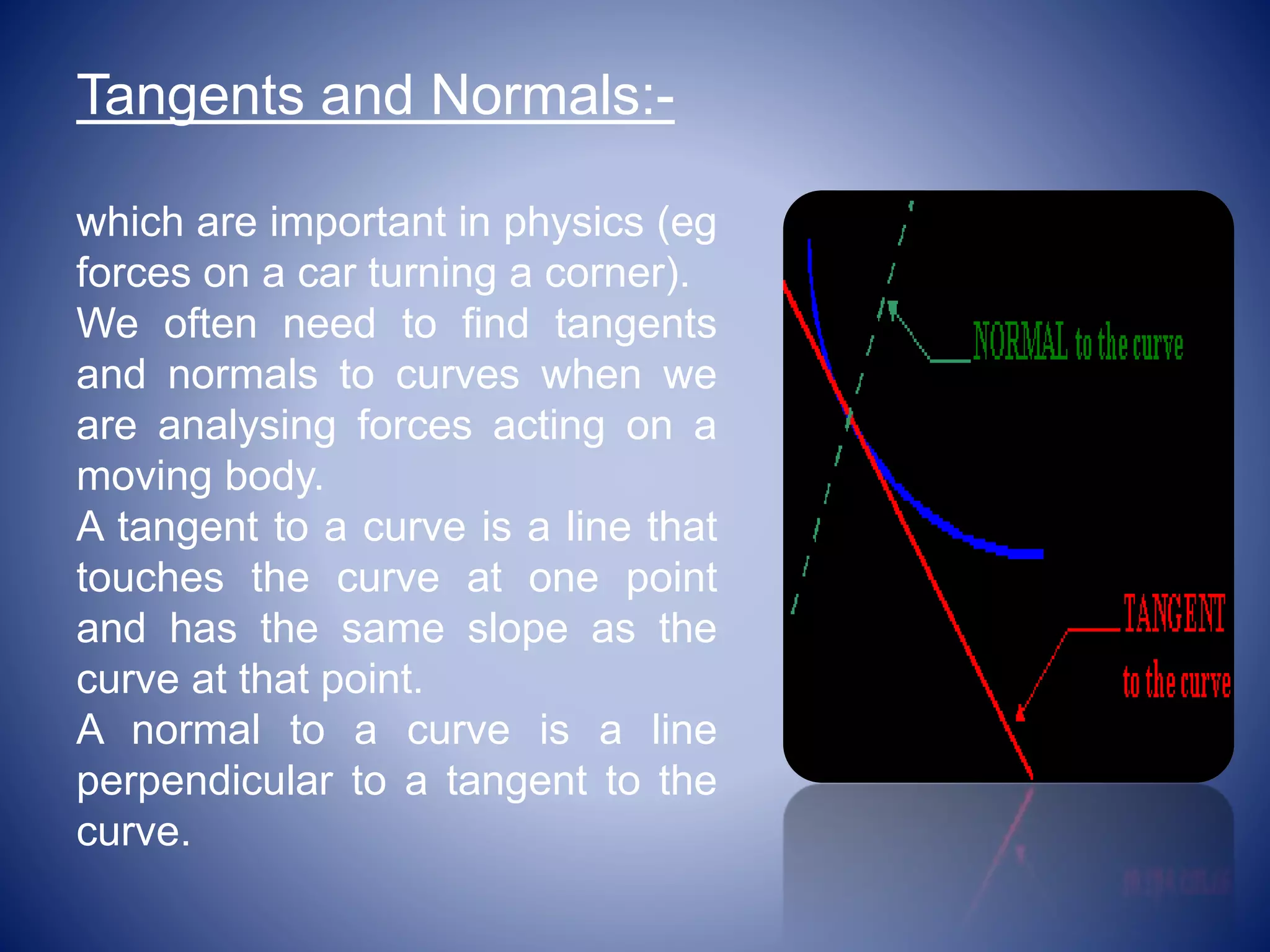
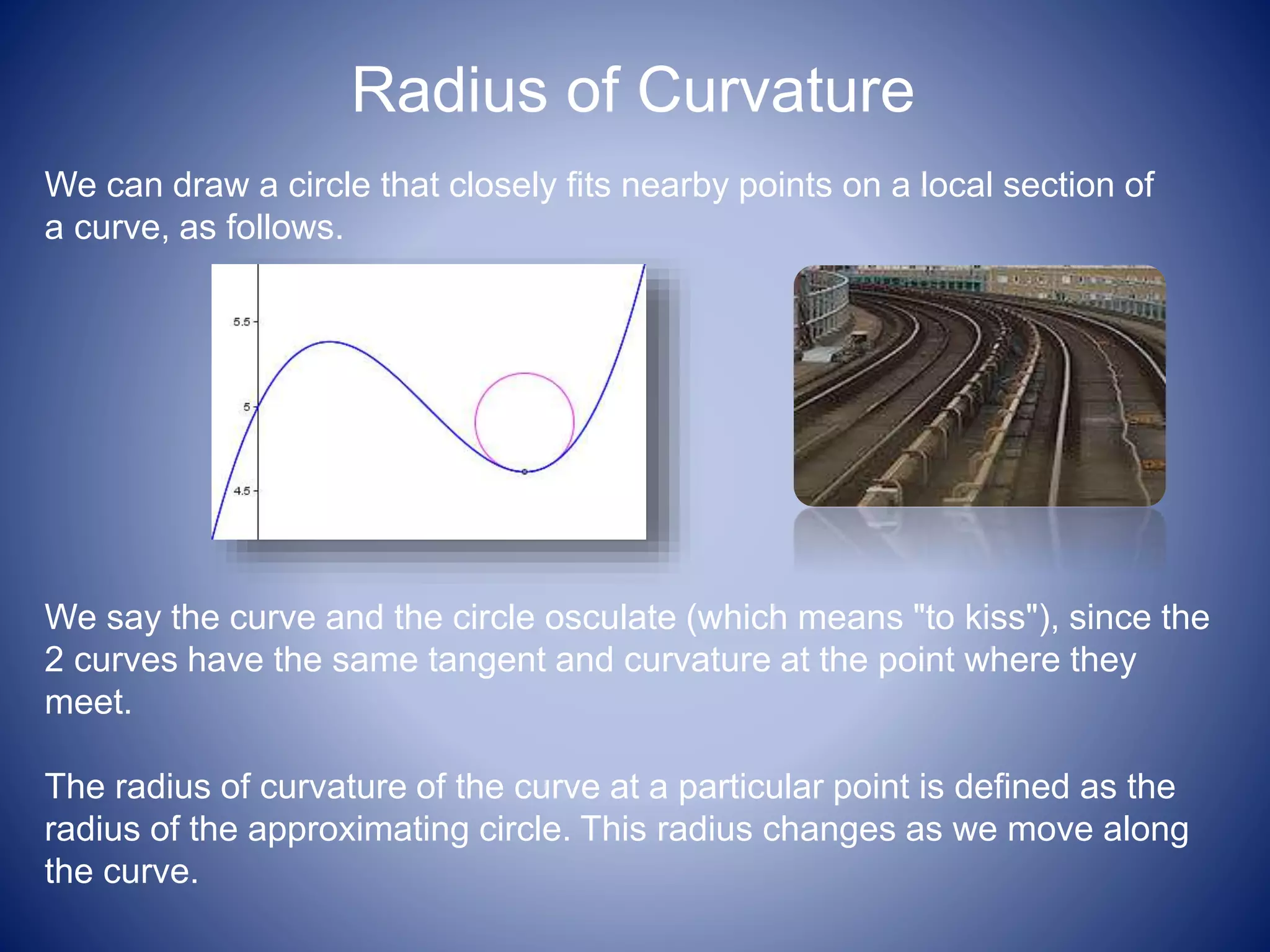
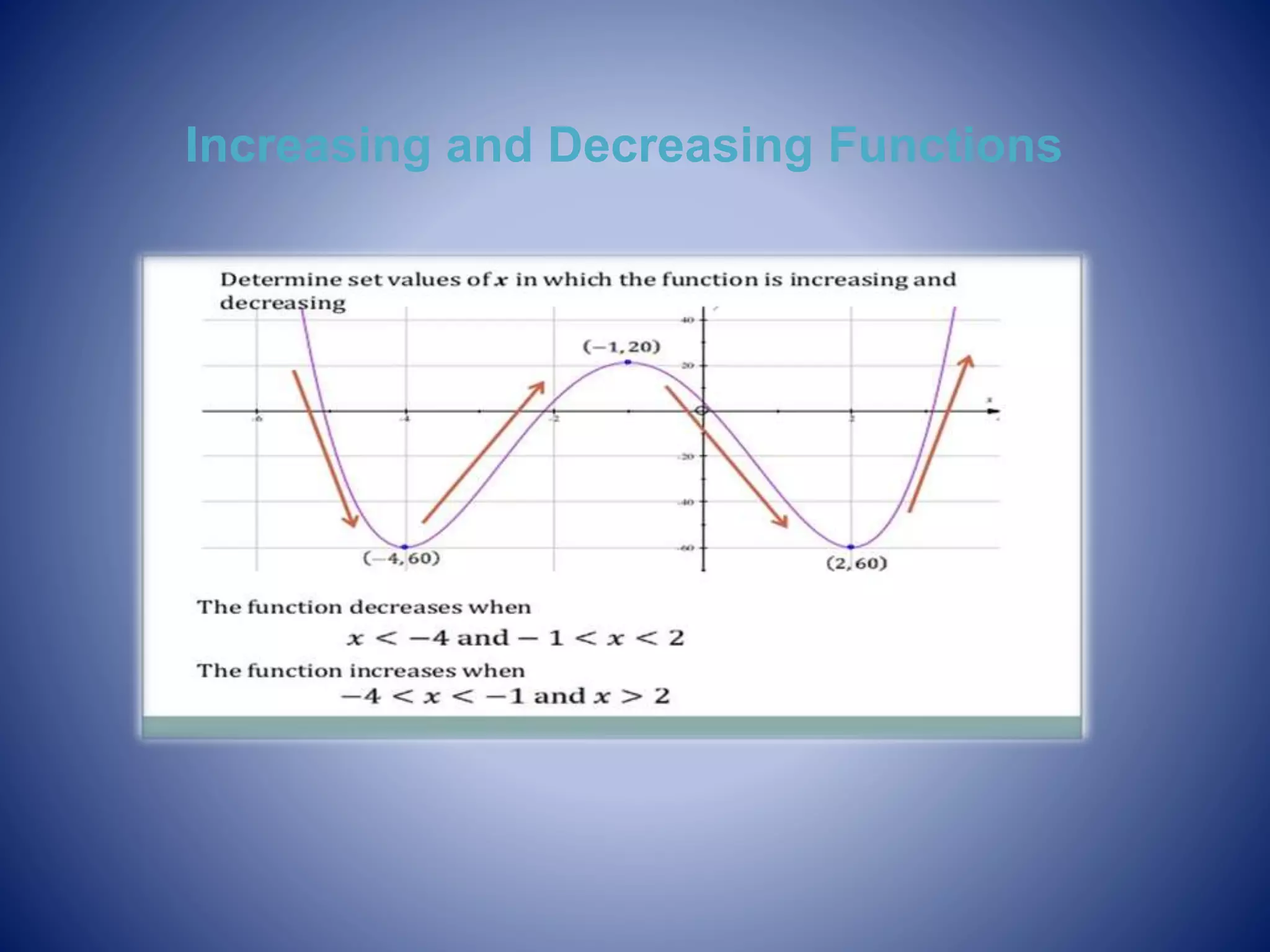
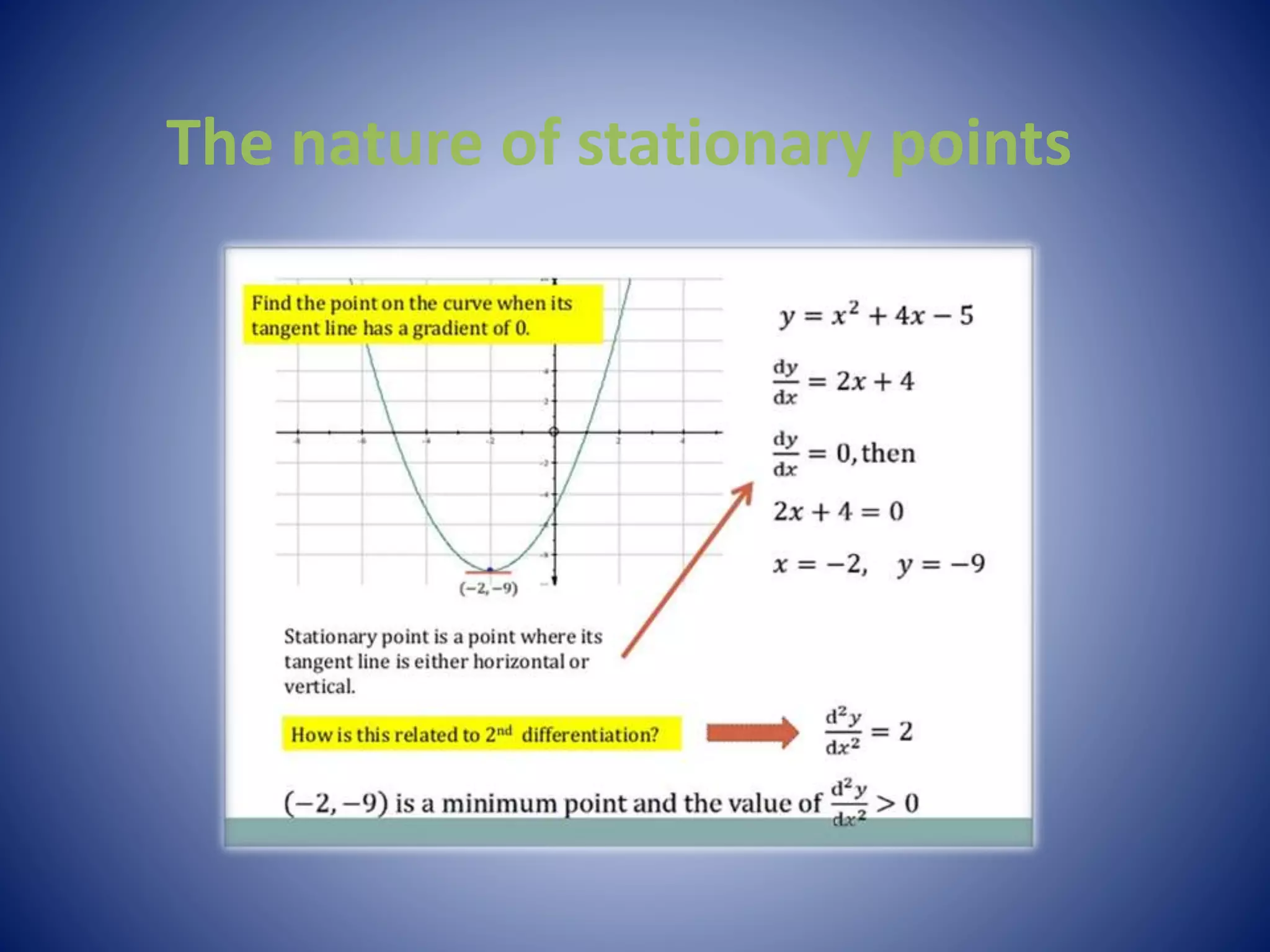
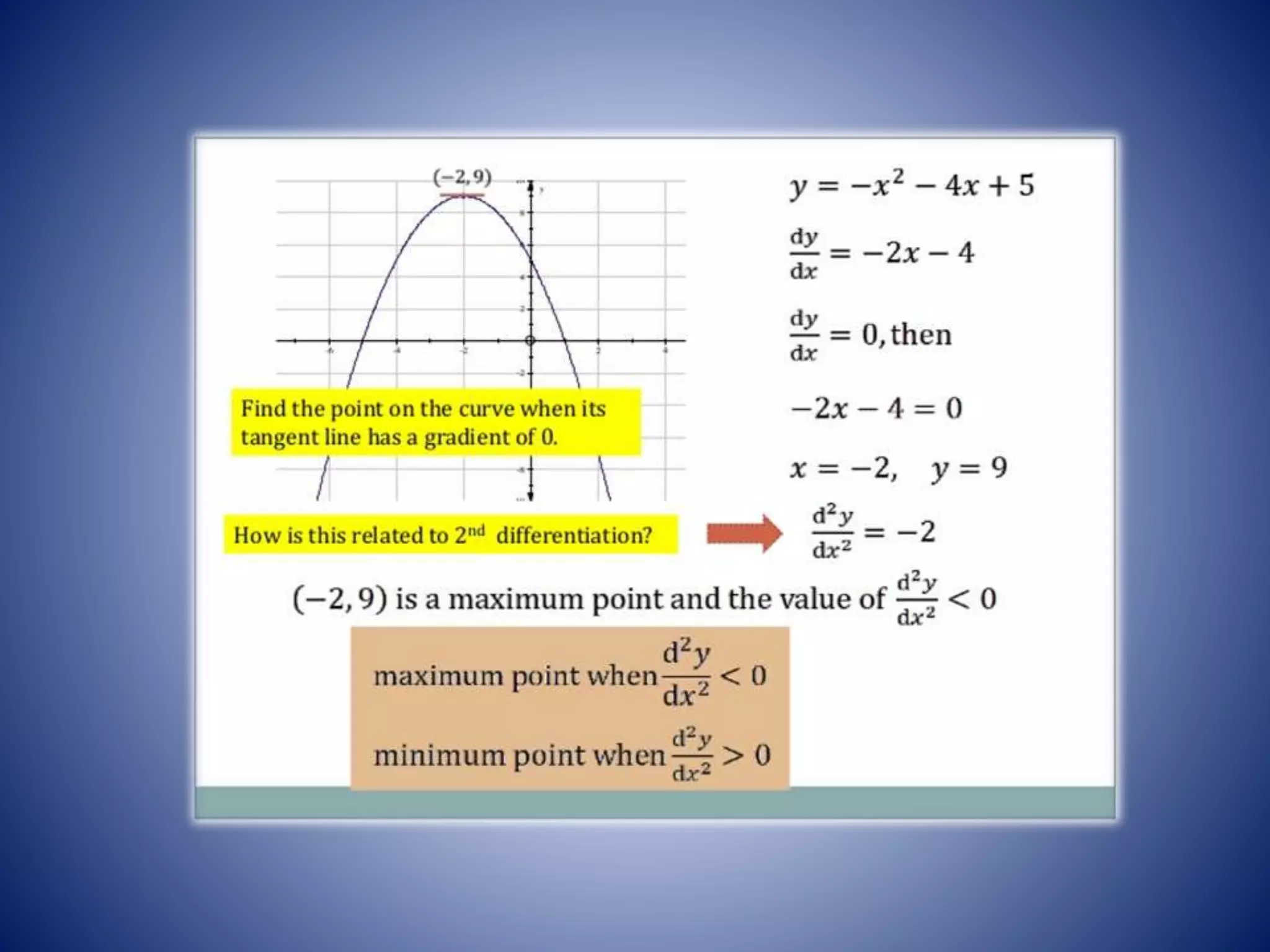
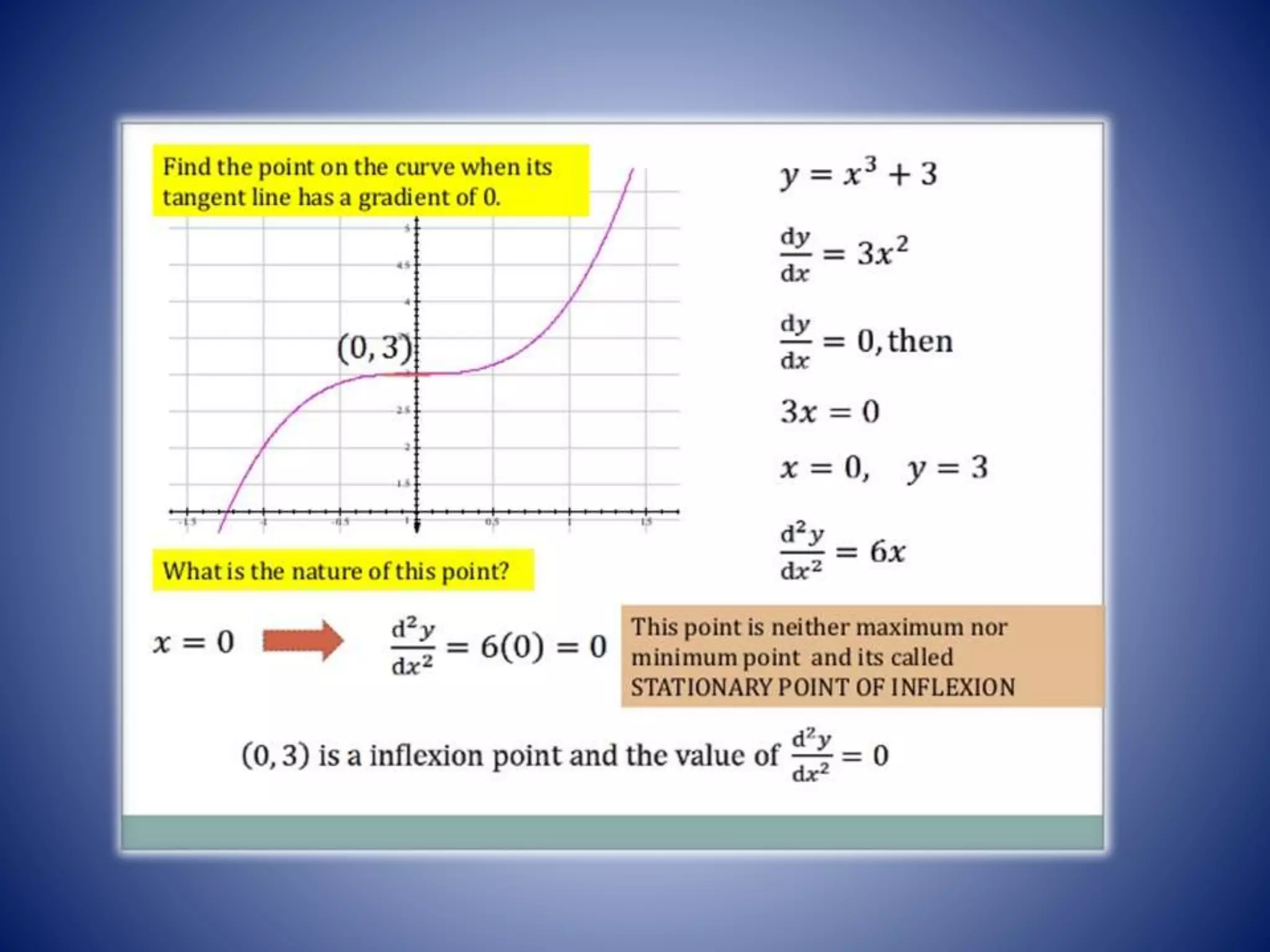
Differentiation allows us to find the rate of change of one variable with respect to another. Calculus helped improve navigation by providing a better understanding of how celestial bodies move. Differentiation and integration can help solve real-world problems like determining maximum/minimum values, finding tangents and normals, solving equations using Newton's method, optimizing costs/profits, and determining radii of curvature. The presentation concludes with information on increasing/decreasing functions and the nature of stationary points.

1. WELCOME
MY
PRESENTATION

2. MY TROPIC IS
DIFFERENTATION OFAPPLICATION
SUBMITTED BY
RAJESH
KUMAR ROY
ID : 163-15-
8494
SECTION : E

3. SUBMITTED TO
MOHAMMAD ABDUL HALIM
LECTURER (MATHEMATICS)
DAFFODIL INTERNATIONAL UNIVERSITY

4. What is Differentiation?
Differentiation is an operation that
allows us to find a function that outputs
the rate of change of one variable with
respect to another variable

5. Introduction to Applications of Differentiation
In Isaac Newton's day, one of the biggest problems was poor
navigation at sea.
Calculus helped improve navigation, less reliance on stars
Before calculus was developed, the stars were vital for navigation.
Shipwrecks occured because the ship was not where the captain
thought it should be. There was not a good enough understanding of
how the Earth, stars and planets moved with respect to each other.
Calculus (differentiation and integration) was developed to improve
this understanding.
Differentiation and integration can help us solve many types of real-
world problems.
We use the derivative to determine the maximum and minimum
values of particular functions (e.g. cost, strength, amount of material
used in a building, profit, loss, etc

6. Tangents and Normals:-
which are important in physics (eg
forces on a car turning a corner).
We often need to find tangents
and normals to curves when we
are analysing forces acting on a
moving body.
A tangent to a curve is a line that
touches the curve at one point
and has the same slope as the
curve at that point.
A normal to a curve is a line
perpendicular to a tangent to the
curve.

7. Newton's Method for Solving
Equations
Computers use iterative methods to solve equations. The
process involves making a guess at the true solution and then
applying a formula to get a better guess and so on until we
arrive at an acceptable approximation for the solution.
If we wish to find x so that f(x)=0 (a common type of problem),
then we guess some initial value x0 which is close to the
desired solution and then we get a better approximation using
Newton's Method.

8. Applied Maximum and Minimum
Problems
The process of finding maximum or minimum values is called
optimisation. We are trying to do things like maximise the
profit in a company, or minimise the costs, or find the least
amount of material to make a particular object.These are very
important in the world of industry.

9. Radius of Curvature
We can draw a circle that closely fits nearby points on a local section of
a curve, as follows.
We say the curve and the circle osculate (which means "to kiss"), since the
2 curves have the same tangent and curvature at the point where they
meet.
The radius of curvature of the curve at a particular point is defined as the
radius of the approximating circle. This radius changes as we move along
the curve.

10. Increasing and Decreasing Functions

11. The nature of stationary points

18. THANK YOU