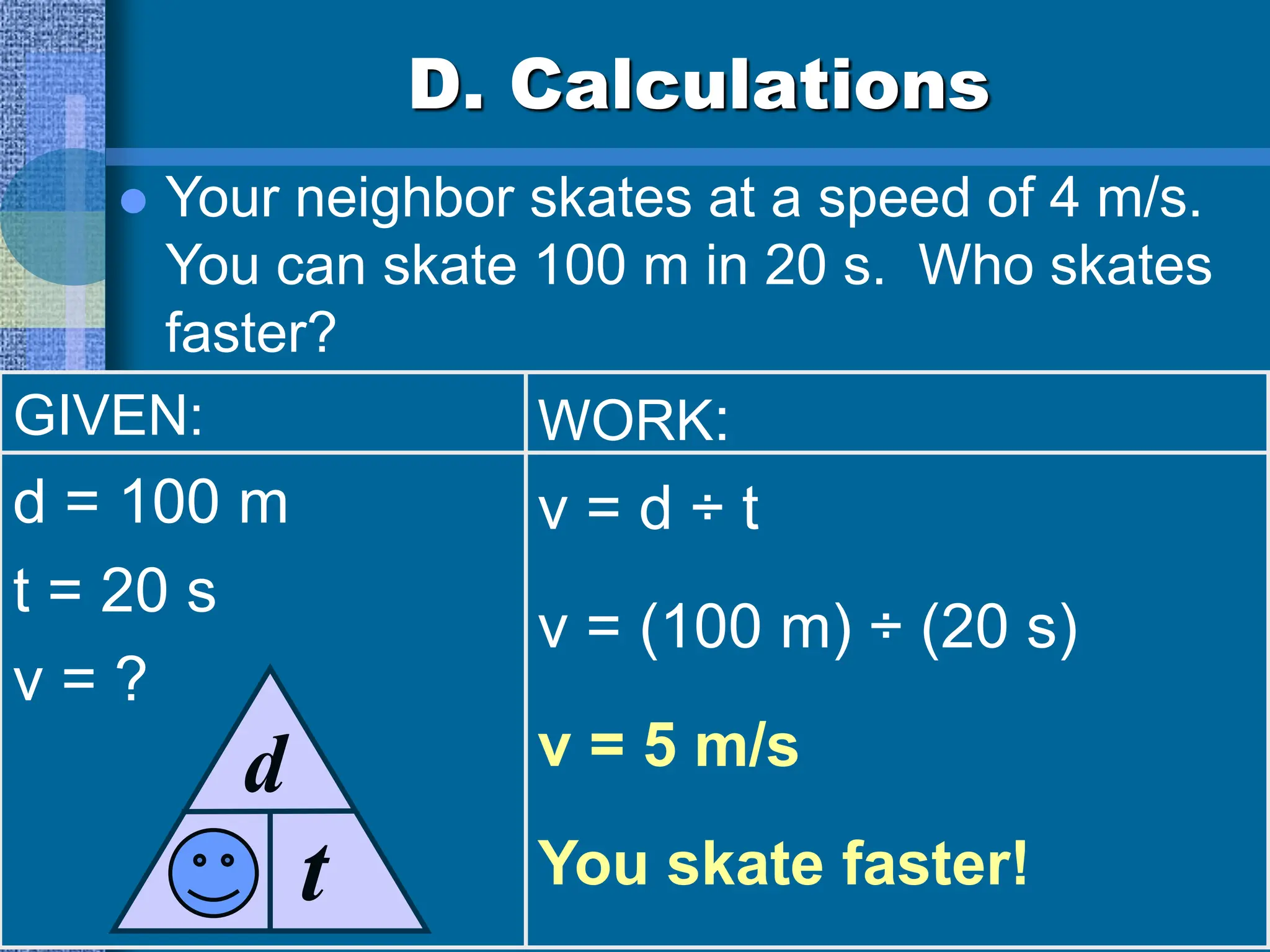
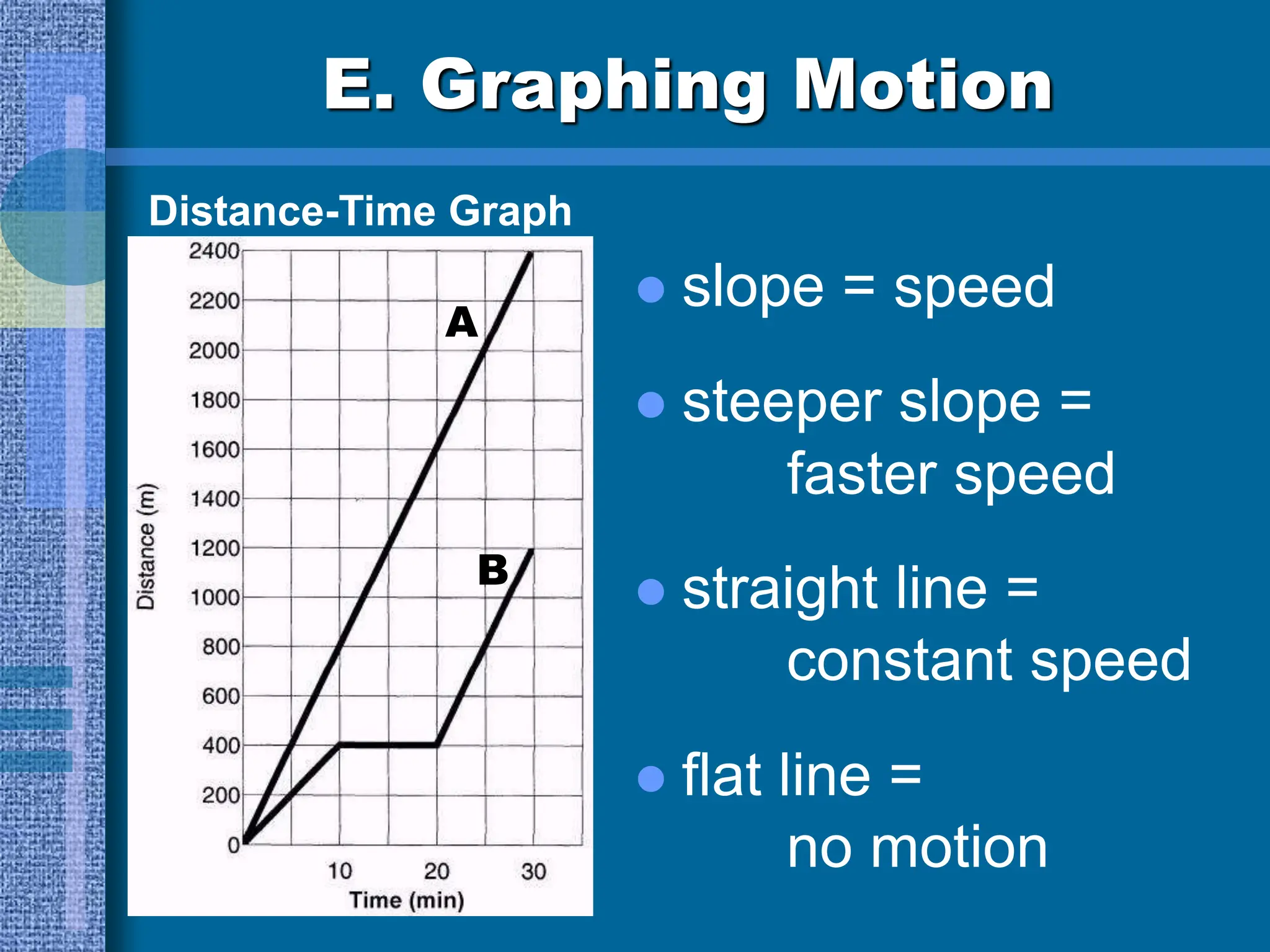
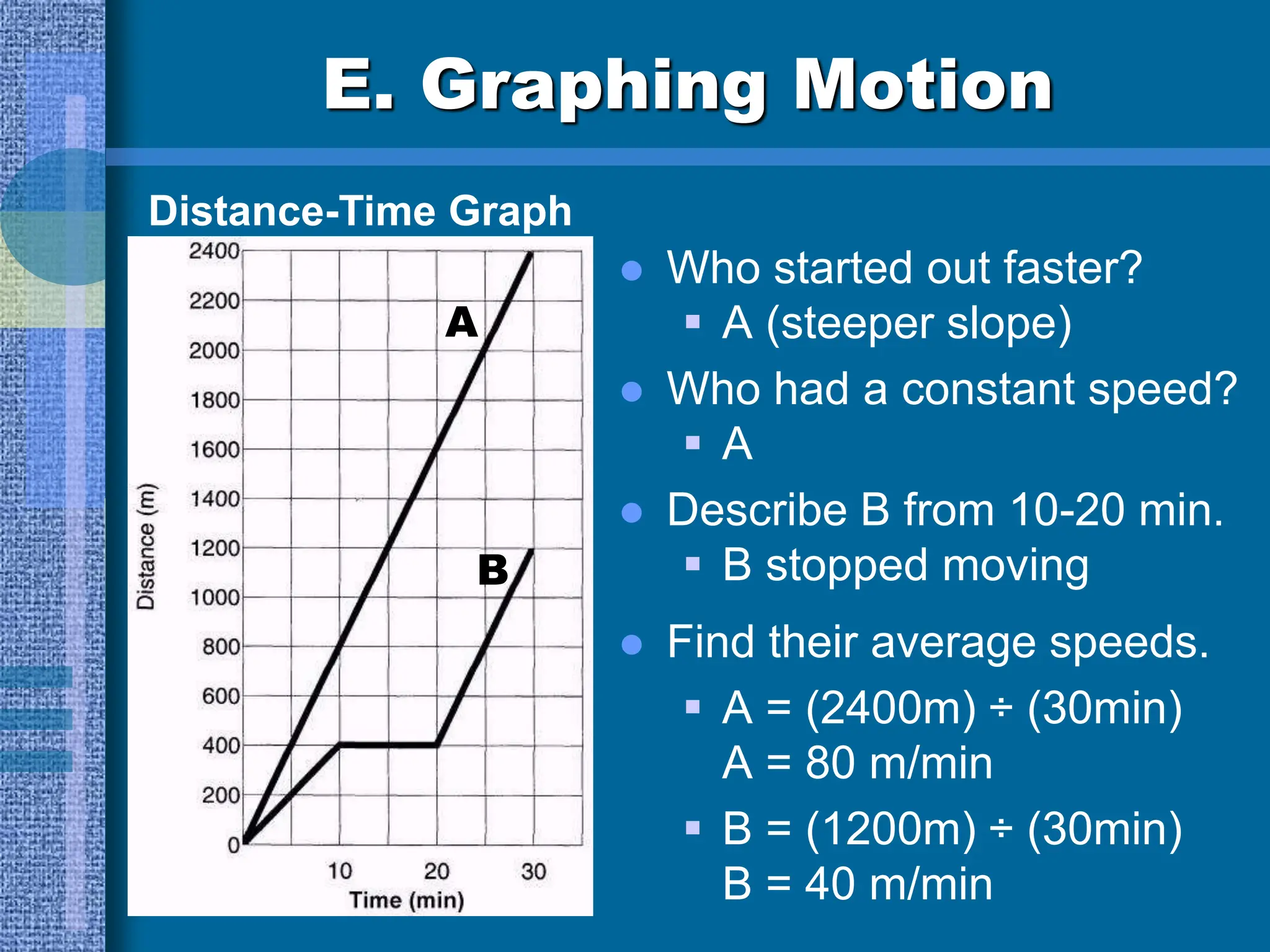
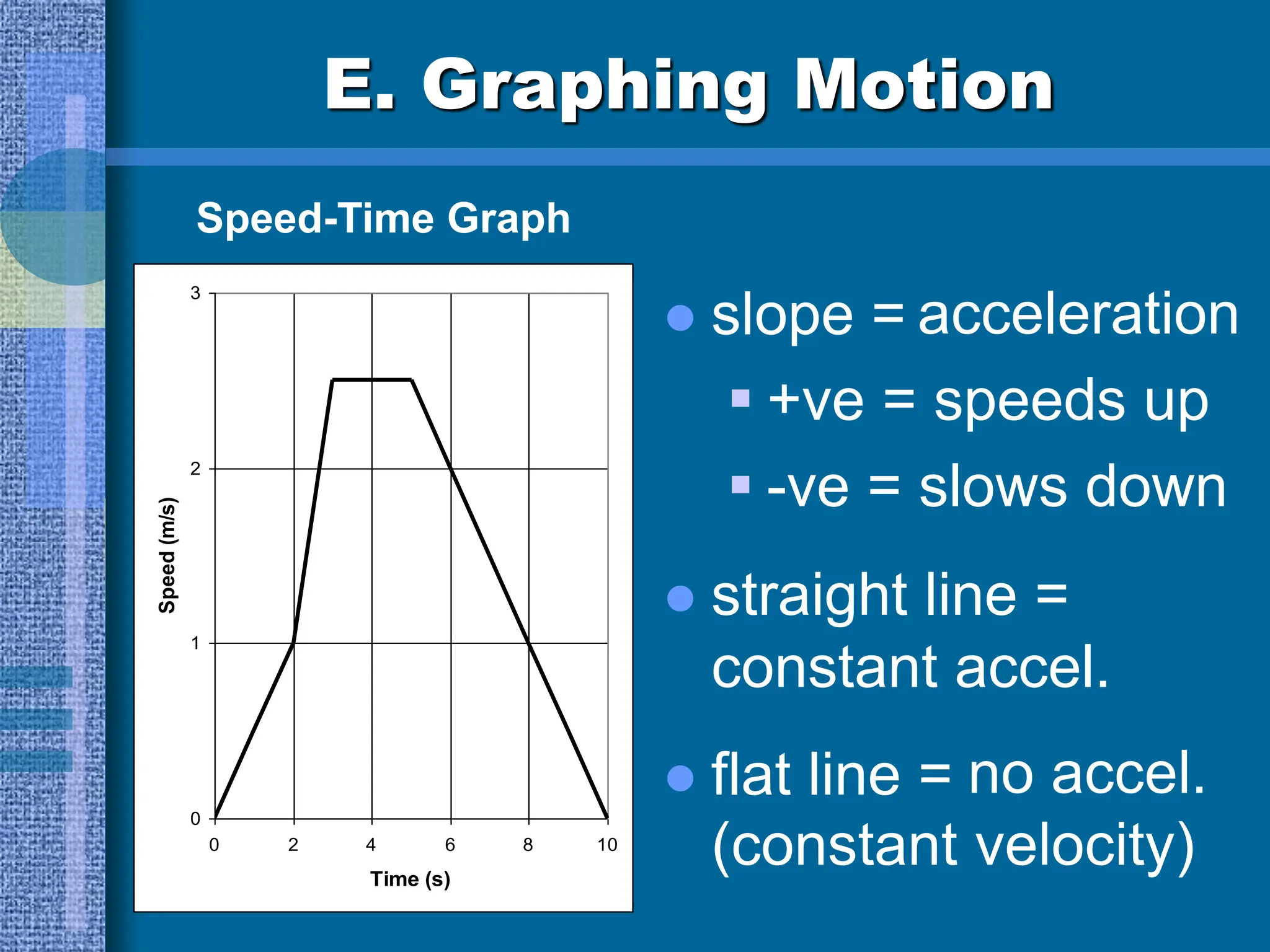
Chapters 3 and 4 cover motion and forces, introducing concepts like speed, velocity, and acceleration as described by Newton's laws. It explains motion relative to a reference point, the distinction between speed and velocity, and how to calculate acceleration and average speed through various examples. The document also discusses graphing motion, including interpreting distance-time and speed-time graphs to analyze movement characteristics.

1. Ch. 3 & 4
Motion & Forces
II. Describing Motion
 Motion
 Speed & Velocity
 Acceleration

2. Newton’s First Law
 Newton’s First Law of Motion
An object at rest will remain at
rest and an object in motion
will continue moving at a
constant velocity unless acted
upon by a net force.
motion
constant velocity
net force

3. A. Motion
 Problem:
Is your desk moving?
 We need a reference point...
nonmoving point from which
motion is measured

4. A. Motion
 Motion
Change in position in relation to
a reference point.
Reference point
Motion

5. A. Motion
Problem:
 You are a passenger in a car
stopped at a stop sign. Out of the
corner of your eye, you notice a
tree on the side of the road begin
to move forward.
 You have mistakenly set yourself
as the reference point.

6. B. Speed & Velocity
 Speed
rate of motion
distance traveled per unit time
time
distance
speed 
v
d
t

7. B. Speed & Velocity
 Instantaneous Speed
speed at a given instant
 Average Speed
time
total
distance
total
speed
avg. 

8. B. Speed & Velocity
 Problem:
A storm is 10 km away and is
moving at a speed of 60 km/h.
Should you be worried?
It depends
on the
storm’s
direction!

9. B. Speed & Velocity
 Velocity
speed in a given direction
can change even when the
speed is constant!

10. C. Acceleration
 Acceleration
the rate of change of velocity
change in speed or direction
t
v
v
a
i
f 

a: acceleration
vf: final velocity
vi: initial velocity
t: time
a
vf - vi
t

11. C. Acceleration
 Positive acceleration
“speeding up”
 Negative acceleration
“slowing down”

12. D. Calculations
 Your neighbor skates at a speed of 4 m/s.
You can skate 100 m in 20 s. Who skates
faster?
GIVEN:
d = 100 m
t = 20 s
v = ?
WORK:
v = d ÷ t
v = (100 m) ÷ (20 s)
v = 5 m/s
You skate faster!
v
d
t

13. D. Calculations
 A roller coaster starts down a hill at 10 m/s.
Three seconds later, its speed is 32 m/s.
What is the roller coaster’s acceleration?
GIVEN:
vi = 10 m/s
t = 3 s
vf = 32 m/s
a = ?
WORK:
a = (vf - vi) ÷ t
a = (32m/s - 10m/s) ÷ (3s)
a = 22 m/s ÷ 3 s
a = 7.3 m/s2
a
vf - vi
t

14. D. Calculations
 Sound travels 330 m/s. If a lightning bolt
strikes the ground 1 km away from you,
how long will it take for you to hear it?
GIVEN:
v = 330 m/s
d = 1km = 1000m
t = ?
WORK:
t = d ÷ v
t = (1000 m) ÷ (330 m/s)
t = 3.03 s
v
d
t

15. D. Calculations
 How long will it take a car traveling 30 m/s
to come to a stop if its acceleration is
-3 m/s2?
GIVEN:
t = ?
vi = 30 m/s
vf = 0 m/s
a = -3 m/s2
WORK:
t = (vf - vi) ÷ a
t = (0m/s-30m/s)÷(-3m/s2)
t = -30 m/s ÷ -3m/s2
t = 10 s
a
vf - vi
t

16. E. Graphing Motion
 slope =
 steeper slope =
 straight line =
 flat line =
Distance-Time Graph
A
B
faster speed
constant speed
no motion
speed

17. E. Graphing Motion
 Who started out faster?
 A (steeper slope)
 Who had a constant speed?
 A
 Describe B from 10-20 min.
 B stopped moving
 Find their average speeds.
 A = (2400m) ÷ (30min)
A = 80 m/min
 B = (1200m) ÷ (30min)
B = 40 m/min
Distance-Time Graph
A
B

18. 0
100
200
300
400
0 5 10 15 20
Time (s)
Distance
(m)
Distance-Time Graph
E. Graphing Motion
 Acceleration is
indicated by a
curve on a
Distance-Time
graph.
 Changing slope =
changing velocity

19. E. Graphing Motion
0
1
2
3
0 2 4 6 8 10
Time (s)
Speed
(m/s)
Speed-Time Graph
 slope =
 straight line =
 flat line =
acceleration
 +ve = speeds up
 -ve = slows down
constant accel.
no accel.
(constant velocity)

20. E. Graphing Motion
0
1
2
3
0 2 4 6 8 10
Time (s)
Speed
(m/s)
Speed-Time Graph
Specify the time period
when the object was...
 slowing down
 5 to 10 seconds
 speeding up
 0 to 3 seconds
 moving at a constant
speed
 3 to 5 seconds
 not moving
 0 & 10 seconds