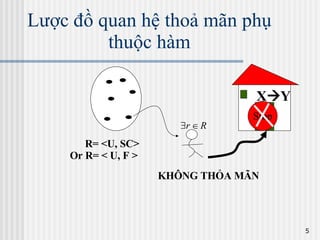
Tài liệu trình bày về lý thuyết phụ thuộc hàm trong cơ sở dữ liệu, bao gồm các khái niệm như phụ thuộc hàm, bao đóng và khóa của lược đồ quan hệ. Nó cũng giới thiệu các hệ tiên đề Armstrong và cách xác định phủ cực tiểu của tập phụ thuộc hàm. Cuối cùng, tài liệu mô tả các giải thuật để tìm các khóa và bổ sung khóa trong lược đồ quan hệ.



![Phụ thuộc hàm r thỏa A C r thỏa B C A B C r = a b c b d c a e c X Y t 1 , t 2 r : t 1 [X] = t 2 [X] t 1 [Y] = t 2 [Y]](https://image.slidesharecdn.com/csdl-nangcao-1213449240597054-8/85/Csdl-Nangcao-4-320.jpg)