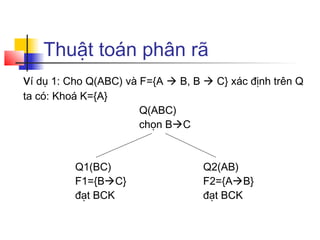
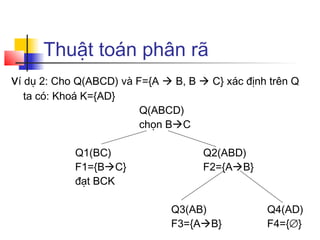
Chương 7 trình bày lý thuyết thiết kế cơ sở dữ liệu với các phụ thuộc hàm và cách xác định khoá trong lược đồ. Nó đề cập đến các dạng chuẩn như 1NF, 2NF, 3NF và BCNF, cùng với các ví dụ minh họa và quy trình chuẩn hóa lược đồ để loại bỏ trùng lắp thông tin. Các thuật toán để tìm bao đóng và xác định khoá cũng được mô tả chi tiết.

1. CHƯƠNG 7
LÝ THUYẾT THIẾT KẾ
CSDL

2. Phụ thuộc hàm
 Định nghĩa:
Cho một LĐQH Q(X,Y,Z) vớI X,Y,Z là các
thuộc tính con của Q+ và X, Y khác rỗng.
Phụ thuộc hàm: X  Y được xác định trên Q
nếu:
q1, q2 ∈ TQ: q1.X = q2.X ⇒ q1.Y =
q2.Y
Ta nói: X xác định Y hay Y phụ thuộc hàm
vào X

3. Phụ thuộc hàm
Ví dụ: xét LĐQH
TD(MSTD, MSPH, GIO_TD, NGAY_TD)
Mỗi trận đấu diễn ra trong một phòng,
vào một ngày và một giờ bắt đầu quy
định.
Ta có:
MSTD → MSPH, GIO_TD, NGAY_TD

4. Các phụ thuộc hàm đặc biệt
 Phụ thuộc hàm hiển nhiên:
X→X
 Phụ thuộc hàm nguyên tố:
X → Y là PTH nguyên tố nếu:
∄ X' ⊆ X và X' <> X mà X'→ Y
 Vd: ChiTietHD(MAHD, MAHH, SL, GIA)
Ta có: MAHD,MAHH → SL
Nhưng: MAHD,MAHH ↛ SL

5. Tập phụ thuộc hàm của 1
quan hệ
 Tập các PTH của Q được ký hiệu là FQ
FQ ={fi: X →Y xác định trên Q}
 Qui ước: FQ chỉ gồm các PTH không
hiển nhiên trong tập F
 Biểu diễn tập PTH bằng đồ thị: xem tài
liệu trang 46

6. Hệ tiên đề Amstrong và các luật
dẫn
 Hệ tiên đề Amstrrong:
Cho LĐQH Q và X, Y, Z ⊆ Q+
• Tính phản xạ:
Y ⊆ X ⇒ X→ Y
• Luật thêm vào:
Nếu X→ Y và Z ⊆ W thì XW→ YZ
• Luật bắc cầu:
Nếu X→ Y và Y→ Z thì X → Z

7. Hệ tiên đề Amstrong và các luật
dẫn
 Các luật dẫn từ hệ tiên đề Amstrrong:
Cho LĐQH Q và X, Y, Z ⊆ Q+
• Tính phân rã:
Nếu X→ Y, Z thì X→ Y và X→ Z
• Tính hội:
Nếu X→ Y và X→ Z thì X→ YZ
• Luật bắc cầu giả:
Nếu X→ Y và YZ→ W thì XZ → W

8. Bao đóng của tập thuộc tính
 Cho LĐQH Q có tập PTH F={f1,f2,…,fn}
và X ⊆ Q+
 Bao đóng của tập thuộc tính X dựa trên
F là tập các thuộc tính phụ thuộc hàm
vào X dựa trên F
X F + = {Y ∈ Q + : X→ Y ∈ F + }
 Ta có thể trả lời câu hỏi một
PTH X→ Y có suy diễn được từ
F ?

9. Thuật tóan xác định X F +
Begin
X F + = X;
do
X’ = X F +
for I = 1 to card(F)
if VT(fi) ∈ X F + :
X F + = X F + ∪ VP(fi)
while (X F + = X’)
end

10. Ví dụ:Cho Q(ABCDEFGH) và tập pth
F = {f1: B → A; f2: DA →CE; f3:D→H; f4:GH
→C; f5:AC →D}
Tìm bao đóng của tập thuộc tính
X={BD}:
 X + = BD
F
 Vì VT(f1) ∈ XF+ nên XF+ = BDA
 Vì VT(f2) ∈ XF+ nên XF+ = BDACE
 Vì VT(f3) ∈ XF+ nên XF+ = BDACEH
 Vì VT(f5) ∈ XF+ nên XF+ = BDACEH : dừng
Vậy XF+ = BDACEH

11. Ví dụ:Cho Q(ABCDEGH) và tập pth
F = {f1: B → A; f2: DA →CE; f3:D→H; f4:GH
→C; f5:AC →D}
Tìm bao đóng của tập thuộc tính X={BCG}
 X + = BCG
F
 Vì VT(f1) ∈ XF+ nên XF+ = BCGA
 Vì VT(f5) ∈ XF+ nên XF+ = BCGAD
 Vì VT(f2) ∈ XF+ nên XF+ = BCGADE
 Vì VT(f3) ∈ XF+ nên XF+ = BCGADEH = Q+ dừng
Vậy XF+ = Q+

12. Nhận xét
 X ∈ XF+
 Y ∈ XF+ ⇔ f: X→ Y ∈ F
 Ví dụ: Cho Q(ABCDEFGH) và tập pth
F = {f1: B → A; f2: DA →CE; f3:D→H;
f4:GH →C; f5:AC →D}
Kiểm tra f: BD → CE có thuộc F+ không?
Ta có (BD)F+ = BDACEH
Vì CE ∈ (BD)F+ nên f: BD → CE thuộc F+

13. Phụ thuộc hàm và khóa
 Định nghĩa: cho LĐQH Q(A1, A2, …, An),
F là tập PTH trên Q.
K ⊆ Q+ được gọi là khóa của Q nếu:
1. K → Q ∈ F
+ +
2. ∄ K’ ⊆ K mà K’ → Q + ∈ F +

14. Thuật tóan xác định tất cả các
khóa của 1 LĐQH
 Qui ước:
 N: tập thuộc tính nguồn, chỉ chứa các nút
thuộc tính không có cung đi tới
 M: tập thuộc tính trung gian, chứa các nút
thuộc tính vừa có cung đi tới, vừa có cung
đi ra.
 Input: <Q,F>
 Output: K{tập các khóa của quan hệ Q}

15. Thuật tóan xác định tất cả các
khóa của 1 LĐQH
Begin
b1: xây dựng tập N và M
b2: xây dựng 2 m tập con của tập M với m=Card(M)
b3: xây dựng tập K chứa các khóa
K=∅
for i=1 to 2 m
Ki = N ∪ M i
nếu Ki không chứa các khóa đã xác định
trước đó và (Ki)F+ = Q+ thì
Ki là 1 khóa của Q: K = K ∪ Ki
end

16. Ví dụ:Cho Q(ABCDEG) và tập pth
F = {f1: AD → B; f2: EG → A; f3:BC→ G}
 Tìm tất cả các khóa của LĐQH Q:
1. N={CDE}
2. M={ABG}
3. Các tập con của M: {∅}, {A}, {B}, {G}, {AB}, {AG},
{BG}, {ABG}
4. Tính bao đóng cho các tập thuộc tính sau:
(CDE)+F = {CDE} ≠ Q+
(CDEA)+F = {CDEABG} = Q+
(CDEB)+F = {CDEBAG} = Q+
(CDEG)+F = {CDEGAB} = Q+
5. Tập các khóa tìm được:
K={K1={CDEA}, K2={CDEB},K3={CDEG}}

17. Các dạng chuẩn
 Sự trùng lắp thông tin là nguyên nhân làm 1
lược đồ CSDL có chất lượng kém.
 Để đánh giá chất lượng của 1 lược đồ CSDL,
người ta đưa ra các dạng chuẩn(normal form)
sau:
 Dạng chuẩn 1 (1NF)
 Dạng chuẩn 2 (2NF)
 Dạng chuẩn 3 (3NF)
 Dạng chuẩn BCK (BCNF)

18. Dạng chuẩn 1
 Định nghĩa DC1: một lược đồ Q đạt dạng
chuẩn 1 nếu mọi thuộc tính của Q đều là
thuộc tính đơn.
 Một thuộc tính được gọi là thuộc tính đơn nếu
giá trị của nó không phải là sự kết hợp bởi
nhiều thông tin có ý nghĩa khác nhau và hệ
thống thường truy xuất trên tòan bộ giá trị của
nó.
 Chú ý: thuộc tính kiểu datetime được xem là
thuộc tính đơn.

19. Dạng chuẩn 1
 Ví dụ: Mỗi giáo viên có thể dạy nhiều môn
ChuyenMon1(MAGV, MAMH)
Mỗi bộ trong ChuyenMon1 cho biết 1 môn mà
giáo viên có thể dạy  đạt DC1.
ChuyenMon2(MAGV, MAMH)
Mỗi bộ trong ChuyenMon2 cho biết nhiều
môn mà giáo viên có thể dạy  không đạt
DC1.

20. Dạng chuẩn 1
 Ví dụ: Mỗi giáo viên có thể dạy nhiều môn
ChuyenMon3(MAGV, MAMH, TENGV,
HOCVI)
Mỗi bộ trong ChuyenMon3 cho biết 1 môn mà
giáo viên có thể dạy  đạt DC1.
 Nhận xét: Chuyenmon3 đạt dạng chuẩn 1
nhưng vẫn còn trùng lắp thông tin

21. Dạng chuẩn 2
 Phụ thuộc đầy đủ: cho pth X  A. Tập thuộc tính A được
gọi là phụ thuộc đầy đủ vào tập thuộc tính X nếu:
∄ X' ⊆ X mà X'→ A
 Ví dụ 1:
ChuyenMon3(MAGV, MAMH, TENGV, HOCVI)
Phụ thuộc hàm: MAGV, MAMH  TENGV, HOCVI
là pth không đầy đủ vì chỉ cần MAGV  TENGV, HOCVI
 Ví dụ 2:
GiaoVien(MAGV, TENGV, HOCVI)
Phụ thuộc hàm: MAGV  TENGV, HOCVI là pth đầy đủ

22. Dạng chuẩn 2
 Định nghĩa DC2:
Một lược đồ quan hệ Q đạt DC2 nếu:
1. Q ở dạng chuẩn 1
2. Mọi thuộc tính không khóa đều phụ thuộc đầy đủ vào
các khóa của Q
 Ví dụ 1:
ChuyenMon3(MAGV, MAMH, TENGV, HOCVI)
Không đạt DC2 vì:MAGV, MAMH  TENGV, HOCVI
là pth không đầy đủ vì chỉ cần
MAGVTENGV,HOCVI

23. Dạng chuẩn 2
 Ví dụ 2:
GiaoVien(MAGV, TENGV, HOCVI)
đạt DC2 vì : MAGV  TENGV, HOCVI
Nên mọi thuộc tính không khóa đều phụ thuộc
đầy đủ vào các khóa

24. Dạng chuẩn 2
 Ví dụ 3:
SinhVien(MASV, HOTEN, NGSINH, MALOP,
TENLOP)
Đạt DC2 vì mọi thuộc tính không khóa:
HOTEN,NGSINH, MALOP, TENLOP đều phụ thuộc
đầy đủ vào các khóa : MASV
 Nhận xét: SinhVien đạt dạng chuẩn 2
nhưng vẫn còn trùng lắp thông tin

25. Dạng chuẩn 3
 Phụ thuộc bắc cầu:
Cho LĐQH Q. Tập thuộc tính A ⊆ Q+ được gọi là
phụ thuộc bắc cầu vào tập thuộc tính X nếu tồn
tại tập thuộc tính Y⊆ Q+ thỏa 4 điều kiện sau:
1. X  Y ∈ F+
2. Y  A ∈ F+
3. Y↛ X
4. A ⊄ {X ∪ Y}

26. Dạng chuẩn 3
 Ví dụ:
SinhVien(MASV, HOTEN, NGSINH, MALOP,
TENLOP)
MASV  HOTEN, NGSINH, MALOP
MALOP  TENLOP
Vậy TENLOP phụ thuộc bắc cầu vào MASV

27. Dạng chuẩn 3
 Định nghĩa DC3:
Một LĐQH Q đạt DC3 nếu:
1. Q đạt DC2
2. Mọi thuộc tính không khóa của Q đều không
phụ thuộc bắc cầu vào khóa của Q.
 Ví dụ:
SinhVien(MASV, HOTEN, NGSINH, MALOP, TENLOP)
Không đạt DC3 vì: TENLOP phụ thuộc bắc cầu vào
MASV do có các pth
MASV  HOTEN, NGSINH, MALOP
MALOP  TENLOP

28. Dạng chuẩn 3
 Ví dụ:
SinhVien(MASV, HOTEN, NGSINH,
MALOP)
đạt DC3
Lop(MALOP, TENLOP)
Đạt DC3

29. Dạng chuẩn 3
 Ví dụ:
KETQUA(MASV, CMND, MAMH, DIEM)
Ta có:
MASV, MAMH  DIEM
CMND, MAMH  DIEM
nên KETQUA đạt DC3
 Nhận xét:
1 LĐQH đạt DC3 vẫn còn trùng lắp thông
tin

30. Dạng chuẩn BCK(Boyce-Codd-
Kent)
 Định nghĩa:
Một LĐQH Q đạt dạng chuẩn BCK nếu
mọi phụ thuộc hàm không hiển nhiên
đều có vế trái chứa khóa.
 Nhận xét: Nếu Q đạt dạng chuẩn BCK
thì mọi vế trái của các pth đều là siêu
khóa.

31. Dạng chuẩn BCK(Boyce-Codd-
Kent)
 Ví dụ:
KETQUA(MASV, CMND, MAMH,
DIEM)
Ta có:
MASV, MAMH  DIEM
CMND, MAMH  DIEM
nên KETQUA đạt DC3
Nhưng : MASV  CMND
nên KETQUA không đạt DC BCK

32. Dạng chuẩn BCK(Boyce-Codd-
Kent)
 Ví dụ:
KETQUA(MASV, MAMH,
DIEM)
Ta có:
MASV, MAMH  DIEM
nên KETQUA đạt DC BCK

33. Dạng chuẩn của một LĐCSDL
 Là dạng chuẩn thấp nhất của những
lược đồ quan hệ có trong lược đồ CSDL
đó.

34. Chuẩn hóa một LĐCSDL
 Định lý DELOBEL(1973):
Cho LĐQH Q và tập pth F.
Nếu f: X A ∈ F+ sao cho X∪A ⊂ Q+ thì phép
phân rã Q thành 2 lược đồ quan hệ có sau là
bảo toàn thông tin:
<Q1(X,A),F1={f ∈ F+:VT(f) ∪VP(f) ⊂ Q1+}>
<Q2(Q+A),F2={f ∈ F+:VT(f) ∪VP(f)⊂ Q2+}>

35. Thuật toán phân rã
Cho LĐQH Q, F+ là tập pth trên Q. Nếu Q
không đạt dạng chuẩn BCK thì chọn X A ∈
F+ mà X không là siêu khoá, khi đó Q được
phân rã thành:
<Q1(X,A),F1={f ∈ F+:VT(f) ∪VP(f) ⊂ Q1+}>
<Q2(Q+A),F2={f ∈ F+:VT(f) ∪VP(f)⊂ Q2+}>
Lặp lại qui trình trên cho Q2 và chỉ xét pth
thuộc F2 cho đến khi các quan hệ con đều
đạt DC BCK thì dừng.

36. Thuật toán phân rã
ví dụ 1: Cho Q(ABC) và F={A  B, B  C} xác định trên Q
ta có: Khoá K={A}
Q(ABC)
chọn BC
Q1(BC) Q2(AB)
F1={BC} F2={AB}
đạt BCK đạt BCK

37. Thuật toán phân rã
ví dụ 2: Cho Q(ABCD) và F={A  B, B  C} xác định trên Q
ta có: Khoá K={AD}
Q(ABCD)
chọn BC
Q1(BC) Q2(ABD)
F1={BC} F2={AB}
đạt BCK
Q3(AB) Q4(AD)
F3={AB} F4={∅}