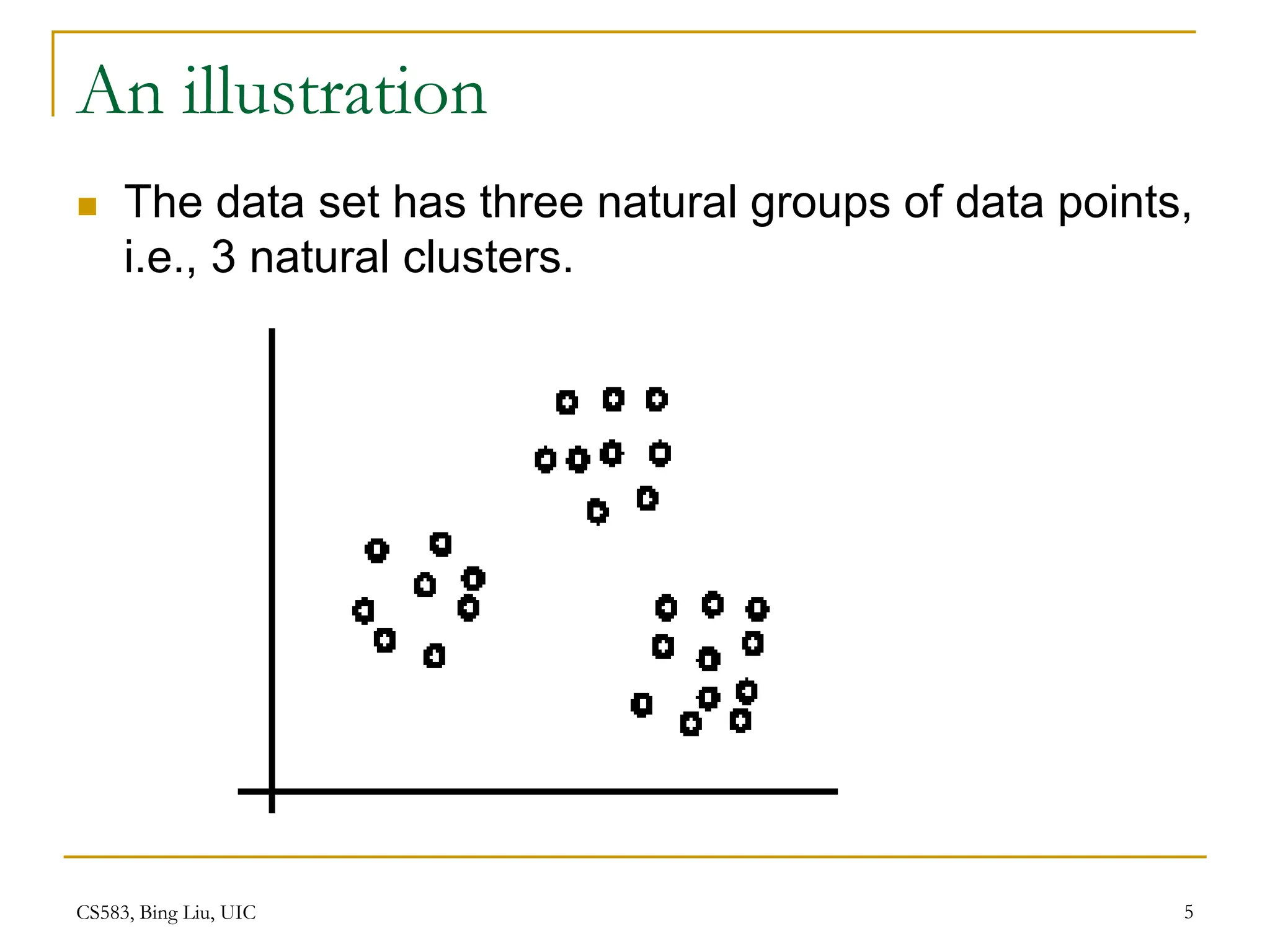
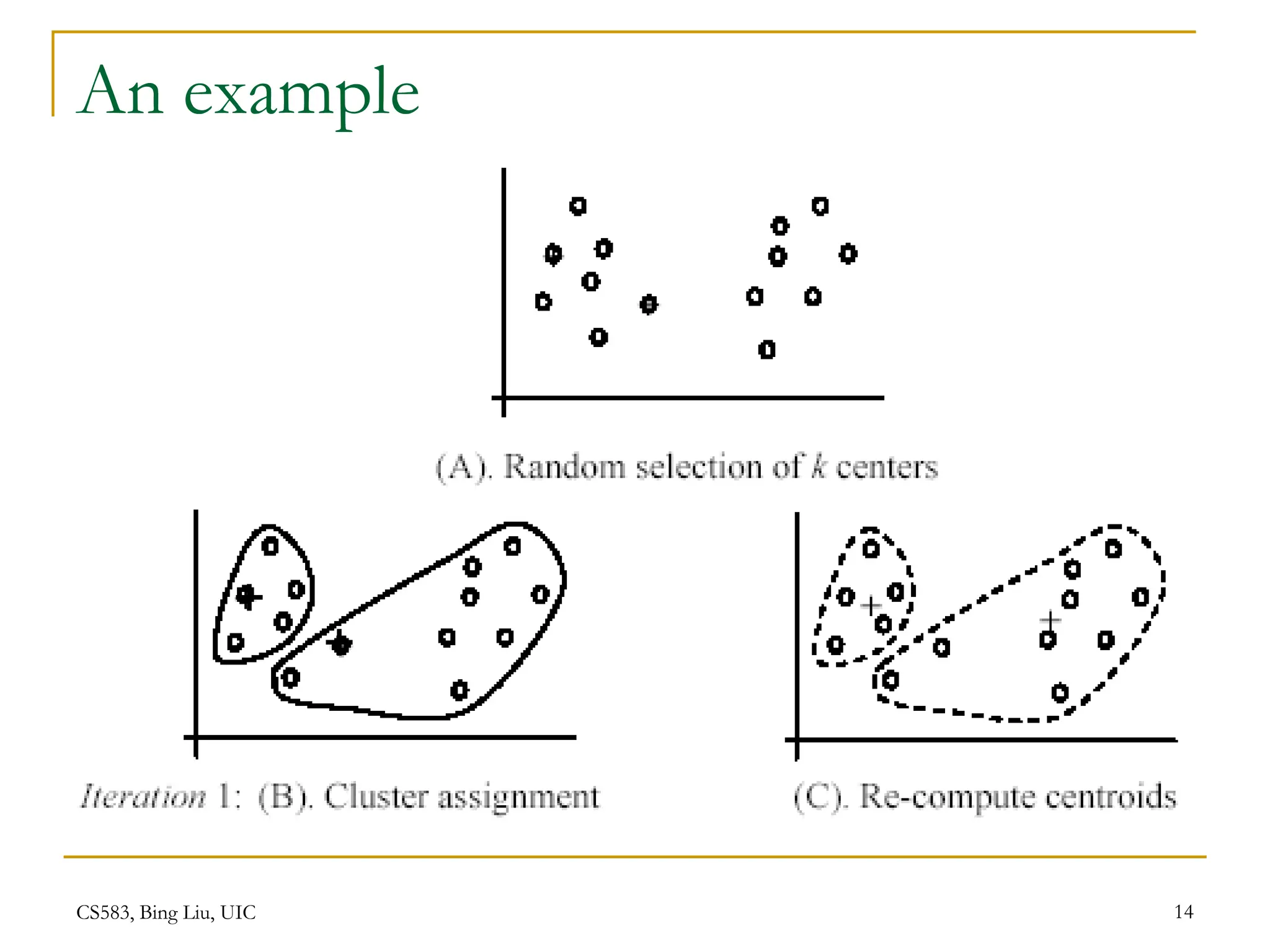
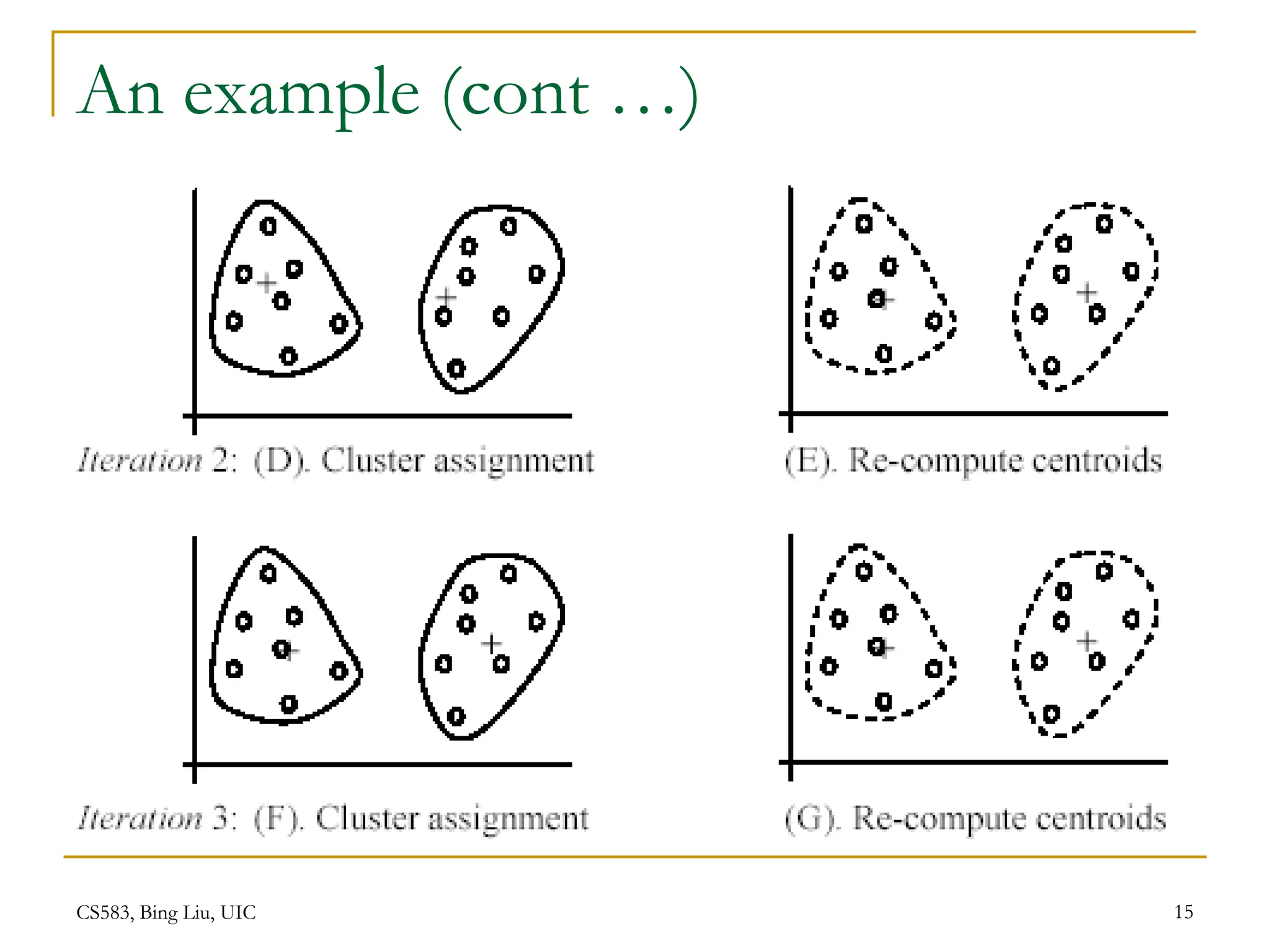
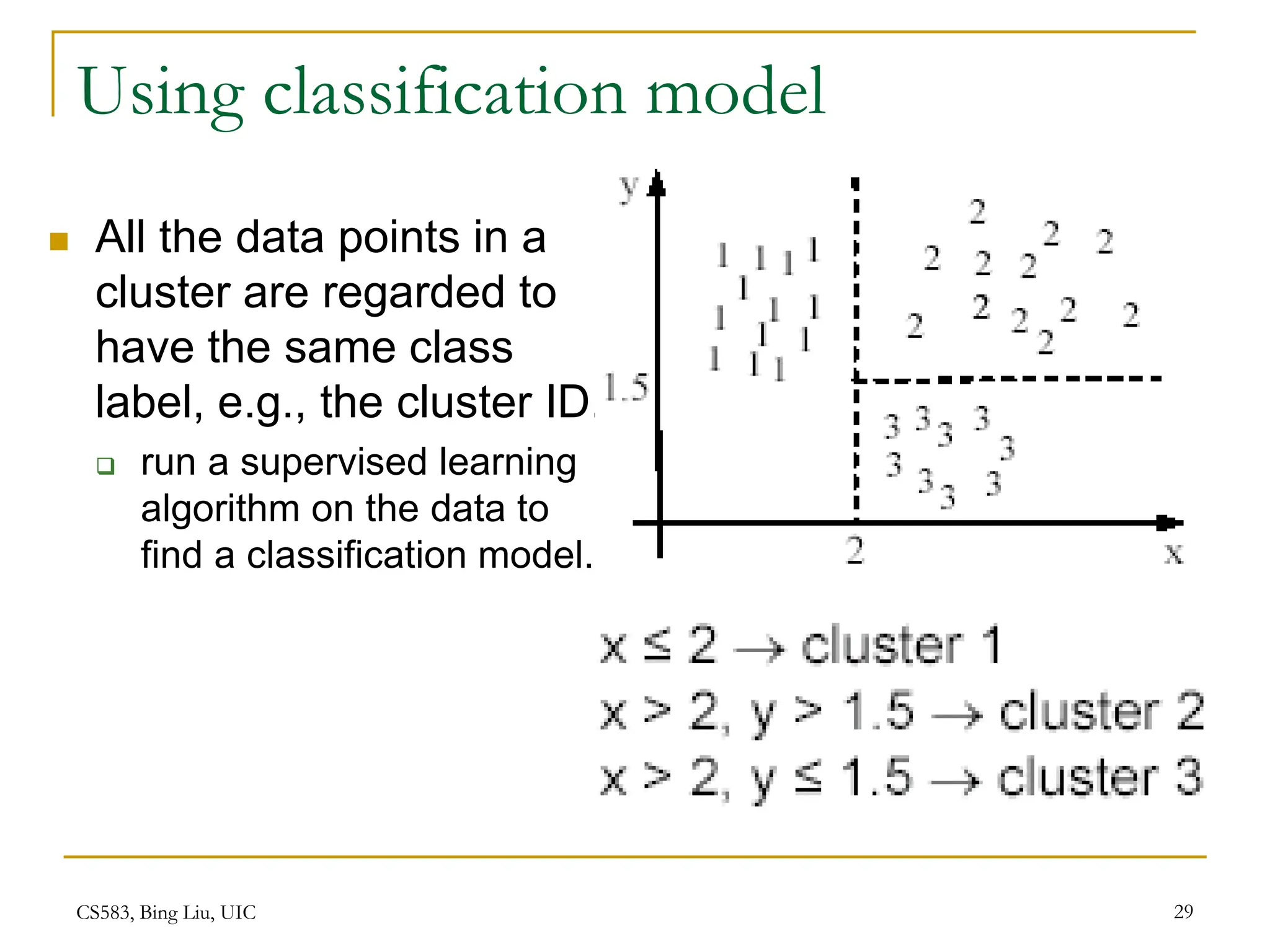
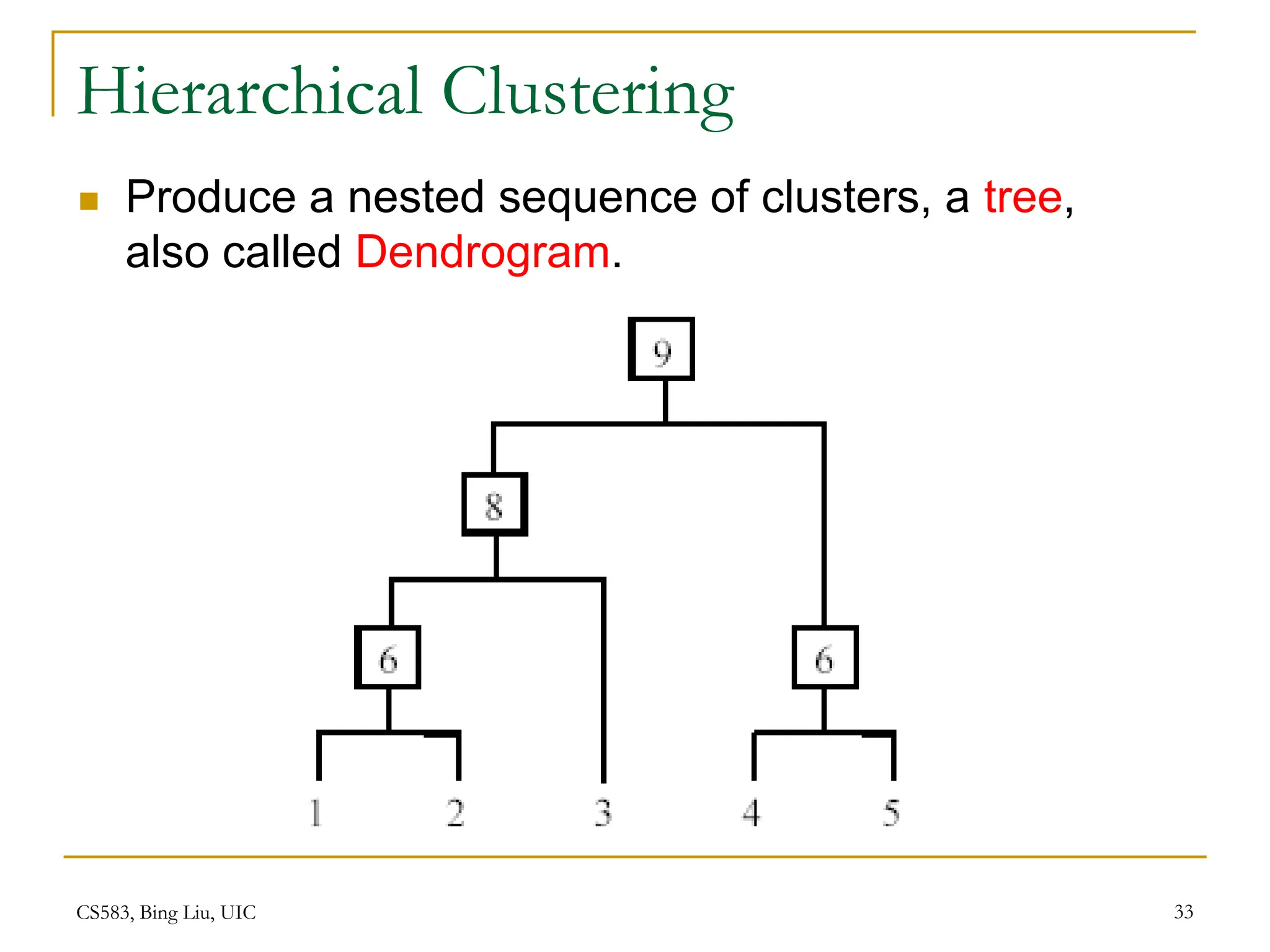
This document provides an overview of unsupervised learning and clustering algorithms. It introduces key concepts in unsupervised learning and how it differs from supervised learning. Clustering is defined as grouping similar data points together into clusters with the goal of maximizing inter-cluster distance and minimizing intra-cluster distance. The k-means algorithm and hierarchical clustering are described as two common clustering techniques. K-means partitions data into k clusters by iteratively assigning points to centroids while hierarchical clustering builds a nested sequence of clusters in a tree structure.