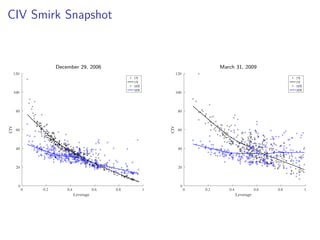
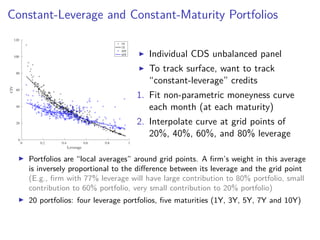
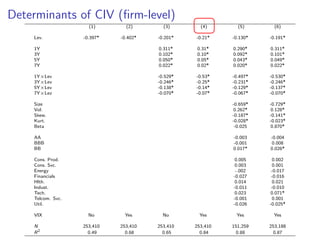
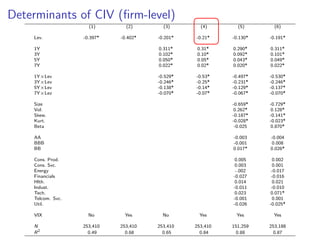
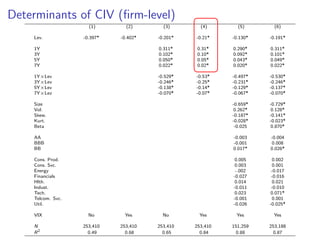
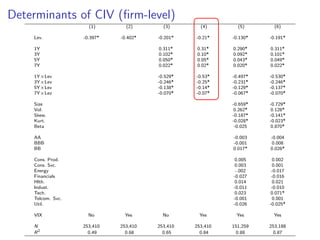
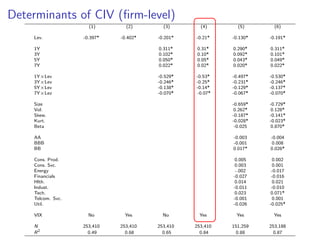
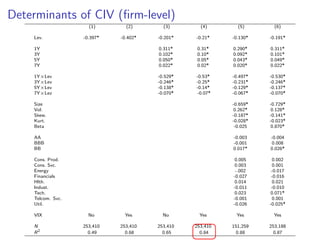
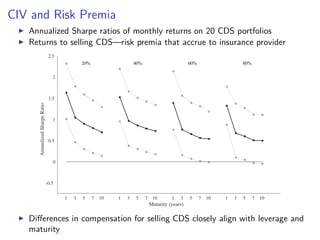
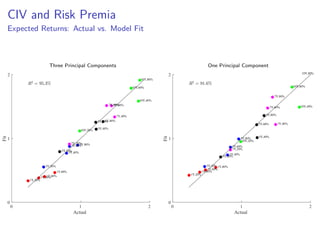
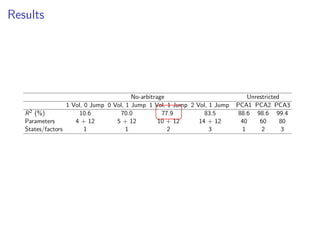
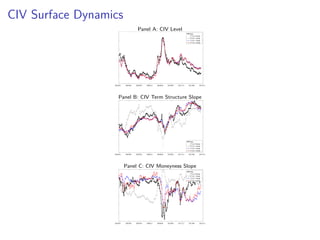
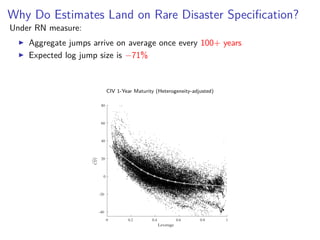
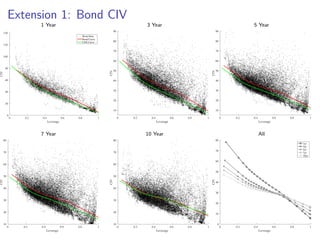
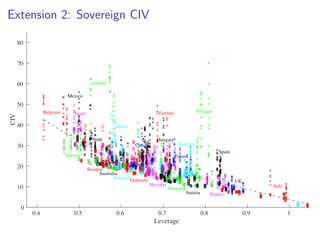
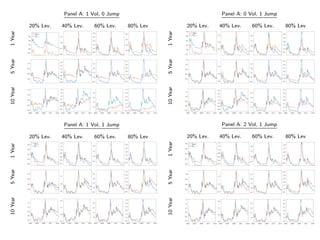
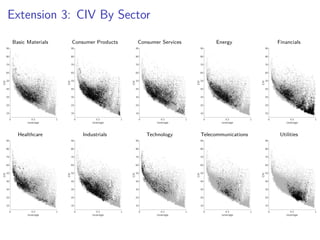
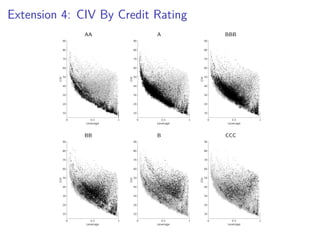
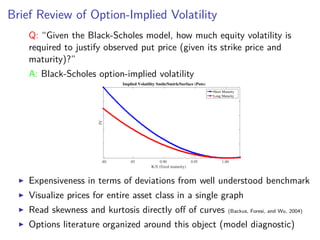
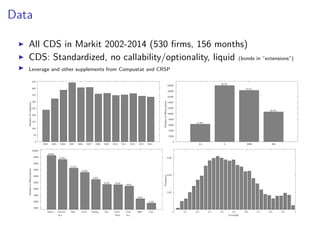
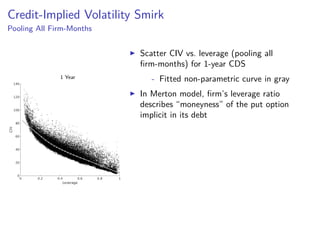
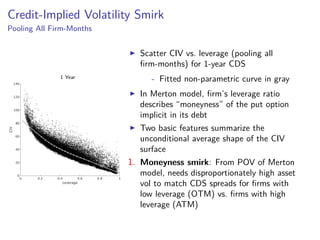
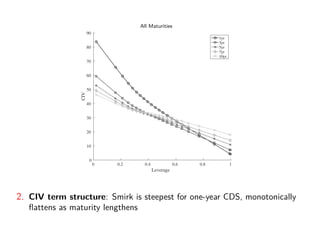
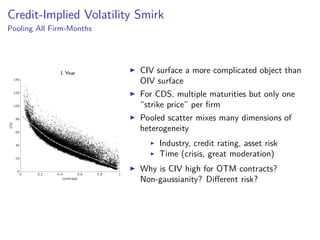
The paper introduces the concept of 'credit-implied volatility' (CIV) surface, which organizes corporate credit price behaviors into visual representations across different firms and maturities. It examines how CIV can be used to infer asset growth distributions and diagnose credit risk models, building on the Merton model framework. Key findings indicate that variations in credit spreads are largely explained by firm leverage, contract maturity, and common state variables.

1. Credit-Implied Volatility
Bryan Kelly
University of Chicago
Gerardo Manzo
Two Sigma
Diogo Palhares
AQR
6th Conference on Fixed Income Markets
August 17-18, 2017

2. This Paper
Introduce “credit-implied volatility” (CIV) surface
Organizes behavior of corporate credit prices into a handful of
easy-to-visualize facts
Across wide range of firms (credit quality)
For short and long maturities
Dynamics
* New stylized facts for credit pricing
Simple visual diagnostic for candidate credit risk models
Infer distribution of asset growth (firms and aggregate)

3. Brief Review of Option-Implied Volatility
Q: “Given the Black-Scholes model, how much equity volatility is
required to justify observed put price (given its strike price and
maturity)?”

4. Brief Review of Option-Implied Volatility
Q: “Given the Black-Scholes model, how much equity volatility is
required to justify observed put price (given its strike price and
maturity)?”
A: Black-Scholes option-implied volatility
K/S (fixed maturity)
.80 .85 0.90 0.95 1.00
IV
Implied Volatility Smile/Smirk/Surface (Puts)
Short Maturity
Long Maturity

5. Brief Review of Option-Implied Volatility
Q: “Given the Black-Scholes model, how much equity volatility is
required to justify observed put price (given its strike price and
maturity)?”
A: Black-Scholes option-implied volatility
K/S (fixed maturity)
.80 .85 0.90 0.95 1.00
IV
Implied Volatility Smile/Smirk/Surface (Puts)
Short Maturity
Long Maturity
Expensiveness in terms of deviations from well understood benchmark
Visualize prices for entire asset class in a single graph
Read skewness and kurtosis directly off of curves (Backus, Foresi, and Wu, 2004)
Options literature organized around this object (model diagnostic)

6. “Debt is a Short Put in a Gaussian World”
Brief Review of Merton Model
Assumptions of Merton (Black-Scholes) Model
1. Asset growth through time T is N µA,σ2
A
2. Debt matures at T, face value of F, can only default at T

7. “Debt is a Short Put in a Gaussian World”
Brief Review of Merton Model
Assumptions of Merton (Black-Scholes) Model
1. Asset growth through time T is N µA,σ2
A
2. Debt matures at T, face value of F, can only default at T
F
Asset Value at Maturity
Debt Payoff at Maturity
Equity Payoff at Maturity
In other words,
Debt is (short) put on AT with strike F
Credit spread simple translation of this put’s price

8. Credit-Implied Volatility Surface
Q: “How much asset volatility does the Merton model require to
justify a firm’s observed credit spread, given its leverage and contract
maturity?”

9. Credit-Implied Volatility Surface
Q: “How much asset volatility does the Merton model require to
justify a firm’s observed credit spread, given its leverage and contract
maturity?”
A: CIV
Note: “moneyness” of put in debt is firm’s leverage ratio

10. Credit-Implied Volatility Surface
Q: “How much asset volatility does the Merton model require to
justify a firm’s observed credit spread, given its leverage and contract
maturity?”
A: CIV
Note: “moneyness” of put in debt is firm’s leverage ratio
Data: Credit Spread (Si,τ ) & Firm Leverage (Li = Fi
Ai
) & Debt
Maturity (τ)
⇓
Merton Formula: Si,τ = f (σA,Li ,τ)
⇓
Invert: CIVi,τ
CIV Surface: Plot CIVi,τ against “moneyness” and maturity of debt

11. Data
All CDS in Markit 2002-2014 (530 firms, 156 months)
CDS: Standardized, no callability/optionality, liquid (bonds in “extensions”)
Leverage and other supplements from Compustat and CRSP
2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014
NumberofCompanies
0
50
100
150
200
250
300
350
400
450
AA A BBB BB
NumberofObservations
0
2000
4000
6000
8000
10000
12000
14000
16000
18000
20000
11.4%
36.2%
33.1%
19.3%
Indust. Telcom.
Svc.
Mat. Tech. Energy Fin. Cons.
Prod.
Cons.
Svc.
Hlth. Util.
NumberofObservations
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
16.8%
15.6%
13.2%
12.0%
9.9%
8.5% 8.4%
8.0%
4.4%
3.2%
Leverage
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Frequency
0.02
0.04
0.06

12. Credit-Implied Volatility Smirk
Pooling All Firm-Months
Scatter CIV vs. leverage (pooling all
firm-months) for 1-year CDS
- Fitted non-parametric curve in gray
In Merton model, firm’s leverage ratio
describes “moneyness” of the put option
implicit in its debt

13. Credit-Implied Volatility Smirk
Pooling All Firm-Months
1 Year
Scatter CIV vs. leverage (pooling all
firm-months) for 1-year CDS
- Fitted non-parametric curve in gray
In Merton model, firm’s leverage ratio
describes “moneyness” of the put option
implicit in its debt

14. Credit-Implied Volatility Smirk
Pooling All Firm-Months
1 Year
Scatter CIV vs. leverage (pooling all
firm-months) for 1-year CDS
- Fitted non-parametric curve in gray
In Merton model, firm’s leverage ratio
describes “moneyness” of the put option
implicit in its debt
Two basic features summarize the
unconditional average shape of the CIV
surface
1. Moneyness smirk: From POV of Merton
model, needs disproportionately high asset
vol to match CDS spreads for firms with
low leverage (OTM) vs. firms with high
leverage (ATM)

15. All Maturities
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
0
10
20
30
40
50
60
70
80
90
1yr
3yr
5yr
7yr
10yr
2. CIV term structure: Smirk is steepest for one-year CDS, monotonically
flattens as maturity lengthens

16. Credit-Implied Volatility Smirk
Pooling All Firm-Months
1 Year CIV surface a more complicated object than
OIV surface
For CDS, multiple maturities but only one
“strike price” per firm
Pooled scatter mixes many dimensions of
heterogeneity
Industry, credit rating, asset risk
Time (crisis, great moderation)
Why is CIV high for OTM contracts?
Non-gaussianity? Different risk?

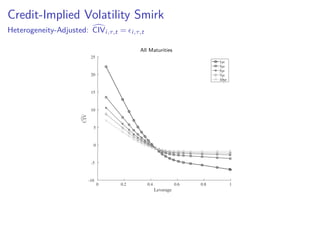
17. Credit-Implied Volatility Smirk (Heterogeneity-Adjusted)
CIVi,τ,t = δ0,τ +δ1,τ [Size,Beta,Vol,Skew,Kurt]i,t
+ Rating FE+Sector FE+Month FE+ i,τ,t,
Regression run separately for each maturity, τ
Soak up all heterogeneity excluding leverage
Noting of course other measures correlated
Plot the residual—“Heterogeneity-adjusted” CIV
CIVi,τ,t = i,τ,t

18. Credit-Implied Volatility Smirk
Heterogeneity-Adjusted: CIVi,τ,t = i,τ,t
All Maturities
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
-10
-5
0
5
10
15
20
25
1yr
3yr
5yr
7yr
10yr

19. Credit Fact 1: IV from credit spreads possesses a steep moneyness smirk
Differences in credit spreads in cross section explained by leverage and
maturity
Fact not explained by non-leverage firm heterogeneity
Suggests (severe) non-normalities in asset growth distribution

20. Dynamics of Credit Spreads

21. CIV Smirk Snapshot
December 29, 2006 March 31, 2009
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
0
20
40
60
80
100
120
1Y
1Y
10Y
10Y
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
0
20
40
60
80
100
120
1Y
1Y
10Y
10Y

22. Constant-Leverage and Constant-Maturity Portfolios
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
0
20
40
60
80
100
120
1Y
1Y
10Y
10Y Individual CDS unbalanced panel
To track surface, want to track
“constant-leverage” credits
1. Fit non-parametric moneyness curve
each month (at each maturity)
2. Interpolate curve at grid points of
20%, 40%, 60%, and 80% leverage
Portfolios are “local averages” around grid points. A firm’s weight in this average
is inversely proportional to the difference between its leverage and the grid point
(E.g., firm with 77% leverage will have large contribution to 80% portfolio, small
contribution to 60% portfolio, very small contribution to 20% portfolio)
20 portfolios: four leverage portfolios, five maturities (1Y, 3Y, 5Y, 7Y and 10Y)

23. Surface Dynamics
High degree of commonality in CIV fluctuations for portfolios sorted by
leverage and maturity
We first analyze the factor structure of CIV surface using PCA on panel of
156×20 month-by-portfolio CIV observations
Five leading components explain 87.4%, 9.6%, 1.8%, 0.4%, and 0.3% of the
panel variation in CIV, respectively
We focus on first three PCs

24. First Component: Surface Level
20 40 60 80 20 40 60 80 20 40 60 80 20 40 60 80 20 40 60 80
1Y 3Y 5Y 7Y 10Y
200201 200308 200504 200612 200808 201004 201112 201308 201412
PC1
Avg. CIV
VIX
Corr(PC1,Avg. CIV) = 99.8%, Corr(PC1,VIX) = 81.2%, Expl. Var = 87.4%
Second Component: Term Structure Slope
20 40 60 80 20 40 60 80 20 40 60 80 20 40 60 80 20 40 60 80
1Y 3Y 5Y 7Y 10Y
200201 200308 200504 200612 200808 201004 201112 201308 201412
PC2
10Y-1Y
Corr. = 93.2%, Expl. Var = 9.6%
Third Component: Moneyness Slope
20 40 60 80 20 40 60 80 20 40 60 80 20 40 60 80 20 40 60 80
1Y 3Y 5Y 7Y 10Y
200201 200308 200504 200612 200808 201004 201112 201308 201412
PC3
10%-90%
Corr. = 56.9%, Expl. Var = 1.8%

25. Credit Fact 2: 99% of panel dynamics in spreads captured with
1. Variation in common level of CIV (~87%)
2. Variation in term structure slope (~10%)
3. Variation in moneyness slope (~2%)
Collectively, Facts 1 + 2 suggest that vast majority of credit spread heterogeneity,
both across individual CDS and over time, is associated with the leverage of the
reference entity, the maturity of the CDS contract, and a small number of
common state variables

26. Determinants of CIV (firm-level)
(1) (2) (3) (4) (5) (6)
Lev. -0.397* -0.402* -0.201* -0.21* -0.130* -0.191*
1Y 0.311* 0.31* 0.290* 0.311*
3Y 0.102* 0.10* 0.092* 0.101*
5Y 0.050* 0.05* 0.043* 0.049*
7Y 0.022* 0.02* 0.020* 0.022*
1Y×Lev -0.529* -0.53* -0.497* -0.530*
3Y×Lev -0.246* -0.25* -0.231* -0.246*
5Y×Lev -0.138* -0.14* -0.129* -0.137*
7Y×Lev -0.070* -0.07* -0.067* -0.070*
Size -0.659* -0.729*
Vol. 0.262* 0.128*
Skew. -0.187* -0.141*
Kurt. -0.028* -0.023*
Beta -0.025 0.870*
AA -0.003 -0.004
BBB -0.001 0.008
BB 0.017* 0.026*
Cons. Prod. 0.005 0.002
Cons. Svc. 0.003 0.001
Energy -.002 -0.017
Financials -0.027 -0.016
Hlth. 0.014 0.021
Indust. -0.011 -0.010
Tech. 0.023 0.071*
Telcom. Svc. -0.001 0.001
Util. -0.026 -0.025*
VIX No Yes No Yes Yes Yes
N 253,410 253,410 253,410 253,410 151,259 253,188
R2
0.49 0.68 0.65 0.84 0.88 0.87

27. Determinants of CIV (firm-level)
(1) (2) (3) (4) (5) (6)
Lev. -0.397* -0.402* -0.201* -0.21* -0.130* -0.191*
1Y 0.311* 0.31* 0.290* 0.311*
3Y 0.102* 0.10* 0.092* 0.101*
5Y 0.050* 0.05* 0.043* 0.049*
7Y 0.022* 0.02* 0.020* 0.022*
1Y×Lev -0.529* -0.53* -0.497* -0.530*
3Y×Lev -0.246* -0.25* -0.231* -0.246*
5Y×Lev -0.138* -0.14* -0.129* -0.137*
7Y×Lev -0.070* -0.07* -0.067* -0.070*
Size -0.659* -0.729*
Vol. 0.262* 0.128*
Skew. -0.187* -0.141*
Kurt. -0.028* -0.023*
Beta -0.025 0.870*
AA -0.003 -0.004
BBB -0.001 0.008
BB 0.017* 0.026*
Cons. Prod. 0.005 0.002
Cons. Svc. 0.003 0.001
Energy -.002 -0.017
Financials -0.027 -0.016
Hlth. 0.014 0.021
Indust. -0.011 -0.010
Tech. 0.023 0.071*
Telcom. Svc. -0.001 0.001
Util. -0.026 -0.025*
VIX No Yes No Yes Yes Yes
N 253,410 253,410 253,410 253,410 151,259 253,188
R2
0.49 0.68 0.65 0.84 0.88 0.87

28. Determinants of CIV (firm-level)
(1) (2) (3) (4) (5) (6)
Lev. -0.397* -0.402* -0.201* -0.21* -0.130* -0.191*
1Y 0.311* 0.31* 0.290* 0.311*
3Y 0.102* 0.10* 0.092* 0.101*
5Y 0.050* 0.05* 0.043* 0.049*
7Y 0.022* 0.02* 0.020* 0.022*
1Y×Lev -0.529* -0.53* -0.497* -0.530*
3Y×Lev -0.246* -0.25* -0.231* -0.246*
5Y×Lev -0.138* -0.14* -0.129* -0.137*
7Y×Lev -0.070* -0.07* -0.067* -0.070*
Size -0.659* -0.729*
Vol. 0.262* 0.128*
Skew. -0.187* -0.141*
Kurt. -0.028* -0.023*
Beta -0.025 0.870*
AA -0.003 -0.004
BBB -0.001 0.008
BB 0.017* 0.026*
Cons. Prod. 0.005 0.002
Cons. Svc. 0.003 0.001
Energy -.002 -0.017
Financials -0.027 -0.016
Hlth. 0.014 0.021
Indust. -0.011 -0.010
Tech. 0.023 0.071*
Telcom. Svc. -0.001 0.001
Util. -0.026 -0.025*
VIX No Yes No Yes Yes Yes
N 253,410 253,410 253,410 253,410 151,259 253,188
R2
0.49 0.68 0.65 0.84 0.88 0.87

29. Determinants of CIV (firm-level)
(1) (2) (3) (4) (5) (6)
Lev. -0.397* -0.402* -0.201* -0.21* -0.130* -0.191*
1Y 0.311* 0.31* 0.290* 0.311*
3Y 0.102* 0.10* 0.092* 0.101*
5Y 0.050* 0.05* 0.043* 0.049*
7Y 0.022* 0.02* 0.020* 0.022*
1Y×Lev -0.529* -0.53* -0.497* -0.530*
3Y×Lev -0.246* -0.25* -0.231* -0.246*
5Y×Lev -0.138* -0.14* -0.129* -0.137*
7Y×Lev -0.070* -0.07* -0.067* -0.070*
Size -0.659* -0.729*
Vol. 0.262* 0.128*
Skew. -0.187* -0.141*
Kurt. -0.028* -0.023*
Beta -0.025 0.870*
AA -0.003 -0.004
BBB -0.001 0.008
BB 0.017* 0.026*
Cons. Prod. 0.005 0.002
Cons. Svc. 0.003 0.001
Energy -.002 -0.017
Financials -0.027 -0.016
Hlth. 0.014 0.021
Indust. -0.011 -0.010
Tech. 0.023 0.071*
Telcom. Svc. -0.001 0.001
Util. -0.026 -0.025*
VIX No Yes No Yes Yes Yes
N 253,410 253,410 253,410 253,410 151,259 253,188
R2
0.49 0.68 0.65 0.84 0.88 0.87

30. Determinants of CIV (firm-level)
(1) (2) (3) (4) (5) (6)
Lev. -0.397* -0.402* -0.201* -0.21* -0.130* -0.191*
1Y 0.311* 0.31* 0.290* 0.311*
3Y 0.102* 0.10* 0.092* 0.101*
5Y 0.050* 0.05* 0.043* 0.049*
7Y 0.022* 0.02* 0.020* 0.022*
1Y×Lev -0.529* -0.53* -0.497* -0.530*
3Y×Lev -0.246* -0.25* -0.231* -0.246*
5Y×Lev -0.138* -0.14* -0.129* -0.137*
7Y×Lev -0.070* -0.07* -0.067* -0.070*
Size -0.659* -0.729*
Vol. 0.262* 0.128*
Skew. -0.187* -0.141*
Kurt. -0.028* -0.023*
Beta -0.025 0.870*
AA -0.003 -0.004
BBB -0.001 0.008
BB 0.017* 0.026*
Cons. Prod. 0.005 0.002
Cons. Svc. 0.003 0.001
Energy -.002 -0.017
Financials -0.027 -0.016
Hlth. 0.014 0.021
Indust. -0.011 -0.010
Tech. 0.023 0.071*
Telcom. Svc. -0.001 0.001
Util. -0.026 -0.025*
VIX No Yes No Yes Yes Yes
N 253,410 253,410 253,410 253,410 151,259 253,188
R2
0.49 0.68 0.65 0.84 0.88 0.87

31. Determinants of CIV (firm-level)
(1) (2) (3) (4) (5) (6)
Lev. -0.397* -0.402* -0.201* -0.21* -0.130* -0.191*
1Y 0.311* 0.31* 0.290* 0.311*
3Y 0.102* 0.10* 0.092* 0.101*
5Y 0.050* 0.05* 0.043* 0.049*
7Y 0.022* 0.02* 0.020* 0.022*
1Y×Lev -0.529* -0.53* -0.497* -0.530*
3Y×Lev -0.246* -0.25* -0.231* -0.246*
5Y×Lev -0.138* -0.14* -0.129* -0.137*
7Y×Lev -0.070* -0.07* -0.067* -0.070*
Size -0.659* -0.729*
Vol. 0.262* 0.128*
Skew. -0.187* -0.141*
Kurt. -0.028* -0.023*
Beta -0.025 0.870*
AA -0.003 -0.004
BBB -0.001 0.008
BB 0.017* 0.026*
Cons. Prod. 0.005 0.002
Cons. Svc. 0.003 0.001
Energy -.002 -0.017
Financials -0.027 -0.016
Hlth. 0.014 0.021
Indust. -0.011 -0.010
Tech. 0.023 0.071*
Telcom. Svc. -0.001 0.001
Util. -0.026 -0.025*
VIX No Yes No Yes Yes Yes
N 253,410 253,410 253,410 253,410 151,259 253,188
R2
0.49 0.68 0.65 0.84 0.88 0.87

32. Patterns of Credit Risk Premia
So far analysis focused on levels of spreads and CIV
Levels all but perfectly explained with two or three common factors
interpretable via differences in leverage and maturity
Next natural question: Do credit risk premia also align with its leverage
and maturity?
Study average returns of 20 leverage/maturity CDS portfolios

33. CIV and Risk Premia
Annualized Sharpe ratios of monthly returns on 20 CDS portfolios
Returns to selling CDS—risk premia that accrue to insurance provider
Maturity (years)
1 3 5 7 10 1 3 5 7 10 1 3 5 7 10 1 3 5 7 10
AnnualizedSharpeRatio
-0.5
0
0.5
1
1.5
2
2.5
20% 40% 60% 80%
Differences in compensation for selling CDS closely align with leverage and
maturity

34. CIV and Risk Premia
Why do credit risk premia align with leverage and maturity?
PCA showed that credit risk for all firms well captured by small number of
shocks
Are these shocks risk factors?
Fama-MacBeth analysis using shocks to PC’s
1. Betas of each portfolio on factor innovations (time series)
2. Do betas align with differences in mean portfolio returns?

35. CIV and Risk Premia
Expected Returns: Actual vs. Model Fit
Three Principal Components One Principal Component
Actual
0 1 2
Fit
0
1
2
1Y,20%
1Y,40%1Y,60%
1Y,80%
3Y,20%
3Y,40%
3Y,60%3Y,80%
5Y,20%
5Y,40%
5Y,60%5Y,80%
7Y,20%
7Y,40%
7Y,60%7Y,80%
10Y,20%
10Y,40%
10Y,60%
10Y,80%
R2
= 95.3%
Actual
0 1 2
Fit
0
1
2
1Y,20%
1Y,40%
1Y,60%
1Y,80%3Y,20%
3Y,40%
3Y,60%
3Y,80%
5Y,20%
5Y,40%
5Y,60%
5Y,80%
7Y,20%
7Y,40%
7Y,60%
7Y,80%
10Y,20%
10Y,40%
10Y,60%
10Y,80%
R2
= 91.6%

36. Credit Fact 3: Differences in average CDS returns align with same
dimensions of CIV surface (leverage and maturity)
These differences are fully explained by differences in exposure to
fluctuations in CIV surface
Much of the credit risk premium is a variance risk premium. Similar behavior
to equity VRP but larger magnitude

37. Model

38. Background: Credit Spread Empirics
No-arbitrage Models
“Structural” or “Reduced-form”
Enforce cross-equation restrictions
Typical estimation approach
calibrates to
- Average spread (no
dynamics)
- Representative credit in
rating category (no cross
section)
Unrestricted Models
Regressions
LHS: Spread levels or changes
RHS: Firm characteristics
Fit full panel (dynamics and
cross section)
We propose no-arbitrage (“structural”) model
Specification based on what we’ve learned from CIV surface
Matches panel of spreads nearly as well as unrestricted
models—across wide range of credit quality and throughout the credit cycle

39. Choosing Specification
What a model should accomplish:
Steep moneyness smirk → (Severe) Excess kurtosis
Smirk flattens with maturity → Mean reversion
Panel dynamics entirely → Exposure to aggregate shocks,
• captured by 2-3 factors → Few state variables,
→ No independent idiosyncratic risk variation

40. Model: “1 Vol, 1 Jump”
Aggregate Asset Growth:
dAm,t
Am,t
= rdt +
√
vtdW m,1
t
Agg. Stochastic Vol
+ e−qm
−1 dJ (λt)−λtξm
Agg. Jump Risk
dv1,t = κv (θv −vt)dt +σv
√
v1,tdW v
t
λt = avt +zt , dzt = κz (θz −zt)dt +σz
√
z,tdW z
t
Firm Asset Growth:
dAi,t
Ai,t
= rdt +βi
dAm,t
Am,t
−rdt
Agg. Exposure
+
√
vi,tdW i
t + e−qi −1 dJ (λt)−λtξi
Common Idios. Risk
vi,t = vi +γi vt , qi ∼ qm

41. Compare Specifications
Stochastic vol only (1-factor)
Jump only (1-factor)
Stochastic Vol + Jump (2-factor)
Two Stochastic Vols + Jump (3-factor)

42. Results
No-arbitrage Unrestricted
1 Vol, 0 Jump 0 Vol, 1 Jump 1 Vol, 1 Jump 2 Vol, 1 Jump PCA1 PCA2 PCA3
R2 (%) 10.6 70.0 77.9 83.5 88.6 98.6 99.4
Parameters 4 + 12 5 + 12 10 + 12 14 + 12 40 60 80
States/factors 1 1 2 3 1 2 3

43. CIV Surface Dynamics
Panel A: CIV Level
200201 200308 200504 200612 200808 201004 201112 201308 201412
Data
1 Vol, 0 Jump
0 Vol, 1 Jump
1 Vol, 1 Jump
2 Vol, 1 Jump
Panel B: CIV Term Structure Slope
200201 200308 200504 200612 200808 201004 201112 201308 201412
Data
1 Vol, 0 Jump
0 Vol, 1 Jump
1 Vol, 1 Jump
2 Vol, 1 Jump
Panel C: CIV Moneyness Slope
200201 200308 200504 200612 200808 201004 201112 201308 201412
Data
1 Vol, 0 Jump
0 Vol, 1 Jump
1 Vol, 1 Jump
2 Vol, 1 Jump

44. Why Do Estimates Land on Rare Disaster Specification?
Under RN measure:
Aggregate jumps arrive on average once every 100+ years
Expected log jump size is −71%
CIV 1-Year Maturity (Heterogeneity-adjusted)
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
-40
-20
0
20
40
60
80

45. What We Learn From the Model
Highly accurate fit of spreads based on
Crash-risky aggregate asset growth
2-factor dynamics in higher moments (stochastic vol, crash risk)
All firms exposed to aggregate shock, inherit its higher moments
By looking at CIV smirk, we read off the (risk-neutral) distribution of
aggregate asset growth, despite not having a cross section of
“strikes.” This is not something we have “seen” before
More work to be done here

46. Extension 1: Bond CIV
1 Year 3 Year 5 Year
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
0
20
40
60
80
100
120
140
Bond Data
Bond Curve
CDS Curve
Leverage
0 0.2 0.4 0.6 0.8 1
CIV10
20
30
40
50
60
70
80
90
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
10
20
30
40
50
60
70
80
90
7 Year 10 Year All
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
10
20
30
40
50
60
70
80
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
10
20
30
40
50
60
70
80
Leverage
0 0.2 0.4 0.6 0.8 1
CIV
0
10
20
30
40
50
60
70
80
1yr
3yr
5yr
7yr
10yr

47. Extension 2: Sovereign CIV
Sovereign CDS for 24 OECD countries
What is “moneyness” of sovereign credit?
From OECD Consolidated National Balance Sheets for General Government
The difference between the financial assets and liabilities held by governments (also known as financial net
worth or as a broad description of net government debt), gives an extensive measure of the government’s
capacity to meet its financial obligation. While financial assets reflect a source of additional funding
and income available to government, liabilities reflect the debts accumulated by government. Thus, an
increase in the financial net worth signals good financial health. Net worth may be depleted by debt
accumulation, indicating a worsening of fiscal position and ultimately forcing governments to either cut
spending or raise taxes.
We define sovereign leverage as the ratio of total financial liabilities (net of shares
and other equity) to financial assets for the general government sector

48. Extension 2: Sovereign CIV
Leverage
0.4 0.5 0.6 0.7 0.8 0.9 1
CIV
0
10
20
30
40
50
60
70
80
Austria
Belgium
Czech
Denmark
Estonia
Finland
France
Germany
Hungary
Ireland
Israel
Italy
Neth.
Norway Poland
Portugal
Slovakia
Slovenia
Spain
Sweden
UK
Mexico
Brazil
Australia

49. Conclusion
CIV surface as organizing framework for empirical analysis of credit
Almost all variation in relative cost of a credit claim lines up with
Moneyness of contract (underlying firm’s leverage)
Contract maturity
Document steep CIV moneyness slope that implies large deviations from
normality in the risk-neutral distribution of aggregate asset growth
Dynamics of surface summarized with three interpretable factors
CIV level
Term structure slope
Moneyness slope
Provides compact and complete description of time-variation in the
entire panel of firm-level credit spreads
A parsimonious structural model with stochastic volatility and jumps
provides an accurate description of CDS spreads for firms across the credit
spectrum, at short and long maturities, and at all points throughout the
credit cycle
Our estimation suggests risk-neutral distribution of aggregate asset growth
effectively described as a rare disaster model

50. Panel A: 1 Vol, 0 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
-0.2 0.0 0.2 0.4 0.6
Fit
-0.2
0.0
0.2
0.4
0.6
0.0 0.5 1.0 1.5
0.0
0.5
1.0
1.5
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
1.0 2.0 3.0 4.0
1.0
2.0
3.0
4.0
5Year
0.4 0.6 0.8 1.0
Fit
0.4
0.6
0.8
1.0
0.5 1.0 1.5
0.4
0.6
0.8
1.0
1.2
1.4
1.6
0.5 1.0 1.5 2.0 2.5
0.5
1.0
1.5
2.0
2.5
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
10Year
Data
0.4 0.6 0.8 1.0 1.2
Fit
0.4
0.6
0.8
1.0
1.2
Data
0.5 1.0 1.5
0.5
1.0
1.5
Data
1.0 1.5 2.0 2.5
1.0
1.5
2.0
2.5
Data
1.0 2.0 3.0
1.0
2.0
3.0
Panel A: 0 Vol, 1 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
-0.2 0.0 0.2 0.4 0.6 0.8
Fit
-0.2
0.0
0.2
0.4
0.6
0.8
0.5 1.0 1.5
0.5
1.0
1.5
0.5 1.0 1.5 2.0
0.5
1.0
1.5
2.0
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
5Year
0.4 0.6 0.8 1.0 1.2
Fit
0.4
0.6
0.8
1.0
1.2
0.5 1.0 1.5
0.5
1.0
1.5
0.5 1.0 1.5 2.0 2.5
0.5
1.0
1.5
2.0
2.5
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
10Year
Data
0.4 0.6 0.8 1.0 1.2
Fit
0.4
0.6
0.8
1.0
1.2
Data
0.5 1.0 1.5
0.5
1.0
1.5
Data
1.0 1.5 2.0 2.5
1.0
1.5
2.0
2.5
Data
1.0 2.0 3.0
1.0
2.0
3.0
Panel A: 1 Vol, 1 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
0.0 0.2 0.4 0.6 0.8
Fit
0.0
0.2
0.4
0.6
0.8
0.2 0.4 0.6 0.8 1.0 1.2 1.4
0.2
0.4
0.6
0.8
1.0
1.2
1.4
0.5 1.0 1.5 2.0
0.5
1.0
1.5
2.0
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
5Year
0.4 0.6 0.8 1.0
Fit
0.4
0.6
0.8
1.0
0.5 1.0 1.5
0.5
1.0
1.5
0.5 1.0 1.5 2.0 2.5
0.5
1.0
1.5
2.0
2.5
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
10Year
Data
0.4 0.6 0.8 1.0 1.2
Fit
0.4
0.6
0.8
1.0
1.2
Data
0.5 1.0 1.5 2.0
0.5
1.0
1.5
2.0
Data
1.0 1.5 2.0 2.5
1.0
1.5
2.0
2.5
Data
1.0 2.0 3.0
1.0
2.0
3.0
Panel A: 2 Vol, 1 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
0.0 0.2 0.4 0.6 0.8
Fit
0.0
0.2
0.4
0.6
0.8
0.2 0.4 0.6 0.8 1.0 1.2 1.4
0.2
0.4
0.6
0.8
1.0
1.2
1.4
0.5 1.0 1.5 2.0
0.5
1.0
1.5
2.0
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
5Year
0.4 0.6 0.8 1.0
Fit
0.4
0.6
0.8
1.0
0.5 1.0 1.5
0.5
1.0
1.5
0.5 1.0 1.5 2.0 2.5
0.5
1.0
1.5
2.0
2.5
1.0 2.0 3.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
10Year
Data
0.4 0.6 0.8 1.0 1.2 1.4
Fit
0.4
0.6
0.8
1.0
1.2
1.4
Data
0.5 1.0 1.5 2.0
0.5
1.0
1.5
2.0
Data
1.0 1.5 2.0 2.5
1.0
1.5
2.0
2.5
Data
1.0 2.0 3.0
1.0
2.0
3.0

51. Panel A: 1 Vol, 0 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
-0.2
0.0
0.2
0.4
0.6
Data
Fit
0.0
0.5
1.0
1.5
0.5
1.0
1.5
2.0
2.5
3.0
1.0
2.0
3.0
4.0
5Year
0.4
0.6
0.8
1.0
0.4
0.6
0.8
1.0
1.2
1.4
1.6
0.5
1.0
1.5
2.0
2.5
0.5
1.0
1.5
2.0
2.5
3.0
3.5
10Year
2002 2005 2008 2011 2014
0.4
0.6
0.8
1.0
1.2
2002 2005 2008 2011 2014
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2002 2005 2008 2011 2014
1.0
1.5
2.0
2.5
2002 2005 2008 2011 2014
0.5
1.0
1.5
2.0
2.5
3.0
3.5
Panel A: 0 Vol, 1 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
-0.2
0.0
0.2
0.4
0.6
0.8
Data
Fit
0.5
1.0
1.5
0.5
1.0
1.5
2.0
0.5
1.0
1.5
2.0
2.5
3.0
5Year
0.4
0.6
0.8
1.0
1.2
0.5
1.0
1.5
0.5
1.0
1.5
2.0
2.5
0.5
1.0
1.5
2.0
2.5
3.0
3.5
10Year
2002 2005 2008 2011 2014
0.4
0.6
0.8
1.0
1.2
2002 2005 2008 2011 2014
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2002 2005 2008 2011 2014
1.0
1.5
2.0
2.5
2002 2005 2008 2011 2014
0.5
1.0
1.5
2.0
2.5
3.0
3.5
Panel A: 1 Vol, 1 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
0.0
0.2
0.4
0.6
0.8 Data
Fit
0.2
0.4
0.6
0.8
1.0
1.2
1.4
0.5
1.0
1.5
2.0
0.5
1.0
1.5
2.0
2.5
3.0
5Year
0.4
0.6
0.8
1.0
0.5
1.0
1.5
0.5
1.0
1.5
2.0
2.5
0.5
1.0
1.5
2.0
2.5
3.0
3.5
10Year
2002 2005 2008 2011 2014
0.4
0.6
0.8
1.0
1.2
2002 2005 2008 2011 2014
0.5
1.0
1.5
2.0
2002 2005 2008 2011 2014
1.0
1.5
2.0
2.5
2002 2005 2008 2011 2014
0.5
1.0
1.5
2.0
2.5
3.0
3.5
Panel A: 2 Vol, 1 Jump
20% Lev. 40% Lev. 60% Lev. 80% Lev
1Year
0.0
0.2
0.4
0.6
0.8 Data
Fit
0.2
0.4
0.6
0.8
1.0
1.2
1.4
0.5
1.0
1.5
2.0
0.5
1.0
1.5
2.0
2.5
3.0
5Year
0.4
0.6
0.8
1.0
0.5
1.0
1.5
0.5
1.0
1.5
2.0
2.5
0.5
1.0
1.5
2.0
2.5
3.0
3.510Year
2002 2005 2008 2011 2014
0.4
0.6
0.8
1.0
1.2
1.4
2002 2005 2008 2011 2014
0.5
1.0
1.5
2.0
2002 2005 2008 2011 2014
1.0
1.5
2.0
2.5
2002 2005 2008 2011 2014
0.5
1.0
1.5
2.0
2.5
3.0
3.5

52. Extension 3: CIV By Sector
Basic Materials Consumer Products Consumer Services Energy Financials
Healthcare Industrials Technology Telecommunications Utilities

53. Extension 4: CIV By Credit Rating
AA A BBB
BB B CCC

54. This document is being distributed for informational and educational purposes only and is not an offer to sell or the solicitation of an offer to buy
any securities or other instruments. The information contained herein is not intended to provide, and should not be relied upon for investment
advice. The views expressed herein are not necessarily the views of Two Sigma Investments, LP or any of its affiliates (collectively, “Two Sigma”).
Such views reflect significant assumptions and subjective of the author(s) of the document and are subject to change without notice. The
document may employ data derived from third-party sources. No representation is made as to the accuracy of such information and the use of
such information in no way implies an endorsement of the source of such information or its validity.
The copyrights and/or trademarks in some of the images, logos or other material used herein may be owned by entities other than Two Sigma. If
so, such copyrights and/or trademarks are most likely owned by the entity that created the material and are used purely for identification and
comment as fair use under international copyright and/or trademark laws. Use of such image, copyright or trademark does not imply any
association with such organization (or endorsement of such organization) by Two Sigma, nor vice versa.