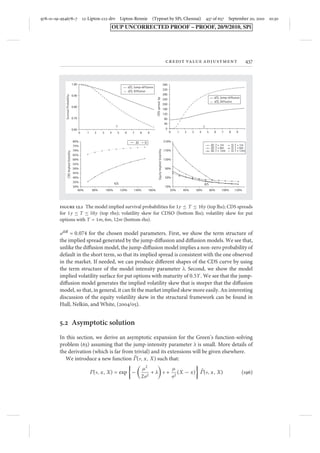
This document discusses credit value adjustment (CVA) in the context of counterparty risk for credit default swaps (CDS), emphasizing the importance of effective risk management following the 2008 financial crisis. It presents a multi-dimensional structural default model which quantitatively estimates counterparty credit risk, illustrating how to integrate correlated dynamics of credit spreads and firm values. The chapter outlines innovative numerical methods for pricing CDS and estimating CVA while addressing limitations in existing approaches, enabling better calibration to market observed spreads.




![978–0–19–954678–7 12-Lipton-c12-drv Lipton-Rennie (Typeset by SPi, Chennai) 410 of 657 September 20, 2010 10:30
OUP UNCORRECTED PROOF – PROOF, 20/9/2010, SPi
410 a. lipton & a. sepp
and numerical methods for solving the 1D pricing problem. In particular, we describe
MC, FFT, and FD methods for solving the calibration problem via forward induction
and the pricing problem via backward induction. In section 6 we present analytical
and numerical methods for solving the 2D pricing problem, including FFT and FD
methods. In section 7 we provide an illustration of our findings by showing how to
calculate CVA for a CDS on Morgan Stanley (MS) sold by JP Morgan (JPM) and a
CDS on JPM sold by MS.We formulate brief conclusions in section 8.
2 Structural model and default event
................................................................................................................................................
In this section we describe our structural default model in one, two, and multi-dimensions.
Qt
2.1 Notation
Throughout the chapter, we model uncertainty by constructing a probability space
(Ÿ,F, F,Q) with the filtration F = {F(t), t ≥ 0} and a martingale measure Q. We
assume that Q is specified by market prices of liquid credit products. The operation
of expectation under Q given information set F(t) at time t is denoted by E[·]. The
imaginary unit is denoted by i, i =
√
−1.
The instantaneous risk-free interest rate r (t) is assumed to be deterministic; the
corresponding discount factor, D(t, T) is given by:
D(t, T) = exp
−
T
t
r (t)dt
(1)
It is applied at valuation time t for cash flows generated at time T, 0 ≤ t ≤ T ∞.
The indicator function of an event ˆ is denoted by 1ˆ:
1ˆ =
1 ifˆ is true
0 ifˆ is false (2)
The Heaviside step function is denoted by H(x),
H(x) = 1{x≥0} (3)
the Dirac delta function is denoted by δ(x); the Kronecker delta function is denoted by
δn,n0 .We also use the following notation
{x}
+ = max{x, 0} (4)
We denote the normal probability density function (PDF) by n (x); and the cumu-lative
normal probability function by N(x); besides, we frequently use the function
P (a, b) defined as follows:](https://image.slidesharecdn.com/12-lipton-c12-drv-140830042846-phpapp01/85/Credit-Value-Adjustment-in-the-Extended-Structural-Default-Model-5-320.jpg)

![978–0–19–954678–7 12-Lipton-c12-drv Lipton-Rennie (Typeset by SPi, Chennai) 412 of 657 September 20, 2010 10:30
OUP UNCORRECTED PROOF – PROOF, 20/9/2010, SPi
412 a. lipton a. sepp
minimizing the value of outstanding bonds. Thus, the optimal debt-to-equity ratio and
the endogenous default barrier are decision variables in this approach. A nice review of
the Black-Cox approach and its extensions is given by Bielecki and Rutkowski (2002),
and Uhrig-Homburg (2002). However, in our view, the endogenous approach is not
realistic given the complicated equity-liability structure of large firms and the actual
relationships between the firm’s management and its equity and debtholders. For
example, in July 2009 the bail-out of a commercial lender CIT was carried out by
debtholders, who proposed debt restructuring, rather than by equity holders, who had
no negotiating power.
In the exogenous approach, the default boundary is one of the model parameters.
The default barrier is typically specified as a fraction of the debt per share estimated
by the recovery ratio of firms with similar characteristics. While still not very realistic,
this approach is more intuitive and practical (see, for instance, Kim and Ramaswamy,
and Sundaresan 1993; Nielsen, and Saa-Requejo, and Santa-Clara 1993; Longstaff and
Schwartz 1995; etc.).
In our approach, similarly to Lipton (2002b); and Stamicar and Finger (2005), we
assume that the default barrier of the firm is a deterministic function of time given by
l (t) = E (t)l (0) (10)
where E (t) is the deterministic growth factor:
E (t) = exp
t
0
(r (t) − Ê(t))dt
(11)
and l (0) is defined by l (0) = RL(0), where R is an average recovery of the firm’s
liabilities and L(0) is its total debt per share. We find L(0) from the balance sheet
as the ratio of the firm’s total liability to the total common shares outstanding; R is
found from CDS quotes, typically, it is assumed that R = 0.4.
2.2.3 Default triggering event
The key variable of the model is the random default time which we denote by Ù. We
assume that Ù is an F-adapted stopping time, Ù ∈ (0,∞]. In general, the default event
can be triggered in three ways.
First, when the firm’s value is monitored only at the debt’s maturity time T, then
the default time is defined by:
Ù =
T, a(T) ≤ l (T)
∞, a(T) l (T) (12)
This is the case of terminal default monitoring (TDM) which we do not use below.
Second, if the firm’s value is monitored at fixed points in time, {tdm
}m=1,. . .,M,
0 td
1 . . . tdM
≤ T, then the default event can only occur at some time tdm
. The
corresponding default time is specified by:](https://image.slidesharecdn.com/12-lipton-c12-drv-140830042846-phpapp01/85/Credit-Value-Adjustment-in-the-Extended-Structural-Default-Model-7-320.jpg)

![978–0–19–954678–7 12-Lipton-c12-drv Lipton-Rennie (Typeset by SPi, Chennai) 414 of 657 September 20, 2010 10:30
OUP UNCORRECTED PROOF – PROOF, 20/9/2010, SPi
414 a. lipton a. sepp
and represent the asset value as follows:
a(t) = E (t)l (0)e x(t) = l (t) e x(t) (16)
where x(t) is driven by the following dynamics under Q:
dx(t) = Ï(t)dt + Û(t)dW(t) + j dN(t) (17)
x(0) = ln
a(0)
l (0)
≡ Ó, Ó 0
Ï(t) = −1
2
Û2(t) − Î(t)Í
We observe that, under this formulation of the firm value process, the default time
is specified by:
Ù = min{t : x(t) ≤ 0} (18)
triggered either discretely or continuously. Accordingly, the default event is deter-mined
only by the dynamics of the stochastic driver x(t).
We note that the shifted process y(t) = x(t) − Ó is an additive process with respect
to the filtration F which is characterized by the following conditions: y(t) is adapted
to F(t), increments of y(t) are independent of F(t), y(t) is continuous in probability,
and y(t) starts from the origin, Sato (1999). The main difference between an additive
process and a Levy process is that the distribution of increments in the former process
is time dependent.
Without loss of generality, we assume that volatility Û(t) and jump intensity Î(t) are
piecewise constant functions of time changing at times {tc
k
}, k = 1, . . . , k:
Û(t) =
k
k=1
Û(k)1{tc
k−1t≤tc
k
} + Û(k)1{ttc
k
} (19)
Î(t) =
k
k=1
Î(k)1{tc
k−1t≤tc
k
} + Î(k)1{ttc
k
}
where Û(k) defines the volatility and Î(k) defines the intensity at time periods (tc
k−1, tc
k ]
0 = 0, k = 1, . . . , k. In the case of DDM we assume that {tc
with tc
k
} is a subset of {tdm
}, so
that parameters do not jump between observation dates.
We consider the firm’s equity share price, which is denoted by s (t), and, following
Stamicar and Finger (2005), assume that the value of s (t) is given by:
s (t) =
a(t) − l (t) = E (t)l (0)
e x(t) − 1
= l (t)
e x(t) − 1
, {t Ù}
0, {t ≥ Ù} (20)
At time t = 0, s (0) is specified by themarket price of the equity share. Accordingly, the
initial value of the firm’s assets is given by:
a(0) = s (0) + l (0) (21)](https://image.slidesharecdn.com/12-lipton-c12-drv-140830042846-phpapp01/85/Credit-Value-Adjustment-in-the-Extended-Structural-Default-Model-9-320.jpg)