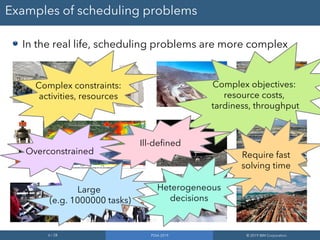
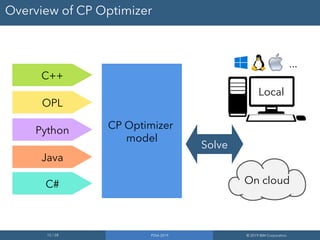
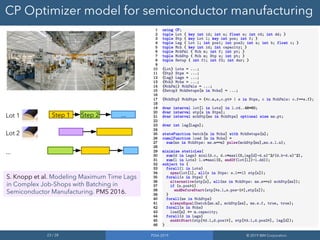
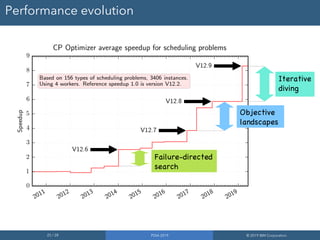
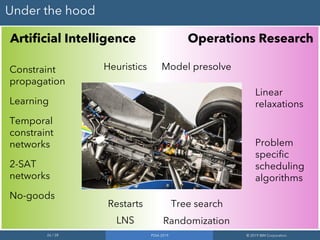
CP Optimizer is a tool for modeling and solving complex scheduling problems. It uses an interval-based approach to integrate temporal reasoning into mixed integer programming models. This allows it to more easily model problems involving time, durations, precedence constraints and resource allocation over time. CP Optimizer uses constraint programming techniques like temporal constraint networks along with artificial intelligence search methods to efficiently solve large, real-world scheduling instances that are difficult for MIP solvers. It has been applied successfully to problems in areas like semiconductor manufacturing.