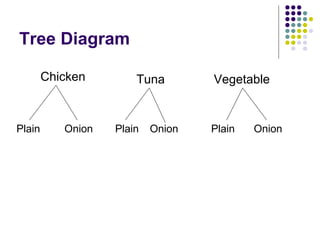
This document provides examples and explanations of probability, permutations, and combinations. It begins with probability questions about drawing cards and coins. It then introduces permutations and combinations, providing examples of counting possible sandwich combinations at a bagel shop and arranging swimmers in a relay. It defines permutations as arrangements where order matters and combinations as arrangements where order does not matter. It gives examples of calculating permutations and combinations using factorials.

1. Warm-up
 What is the probability that you will pick one card
that is a number 12 out of a regular deck of
playing cards?
 What is the probability that you will pick an even
number out of the numbers 2, 4, 6, 8, 10?

2. Counting Principle
Permutations
Combinations
After today, you will be able to
count outcomes, use
permutations, and use
combinations.

3. Bagel Mania!
 Bagel Mania offers chicken, tuna, and
vegetable sandwiches on plain or onion
bagels. How many possible sandwiches are
there?

4. Tree Diagram
Chicken Tuna Vegetable
Plain Onion PlainPlain OnionOnion

5. Counting Principle
 To find the total number of outcomes, multiply
your options together.
 EX) 8 different pizza toppings and 3 types of
crust (stuffed, thick, thin). How many different
combinations for a one-topping pizza?
 EX) Four coins are tossed.

6.  How many different ways can you order an ice
cream if the choices are:
 What is the probability the ice cream will be in a
sugar cone?
Type of cone Number of
scoops
Ice cream
flavor
Toppings
Sugar or waffle One or two Chocolate,
vanilla, coffee
or pistachio
Sprinkles,
syrup, or none

7. Permutations
 Permutation- an arrangement or listing in
which order is important.
 How many arrangements are possible with a
4-swimmer relay?
 4 x 3 x 2 x 1 or 4P4 in your calculator
 How many arrangements are possible with 5
swimmers for a 4-swimmer relay?
 5 x 4 x 3 x 2 or 5P4 in your calculator

8. Permutations
 Find P(8,3)
 P(8,3) means the number of orders of 8 things
taken 3 at a time.

9. Combinations
 Combination- arrangements where order is NOT
important.
 Examples:

10. Combinations
 Ex) In gym class Mr. Merrill picked 10
students to compete in the 100m dash. The
top three finishers each received a free
t-shirt. How many combinations of winners
could there be?

11. Permutation OR Combination?
 Four books in a row
 6 CDs from a group of 20
 A team of 6 players from 12
 Ten people in line to buy tickets

12. Permutations
 What is 4!
 4! Is read as “four factorial”
 Find 6!