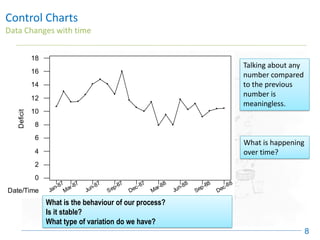
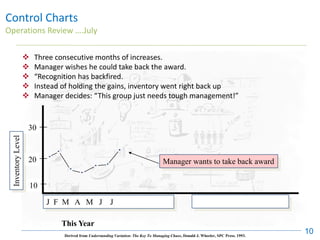
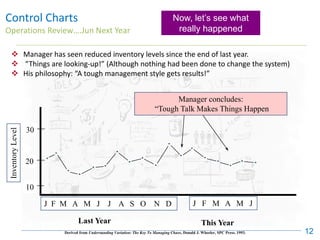
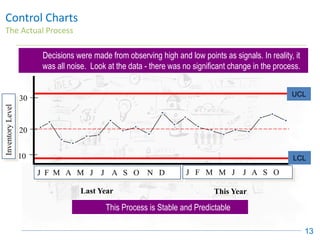
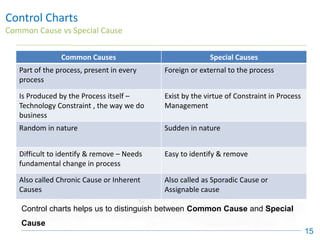
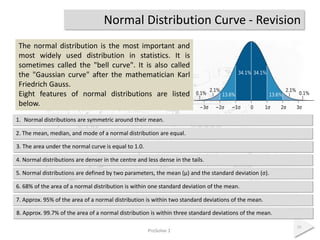
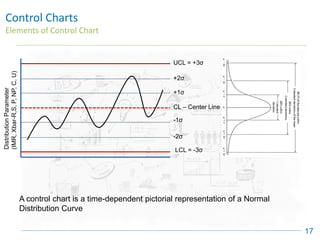
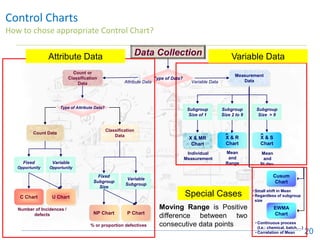
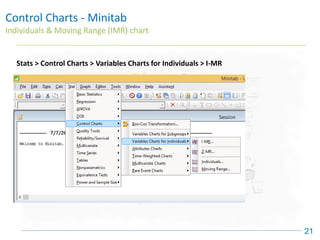
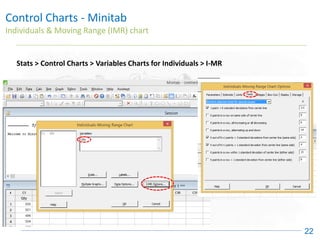
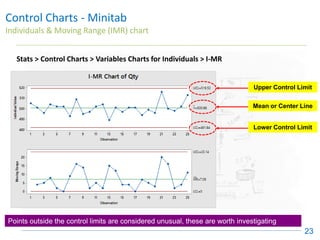
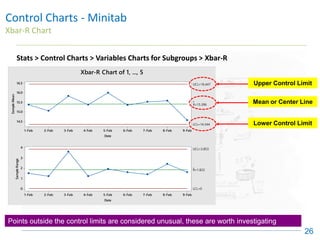
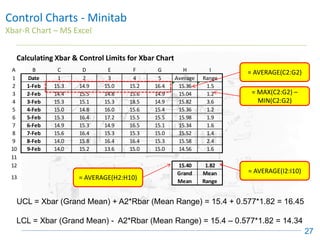
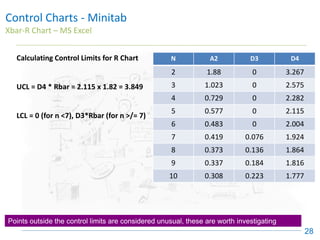
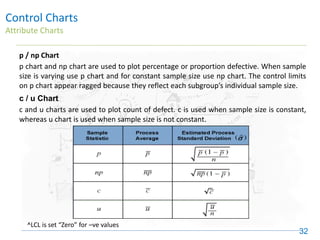
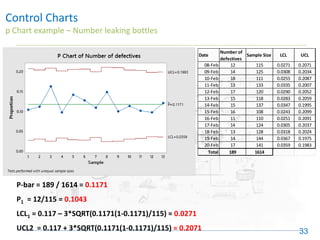
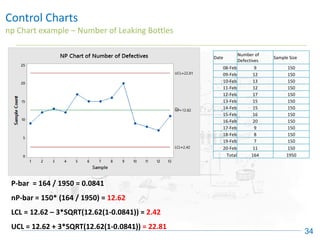
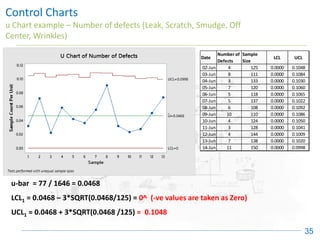
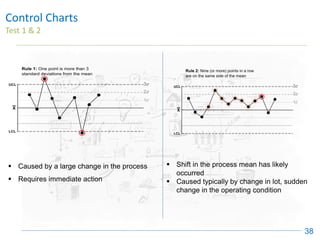
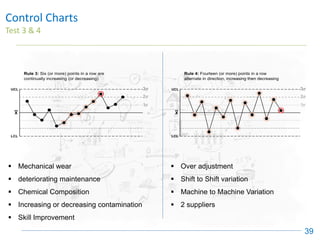
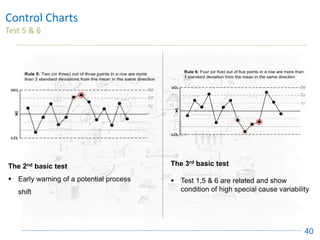
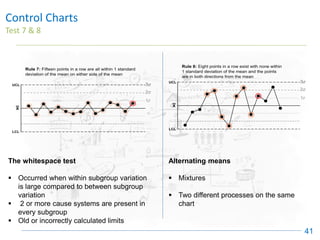
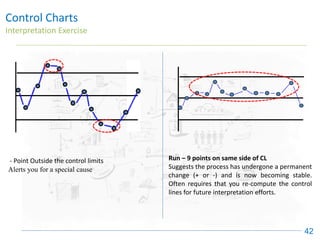
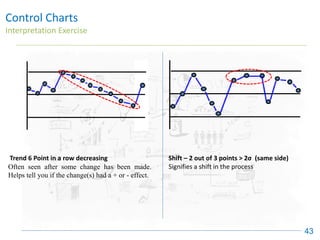
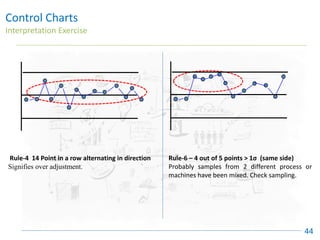
The document discusses control charts, emphasizing their purpose of distinguishing between special and common causes of variation in processes, allowing for improved decision-making and process stability. It highlights the limitations of traditional data analysis methods and introduces control limits, variation interpretation, and historical context for the development of control charts. Additionally, the document describes different types of charts used for statistical process control, helping users identify real process changes and maintain quality.