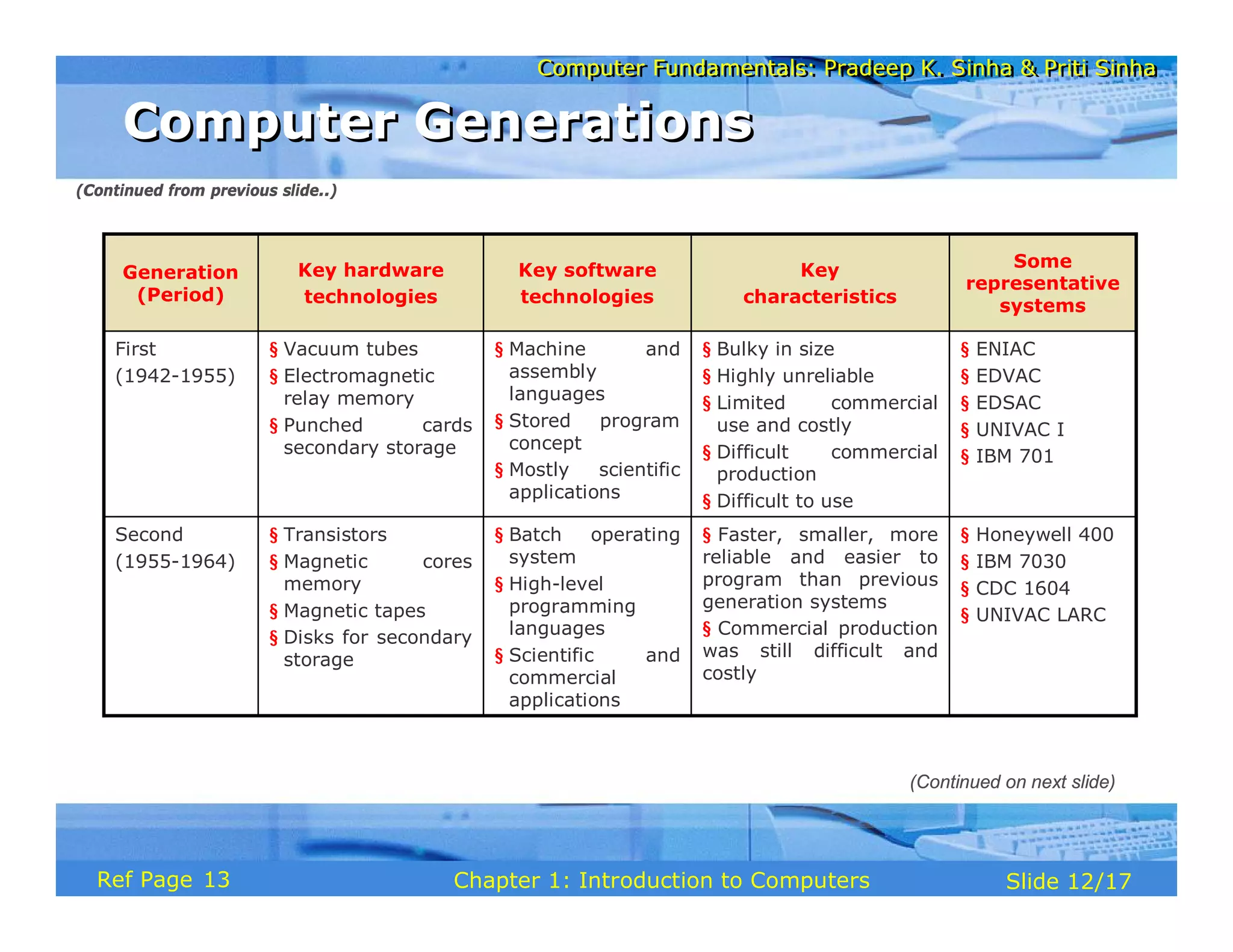
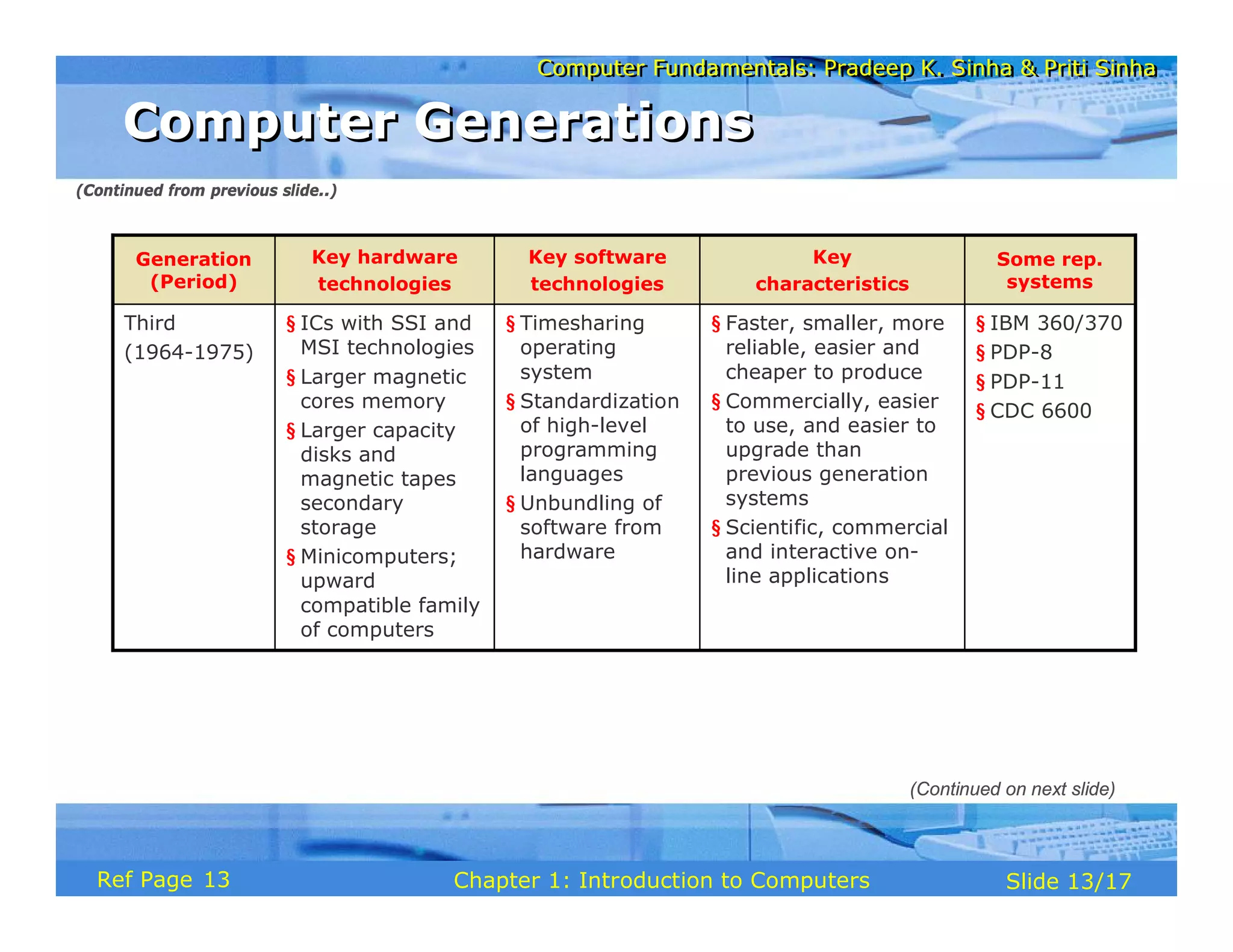
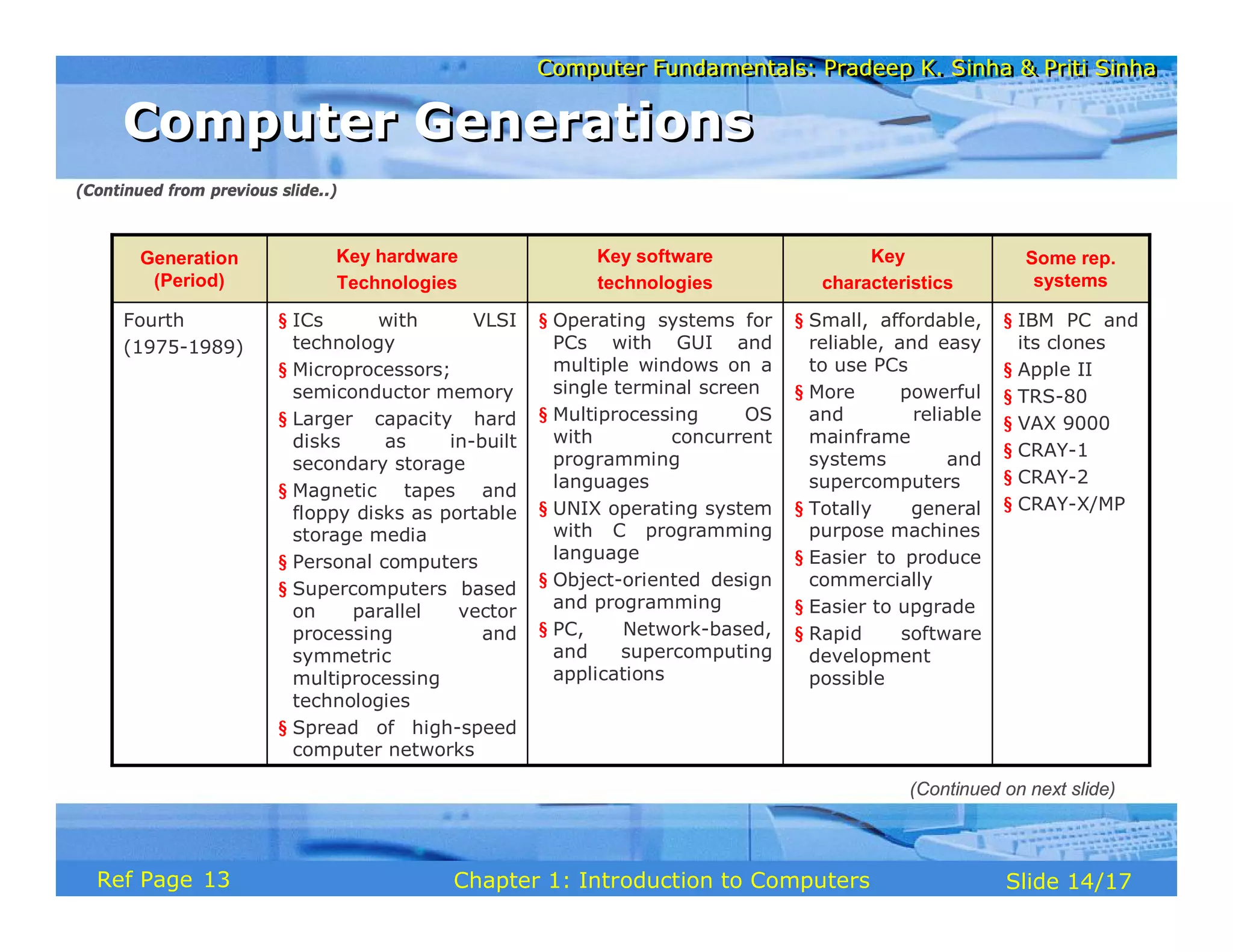
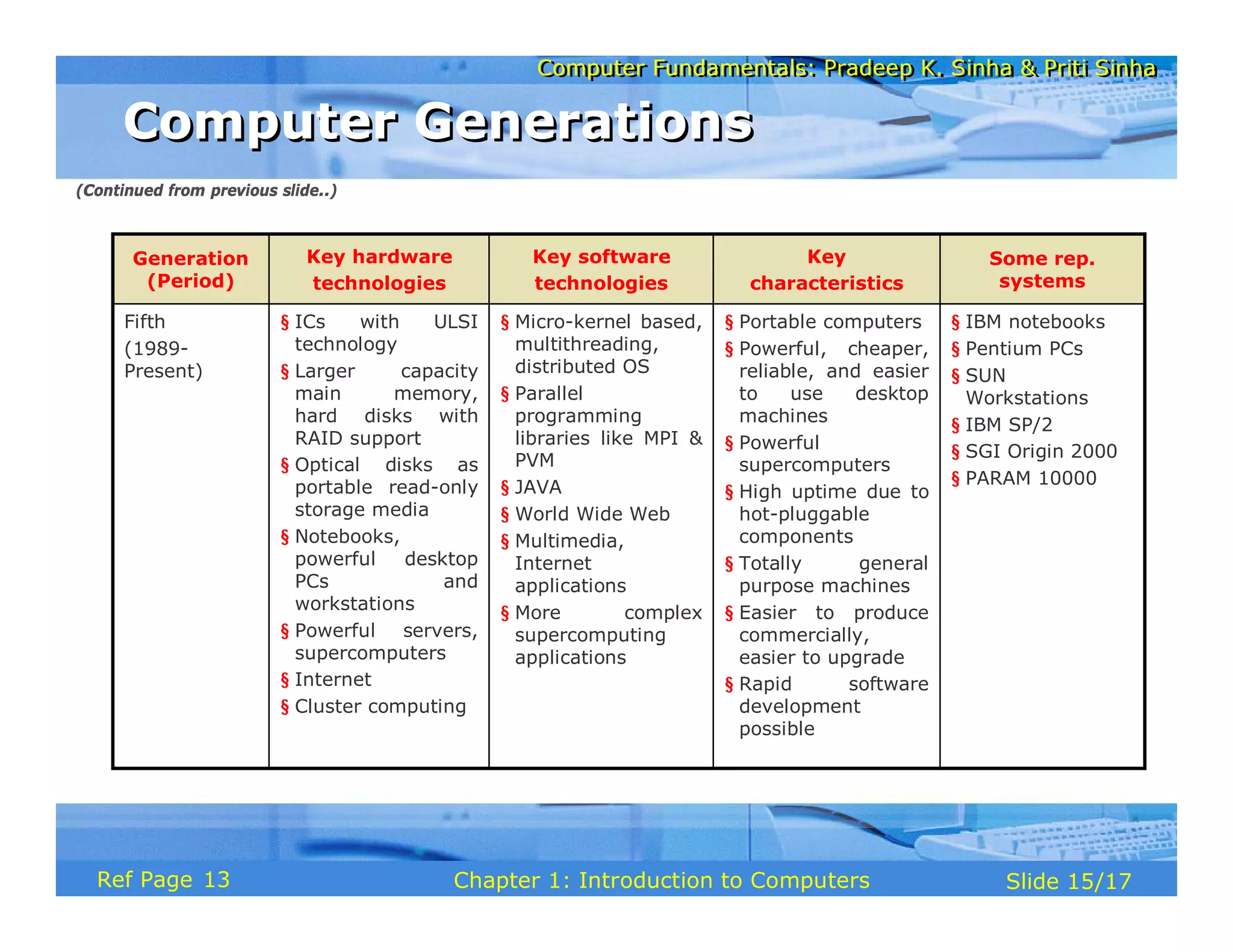
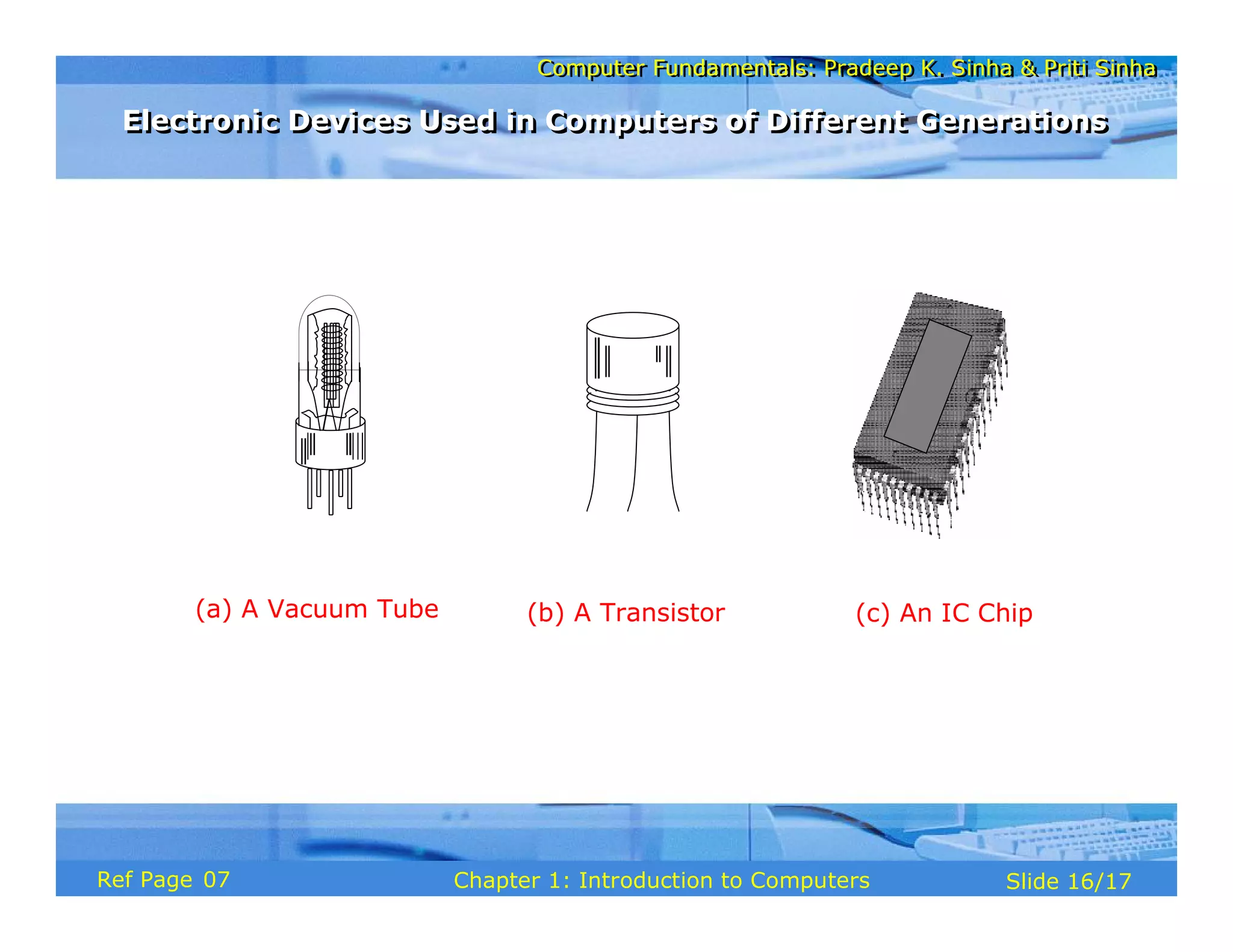
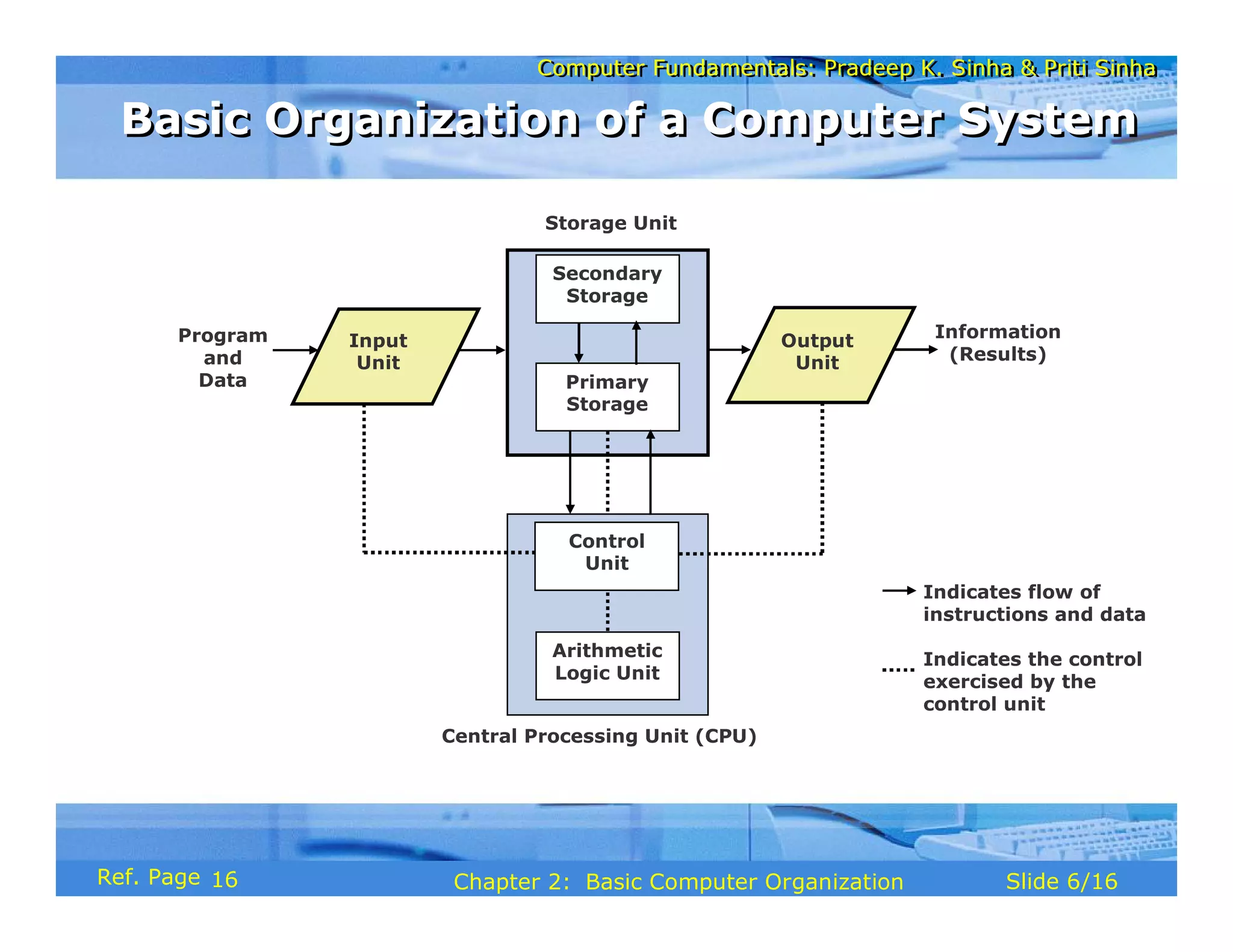
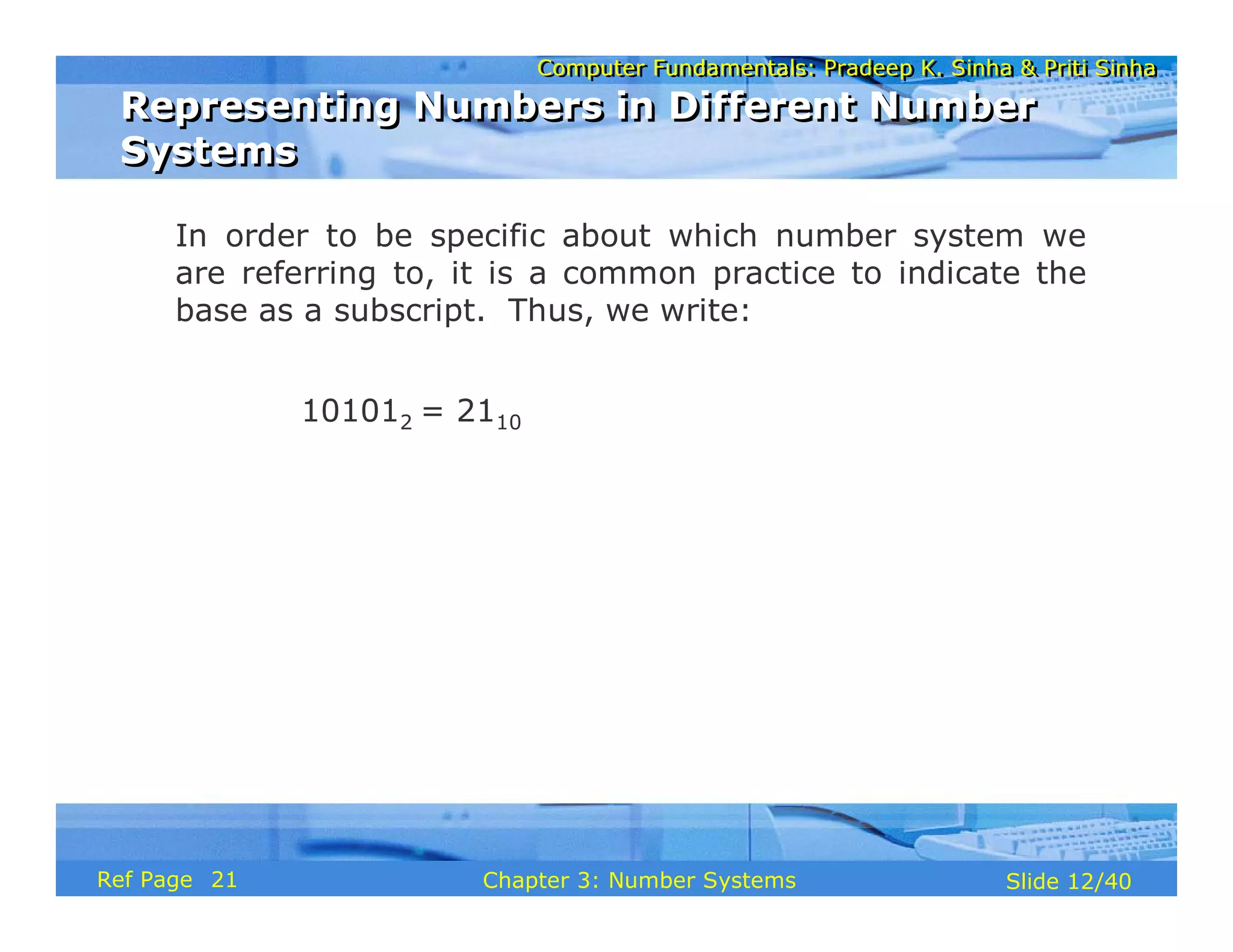
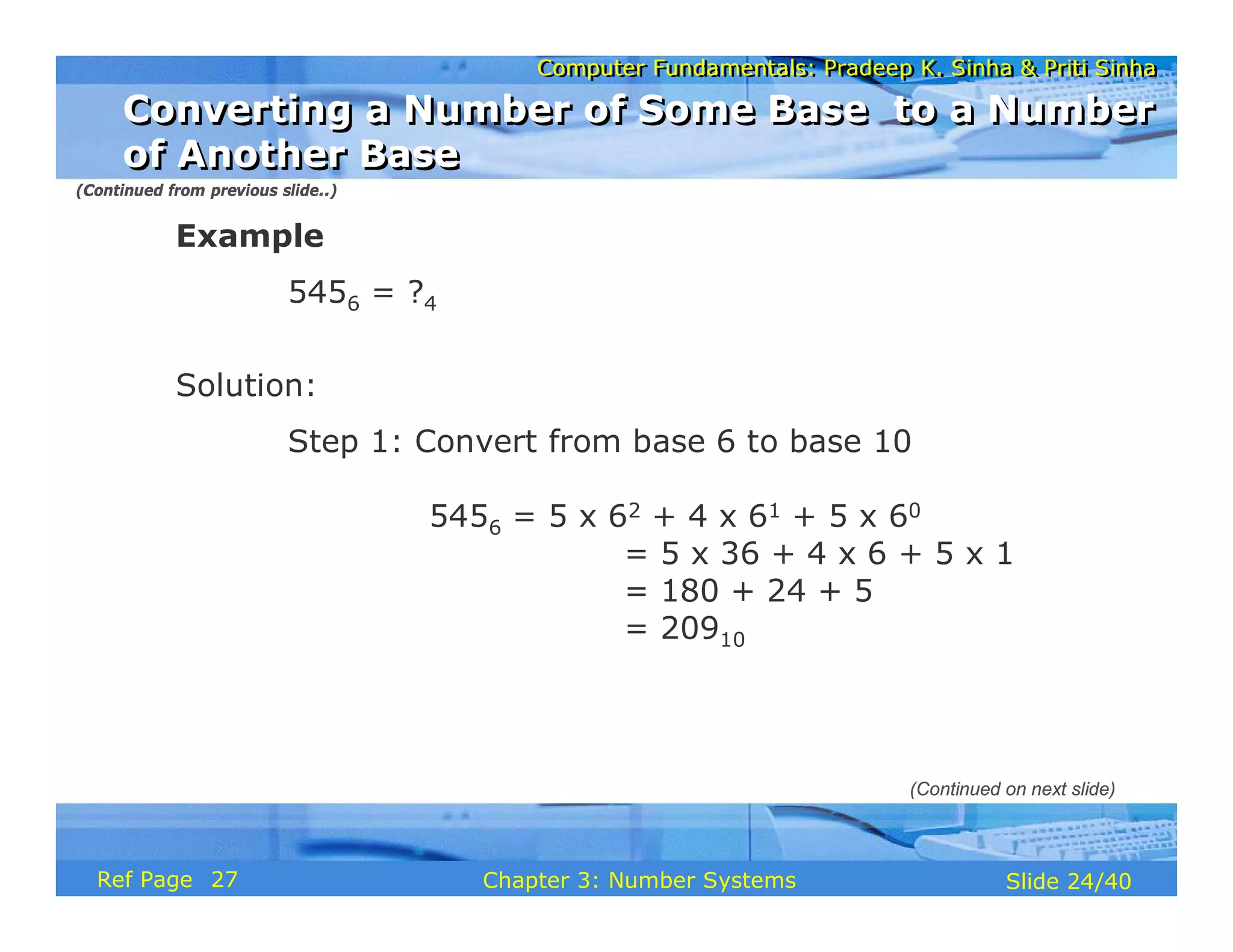
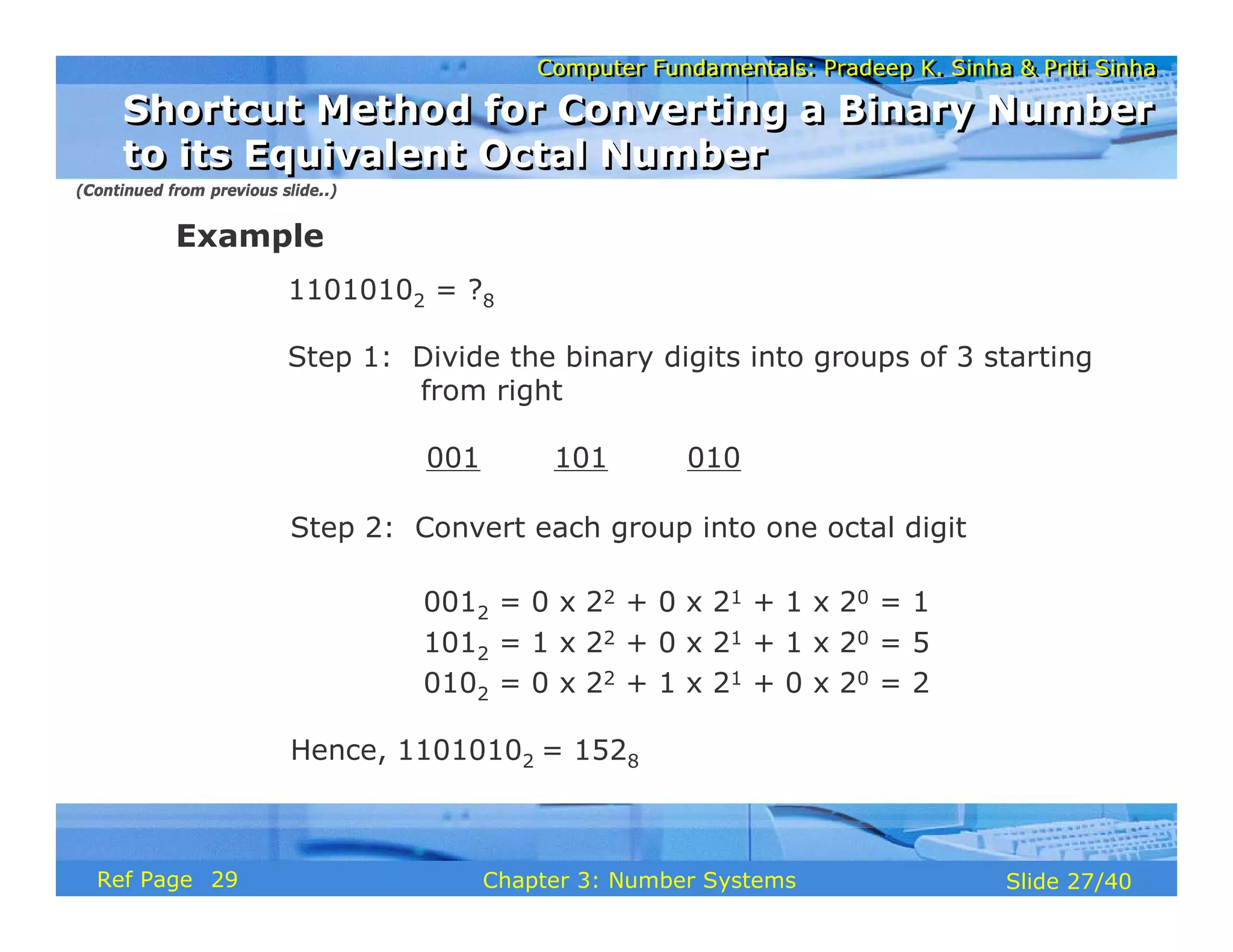
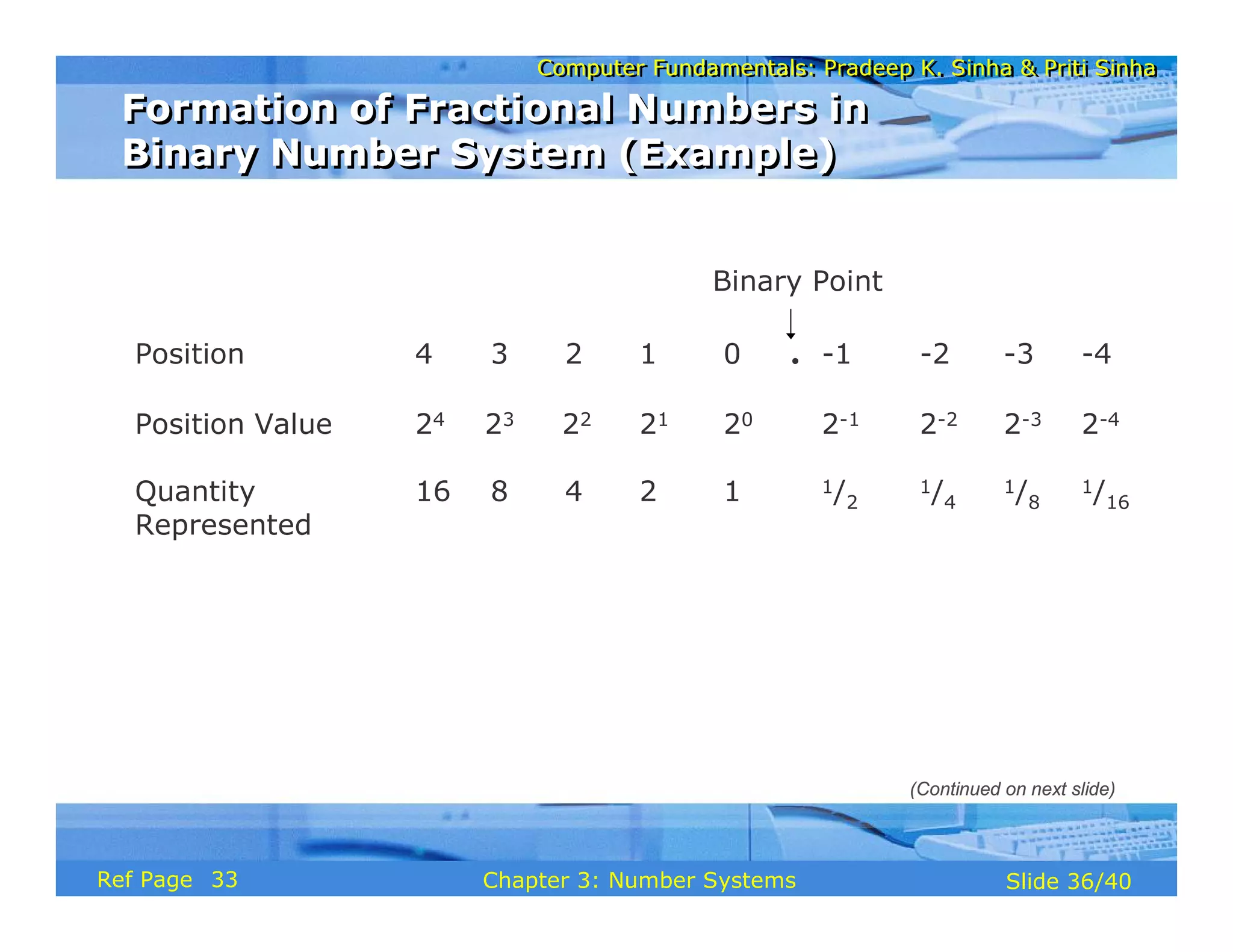
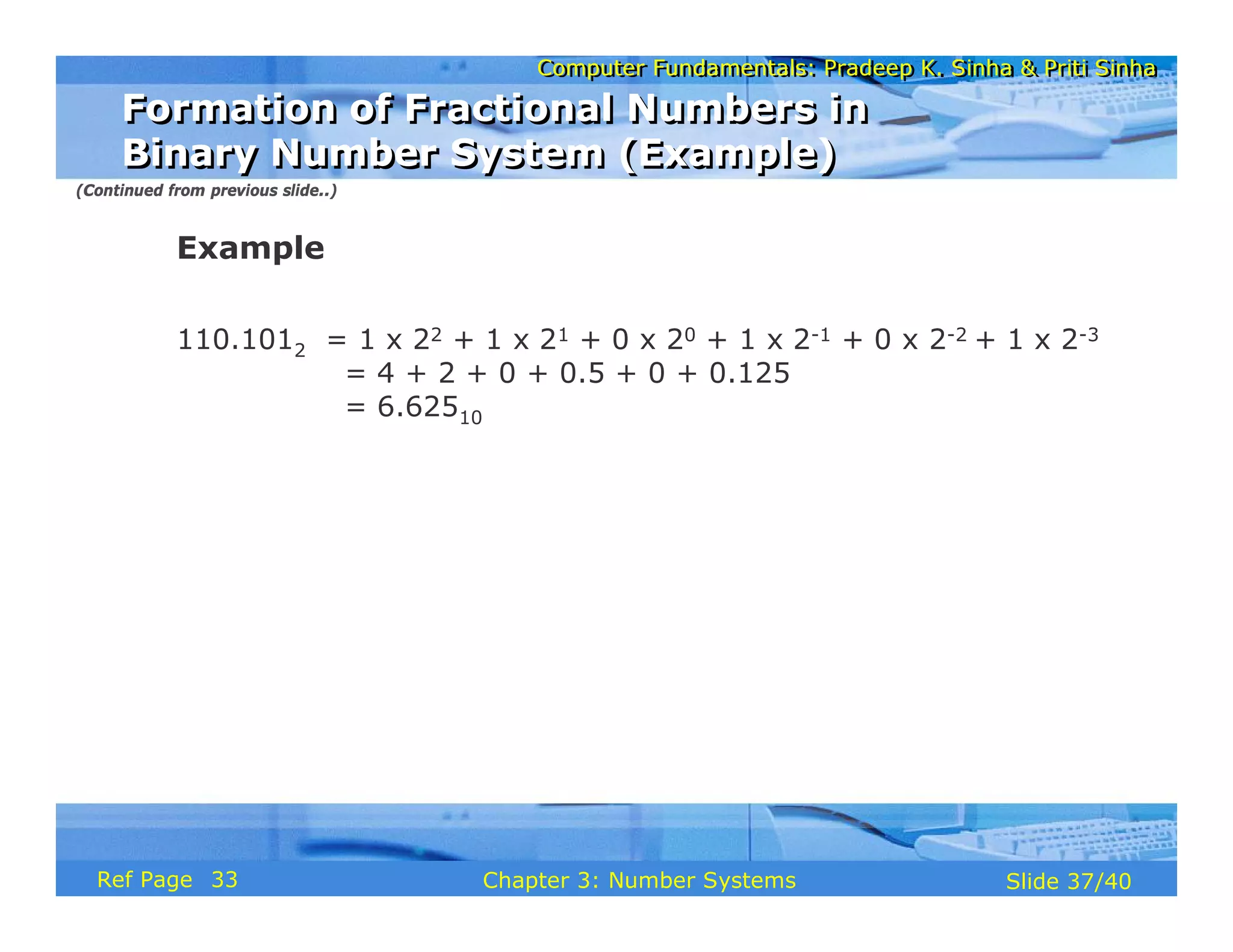
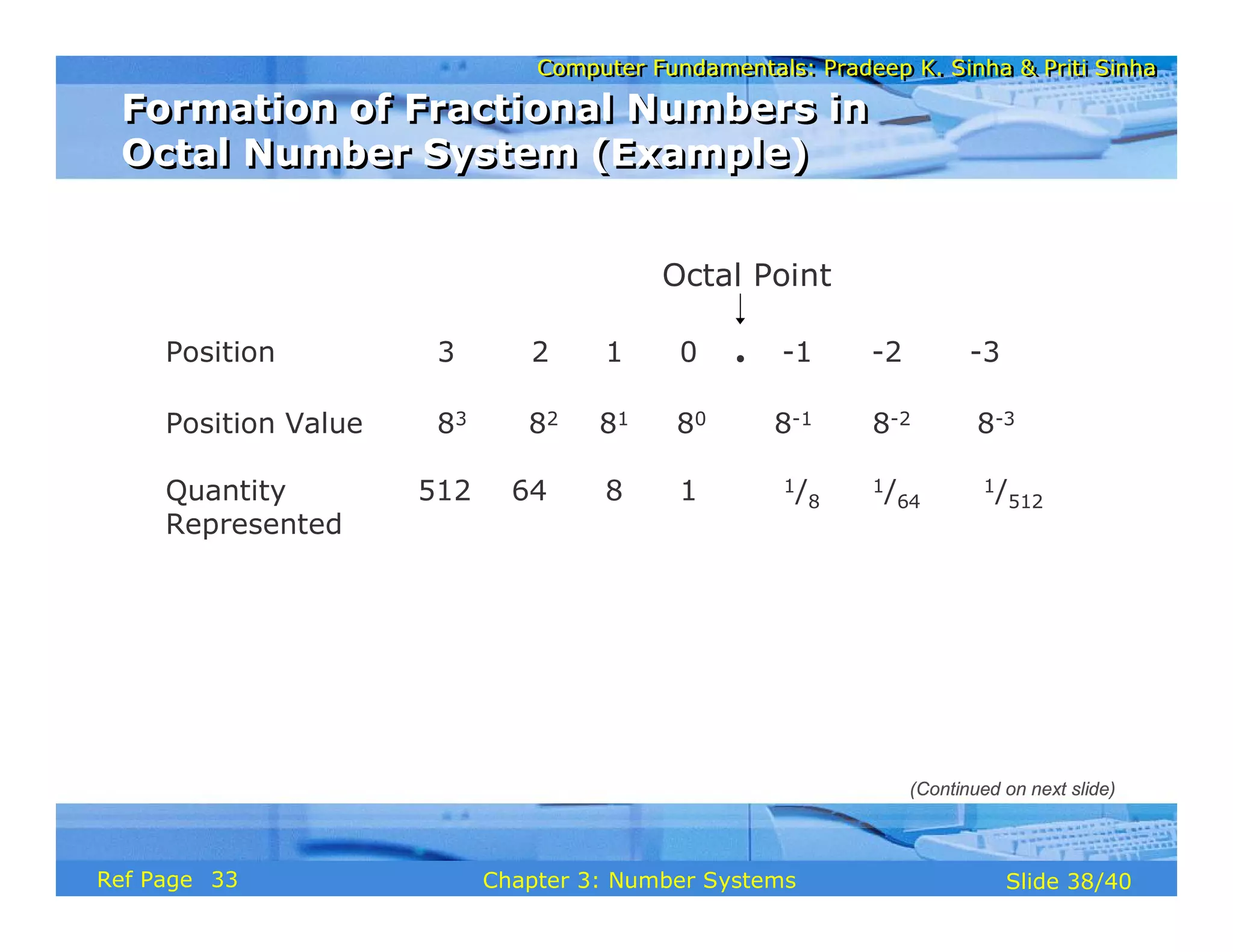
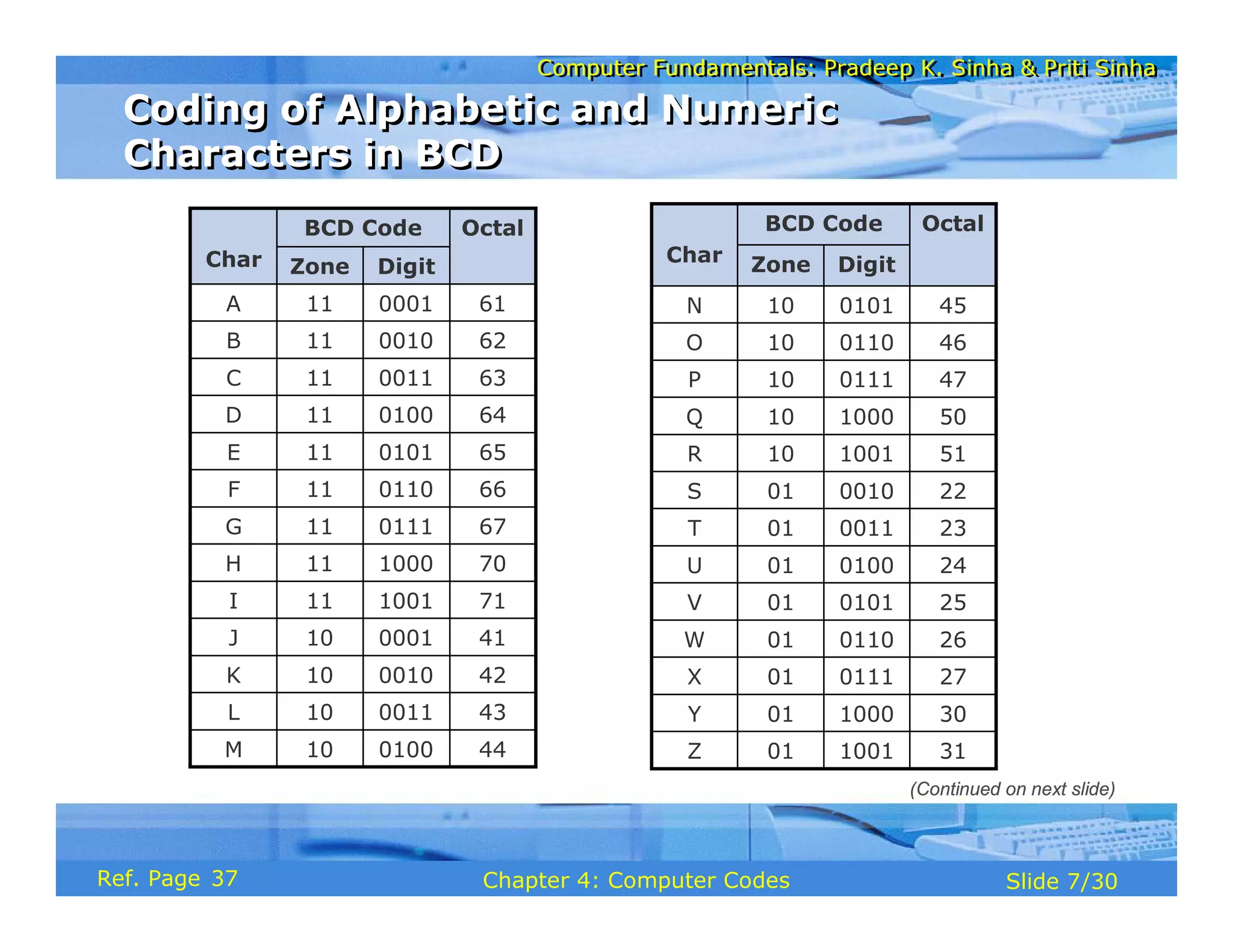
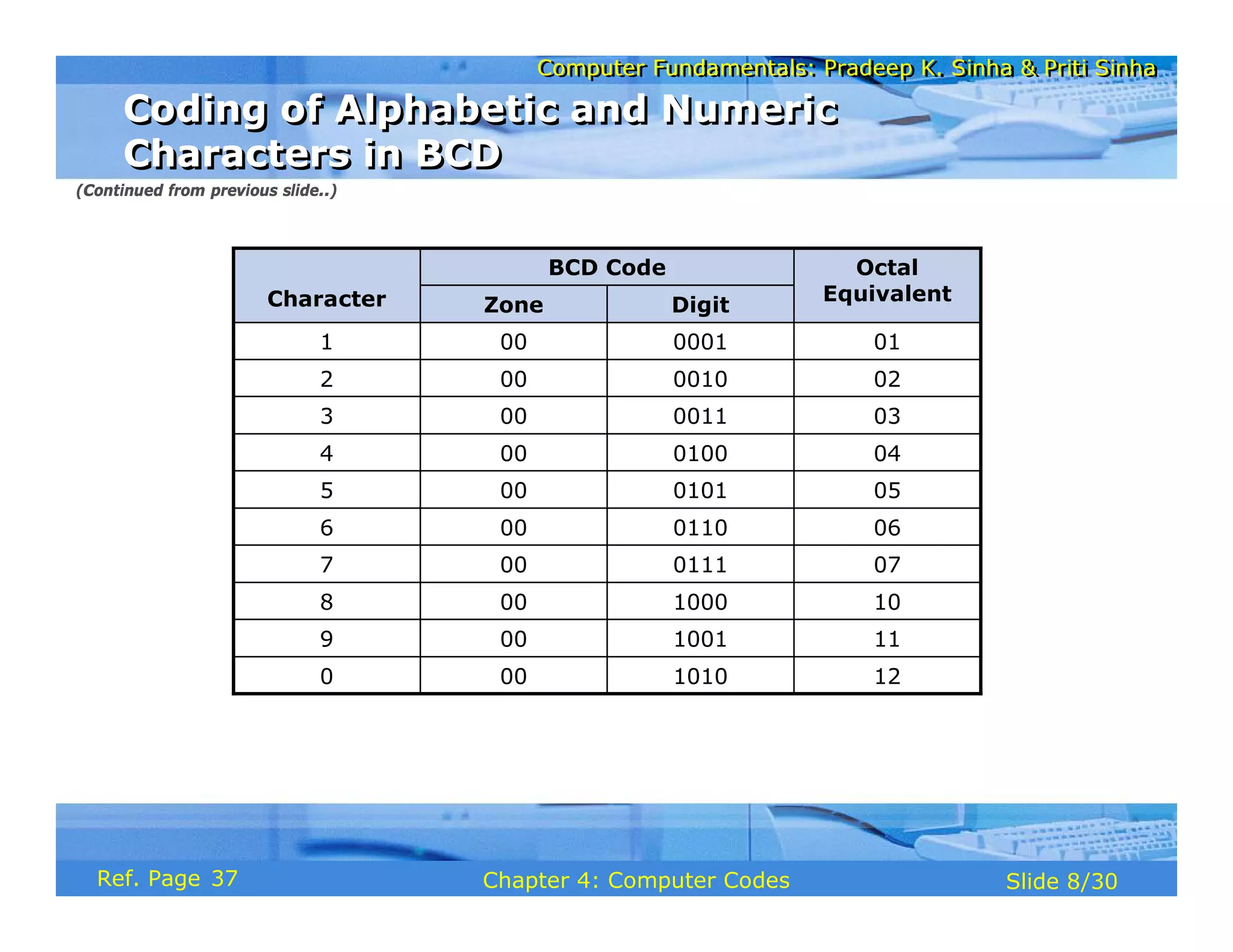
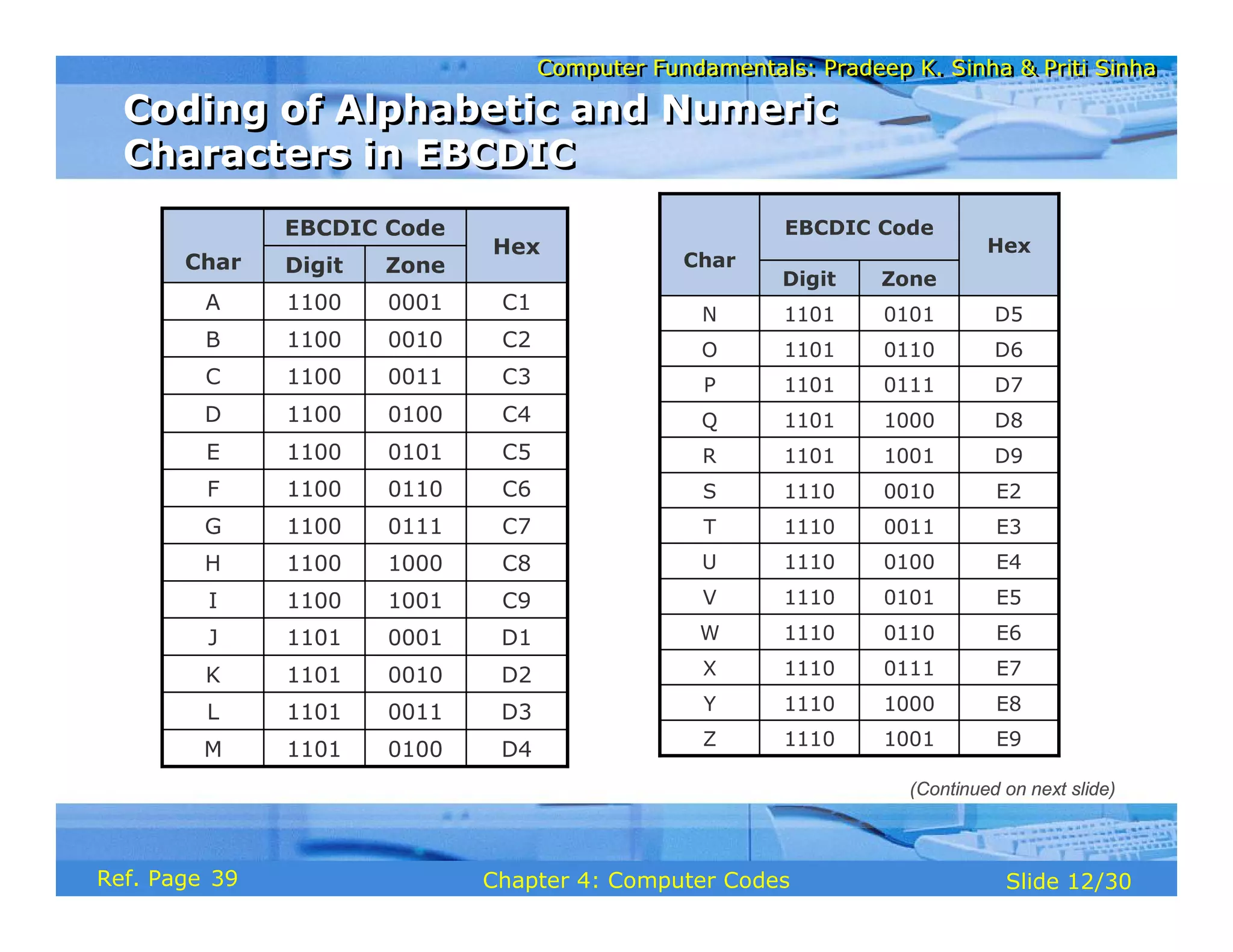
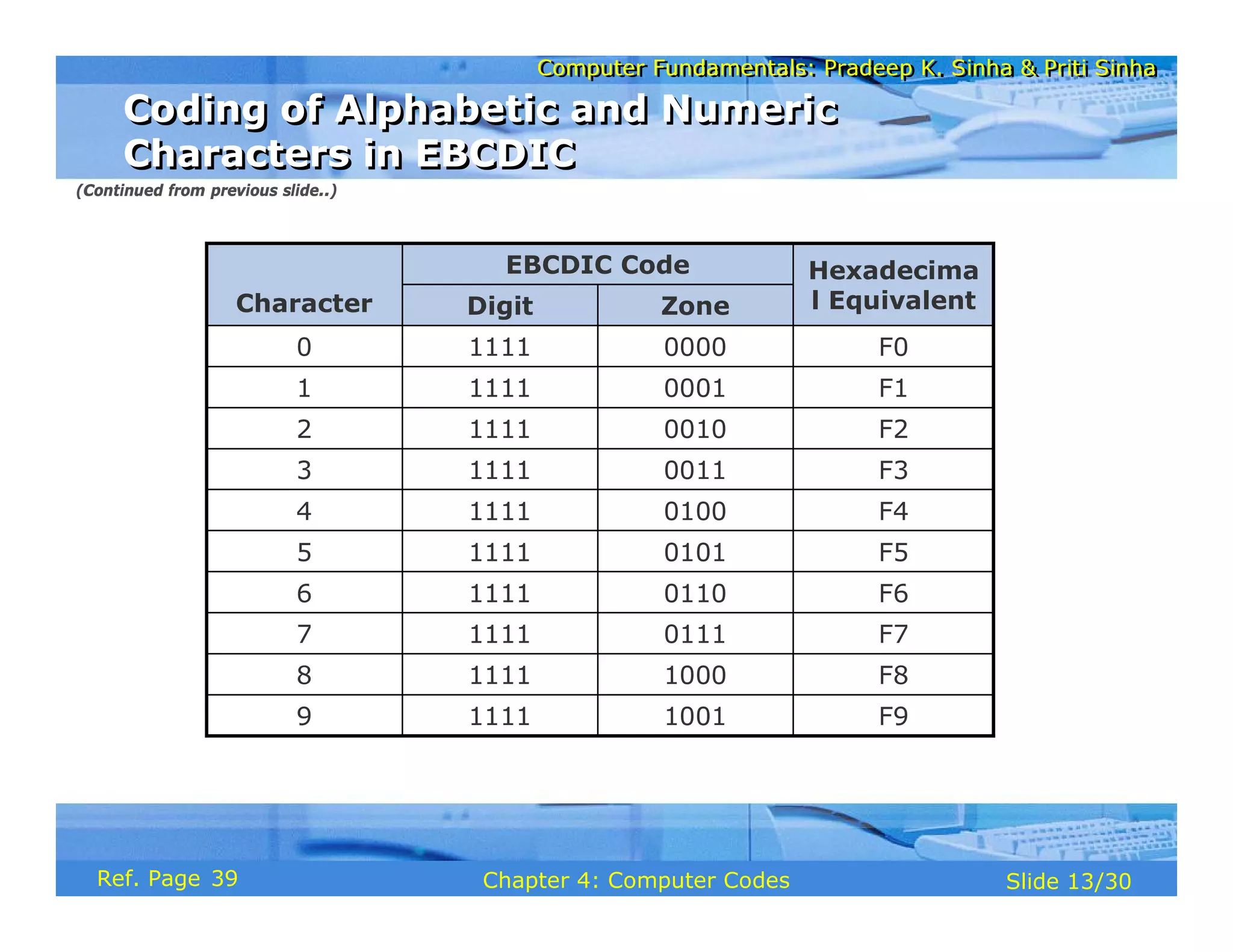
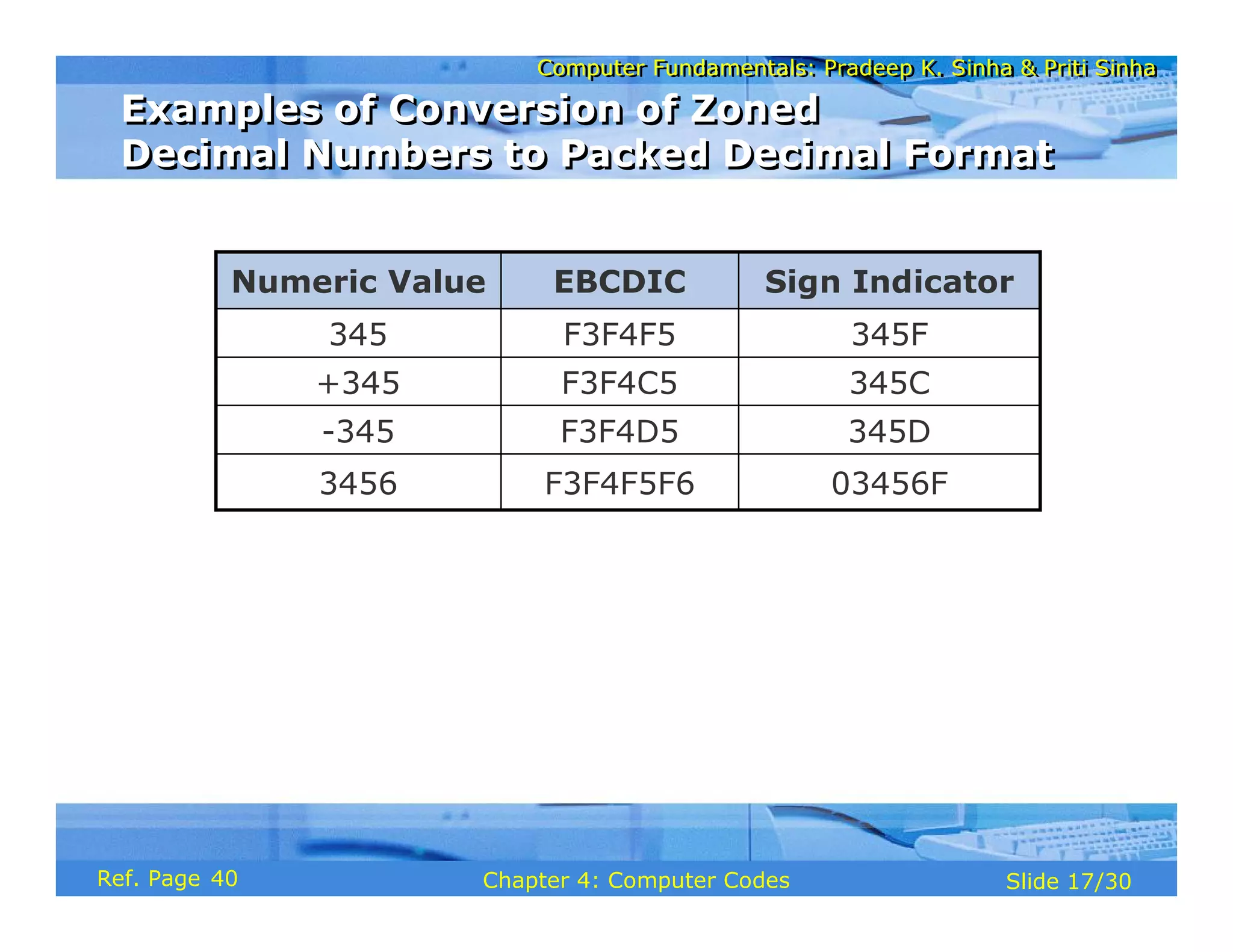
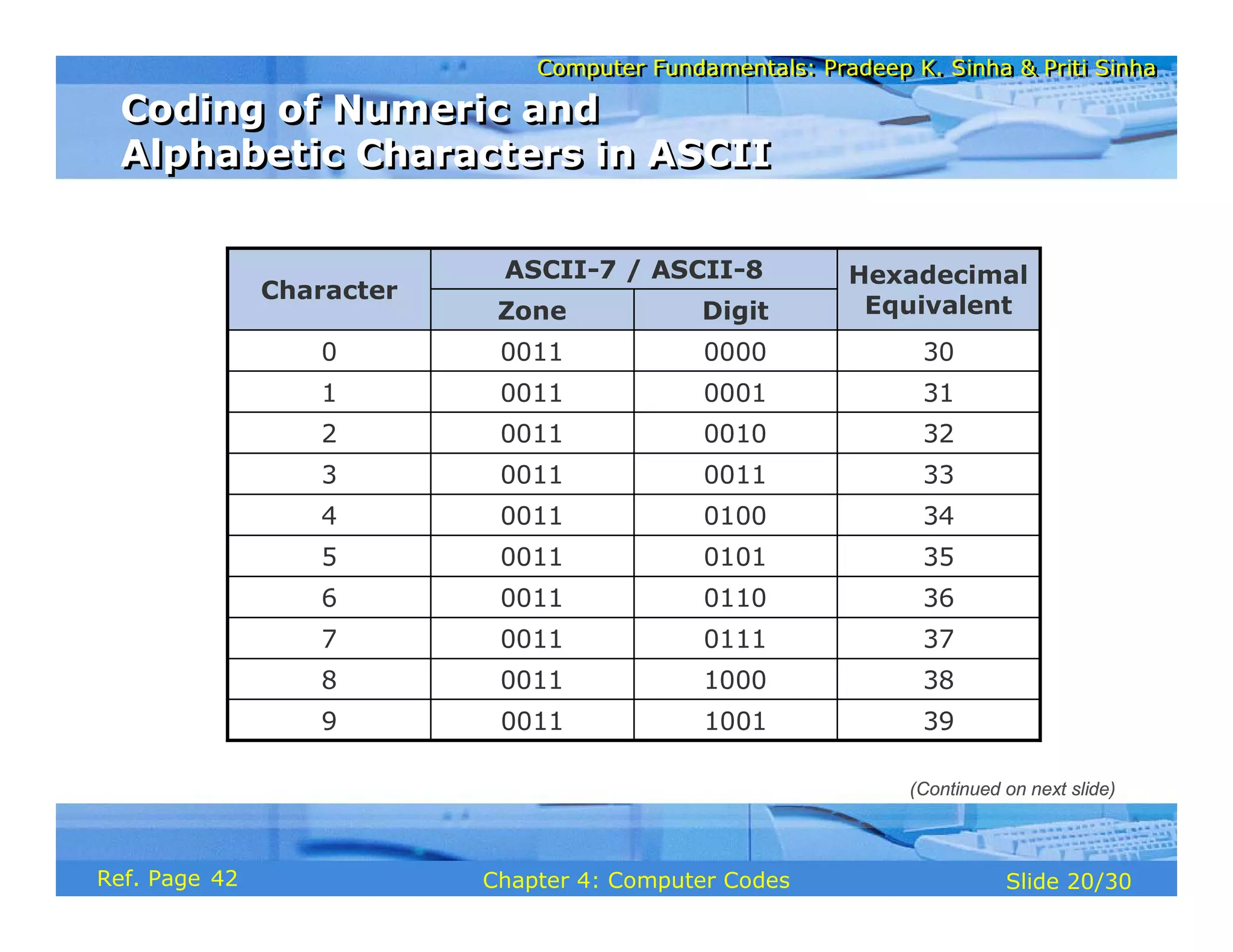
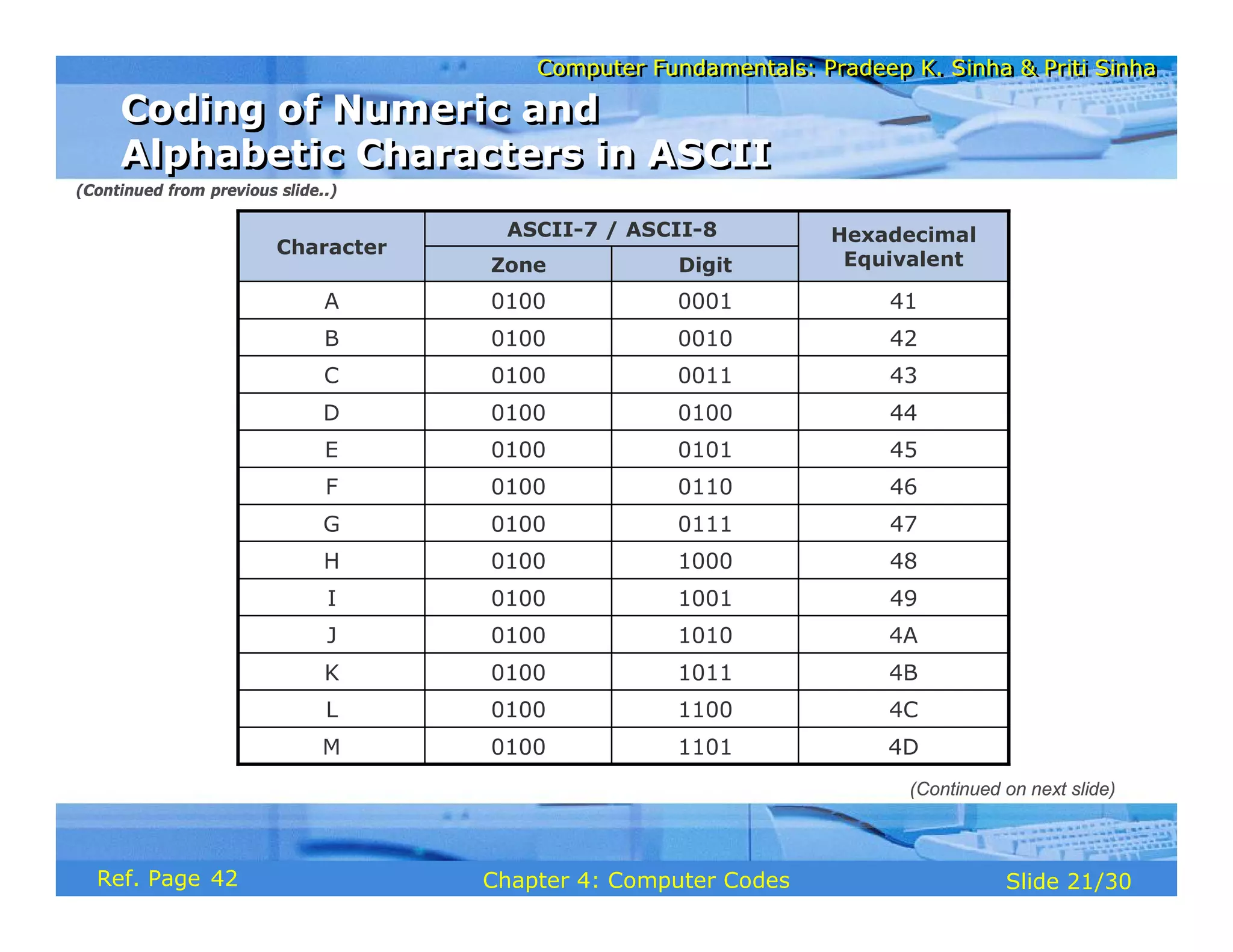
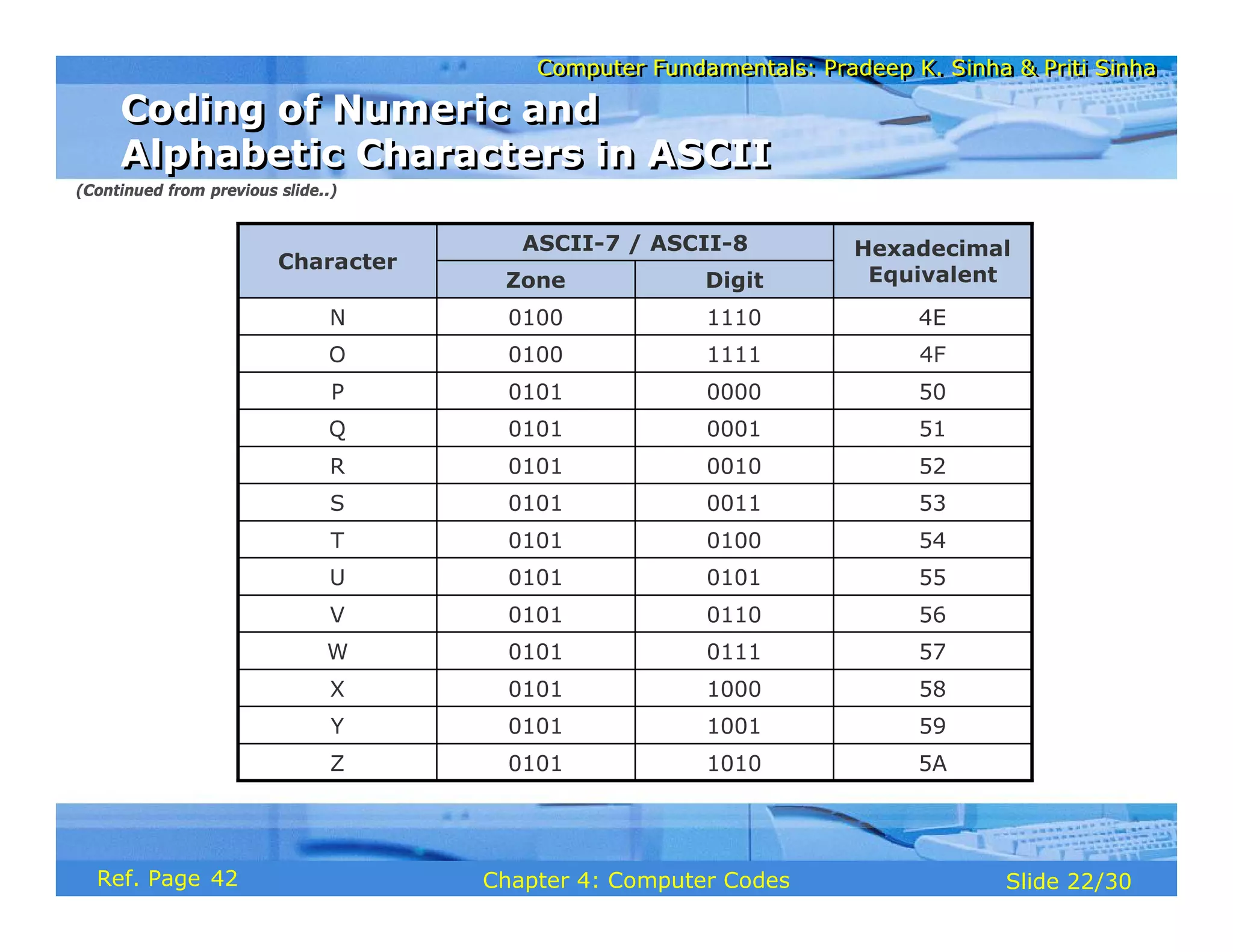
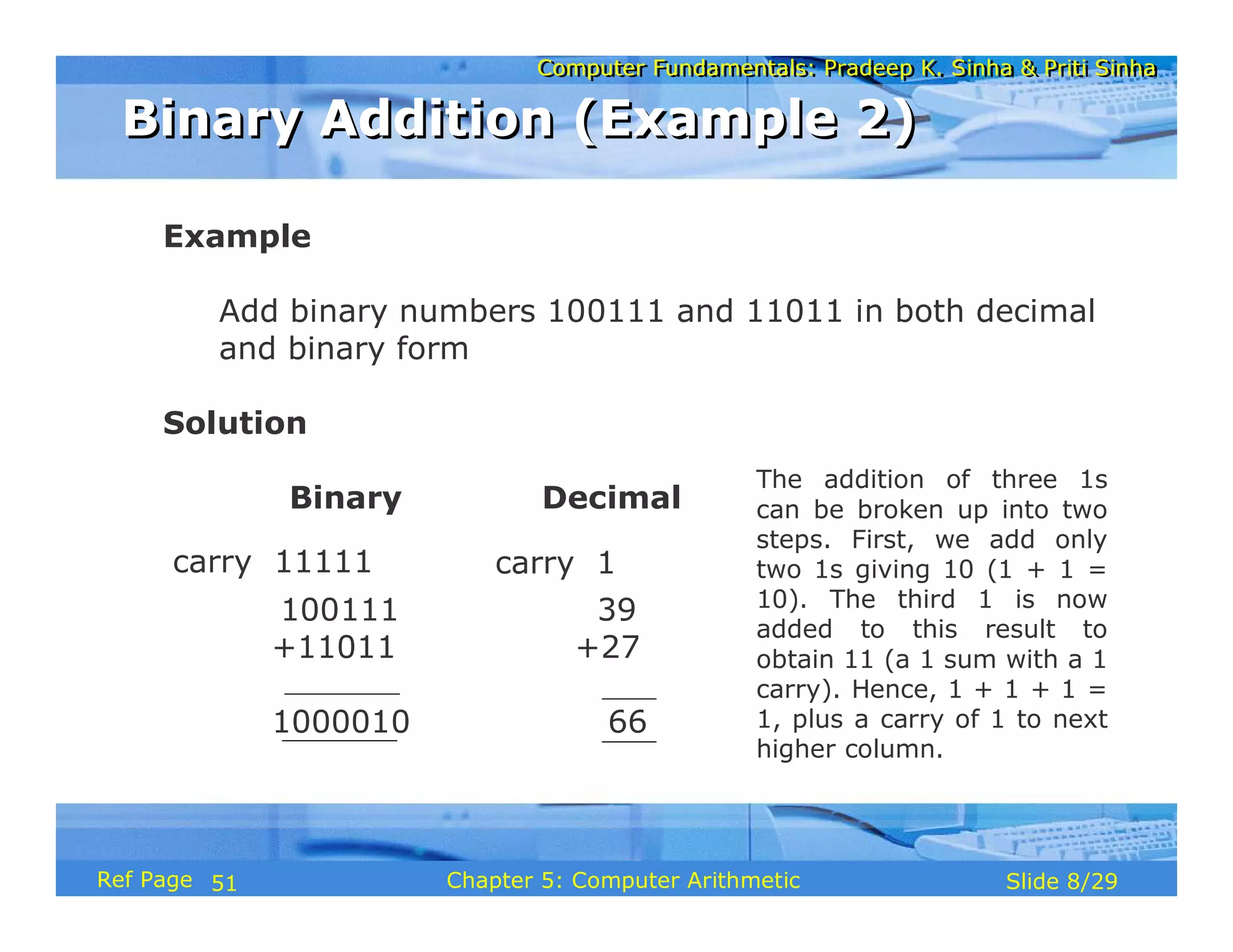
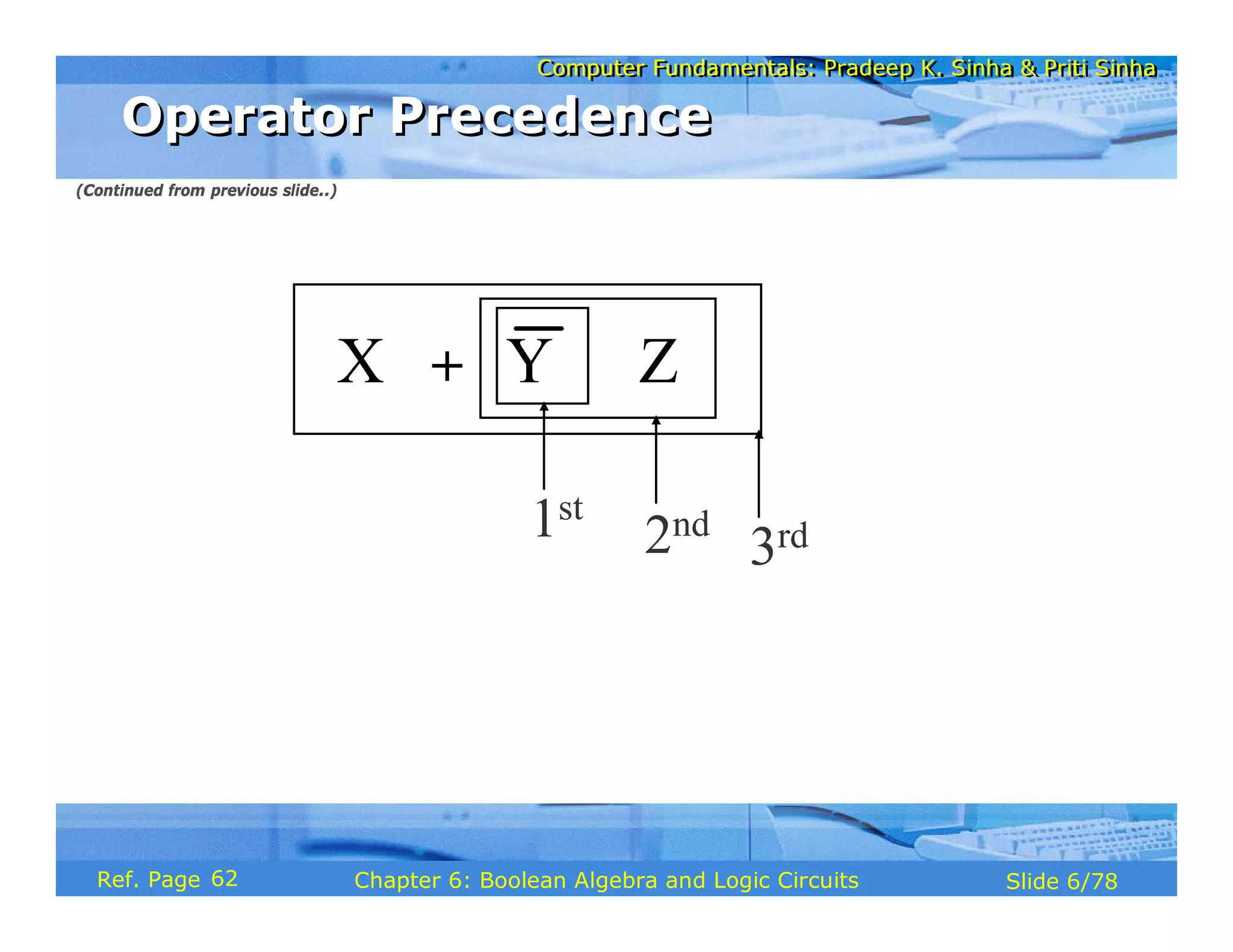
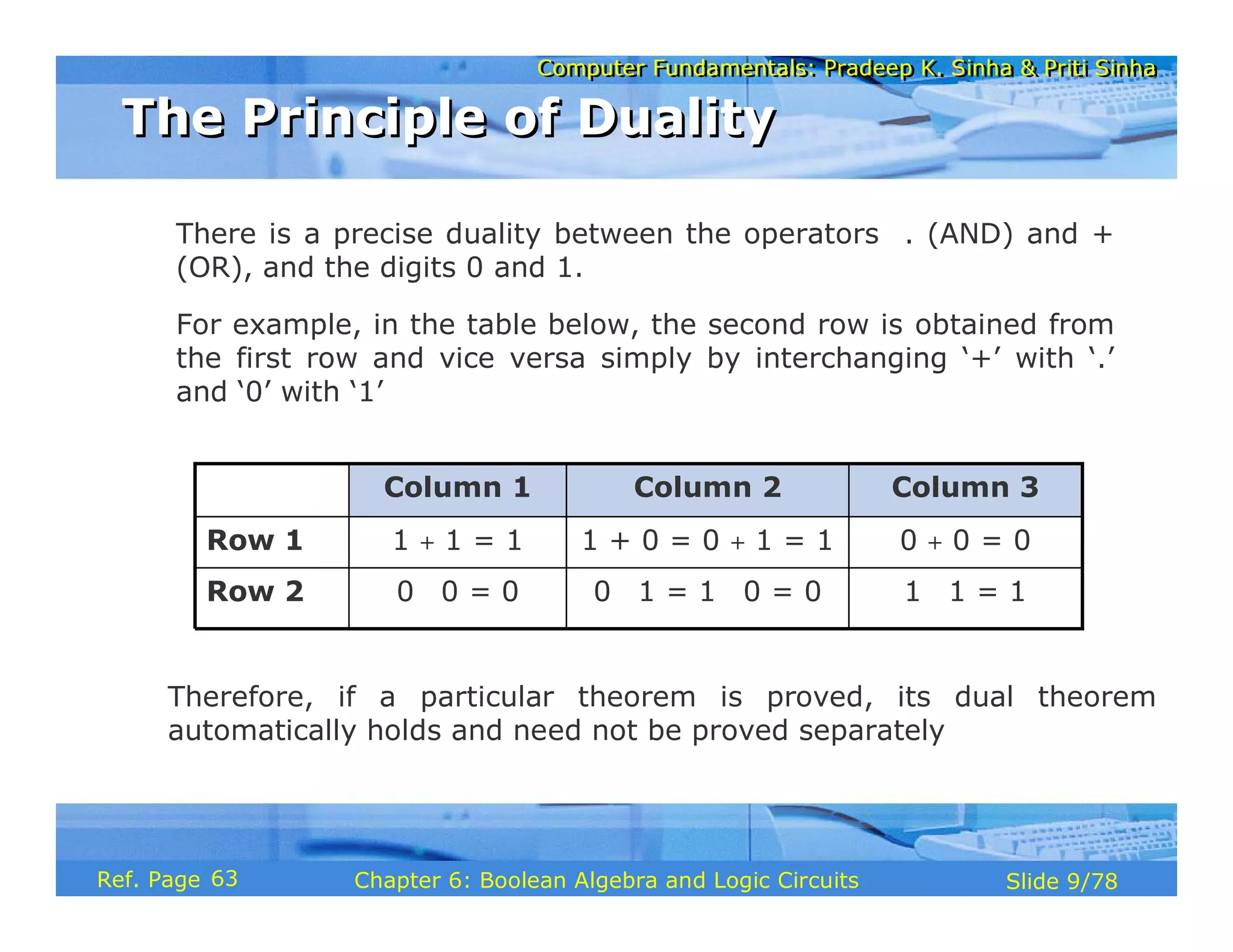
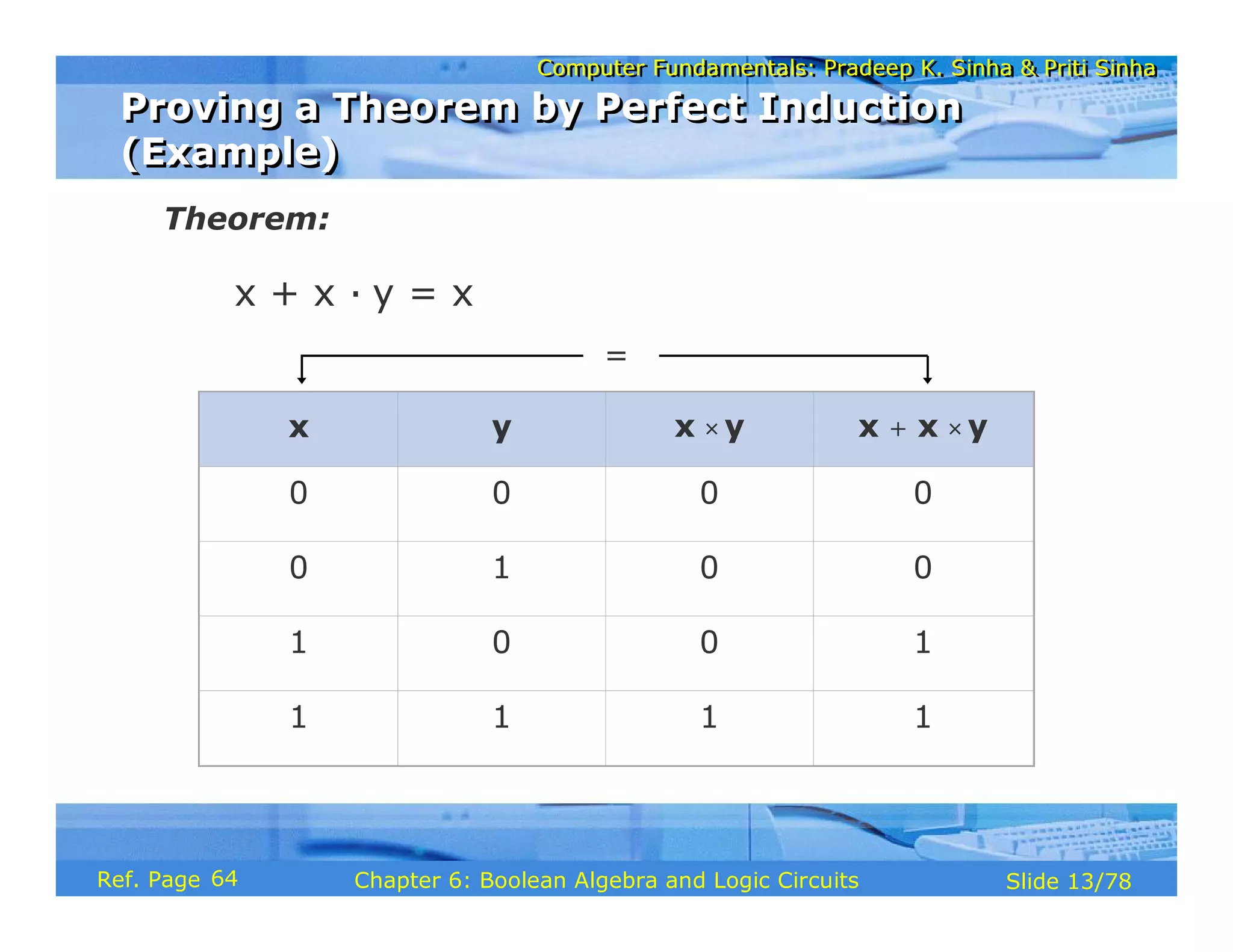
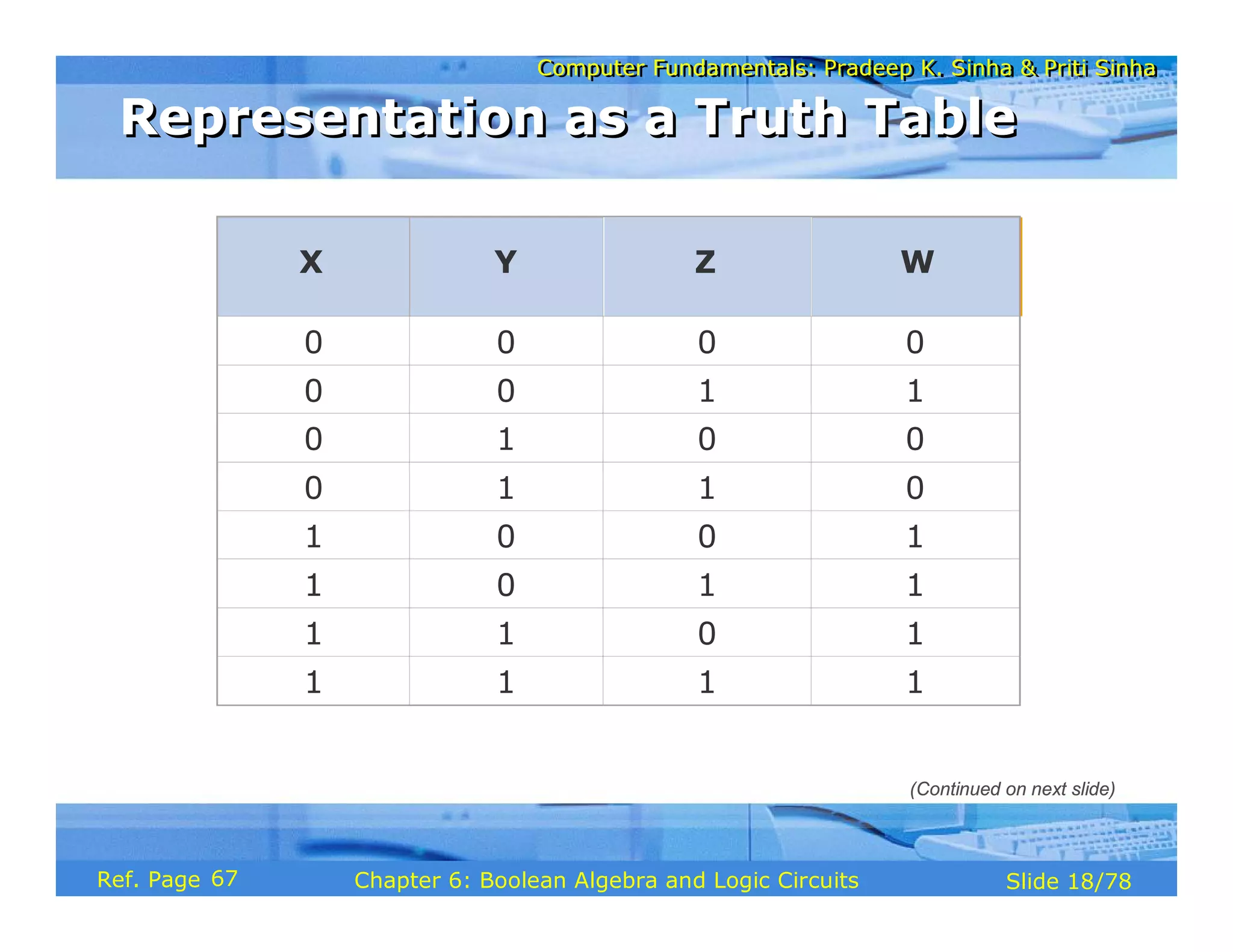
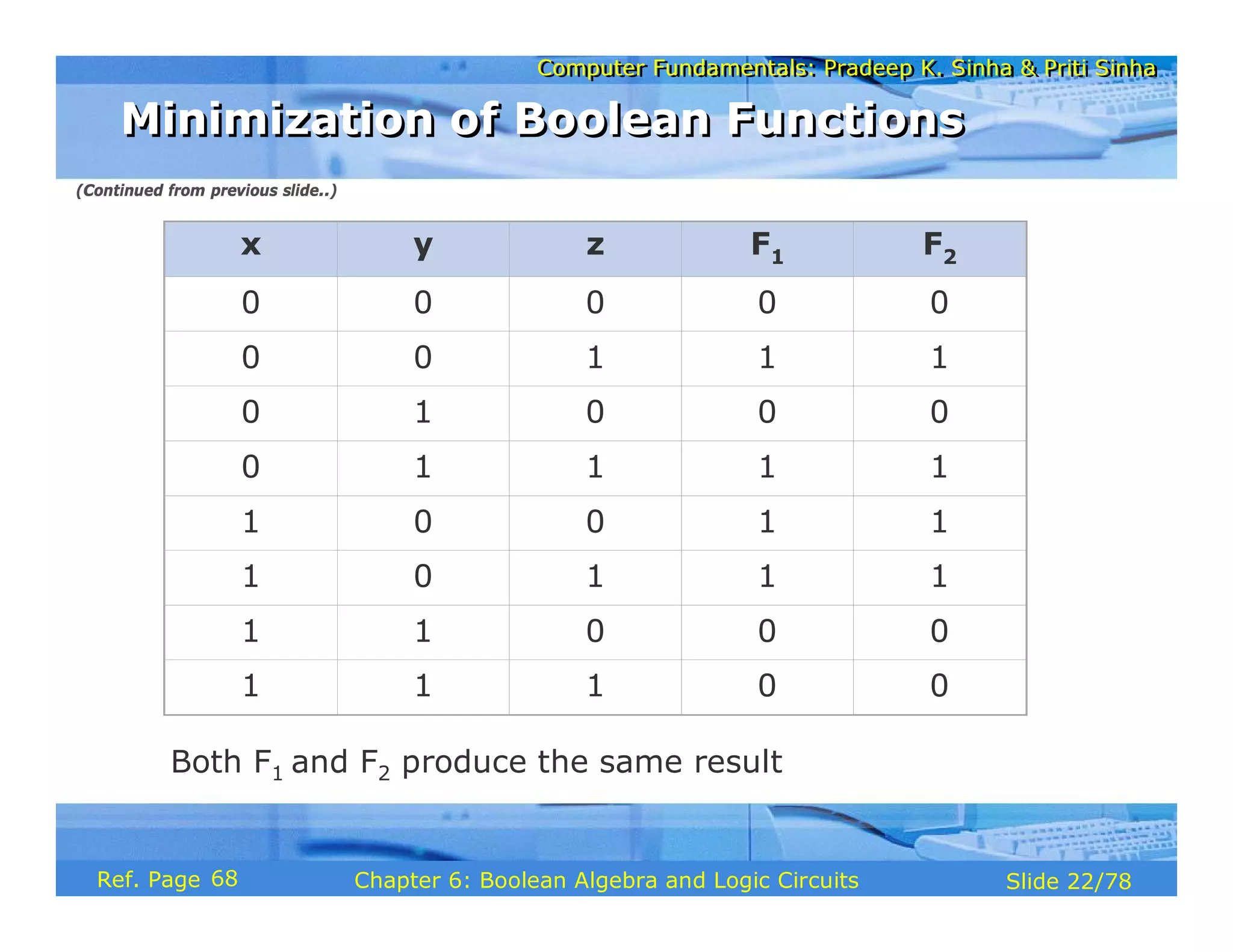
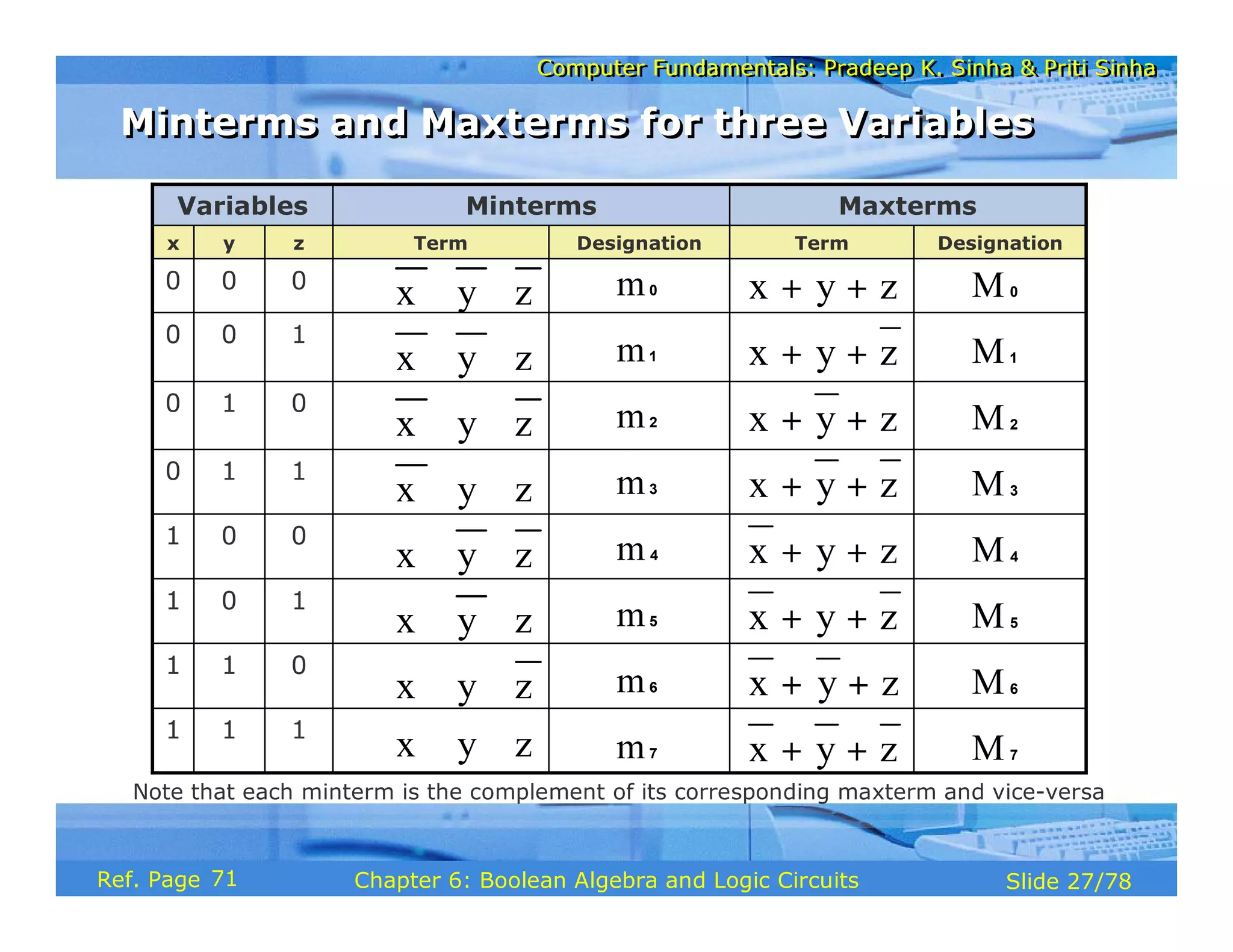
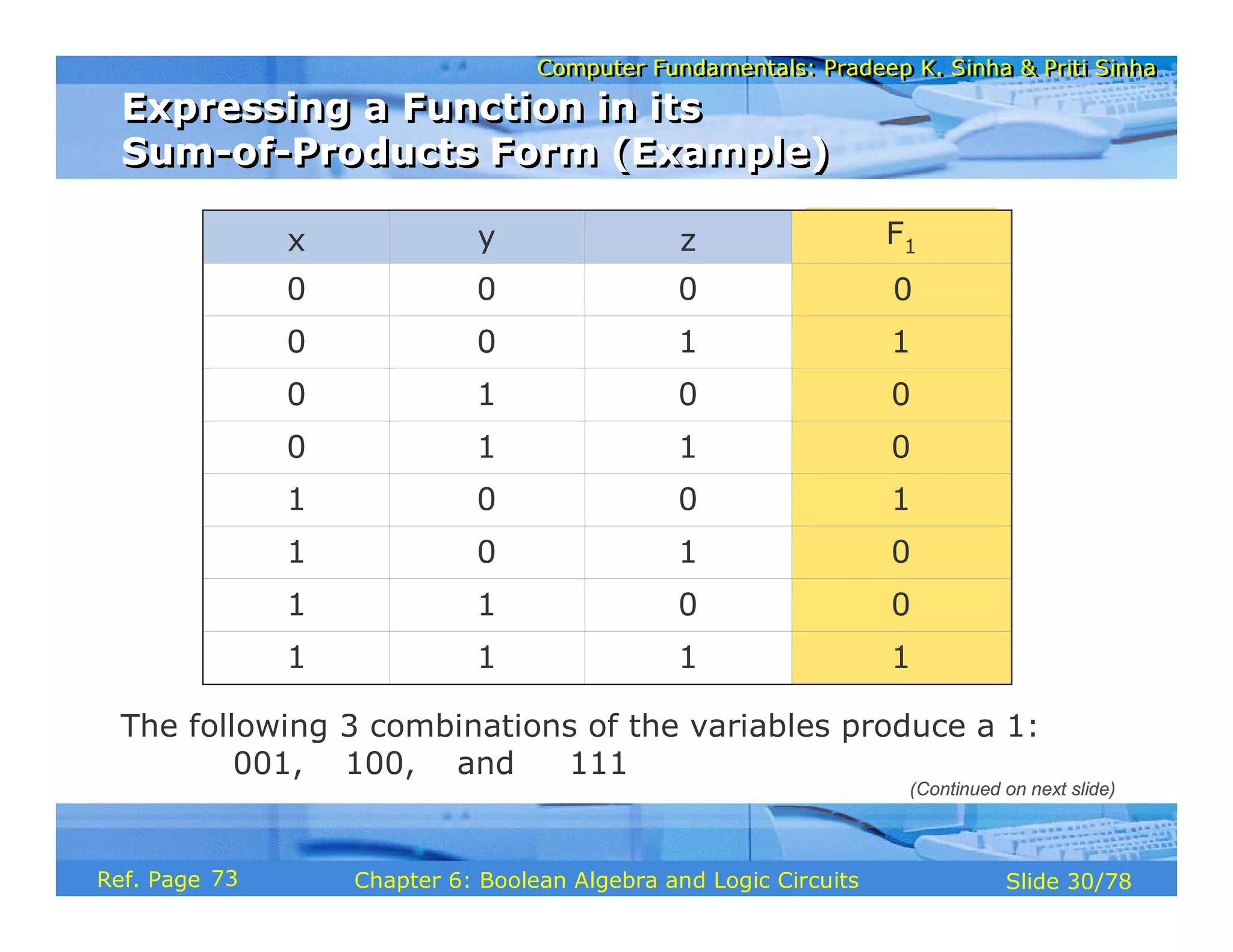
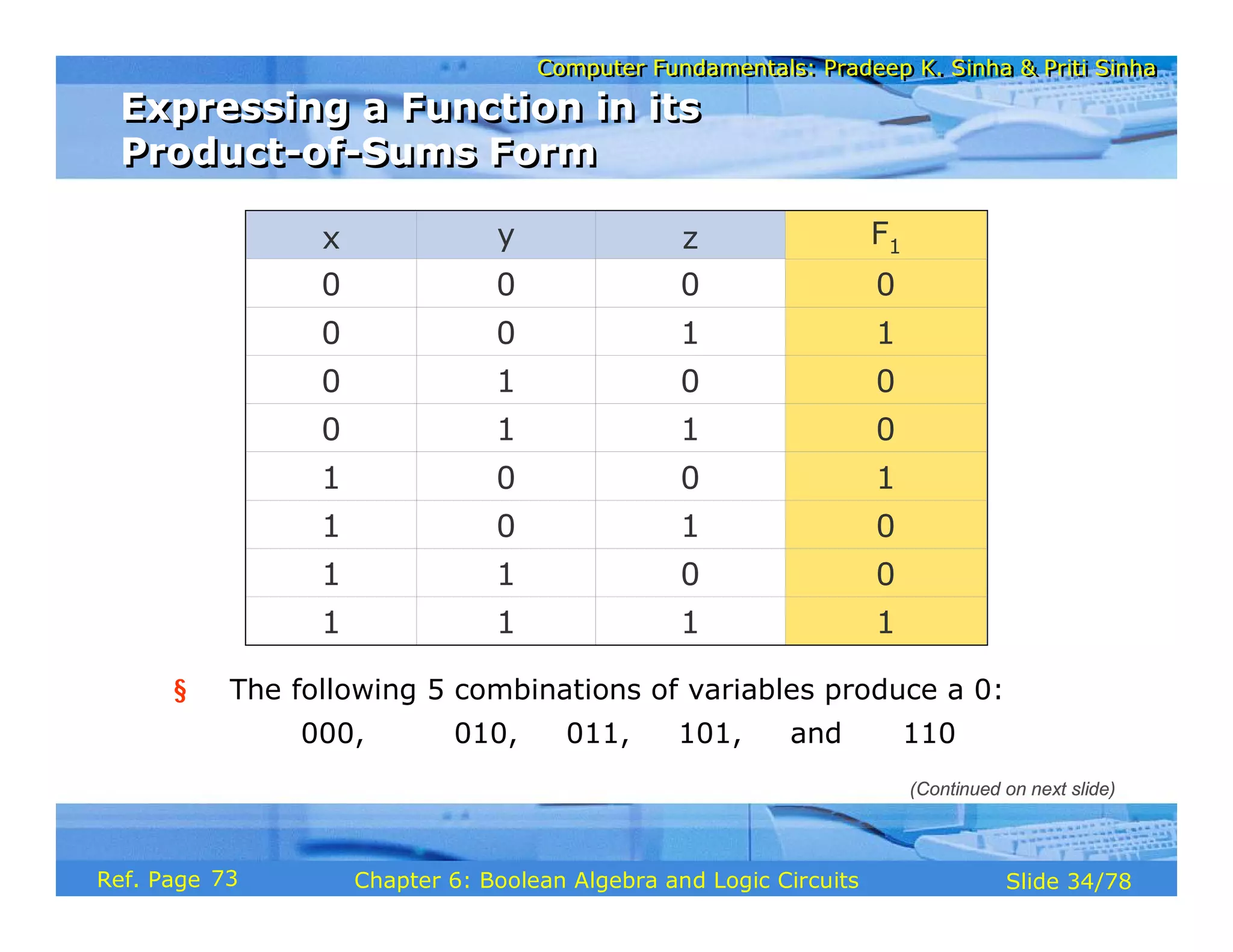
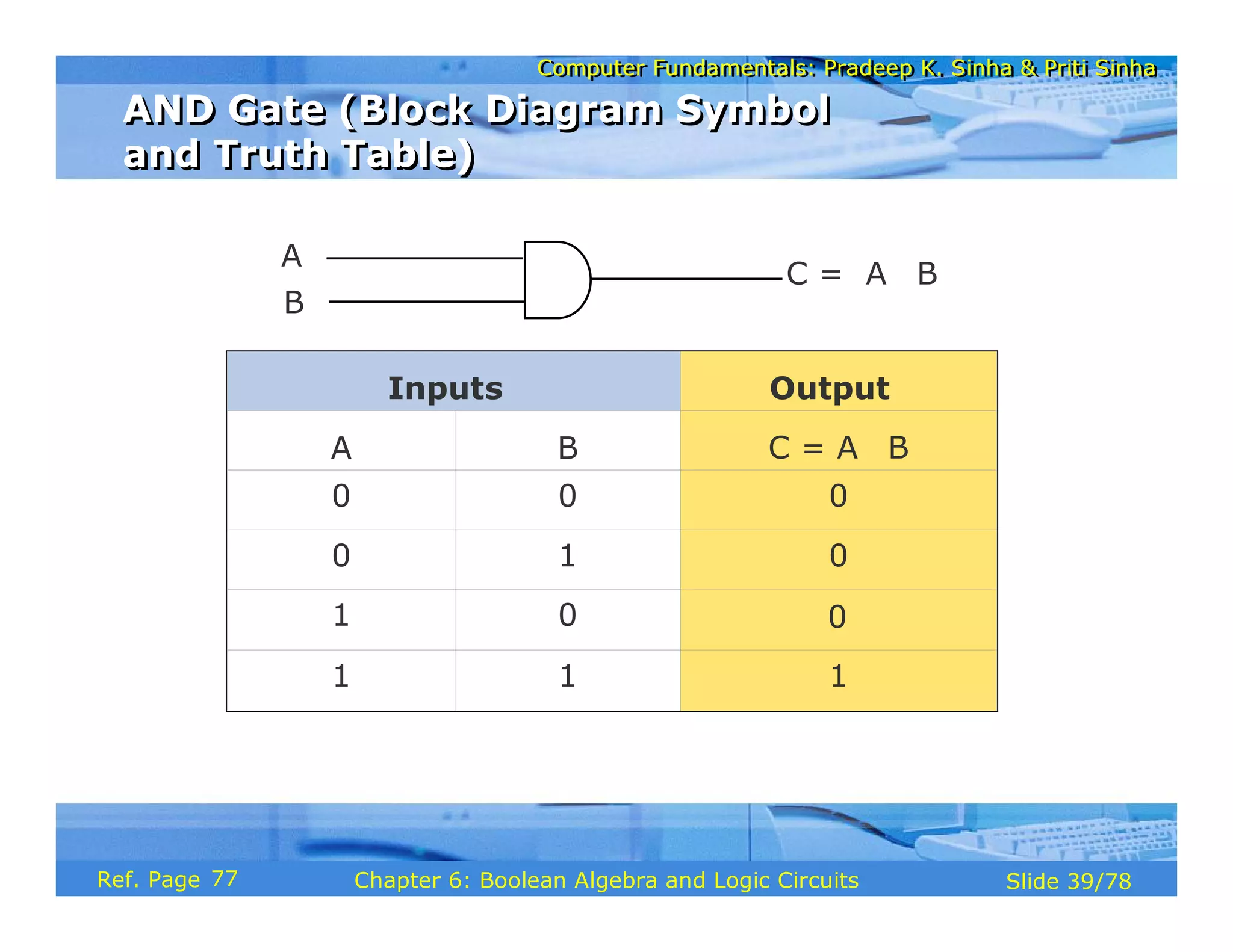
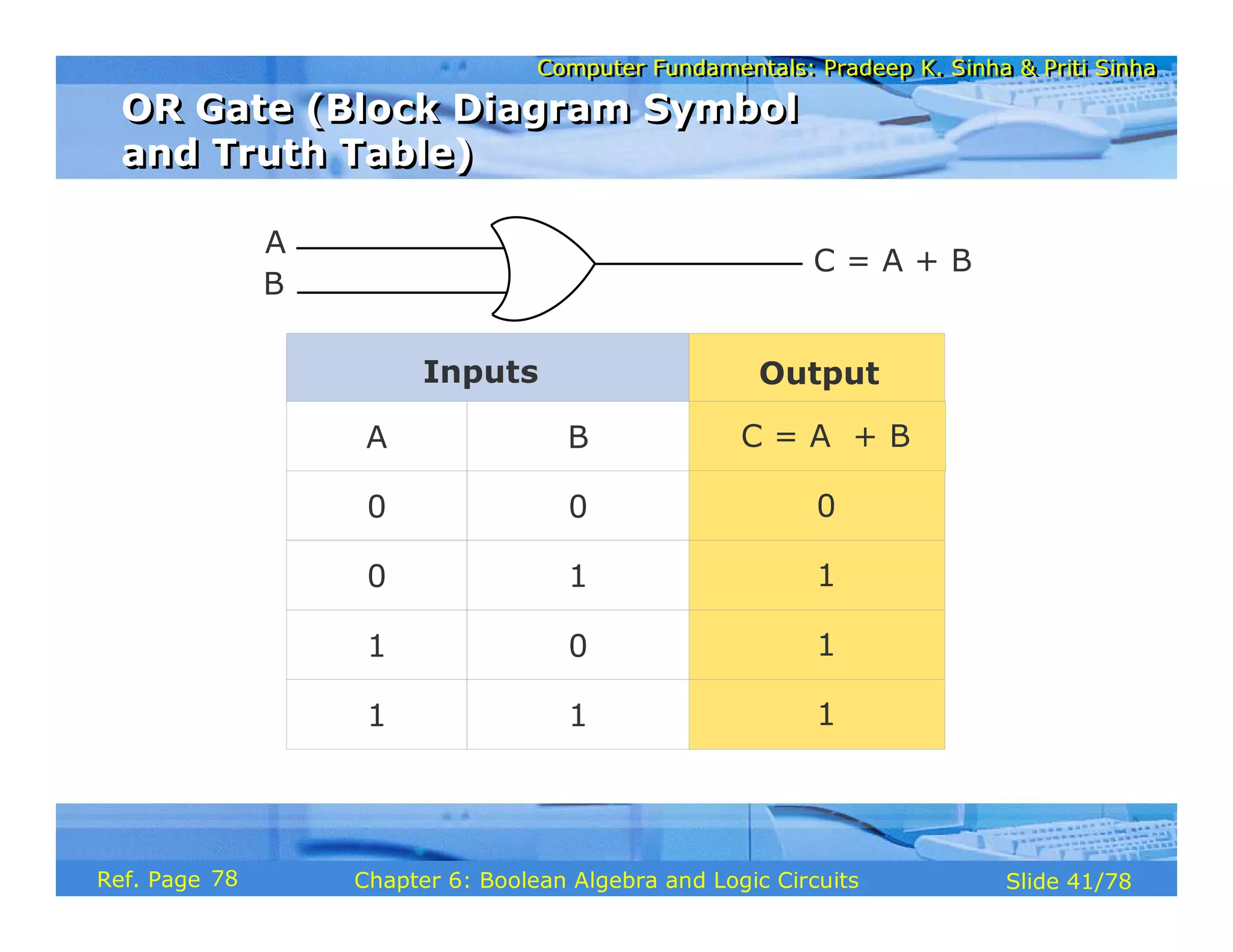
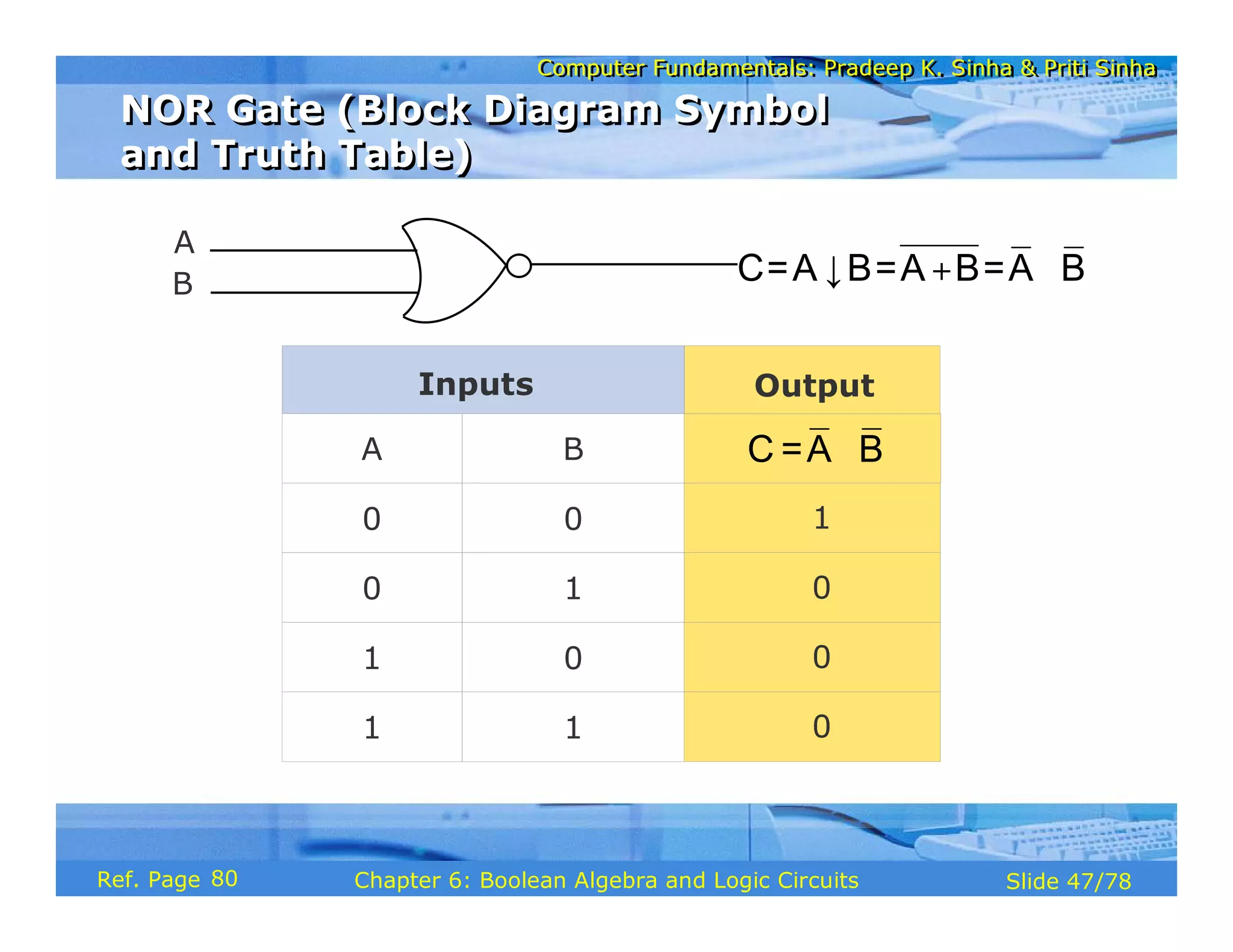
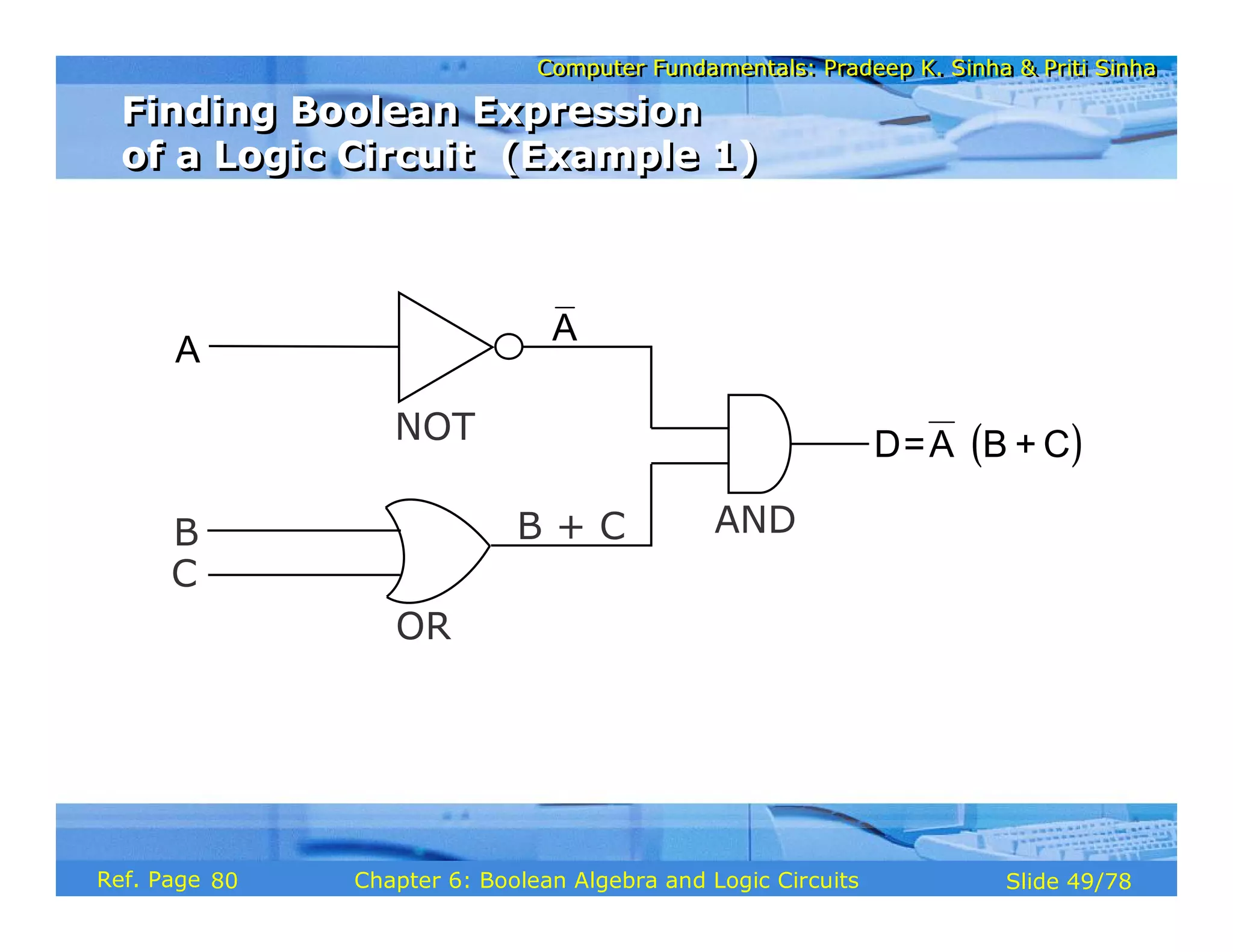
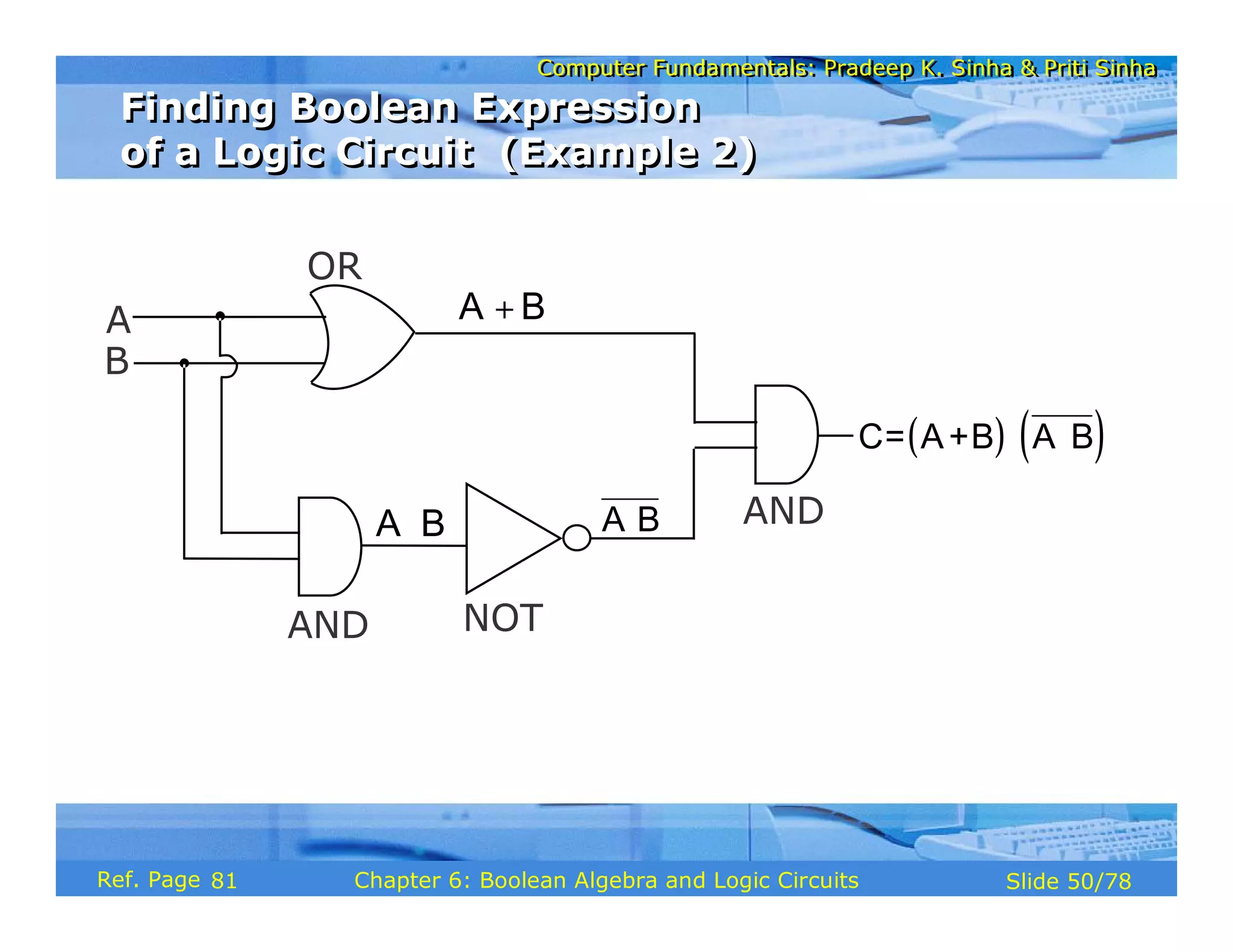
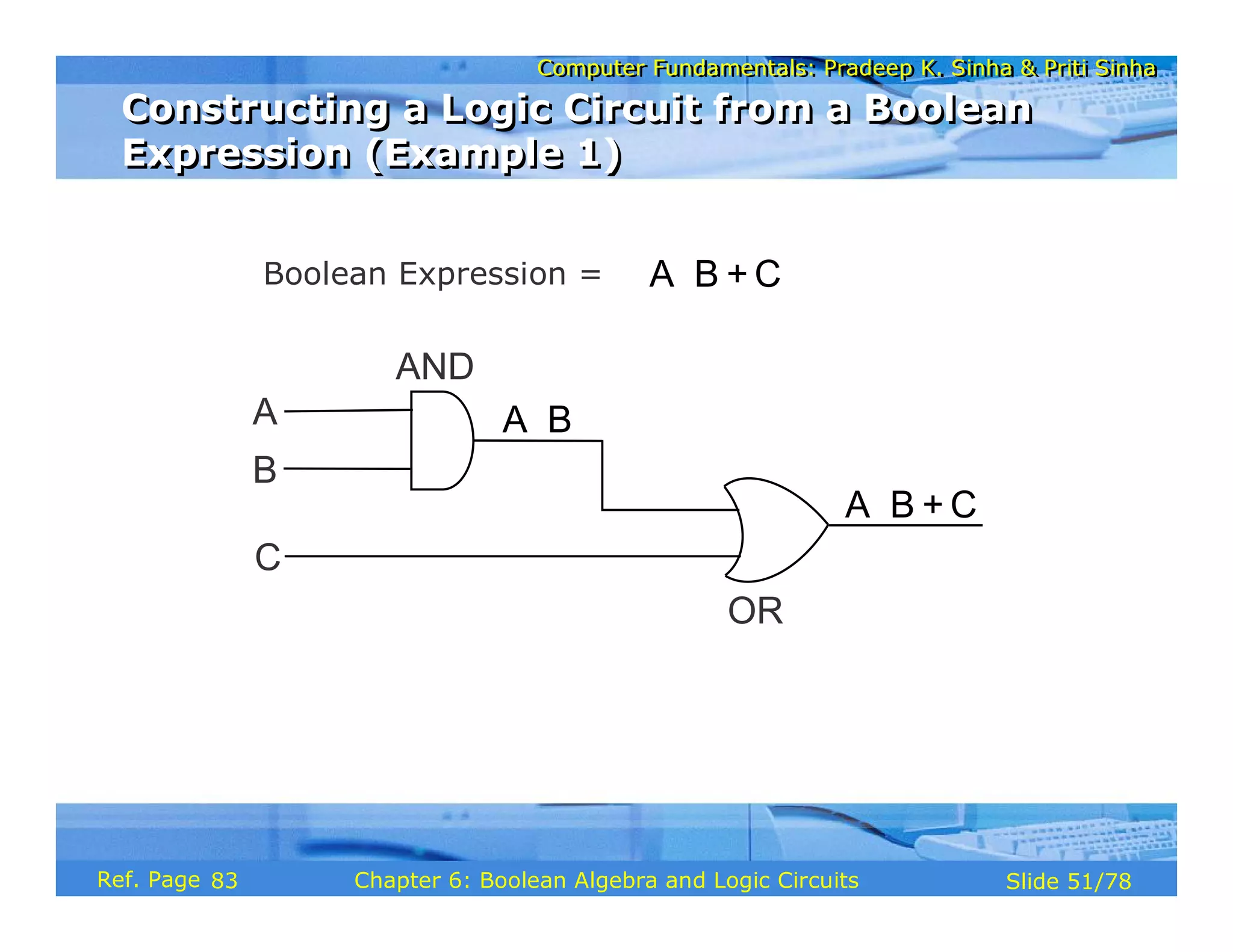
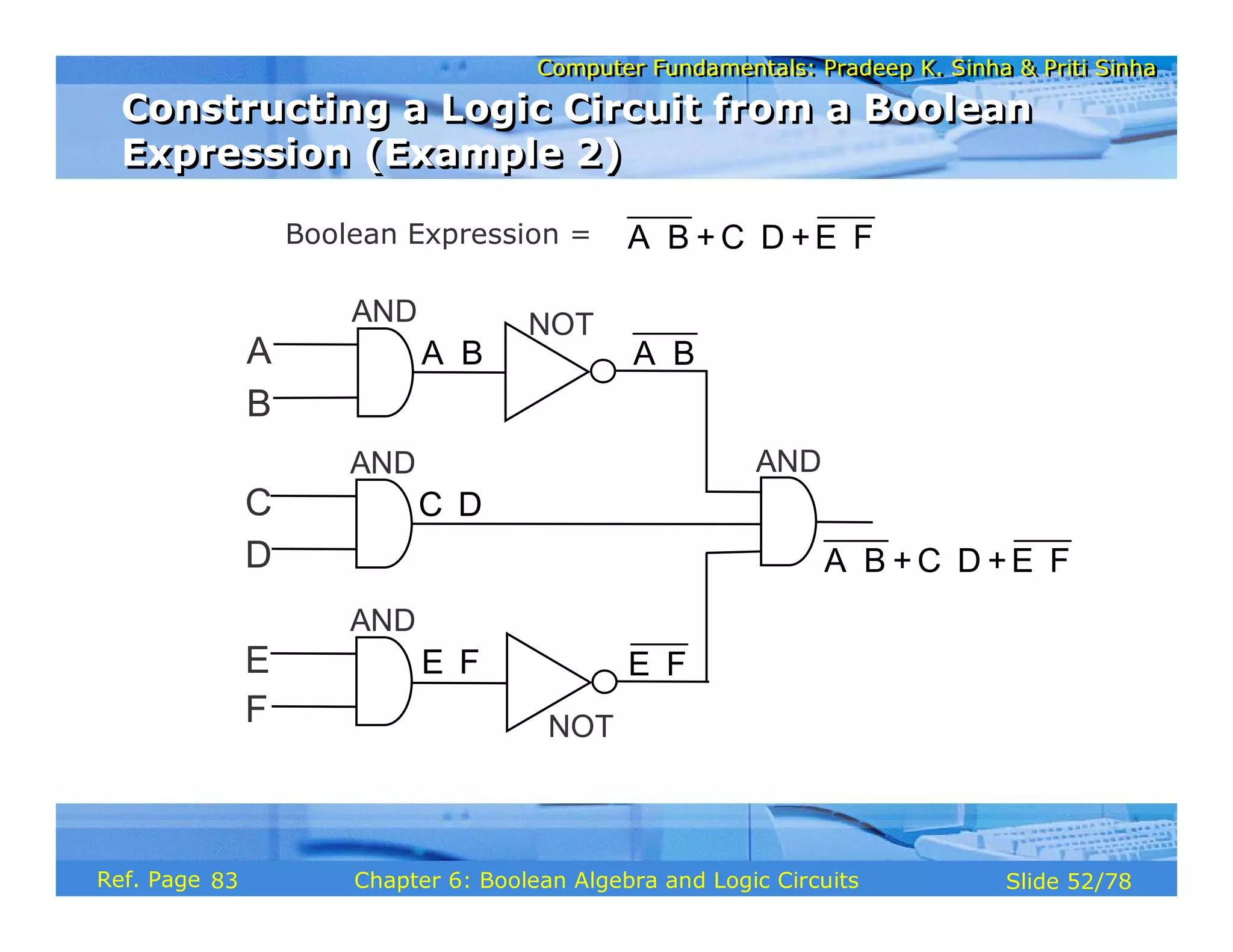
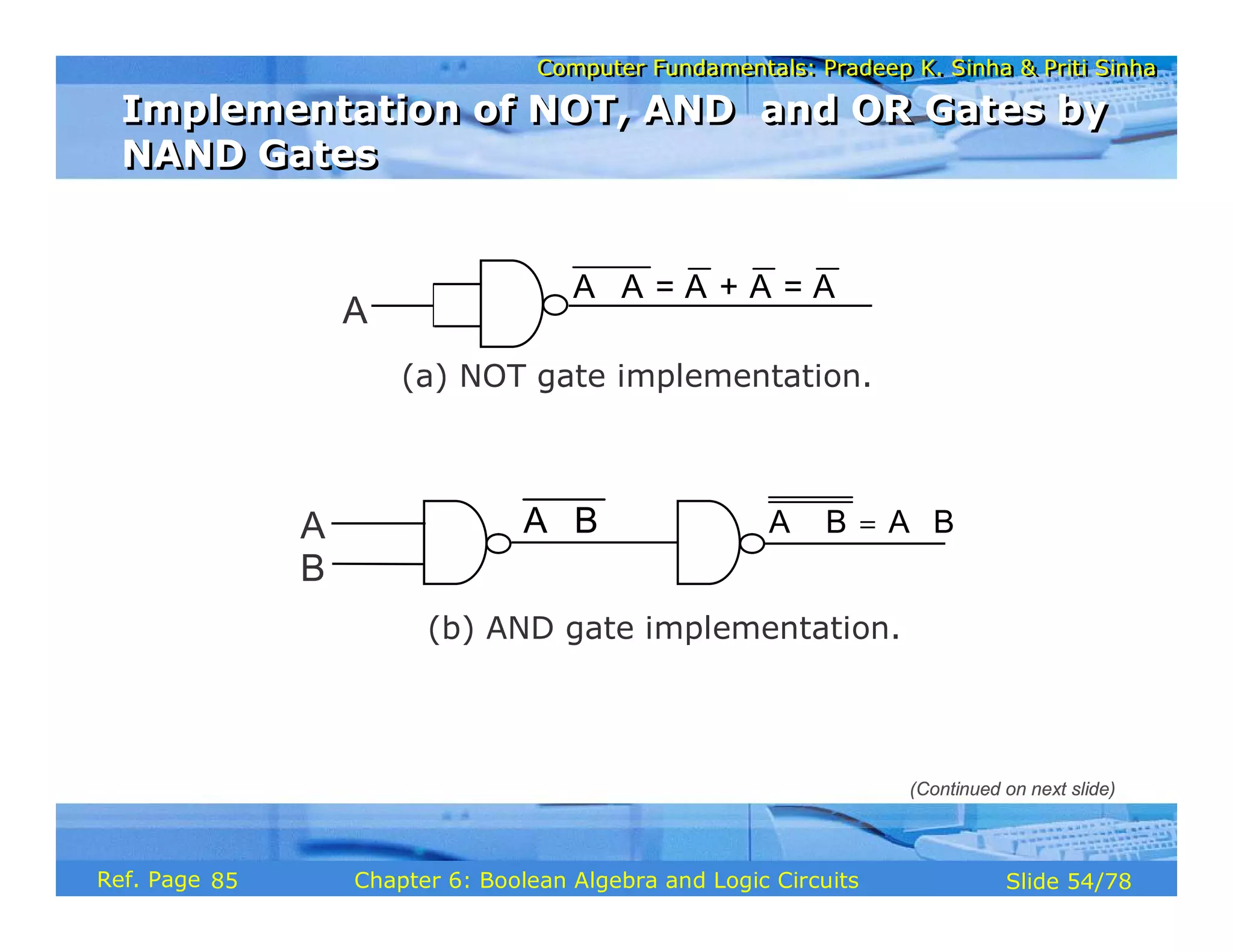
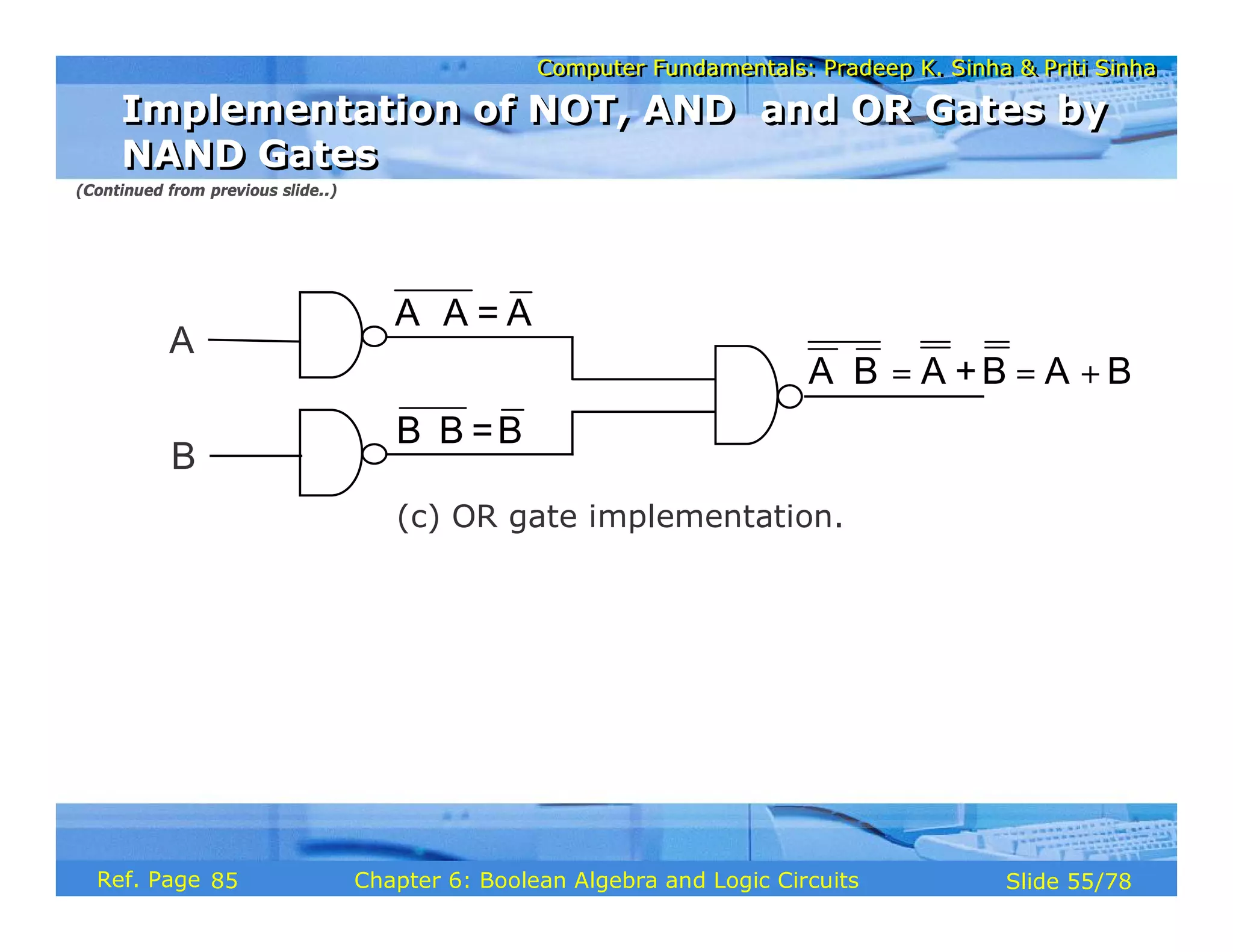
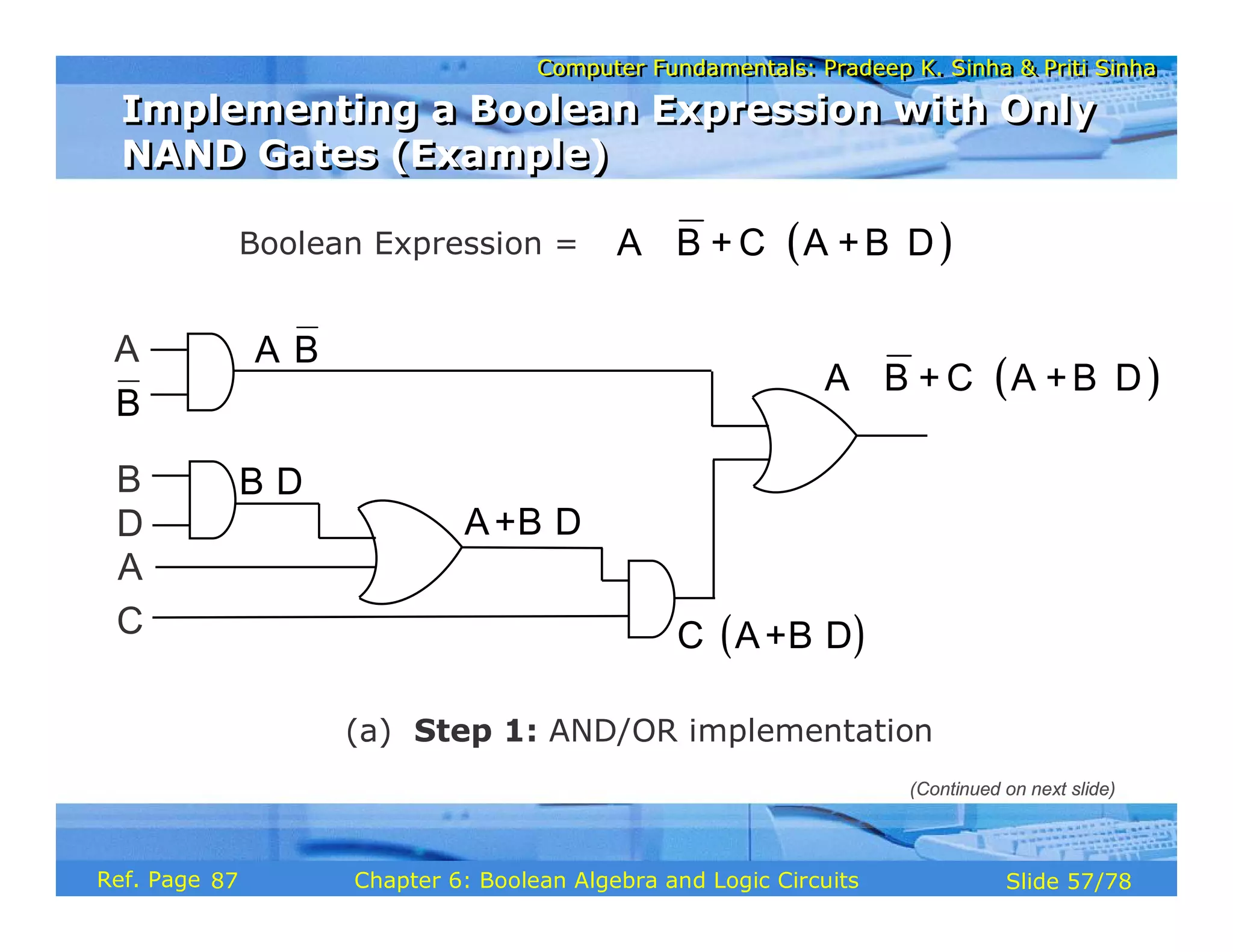
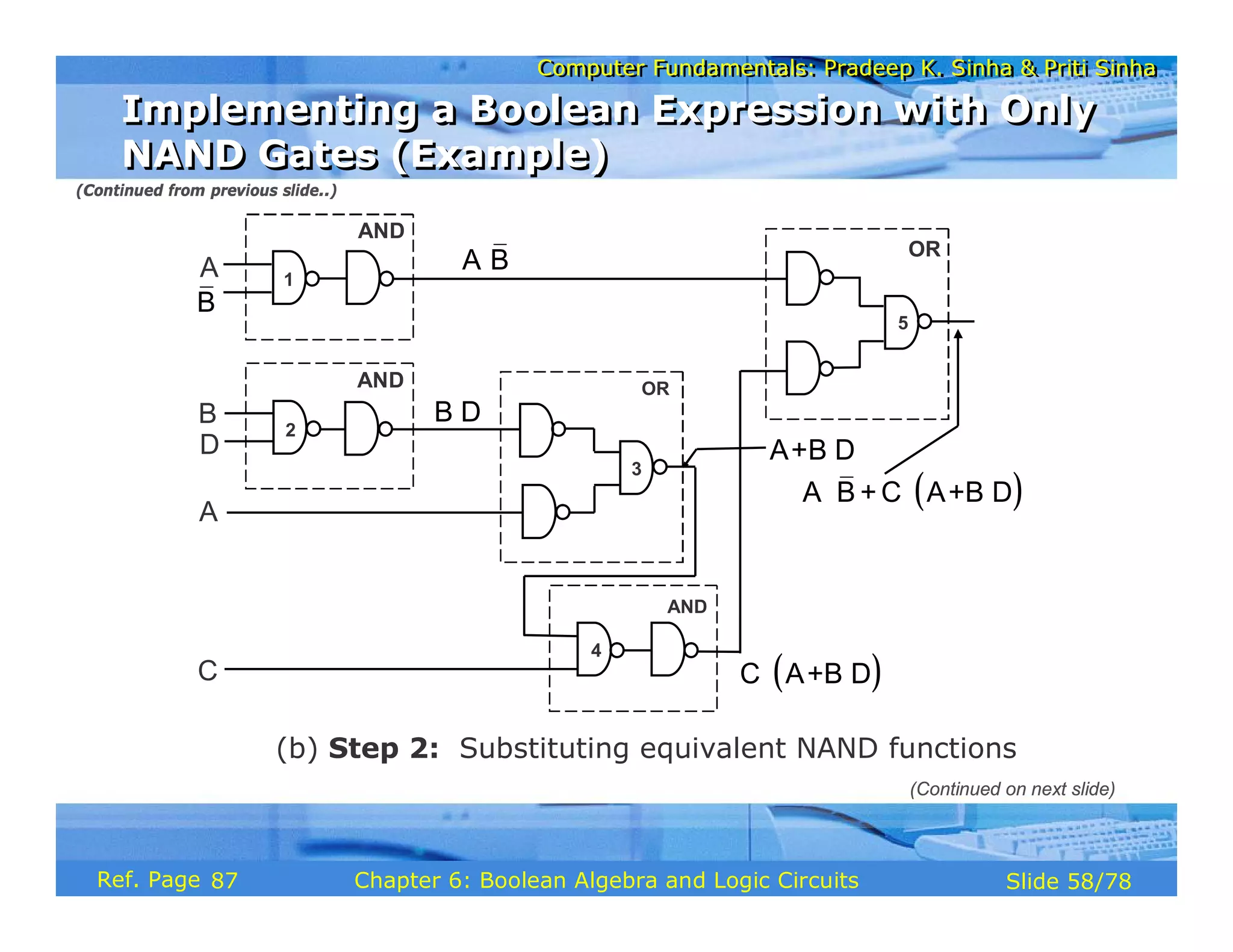
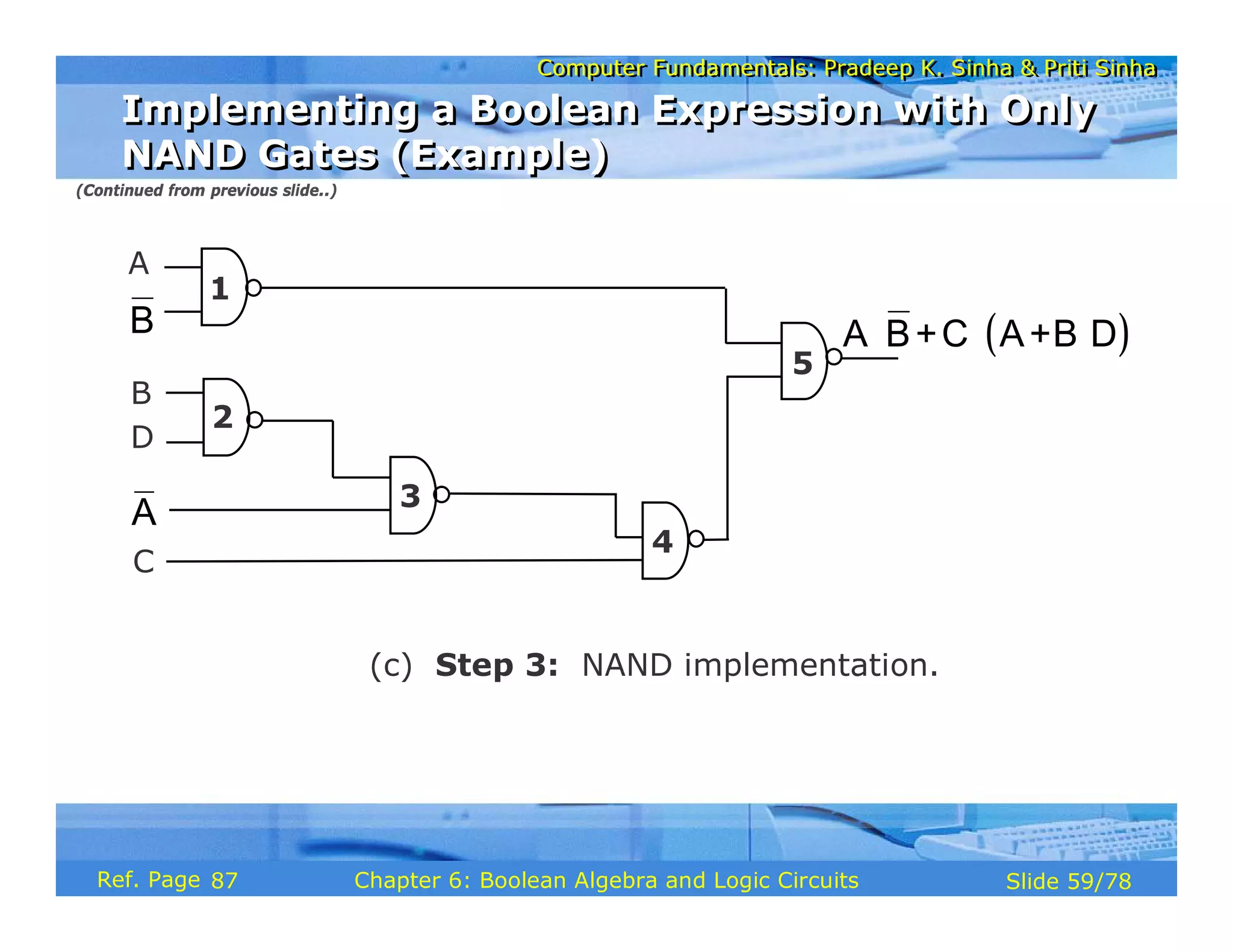
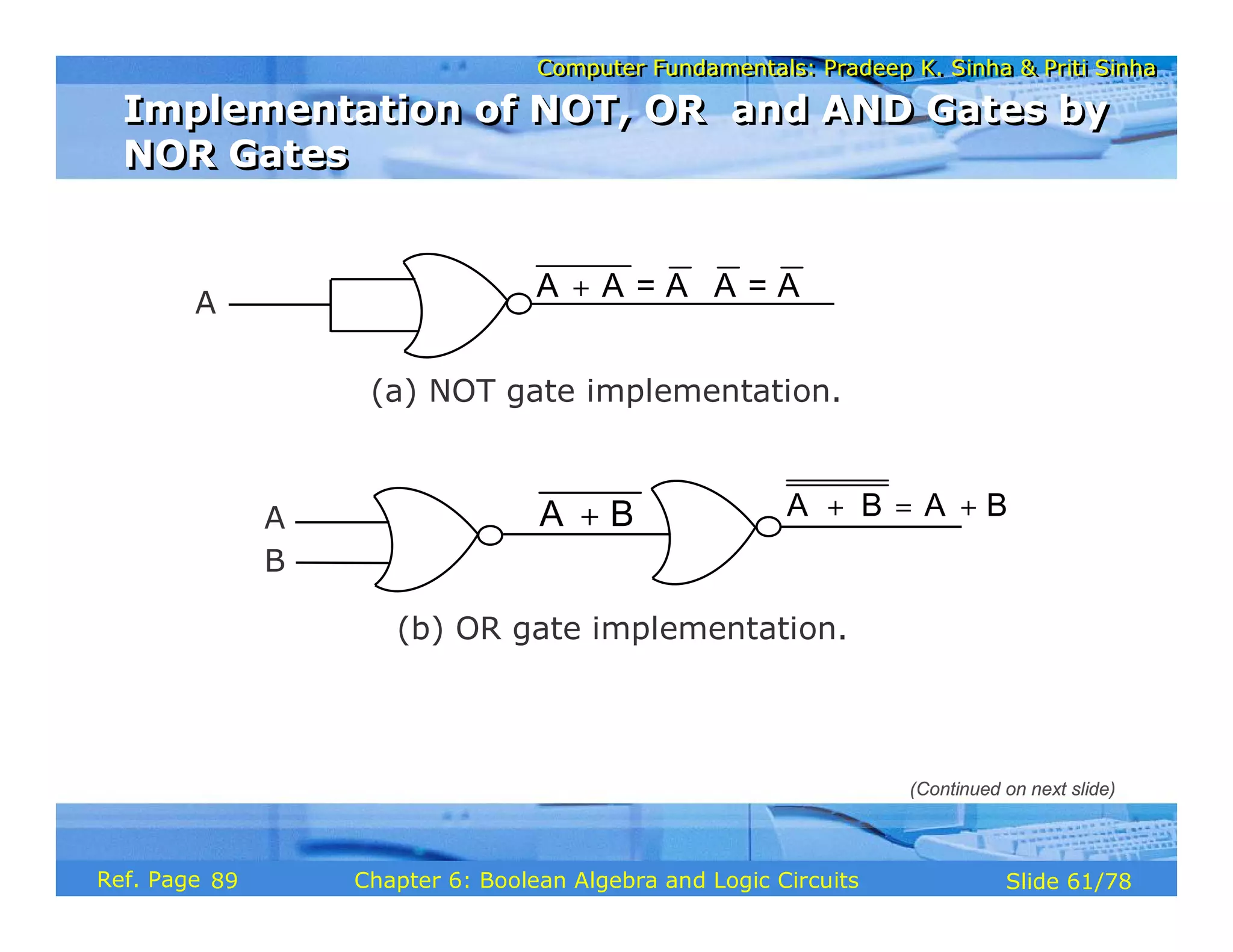
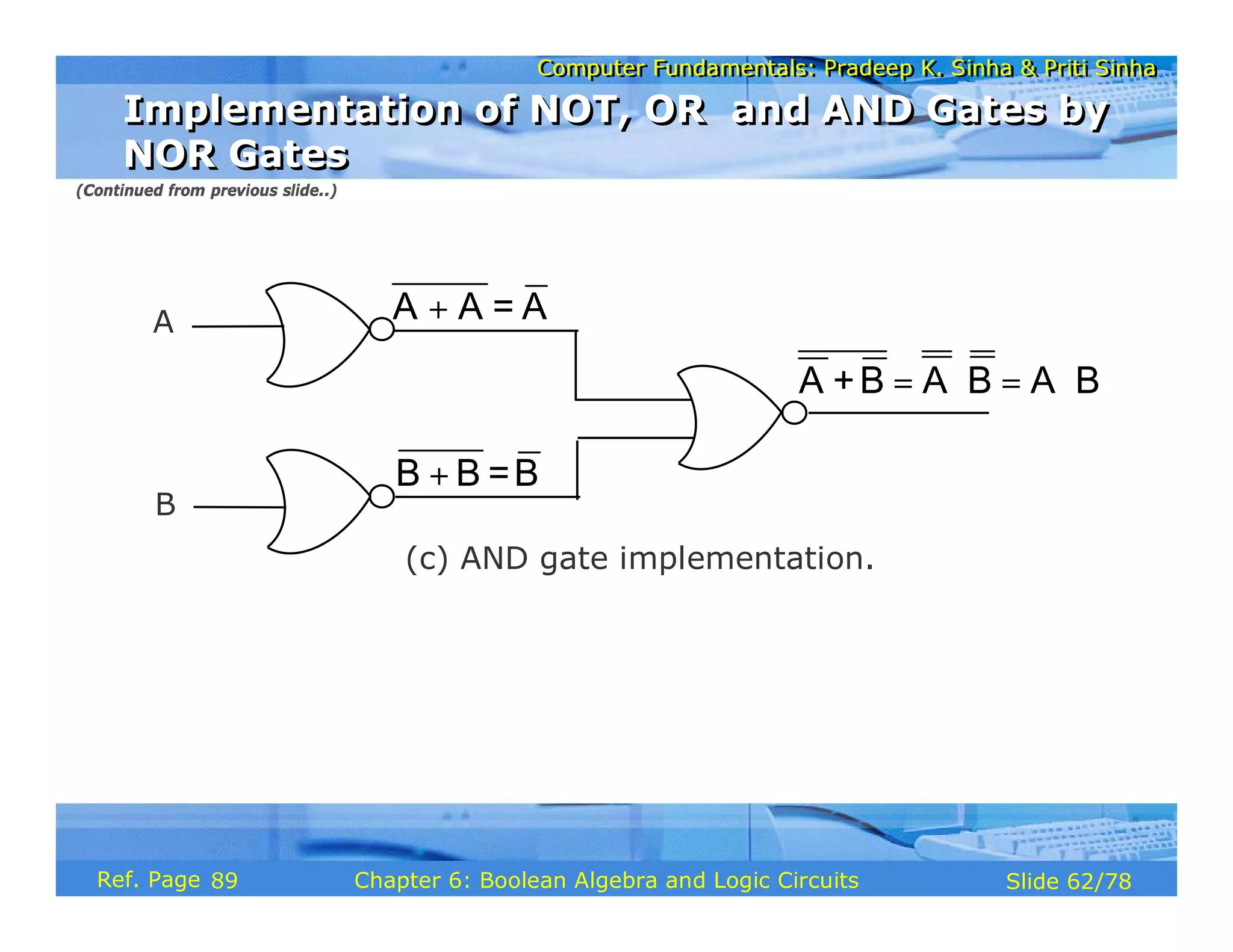
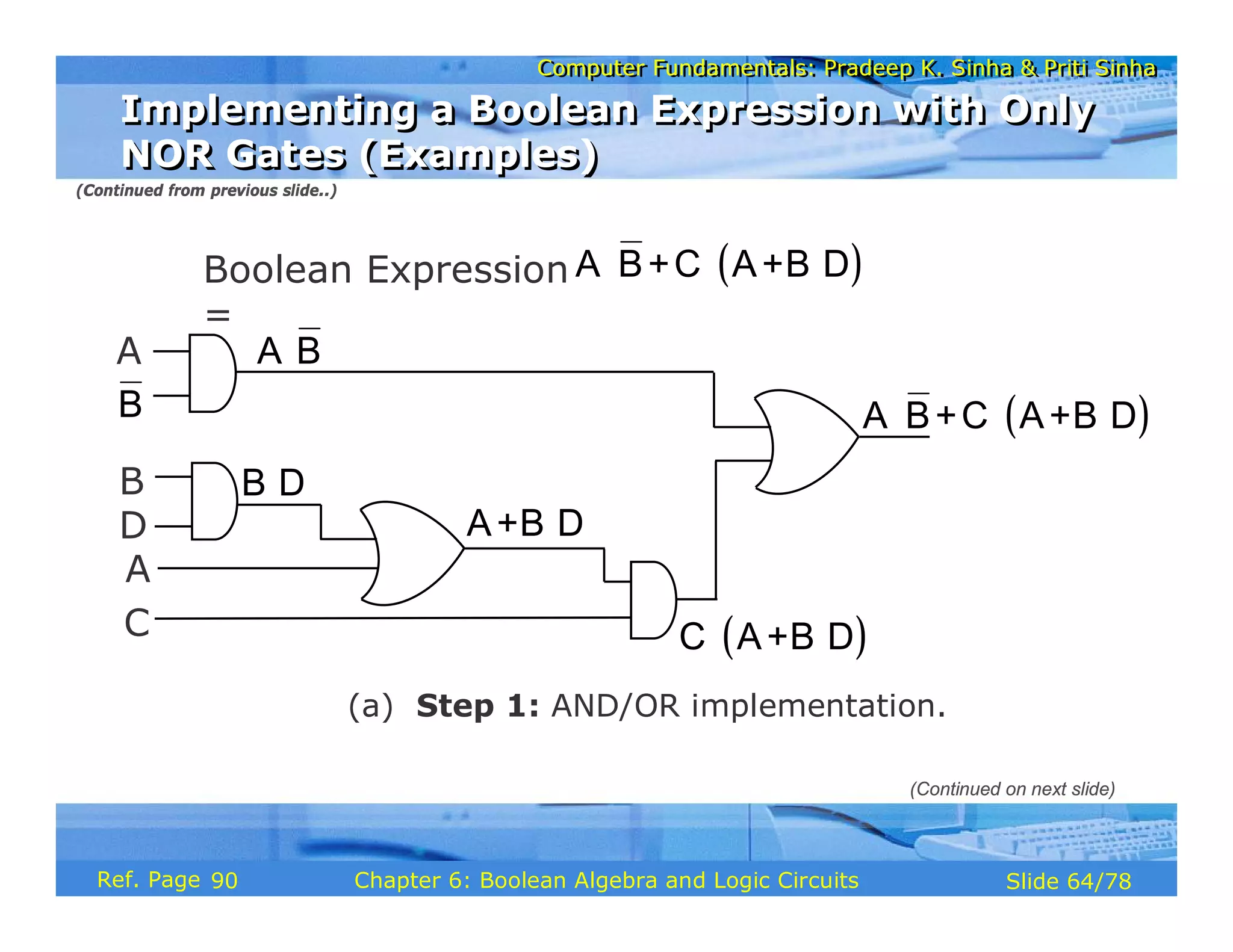
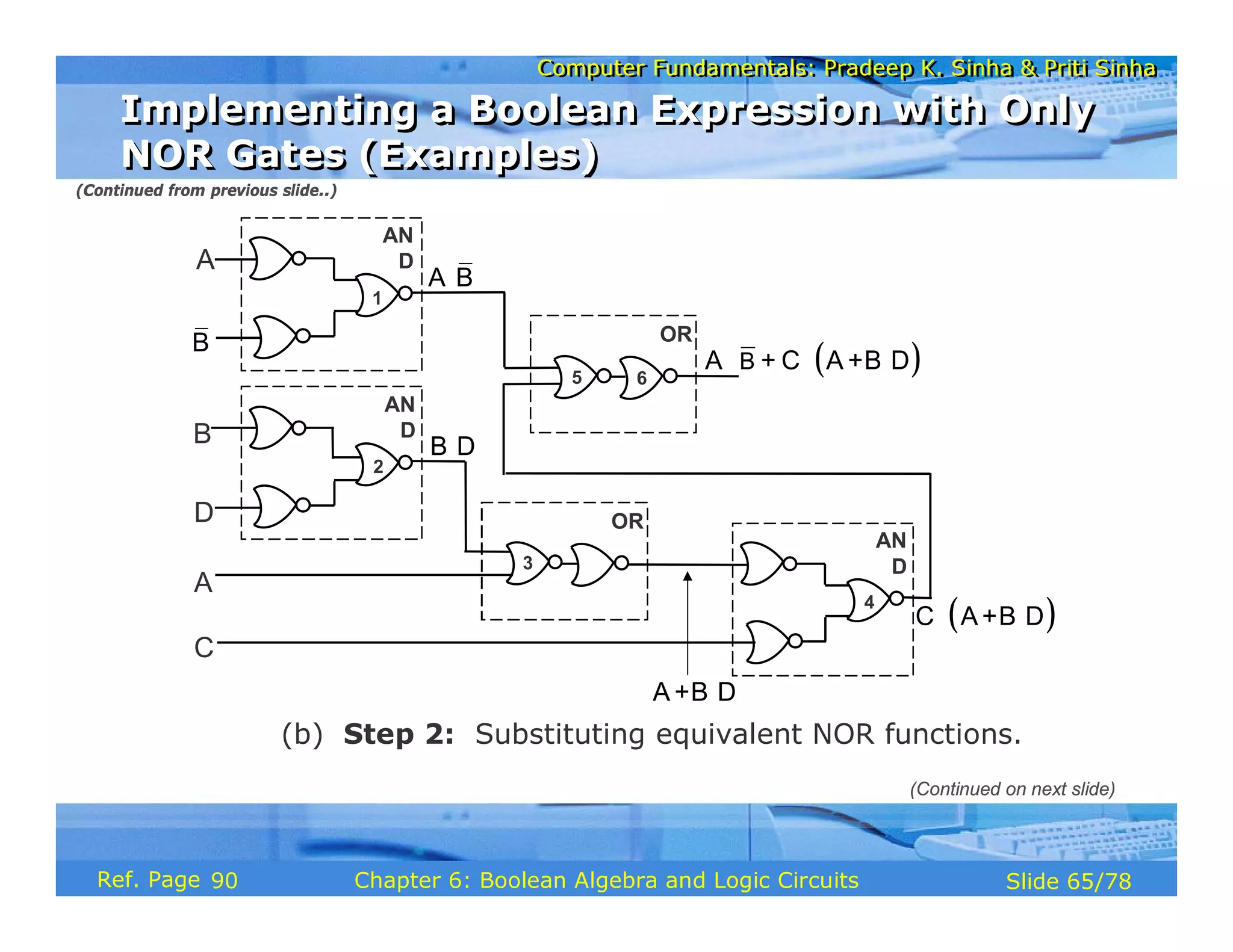
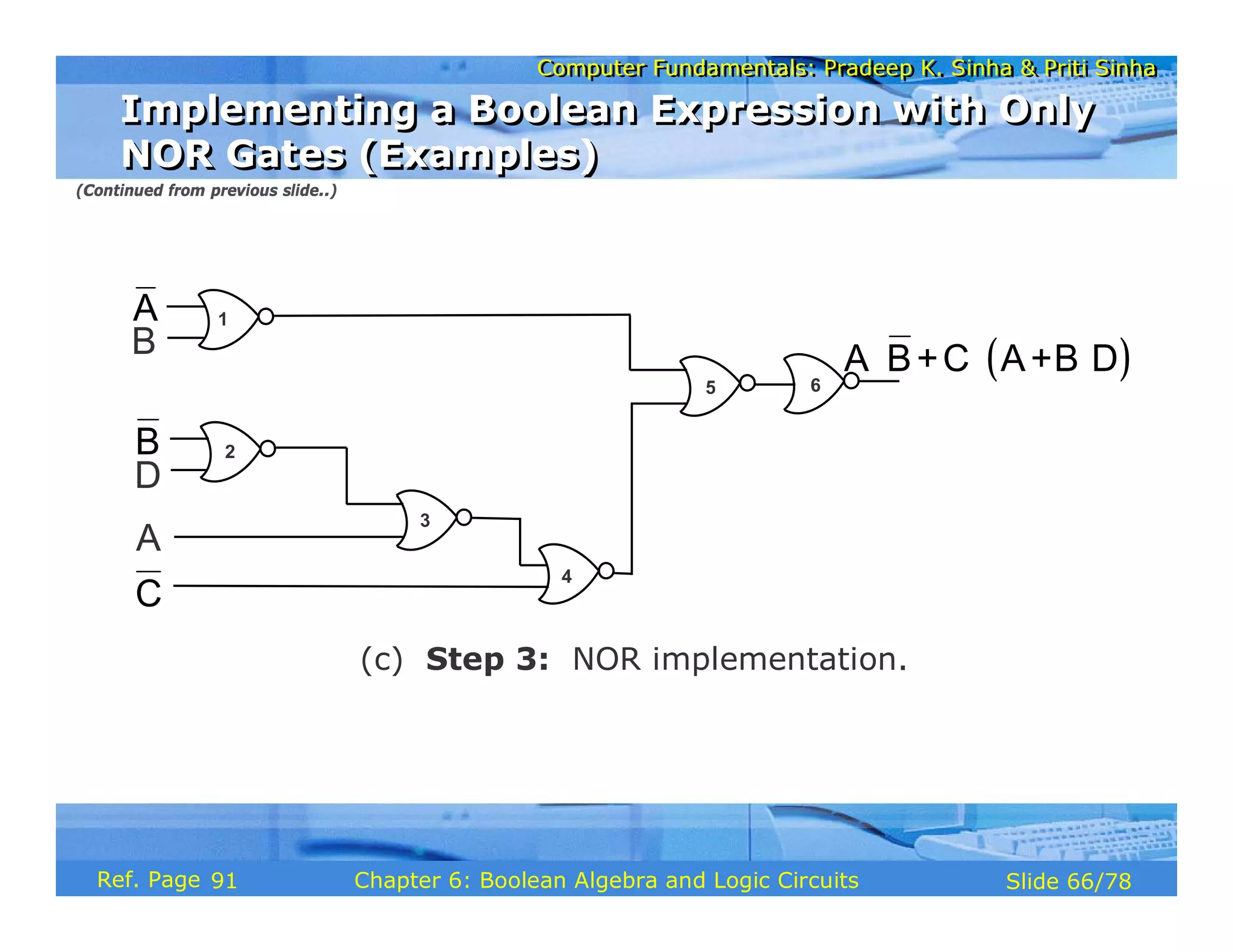
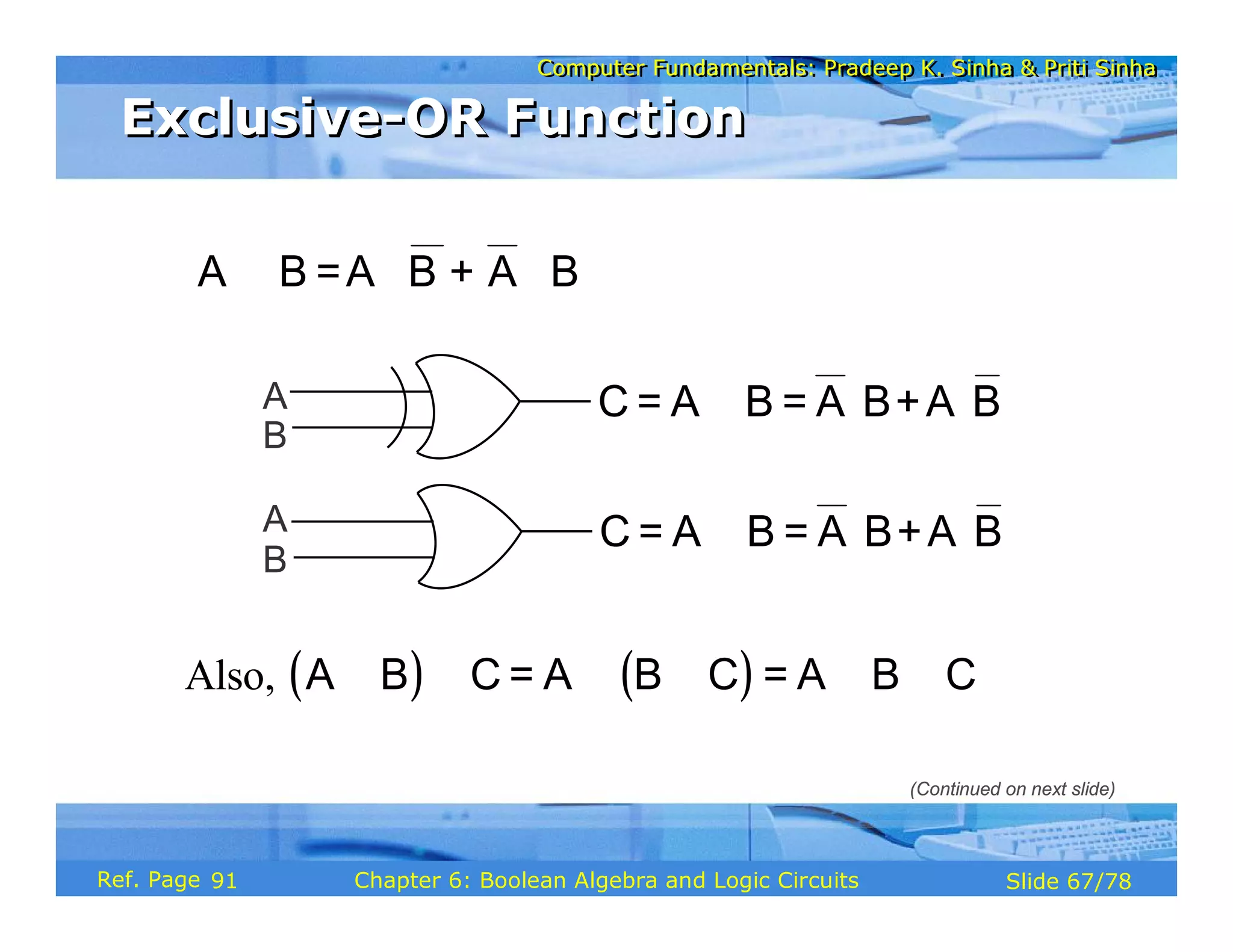
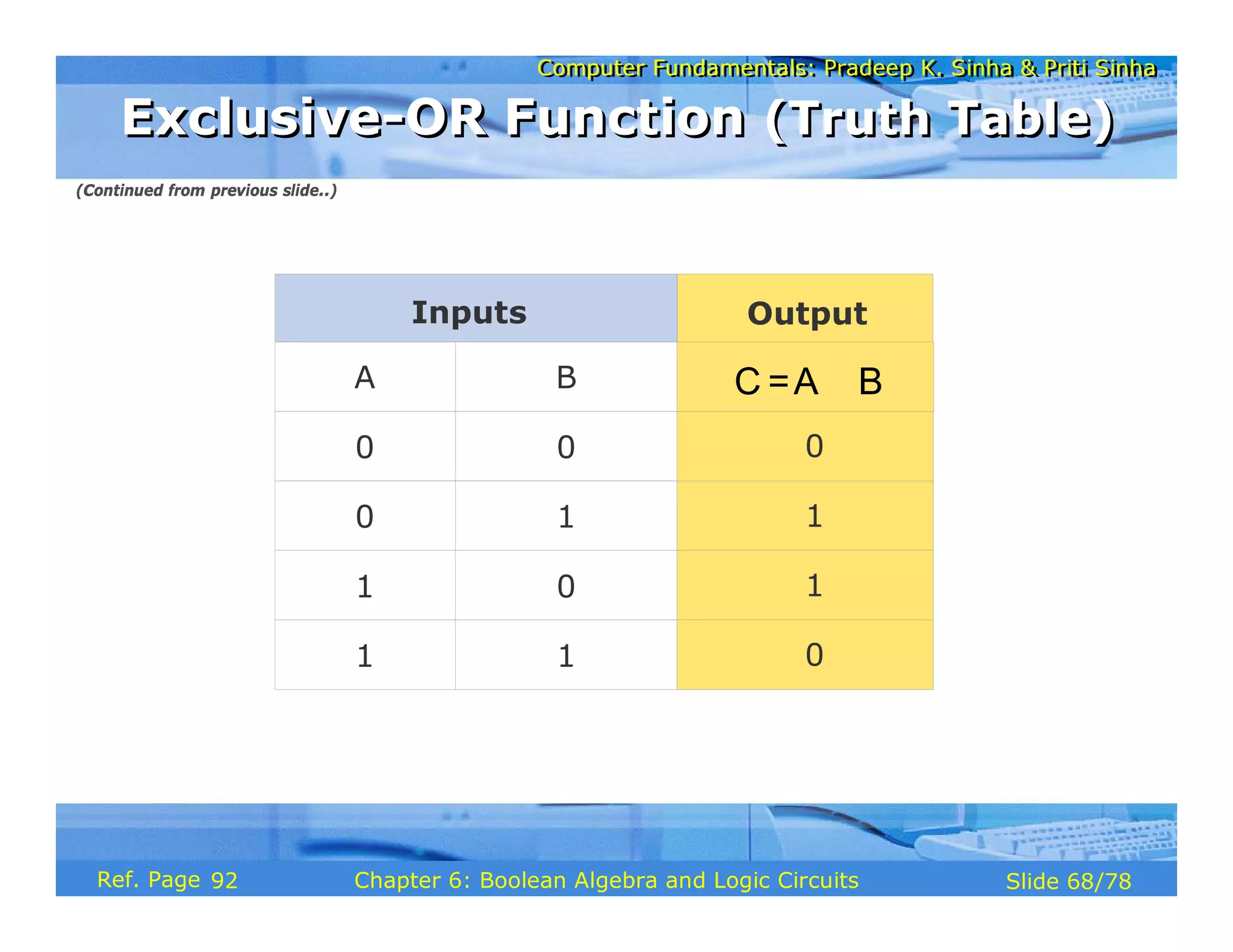
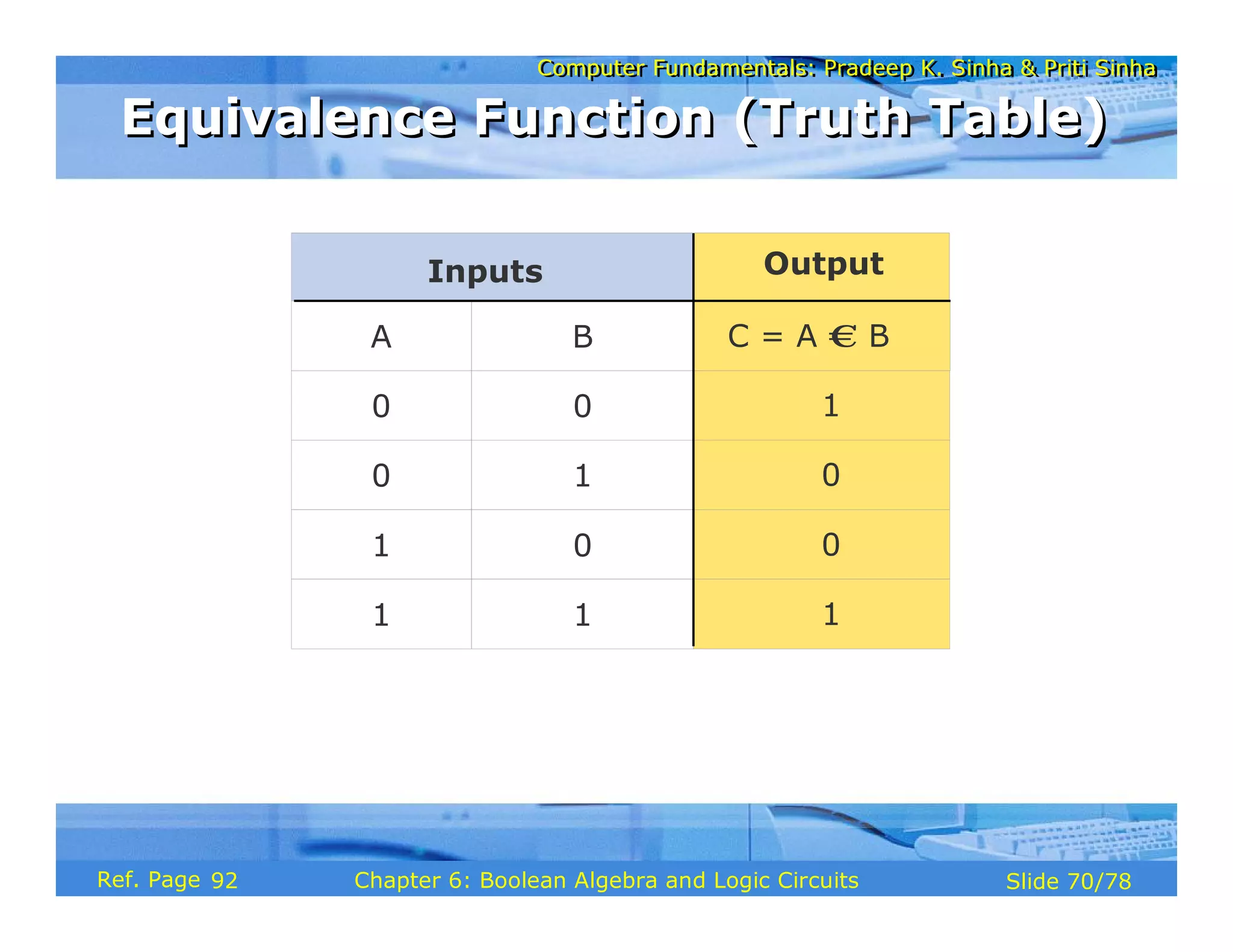
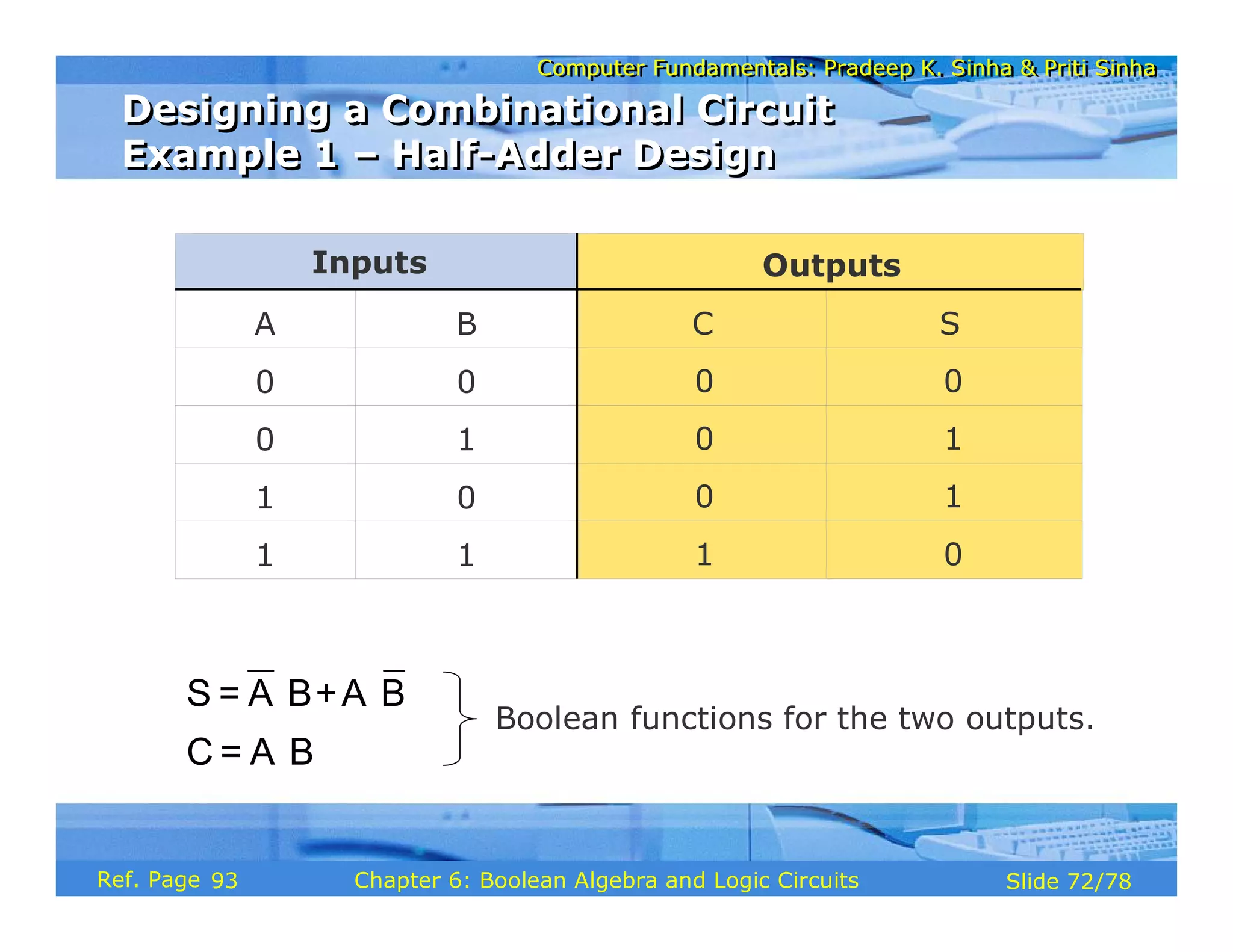
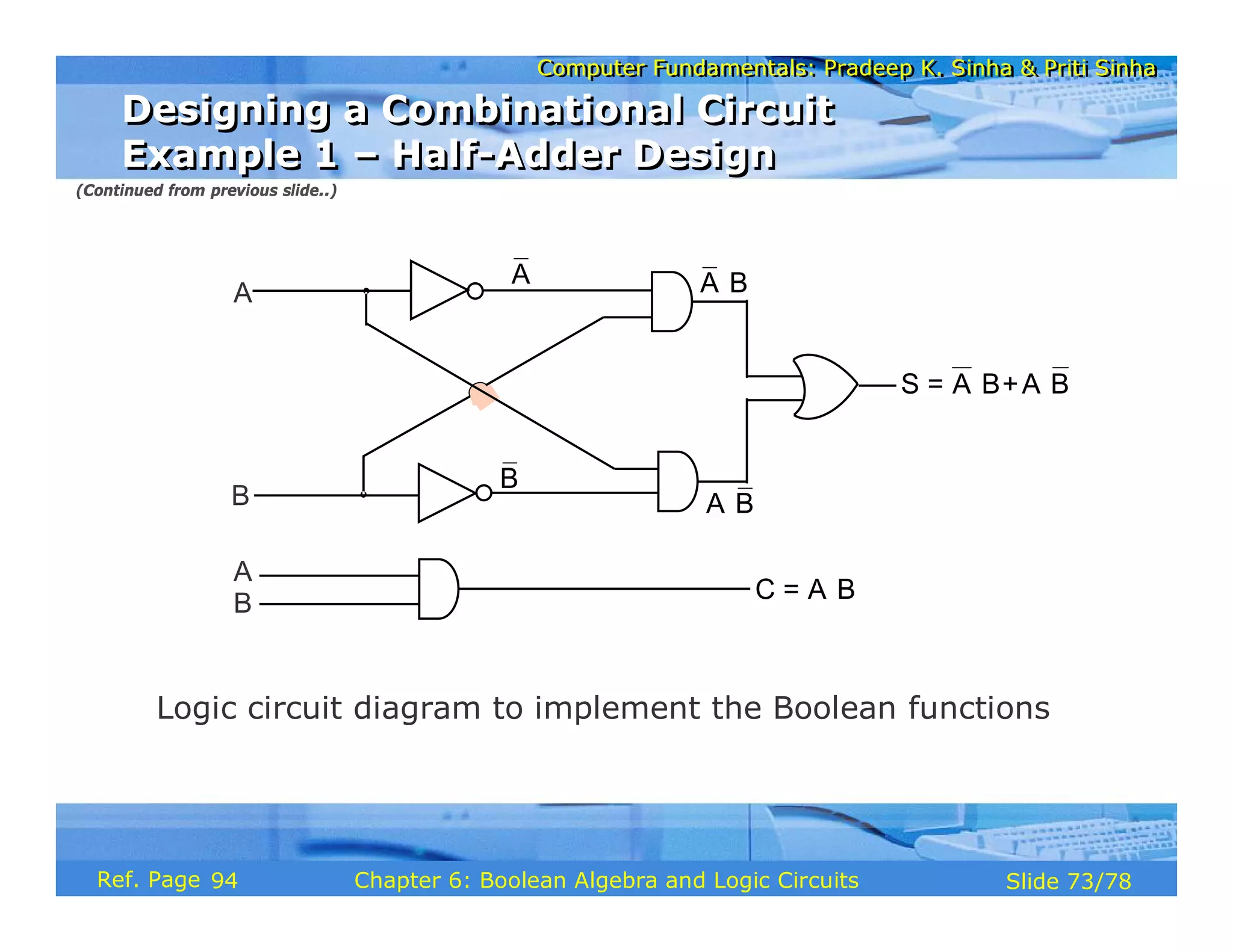
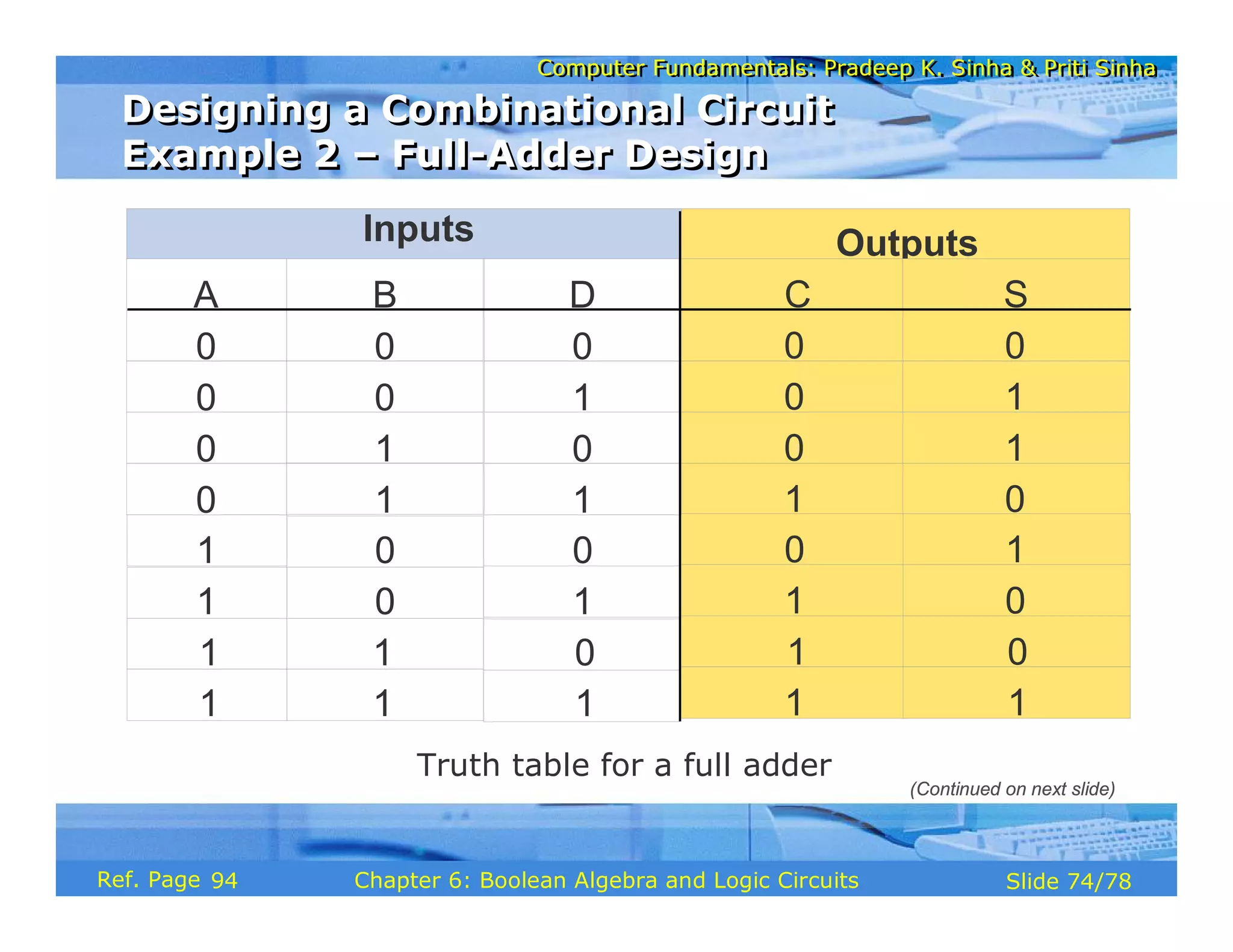
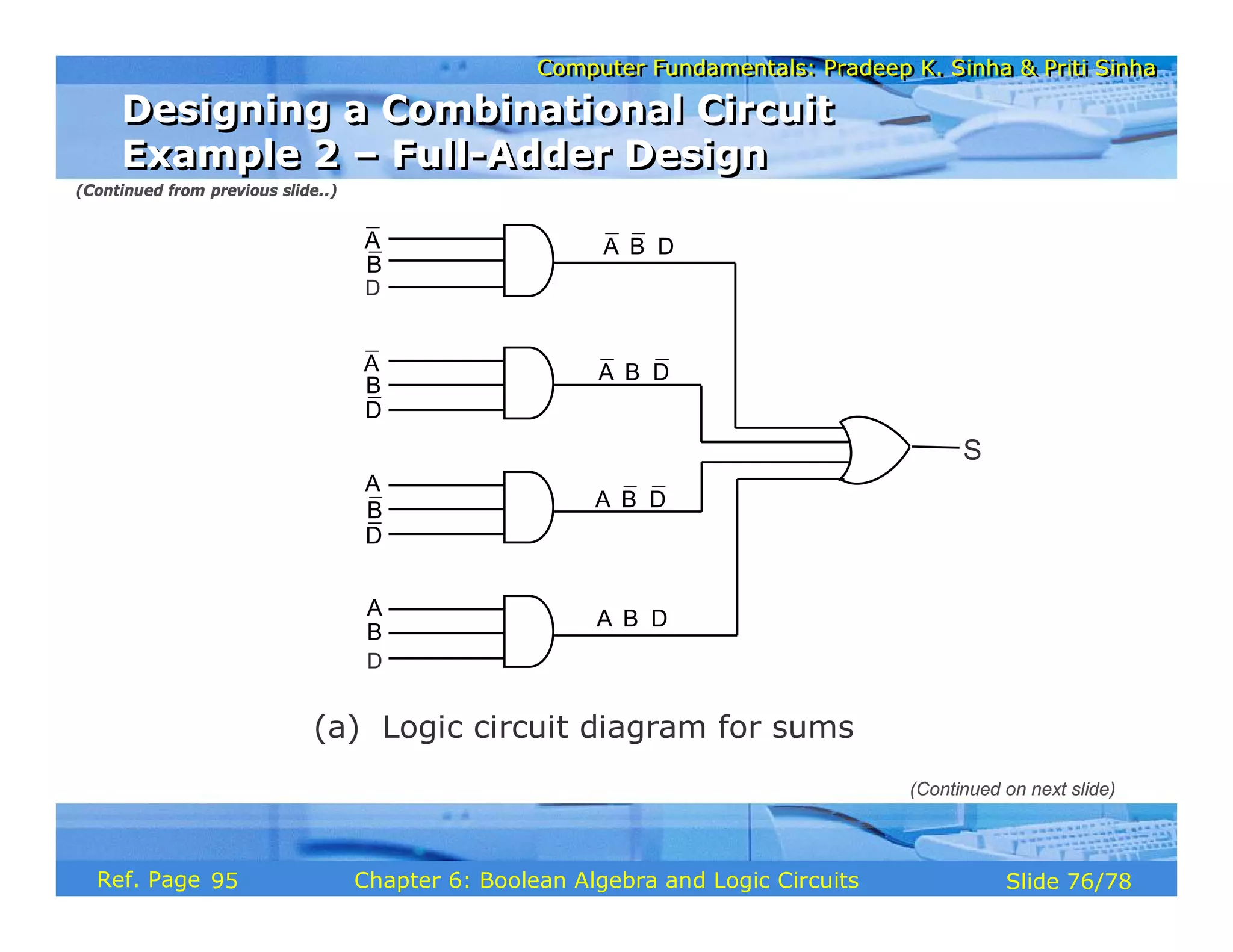
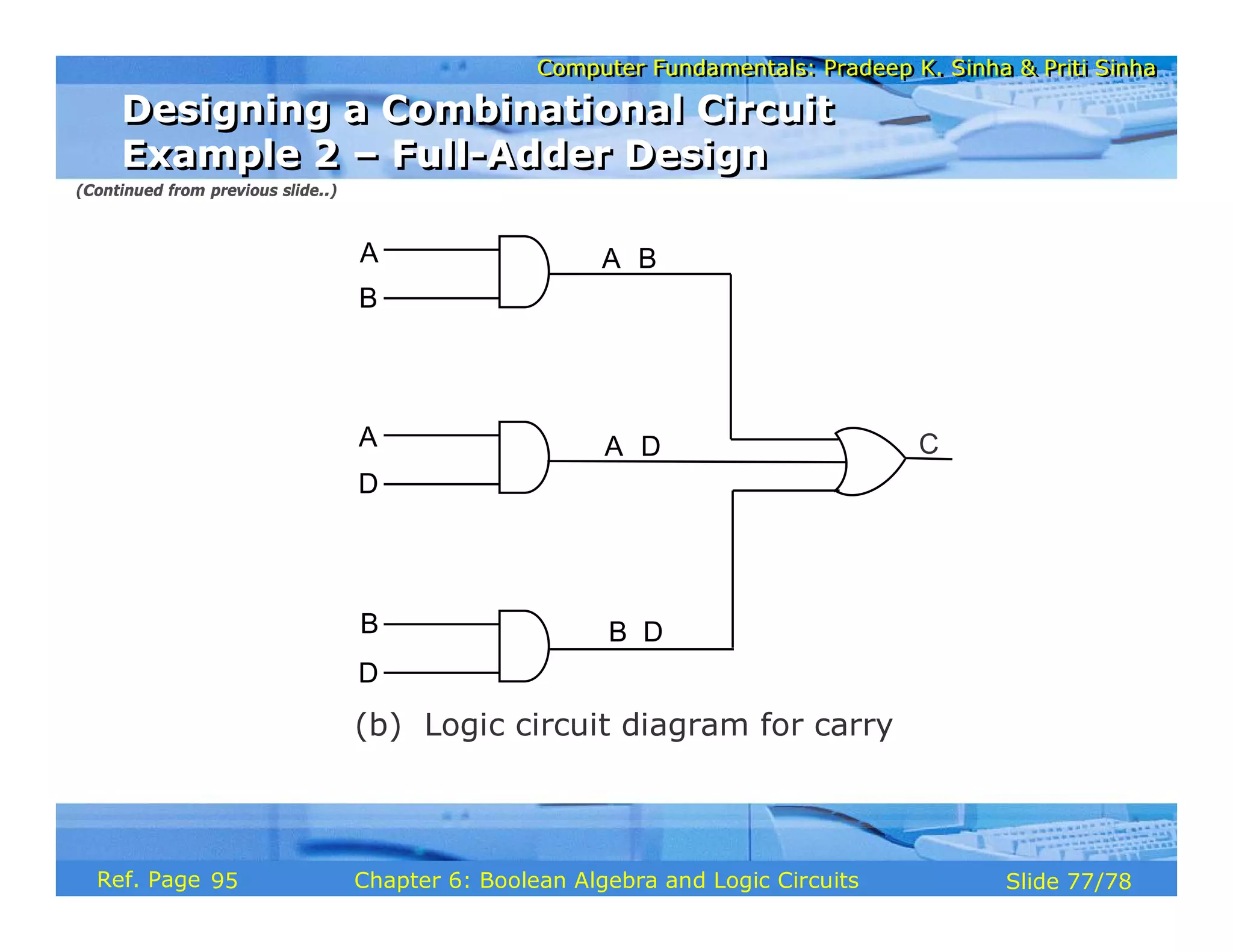
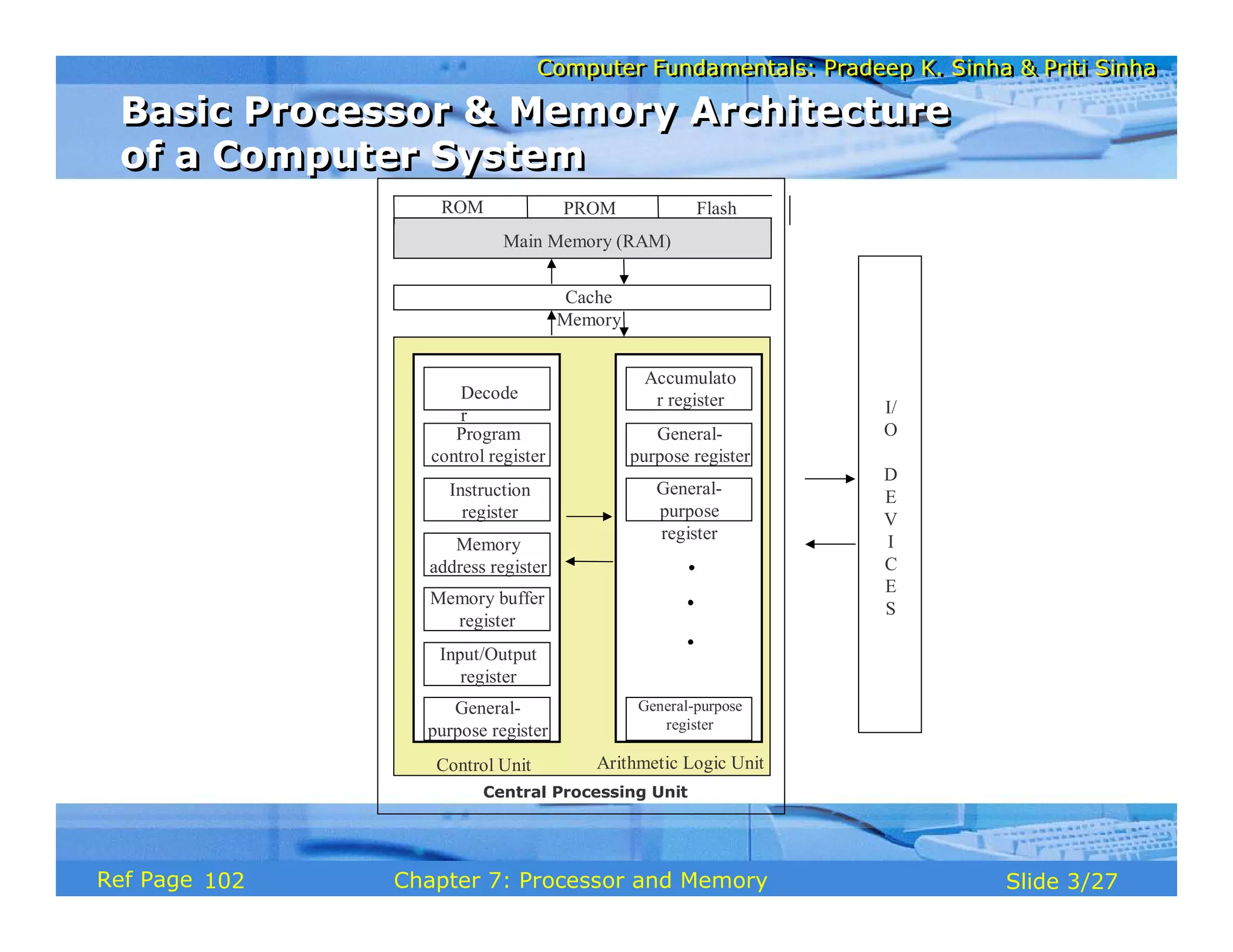
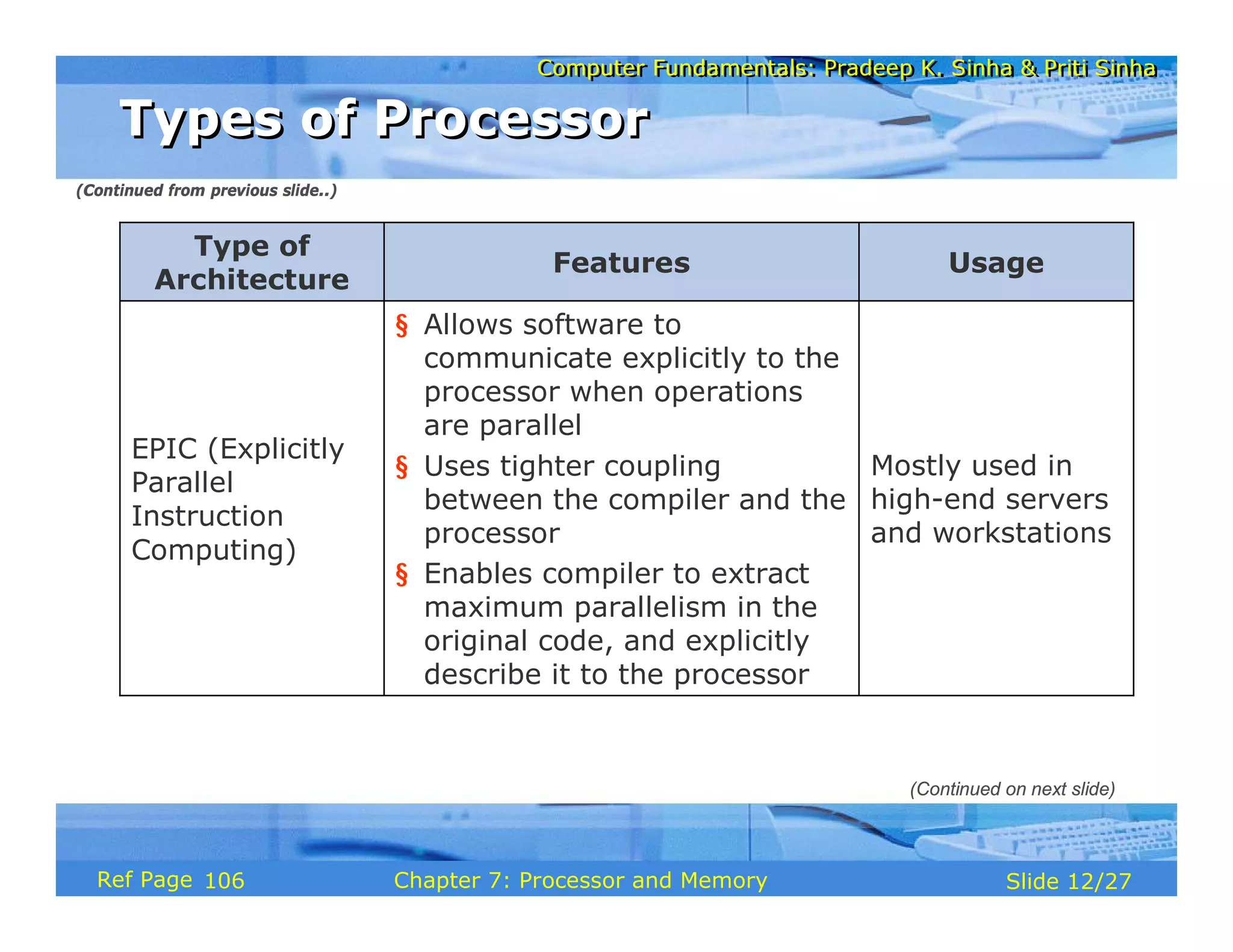
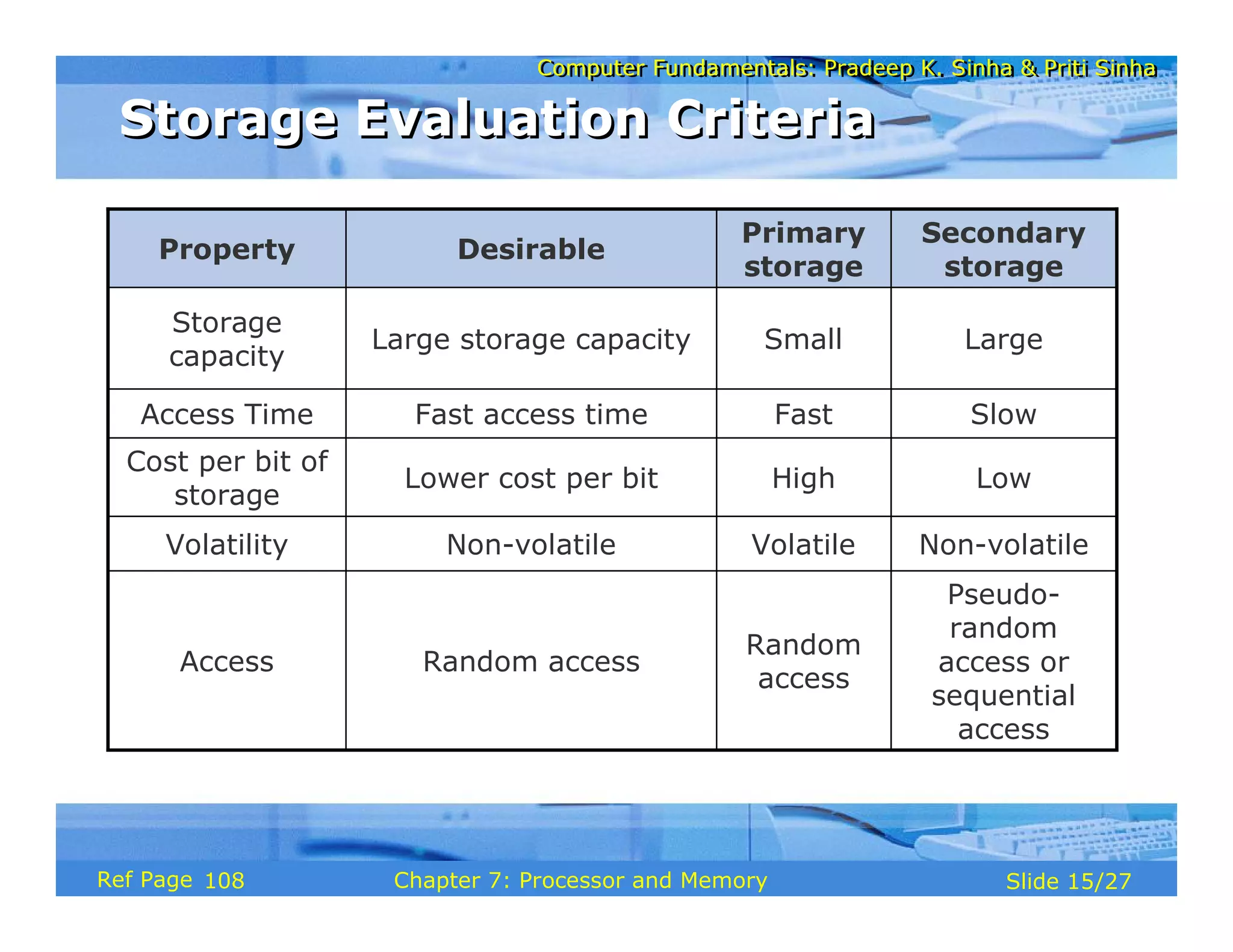
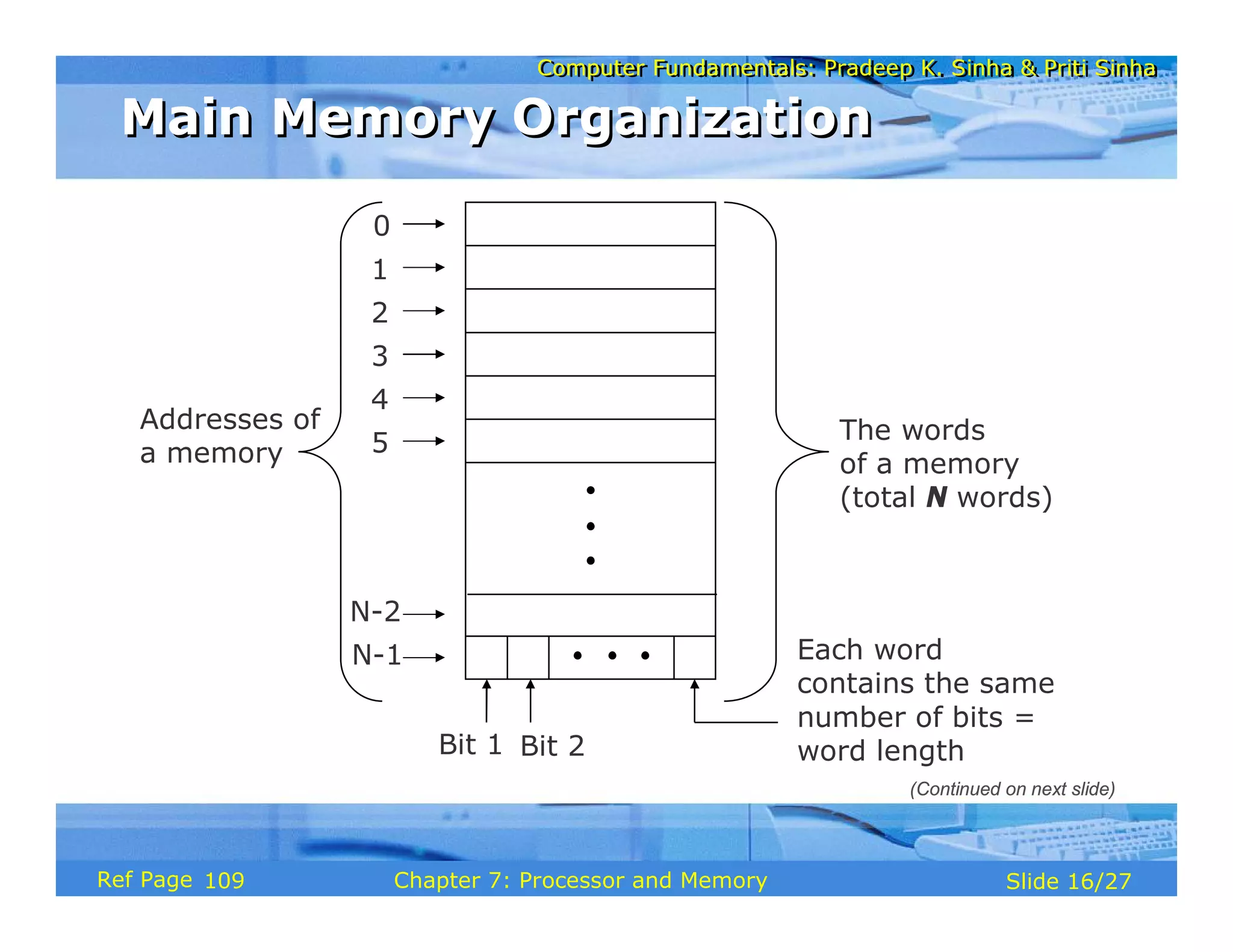
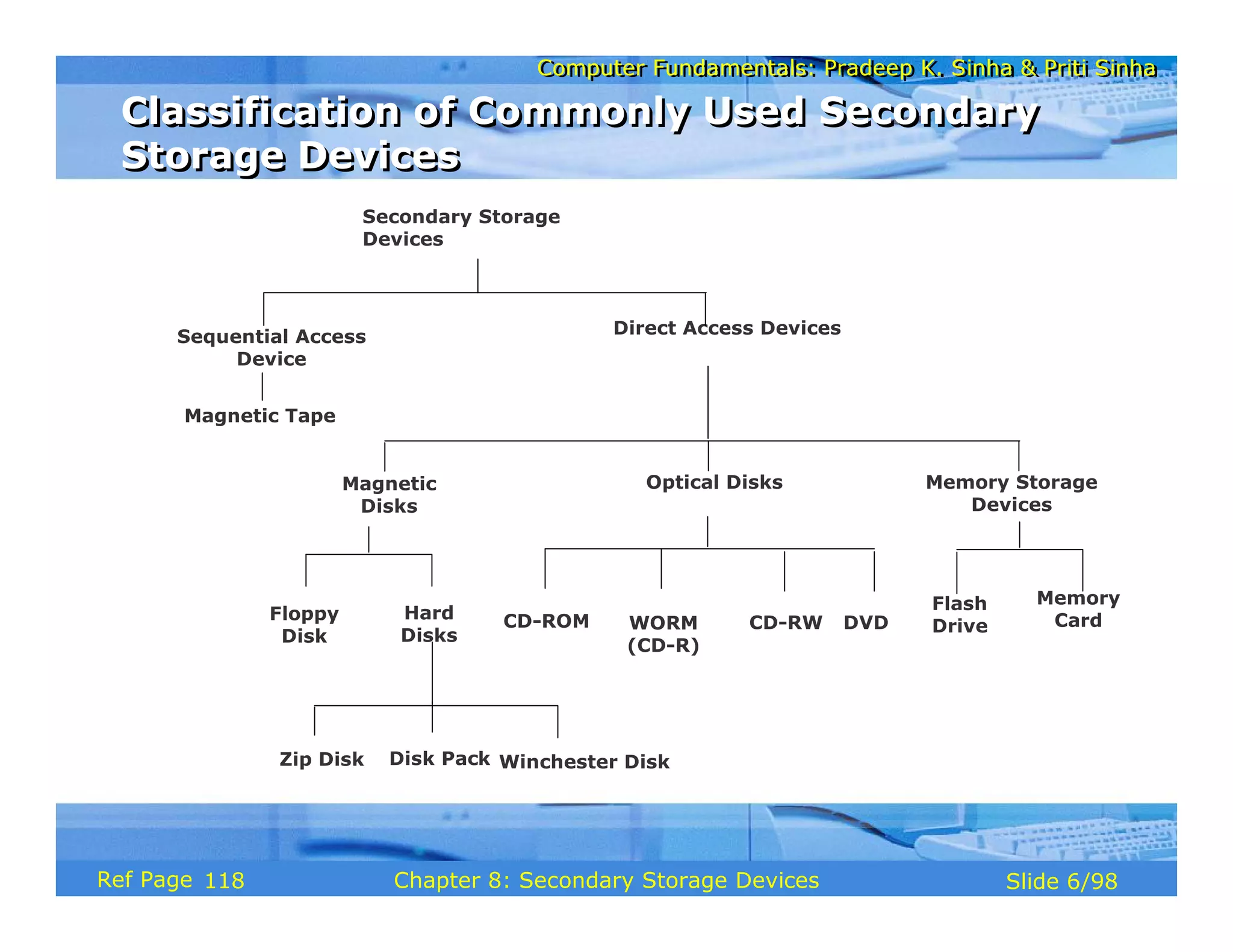
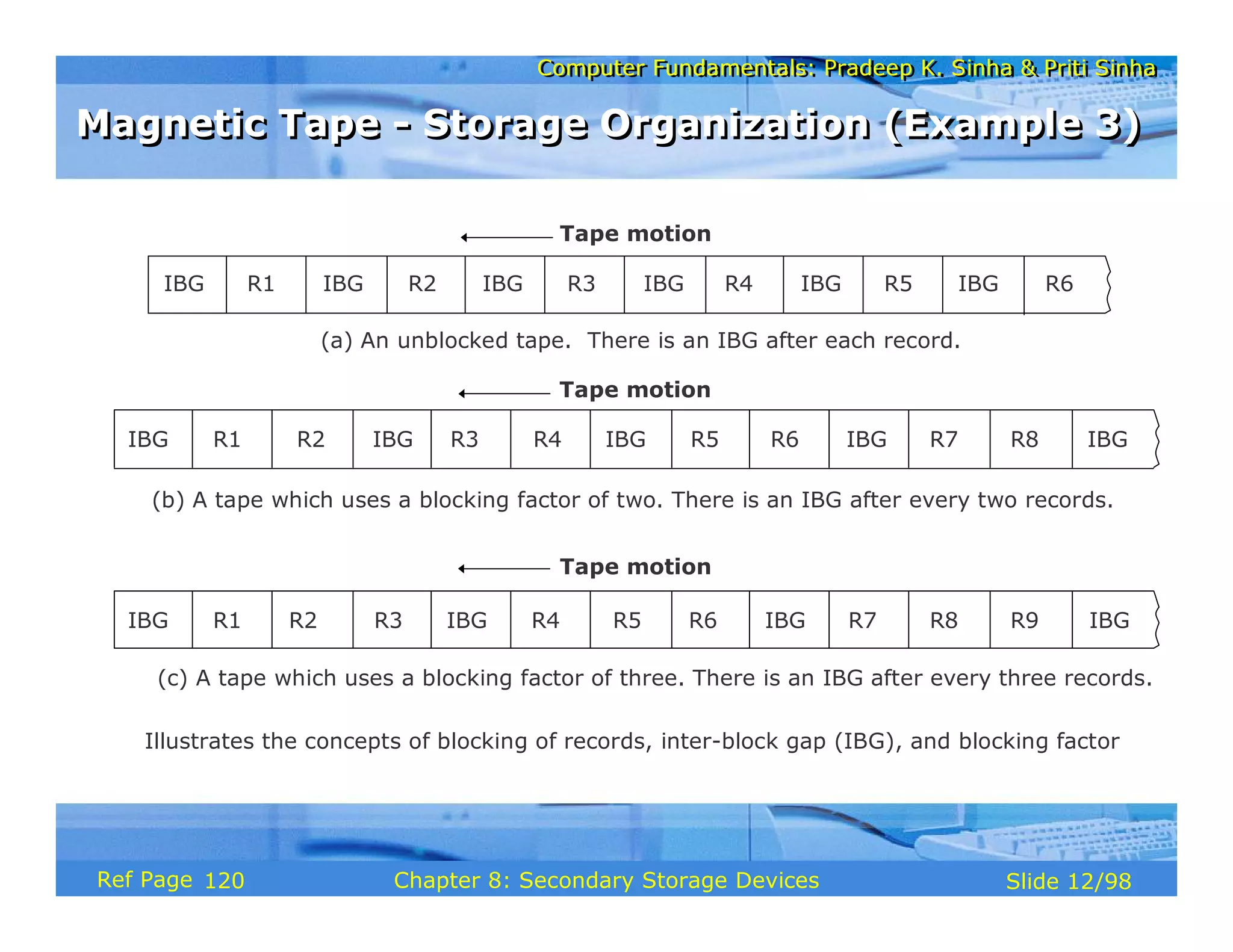
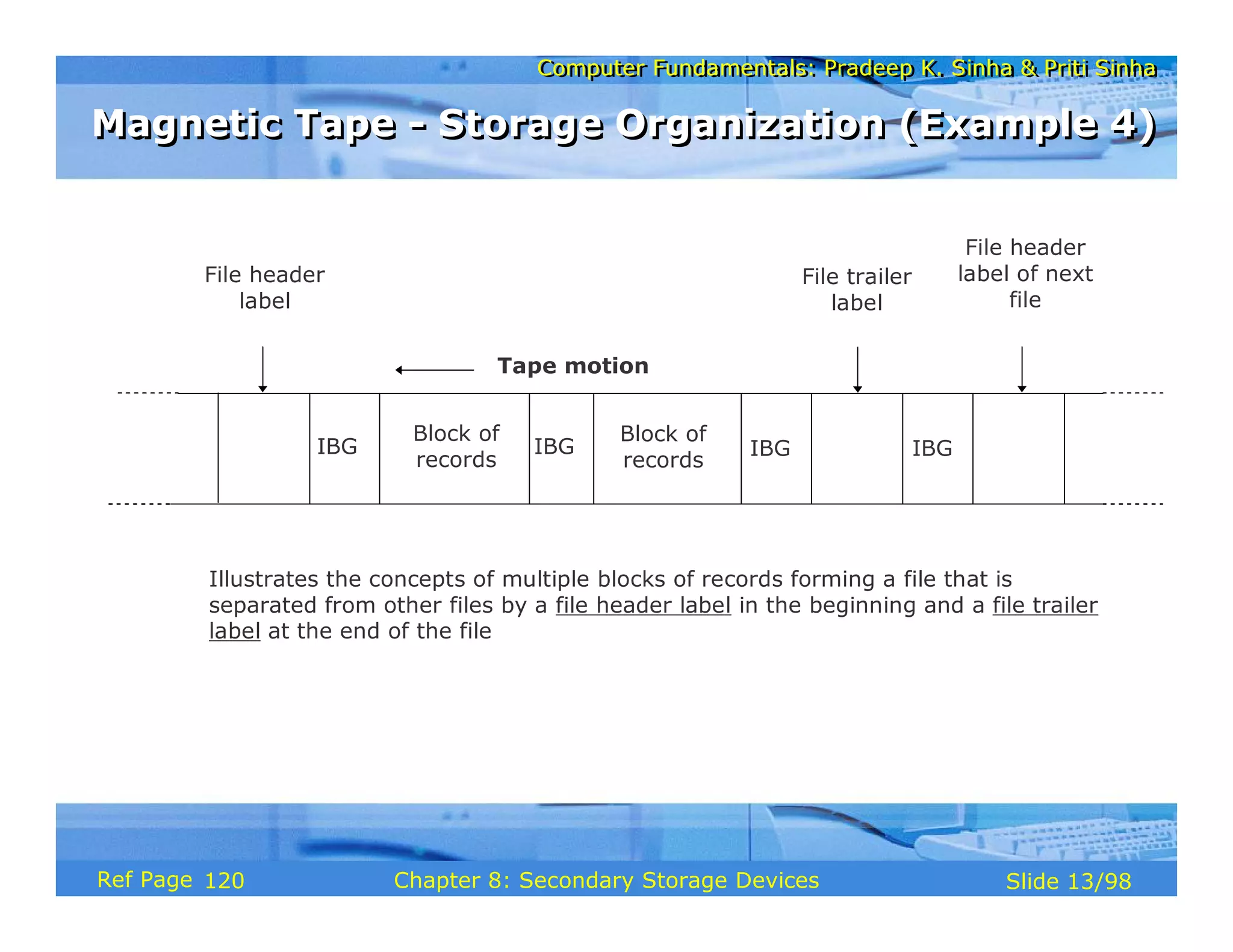
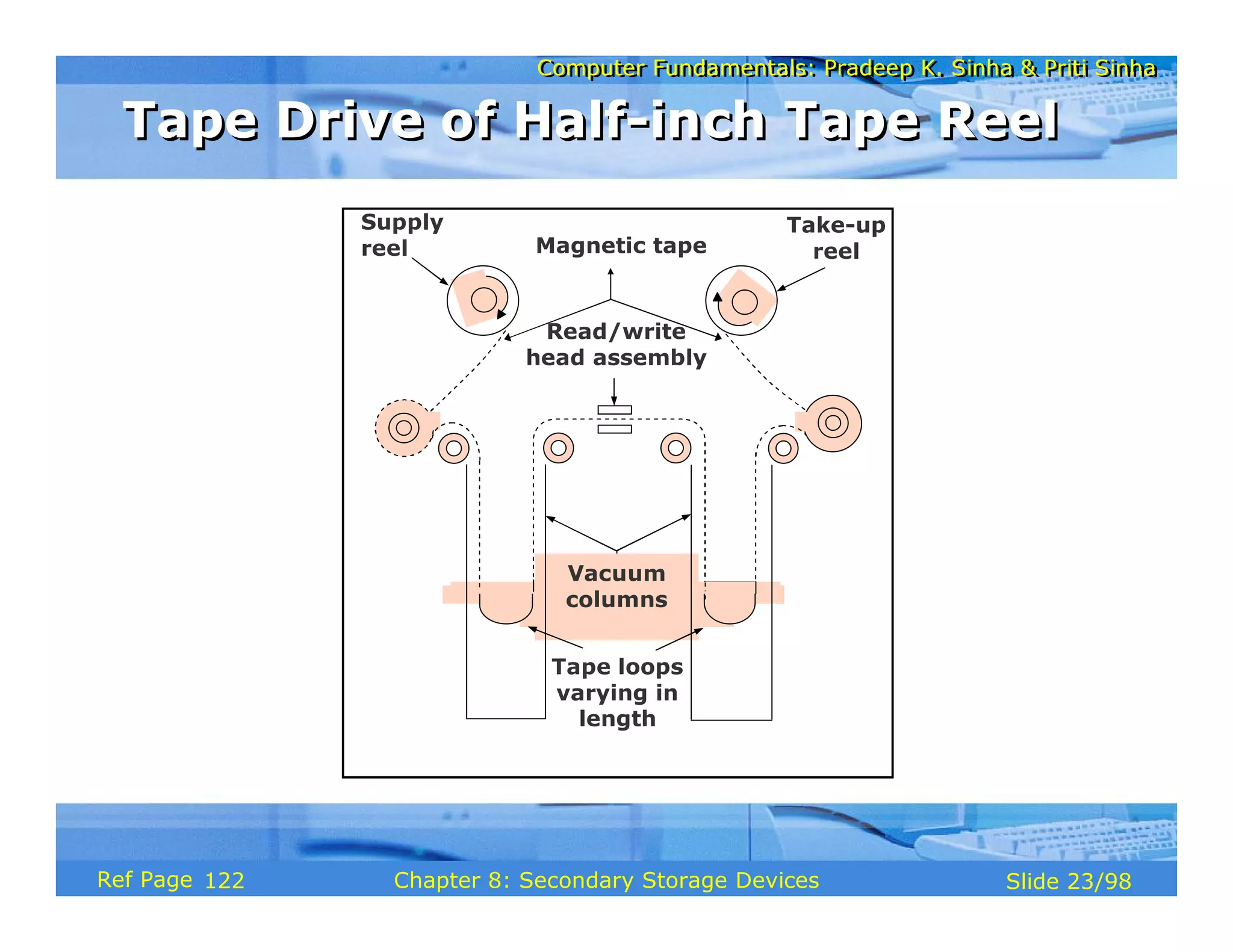
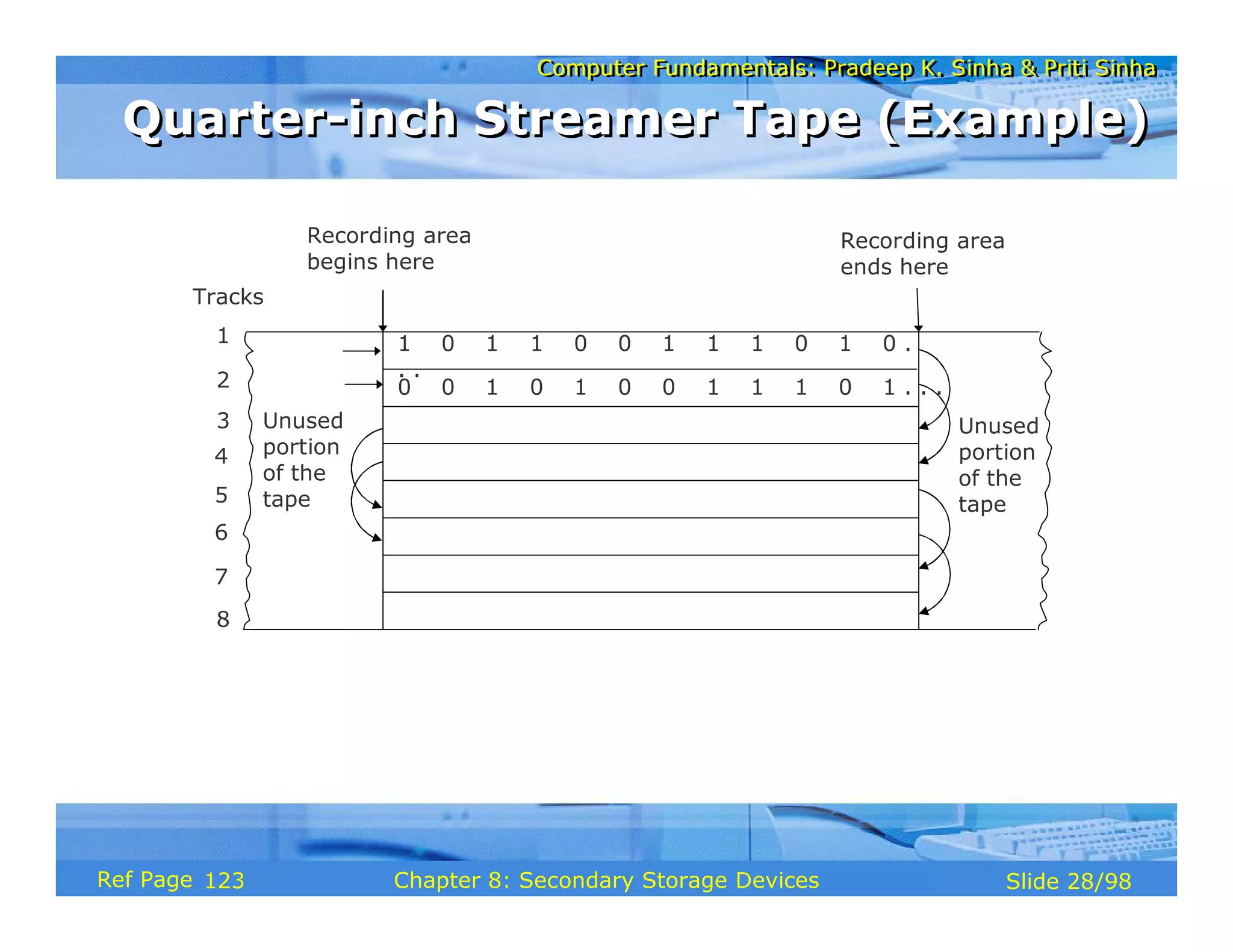
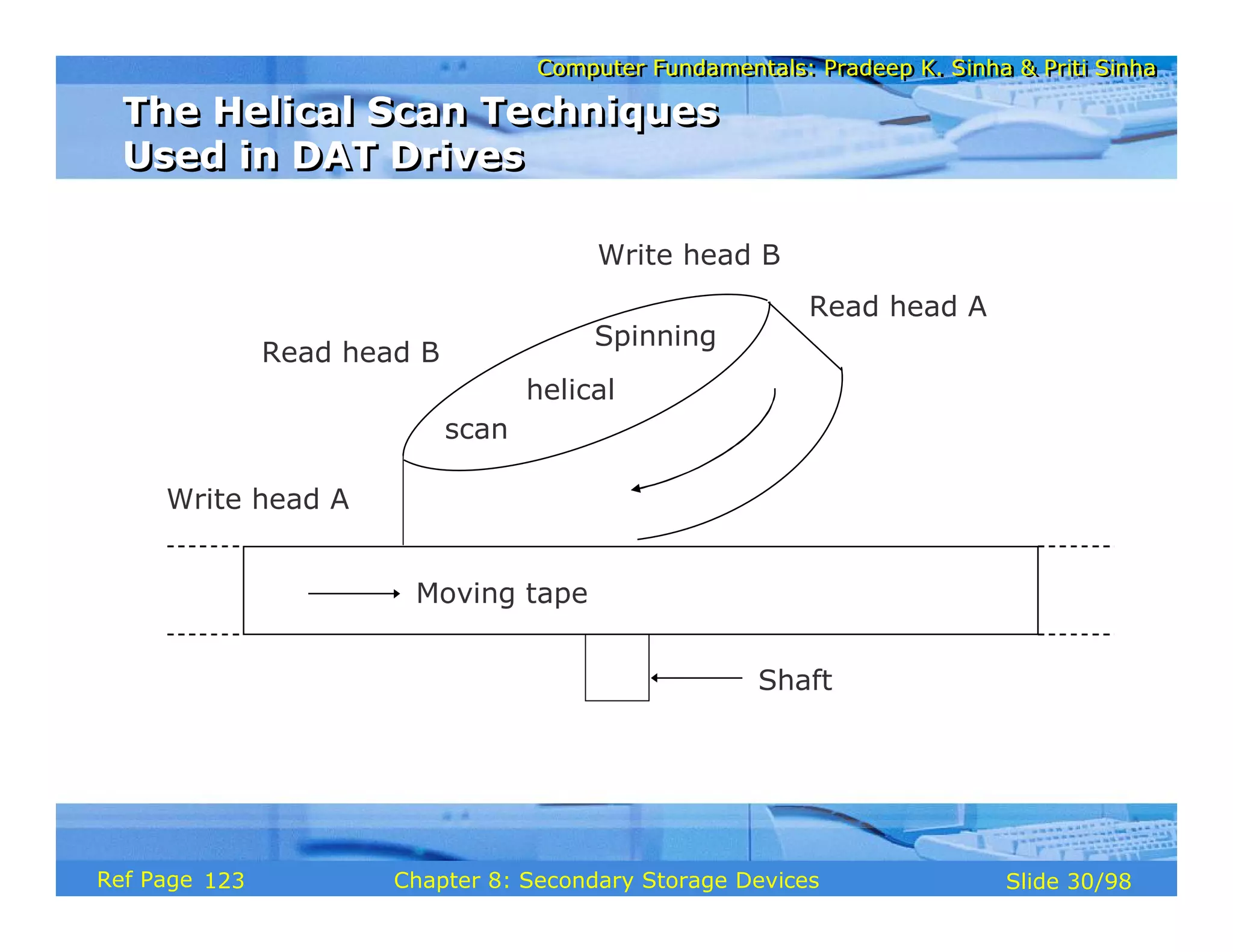
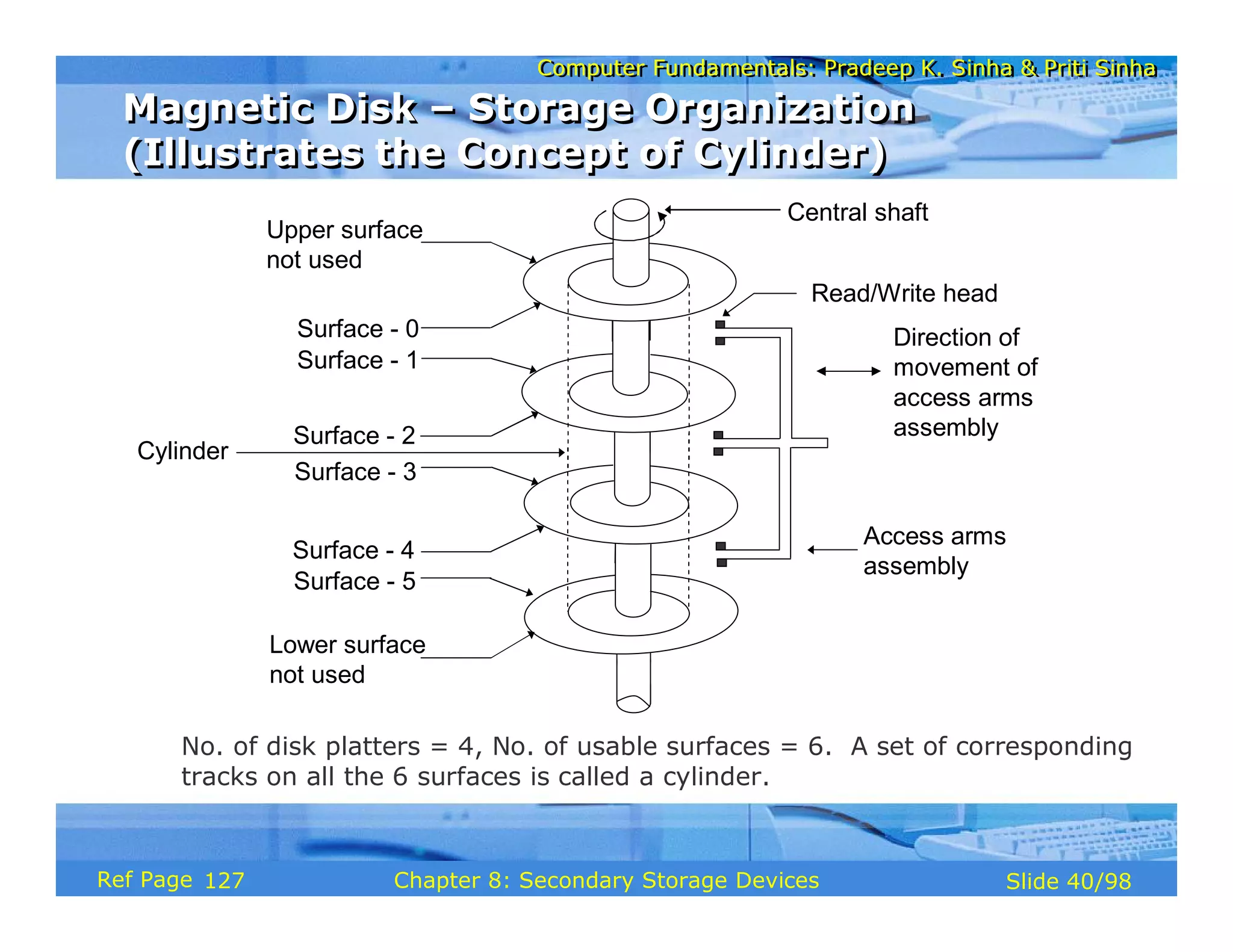
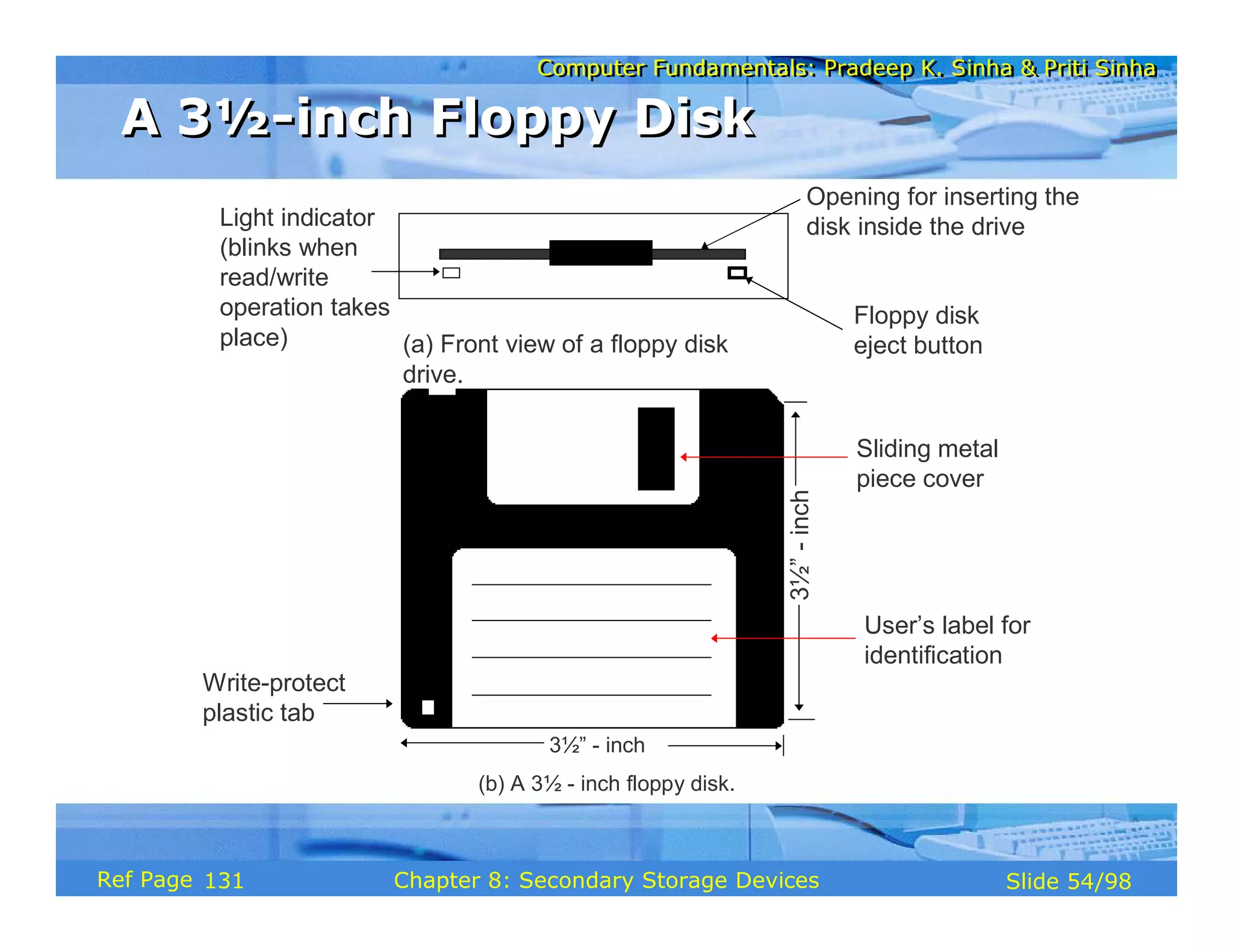
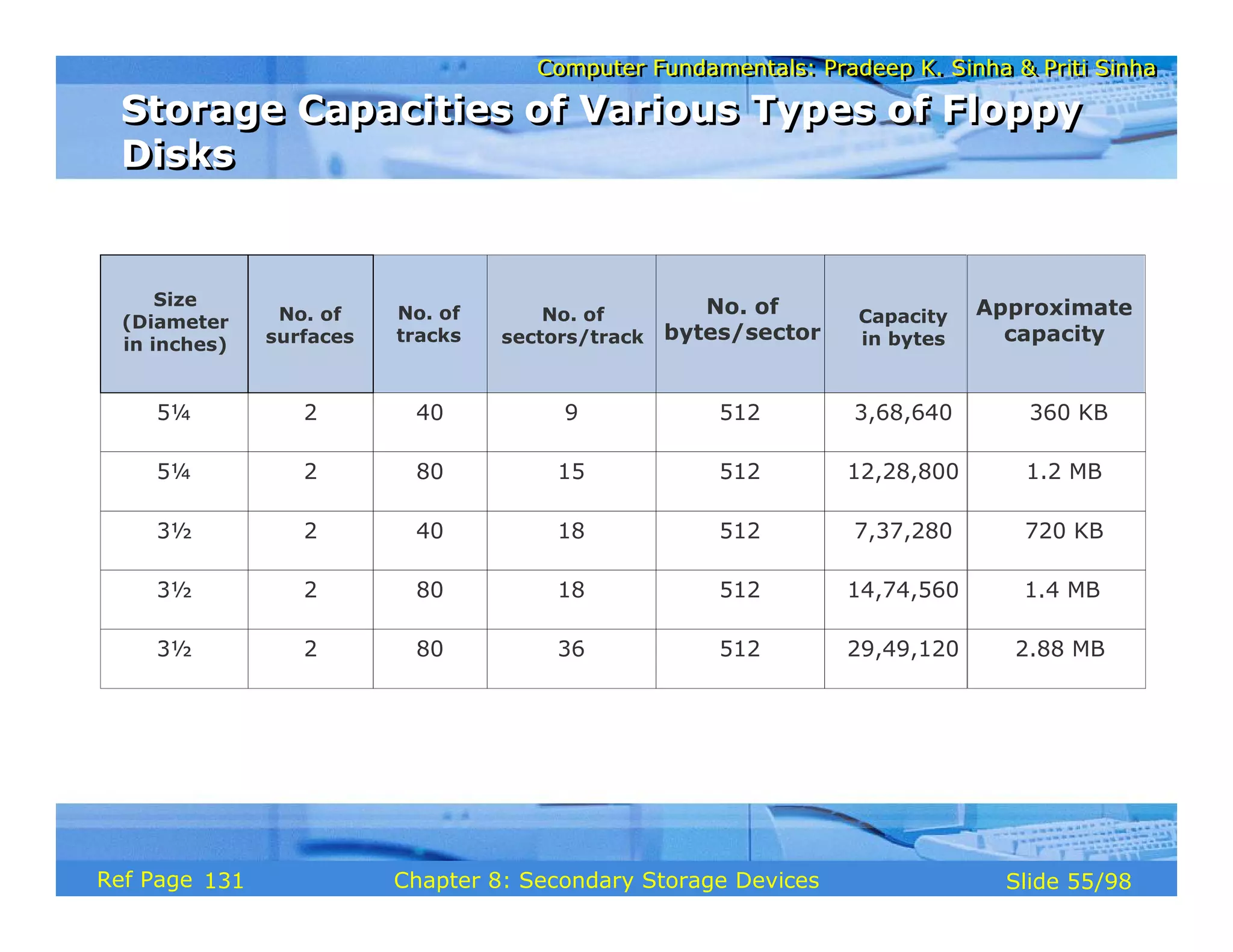
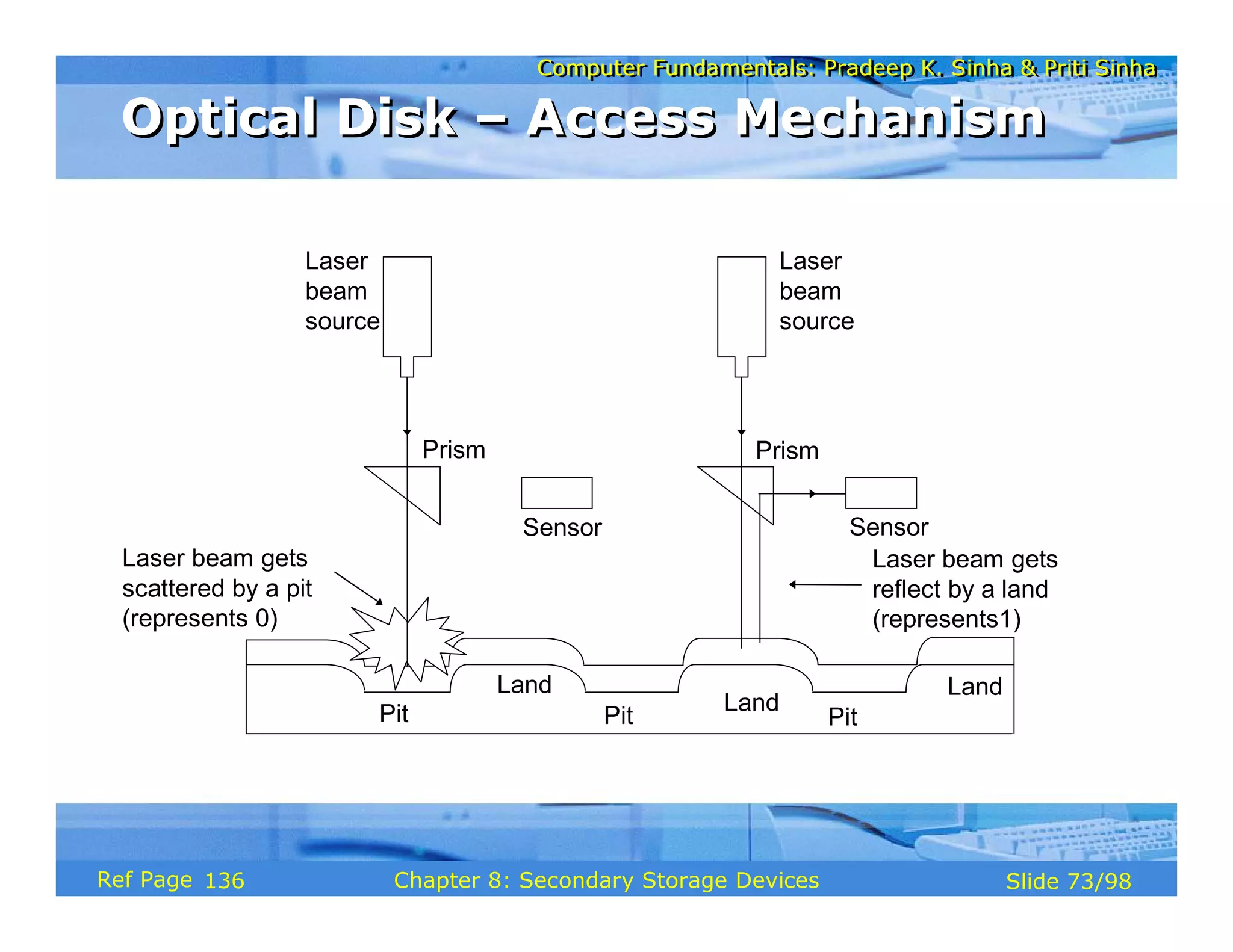
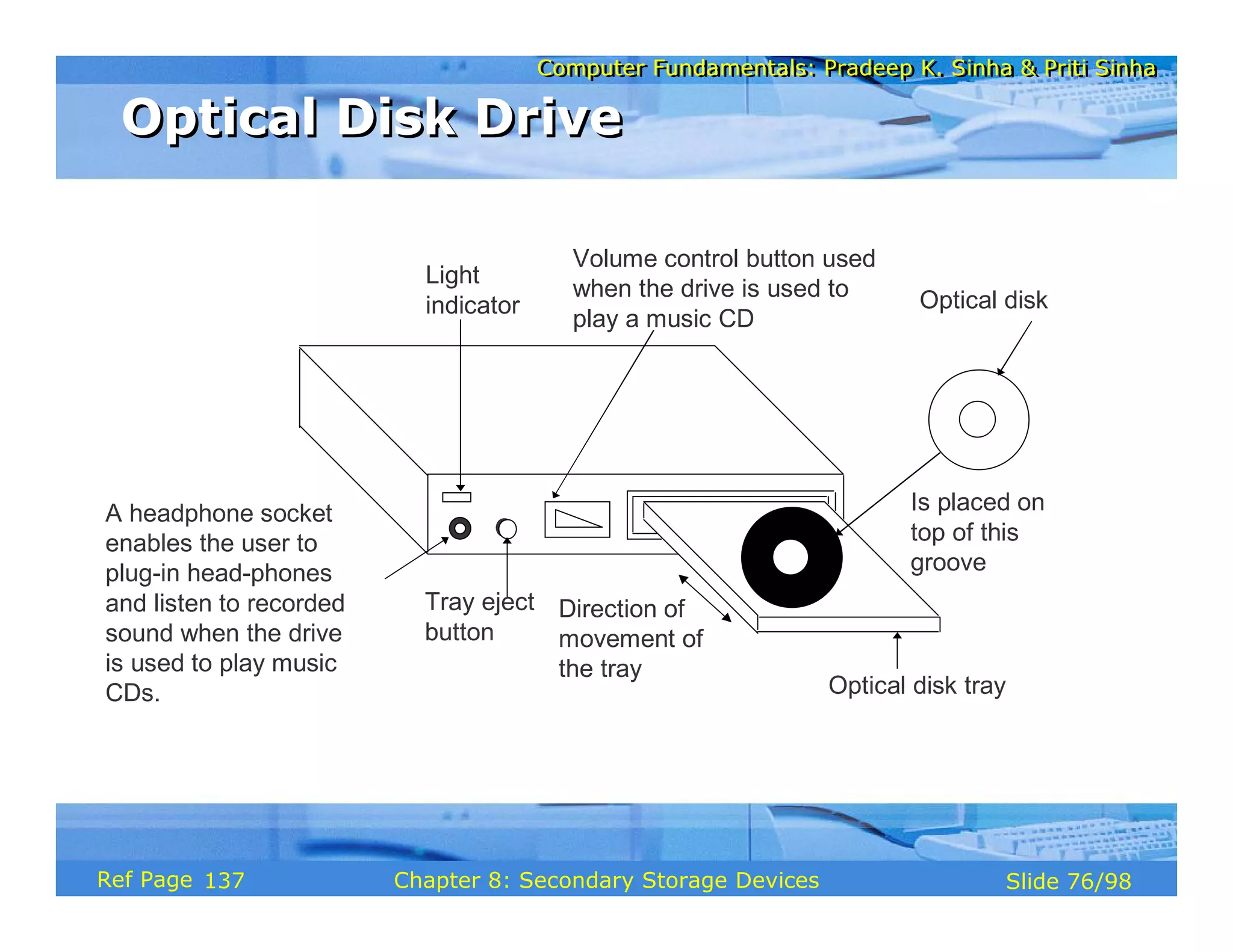
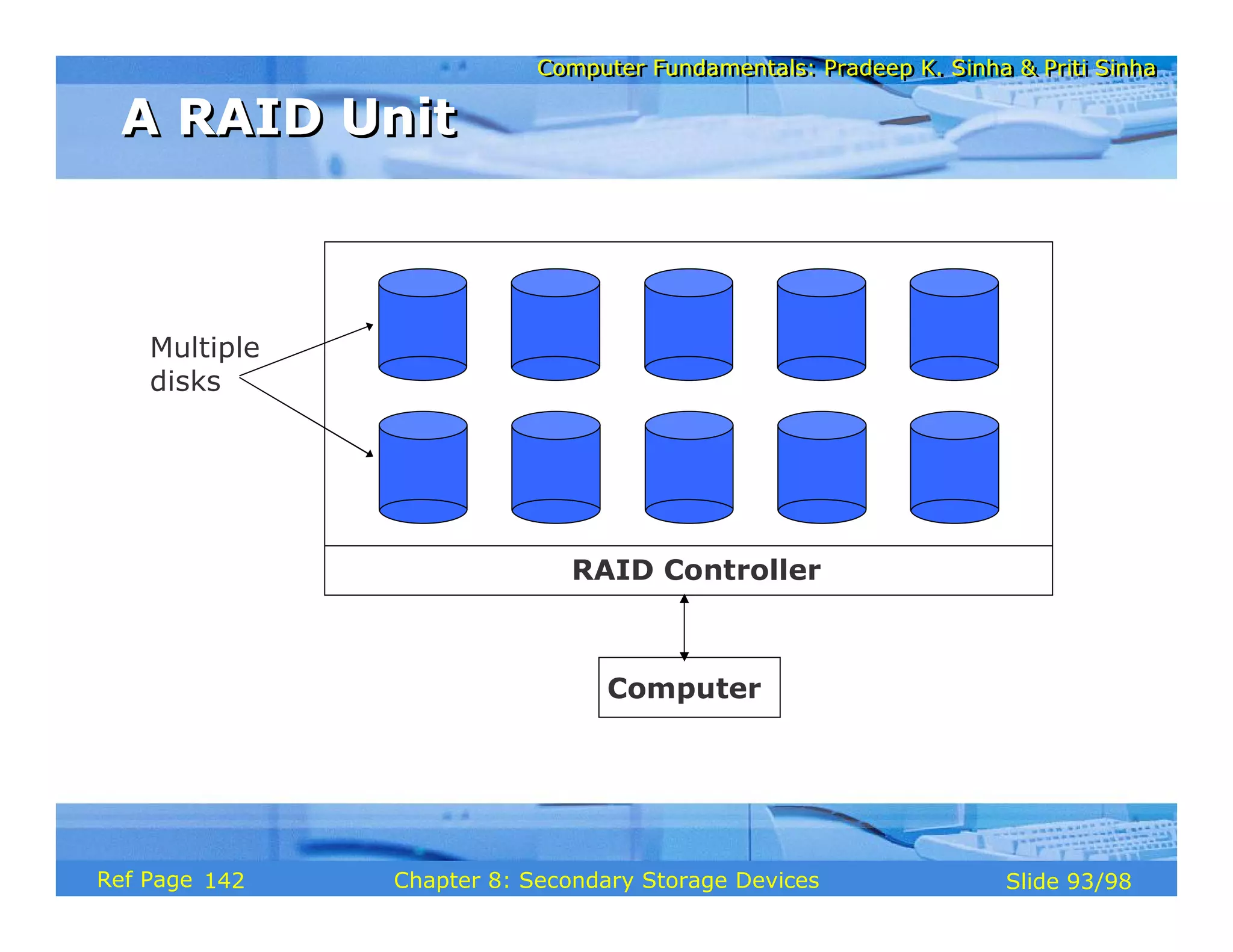
The document discusses the basic organization and operations of a computer system. It covers the five basic operations of inputting, storing, processing, outputting, and controlling. It describes the main components of a computer system including the input and output units, storage unit, arithmetic logic unit, control unit, and central processing unit. It also provides an overview of computer generations and the evolution of computers from the first generation using vacuum tubes to the modern fifth generation using microprocessors and integrated circuits.