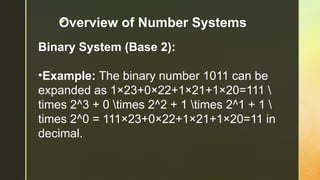
COMPUTER NUMBER SYSTEM( ACTIVITIES)INFORMATION AND COMMUNICATIONS TECHNOLOGY GRADE 7 LEARNING AREA..........................................................................................................................................................................

1. z
COMPUTER NUMBER
SYSTEM
GRADE 7_LESSON 3

2. z
The computer number system is fundamental
to understanding how computers process and
store data. For Grade 7 students, this topic
introduces them to the basic concepts of
binary, decimal, octal, and hexadecimal
number systems. These systems are essential
for grasping how computers perform
calculations, store data, and communicate
information.
Introduction

3. z

4. z

5. z

6. z

7. z

8. z

9. z

10. z

11. z

12. z

13. z

14. z

15. z

16. z

17. z

18. z
1. Decimal System (Base 10):
•The decimal system is the most familiar number
system, using digits 0-9. It’s based on powers of
10, with each digit representing a different
power.
Overview of Number Systems

19. z
1. Decimal System (Base 10):
•Example: The number 325 in decimal can be
expanded as 3×102+2×101+5×1003 times
10^2 + 2 times 10^1 + 5 times
10^03×102+2×101+5×100.
Overview of Number Systems

20. z
Binary System (Base 2):
•The binary system is the foundation of
computer operations. It uses only two digits: 0
and 1. Each digit represents a power of 2.
Overview of Number Systems

21. z
The positional notation method is one in which the
value of a digit in a number is determined by a
weight based on its position. The steps to convert
binary to decimal are as follows:
•Step 1: Multiply each digit starting from the
rightmost digit by the powers of 2. Here, we start
with 20
and increase the exponent by 1 as we move
onto the left side.
•Step 2: The sum of all these values obtained for each
digit gives the equivalent value of the given binary
Binary to Decimal Conversion Using Positional Notation
Method

22. z
Example: Convert the binary number
1011012 to a decimal number.
Solution: Observe the following steps to
understand the binary to decimal conversion.
In any binary number, the rightmost digit is
called the 'Least Significant Bit' (LSB) and the
left-most digit is called the 'Most Significant
Bit' (MSB). For a binary number with 'n' digits,
the least significant bit has a weight of 20
and
Let us understand this with the help of examples.

23. z
•Step 1: List out the exponents of 2 for all the digits starting
from the rightmost position. The first power would be
20
and as we move on to the left side it will be 21
, 22
, 23
, 24
,
25
,... In the given example, there are 6 digits, therefore,
starting from the rightmost digit, the weight of each
position from right to left is 20
, 21
, 22
, 23
, 24
, and 25
.

24. z
•Step 2: Now multiply each digit in the binary number
starting from the right with its respective weight based on
its position and evaluate the product. Observe the figure
shown below to relate to the step.

25. z

26. z
Binary System (Base 2):
•Example: The binary number 1011 can be
expanded as 1×23+0×22+1×21+1×20=111
times 2^3 + 0 times 2^2 + 1 times 2^1 + 1
times 2^0 = 111×23+0×22+1×21+1×20=11 in
decimal.
Overview of Number Systems

27. z
Octal System (Base 8):
•The octal system uses digits from 0 to 7 and is
sometimes used in computing as a more
compact representation of binary numbers.
Overview of Number Systems

28. z
Octal System (Base 8):
•Example: The octal number 57 can be
converted to decimal by expanding as
5×81+7×80=475 times 8^1 + 7 times 8^0 =
475×81+7×80=47.
Overview of Number Systems

29. z
Hexadecimal System (Base 16):
•The hexadecimal system uses digits 0-9 and
letters A-F to represent values. It is commonly
used in computing because it can represent
binary numbers more compactly.
Overview of Number Systems

30. z
Hexadecimal System (Base 16):
•Example: The hexadecimal number 1A3 can
be converted to decimal as
1×162+10×161+3×160=4191 times 16^2 + 10
times 16^1 + 3 times 16^0 =
4191×162+10×161+3×160=419.
Overview of Number Systems