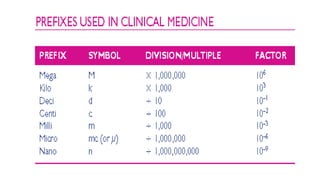
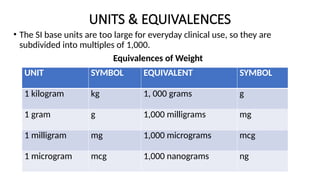
The document presents a comprehensive guide for healthcare professionals on drug calculations, emphasizing the importance of understanding and accurately performing arithmetic related to medication dosages. It covers fundamental mathematical concepts, estimation techniques, and the significance of unit conversions, alongside methods for drug dosage calculations and infusion rate determinations. The resource aims to enhance mathematical skills in clinical contexts to minimize potential medication errors.