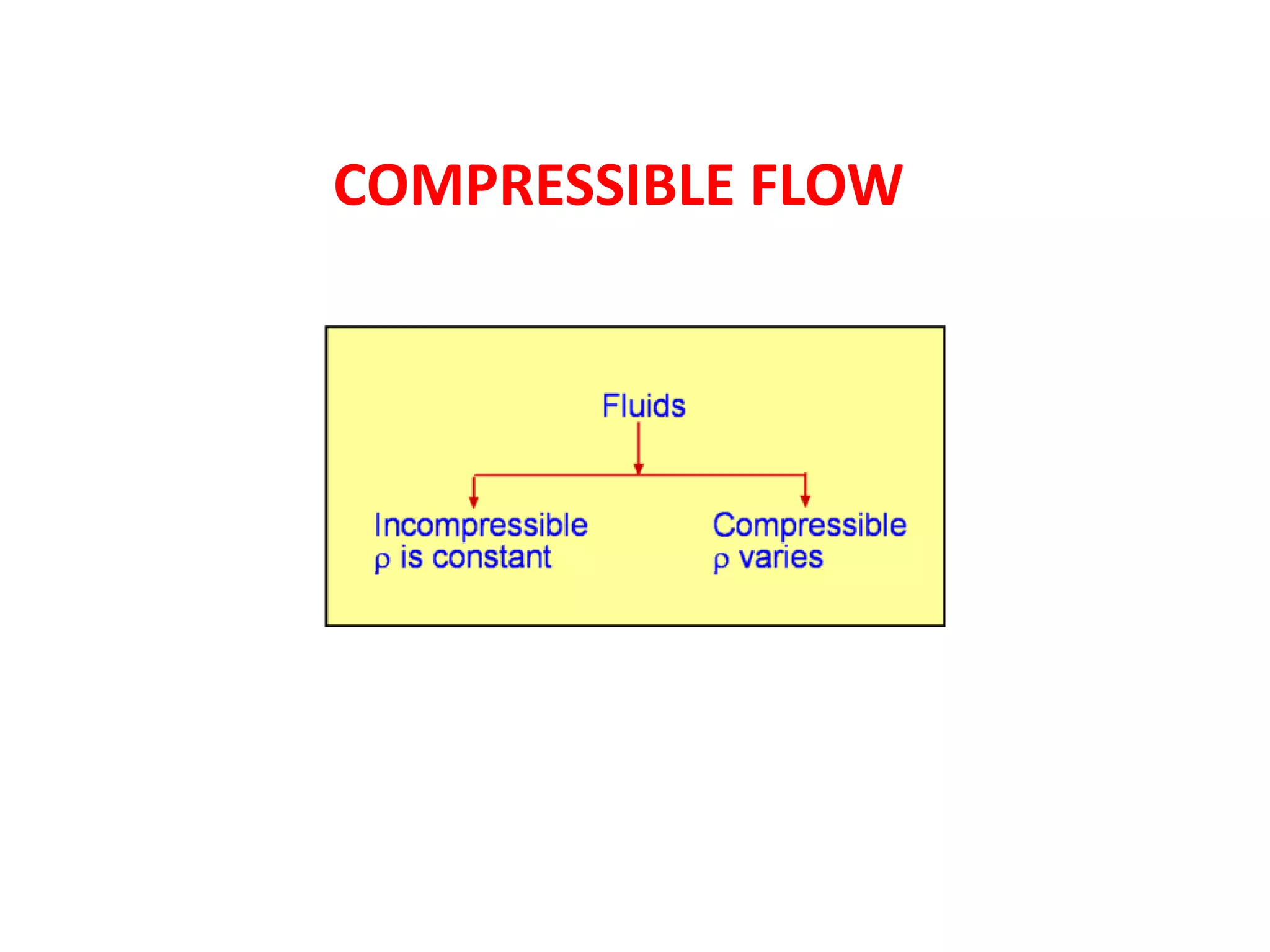
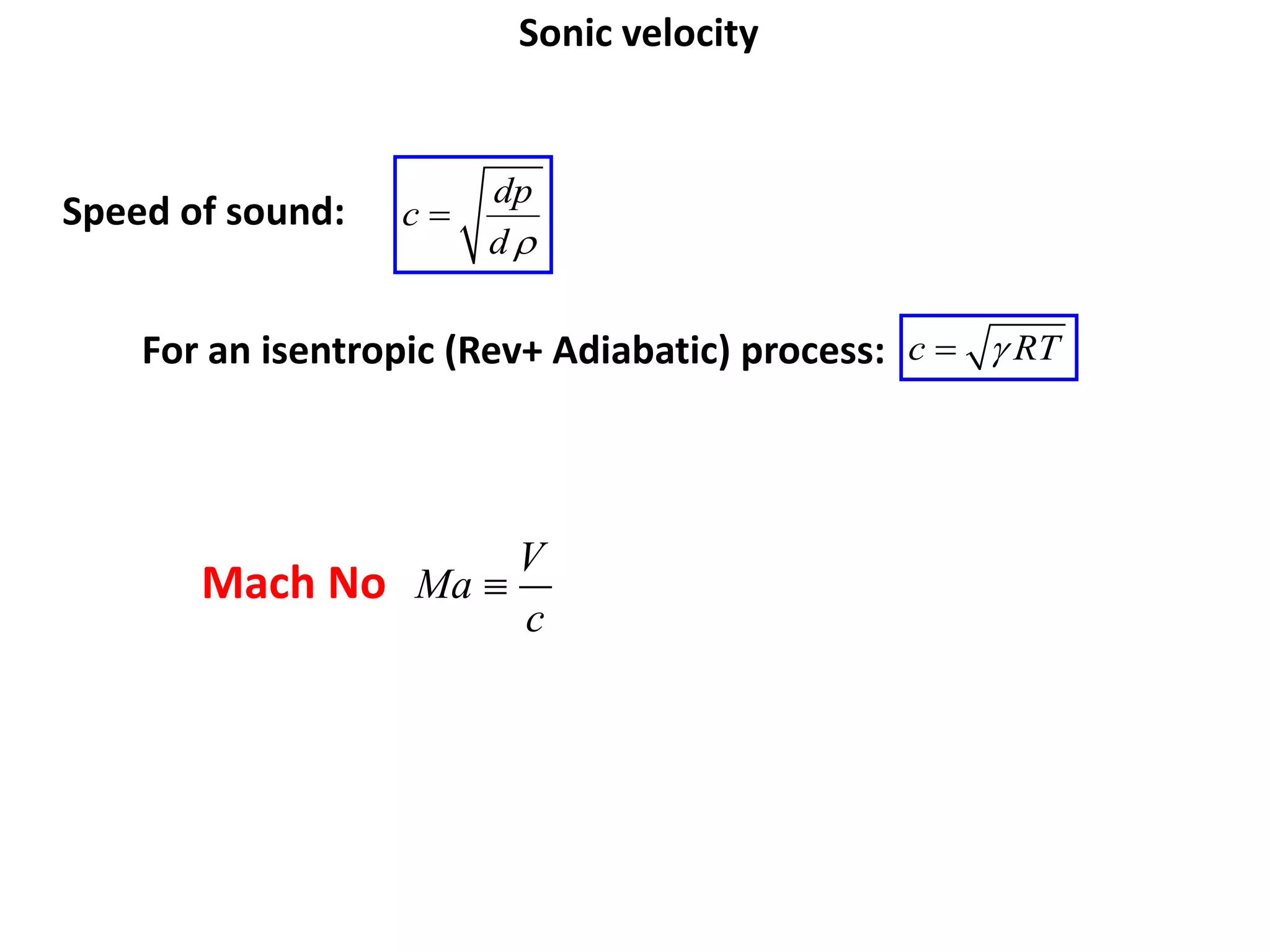
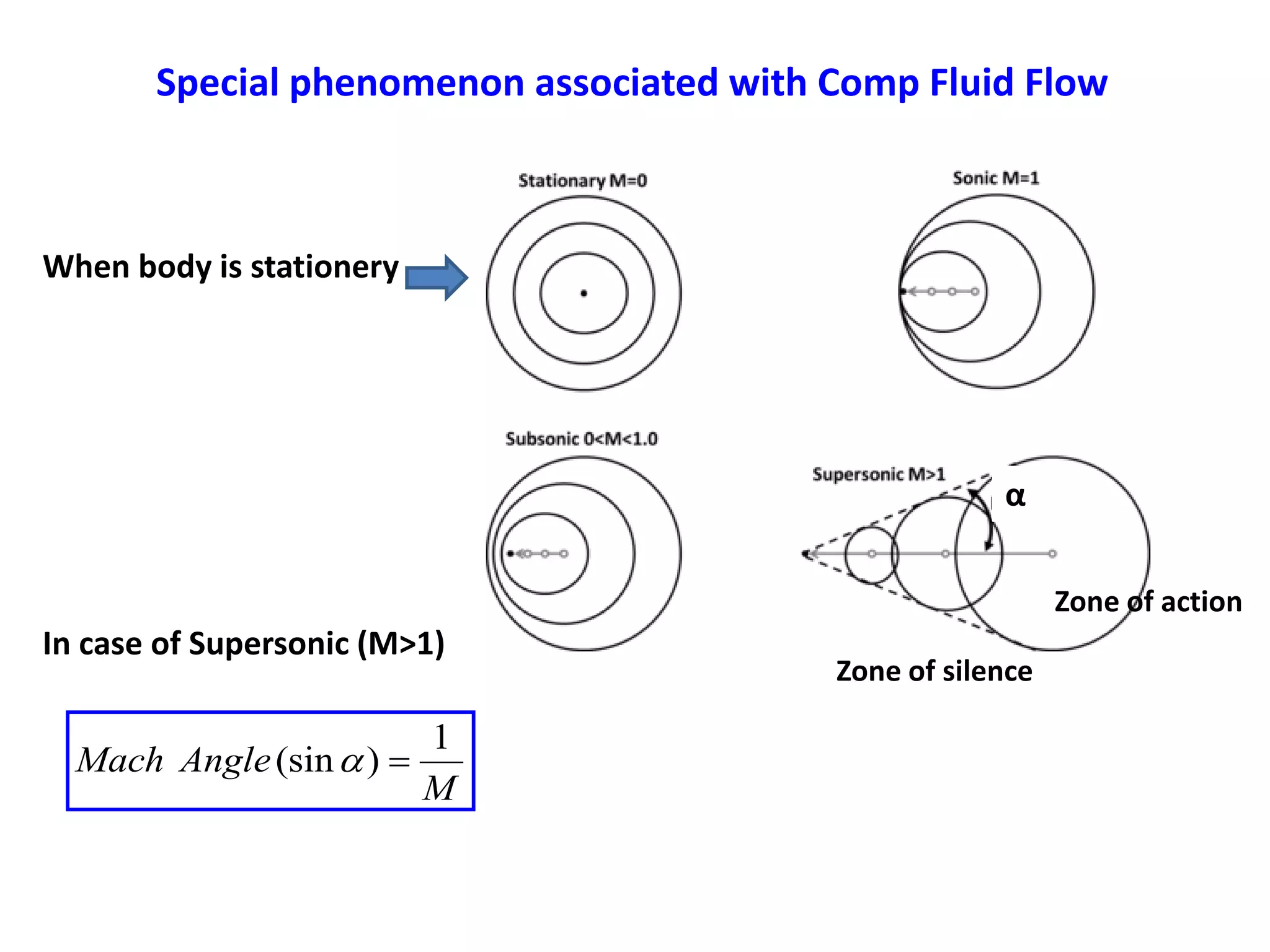
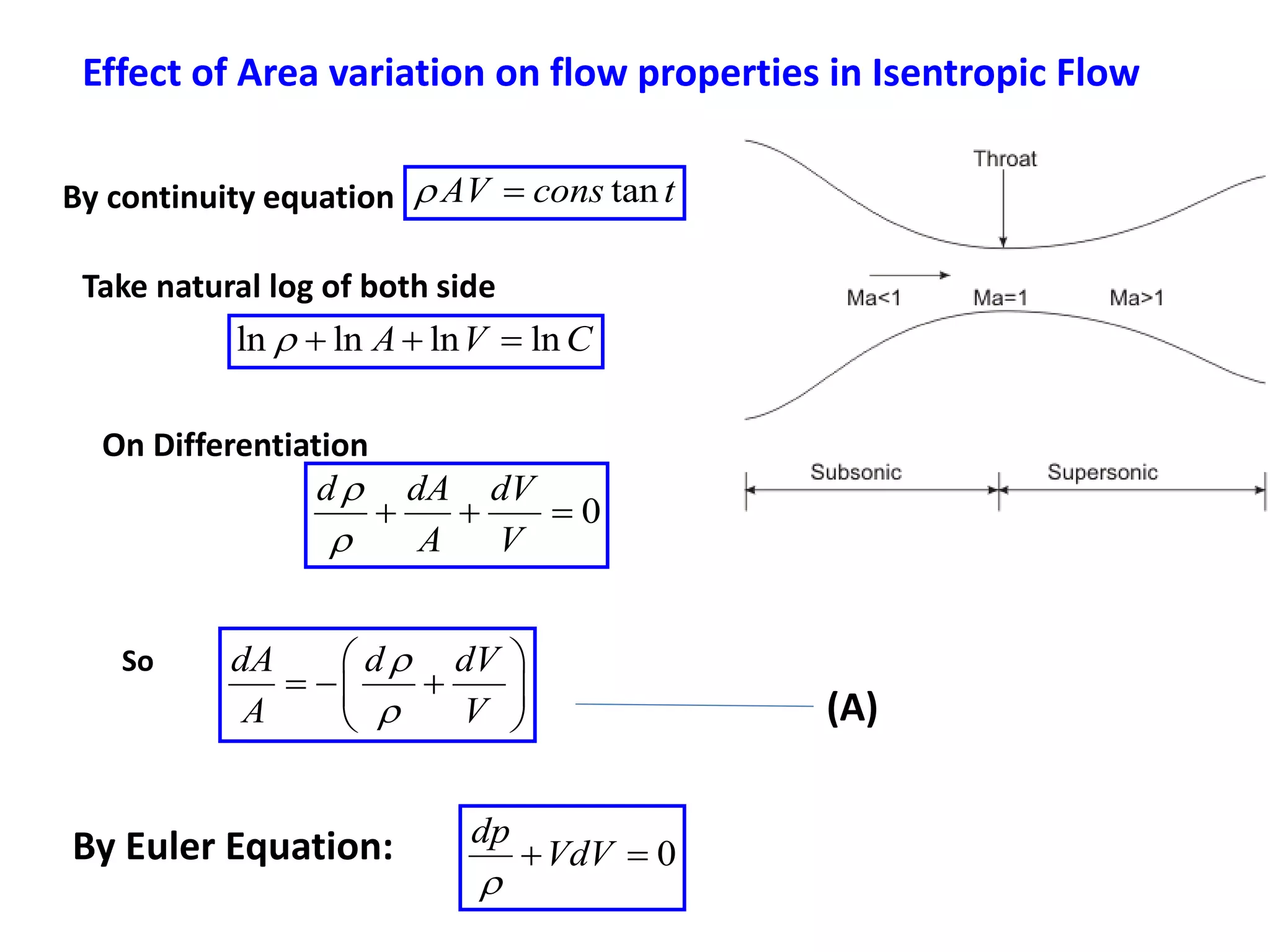
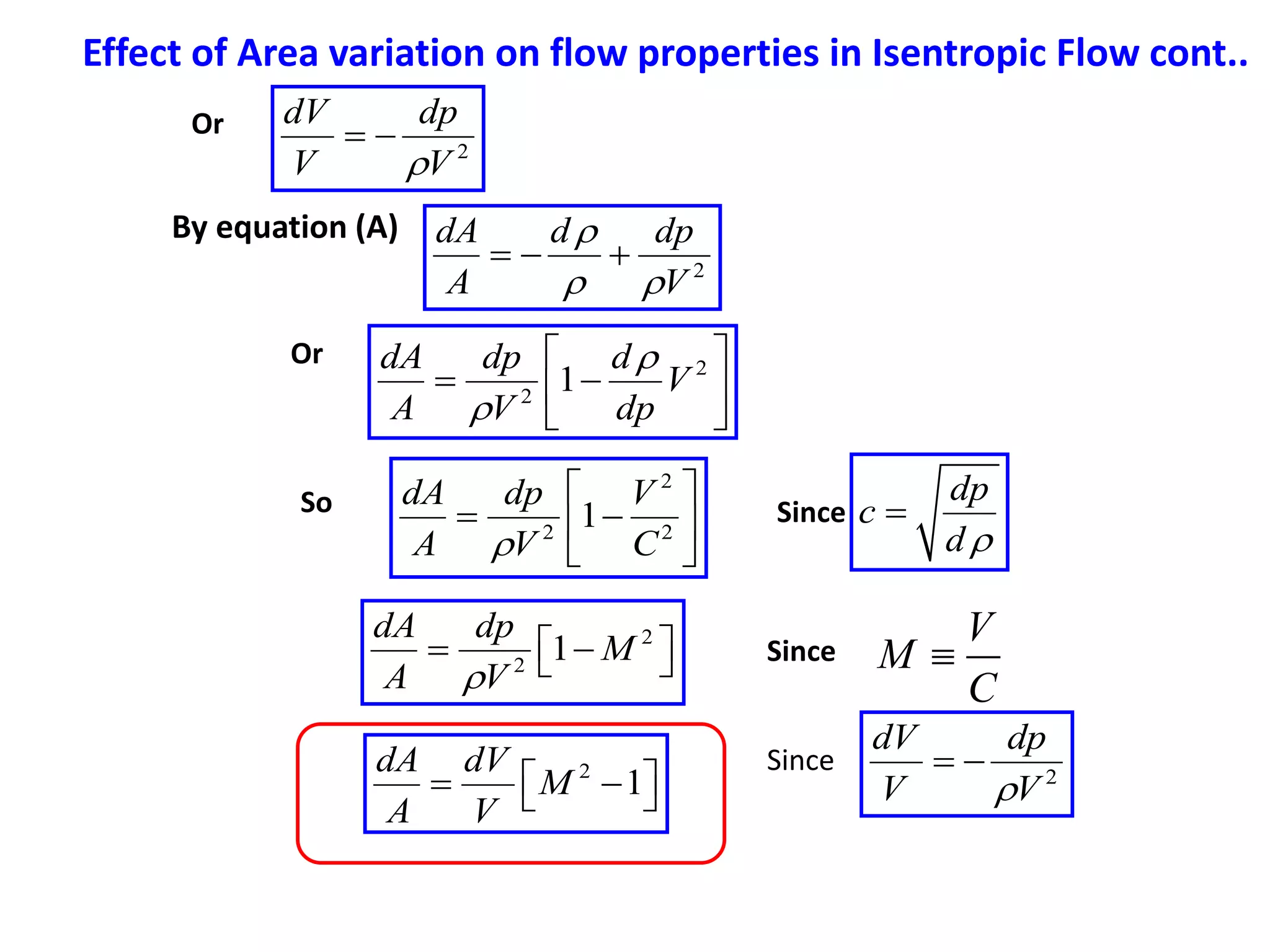
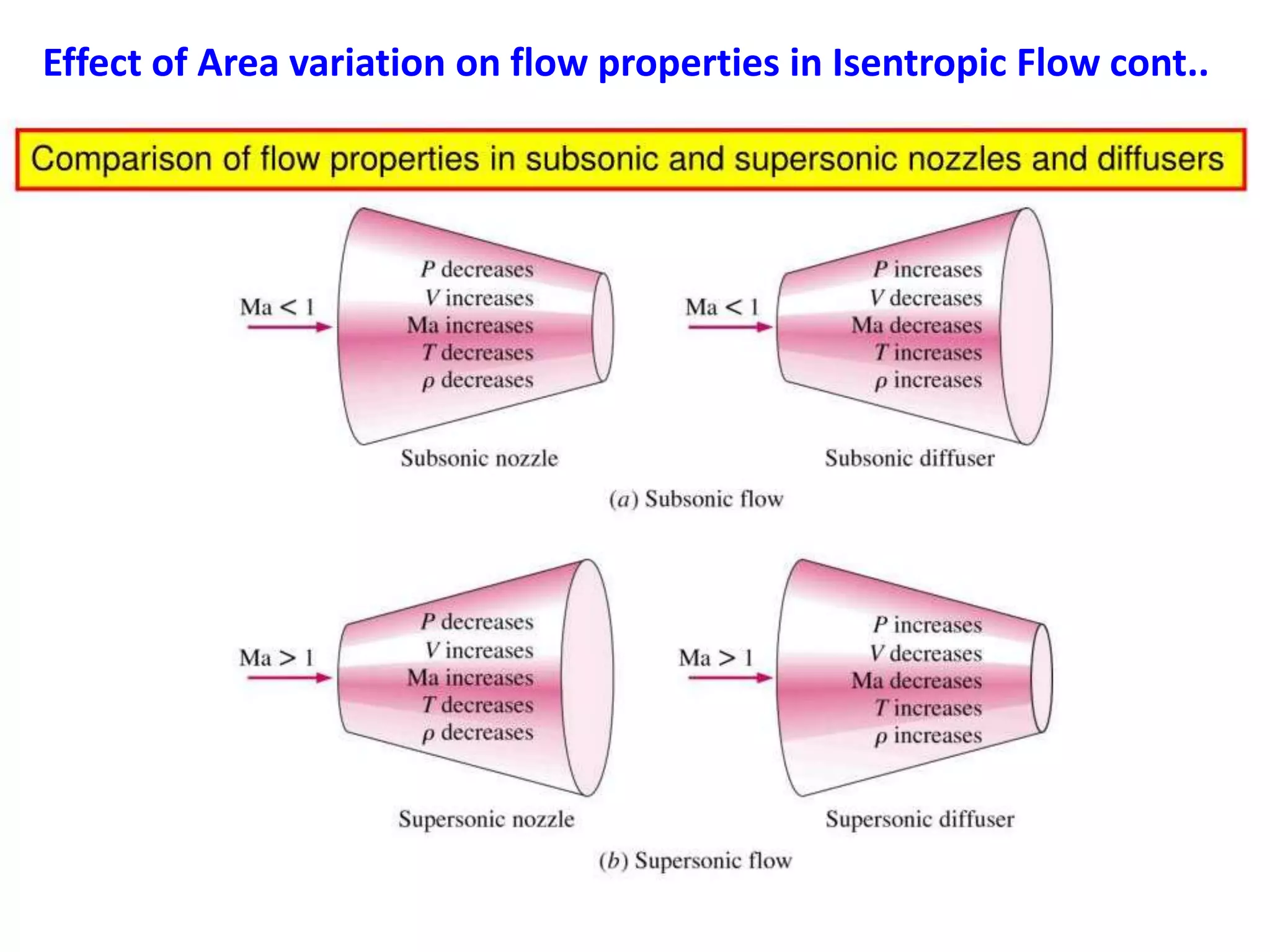
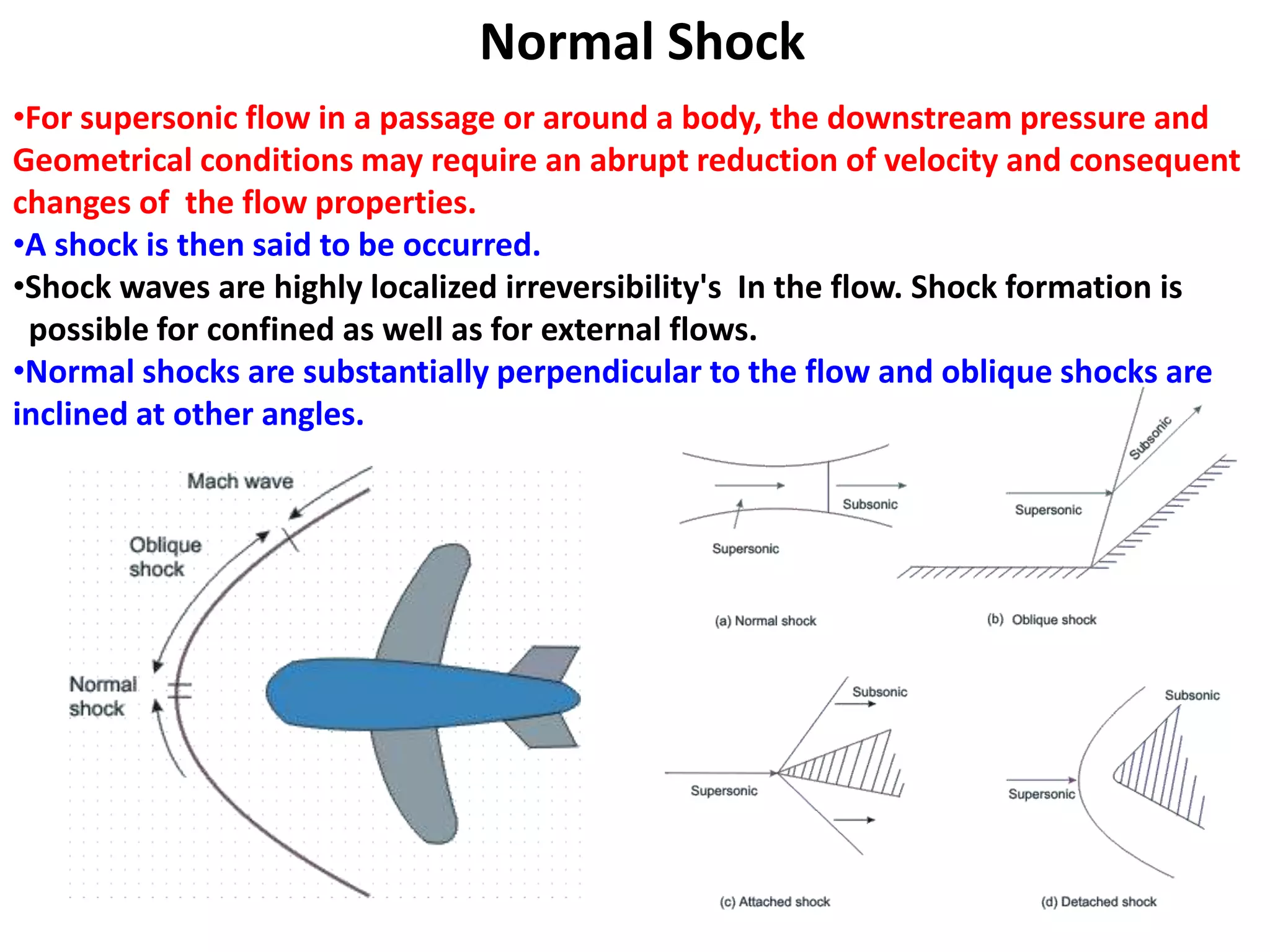
1) A normal shock wave occurs when the flow velocity decreases abruptly from supersonic to subsonic speeds. Flow properties like pressure, temperature, and density change discontinuously across the shock. 2) The flow Mach number decreases from a value greater than 1 upstream to less than 1 downstream. Pressure and temperature increase across the normal shock. 3) Normal shock waves are analyzed using the Rankine-Hugoniot equations which relate flow properties on both sides of the shock based on conservation of mass, momentum, and energy. Examples show how to calculate post-shock properties given pre-shock conditions.

1. COMPRESSIBLE FLOW

2. V
Ma
c

Mach No
7.0
Ma 
c = Speed of sound
V = Flow velocity

3. Sonic velocity
dp
c
d

For an isentropic (Rev+ Adiabatic) process: c RT


Speed of sound:
Mach No
V
Ma
c


4. Special phenomenon associated with Comp Fluid Flow
1
(sin )
Mach Angle
M
 
α
When body is stationery
In case of Supersonic (M>1)
Zone of action
Zone of silence

5. Determine the velocity of a bullet fired in the air if the Mach angle is observed to
be 300 . Given that the temperature of the air is 22 0C, density 1.2 kg/m3, ϒ = 1.4
R = 287.4 J/kg K.
Ans: C = 344.6 m/s, U = 2481 km/hr
An observer on the ground hears the sonic boom of a plane 15 km above when
The plane has gone 20 km ahead of him. Estimate the speed of flight of the plane.
Ans: M = 1.67
Calculate the velocity and Mach No of a supersonic aircraft flying at an altitude of
1000 m where the temperature is 280 0K. Sound of the aircraft is heard 2.15 sec
After the passage of aircraft an the head of on observer. Take ϒ = 1.4, R = 287.4 J/kg K.
Ans: V= 488.68 m/sec, M = 1.45
15 KM
20 KM

6. Effect of Area variation on flow properties in Isentropic Flow
By continuity equation tan
AV cons t
 
Take natural log of both side
ln ln ln ln
A V C
   
On Differentiation
0
d dA dV
A V


  
So dA d dV
A V


 
  
 
 
By Euler Equation: 0
dp
VdV

 
(A)

7. 2
dV dp
V V

 
Or
By equation (A)
2
dA d dp
A V

 
  
2
2
1
dA dp d
V
A V dp


 
 
 
 
Or
2
2 2
1
dA dp V
A V C

 
 
 
 
2
2
1
dA dp
M
A V

 
 
 
2
1
dA dV
M
A V
 
 
 
So Since
dp
c
d

V
M
C

Since
2
dV dp
V V

 
Since
Effect of Area variation on flow properties in Isentropic Flow cont..

8. Effect of Area variation on flow properties in Isentropic Flow cont..

9. Stagnation and Sonic Properties
2
0
1
2
h h V
 
Stagnation enthalpy (ho) is given by
We knew that h = CpT
So
Hence,
2
0
1
2
p p
C T C T V
 
2
2
0 1 1
1 1
2 2
p
T V
V
T TC RT



   
Or 2
0 1
1
2
T
M
T
 
 
Since Cp = ϒR/(ϒ-1)
Similarly 1 1
2
0 0 1
1
2
p T
M
p T
 
 

 

   
  
   
 
 
1 1
1 1
2
0 0 1
1
2
T
M
T
 
 

 

   
  
   
 
 
h
T
p
ρ
h0
T0
p0
ρ0

10. Stagnation and Sonic Properties contt.
There is another set of condition where the flow is sonic i.e. M=1
These Sonic or Critical properties are denoted by asterisks: p*, T* etc
2
0
1
2
p p
C T C T V
 
We know that
 
1/2
0
2
1
R
V T T


 
 
 

 
or
Max velocity is given by
1/2
max 0
2
1
R
V T


 
  

 
At M = 1, we can write the previous equations as
0 1
2
T
T




1
0 1
2
p
p


 


 
  
 
1
1
0 1
2

 




 
  
 

11. An aeroplane is flying at 1000 km/hr through still air having a pressure of 78.5 kN/m2
(abs) and temperature -8 0C. Calculate on the stagnation point on the nose of the
Plane: Stagnation Pressure, Stag. Temperature and Stag. density. . Take for air =
R = 287 J/kg K and ϒ = 1.4.
Ans: p0 = 126.1 kN/m2, T0 = 30.4 0C, ρ0 = 1.448 kg/m3
Air has a velocity of 1000 km/hr at a pressure of 9.81 kN/m2 vacuum and a temp of
47 oC. Compute its stagnation properties and the local Mach No. Take atm air =
98.1 kN/m2, R = 287 J/kg K and ϒ = 1.4.
Ans: p0 = 131.3 kN/m2, T0 = 85.4 0C, ρ0 = 1.276 kg/m3

12. Normal Shock
•For supersonic flow in a passage or around a body, the downstream pressure and
Geometrical conditions may require an abrupt reduction of velocity and consequent
changes of the flow properties.
•A shock is then said to be occurred.
•Shock waves are highly localized irreversibility's In the flow. Shock formation is
possible for confined as well as for external flows.
•Normal shocks are substantially perpendicular to the flow and oblique shocks are
inclined at other angles.

14. Flow Properties Across a Normal Shock
1 2
A1
P1
T1
M1
A2
P2
T2
M2
Normal
Shock
 
 
2
1
2
2
1 2
1
1
M
p
p M





 
 
2
1
2
2
1 2
1 1 2
1 1 2
M
T
T M


 
 
 

 
 
 
Mach No of a normal shock wave is always greater than
Unity in the upstream and less than Unity in the downstream.
 
 
2
1
2
2 2
1
1 2
2 1
M
M
M

 
 

 
Shock strength is defined by:
 
2
2 1
1
1
2
1
1
p p
Shock Strength M
p



  

 
 
2
1
2
2
1 1
1
1 2
M
M


 


 
Rankine – Hugoniot Equations

15. Calculate the downstream Mach No, pressure, temperature and shock strength of a
Normal shock wave observed to occur in an air nozzle at
M1 = 2, p1 = 20 kN/m2, T1 = 300 K
Ans: p2 = 90 kN/m2, M2 = 0.575, T2 = 510 K, Shock strength = 3.5
For a normal shock wave in air, Mach No is 2. If the atmospheric pressure and air
Density are 26.5 kN/m2 and 0.413 kg/m3 respectively, determine the flow conditions
Before and after the shock wave. Take ϒ = 1.4.
Ans: M2 = 0.577, p2 = 119.25 kN/m2, ρ2 = 1.101 kg/m3, T1 = -49.4 0C
T2 = 104.3 0C, V1 = 599.4 m/s, V2 = 224.6 m/s

16. Conclusion from 1D analysis of a Normal Shock:
• A normal shock can occur only if M1 >1
• M2 must be less than 1 for a normal shock
• Entropy rise across a shock increases
• p2/p1 and T2/T1 increases with M1

17. Thank You