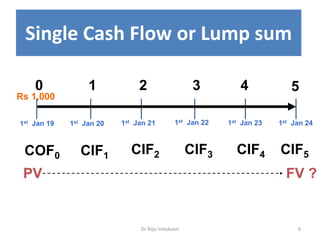
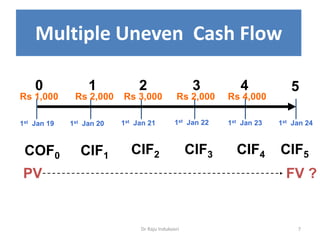
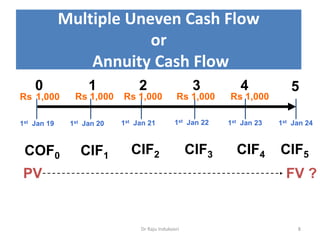
This document discusses the concept of compounding in finance. It defines compounding as the process of earning interest on interest over multiple periods of time. The document outlines tools for calculating the future value of single and multiple cash flows using compound interest formulas. These include formulas for determining the future value of a lump sum, annuities with regular payments, and sinking funds. The document also explores how the frequency of compounding affects interest earned, with more frequent compounding resulting in higher returns.

1. Dr Raju Indukoori 1
Compounding
(Future Value of Money)
S S N Raju Indukoori

2. Dr Raju Indukoori 2
Future Value of Money (FVM)
COMPOUNDING

3. Dr Raju Indukoori 3
Future Value of Money
It is the Process of
Compounding
PV of money
for a
Future Period of Time

4. Dr Raju Indukoori 4
Purpose of compounding
1) To Know Future value of single CF
• Bank Deposits
• Retirement plan
2) To Know Future value of multiple CF
1) Irregular
» Portfolio Investments
» Business Participation
2) Regular
a) Even CF
» Recurring Deposits
» Future redemption (Sinking fund)
b) Uneven CF
» Chit funds

5. Compounding – Time Line

6. Dr Raju Indukoori 6
Single Cash Flow or Lump sum
0 1 2 3 54
1st Jan 19
CIF2 CIF3 CIF4CIF1 CIF5COF0
Rs 1,000
1st Jan 20 1st Jan 221st Jan 21 1st Jan 23 1st Jan 24
PV FV ?

7. Dr Raju Indukoori 7
Multiple Uneven Cash Flow
0 1 2 3 54
1st Jan 19
CIF2 CIF3 CIF4CIF1 CIF5COF0
Rs 1,000
1st Jan 20 1st Jan 221st Jan 21 1st Jan 23 1st Jan 24
PV FV ?
Rs 2,000 Rs 3,000 Rs 2,000 Rs 4,000

8. Dr Raju Indukoori 8
Multiple Uneven Cash Flow
or
Annuity Cash Flow
0 1 2 3 54
1st Jan 19
CIF2 CIF3 CIF4CIF1 CIF5COF0
Rs 1,000
1st Jan 20 1st Jan 221st Jan 21 1st Jan 23 1st Jan 24
PV FV ?
Rs 1,000 Rs 1,000 Rs 1,000 Rs 1,000

9. Compounding Tools

10. Dr Raju Indukoori 10
Compounding Tools
1) Future value of a Single CF
2) Future value of Multiple CF
a) Regular Cash Flows
• Even Cash Flows (Annuities)
• Uneven Cash Flows
b) Irregular Cash Flows
3) Sinking fund factor

11. Dr Raju Indukoori 11
Future Value of a Single Cash Flow
FV = PV(1+r)n
= PV (FVIFnR)

12. Dr Raju Indukoori 12
FUTURE VALUE OF SINGLE CASH FLOW
An Example
• Deposit with a Bank : Rs 1,00,000
• Rate of Interest (k) : 9%
• Period (n) : 5 Years
FV = 1,00,000(1+0.09)5 = Rs 1,53,862
Or using Time value compounding table
FV = 1,00,000 (1.5386) = Rs 1,53,860

13. Dr Raju Indukoori 13
FUTURE VALUE OF ANNUITIES
FV = A (FVIFA)







 

r
1-r)(1
A
n
FVn

14. Dr Raju Indukoori 14
FUTURE VALUE OF ANNUITIES
- An Example
• Annual Insurance Premium : Rs 50,000
• Rate of Interest (k) : 9%
• Period (n) : 20 Years
FV = = 25,58,000
Or
FV = 50000 (51.1601) = 25,58,005







 
0.09
1-200.09)(1
50000

15. Dr Raju Indukoori 15
Sinking Fund Factor
Equated Annual Installment to meet future redemption
A = FVA (Sinking Fund Factor)










1r)(1
r
FVn
n







FVIFA
1
FVn

16. Dr Raju Indukoori 16
Sinking Fund Factor
An Example
• Future Payment : Rs 1,00,000
• Rate of Interest (k) : 10%
• Period (n) : 5 Years
A = 16,380
Or
= 16,380










15.10)0(1
0.10
1,00,000







6.105
1
1,00,000

17. Dr Raju Indukoori 17
Yearly Compoundingm = 1
Role of Multiple Compounding
m=Frequency of Compounding
m = 2
m = 3
m = 4
m = 8
m = 12
m = 52
m = 365
m = ∞
Semi Annual Compounding
Once in 4 months
Quarterly Compounding
Once in 45 days
Monthly Compounding
Weekly Compounding
Daily Compounding
Continuous Compounding

18. Dr Raju Indukoori 18
Role of Multiple Compounding
‘m’ and TVM
• As ‘m’ increases, compounded value
increases, vice versa
• As ‘m’ increases, discounted value decreases,
vice versa

19. Dr Raju Indukoori 19
Role of Multiple Compounding
• Minimum value of ‘m’ is 1
If m = 1, then ERR = R
• As ‘m’ increases r also
increases, Vice versa
If m > 1, then R > ERR
• Maximum value of ‘ERR’ is
there when ‘m’ is at
continuous compounding
100*)1m
r
1(ERR
365m1








m
 
7183.2
1ERR e
gCompoundinContinous


e
r
‘m’ and Effective Rate of Return (ERR)

20. Dr Raju Indukoori 20
ERR = 10.00m = 1
EXAMPLE
Multiple Compounding
PV: 1,00,000, Rate of Interest (R): 10%, Period (n) : 5 Years
m = 2
m = 3
m = 4
m = 8
m = 12
m = 52
m = 365
m = ∞
FV = 110,000
FV = 110,337
FV = 110,381
FV = 110,449
FV = 110,471
FV = 110,506
FV = 110,515
FV = 110,517
FV = 110,250
ERR = 10.51
ERR = 10.52
ERR = 10.52
ERR = 10.38
ERR = 10.45
ERR = 10.47
ERR = 10.25
ERR = 10.34

21. Dr Raju Indukoori 21
Any Questions

22. Dr Raju Indukoori 22
Thank You
Dr Raju Indukoori