The document details the principles and applications of EDTA titrations, emphasizing its role as a chelating agent for complexometric titrations of divalent and polyvalent metal ions, with a stoichiometry typically of 1:1. It discusses the formation constants of EDTA complexes, the effect of pH on titration curves, and the use of indicators in these titrations, along with several practical examples and calculations. Overall, this document serves as a comprehensive guide on the methodologies and chemical dynamics involved in EDTA titrations.

1. 1
EDTA Titrations
Ethylenediaminetetraacetic acid disodium salt
(EDTA) is the most frequently used chelate in
complexometric titrations. Usually, the
disodium salt is used due to its good
solubility. EDTA is used for titrations of
divalent and polyvalent metal ions. The
stoichiometry of EDTA reactions with metal
ions is usually 1:1. Therefore, calculations
involved are simple and straightforward.
Since EDTA is a polydentate ligand, it is a
good chelating agent and its chelates with
metal ions have good stability.

2. 2

3. 3
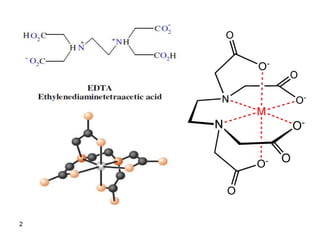
EDTA Equilibria
EDTA can be regarded as H4Y where in solution
we will have, in addition to H4Y, the following
species: H3Y-, H2Y2-, HY3-, and Y4-. The
amount of each species depends on the pH
of the solution where:
a4 = [Y4-]/CT where:
CT = [H4Y] + [H3Y-] + [H2Y2-] + [HY3-] + [Y4-]
The species Y4- is the ligand species in EDTA
titrations and thus should be looked at
carefully.

4. 4

5. 5
The Formation Constant
Reaction of EDTA with a metal ion to form a
chelate is a simple reaction. For example, EDTA
reacts with Ca2+ ions to form a Ca-EDTA chelate
forming the basis for estimation of water
hardness. The reaction can be represented by
the following equation:
Ca2+ + Y4- = CaY2- kf = 5.0x1010
Kf = [CaY2-]/[Ca2+][Y4-]
The formation constant is very high and the
reaction between Ca2+ and Y4- can be considered
quantitative. Therefore, if equivalent amounts of
Ca2+ and Y4- were mixed together, an equivalent
amount of CaY2- will be formed.

6. 6
Formation Constants for EDTA Complexes
Cation KMY Cation KMY
Ag+ 2.1 x 107 Cu2+ 6.3 x 1018
Mg2+ 4.9 x 108 Zn2+ 3.2 x 1016
Ca2+ 5.0 x1010 Cd2+ 2.9 x 1016
Sr2+ 4.3 x 108 Hg2+ 6.3 x 1021
Ba2+ 5.8 x 107 Pb2+ 1.1 x 1018
Mn2+ 6.2 x1013 Al3+ 1.3 x 1016
Fe2+ 2.1 x1014 Fe3+ 1.3 x 1025
Co2+ 2.0 x1016 V3+ 7.9 x 1025
Ni2+ 4.2 x1018 Th4+ 1.6 x 1023

7. 7
Minimum pH for effective titrations
of various metal ions with EDTA.

8. 8

9. 9
Titration Curves
In most cases, a titration is performed by addition of
the titrant (EDTA) to the metal ion solution adjusted
to appropriate pH and in presence of a suitable
indicator. The break in the titration curve is
dependent on:
1. The value of the formation constant.
2. The concentrations of EDTA and metal ion.
3. The pH of the solution
As for acid-base titrations, the break in the titration
curve increases as kf increases and as the
concentration of reactants is increased. The pH
effect on the break of the titration curve is such that
sharper breaks are obtained at higher pH values.

10. 10

11. 11
Indicators
The indicator is usually a weaker chelate
forming ligand. The indicator has a
color when free in solution and has a
clearly different color in the chelate.
The following equilibrium describes the
function of an indicator (H3In) in a Mg2+
reaction with EDTA:
MgIn- (Color 1) + Y4- D MgY2- + In3- (Color 2)

12. 12

13. 13

14. 14
Example
Calculate the pCa of a solution at pH 10 after
addition of 100 mL of 0.10 M Ca2+ to 100 mL
of 0.10 M EDTA. a4 at pH 10 is 0.35. kf =
5.0x1010
Solution
Ca2+ + Y4- = CaY2-
mmol Ca2+ = 0.10 x 100 = 10
mmol EDTA = 0.10 x 100 = 10
mmol CaY2- = 10
[CaY2-] = 10/200 = 0.05 M
Therefore, Ca2+ will be produced from partial
dissociation of the complex

15. 15
Ca2+ + Y4- D CaY2-
CT = [H4Y] + [H3Y-] + [H2Y2-] + [HY3-] + [Y4-]
Kf = [CaY2-]/[Ca2+]a4CT
[Ca2+] = CT
5.0x1010 = 0.05/([Ca2+]2 x 0.35)
[Ca2+] = 1.7x10-6 M
pCa = 5.77
Using the same type of calculation we
are used to perform, one can write the
following:

16. 16
Kf = [CaY2-]/[Ca2+][Y4-]
5.0x1010 = (0.05 – x)/(x* a4 x)
assume that 0.05>>x
x = 1.7x10-6
Relative error = (1.7x10-6/0.05) x 100 = 3.4x10-3%
[Ca2+] = 1.7x10-6 M
pCa = 5.77

17. 17
Calculate the titer of a 0.100 M EDTA solution in
terms of mg CaCO3 (FW = 100.0) per mL
EDTA
The EDTA concentration is 0.100 mmol/mL, therefore,
the point here is to calculate the mg CaCO3 reacting
with 0.100 mmol EDTA. We know that EDTA reacts
with metal ions in a 1:1 ratio. Therefore 0.100 mmol
EDTA will react with 0.100 mmol CaCO3.
mmol CaCO3 = mmol EDTA
mg CaCO3/100 = 0.1 * 1
mg CaCO3 = 10.0

18. 18
Example
An EDTA solution is standardized against high
purity CaCO3 by dissolving 0.3982 g of
CaCO3 in HCl and adjusting the pH to 10. The
solution is then titrated with EDTA requiring
38.26 mL. Find the molarity of EDTA.
Solution
EDTA reacts with metal ions in a 1:1 ratio.
Therefore,
mmol CaCO3 = mmol EDTA
mg/FW = Molarity x VmL
398.2/100.0 = M x 38.26, MEDTA = 0.1041

19. 19
Example
Find pCa in a 100 mL solution of 0.10 M Ca2+ at pH
10 after addition of 0, 25, 50, 100, 150, and 200
mL of 0.10 M EDTA. a4 at pH 10 is 0.35. kf =
5x1010
Solution
Again, we should remember that EDTA reactions
with metal ions are 1:1 reactions. Therefore, we
have:
Ca2+ + Y4- D CaY2- kf = 5.0x1010
1. After addition of 0 mL EDTA
[Ca2+] = 0.10 M pCa = 1.00

20. 20
2. After addition of 25 mL EDTA
Initial mmol Ca2+ = 0.10 x 100 = 10
mmol EDTA added = 0.10 x 25 = 2.5
mmol Ca2+ left = 10 – 2.5 = 7.5
[Ca2+]left = 7.5/125 = 0.06 M
In fact, this calcium concentration is the major source
of calcium in solution since the amount of calcium
coming from dissociation of the chelate is very
small, especially in presence of Ca2+ left in solution.
However, let us calculate the amount of calcium
released from the chelate:
mmol CaY2- formed = 2.5
[CaY2-] = 2.5/125 = 0.02 M

21. 21
Kf = [CaY2-]/[Ca2+][Y4-]
5x1010 = (0.02 – x)/((0.06 + x) * a4 x)
assume that 0.02>>x
x = 1.9x10-11
The assumption is valid even without verification.
[Ca2+] = 0.06 + 1.9x10-11 = 0.06 M
pCa = 1.22

22. 22
3. After addition of 50 mL EDTA
mmol EDTA added = 0.10 x 50 = 5.0
mmol Ca2+ left = 10 – 5.0 = 5.0
[Ca2+]left = 5.0/150 = 0.033 M
We will see by similar calculation as in step
above that the amount of Ca2+ coming from
dissociation of the chelate is exceedingly
small as compared to amount left. However,
for the sake of practice let us perform the
calculation:
mmol CaY2- formed = 5.0
[CaY2-] = 5.0/150 = 0.033 M

23. 23
Kf = [CaY2-]/[Ca2+][Y4-]
5x1010 = (0.033 – x)/((0.033 + x)* a4 x)
assume that 0.033>>x
x = 5.7x10-11
The assumption is valid even without verification.
[Ca2+] = 0.033+ 5.7x10-11 = 0.033 M
pCa = 1.48

24. 24
4. After addition of 100 mL EDTA
mmol EDTA added = 0.10 x 100 = 10
mmol Ca2+ left = 10 – 10 = 0
This is the equivalence point. The only source for Ca2+
is the dissociation of the Chelate
mmol CaY2- formed = 10
[CaY2-] = 10/200 = 0.05 M
Ca2+ + Y4- D CaY2- kf = 5.0x1010

25. 25
Kf = [CaY2-]/[Ca2+][Y4-]
5x105 = (0.05 – x)/(x* a4 x)
assume that 0.05>>x, x = 1.7x10-6
Relative error = (1.7x10-6/0.05) x 100 = 3.4x10-3%
[Ca2+] = 1.7x10-6 M, pCa = 5.77
5. After addition of 150 mL EDTA
mmol EDTA added = 0.10 x 150 = 15
mmol EDTA excess = 15 – 10 = 5.0
CT = 5.0/250 = 0.02 M
mmol CaY2- = 10
[CaY2-] = 10/250 = 0.04 M
Ca2+ + Y4- D CaY2- kf = 5.0x1010

26. 26
Kf = [CaY2-]/[Ca2+][Y4-]
5x1010 = (0.04 – x)/(x* a4(0.02 + x) )
assume that 0.02>>x
x = 1.1x10-10
The assumption is valid
[Ca2+] = 1.1x10-10 M
pCa = 9.95

27. 27
6. After addition of 200 mL EDTA
mmol EDTA added = 0.10 x 200 = 20
mmol EDTA excess = 20 – 10 = 10
CT = 10/300 = 0.033 M
mmol CaY2- = 10
[CaY2-] = 10/300 = 0.033 M
Ca2+ + Y4- D CaY2- kf = 5.0x1010

28. 28
Kf = [CaY2-]/[Ca2+][Y4-]
5x1010 = (0.033 – x)/(x* a4(0.033 + x) )
assume that 0.033>>x
x = 5.7x10-11
The assumption is undoubtedly valid
[Ca2+] = 5.7 x10-11 M
pCa = 10.24