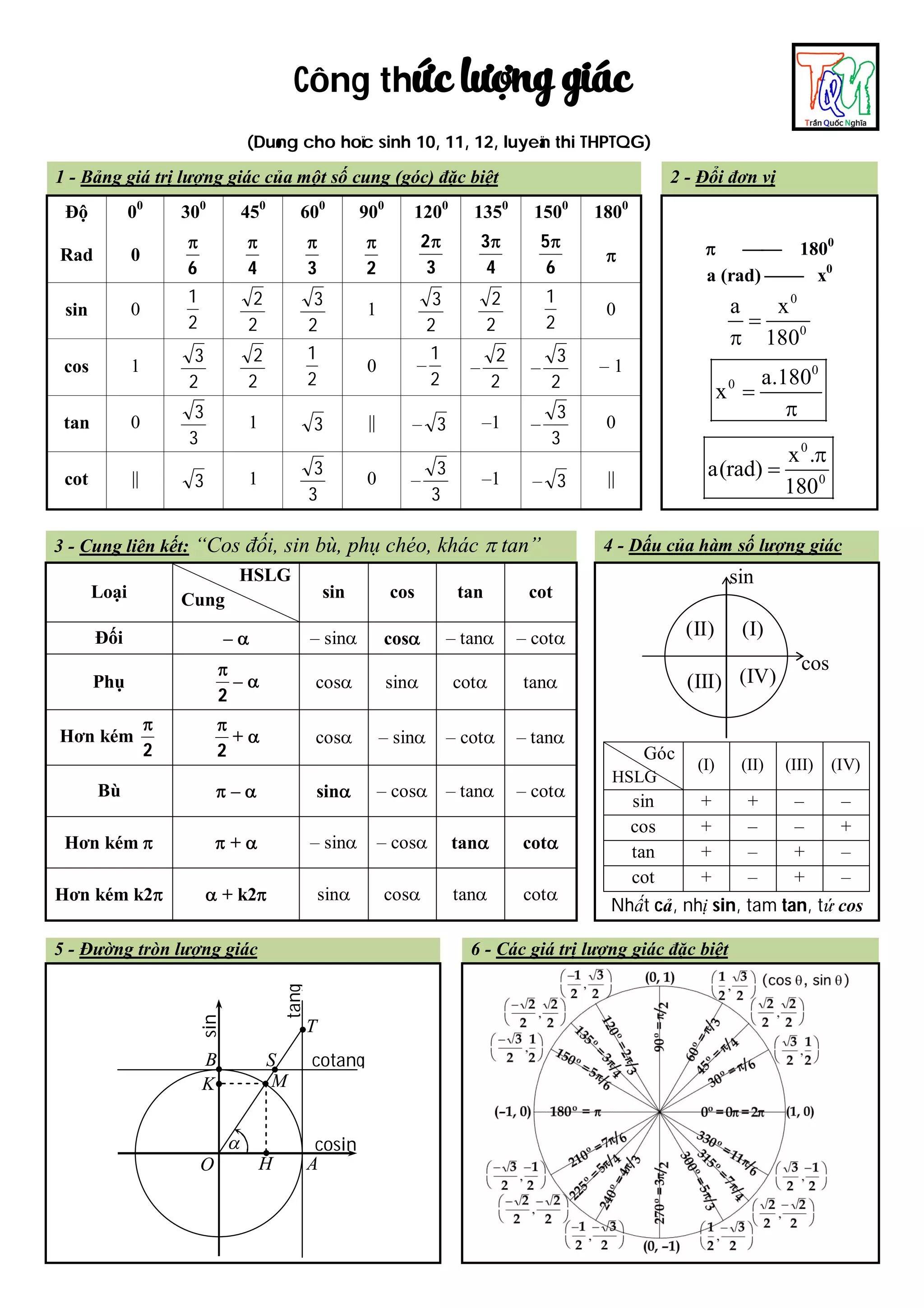
Tài liệu trình bày các công thức lượng giác quan trọng cho học sinh lớp 10, 11, 12, bao gồm bảng giá trị lượng giác của một số cung đặc biệt, dấu hiệu của hàm số lượng giác, và công thức biến đổi giữa các hàm số lượng giác. Nó cũng bao gồm các công thức cộng, nhân đôi, hạ bậc và biến đổi tích thành tổng cũng như tổng thành tích. Tài liệu là một tài liệu học tập thiết thực cho việc ôn thi THPT Quốc gia.

1. Công thức lượng giác
(Duøng cho hoïc sinh 10, 11, 12, luyeän thi THPTQG)
1 - Bảng giá trị lượng giác của một số cung (góc) đặc biệt 2 - Đổi đơn vị
Độ 00
300
450
600
900
1200
1350
1500
1800
  1800
a (rad)  x0
0
0
a x
180


0
0 a.180
x 

0
0
x .
a(rad)
180


Rad 0
6

4

3

2

3
2
4
3
6
5

sin 0
2
1
2
2
2
3
1
2
3
2
2
2
1
0
cos 1
2
3
2
2
2
1
0 –
2
1
–
2
2
–
2
3
– 1
tan 0
3
3
1 3 || – 3 –1 –
3
3
0
cot || 3 1
3
3
0 –
3
3
–1 – 3 ||
3 - Cung liên kết: “Cos đối, sin bù, phụ chéo, khác  tan” 4 - Dấu của hàm số lượng giác
Loại
HSLG
Cung sin cos tan cot
Góc
HSLG
(I) (II) (III) (IV)
sin + + – –
cos + – – +
tan + – + –
cot + – + –
Nhất cả, nhị sin, tam tan, tứ cos
Đối –  – sin cos – tan – cot
Phụ
2

–  cos sin cot tan
Hơn kém
2

2

+  cos – sin – cot – tan
Bù  –  sin – cos – tan – cot
Hơn kém   +  – sin – cos tan cot
Hơn kém k2  + k2 sin cos tan cot
5 - Đường tròn lượng giác 6 - Các giá trị lượng giác đặc biệt
sin
tang
cotang
cosin
O H A
K M
SB
T
sin
cos
(I)(II)
(III) (IV)

2. 7 - Công thức cơ bản: 8 - Các biến đổi thường gặp:
①    2 2
sin cos 1 ①            3 3
sin cos sin cos 1 sin cos
②

      tan .cot 1, k ,
2
k ②            3 3
sin cos sin cos 1 sin cos
③
 
      


sin
tan , ,
cos 2
k k ③             4 4 2 2 21 3 1
sin cos 1 2 sin cos 1 sin 2 cos 4
2 4 4
④

     


cos
cot , ,
sin
k k ④          4 4 2 2
sin cos sin cos cos2
⑤

      

2
2
1
1 tan ,
2cos
k ⑤             6 6 2 2 23 5 3
sin cos 1 3 sin cos 1 sin 2 cos 4
4 8 8
⑥       

2
2
1
1 cot , ,
sin
k k ⑥          6 6 2 2
sin cos 2 cos2 1 sin cos
9 - Công thức cộng 10 - Công thức nhân đôi, nhân ba
①    sin sin cos cos sina b a b a b ① sin2 2 sin cosa a a
②    sin sin cos cos sina b a b a b ②           2 2 2 2
cos2 cos sin 2 cos 1 1 2 sin
③    cos cos cos sin sina b a b a b ③

 
 2
2 tan
tan2
1 tan
④    cos cos cos sin sina b a b a b ④     3
sin 3 3 sin 4 sin (chứng minh)
⑤   
 

tan tan
tan
1 tan tan
a b
a b
a b
⑤     3
cos 3 4 cos 3 cos (chứng minh)
⑥   
 

tan tan
tan
1 tan tan
a b
a b
a b
⑥
  
 
 
3
2
3 tan tan
tan 3
1 3 tan
(chứng minh)
11 - Công thức hạ bậc: 12 - Các hệ quả:
①
 
 2 1 cos2
cos
2
②
 
 2 1 cos2
sin
2
①    
1
sin cos sin 2
2
②    2 2 21
sin cos sin 2
4
③
 
 
 
2 1 cos2
tan
1 cos2
③   2
1 cos 2 cos
2
ka
ka ④   2
1 cos 2 sin
2
ka
ka
④
  
 3 3 cos cos 3
cos
4
⑤
 
   
 
2
1 sin sin cos
2 2
ka ka
ka ⑦    
2
1 sin 2 sin cosa a a
⑤
  
 3 3 sin sin 3
sin
4
⑥
 
   
 
2
1 sin sin cos
2 2
ka ka
ka ⑧    
2
1 sin 2 sin cosa a a
13 - Công thức biến đổi tích thành tổng:
①        
 
1
sin .cos sin sin
2
a b a b a b ②        
 
1
cos .sin sin sin
2
a b a b a b
③        
 
1
cos .cos cos cos
2
a b a b a b ④         
 
1
sin .sin cos cos
2
a b a b a b
14a - Công thức biến đổi tổng thành tích: 14b - Đặc biệt khi a = b = :
①
 
 sin sin 2 sin cos
2 2
a b a b
a b ①
 
      
 
sin cos 2 sin
4
②
 
 sin sin 2 cos sin
2 2
a b a b
a b ②
 
      
 
sin cos 2 sin
4
③
 
 cos cos 2 cos cos
2 2
a b a b
a b ③
 
      
 
cos sin 2 cos
4
④
 
  cos cos 2 sin sin
2 2
a b a b
a b ④
 
      
 
cos sin 2 cos
4