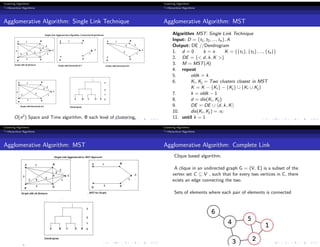
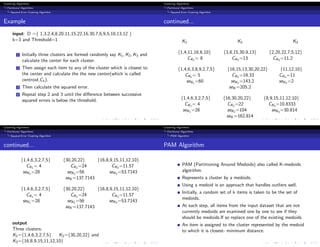
This document discusses various clustering algorithms. It begins by defining clustering as assigning objects into groups so that objects in the same cluster are more similar to each other than objects in other clusters. It then discusses hierarchical and partitional clustering algorithms. Hierarchical algorithms produce nested clusters and can be agglomerative (bottom-up) or divisive (top-down). Partitional algorithms create all clusters in one step by optimizing a criterion function like squared error. Popular algorithms discussed include K-means, single and complete link hierarchical clustering, and squared error clustering.

1. Clustering Algorithms
CONTENTS
1 What is Clustering
2 Similarity Measures
3 Hierarchical Algorithms
4 Partitional Algorithms
K-Means Clustering
Squared Error Clustring Algorithm
PAM Algorithm
Minimum Spanning Tree
Clustering Algorithms
What is Clustering
What is Clustering
Clustering is the task of assigning a set of objects into groups
(called clusters) so that the objects in the same cluster are more
similar (in some sense or another) to each other than to those in
other clusters.
Issues
Outlier handling is difficult
The element do not fall into any cluster, are viewed as solitary
clusters
Dynamic data
Cluster memebership change over time
Semantic meaning
interpreting semantic meaning of each cluster may be difficult,
i.e. domain expert is needed to assign a label for each cluster
No correct answer
There is no one correct answer to clustering problem. The
exact number of clusters required is not easy to determine.
Clustering Algorithms
What is Clustering
Clustering problem
Definition
Given a database D={t1, t2, , tn} of tuples and an integer value k,
the Clustering Problem is to define a mapping f : D → {1, .., k}
where each ti is assigned to one cluster Kj , 1 ≤ j ≤ k. A Cluster,
Kj , contains precisely those tuples mapped to it.
i.e.Kj = {ti |f (ti ) = Kj , 1 ≤ i ≤ n, andti ∈ D}
Clustering Algorithms
What is Clustering
Classification of Clustering Algorithm

2. Clustering Algorithms
Similarity Measures
Similarity Measures
Similarity measure is well known in the field of internet search,
where the similarity is based on the query the user stated,
retrieved pages are similar if they all contain the specified
query words.
Documents that are more alike have a higher degree of
similarity.
Useful in clustering and classification problems
Most similarity measures assume numeric values, so difficult
use with general data types
A mapping from the attribute domain to subset of integers
required
Clustering Algorithms
Similarity Measures
Similarity Measures
Definition
Similarity between two tuples ti and tj , sim(ti , tj ), in a database D
is a mapping from D × D to the range [0,1]. Thus sim(ti , tj ) ∈
[0,1].
The following desirable characteristics of good similarity measures
∀ti ∈ D, sim(ti , ti ) = 1
∀ti , tj ∈ D, sim(ti , tj ) = 0 if ti and tj are not like at all
∀ti , tj , tk ∈ D, sim(ti , tj ) < sim(ti , tk) if ti is more like tk
than it is like tj
Clustering Algorithms
Similarity Measures
Some Important Similarity Measures
Important similarity measures used in information retrieval system
and search engines are
Clustering Algorithms
Similarity Measures
Distance Measures
Distance or dissimilarity measures measure how unlike items are.
Definition
Given a cluster, Kj , ∀ tjl , tjm ∈ Kj and ti /
∈ Kj , dis(tjl , tjm) ≤
dis(tjl , ti )
Some important distance measures in a two dimensional space are

3. Clustering Algorithms
Similarity Measures
Characteristic values of a cluster
Given a cluster Km of N points{tm1, tm2, .......tmN}
Clustering Algorithms
Similarity Measures
Centroid is the middle of the cluster. It need not be an
actual point in the cluster. Medoid is the centrally located
object in the cluster.
Radius is the square root of the average mean squared
distance from any point in the cluster to the centroid.
Diameter is the square root of the average mean squared
distance between all pairs of points in the cluster.
Clustering Algorithms
Hierarchical Algorithms
Hierarchical Algorithms
Lets start with a Simple Example!!!
In Ramayana, Rama, Bharatha, Lakshmana and Sathrugna are the
sons of King Dasradha. The hierarchical clustering of this data is
as follows:
At leaf level, Rama, Bharatha, Lakshmana and Sathrugna are
individual clusters
Then Rama and Lakshmana, Bharatha and Sathrugna form
cluster of two elements
As the sons of King Dasradha, Rama, Bharatha, Lakshmana
and Sathrugna form a single cluster.
Clustering Algorithms
Hierarchical Algorithms
Hierarchical Algorithms
Produce a nested set of clusters
Each level in hierarchy, has a separate set of cluster
At lowest level, each item belonging to its own unique cluster
Other extreme, all item belonging to single cluster.

4. Clustering Algorithms
Hierarchical Algorithms
Hierarchical Algorithms
Used to illustrate the hierarchical clustering
The root of dendrogram tree contains one cluster, where all
elements together
The leaves of dendrogram tree consist of a single element
cluster
Internal nodes represents clusters formed by merging the
clusters that appear as its children in the tree.
Clustering Algorithms
Hierarchical Algorithms
Hierarchical Algorithms
Clustering Algorithms
Hierarchical Algorithms
Comparison
Table: Comparison
Sl. Flat(Partional) Algorithms Hierarchical Algorithms
1 Not include structural information Hierarchical structure, So more in-
formative
2 Pre-specification of number of re-
quired clusters
No such pre-specification required
3 Create only one set of cluster Each level of hierarchy create a set
of cluster
4 Complexity is linear Complexity is Quadratic
Clustering Algorithms
Hierarchical Algorithms
Hierarchical Algorithms: Types
We’ll Cover.....
Agglomerative (bottom up approach)
Single Link Technique
Complete Link Technique
Average Link Technique
Divisive Algorithms

5. Clustering Algorithms
Hierarchical Algorithms
Agglomerative
The act of process of gathering into a mass
Input: Set of elements and distance between them as Adjacency
matrix.
Output: Dendrogram
Algorithm (General):
Keep each individual items in to its own Clustering
Repeat
Merge Clusters based on the distance between elements in
the cluster and threshold distance
Until All items belonging to one cluster.
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm
Algorithm Agglomerative Clustering
Input: D = {t1, t2, ..., tn}, A
Output: DE //Dendrogram
1. d = 0 k = n K = {{t1}, {t2}, ..., {tn}}
2. DE = {< d, k, K >}
3. repeat
4. oldk = k
5. d = d + 1
6. Ad = Vertex Adjacency matrix for threshold d
7. < k, K >= NewCluster(Ad , D) //procedure to create
next level of clusters
8. if oldk 6= k
9. then DE = DE ∪ hd, k, Ki
10. until k = 1
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Single Link Technique
Find Maximal Connected Component
Two clusters are merged if there is at least one edge that
connects the two clusters
The minimum distance that between any two point is less
than or equal to the threshold distance being considered
Also called nearest neighboring clustering technique
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Single Link Technique
Example:
Data = {A, B, C, D, E}
Table: Adjacency Matrix
Item A B C D E
A 0 1 2 2 3
B 1 0 2 4 3
C 2 2 0 1 5
D 2 4 1 0 3
E 3 3 5 3 0
Output:
Iteration-1: h0, 5, {{A}, {B}, {C}, {D}, {E}}i
Iteration-2: h1, 3, {{{{A, B}, {C, D}, {E}}i
Iteration-3: h2, 2, {{A, B, C, D}, {E}}i
Iteration-4: h3, 1, {A, B, C, D, E}i

6. Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Single Link Technique
O(n2) Space and Time algorithm, @ each level of clustering.
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: MST
Algorithm MST: Single Link Technique
Input: D = {t1, t2, ..., tn}, A
Output: DE //Dendrogram
1. d = 0 k = n K = {{t1}, {t2}, ..., {tn}}
2. DE = {< d, k, K >}
3. M = MST(A)
4. repeat
5. oldk = k
6. Ki , Kj = Two clusters closest in MST
K = K − {Ki } − {Kj } ∪ {Ki ∪ Kj }
7. k = oldk − 1
8. d = dis(Ki , Kj )
9. DE = DE ∪ hd, k, Ki
10. dis(Ki , Kj ) = ∞
11. until k = 1
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: MST
2
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Complete Link
Clique based algorithm.
A clique in an undirected graph G = (V, E) is a subset of the
vertex set C ⊆ V , such that for every two vertices in C, there
exists an edge connecting the two.
Sets of elements where each pair of elements is connected

7. Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Complete Link
Complete Link approach is similar to single link approach, instead
of finding connected graph, it look for Cliques.
Find maximum distance between any clusters, so that two clusters
are merged if the maximum distance is less than or equal to the
distance threshold.
It is also called farthest neighbor algorithm
O(n2) algorithm.
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Complete Link
Algorithm Complete Link Technique
Input: D = {t1, t2, ..., tn}, A
Output: DE //Dendrogram
1. d = 0 k = n K = {{t1}, {t2}, ..., {tn}}
2. DE = {< d, k, K >}
3. M = CLIQUE(A)
4. repeat
5. oldk = k
6. Ki , Kj = Two clusters farthest in Clique
K = K − {Ki } − {Kj } ∪ {Ki ∪ Kj }
7. k = oldk − 1
8. d = dis(Ki , Kj )
9. DE = DE ∪ hd, k, Ki
10. dis(Ki , Kj ) = 0
11. until k = 1
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Complete Link
Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Average Link
Merges two clusters if the distance between any two points in the
two target cluster is below the distance threshold.
In the example above, produces the same cluster as in Single Link
approach.

8. Clustering Algorithms
Hierarchical Algorithms
Agglomerative Algorithm: Average Link
Algorithm Average Link Technique
Input: D = {t1, t2, ..., tn}, A
Output: DE //Dendrogram
1. d = 0, k = n
2. K = {{t1}, {t2}, ..., {tn}}
3. DE = {< d, k, K >}
4. repeat
5. oldk = k
6. d = d + 0.5
7. for each pair of Ki , Kj ∈ K do
8. ave = average distance(ti , tj ) ∀ ti ∈ Ki and tj ∈ Kj
9. if ave ≤ d,
10. then K = K − {Ki } − {Kj } ∪ {Ki ∪ Kj }
11. k = oldk − 1
12. DE = DE ∪ hd, k, Ki
13. until k = 1
Clustering Algorithms
Hierarchical Algorithms
Divisive Algorithm
Items are initially placed in one cluster
Clusters are repeatedly split into two until all items are in their
own clusters.
MST based single link approach is commonly used.
Cut out edges from the MST from largest to the smallest.
Reverse of Agglomerative approach.
Clustering Algorithms
Hierarchical Algorithms
Divisive Algorithm
Clustering Algorithms
Hierarchical Algorithms
Summary
Table: Summary
Item Single Link Complete
Link
Average
Link
Divisive
Idea Connected
Compo-
nents/MST
Cliques Average Dis-
tance
MST
Criteria minimum
distance be-
tween two
points less
than or equal
to threshold
maximum
distance be-
tween two
points less
than or equal
to threshold
Average
distance be-
tween two
points less
than or equal
to threshold
Split if two
elements are
sufficiently
close to other
element
Complexity O(n2
) at each
level
O(n2
) O(n2
) O(n2
)

9. Clustering Algorithms
Partitional Algorithms
Partitional Clustering
Nonhierarchical
Creates clusters in one step as opposed to several steps.
Since only one set of clusters is output, the user normally has
to input the desired number of clusters, k.
Some metric or criterion function is used to dtermine the
goodness of any proposed solution
one common metric is Squared Error Metric
Pk
m=1
P
tmi ∈Km
dis(Cm, tmi )2
Clustering Algorithms
Partitional Algorithms
K-Means Clustering
K-Means clustering
K-means (MacQueen, 1967) is one of the simplest
unsupervised learning algorithms that solve the clustering
problem.
It is an iterative clustering in which items are moved among
sets of clusters until the desired cluster is obtained.
It may be considered as a type of squared error algorithm.
This algorithms give a high degree of similarity between
elements in the clusters and high degree of dissimilarity
between elements in different clusters.
Clustering Algorithms
Partitional Algorithms
K-Means Clustering
K-means Clustering Algorithm
The procedure classify a given data set into a fixed number of
clusters (assume k clusters).
The main idea is to define k centroids (cluster mean), one for
each cluster, initially selected arbitrarily from the data set or
first k elements of the data set.
The selection initial values for centroid are important-i. e.
different location causes different result. So, the better choice
is to place them as much as possible far away from each other.
Assign each point belonging to a given data set to the nearest
centroid.
Recalculate the mean and associate data set to this new
mean. Repeat this until a convergence criterion is met.
Clustering Algorithms
Partitional Algorithms
K-Means Clustering
K-Means clustering algorithm
Algorithm K-Means Clustering
Input:
1. D = {t1, t2, t3, ...., tn} //Set of elements
2. k //Number of desired clusters
Output: K //Set of clusters.
3. K-means algorithm:
4. assign initial values for means m1, m2, ........, mk;
5. repeat
6. assign each item ti to the cluster which has the closest
mean;
7. calculate new mean for each cluster;
8. until convergence criteria is met;

10. Clustering Algorithms
Partitional Algorithms
K-Means Clustering
Example
input: D ={ 2,4,10,12,3,20,30,11,25 }
k=2
Algorithm
m1 m2 K1 K2
2 4 {2,3} {4,10,12,20,30,11,25}
2.5 16 {2,3,4} {10,12,20,30,11,25}
3 18 {2,3,4,10} {12,20,30,11,25}
4.75 19.6 {2,3,4,10,11,12} {20,30,25}
7 25 {2,3,4,10,11,12} {20,30,25}
output
Two clusters:
K1 = {2, 3, 4, 10, 11, 12} K2 = {20, 30, 25}
Clustering Algorithms
Partitional Algorithms
Squared Error Clustring Algorithm
Squared Error Clustring Algorithm
Given a cluster Ki , let the set of items mapped to that cluster be
ti1, ti2..........tim. The squared error is defined as
seKi
=
Pm
j=1 || tij − Ck ||2
Given a set of clusters K= K1, K1,.... Kk, the squared error for K
is defined as
seK =
Pk
j=1 seKj
Clustering Algorithms
Partitional Algorithms
Squared Error Clustring Algorithm
Squared Error Clustring Algorithm
Algorithm Squared Error Clustring Algorithm
Input:
1. D={t1, t2.....tn}
2. Set of elements k //Number of desired clusters
Output: K//set of clusters
Squared error algorithm:
3. assign each item ti to a cluster;
4. calculate center for each cluster;
5. repeat
6. assign each item ti to the cluster which has the closest
center;
7. calculate new center for each cluster;
8. calculate squared error;
9. until The difference between successive squared errors are
below the threshold;
Clustering Algorithms
Partitional Algorithms
Squared Error Clustring Algorithm
continued...
For each iteration, each tuple is assigned to the cluster with
the closest center.
Since there are k clusters and n items, this is a O(kn)
operation.
Assuming t iterations, the time complexity is O(tkn).
Space complexity is O(n)

11. Clustering Algorithms
Partitional Algorithms
Squared Error Clustring Algorithm
Example
input: D ={ 1,3,2,4,8,20,11,15,22,16,30,7,6,9,5,10,13,12 }
k=3 and Threshold=1
1 Initially three clusters are formed randomly say K1, K2, K3 and
calculate the center for each cluster.
2 Then assign each item to any of the cluster which is closest to
the center and calculate the the new center(which is called
centroid,Ck).
3 Then calculate the squared error.
4 Repeat step 2 and 3 until the difference between successive
squared errors is below the threshold.
Clustering Algorithms
Partitional Algorithms
Squared Error Clustring Algorithm
continued...
K1 K2 K3
{1,4,11,16,6,10} {3,8,15,30,9,13} {2,20,22,7,5,12}
CK1 = 8 CK2 =13 CK3 =11.2
{1,4,6,3,8,9,2,7,5} {16,15,13,30,20,22} {11,12,10}
CK1 = 5 CK2 =19.33 CK3 =11
seK1 =60 seK2 =143.2 seK3 =2
seK =205.2
{1,4,6,3,2,7,5} {16,30,20,22} {8,9,15,11,12,10}
CK1 = 4 CK2 =22 CK3 =10.8333
seK1 =28 seK2 =104 seK3 =30.814
seK =162.814
Clustering Algorithms
Partitional Algorithms
Squared Error Clustring Algorithm
continued...
{1,4,6,3,2,7,5} {30,20,22} {16,8,9,15,11,12,10}
CK1 = 4 CK2 =24 CK3 =11.57
seK1 =28 seK2 =56 seK3 =53.7143
seK =137.7143
{1,4,6,3,2,7,5} {30,20,22} {16,8,9,15,11,12,10}
CK1 = 4 CK2 =24 CK3 =11.57
seK1 =28 seK2 =56 seK3 =53.7143
seK =137.7143
output
Three clusters:
K1={1,4,6,3,2,7,5} K2={30,20,22} and
K3={16,8,9,15,11,12,10}
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
PAM Algorithm
PAM (Partitioning Around Medoids) also called K-medoids
algorithm.
Represents a cluster by a medoids.
Using a medoid is an approach that handles outliers well.
Initially, a random set of k items is taken to be the set of
medoids.
At each step, all items from the input dataset that are not
currently medoids are examined one by one to see if they
should be medoids.If so replace one of the existing medoids
An item is assigned to the cluster represented by the medoid
to which it is closest- minimum distance.

12. Clustering Algorithms
Partitional Algorithms
PAM Algorithm
Assume Ki cluster represented by medoid ti
We wish to determine whether ti should be exchanged with a
non-medoid th
We will do this swap only if the overall impact to the cost(sum
of distancesto cluster medoids) represents an improvement.
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
We use Cjih to be the cost change for an item tj associated
with swapping medoid ti with non-medoid th
The cost is the change to the sum of all distances from items
to their cluster medoids.
The total impact to quality by a medoid change TCih then is
given by
TCih=
Pn
j=1 Cjih
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
PAM Algorithm
Algorithm PAM Algorithm
1.
Input:
2. D = {t1, t2, ..., tn}, A//AdjacenncyMatrix, k//numberofclusters
Output: K // Set of clusters
3. PAM algorithm:
4. arbitrarily select k medoids from D;
5. repeat
6. for each th not a medoid do
7. for each medoid ti do
8. calculate TCih;
9. find i,h where TCih is the smallest;
10. if TCih < 0 then replace medoid ti with th;
11. until TCih ≥ 0;
12. for each ti ∈ D do
13. assign ti to Kj , where dis(ti ,tj ) is the smallest over all
medoids;
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
Example
Initially chosen medoids are A and B.
We have six costs to determine:
TCAC , TCAD, TCAE , TCBC , TCBD, TCBE
We obtain the following:
TCAC = CAAC + CBAC + CCAC + CDAC + CEAC
= 1+0-2-1+0=-2
A is no longer a medoid, and since it is closer to B, it will be
placed in the cluster with B as medoid
its cost ic CAAC = 1
Cost for B is 0because it stays a cluster medoid.
C is now a medoid, so it has a negative cost based on its
distance to the old medoid
CCAB = −2

13. Clustering Algorithms
Partitional Algorithms
PAM Algorithm
D is closer to C than it was to A by a distance of 1. So its cost
CDAC = −1
E stays in the same cluster with the same distance, so its cost
change to 0.
Overall cost is a reduction of 2.
Figure shows calculation of these six costs.
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
Cost calculation
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
Algorithm
Here minimum cost is 2. There are several ways to reduce this
cost.
Arbitrarily choosing the first swap, we get C and B as the new
medoids with the clusters being {C, D} and {B, A, E}.
At the next iteration, changing medoids again and pick the
choice that bestreduces the cost.
Iterations stop when no changes will reduce the cost.
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
Algorithm
PAM does not scale well to large datasets because of its
computational complexity.
For each iteration, k(n-k) pairs of objects i, h for which a
cost, TCih , should be determined.
Calculating the cost during each iteration requires that the
cost be calculated for all other non-medoids Tj . There are n-k
of these.
Total complexity per iteration is n(n − k)2

14. Clustering Algorithms
Partitional Algorithms
PAM Algorithm
CLARA
Clustering LARge Applications
Clustering algorithm based on PAM targeted to large datasets.
Applying PAM to a sample of the underlying database and
then uses the medoids found as the medoids for the complete
clustering
Each item from the complete database is then assigned to the
cluster with the medoid to which it is closest.
Because of the sampling , CLARA is more efficient than PAM
for large databases.
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
CLARANS
Clustering large applications based upon randomized search
CLARANS improves on CLARA by using multiple different
samples.
It requires two additional parameters: maxneighbor and
numlocal.
Maxneighbor is the number of nighbors of a node to which
any specific node can be compared.
Numlocal indicates the number of samples to be taken
Clustering Algorithms
Partitional Algorithms
PAM Algorithm
CLARANS
As maxneighbor increases, CLARANS looks more and more
like PAM, because all nodes will be examined.
Performance studies indicates that numlocal = 2 and
maxneighbor = max((0.0125 X k(n-k)), 250) are good
choices.
CLARANS is shown to be more efficient than either PAM or
CLARA for any size dataset.
Clustering Algorithms
Partitional Algorithms
Minimum Spanning Tree
Minimum Spanning Tree
Algorithm MST
Input:
1. D = {t1, t2, ..., tn}, A
2. A // Adjacency matrix showing distance between elements
3. k // Number of desired clusters
Output:
4. f //Mapping represented as a set of ordered pairs
Partitional MST algorithm
5. M = MST(A)
6. identify inconsistent edges in M;
7. remove k -1 inconsistent edges
8. create output representation

15. Clustering Algorithms
Partitional Algorithms
Minimum Spanning Tree
Minimum Spanning Tree
The problem is how to define ”inconsistent”. One mechanism
is to remove the largest k − 1 edges from the completely connected
graph. But, this is poor solution, more reasonable solutions are
proposed
Time Complexity
MST : O(n2)
remove (k-1)edges :O(k − 1)
determining inconsistent :O(k2)
(looking at each edge, there are (k-2) adjacent edges)
Complexity of Total Algorithm : O(n2)