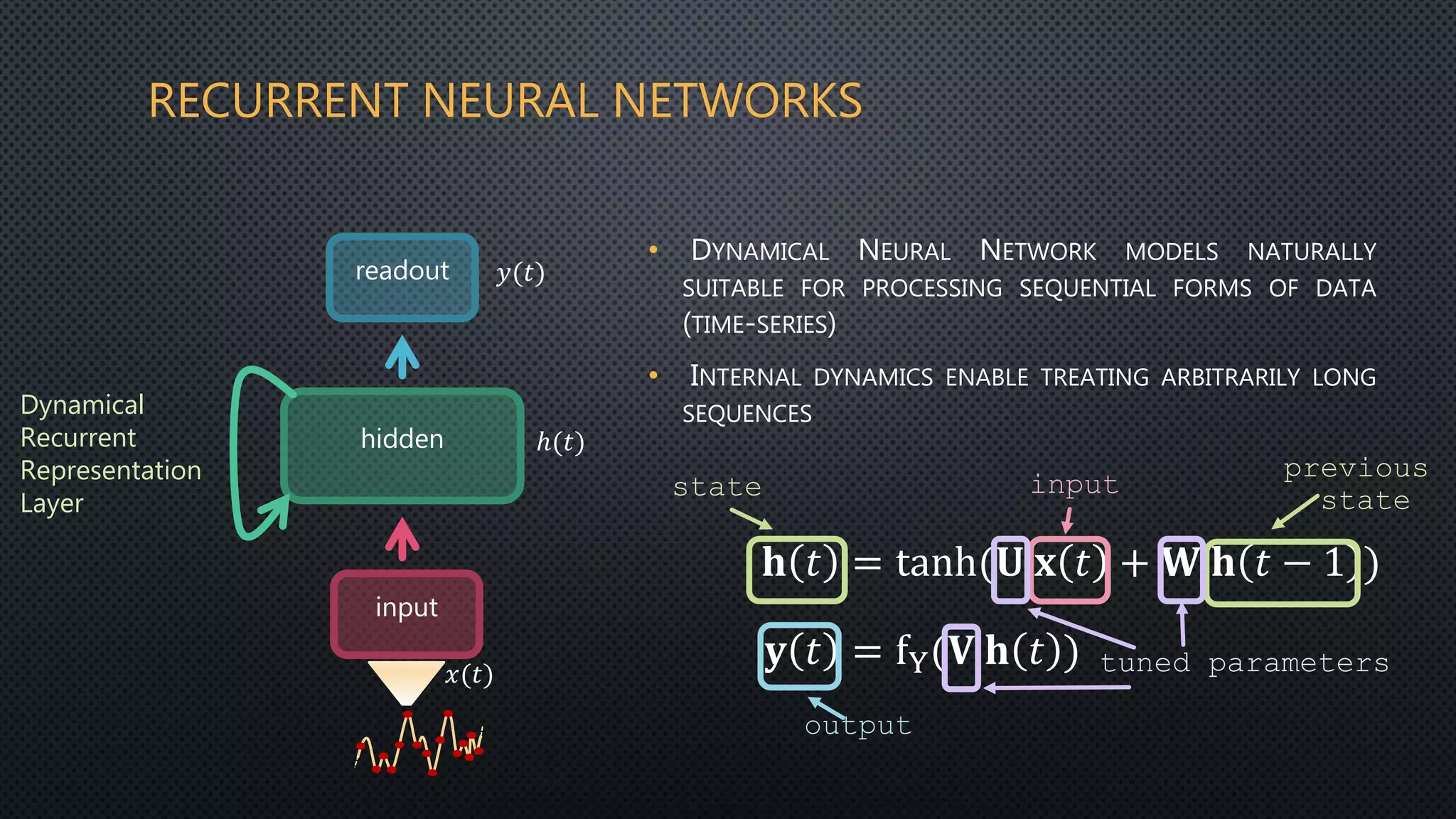
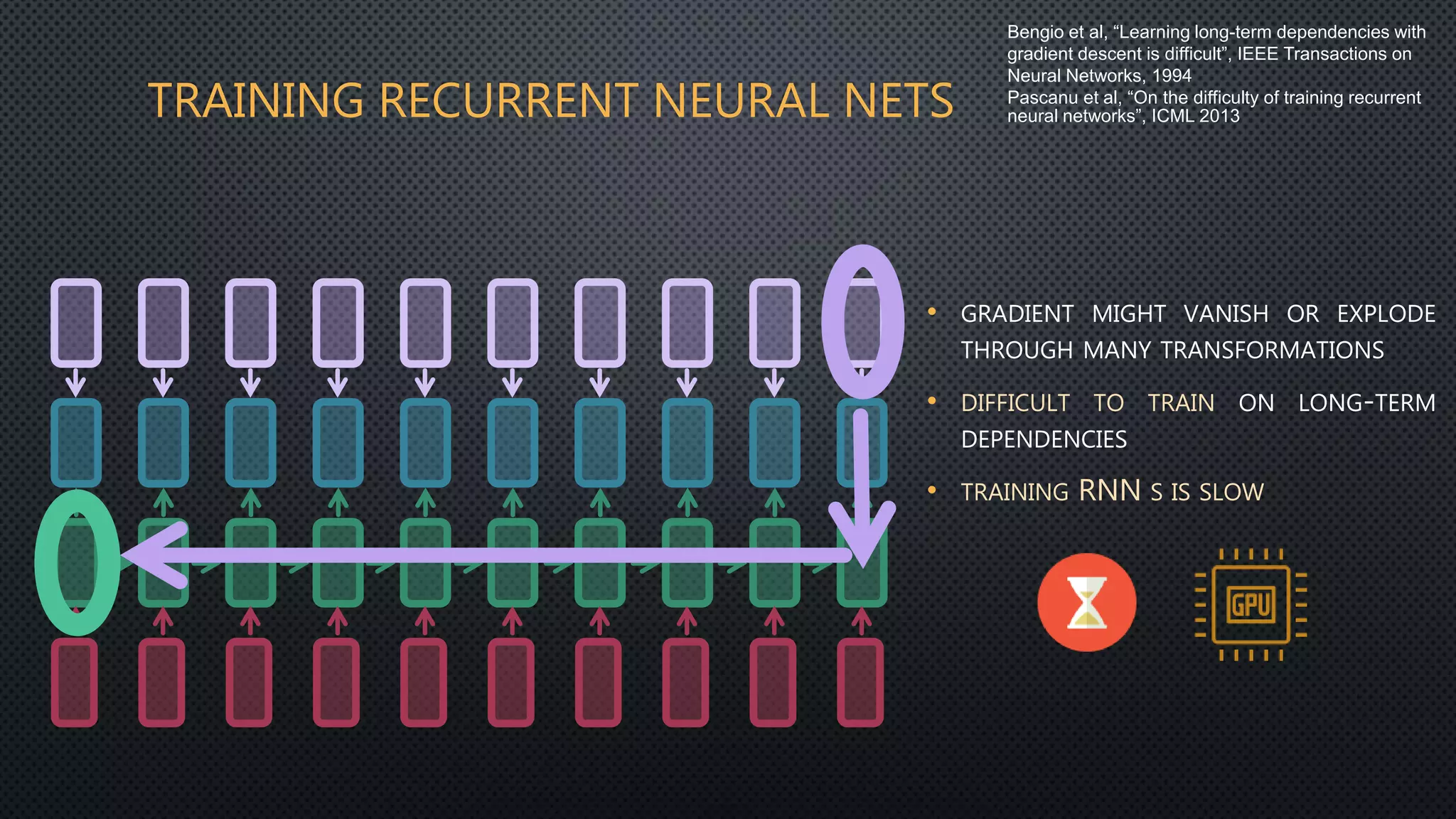
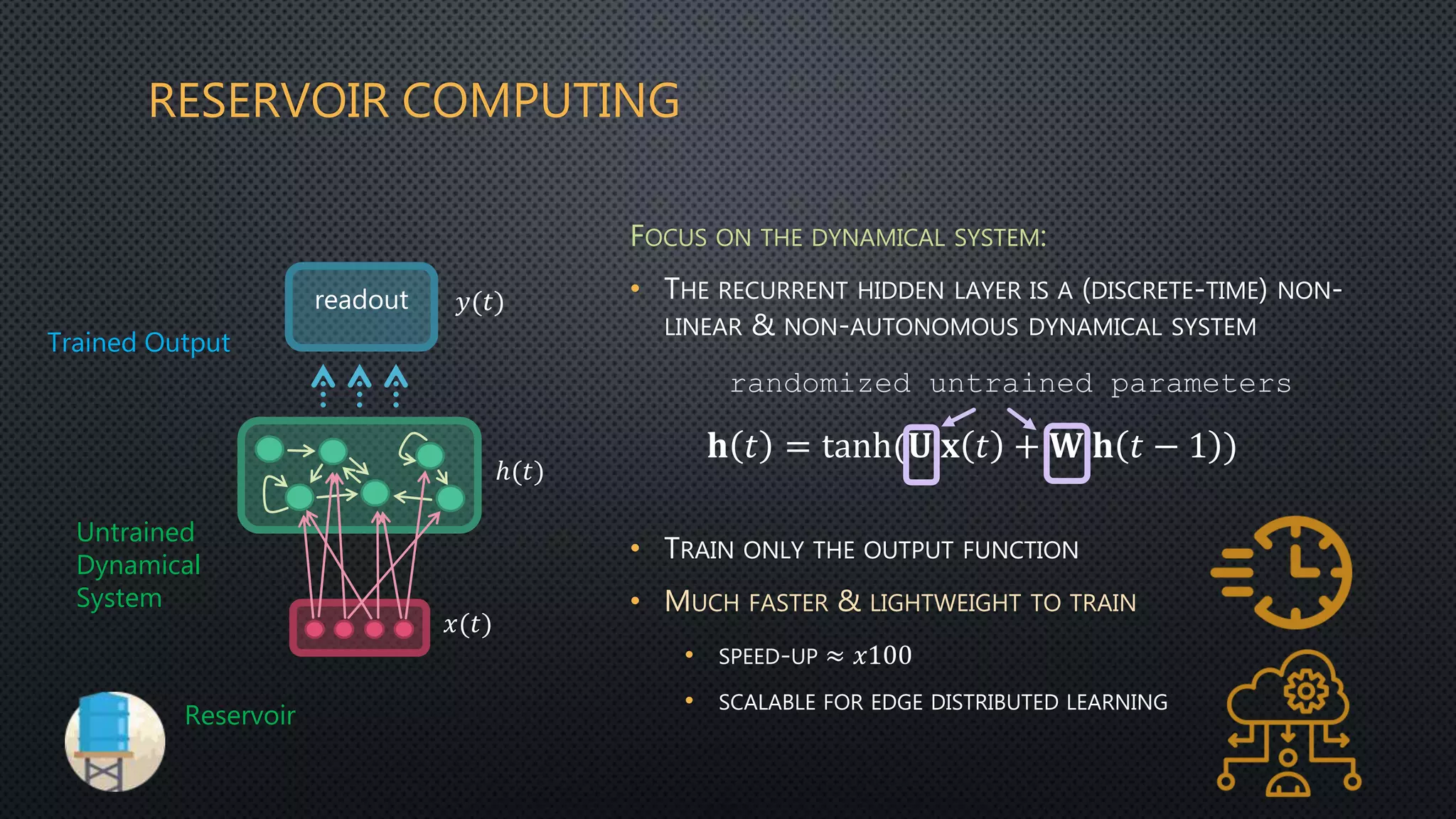
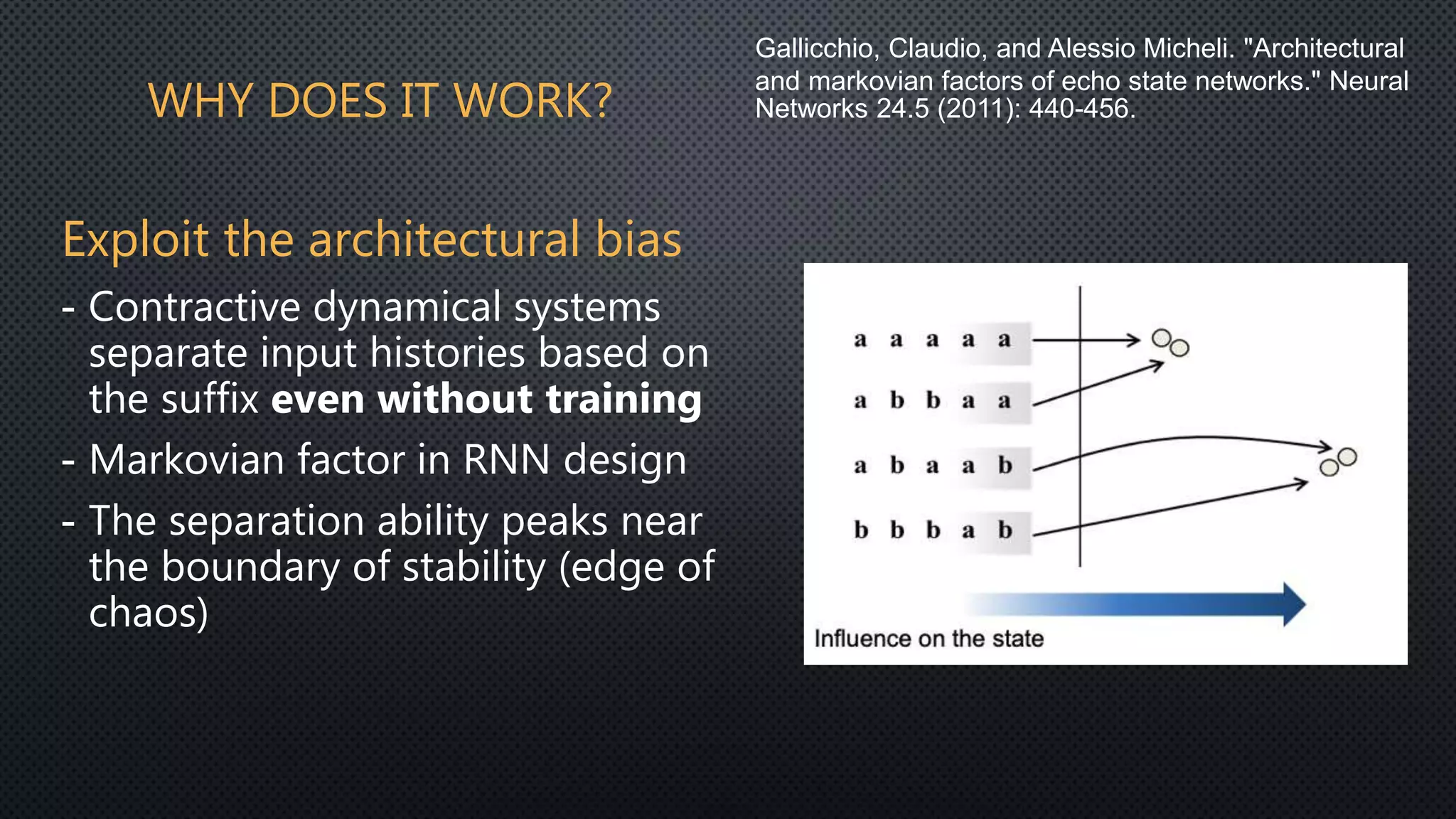
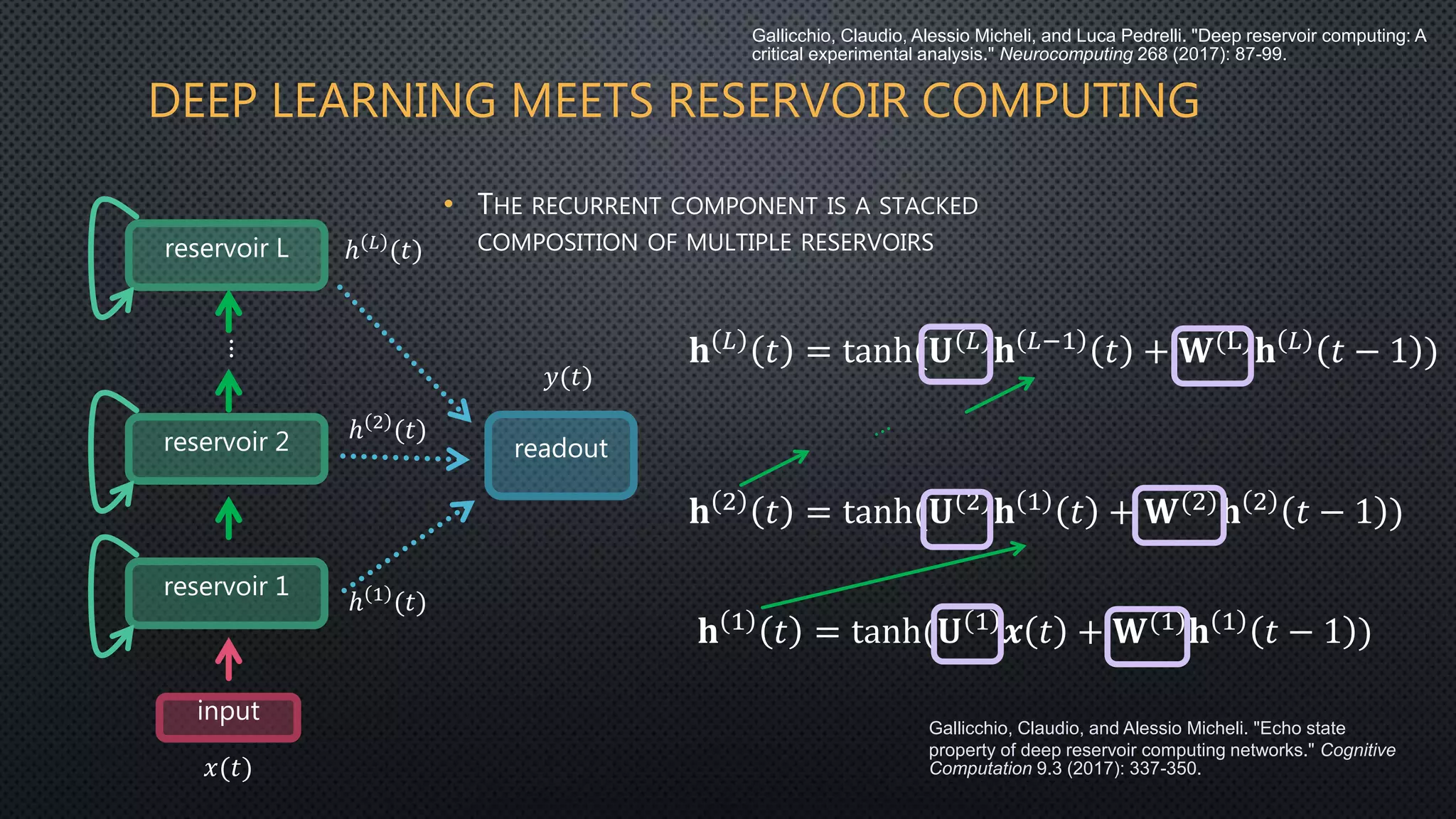
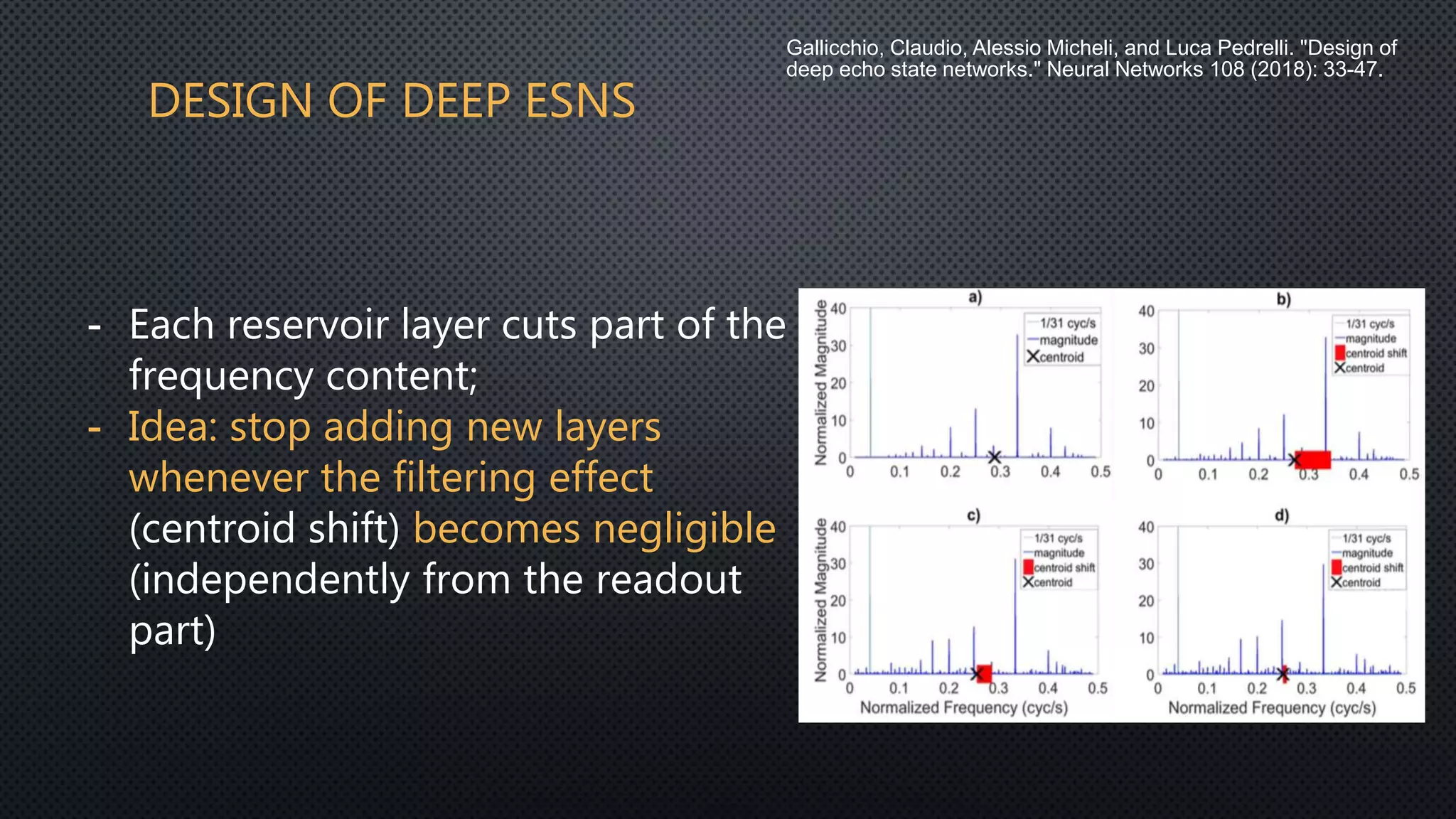
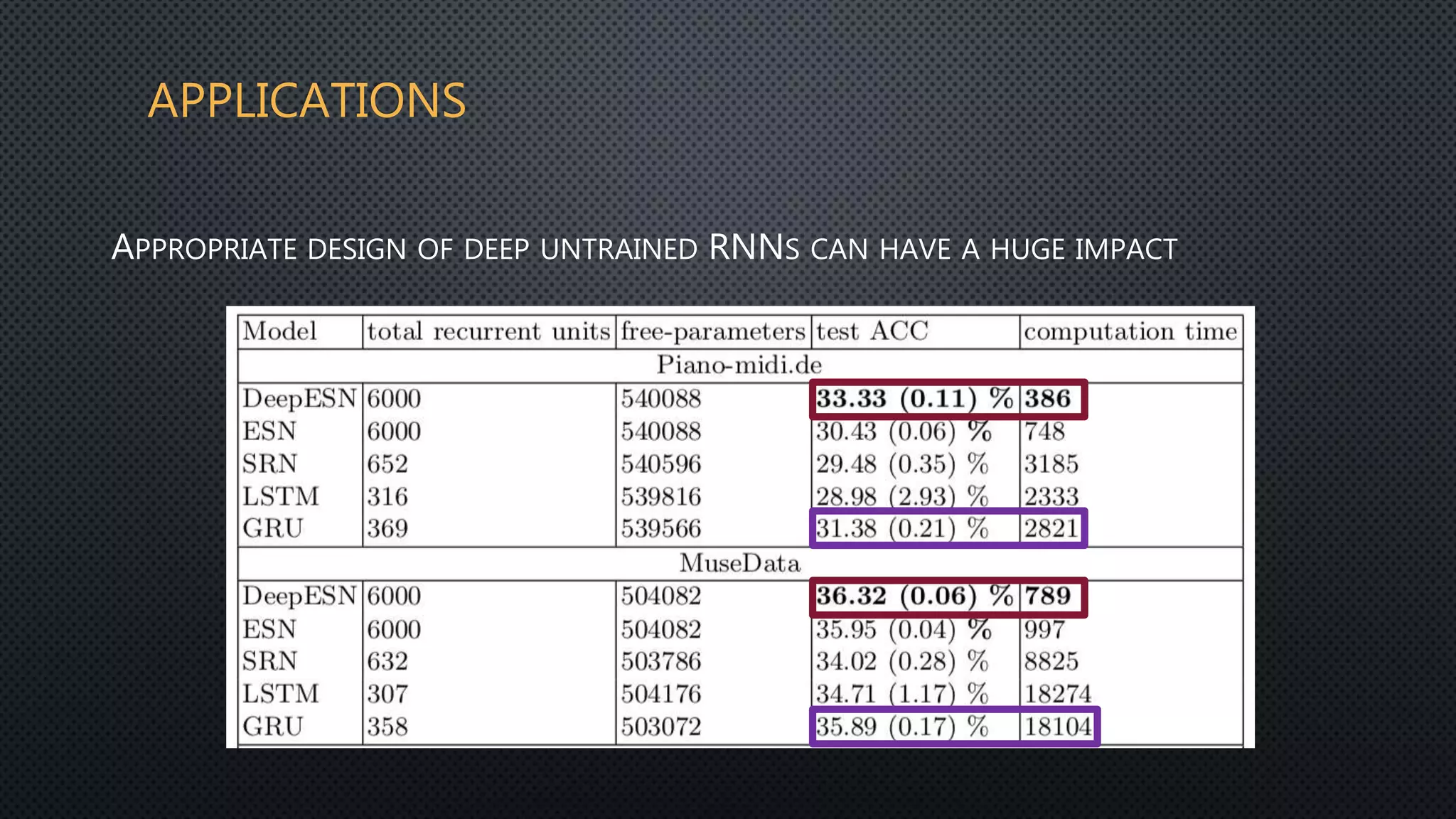
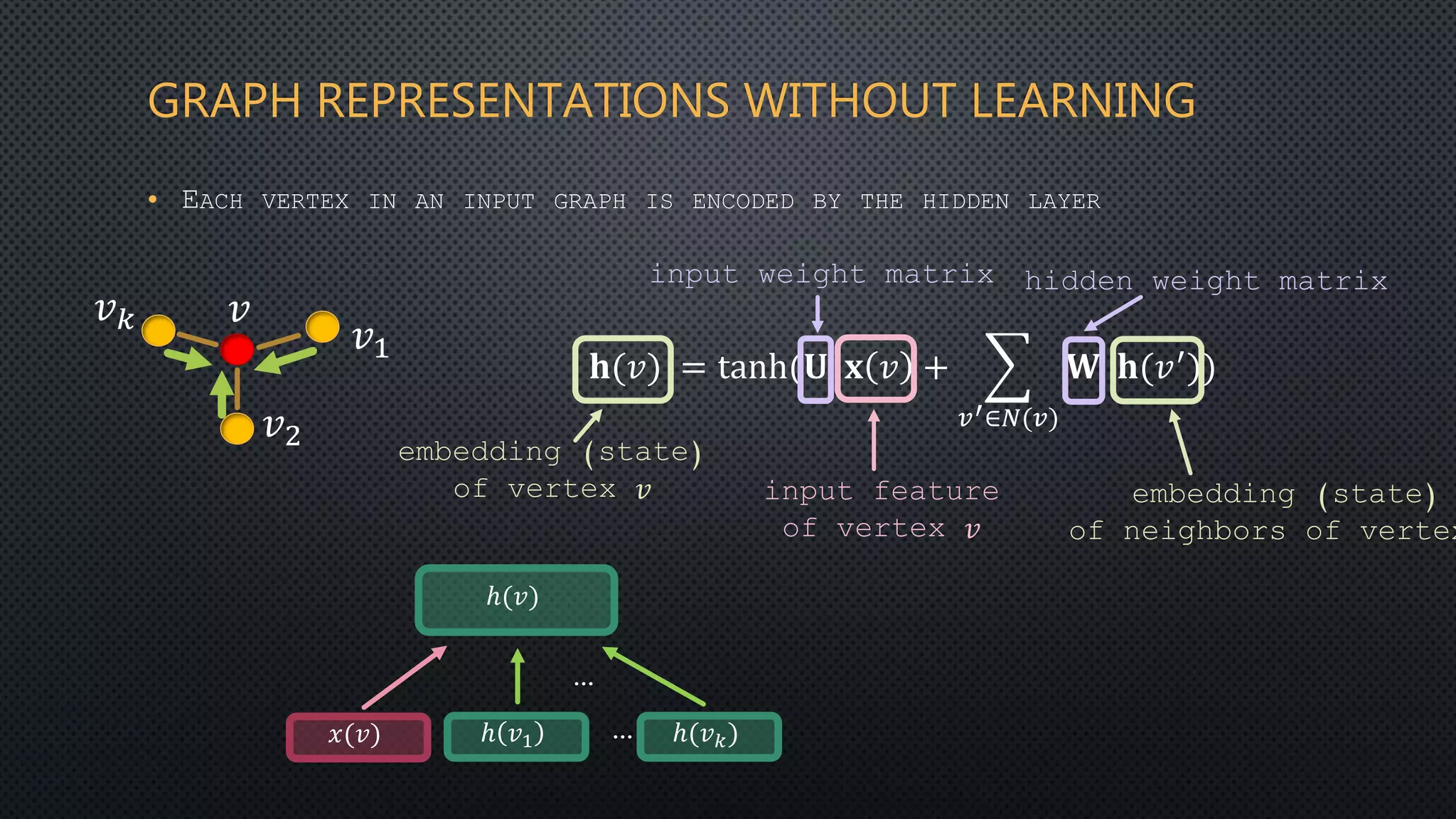
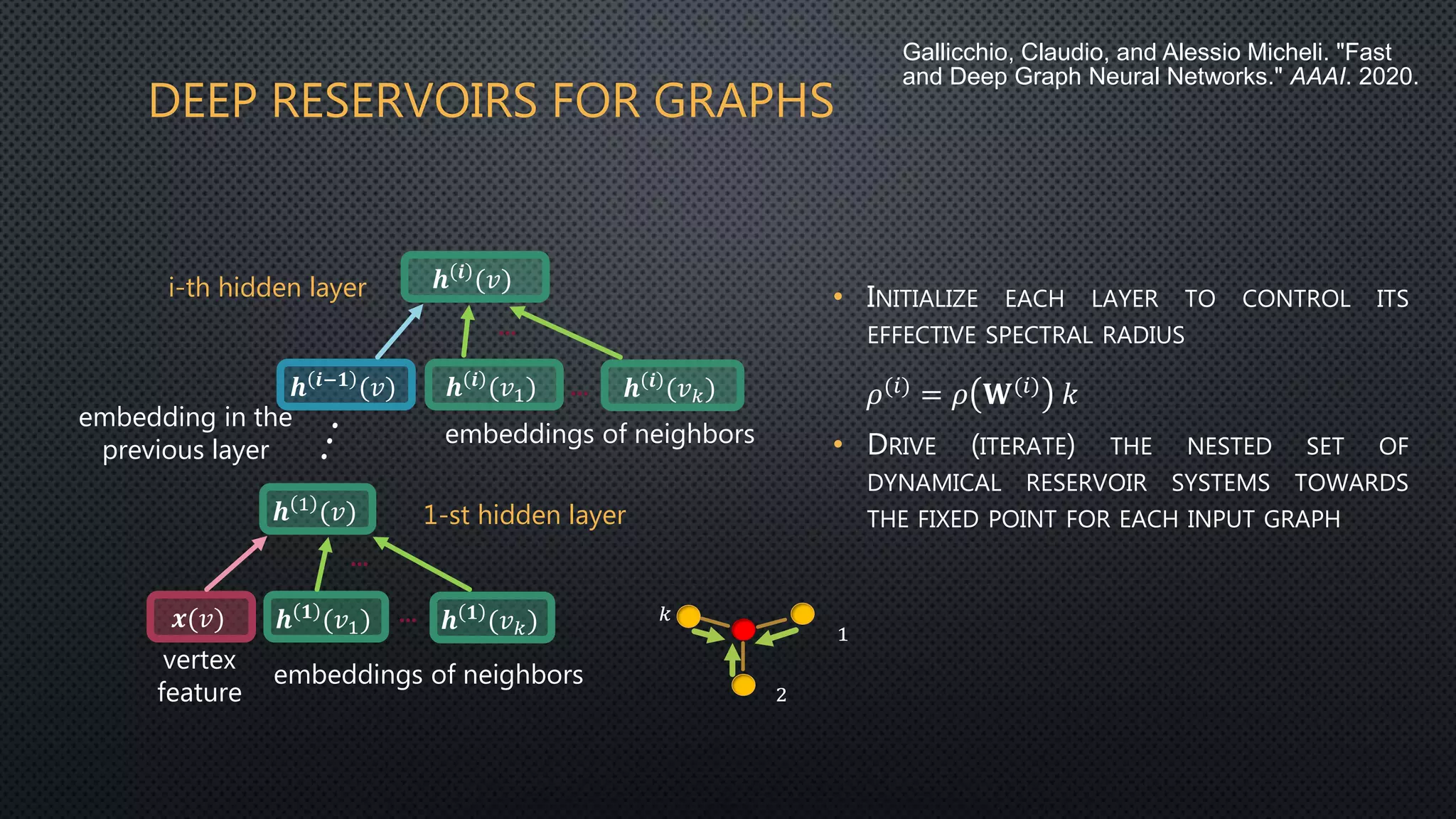
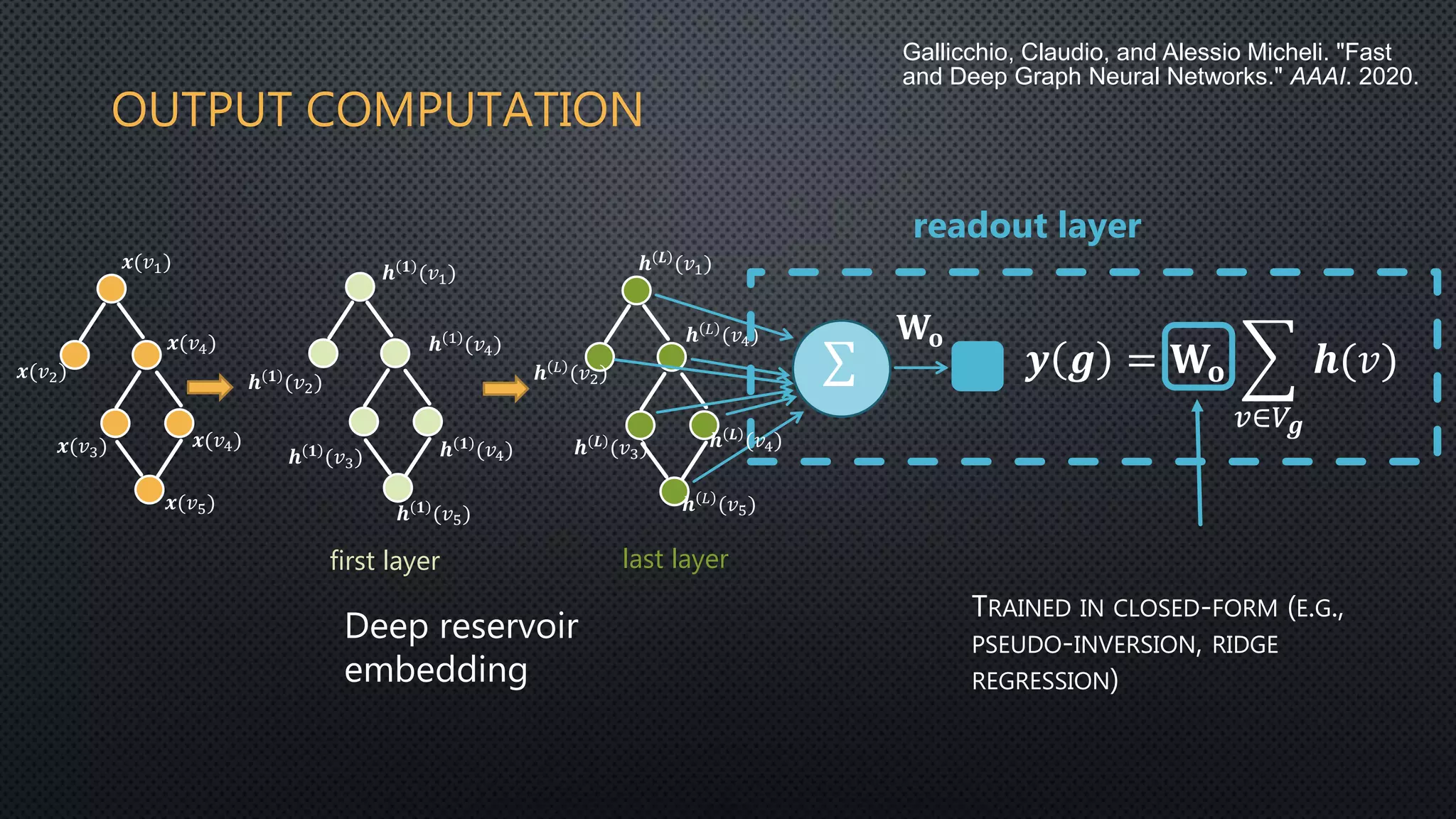
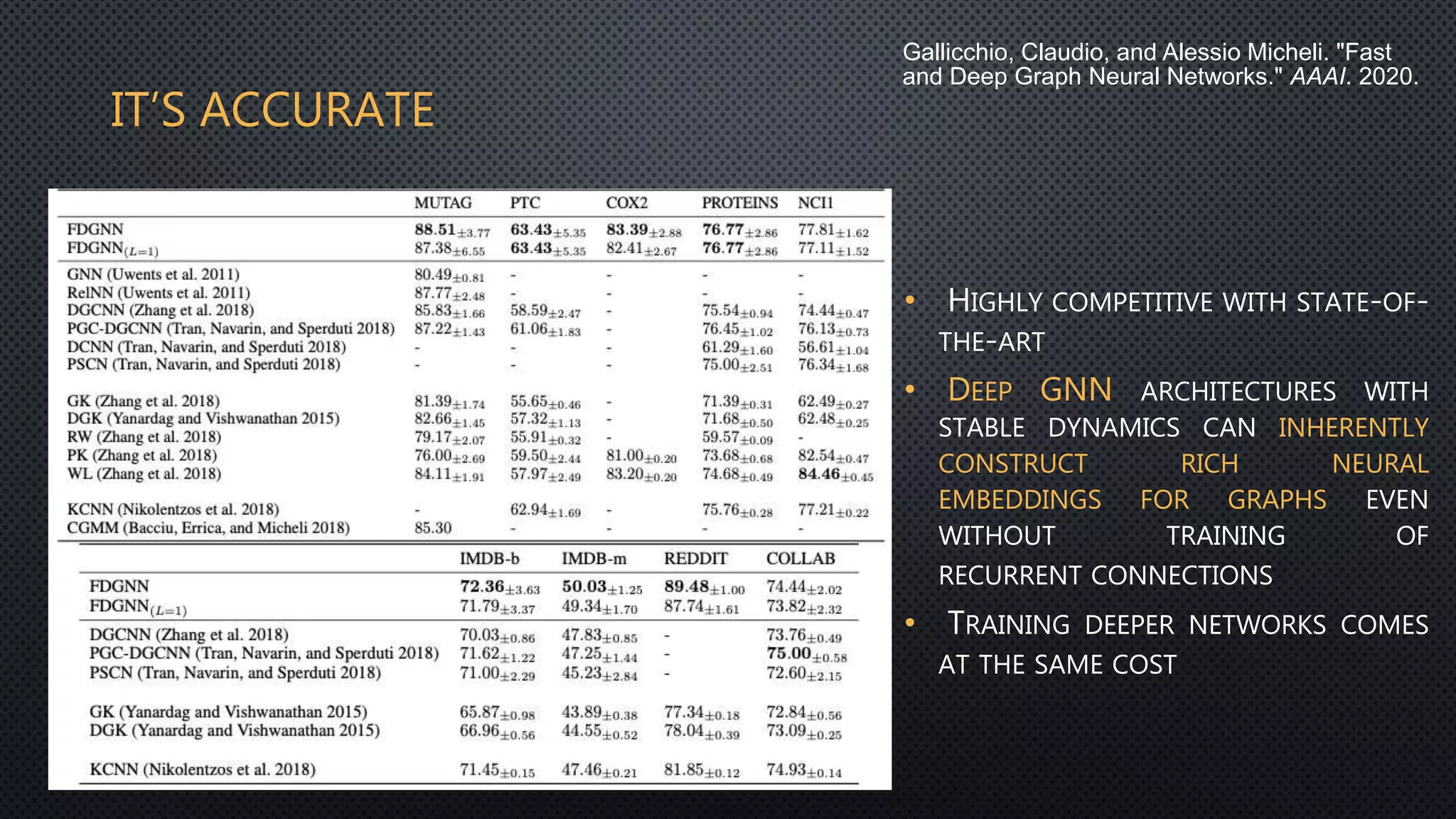
This document discusses deep reservoir computing for structured data like time-series and graphs. Recurrent neural networks are naturally suited for sequential data but are difficult to train. Reservoir computing addresses this by only training the output layer, leaving the recurrent hidden layer untrained. Stacking multiple reservoir layers leads to deep reservoir computing, which develops richer dynamics. For graphs, each node is encoded by the fixed point of a dynamical system implemented as a reservoir network. Deep reservoirs can inherently construct rich embeddings for graphs without training recurrent connections. This makes graph neural networks accurate yet fast compared to state-of-the-art methods that require training deep architectures.

1. DEEP RESERVOIR COMPUTING
FOR STRUCTURED DATA
CLAUDIO GALLICCHIO
UNIVERSITY OF PISA

2. DEEP LEARNING
• DEVELOP MULTIPLE REPRESENTATIONS (NON-LINEARLY)
• ARTIFICIAL NEURAL ARCHITECTURES
• TRAINING ALGORITHMS
• INITIALIZATION SCHEMES
Deep Randomized Neural Networks
Gallicchio C., Scardapane S. (2020)
Deep Randomized Neural Networks. In: Oneto
L., Navarin N., Sperduti A., Anguita D. (eds)
Recent Trends in Learning From Data. Studies
in Computational Intelligence, vol 896.
Springer, Cham
https://arxiv.org/pdf/2002.12287
AAAI-2021 TUTORIAL
FEBRUARY 3, 2021

3. STRUCTURED DATA
time-series graphs

4. RECURRENT NEURAL NETWORKS
• DYNAMICAL NEURAL NETWORK MODELS NATURALLY
SUITABLE FOR PROCESSING SEQUENTIAL FORMS OF DATA
(TIME-SERIES)
• INTERNAL DYNAMICS ENABLE TREATING ARBITRARILY LONG
SEQUENCES
input
hidden
readout
𝑥(𝑡)
ℎ(𝑡)
𝑦(𝑡)
Dynamical
Recurrent
Representation
Layer
𝐡 𝑡 = tanh(𝐔 𝐱 𝑡 + 𝐖 𝐡 𝑡 − 1 )
𝐲 𝑡 = fY(𝐕 𝐡 𝑡 )
state input
previous
state
output
tuned parameters

5. TRAINING RECURRENT NEURAL NETS
• GRADIENT MIGHT VANISH OR EXPLODE
THROUGH MANY TRANSFORMATIONS
• DIFFICULT TO TRAIN ON LONG-TERM
DEPENDENCIES
• TRAINING RNN S IS SLOW
Bengio et al, “Learning long-term dependencies with
gradient descent is difficult”, IEEE Transactions on
Neural Networks, 1994
Pascanu et al, “On the difficulty of training recurrent
neural networks”, ICML 2013

6. RESERVOIR COMPUTING
FOCUS ON THE DYNAMICAL SYSTEM:
• THE RECURRENT HIDDEN LAYER IS A (DISCRETE-TIME) NON-
LINEAR & NON-AUTONOMOUS DYNAMICAL SYSTEM
• TRAIN ONLY THE OUTPUT FUNCTION
• MUCH FASTER & LIGHTWEIGHT TO TRAIN
• SPEED-UP ≈ 𝑥100
• SCALABLE FOR EDGE DISTRIBUTED LEARNING
readout
𝑥(𝑡)
ℎ(𝑡)
𝑦(𝑡)
Untrained
Dynamical
System
Trained Output
𝐡 𝑡 = tanh(𝐔 𝐱 𝑡 + 𝐖 𝐡 𝑡 − 1 )
randomized untrained parameters
Reservoir

7. RESERVOIR COMPUTING – INITIALIZATION
𝐡 𝑡 = tanh(𝐔 𝐱 𝑡 + 𝐖 𝐡 𝑡 − 1 )

8. RESERVOIR COMPUTING – INITIALIZATION
𝐡 𝑡 = tanh(𝜔𝐔 𝐱 𝑡 + 𝝆𝐖 𝐡 𝑡 − 1 )
• HOW TO SCALE THE WEIGHT MATRICES?
• FULFILL THE “ECHO STATE PROPERTY”
• GLOBAL ASYMPTOTIC LYAPUNOV STABILITY CONDITION
• SPECTRAL RADIUS < 1
RANDOMLY INITIALIZED + SPARSELY CONNECTED
Yildiz, Izzet B., Herbert Jaeger, and Stefan J. Kiebel. "Re-visiting
the echo state property." Neural networks 35 (2012): 1-9.

9. WHY DOES IT WORK?
Gallicchio, Claudio, and Alessio Micheli. "Architectural
and markovian factors of echo state networks." Neural
Networks 24.5 (2011): 440-456.
Exploit the architectural bias
- Contractive dynamical systems
separate input histories based on
the suffix even without training
- Markovian factor in RNN design
- The separation ability peaks near
the boundary of stability (edge of
chaos)

10. ADVANTAGES
1. FASTER LEARNING
2. CLEAN MATHEMATICAL ANALYSIS
• ARCHITECTURAL BIAS OF RECURRENT NEURAL NETWORKS
3. UNCONVENTIONAL HARDWARE IMPLEMENTATIONS
• E.G., IN PHOTONICS (MORE EFFICIENT, FASTER)
Brunner, Daniel, Miguel C. Soriano, and Guy Van der Sande,
eds. Photonic Reservoir Computing: Optical Recurrent Neural
Networks. Walter de Gruyter GmbH & Co KG, 2019.
Tino, Peter, Michal Cernansky, and Lubica Benuskova.
"Markovian architectural bias of recurrent neural networks." IEEE
Transactions on Neural Networks 15.1 (2004): 6-15.

11. APPLICATIONS
• AMBIENT INTELLIGENCE: DEPLOY EFFICIENTLY TRAINABLE RNNS IN RESOURCE-CONSTRAINED DEVICES
• HUMAN ACTIVITY RECOGNITION
• ROBOT LOCALIZATION (E.G., IN HOSPITAL ENVIRONMENTS)
• EARLY IDENTIFICATION OF EARTHQUAKES
• MEDICAL APPLICATIONS
• ESTIMATION OF CLINICAL EXAMS OUTCOMES (E.G., POSTURE AND BALANCE SKILLS)
• EARLY IDENTIFICATION OF (RARE) HEART DISEASES
• HUMAN-CENTRIC INTERACTIONS IN CYBER-PHYSICAL SYSTEMS OF SYSTEMS
https://www.teaching-h2020.eu
http://fp7rubicon.eu/

12. IMPLEMENTATIONS
HTTPS://GITHUB.COM/GALLICCH/DEEPESN

13. DEEP LEARNING MEETS RESERVOIR COMPUTING
• THE RECURRENT COMPONENT IS A STACKED
COMPOSITION OF MULTIPLE RESERVOIRS
input
readout
𝑥(𝑡)
ℎ 1
(𝑡)
𝑦(𝑡)
reservoir 1
reservoir 2
reservoir L
⋮
ℎ 2 (𝑡)
ℎ 𝐿
(𝑡)
𝐡 1
𝑡 = tanh(𝐔 1
𝒙 𝑡 + 𝐖(1)
𝐡 1
𝑡 − 1 )
𝐡 2
𝑡 = tanh(𝐔 2
𝐡 1
𝑡 + 𝐖(2)
𝐡 2
𝑡 − 1 )
𝐡 𝐿 𝑡 = tanh(𝐔 𝐿 𝐡 𝐿−1 𝑡 + 𝐖(L) 𝐡 𝐿 𝑡 − 1 )
Gallicchio, Claudio, Alessio Micheli, and Luca Pedrelli. "Deep reservoir computing: A
critical experimental analysis." Neurocomputing 268 (2017): 87-99.
Gallicchio, Claudio, and Alessio Micheli. "Echo state
property of deep reservoir computing networks." Cognitive
Computation 9.3 (2017): 337-350.

14. DEPTH IN RECURRENT NEURAL SYSTEMS
• DEVELOP RICHER DYNAMICS EVEN WITHOUT TRAINING OF THE RECURRENT CONNECTIONS
• MULTIPLE TIME-SCALES
• MULTIPLE FREQUENCIES
• NATURALLY BOOST THE PERFORMANCE OF DYNAMICAL NEURAL SYSTEMS EFFICIENTLY
Gallicchio, Claudio and Alessio Micheli. “Deep
Reservoir Computing” (2020). To appear in
"Reservoir Computing: Theory and Physical
Implementations", K. Nakajima and I. Fischer,
eds., Springer.

15. DESIGN OF DEEP ESNS
- Each reservoir layer cuts part of the
frequency content;
- Idea: stop adding new layers
whenever the filtering effect
(centroid shift) becomes negligible
(independently from the readout
part)
Gallicchio, Claudio, Alessio Micheli, and Luca Pedrelli. "Design of
deep echo state networks." Neural Networks 108 (2018): 33-47.

16. APPLICATIONS
APPROPRIATE DESIGN OF DEEP UNTRAINED RNNS CAN HAVE A HUGE IMPACT

17. RESERVOIR COMPUTING FOR GRAPHS
• BASIC IDEA: EACH INPUT GRAPH IS ENCODED BY THE FIXED POINT OF A DYNAMICAL SYSTEM
• THE DYNAMICAL SYSTEM IS IMPLEMENTED BY A HIDDEN LAYER OF RECURRENT RESERVOIR
NEURONS
• RESERVOIR COMPUTING (RC):
• THE RESERVOIR NEURONS DO NOT REQUIRE LEARNING
• FAST DEEP NEURAL NETWORKS FOR GRAPHS
Deep Neural
Network ?

18. GRAPH REPRESENTATIONS WITHOUT LEARNING
• EACH VERTEX IN AN INPUT GRAPH IS ENCODED BY THE HIDDEN LAYER
𝑣
𝑣1
𝑣2
𝑣 𝑘
𝑥(𝑣)
ℎ(𝑣)
ℎ 𝑣1 ℎ(𝑣 𝑘)
⋮
⋮
embedding (state)
of vertex 𝑣 input feature
of vertex 𝑣
embedding (state)
of neighbors of vertex
input weight matrix hidden weight matrix
𝐡(𝑣) = tanh(𝐔 𝐱 𝑣 +
𝑣′∈𝑁(𝑣)
𝐖 𝐡(𝑣′))

19. GRAPH REPRESENTATIONS WITHOUT LEARNING
• EQUATIONS CAN BE COLLECTIVELY GROUPED
𝑣
𝑣1
𝑣2
𝑣 𝑘
𝐇 = F X, H = tanh(𝐔 𝐗 + 𝐖 𝐇 𝐀)
state
input feature matrixadjacency matrix
Existence (and uniqueness) of solutions is not guaranteed in case of
mutual dependencies (e.g., cycles, undirected edges)

20. GRAPH EMBEDDING BY LEARNING-FREE NEURONS
• THE ENCODING EQUATION CAN BE SEEN AS A DISCRETE TIME DYNAMICAL SYSTEM
• EXISTENCE UNIQUENESS OF THE SOLUTION IS GUARANTEED BY STUDYING LOCAL ASYMPTOTIC
STABILITY OF THE ABOVE EQUATION
• GRAPH EMBEDDING STABILITY (GES): GLOBAL (LYAPUNOV) ASYMPTOTIC STABILITY OF THE
ENCODING PROCESS
INITIALIZE THE DYNAMICAL LAYER UNDER THE GES CONDITION AND THEN LEAVE IT UNTRAINED
RESERVOIR COMPUTING FOR GRAPHS
𝐇 = F X, H = tanh(𝐔 𝐗 + 𝐖 𝐇 𝐀)
𝑣
𝑣1
𝑣2
𝑣 𝑘

21. DEEP RESERVOIRS FOR GRAPHS
• INITIALIZE EACH LAYER TO CONTROL ITS
EFFECTIVE SPECTRAL RADIUS
𝜌(𝑖)
= 𝜌 𝐖(𝑖)
𝑘
• DRIVE (ITERATE) THE NESTED SET OF
DYNAMICAL RESERVOIR SYSTEMS TOWARDS
THE FIXED POINT FOR EACH INPUT GRAPH𝒉 1 (𝑣)
𝒙(𝑣) 𝒉 𝟏
(𝑣1) 𝒉 𝟏
(𝑣 𝑘)…
…
𝒉 𝒊
(𝑣)
𝒉 𝒊−𝟏
(𝑣) 𝒉 𝒊
(𝑣1) 𝒉 𝒊
(𝑣 𝑘)…
…
vertex
feature
embeddings of neighbors
embeddings of neighbors
embedding in the
previous layer
1-st hidden layer
i-th hidden layer
�
�
�
�
Gallicchio, Claudio, and Alessio Micheli. "Fast
and Deep Graph Neural Networks." AAAI. 2020.

22. OUTPUT COMPUTATION
TRAINED IN CLOSED-FORM (E.G.,
PSEUDO-INVERSION, RIDGE
REGRESSION)
𝒚 𝒈 = 𝐖𝐨
𝑣∈𝑉𝒈
𝒉(𝑣)
Deep reservoir
embedding
𝒙(𝑣5)
𝒙(𝑣4)
𝒙(𝑣1)
𝒙(𝑣2)
𝒙(𝑣3)
𝒙(𝑣4)
𝒉 𝐿
(𝑣5)
𝒉 𝑳
(𝑣1)
𝒉 𝐿
(𝑣2)
𝒉 𝑳
(𝑣3)
𝒉 𝐿
(𝑣4)
∑
𝐖𝐨
readout layer
𝒉 𝟏
(𝑣5)
𝒉 𝟏
(𝑣1)
𝒉 𝟏
(𝑣2)
𝒉 𝟏
(𝑣3)
𝒉 1
(𝑣4)
𝒉 𝟏
(𝑣4)
first layer last layer
𝒉 𝑳
(𝑣4)
Gallicchio, Claudio, and Alessio Micheli. "Fast
and Deep Graph Neural Networks." AAAI. 2020.

23. IT’S ACCURATE
• HIGHLY COMPETITIVE WITH STATE-OF-
THE-ART
• DEEP GNN ARCHITECTURES WITH
STABLE DYNAMICS CAN INHERENTLY
CONSTRUCT RICH NEURAL
EMBEDDINGS FOR GRAPHS EVEN
WITHOUT TRAINING OF
RECURRENT CONNECTIONS
• TRAINING DEEPER NETWORKS COMES
AT THE SAME COST
Gallicchio, Claudio, and Alessio Micheli. "Fast
and Deep Graph Neural Networks." AAAI. 2020.

24. IT’S FAST
• UNTRAINED EMBEDDINGS, LINEAR COMPLEXITY
IN THE # OF VERTICES
• SPARSE AND DEEP ARCHITECTURE
• A VERY SMALL NUMBER OF TRAINABLE WEIGHTS
(MAX. 1001 IN OUR EXPERIMENTS)
Gallicchio, Claudio, and Alessio Micheli. "Fast
and Deep Graph Neural Networks." AAAI. 2020.

25. CONCLUSIONS
• DEEP RESERVOIR COMPUTING ENABLES FAST YET EFFECTIVE LEARNING IN
STRUCTURED DOMAINS
• SEQUENCES, GRAPH DOMAINS
• THE APPROACH HIGHLIGHTS THE INHERENT POSITIVE ARCHITECTURAL BIAS OF
RECURSIVE NEURAL NETWORKS ON GRAPHS
• STABLE AND DEEP ARCHITECTURE ENABLE RICH UNTRAINED EMBEDDINGS
• IT’S ACCURATE AND FAST

26. DEEP RESERVOIR COMPUTING
FOR STRUCTURED DATA
CLAUDIO GALLICCHIO
gallicch@di.unipi.it