ML Types

1. Course
Outcomes
After completion of this course, students will be able to
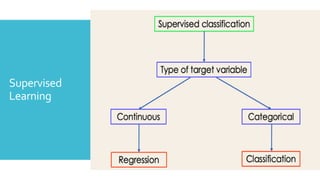
 Understand machine-learning concepts.
 Understand and implement Classification concepts.
 Understand and analyse the different Regression
algorithms.
 Apply the concept of Unsupervised Learning.
 Apply the concepts ofArtificial Neural Networks.

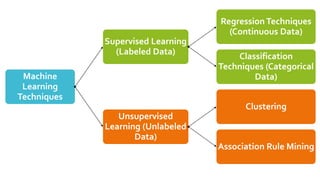
2. Topics -
Supervised
Learning
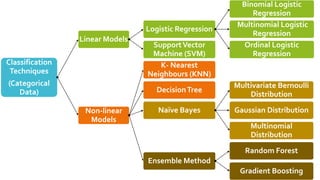
Classification Techniques:
 Naive Bayes Classification
 Fitting Multivariate Bernoulli
Distribution
 Gaussian Distribution and
Multinomial Distribution
 K- Nearest Neighbours
 Decision tree
 Random Forest
 Ensemble Learning
 SupportVector Machines
 Evaluation metrics for
ClassificationTechniques:
Confusion Matrix, Accuracy,
Precision, Recall, F1 Score,
Threshold, AUC-ROC
RegressionTechniques:
 Basic concepts and
applications of Regression
 Simple Linear Regression -
Gradient Descent and Normal
Equation Method
 Multiple Linear Regression
 Non-Linear Regression
 Linear Regression with
Regularization
 Overfitting and Underfitting
 Hyperparameter tuning
 Evaluation Measures for
Regression Techniques: MSE,
RMSE, MAE, R2

3. Algorithms
Machine
Learning
Techniques
Supervised Learning
(Labeled Data)
Regression Techniques
(Continuous Data)
Classification
Techniques (Categorical
Data)
Unsupervised
Learning (Unlabeled
Data)
Clustering
Association Rule Mining

4. Supervised
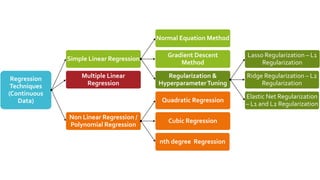
Learning

5. Algorithms
Regression
Techniques
(Continuous
Data)
Simple Linear Regression
Normal Equation Method
Gradient Descent
Method
Regularization &
HyperparameterTuning
Lasso Regularization – L1
Regularization
Ridge Regularization – L2
Regularization
Elastic Net Regularization
– L1 and L2 Regularization
Multiple Linear
Regression
Non Linear Regression /
Polynomial Regression
Quadratic Regression
Cubic Regression
nth degree Regression

6. Algorithms
Classification
Techniques
(Categorical
Data)
Linear Models
Logistic Regression
Binomial Logistic
Regression
Multinomial Logistic
Regression
Ordinal Logistic
Regression
SupportVector
Machine (SVM)
Non-linear
Models
K- Nearest
Neighbours (KNN)
DecisionTree
Naïve Bayes
Multivariate Bernoulli
Distribution
Gaussian Distribution
Multinomial
Distribution
Ensemble Method
Random Forest
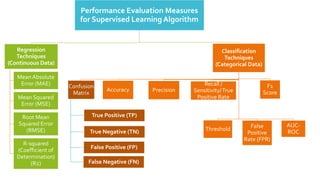
Gradient Boosting

7. Performance Evaluation Measures
for Supervised Learning Algorithm
Regression
Techniques
(Continuous Data)
Mean Absolute
Error (MAE)
Mean Squared
Error (MSE)
Root Mean
Squared Error
(RMSE)
R-squared
(Coefficient of
Determination)
(R2)
Classification
Techniques
(Categorical Data)
Confusion
Matrix
True Positive (TP)
True Negative (TN)
False Positive (FP)
False Negative (FN)
Accuracy Precision
Recall /
Sensitivity/True
Positive Rate
F1
Score
Threshold False
Positive
Rate (FPR)
AUC-
ROC

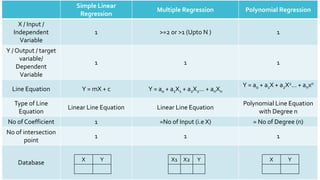
8. Simple Linear
Regression
Multiple Regression Polynomial Regression
X / Input /
Independent
Variable
1 >=2 or >1 (Upto N ) 1
Y / Output / target
variable/
Dependent
Variable
1 1 1
Line Equation Y = mX + c Y = a0 + a1X1 + a2X2… + anXn
Y = a0 + a1X + a2X2… + anxn
Type of Line
Equation
Linear Line Equation Linear Line Equation
Polynomial Line Equation
with Degree n
No of Coefficient 1 =No of Input (i.e X) = No of Degree (n)
No of intersection
point
1 1 1
Database X Y X Y
X1 X2 Y