Chuanhk1

Họ và tên HS:…………………………..……….Lớp:….....
Năm học 2014-2015
-Lƣu hành nội bộ-
TAØI LIEÄU HOÏC TAÄP
MOÂNTOAÙN11
HK1

THPT ERNST THÄLMANN GV. LÊ QUỐC HUY
Tài liệu học tập Toán 11-HK1/2014/2015 Lưu hành nội bộ lớp Trang 2
MỤC LỤC
Chƣơng 1. PHƢƠNG TRÌNH LƢỢNG GIÁC .............................. 6
CHỦ ĐỀ 1: HÀM SỐ LƢỢNG GIÁC. ...............................................8
Vấn đề 1: Tìm TXĐ của các hàm số lƣợng giác:...............................8
Vấn đề 2: Tìm GTLN- GTNN của các hàm số lƣợng giác:...............10
CHỦ ĐỀ 2: PHƢƠNG TRÌNH LƢỢNG GIÁC .................................10
Vấn đề 1: Phƣơng trình lƣợng giác cơ bản: ....................................12
 Vấn đề 2: Phƣơng trình bậc hai hoặc phƣơng trình đƣa về đƣợc bậc hai
theo một hàm số lƣợng giác:............................................................19
 Vấn đề 3: Phƣơng trình cổ điển (bậc nhất theo sin, cos): .................20
 Vấn đề 4: [Đọc thêm]Phƣơng trình đẳng cấp bậc hai ......................22
 Vấn đề 5: Phƣơng trình đƣa về dạng tích:......................................23
 Vấn đề 6: [Nâng cao] Phƣơng trình đối xứng:................................24
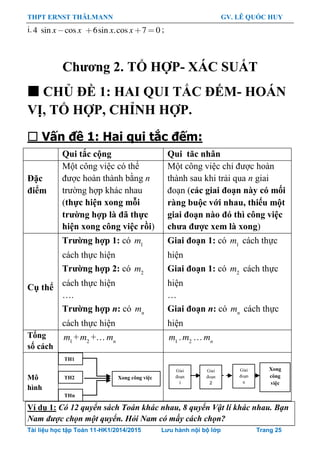
Chƣơng 2. TỔ HỢP- XÁC SUẤT................................................ 25
 CHỦ ĐỀ 1: HAI QUI TẮC ĐẾM- HOÁN VỊ, TỔ HỢP, CHỈNH HỢP.
.......................................................................................................25
 Vấn đề 1: Hai qui tắc đếm:..........................................................25
 Vấn đề 2: Hoán vị- tổ hợp- chỉnh hợp:..........................................28
 Vấn đề 3: Vận dụng công thức tính số tổ hợp, số chỉnh hợp, số hoán
vị- Giải phƣơng trình, bất phƣơng trình tổ hợp đơn giản: ....................35
CHỦ ĐỀ 2: NHỊ THỨC NEWTON..................................................37
 Vấn đề 1: Khai triển nhị thức Newton:..........................................38
 Vấn đề 2: Tìm hệ số, số hạng của nhị thức Newton: .......................39

 Vấn đề 3: [Nâng cao] Một số bài toán nâng cao liên quan nhị thức
Newton:........................................................................................41
CHỦ ĐỀ 3: XÁC SUẤT .................................................................42
Chƣơng 3: DÃY SỐ- CẤP SỐ CỘNG- CẤP SỐ NHÂN............ 49
CHỦ ĐỀ 1. PHƢƠNG PHÁP QUY NẠP TOÁN HỌC.......................49
CHỦ ĐỀ 2. DÃY SỐ......................................................................52
 Vấn đề 1: Số hạng, số hạng tổng quát của dãy số: ..........................52
 Vấn đề 2: Dãy số tăng, dãy số giảm:.............................................53
 Vấn đề 3: Dãy số bị chặn: ...........................................................53
Chƣơng 4: PHÉP DỜI HÌNH- PHÉP ĐỒNG DẠNG TRONG
MẶT PHẲNG............................................................................... 54
CHỦ ĐỀ 1: PHÉP TỊNH TIẾN: .......................................................55
CHỦ ĐỀ 2: PHÉP ĐỐI XỨNG TRỤC:.............................................57
CHỦ ĐỀ 3: PHÉP ĐỐI XỨNG TÂM:...............................................59
CHỦ ĐỀ 4: PHÉP VỊ TỰ: ...............................................................60
CHỦ ĐỀ 5: PHÉP QUAY................................................................62
BÀI TỔNG HỢP: ...........................................................................62
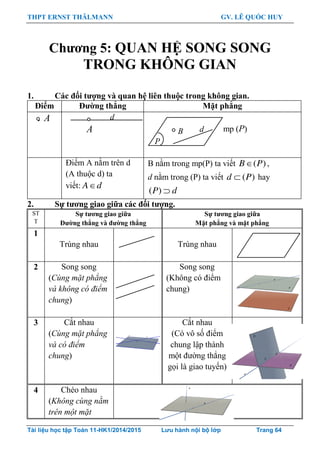
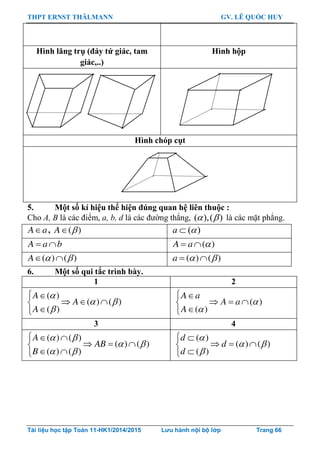
Chƣơng 5: QUAN HỆ SONG SONG TRONG KHÔNG GIAN . 64
CHỦ ĐỀ 1: GIAO TUYẾN, GIAO ĐIỂM.........................................67
 Vấn đề 1: Giao tuyến của hai mặt phẳng: ......................................67
 Vấn đề 2: Các bài tập tìm giao tuyến bằng cách tìm phƣơng giao tuyến:
....................................................................................................69

 Vấn đề 3: Giao điểm của đƣờng thẳng với mặt phẳng:....................69
CHỦ ĐỀ 2: QUAN HỆ SONG SONG ..............................................72
 Vấn đề 1: Đƣờng thẳng song song với đƣờng thẳng:.......................72
 Vấn đề 2: Đƣờng thẳng song song với mặt phẳng:..........................73
 Vấn đề 3: Mặt phẳng song song với mặt phẳng:.............................74
CHỦ ĐỀ 3: THIẾT DIỆN CỦA HÌNH CHÓP VỚI MỘT MẶT PHẲNG
.......................................................................................................76
 BÀI TỔNG HỢP...........................................................................77
PHỤ LỤC ..................................................................................... 81
Phụ lục 1:ĐỀ ÔN THI GIỮA HK1 ...................................................81
Đề số 1......................................................................................82
Đề số 2......................................................................................83
Đề số 3......................................................................................83
Đề số 4......................................................................................84
Đề số 5......................................................................................85
Đề số 6......................................................................................85
Phụ lục 2: ĐỀ THI GIỮA HK1 các năm trƣớc....................................86
Đề giữa Hk1 năm 2008- 2009 (đề A).............................................86
Đề giữa Hk1 2009- 2010 (đề A)....................................................86
Đề giữa Hk1 2011- 2012 (đề A)....................................................87
Phụ lục 3: BỘ ĐỀ ÔN THI HK1.......................................................87
Đề số 1......................................................................................87

Đề số 2......................................................................................88
Đề số 3......................................................................................89
Đề số 4......................................................................................89
Đề số 5......................................................................................90
Đề số 6......................................................................................91
Đề số 7......................................................................................91
Đề số 8......................................................................................92
Đề số 9......................................................................................92
Đề số 10 ....................................................................................93
Đề số 11 ....................................................................................94
Phụ lục 4: ĐỀ THI HK1 các năm trƣớc..............................................94
Đề thi HK 1 năm 2008- 2009 .......................................................94
Đề thi HK 1 năm 2009- 2010 (đề A) .............................................95
Đề thi HK 1 năm 2010- 2011 (đề A) .............................................95
Đề thi HK 1 năm 2011- 2012 (đề A) .............................................96

Chƣơng 1. PHƢƠNG TRÌNH LƢỢNG
GIÁC
HỆ THỨC CƠ BẢN
2 2
sin cos 1x x  ; 2
2
1
1 tan
cos
x
x
 
2
2
1
1 cot
sin
x
x
  ;
1
tan .cot 1 hay tan
cot
 x x x
x
;
sin( 2 ) sin
os( 2 ) os
,
tan( 2 ) tan
cot( 2 ) cot




 
  

 
  
x k x
c x k c x
k Z
x k x
x k x
.
DẤU CỦA CÁC GIÁ TRỊ LƢỢNG GIÁC
GHI NHỚ:
NHẤT CẢ- NHÌ SIN
TAM TAN COT- TỨ COS
CUNG ĐỐI
cos( ) cos ;
sin( ) sin ;
 
  
x x
x x
tan( ) tan ;
cot( ) cot .
  
  
x x
x x
CUNG BÙ
cos( ) cos ;
sin( ) sin ;


  
 
x x
x x
tan( ) tan ;
cot( ) cot .


  
  
x x
x x
CUNG HƠN KÉM 
cos( ) cos ;
sin( ) sin ;


  
  
x x
x x
tan( ) tan ;
cot( ) cot


 
 
x x
x x
CUNG PHỤ
cos
sin
III
III IV

sin( ) cos ;
2
cos( ) sin ;
2


 
 
x x
x x
tan( ) cot ;
2
cot( ) tan .
2


 
 
x x
x x
GHI NHỚ: cos ĐỐI, sin BÙ, tan cot  , phụ CHÉO.
CÔNG THỨC CỘNG
sin( ) sin cos cos sin  a b a b a b;
os( ) cos cos sin sin c a b a b a b ;
tan tan
tan( )
1 tan tan

 
a b
a b
a b
.
GHI NHỚ:
Sin thì sincos cossin Cos thì coscos sinsin dấu trừ
CÔNG THỨC NHÂN ĐÔI
sin2 2sin .cosa a a ;
2
2tan
tan 2
1 tan


a
a
a
;
2 2
2
2
cos2 cos sin
2cos 1
1 2sin .
 
 
 
a a a
a
a
CÔNG THỨC HẠ BẬC
2 1 os2
sin
2
c a
a

 ;
2 1 os2
os
2
c a
c a

 .
2 1 os2
tan
1 os2



c a
a
c a
;
2 1 cos2
cot
1 cos2



a
a
a
.
CÔNG THỨC TỔNG THÀNH TÍCH
2cos cos
2 2
a b a b
cosa cosb
 
  ;
2sin sin
2 2
a b a b
cosa cosb
 
   ;
sin sin 2sin cos
2 2
a b a b
a b
 
  ;
sin sin 2 os sin
2 2
a b a b
a b c
 
  .
GHI NHỚ:
Cos cộng cos bằng 2coscos; cos trừ cos ngược dấu 2sinsin;
sin cộng sin bằng 2sincos, sin trừ sin bằng 2cossin
CÔNG THỨC TÍCH THÀNH TỔNG
1
cos .cos cos( ) cos( )
2
a b a b a b     

1
sin .sin cos( ) cos( )
2
a b a b a b     
1
sin .cos sin( ) sin( )
2
a b a b a b     
ĐẶC BIỆT:
sin cos 2 sin
4
u u u
 
   
 
sin cos 2 sin
4
u u u
 
   
 
CHỦ ĐỀ 1: HÀM SỐ LƢỢNG GIÁC.
Hàm số sin: Hàm số siny x Hàm số cosin: Hàm số cosy x
Tập xác định: D= ;
Tập giá trị : [ 1;1] ;
Tính chẵn lẻ: Lẻ;
Tuần hoàn với chu kỳ T= 2
Tập xác định: D= ;
Tập giá trị : [ 1;1] ;
 Tính chẵn lẻ: Chẵn;
Tuần hoàn với chu kỳ T= 2
Hàm số tan: Hàm số tany x Hàm số cot: Hàm số coty x
Tập xác định:
,
2
D R k k Z


 
   
 
;
Tập giá trị: ;
 Tính chẵn lẻ: Lẻ;
Tuần hoàn với chu kỳ T=
Tập xác định:
  ,D R k k Z  ;
Tập giá trị: ;
 Tính chẵn lẻ: Lẻ;
Tuần hoàn với chu kỳ T=
Vấn đề 1: Tìm TXĐ của các hàm số lượng
giác:
 Với A, B là các biểu thức :

A
y
B
xác định   0B ; y B xác định   0B ;


A
y
B
xác định   0B ; 
A
y
B
xác định 
 


0
0
A
B
;
 Đối với các hàm số lƣợng giác cần chú ý thêm miền xác định của
tan, cot.
Ví dụ 1: Tìm miền xác định của hàm số:
3sin 2
2sin5 1
x
y
x



Giải: Hàm số có nghĩa
5
1 62sin5 1 sin5
2
5
6
x k
x x
x k



 

 
     
   

Ví dụ 2: 

sin
sin3 2
x
y
x
Giải: Hàm số có nghĩa    sin3 2x x
Ví dụ 3: Phƣơng trình sau có nghĩa khi nào?
sin 2 2cos sin 1
0 (1)
tan 3
x x x
x
  


(ĐẠI HỌC KHỐI D NĂM 2011)
Giải: Phƣơng trình (1) có nghĩa
 
 
 
cos 0 (ñieàu kieän cuûa tan)
tan 3 (ñieàu kieän cuûa maãu)
x
x



 

 
  

( , )
3
x k
k m
x m
.
Bài 1: Tìm miền xác định của các hàm số:
a.
1 sin
cos
x
y
x

 ; b.
1 sin
1 sin
x
y
x



; c. tan(2 )
6
y x

  ;
d. y = cot ( 3x – )
4

; e.y = sin ( )
1
2
x
x
; f.y = cot ( )
43


x
;

g.y = 1sin x ; h. 

tan
sin 1
x
y
x
; j.y =
xx sin3sin
3

;
k.y = cos
x
x


1
1
; l.y =
1cos
cot
x
x
; m.y =
1cos
2sin


x
x
;
n.y = xsin3 ; o.y =
x
x
2sin
cos1
; p.y = sin
x
x


1
1
;
q.y = tan (2x + )
3

; r. 
2 2
2
cos sin
y
x x
;
Vấn đề 2: Tìm GTLN- GTNN của các hàm
số lượng giác:
Chú ý:     1 sin ,cos 1,u u u .
Bài 2:
a.y= 2 sin 1x  ; b.y = 2 – 3cosx; c.y = 3 + 2 sinx;
d.y = 5 – 4 sin2x cos2x; e.y =
2
sin41 2
x
; f.y = 2 cos2
x – 3 cos2x;
g.y = 3 – 2 xsin ; h.y = cosx + cos ( x - )
3

;
i.y = sinx – cosx; j.y = 2 sin2x – cos2x; k. 2 2
5 2cos siny x x  ;
l.y = 3 – 4sinx; m.y = 2 – xcos ; n.y = 2 cos ( x + 3)
3


;
o.y = 4 sin x ; p. 2
1 sin( ) 1y x  
CHỦ ĐỀ 2: PHƢƠNG TRÌNH LƢỢNG
GIÁC

Công thức nghiệm thông thƣờng.

2
sin sin
2
u v k
u v
u v k

 
 
     

2
cos cos
2
u v k
u v
u v k


 
     
 tan tanu v u v k    cot cotu v u v k   
Công thức nghiệm đặc biệt.
sin 0u u k    tan 0u u k  
sin 1 2
2
u u k

     tan 1
4
u u k

   
sin 1 2
2
u u k

       tan 1
4
u u k

     
cos 0
2
u u k

    cot 0
2
u u k

   
cos 1 2u u k   
cot 1
4
u u k

   
cos 1 2u u k     
cot 1
4
u u k

     
Chú ý:
Giải  cot (vôùi 0)u a a ta biến đổi thành tan 1/u a rồi dùng máy
tính bấm shift tan (1/ a) suy ra góc  ,chuyển thành tan tanu v . Còn
cot 0 cos 0 / 2u u u k      
Nếu bấm shift sin, shift cos, shift tan, mà ra giá trị “xấu” thì dùng
arcsin, arcos, arctan.
Chuyển từ sin sang cos, cos sang sin, tan sang cot hay cot sang tan thì
ta sử dụng công thức “PHỤ CHÉO”.
Làm mất dấu trừ:
sin(...) sin[ (...)]   cos(...) cos[ (...)]  
tan(...) tan[ (...)]   cot(...) cot[ (...)]  
Điều kiện của tan, cot:
tanu cotu
cos 0 / 2u u k     sin 0u u k  
Nhớ: Cô tang thì khác k /Còn tan chẳng phải nghĩ gì mất công/90
cộng với nửa vòng…là xong!

Vấn đề 1: Phương trình lượng giác cơ
bản:
Phƣơng trình sin sinu v .
Cách
giải  
2
sin sin ,
2
u v k
u v k Z
u v k

 
 
     
Chú ý  Nếu gặp sin u a thì tìm v để sin sin u a v rồi giải nhƣ
trên
 Nếu góc v không “đẹp”, thì lấy arcsinv a
Các
trƣờng
hợp đặc
biệt
sin 0
sin 1 2 ( )
2
sin 1 2
2






   

       


    

u u k
u u k k Z
u u k
Làm mất
dấu trừ
sin sin sin sin( )    u v u v
Phƣơng trình cos cosu v.
Cách
giải  
2
cos cos
2


 
     
u v k
u v k Z
u v k
Chú ý Nếu gặp cos u a thì tìm v để cos cos u a v rồi giải nhƣ
trên
 Nếu góc v không “đẹp”, thì lấy arccosv a
Đặc biệt
cos 0
2
cos 1 2 ( )
cos 1 2


 


   

     
   


u u k
u u k k Z
u u k
Làm mất
dấu trừ
cos cos cos cos( )    u v u v
Phƣơng trình tan tanu v.

Cách
giải
 tan tan     u v u v k k Z
(Điều kiện: ,
2
u v k

  )
Chú ý Nếu gặp tan u a thì tìm v để tan tan u a v rồi giải nhƣ
trên
Nếu góc v không “đẹp”, thì lấy arctanv a
Đặc biệt
tan 0 sin 0
tan 1 ( )
4
tan 1
4






     

       


    

u u u k
u u k k Z
u u k
Làm mất
dấu trừ
tan tan tan tan( )    u v u v
Phƣơng trình cot cotu v.
Cách
giải
 cot cot     u v u v k k Z
(Điều kiện: ,u v k )
Chú ý Nếu gặp cot u a thì tìm v để cot cot u a v rồi giải nhƣ
trên
Nếu góc v không “đẹp”, thì lấy arccotv a
Đặc biệt
cot 0 cos 0
2
cot 1 ( )
4
cot 1
4







     

       


    

u u u k
u u k k Z
u u k
Làm mất
dấu trừ
cot cot cot cot( )    u v u v
Ví dụ: Giải các phương trình sau:
a.  0
2sin 2 30 1 0x   
Giải:

 0
2sin 2 30 1 0x      0 1
sin 2 30
2
x    
 0 0
sin 2 30 sin( 30 )x   

0 0 0
0 0 0 0
2 30 30 360
2 30 180 ( 30 ) 360
x k
x k
    

    

0 0 0
0 0 0 0
2 30 30 360
2 180 ( 30 ) 30 360
x k
x k
    

    

0
0 0
2 360
2 240 360
x k
x k
 

 

0
0 0
180
120 180
x k
x k
 

 
.
b.
2
cos 2 cos2 0
3
 
   
 
x x
Giải:
2
cos 2 cos2 0
3
 
   
 
x x  2
cos 2 cos2 0
3
 
   
 
x x

2
2 2 2
3
2
2 2 2
3
x x k
x x k





  

    


2
0 2 ( ô lý)
3
2
4 2
3
x k v
x k





  

   


6 2
k
x
 
   .
c. 0
tan(45 ) tan3 0x x   (1)
Giải: ĐK:
0 0 0 0 0
0 0 0 0
45 90 180 45 180
3 90 180 30 60
x k x k
x k x k
       
 
     
(1)  0
tan(45 ) tan3x x    0
tan(45 ) tan( 3 )x x  
 0 0
45 3 180x x k   
 0 0
2 45 180x k   
0
045
90
2
x k  
d. 2
cot 2 3x  (2)
Giải: (2) cot2 3x  
TH1: cot2 3x   1
tan2
3
x   0
tan2 tan30x 
0 0 0 0
2 30 180 15 90x k x k     

TH2: cot2 3x    1
tan2
3
x    0
tan2 tan( 30 )x  
0 0 0 0
2 30 180 15 90x k x k       
e. 0 0
sin(2 30 ) sin(45 2 ) 0x x   
Giải:
0 0
sin(2 30 ) sin(45 2 ) 0x x     0 0
sin(2 30 ) sin(45 2 )x x   
 0 0
sin(2 30 ) sin( 45 2 )x x   
........
........

 

f. 0 0
cos(2 30 ) cos(45 2 ) 0x x   
Giải: 0 0
cos(2 30 ) cos(45 2 )x x     0 0 0
cos(2 30 ) cos 180 (45 2 )x x     
 0 0
cos(2 30 ) cos(135 2 )x x  
........
........

 

g. sin2 cos 0
3
x x
 
   
 
Giải: sin2 cos
3
x x
 
  
 
 cos sin2
3
x x
 
  
 
 cos cos 2
3 2
x x
    
     
   
........
........

 

h. (1 2sin2 )(3 2cos ) 0x x  
Giải:
(1 2sin2 )(3 2cos ) 0x x  
1 2sin2 0
3 2cos 0
x
sx
  
 
 
1 2sin2 0
3 2cos 0
x
sx
  
 
 
1
sin2
2
3
cos (voâ nghieäm)
2
x
x

 
 
 
01
sin2 sin2 sin( 30 )
2
x x     
.....
.....

 

Bài 3: (sinu=a, cosu=a, tanu=a, cotu=a)

a. 0
2sin( 30 ) 2 0x    ; b. 1 2cos( 2 ) 2
4
x

   ;
c. 0
3 3tan(3 60 ) 0x   ; d. 3 3 cot(4 ) 4
4
x

   ;
e.
2
sin 2
6 2
x
 
   
 
; f.  0 3
cos 45
2
x   ;
g.  0
cot 3 45 3 0  x ; h. 1
tan 3
2 3
x
 
  
 
;
i.  0
3cot 135 3  x ; j. 2sin 3 3 0
4
x
 
   
 
;
k.
2
3tan 4 3 0
5
x
 
   
 
; l. 2
2cos( ) 1 0
3 4
x 
   ;
m.  0 1
cot 2 10
3
x    ; n.  2cos 3 1 3 0  x ;
o. 2sin(2 ) 1 0
4

  x ; p.  tan 2 70 3o
x   ;
q. 01)
4
tan(3 

x ; r. 2cos (3x – 20o
) + 03 
s.  0
2sin 2 30 3 0  x ; t. 3cot( 20 ) 3 0
3
ox
  
Bài 4:(sinu=sinv, cosu=cosv, tanu=tanv, cotu=cotv)
a. sin(2 ) sin 0
6
x x

   ; b. 0
cos3 cos(60 2 ) 0x x   ;
c. tan( ) tan(3 ) 0
4 3
x x
 
    ; d. 0 0
cot(4 120 ) cot( 30 ) 0x x   
Bài 5: (Làm mất dấu trừ)
a. 0
sin(2 60 ) sin 0x x   ; b. cos2 cos( 3 ) 0
4
x x

   ;
c. 0 0
tan(45 ) tan(3 45 ) 0x x    ; d. cot( ) cot(3 ) 0
3 6
x x
 
   
Bài 6: (Phụ chéo)

a. 0
sin( 120 ) cos3 0x x   ; b. cos2 sin( ) 0
4
x x

   ;
c. tan( 2 ) cot( ) 0
3 4
x x
 
    ; d. 0 0
cot(2 135 ) tan( 120 ) 0x x   
Bài 7: (Làm mất dấu trừ + Phụ chéo)
a. 0
sin(2 60 ) cos3 0x x   ; b. cos3 sin( 2 ) 0
4
x x

   ;
c. tan( ) cot(2 ) 0
3 4
x x
 
    ; d. cot( ) tan(3 ) 0
4 3
x x
 
   
Bài 8: (Trƣờng hợp nghiệm đặc biệt)
a. 0
sin(2 40 ) 0x   ; b. cos(3 ) 0
4
x

  ; c. tan( ) 0
3
x

  ;
d. cot( ) 0
4
x

  ; e.
2
sin(3 ) 1
3
x

  ; f. cos( 5 ) 1
3
x

  ;
g.
2
tan( 7 ) 1
3
x

  ; h. 0
cot(2 10 ) 1x   ; i. sin(4 ) 1
3
x

  
j. 0
cos(5 30 ) 1x    ; k. 0
tan(135 3 ) 1x   ; l.
3
cot(2 ) 1
4
x

   ;
Bài 9: (Vô nghiệm)
a. 0
sin( 70 ) 2x   ; b. 2cos3 3 0x   ; c. 5 4sin( ) 0
3
x

   ;
d.

  cos( ) 4 0
4
x ; e. 2 os2 3 0c x   ; f.   0
3sin( 70 ) 4x .
g/ sin .cos 1x x  ; h/ 2 2
cos sin 3x x 
Bài 10: (Dùng arc)
a. 0
3sin(2 40 ) 2x   ; b. 1 3cos( ) 0
4
x

   ;
c. 4 tan( 3 ) 0
3
x

   ; d. 2cot(2 ) 4 0
4
x

   ;
e. 5cos2 4 0 x ; f.  0
3sin 2 45 2  x ;

g. 3tan2 5 0x   ; h. 0
6 3cot( 135 ) 12x  
Bài 11: (Lấy căn hoặc hạ bậc)
a. 2 3
sin 2
4
x  ; b. 2 0 1
cos (3 30 )
2
x   ;
c. 2 1
tan 4
3
x  ; d. 2
cot (5 ) 3
4
x

 
Bài 12: (phƣơng trình tích)
a. cos2 .sin3 0x x  ; b. 3
cos 4 .tan 0x x  ;
c. 6
sin3 .cot 0x x  ; d.    0 0
tan 30 .cos 2 150 0x x   ;
e.   3tan 3 2sin 1 0x x   ; f.   sin3 1 2 sin 0x x   ;
g.  2
sin3 1 cos 2 0 x x ; h.   5
sin 2 cos 7 0x x ;
i.    0 2
cos(2 30 ) 1 cos 5 0x x ; j.  2
(tan 4 1)cos 0x x ;
Bài 13: (Tổng hợp)
a. 0
cos2 cos(120 2 ) 0  x x ; b. cos4 cos3 0x x  ;
c. 0
sin2 sin(45 4 ) 0  x x ; d. sin2 sin4 0x x  ;
e. tan3 .cot5 1x x  ; f. sin(3 ) cos2 0
4
x x

   ;
g. sin 3 cos2 0
4
x x
 
   
 
; h. tan cot2 0
3
x x
 
   
 
;
i.tan cot2 0
3
x x
 
   
 
; j.
    
     
   
cot 2 .tan 3 1
3 4
x x ;
k.sin (x + )
3
2
= cos3x; l.
5
sin(3 ) cos( 3 ) 0
6 4
x x
 
    ;
m.cos
2
x
= – cos (2x – 30o
); n.sin3x – cos2x = 0;
o. cos3x – sin5x = 0; p.tan ( xx 2cot)
4


;

 Vấn đề 2: Phương trình bậc hai hoặc
phương trình đưa về được bậc hai theo một
hàm số lượng giác:
Dạng: 2
0( 0)at bt c a    với  sin ,cos ,tan ,cott u u u u.
Giải nhƣ giải phƣơng trình bậc hai, chú ý điều kiện
a. 2
2sin 5sin 3 0x x  
Giải:
Đặt sin ( 1 1)t x t    , ta có 2
2 5 3 0t t  
1( )
3
( )
2
t nhaän
t loaïi
 

 

 1 sin 1 2
2
t x x k

      .
b. 2
sin 4cos 4 0x x  
Giải:  2
sin 4cos 4 0x x    2
1 cos 4cos 4 0x x   
 2
cos 4cos 3 0x x    
cos 1(nhaän)
cos 3(loaïi)
x
x
 


.
Ta có cos 1 2x x k    .
Bài 14.
a. 2
3sin 3 5sin3 2=0 x x ; b. 2
2cos 2 5cos2 3 0  x x ;
c. 2
tan ( ) 4tan( ) 3 0
3 3
x x
 
     ; d.  2
cot 1 3 cot 3 0x x    ;
e. 4 2
tan 4tan 3 0x x   ; f. 2
4sin 2( 3 1)sin + 3 0  x x .
Bài 15. (Chứa   2 2
sin ,cos ; cos ,sinu u u u ) :
a. 2
sin 2 4cos2 4 0x x   ; b. 2
2cos 2 3sin2 2 0x x   ;
c.  2
3sin 2 4 4cos2x x ; d. 2
2cos 3 3sin3 3x x   ;

e. 2
sin cos +1=0x x ; f. 2 2 3
sin 2 2cos 0
4
x x   ;
g. 2
3cos 6 8cos3 sin3 4 0x x x   ; h. 2
2cos 3sin .x x ;
i. 2
6cos 5sin 2 0x x   .
Bài 16. (Chứa    cos2 ,cos ; cos2 ,sinu u u u ) :
a. cos2 4sin 5x x   ; b. 2cos2 1 cosx x  ;
c. 1 cos4 cos2x x  ; d. cos4 cos2 2 0x x   ;
e. 3cos2 sin 4 0x x   ; f. os2 +9cos +5=0c x x ;
Bài 17. Chứa      2 2
tan ,cot ; 1/ cos ,tan ; 1/ sin ,cotu u u u u u :
a. tan 2cot 1 0x x   ; b. 3 tan 6cot +2 3 3 0x x   ;
c. 2
5
9 cot
sin
x
x
   ; d. 2
3
tan 5
cos
x
x
  ; e. tan2 cot 2 2 x x
Bài 18. Chứa   2 2 2 2
cos ,sin ,cos cos ,sin ,sinu u u u u u :
a. 2 2
cos sin 3cos 4 0x x x    ; b. 2 2
2sin cos sin 3x x x    ;
Bài 19. Chứa    2 2
cos2 ,cos ,sin , cos2 ,sin ,cosu u u u u u :
a. 2
cos cos2 4sin 3x x x   ; b. 2
cos2 sin 1 2cosx x x   
Bài 20.
a. 2 2
2sin 3cos 5 0
2
x
x   ; b. 2 2
2cos sin 0
2
x
x  .
 Vấn đề 3: Phương trình cổ điển (bậc nhất
theo sin, cos):
Dạng: sin cosa u b u c  .
Điều kiện có nghiệm: 2 2 2
a b c 
Cách giải: Chia 2 vế cho 2 2
a b , ta đƣợc
2 2 2 2 2 2
sin cos (1)
a b c
u u
a b a b a b
 
  

Sau đó tìm góc  để
2 2 2 2
cos ,sin
a b
a b a b
  
 
.
Khi đó:
2 2 2 2
(1) cos sin sin cos sin( )
c c
u u u
a b a b
       
 
Ví dụ: Giải phương trình 0 0
sin(2 10 ) 3cos(2 10 ) 1x x   
Giải:  1; 3; 1a b c    2 2 2 2 2 2
1 ( 3) 4 1a b c       
 Chia hai vế cho 2 2
2a b  ta được:
0 01 3 1
sin(2 10 ) cos(2 10 )
2 2 2
x x   
 0 0 0 0 1
cos60 sin(2 10 ) sin60 cos(2 10 )
2
x x   
  0 0 1
sin 2 10 60
2
x   
  0 0
sin 2 70 sin30x   
0 0 0
0 0 0 0
2 70 30 360
2 70 180 30 360
x k
x k
   

   

0 0 0 0
0 0 0 0
2 100 360 50 180
2 220 360 110 180
x k x k
x k x k
    
 
    
. 
Bài 21 : a.sin 3cos 2x x  ; b. 3cos2 3sin2 3x x   ;
c. cos sin 2x x    ; d. sin(3 ) 1 3cos(3 ) 0
3 3
 
    x x ;
e. 2sin 3 6cos 3 2 0
4 4
x x
    
       
   
; f. 2 cos4 6sin4 2x x   ;
g.cos2 3sin2 2x x  ; h. 0 0
2 3cos(30 ) sin(30 ) 0x x     ;
i.
2 2
3cos( ) 3sin( ) 3
3 3
x x
 
    .

 Vấn đề 4: [Đọc thêm]Phương trình đẳng
cấp bậc hai
Dạng: 2 2
sin sin cos cosa u b u u c u d   .
Cách giải: Xét hai trƣờng hợp:
TH1: 2
cos 0: sin 1u u   . Thay vào phƣơng trình.
TH2: cos 0u  : Chia 2 vế cho 2
cos u , đƣa phƣơng trình về phƣơng
trình bậc hai theo tanu với chú ý  2
2
1 tan
cos
d
d u
u
 
Xem ví dụ minh họa sẽ rõ hơn.
a. 2 2
5sin 2sin2 3cos 2x x x  
Giải:
2 2 2 2
5sin 2sin2 3cos 2 5sin 4sin cos 3cos 2x x x x x x x      
TH1: cos 0x  : 2 2
sin 1 cos 1 0 1x x     .
Thay vào phƣơng trình ta có: 5.1 4.sin .0 3.0 2x   (vô lý)
TH2: cos 0x  : Chia cả hai vế phƣơng trình cho 2
cos x :
2 2
2 2 2 2
sin sin cos cos 2
5 4 3
cos cos cos cos
x x x x
x x x x
  
 2 2
5tan 4tan 3 2(1 tan )x x x   
 2 2
5tan 4tan 3 2 2tan 0x x x      2
3tan 4tan 1 0x x  

tan 1
1
tan
3
x
x
 

 

4
1
arctan
3
x k
x k




 

 
  
 
b. 2 2
4sin 3 6 3sin3 .cos3 2cos 3 4x x x x  
Giải:
TH1: cos3 0x  :ta có 2
sin 3 1x  . Thay vào đƣợc: 4=4 (đúng).
Giải cos3 0 3
2 6 3
k
x x k x
  
       là nghiệm.

TH2: cos3 0x  : Chia 2 vế cho 2
cos 3x ta đƣợc
2 2
2 2 2 2
sin 3 sin3 .cos3 cos 3 4
4 6 3 2
cos 3 cos 3 cos 3 cos 3
x x x x
x x x x
  
 2 2
4tan 3 6 3 tan3 2 4(1 tan 3 )x x x   
 6 3 tan3 2 4x    6 3 tan3 6x  
6 1
tan3
6 3 3
x   
tan3 tan
6
x

 3
6 18 3
k
x k x
  
      . 
Bài 22:
a. 2 2
cos 3sin cos 2sin 0x x x x   ; b. 2 2
sin (1 3)sin cos 3cos 0x x x x    ;
c. 2 2
5sin 2sin2 2 3cos 0x x x    ; d. 2 2 1
sin 2 sin4 2cos 2
2
x x x   ;
e.    2
3sin 3 3sin3 .cos3 cos6 1 0x x x x ; f. 2 2
2sin 2 sin2 cos2 cos 2 2  x x x x
g. 2 2
2sin 3 sin3 cos3 3cos 3 0x x x x   ; h. 2 2
4sin 2sin2 3cos 1x x x   ;
i. 2 2
2cos 3 3sin2 4sin 4x x x   ; j. 2 2
4cos 3sin cos 3 sinx x x x   ;
 Vấn đề 5: Phương trình đưa về dạng
tích:
Sau những bƣớc biến đổi thích hợp ta có phƣơng trình dạng:
0
. 0
0
A
A B
B
 
  

.
Mở rộng:
1
2
1 2
0
0
. ... 0
...
0
n
n
A
A
A A A
A
 

 



Bài 23:

a.sin4 2cos2 0x x  ; b. 2
sin2 2cos 0x x  ;
c. 2 2
sin (3 ) cos 2 0
4
x x

   ; d. 2sin2 2 sin4 0x x 
e. 2 2
sin (2 ) cos 3 1
5
x x

   ; f.5cos 2sin2 0x x  ;
g. tan2 2tan 0x x  ; h. 2
2cos cos2 2x x 
i. 2
2sin 3cos2 2x x  ; j.cos3x – cos4x + cos5x = 0
k.sin7 sin3 cos5x x x  ; l. 2 2
cos sin sin3 cos4x x x x  
m.cos2x – cosx = 2 sin2
2
3x
; n. cos2 sin 1 0x x  
o. cos2 .cos 1 sin2 .sinx x x x  ; p. cos sin2 0x x 
q.sin2
(x + 0)
3
2(sin)
3
2 2


x ; r.tan 3cotx x
s.sin 2sin3 sin5x x x   t. cos5 .cos cos4x x x
u.
1
sin .sin2 .sin3 sin4
4
x x x x ; v. 4 4 21
sin cos cos 2
2
x x x 
 Vấn đề 6: [Nâng cao] Phương trình đối
xứng:
Dạng: (sin cos ) sin .cos 0 (1)a x x b x x c
Cách giải: Đặt  sin cos 2sin , 2 2
4
t x x x t
 
       
 
suy ra 2
1 2sin cost x x  nên ta có
2
1
sin cos
2
t
x x



.
Sau đó thay vào phƣơng trình (1), đƣợc một phƣơng trình theo ẩn t, giải tìm t,
từ đó giải tìm x.
Bài 24:
a.sin cos 2sin .cos 1 0x x x x ; b. 3 sin cos 4sin .cos 0x x x x .
c.12 sin cos 2sin .cos 12 0x x x x ; d. 1 sin 1 cos 2x x .
e.3 sin cos sin .cos 3x x x x ; f. sin cos 3sin .cos 1x x x x ;
g. 2 sin cos 10sin .cos 2x x x x ; h.sin cos 3sin .cos 1x x x x

i.4 sin cos 6sin .cos 7 0x x x x ;
Chƣơng 2. TỔ HỢP- XÁC SUẤT
 CHỦ ĐỀ 1: HAI QUI TẮC ĐẾM- HOÁN
VỊ, TỔ HỢP, CHỈNH HỢP.
 Vấn đề 1: Hai qui tắc đếm:
Qui tắc cộng Qui tăc nhân
Đặc
điểm
Một công việc có thể
đƣợc hoàn thành bằng n
trƣờng hợp khác nhau
(thực hiện xong mỗi
trƣờng hợp là đã thực
hiện xong công việc rồi)
Một công việc chỉ đƣợc hoàn
thành sau khi trải qua n giai
đoạn (các giai đoạn này có mối
ràng buộc với nhau, thiếu một
giai đoạn nào đó thì công việc
chƣa đƣợc xem là xong)
Cụ thể
Trƣờng hợp 1: có 1
m
cách thực hiện
Trƣờng hợp 2: có 2
m
cách thực hiện
….
Trƣờng hợp n: có n
m
cách thực hiện
Giai đoạn 1: có 1
m cách thực
hiện
Giai đoạn 1: có 2
m cách thực
hiện
…
Giai đoạn n: có n
m cách thực
hiện
Tổng
số cách
1
m + 2
m +… n
m 1
m . 2
m … n
m
Mô
hình
Ví dụ 1: Có 12 quyển sách Toán khác nhau, 8 quyển Vật lí khác nhau. Bạn
Nam được chọn một quyển. Hỏi Nam có mấy cách chọn?
Giai
đoạn
1
Giai
đoạn
2
Giai
đoạn
n
Xong
công
việc
TH1
TH2
THn
Xong công việc

Giải:
Có 2 trƣờng hợp:
TH 1: Chọn sách Toán: 12 cách chọn
TH 2: Chọn sách Vật lí: 8 cách chọn
Rõ ràng không cần phải thực hiện hết cả 2 trƣờng hợp, chỉ cần một trƣờng hợp
cũng đƣợc. Do đó ta sẽ áp dụng Qui tắc cộng.
Theo Qui tắc cộng có 12+8=20 cách chọn.
Ví dụ 2: Từ thành phố A đến thành phố B có 3 con đường, từ thành phố B
đến thành phố C có 4 con đường. Hỏi có bao nhiêu cách đi từ A đến C qua
B?
Giải: Từ A đến C phải qua 2 giai đoạn
Giai đoạn 1: Từ A đến B: có 3 cách
Giai đoạn 2: Từ B đến C: có 4 cách
Rõ rang, để đi từ A tới C thì không đƣợc bỏ bớt giai đoạn nào. Do đó, ta sẽ áp
dụng Qui tắc nhân.
Theo Qui tắc nhân có 3.4=12 cách.
Bài 1: Trong một lớp có 18 bạn nam, 12 bạn nữ. Hỏi có bao nhiêu cách chọn:
a.một bạn làm thủ quỹ?; b.Hai bạn trong đó có một nam và một nữ
Bài 2: Nam đến cửa hàng văn phòng phẩm để mua quà tặng. Trong cửa hàng
có 3 mặt hàng: Bút, vở và thƣớc trong đó có 5 loại bút, 4 loại vở và 3 loại
thƣớc. Hỏi có bao nhiêu cách chọn một món quà gồm một bút, một vở và một
thƣớc?
Bài 3: Trong một đội văn nghệ có 8 bạn nam và 6 bạn nữ. Hỏi có bao nhiêu
cách chọn một đôi song ca nam- nữ?
Bài 4: Có 8 phần thƣởng khác nhau đƣợc đem tặng cho 3 học sinh A, B, C sao
cho: học sinh A đƣợc 4 phần, học sinh B đƣợc 3 phần và học sinh C đƣợc 1
phần. Hỏi có bao nhiêu phƣơng án tặng khác nhau?
Bài 5: Có 10 cặp vợ chồng di dự tiệc. Tính số cách chọn một ngƣời đàn ông và
một ngƣời đàn bà trong bữa tiệc để phát biểu ý kiến, sao cho:
a. Hai ngƣời đó là vợ chồng; b. Hai ngƣời đó không là vợ chồng

Bài 6: Ngƣời ta muốn chọn 5 cặp nam nữ để khiêu vũ trong một buổi dạ tiệc,
trong đó có 10 nam và 8 nữ. Hỏi có bao nhiêu cách chọn?
Bài 7: Một công ty gồm 3 trƣởng phòng và 10 nhân viên. Công ty cần lập ra
một đoàn công tác tỉnh xa gồm một trƣởng phòng làm trƣởng đoàn, 5 nhân
viên khác làm đoàn viên. Hỏi có bao nhiêu cách thành lập đoàn công tác?
Bài 8: Trên một giá sách có 15 quyển sách Tiếng Việt khác nhau, 10 quyển
sách Tiếng Anh khác nhau, 8 quyển sách Tiếng Pháp khác nhau. Hỏi có bao
nhiêu cách chọn: a. một quyển sách? b.Hai quyển sách tiếng khác nhau?
c.Ba quyển sách tiếng khác nhau?
Bài 9: Có 12 cặp vợ chồng đi dự tiệc. Tính số cách chọn 1 ngƣời đàn ông và 1
ngƣời đàn bà trong bữa tiệc để phát biểu ý kiến sao cho:
a.Hai ngƣời đó là vợ chồng?; b.Hai ngƣời đó không là vợ chồng?
Bài10: Từ thành phố A đến thành phố B có 5 con đƣờng. Hỏi có bao nhiêu
cách đi từ A đến B, sau đó quay lại A mà không có con đƣờng nào đƣợc đi quá
1 lần?
Bài 11: Từ thành phố A đến thành phố B có 3 con đƣờng, từ thành phố B đến
thành phố C có 4 con đƣờng. Có bao nhiêu cách đi từ A đến C, qua B mà
không có con đƣờng nào đƣợc đi 2 lần?
Bài 12: Trong 100000 số tự nhiên đầu tiên có bao nhiêu số cả ba chữ số 3, 4, 5
trong đó 3, 4, 5 chỉ xuất hiện đúng một lần?
Bài 13: Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập đƣợc bao nhiêu số tự nhiên
chẵn có 3 chữ số?
Bài 14: Có bao nhiêu số tự nhiên có 5 chữ số trong đó các số cách đều số đứng
giữa thì giống nhau?
Bài 15: Các vé xem phim đƣợc đánh số từ 0000 đến 9999. Hỏi số vé gồm 4
chữ số khác nhau là bao nhiêu?
Bài 16: Có bao nhiêu ƣớc số nguyên dƣơng của 360, của 1000000.
Bài 17: Với các chữ số 1; 2; 3; 4; 5; 6 ta lập đƣợc bao nhiêu số có 5 chữ số
khác nhau nếu:
a.Phải có mặt chữ số 1? b.Phải có mặt hai chữ số 1 và 2?
Bài 18: Có bao nhiêu số tự nhiên có tính chất:
a. Là số chẵn và có hai chữ số (không nhất thiết khác nhau)
b. Là số lẻ và có hai chữ số (không nhất thiết khác nhau)
c. Là số lẻ và có hai chữ số khác nhau;
d. Là số chẵn và có hai chữ số khác nhau
Bài 19: Từ các chữ số 1; 3; 5; 7 có thể lập đƣợc bao nhiêu số tự nhiên có 4 chữ
số?

Bài 20: Từ các số 1,2,3,…,9 có bao nhiêu cách chọn một số hoặc là số chẵn
hoặc là số nguyên tố?
Bài 21: Có bao nhiêu số tự nhiên có tính chất:
a.Là số chẵn có hai chữ số?; b. Là số lẻ có hai chữ số?
c. Là số chẵn có hai chữ số khác nhau ?
Bài 22: Trong 100,000 số nguyên dƣơng đầu tiên có bao nhiêu số chứa một
chữ số 2, một chữ số3, một chữ số 4 ?
Bài 23: Có bao nhiêu số nguyên dƣơng gồm không quá 3 chữ số khác nhau?
Bài 24: Từ các số 1,3,5,7 có thể lập đƣợc bao nhiêu số tự nhiên có 4 chữ số ?
Bài 25: Từ các số 0,1,2,3,4,5,6 có thể lập đƣợc bao nhiêu số tự nhiên chẵn có
3 chữ số ?
Bài 26: Có bao nhiêu số tự nhiên có 5 chữ số trong đó các số cách đều số đứng
giữa thì giống nhau?
Bài 27: Có bao nhiêu số tự nhiên có 6 chữ số và chia hết cho 5?
 Vấn đề 2: Hoán vị- tổ hợp- chỉnh hợp:
Nhớ: ! .( 1).( 2)...3.2.1n n n n  
Ví dụ: 3! 3.2.1 6  ; 5! 5.4.3.2.1 60 
Qui ƣớc: 0! 1
CÁCH PHÂN BIỆT HOÁN VỊ- TỔ HỢP- CHỈNH HỢP
Gom hết Hoán vị Chỉnh hợp Tổ hợp
Số đối tƣợng
có (n)
n n n n
Số đối tƣợng
lấy (k)
n n (k=n) k (k<n) k (k<n)
Vị trí, vai
trò, thứ tự
của các đối
tƣợng lấy
Như nhau
(không
phân biệt)
Khác nhau
(Phân biệt)
Khác nhau
(Phân biệt)
Như nhau
(Không phân
biệt)
Công thức
tính (Số
cách)
1 !nP n
!
( )!
k
n
n
A
n k


!
!.( )!
k
n
n
C
k n k


Ví dụ 1: Có bao nhiêu cách sắp xếp 4 bạn An, Bình, Chi, Dung ngồi vào
một bàn học gồm 4 chỗ?
Giải:

Mỗi cách xếp là một hoán vị của 4 phần tử, vậy có  4! 4.3.2.1 24 (cách)
Ví dụ 2: Từ 5 chữ số của tập X={1; 2; 3; 4; 5}có thể lập được bao nhiêu số
có 5 chữ số khác nhau từng đôi một?
Giải:
Mỗi số là một hoán vị của 5 phần tử. vậy có  5! 5.4.3.2.1 120 (số)
Ví dụ 3: Có bao nhiêu cách bầu một ban cán sự gồm 4 người: Lớp trưởng,
Lớp phó học tập, lớp phó lao động và Thủ quỹ trong một lớp học gồm 20 học
sinh.
Giải:
Cách 1: Qua 4 giai đoạn:
Chọn Lớp trƣởng: có 20 cách
Chọn Lớp phó học tập: có 19 cách (bỏ đi em đã đƣợc chọn làm lớp trƣởng)
Chọn Lớp phó lao động: có 18 cách (bỏ đi 2 em đã đƣợc chọn làm lớp trƣởng
và lớp phó học tập).
Chọn Thủ quĩ: có 17 cách (bỏ đi 3 em đã chọn làm Lớp trƣởng, Lớp phó học
tập và Lớp phó lao động)
Theo Qui tắc nhân có: 20.19.18.17=116280
Cách 2: Mỗi cách chọn là một chỉnh hợp chập 4 của 20 phần tử, vậy có
 4
20
20.19.18.17 116280A .
Ví dụ 4: Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau được lập
từ các chữ số {1; 2; 3; 4; 5; 6; 7; 8; 9}.
Giải:
Cách 1: Mỗi số ứng với một cách lấy 4 chữ số khác nhau trong {1; 2; 3; 4; 5;
6; 7; 8; 9} mà mỗi cách lấy là một chỉnh hợp chập 4 của 9 phần tử .
Vậy có:  4
9
9.8.7.6 3024A (số)
Cách 2: Gọi số đƣợc lập là abcd . Qua 4 giai đoạn:
Chọn a: Có 9 cách.
 Chọn b: có 8 cách (bỏ đi số đã chọn cho a)
Chọn c: có 7 cách (bỏ đi số đã chọn cho a và b)
Chọn d: Có 6 cách (bỏ đi số đã chọn cho a, b và c).
Theo Qui tắc nhân: có 9.8.7.6=3024(số)
Ví dụ 5: Một giải bóng đá có 6 đội, thi đấu vòng tròn một lượt. Hỏi có tất cả
bao nhiêu trận đấu?
Giải:

Để có một trận đấu cần phải lấy 2 đội từ 6 đội (2 đội này không phân biệt vai
trò, thứ tự). Do đó, mỗi trận đấu là một tổ hợp chập 2 của 6 phần từ, vậy sẽ có
 2
6
6.5
15
2.1
C (trận đấu)
Ví dụ 6: Trong một lớp có 10 Đoàn viên, có bao nhiêu cách để GVCN:
a. chọn ra 5 em đi dự Đại hội Đoàn trường;
b. chọn ra 5 em làm Ban cán sự lớp, mỗi em một nhiệm vụ: Lớp trưởng, Lớp
phó học tập, Lớp phó lao động, Lớp phó kỉ luật và Thủ quĩ?
c. phân công 10 em làm 10 món quà khác nhau nhân ngày 20-11.
d. Chọn 4 em trong đó 2 em thi cắm hoa và 2 em thi viết Thư pháp.
Giải:
a. Chọn 5 em đi dự ĐH đoàn trƣờng, mỗi cách chọn là một tổ hợp chập 5 của
10 phần tử, có:  5
10
10.9.8.7.6
252
5.4.3.2.1
C (cách)
b. Mỗi cách chọn là một chỉnh hợp chập 5 của 10 phần tử, có:
 5
10
10.9.8.7.6 30240A (cách)
c. Mỗi cách phân công là một hoán vị của 10 phần tử, có
10! 3628800(cách)
d. Chọn 2 em cắm hoa: Mỗi cách chọn là một tổ hợp chập 2 của 10 phần tử
nên có  2
10
10.9
45
2.1
C (cách);
 Sau đó chọn 2 em viết thƣ pháp trong 8 em còn lại: mỗi cách chọn là một tổ
hợp chập 2 của 8 phần tử nên có  2
8
8.7
28
2.1
C (cách)
Theo Qui tắc nhân có: 45.28 1260 (cách).
Bài 28: Có 6 bài toán Đại số (ĐS), 5 bài toán Hình học (HH), 4 bài toán
Lƣợng giác (LG). Từ các bài toán trên có bao nhiêu cách tạo ra một đề kiểm
tra gồm 3 bài: 1 ĐS, 1 HH, 1 LG?
Bài 29: Một tổ gồm 8 nam và 6 nữ. Cần lấy một nhóm 5 ngƣời trong đó có
không quá 3 nữ. Hỏi có bao nhiêu cách chọn?
Bài 30: Một lớp có 25 nam và 15 nữ, GVCN muốn chọn 4 học sinh vào ban
cán sự lớp. Hỏi có bao nhiêu cách chọn nếu:
a.Số nam, nữ là tùy ý b. Số nam, nữ bằng nhau

c. Ít nhất phải có nam d. Bầu 1 lớp trƣởng và 3 lớp phó
e. Bầu 1 lớp trƣởng và 3 lớp phó khác nhau
Bài 31: Có 9 bông hồng và 6 bông cúc, chọn ra 5 bông. Hỏi có bao nhiêu cách
chọn sao cho:
a. Có 3 bông hồng và 2 bông cúc; b. không có bông hông nào;
c. Có ít nhất một bông cúc; d. Số bông cúc ít hơn 3.
Bài 32: Đội thanh niên xung kích của một trƣờng phổ thông có 12 học sinh
gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học
sinh đi làm nhiệm vụ, sao cho 4 học sinh này không thuộc quá 2 trong 3 lớp
trên. Hỏi có bao nhiêu cách chọn nhƣ vậy?
Bài 33: Có 7 chiếc cặp khác nhau đƣợc phát thƣởng cho 4 học sinh. Hỏi có
bao nhiêu cách phát thƣởng sao cho:
a. Mỗi học sinh đƣợc 1 chiếc cặp; b. Một học sinh giỏi nhất đƣợc phát
hai chiếc, 3 học sinh còn lại mỗi em đƣợc 1 chiếc.
Bài 34: Một đội văn nghệ có 20 ngƣời, trong đó có 10 nam và 10 nữ. Hỏi có
bao nhiêu cách chọn 5 ngƣời sao cho:
a.Có đúng 2 nam trong 5 ngƣời đó;
b. Có ít nhất 2 nam và ít nhất 1 nữ trong 5 ngƣời đó.
Bài 35: Trong mặt phẳng cho 10 điểm phân biệt. Có bao nhiêu vector khác
0 có điểm đầu và điểm cuối thuộc tập các điểm đã cho?
Bài 36: Trong một cuộc đua ngựa có 12 con ngựa cùng xuất phát. Hỏi có bao
nhiêu khả năng xếp loại:
a.ba con ngựa về nhất, nhì, ba? b.Ba con ngựa về đích đầu tiên?
Bài 37: Có bao nhiêu cách sắp xếp 5 bạn nam và 5 bạn nữ vào 10 ghế đƣợc kê
thành hàng ngang sao cho:
a.Nam nữ ngồi xen kẽ nhau; b.Các bạn nam ngồi liền nhau
Bài 38: Có 10 bạn đƣợc xếp vào 10 ghế hàng ngang. Có bao nhiêu cách xếp
sao cho bạn An luôn cạnh bạn Bình?
Bài 39: Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt, có mặt đủ 3 chữ số
1; 2; 3?
Bài 40: Tập hợp X={1;3;4;7;8}. Có bao nhiêu cách lập ra một số có 3 chữ số
khác nhua từ X sao cho:
a.Số tạo thành là số chẵn?; b.Số tạo thành là số không có chữ số 4?
c.Số tạo thành là một số nhỏ hơn 378?;
Bài 41: Từ các chữ số 1; 3; 5; 7;9 có thể lập đƣợc bao nhiêu:
a.Số tự nhiên có 5 chữ số?
b.Số tự nhiên có 5 chữ số khác nhau?
c.Số tự nhiên có 3 chữ số khác nhau?
d.Số tự nhiên có 3 chữ số khác nhau và số đó chia hết cho 3?
Bài 42: Có bao nhiêu số tự nhiên:

a.Có 5 chữ số mà 5 chữ số đều là số chẵn?
b.Có 5 chữ số trong đó các chữ số cách đều chữ số đứng giữa thì giống nhau?
Bài 43: Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập đƣợc bao nhiêu số chẵn có
5 chƣ số đôi một khác nhau?
Bài 44: Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7 có thể lập đƣợc bao nhiêu số gồm
4 chữ số, trong đó:
a.Có đúng một chữ số l?
b.Có đúng một chữ số 1 và các chữ số phân biệt?
Bài 45: Trong một lớp học, thầy giáo phát phiếu thăm dò yêu cầu học
sinh ghi thứ tự 3 môn Toán, Lý, Hóa đang học theo mức độ yêu thích
giảm dần. Hỏi có bao nhiêu cách ghi khác nhau?
Bài 46: Có 10 cuốn sách khác nhau và 7 cây bút máy khác nhau. Cần
chọn ra 3 cuốn sách và 3 cây bút máy để tặng cho 3 học sinh, mỗi em
một cuốn sách và một cây bút máy. Hỏi có mấy cách?
Bài 47: Có bao nhiêu cách xếp 5 bạn A, B, C, D, E vào 5 chiếc ghế kê hàng
ngang ?
Bài 48: Có bao nhiêu cách chia 20 ngƣời thành 3 nhóm: nhóm 1 có 10 ngƣời,
nhóm 2 có 7 ngƣời và nhóm 3 có 3 ngƣời? ĐS: 10 7 3
20 10 3. .C C C
Bài 49: Một lớp có 40 học sinh gồm 25 nam và 15 nữ. Có bao nhiêu cách chọn
một nhóm gồm 7 ngƣời vào ban lao động sao cho:
a. Số nam nữ là tùy ý? ĐS: 7
40C ;
b. 5 nam 2 nữ? ĐS: 5 2
25 15.C C ;
c. Ít hơn 3 nữ? ĐS: 7 0 6 1 5 2
25 15 25 15 25 15. . .C C C C C C  ;
d. Ít nhất là 6 nam? ĐS: 7 0 6 1
25 15 25 15. .C C C C
e. Không ít hơn 4 nam? ĐS: 7 0 6 1 5 2 4 3
25 15 25 15 25 15 25 15. . . .C C C C C C C C   ;
Bài 50: Có 30 bác sĩ phẫu thuật. Có bao nhiêu cách chọn:
a.Một bác sĩ mổ, một bác sĩ phụ mổ? ĐS: 2
30A hoặc 30.29 hoặc 1 1
30 29.C C
b.Một bác sĩ mổ, 4 bác sĩ phụ mổ? ĐS: 1 4
30 29.C C
Bài 51: Có bao nhiêu số nguyên dƣơng gồm 4 chữ số khác không và khác
nhau đôi một?
Bài 52: Cần phân công 4 bạn trong một tổ có 12 ngƣời làm trực nhật. Hỏi có
bao nhiêu cách phân công khác nhau?
Bài 53: Có bao nhiêu cách xếp 6 bạn nam và 6 bạn nữ vào 12 chiếc ghế kê
hàng ngang sao cho:
a.Nam nữ ngồi xen kẽ? b.Các bạn nữ ngồi liền nhau?

Bài 54: Có bao nhiêu cách xếp chỗ ngồi cho 8 bạn ( trong đó có Ngân và
Dũng) vào 8 ghế hàng ngang, sao cho:
a.Ngân và Dũng ngồi cạnh nhau? b.Ngân và Dũng không ngồi cạnh nhau?
Bài 55: Ba quả cầu đặt vào ba cái hộp khác nhau (không nhất thiết hộp nào
cũng phải có quả cầu). Hỏi có bao nhiêu cách đặt nếu:
a.Các quả cầu giống nhau? b.Các quả cầu khác nhau?
Bài 56: Có bao nhiêu cách chia 10 ngƣời thành:
a.Hai nhóm, một nhóm 4 ngƣời, một nhóm 6 ngƣời?
b.Ba nhóm tƣơng ứng là 2,3,5 ngƣời ?
Bài 57: Chia 5 quả táo, 3 quả cam, 2 quả chuối cho 10 em (mỗi em một quả).
Hỏi có bao nhiêu cách chia?
Bài 58: Có bao nhiêu cách xếp 4 nam và 6 nữ ngồi vào 10 ghế mà không có
hai bạn nam nào ngồi gần nhau.
a.Ghế xếp hàng ngang? b.Ghế xếp vòng tròn?
Bài 59: Có bao nhiêu số tự nhiên gồm 3 chữ số khác nhau và khác không, biết
tổng 3 chữ số này bẳng 8 ?
Bài 60: Khoa ngoại bệnh viện có 40 bác sĩ. Hỏi có bao nhiêu cách lập một
êkíp mổ:
a.Nếu mỗi êkíp có 1 ngƣời mổ và 1 ngƣời phụ mổ?
b.Nếu mỗi êkíp có 1 ngƣời mổ và 4 ngƣời phụ mổ?
Bài 61: Một hội đồng quản trị có 11 ngƣời gồm 7 nam và 4 nữ. Hỏi có bao
nhiêu cách lập 1 ban thƣờng trực gồm 3 ngƣời biết rằng trong đó phải có ít
nhất 1 nam?
Bài 62: Có bao nhiêu đƣờng chéo trong một hình thập giác lồi?
Bài 63: Cho tập B={1; 2; 4; 5; 7}. Có thể thành lập từ B đƣợc:
a.Bao nhiêu số gồm 4 chữ số khác nhau? ĐS: 120
b.Bao nhiêu số chẵn gồm 4 chữ số khác nhau? ĐS: 48
c.Bao nhiêu số lẻ gồm 4 chữ số khác nhau? ĐS: 72
Bài 64: Cho tập B={0;1;2;3} có thể thành lập đƣợc:
a.Bao nhiêu số gồm 4 chữ số khác nhau? ĐS: 18
b.Bao nhiêu số chẵn gồm 4 chữ số khác nhau? ĐS: 10
c.Bao nhiêu số lẻ gồm 4 chữ số khác nhau? ĐS: 8
Bài 65: Có bao nhiêu số gồm 3 chữ số trong đó chỉ có đúng một chữ số 4?
ĐS: 225
Bài 66: Có 5 con đƣờng nối hai thành phố X và Y, có 4 con đƣờng nối Y và Z.
a.Có bao nhiêu cách chọn đƣờng đi từ X đến Z qua Y? ĐS: 20
b.Có bao nhiêu cách chọn đƣờng đi từ X đến Z qua Y rồi về lại X trong đó
không có con đƣờng nào đi quá một lần? ĐS: 5.4.3.4=240

Bài 67: Có bao nhiêu số tự nhiên có 2 chữ số mà hai chữ số đều là chẵn đƣợc
thành lập từ các số 0; 2; 4; 6; 8? ĐS: 20
Bài 68: Có bao nhiêu cách sắp xếp 4 học sinh vào ngồi trong một bàn dài đủ 4
chỗ ngồi? ĐS: 4!
Bài 69: Trong một phòng học có hai bàn dài, mỗi bàn có 5 ghế. Ngƣời ta
muốn xếp chỗ ngồi cho 10 học sinh gồm 5 nam và 5 nữ. Hỏi có bao nhiêu cách
sắp xếp chỗ ngồi nếu:
a.Tất cả học sinh ngồi tùy ý. ĐS: 10! ;
b. Tất cả học sinh nam ngồi một bàn và học sinh nữ ngồi một bàn. ĐS: 5!5!2!
Bài 70: Có bao nhiêu cách phân công 5 bạn vào 5 nhiệm vụ sau: lau bảng, quét
lớp, cạo bàn, đổ rác, xếp bàn ghế? ĐS: 5!
Bài 71: Xếp thẳng hàng 7 quyển sách Toán, Lý, Hóa, Anh, Văn, Sử, Địa. Hỏi
có bao nhiêu cách xếp nhƣ thế? ĐS: 7!
Bài 72: Từ tập B={1; 2; 3; 4; 5; 6} có thể lập đƣợc bao nhiêu số tự nhiên gồm
8 chữ số trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng 1 lần?
Gợi ý: Đặt các chữ số 2; 3; 4; 5; 6 vào trước, số cách lần lượt là 8, 7, 6, 5, 4.
Cuối cùng đặt 3 chữ số 1 vào 3 vị trí còn lại có 1 cách. Vậy
ĐS: 8.7.6.5.4.1
Bài 73: Có bao nhiêu cách xếp 5 học sinh A, B, C, D, E vào một chiếc ghế dài
sao cho:
a.Bạn C ngồi chính giữa? ĐS: 4! ;
b. Hai bạn A, E ở hai đầu ghế? ĐS: 2!3!
c.Hai bạn B, D ngồi kề nhau? ĐS: 2!4!
d.Hai bạn B, D không ngồi kề nhau? ĐS: 5!-(2!4!)
e. Hai bạn B, D cách nhau một ghế? ĐS: 2!3!+2!3!+2!3!
Bài 74: Một tổ học sinh có 5 nam và 5 nữ xếp thành một hàng dọc.
a.Có bao nhiêu cách sắp xếp khác nhau? ĐS: 10!
b.Có bao nhiêu cách sắp xếp sao cho không có học sinh cùng giới tính đứng kề
nhau? ĐS: TH1: Nam trước- Nữ sau: 5!5! cách, TH2: Nữ trước- Nam sau:
5!5! cách. Do đó có 5!5!+5!5! cách
Bài 75: Xét các số tự nhiên có 5 chữ số khác nhau lập từ {1; 2; 3; 4; 5}. Hỏi
trong các số đó có bao nhiêu số:
a. Bắt đầu bởi chữ số 5? ĐS: 4!;
b.Không bắt đầu bởi chữ số 1? ĐS: 4.4.3.2.1=96 (hoặc 5! 4!=96)
c. Bắt đầu bởi 23? ĐS: 3!
d. Không bắt đầu bởi 345? ĐS: 5!  2!=118.
Bài 76: Có thể lập đƣợc bao nhiêu số chẵn có 5 chữ số khác nhau lấy từ các số
0; 2; 3; 6; 9?

Gợi ý: Xét 2 trường hợp: TH1: 5 0a  (có 4! cách) ; TH2: 5 0a  (có
2.3.3.2.1=36 cách)
Bài 77: Có bao nhiêu số tự nhiên chẵn có 3 chữ số đôi một khác nhau?
ĐS: 9.8+4.8.8=328
Bài 78: Cho bốn chữ số 1; 2; 3; 4. Lập đƣợc bao nhiêu số gồm bốn chữ số
khác nhau từ 4 chữ số đó? ĐS: 4!
Bài 79: Có bao nhiêu số nguyên dƣơng gồm 5 chữ số sao cho:
a. Là số chẵn? Là số lẻ? ĐS: 5.9.10.10.10;
b. Số đầu tiên là 1? ĐS:10.10.10.10
c. Số đầu tiên khác 1? ĐS: 8.10.10.10.10;
d.Hai chữ số kề nhau thì khác nhau? ĐS: 9.9.9.9.9
Bài 80: Với các số 1; 2; 3; 4; 5 có thể thành lập đƣợc bao nhiêu số:
a. Là số chẵn có 3 chữ số khác nhau? ĐS: 24 b.Gồm ba chữ số khác nhau?
ĐS: 3
5A
c. Là số chẵn có 3 chữ số khác nhau và không lớn hơn 345? ĐS:
Bài 81: Biển số xe gắn máy có 4 chữ số (chữ số đầu tiên có thể bằng 0). Có
bao nhiêu biển số trong đó:
a.Hai chữ số kề nhau phải giống nhau? ĐS: 10
b.Hai chữ số kề nhau phải khác nhau? ĐS:10.9.9.9= 7290 (Gợi ý: biển số
có dạng abcd . Chọn a: 10 cách (kể cả chữ số 0), chọn b: 9 cách (bỏ đi chữ số
đã chọn cho a), chọn c: 9 cách (bỏ đi chữ số đã chọn cho b, chọn d: 9 cách (bỏ
đi chữ số đã chọn cho c).
c.Các chữ số khác nhau đôi một. ĐS: 4
10A
Bài 82: Hình bát giác có tất cả bao nhiêu đƣờng chéo? ĐS: 2
8 8C  =20.
Bài 83: Trong mặt phẳng, một đa giác lồi có n đỉnh ( 3n  ). Tìm n biết đa
giác đó có 27 đƣờng chéo. ĐS: n=9.
 Vấn đề 3: Vận dụng công thức tính số tổ
hợp, số chỉnh hợp, số hoán vị- Giải phương
trình, bất phương trình tổ hợp đơn giản:
 ! .( 1)...3.2.1n
P n n n  
Ví dụ: 5
5! 5.4.3.2.1 120P    ; 6
6! 6.5.4.3.2.1 720P    ;
Nhận xét: ! .[( 1)!] .( 1).[( 2)!] ..n n n n n n     

 ! .( 1)...( 1)
!( )! .( 1)...2.1
k
n
n n n n k
C
k n k k k
  
 
 
Chẳng hạn: 3
5
5.4.3
10
3.2.1
C   ; 2
7
7.6
21
2.1
C   ; 4
8
8.7.6.5
70
4.3.2.1
C   ;
Nhận xét: 0
1n
n n
C C  ; k n k
n n
C C 
 .
 !
.( 1)...( 1)
( )!
k
n
n
A n n n k
n k
    

Chẳng hạn: 3
5
5.4.3 60A   ; 2
7
7.6 42A   ; 4
8
8.7.6.5 1680A   ;
Ví dụ: Biết hệ số của 2
x trong khai triển của  1 3
n
x là 90. Tìm n. ĐS:
n=5
Giải:  Số hạng tổng quát: ( 1) 1 (3 ) ( 1) 3k k n k k k k k k
n n
C x C x
  
 2
x ứng với 2k  . Hệ số của 2
x là 2 2 2
( 1) 3 n
C .
 Do đó ta có :
2 2 2 2 2 4 (loaïi)( 1)
( 1) 3 9 10 10 20 0
2.1 5 (nhaän)n n
nn n
C C n n
n
  
           

Kết luận: Vậy 5n  là giá trị cần tìm.
Bài 84:
a. Biết hệ số của 2
x trong khai triển của  1 3
n
x là 90. Tìm n. ĐS: n=5
b. Biết hệ số của 6
x trong khai triển của  3
1
n
x là 28. Tìm n. ĐS: n=8;
c. Biết hệ số của 4
x trong khai triển của 2
2
1
 
 
 
n
x
là 60. Tìm n. ĐS: n=6.
d. Trong khai triển của  1
n
ax ta có số hạng đầu là 1, Số hạng thứ hai là
24x , số hạng thứ ba là 2
252x . Tìm a và n.
Bài 85: Giải các phƣơng trình, bất phƣơng trình sau:
a. 2
2 3
8P x P x  ; b. 1
1
1
6
x x
x
P P
P



 ; c. 4
2 1
15
.
n
n n n
P
P P P

 
 ;
a. 2 2
2
2 50 ,x x
A A x   ; b. 3 2
5 2( 15)n n
A A n   ;

c. 2 2
2
3 42 0n n
A A   ; d. 2 2
2 6 12n n n n
P A P A   ;
e. 10 9 8
9x x x
A A A  ; f.
4
2
2 1
143
0
4
n
n n
A
P P

 
  ; g.
4
4 15
( 2)! ( 1)!
n
A
n n


 
a. 1 2 3 7
2x x x
C C C x   ; b. 3 2 2
1 1 2
2
3x x x
C C A  
  ;
c. 1 2 1
1 4
1 1 7
6x x x
C C C 
  ; d. 2 2
1
2 3 20x x
C A
  ;
e/
( 1)!
72
( 1)!
n
n



f/ 3 2 2
3 2 3n n n
C C A  ,
g/
4
1
33
1
14 ,x
z
z
A
P x
C



  , h/ 2 1
1
79x x
A C
 
i/ 1 2
3 1
12 55x
x x
C A
 

Bài 87: Thực hiện theo yêu cầu trong từng câu:
a. Biết 1 2 2
2 25n n n
C C A    . Tìm n; b. Tìm n biết 0 1 2
16n n n
C C C   ;
c. Giải bất phƣơng trình 2 2 3
2
1 6
10
2 x x x
A A C
x
   ;
d. Biết rằng 1
4 3
7( 3)n n
n n
C C n
 
   . Hãy tìm n;
e. Cho r thỏa 2
18 18
r r
C C 
 . Hãy tính 5
r
C ;
f. Cho
4
3 4
1
24
23
n
n
n n
A
A C 



. Tính n; g. Biết
4 5 6
1 1 1
k k k
C C C
  . Tìm k;
h. Biết 2 2 2 2
1 2 3 4
2 2 149n n n n
C C C C   
    . Tìm n.
CHỦ ĐỀ 2: NHỊ THỨC NEWTON
 0 1 1
0
( ) ...
n
n n n n n k n k k
n n n n
k
a b C a C a b C b C a b 

       ;
Số hạng tổng quát là k n k k
nC a b
;


0
( ) ( 1)
n
n k k n k k
n
k
a b C a b

  
Số hạng tổng quát là ( 1)k k n k k
nC a b
 ;
 Số hạng thứ m+1 ứng với k=m;
 Các qui tắc lũy thừa:
.m n m n
a a a 
 ;
m
m n
n
a
a
a

 ;
1 n
n
a
a

 ;
1
2
a a ;
  .nm m n
a a ; ( . ) .n n n
a b a b ;
n n
n
a a
b b
 
 
 
 Vấn đề 1: Khai triển nhị thức Newton:
Ví dụ 1: Khai triển biểu thức sau thành tổng các đơn thức:  
5
2x y
Giải:
   
5
5 5
5
0
2 2

  
kk k
k
x y C x y
       
2 3 4 50 5 0 1 4 1 2 3 3 2 4 5
5 5 5 5 5 5(2 ) (2 ) 2 2 2 2     C x y C x y C x y C x y C x y C y
5 4 3 2 2 3 4 5
10 40 80 80 32     x x y x y x y xy y
Ví dụ 2: Khai triển biểu thức:  
4
2 3x 
Giải:
   
4
4 4
4
0
2 3 ( 1) 2 3


  
kk k k
k
x C x
         
4 3 2 1 00 0 0 1 1 1 2 2 2 3 3 3 4 4 4
4 4 4 4 4( 1) 2 3 ( 1) 2 3 ( 1) 2 3 ( 1) 2 3 ( 1) 2 3         C x C x C x C x C x
4 3 2
16 96 216 216 81    x x x x .
Bài: Khai triển các nhị thức sau thành tổng các đơn thức:
a.
3
2 1
x
x
 
 
 
; b.  
4
2 2a ; c.  
3
3 2a b ; d. 
4
2 3x .

 Vấn đề 2: Tìm hệ số, số hạng của nhị
thức Newton:
Ví dụ : Trong khai triển của
8
2
3x
x
 
 
 
a.Tìm hệ số của số hạng chứa 2
x ; b.Tìm số hạng không chứa x;
c. Tìm hệ số của số hạng chính giữa; d. Hệ số của số hạng thứ 7;
e. Số hạng đầu; f. Hệ số của số hạng cuối.
Giải: Số hạng tổng quát:
8
8 2 8
8 8
2
( 1) (3 ) ( 1) 2 3
k
k k k k k k k k
C x C x
x

  
   
 
a. Số hạng chứa 2
x ứng với    2 8 2 5k k .
Do đó hệ số cần tìm là 5 5 8 5 5
8( 1) 2 3 108864C 
   .
b.Số hạng không chứa x ứng với    2 8 0 4k k .
Do đó số hạng cần tìm là 4 4 8 4 4
8( 1) 2 3 90720C 
  .
c. Số hạng chính giữa ứng với   
8
4
2 2
n
k .
Do đó số hạng cần tìm là 4 4 8 4 4
8( 1) 2 3 90720C 
  .
d. Số hạng thứ 7 ứng với  6k .
Do đó hệ số cần tìm là 6 6 8 6 6
8( 1) 2 3 81648C 
  ;
e. Số hạng đầu ứng với  0k ;……
f. Số hạng cuối ứng với  8k ;……
Bài 83:
a. Tìm hệ số của số hạng chứa 3
x trong khai triển của
6
2
2
x
x
 
 
 
;ĐS: 12
b. Tìm số hạng chứa 3
5
3 3
x
x
 
 
 
; ĐS: 3 3 3 3
5( 1) 3 C x
c. Tìm hệ số của số hạng chứa
8
5
x
y
trong khai triển của
7
4 2
x
y
 
 
 
;
ĐS: 5 5 5
7( 1) 2 C (k=5)

d. Tìm số hạng chứa 8
5
3
2
2
3
 
 
 
x
x
; ĐS: không có
e. Tìm số hạng chính giữa trong khai triển của
6
5
7
5
x
x
 
 
 
;
ĐS:
3
3 12
6 3
7
5
C x
(k=3)
f. Tìm hệ số của số hạng chính giữa trong khai triển của
10
2
3
2
9a
a
 
 
 
;
ĐS: 5 5 5 5
10( 1) 9 .2C (k=5)
g. Tìm hai số hạng chính giữa trong khai triển của
73
2
2
3
 
 
 
x
x
;
ĐS:
4
3 3
7 3
2
( 1)
3
 C x ;
3
4 4 6
7 4
2
( 1)
3
 C x (k=3;k=4)
h. Tìm hệ số của hai số hạng chính giữa trong khai triển của
113
7
5 7
3 2
x
x
 
 
 
;
ĐS:
6 5
5 5
11
5 7
( 1)
3 2
C
   
    
   
;
5 6
6 6
11
5 7
( 1)
3 2
C
   
    
   
(k=5;k=6)
i. Tìm số hạng thứ 4 trong khai triển của
74
3
4 5
11 2
x
x
 
 
 
;
ĐS:
34 4
3
7 3
4 5
11 2
x
C
x
  
  
   
(k=3)
j. Tìm hệ số của số hạng thứ 5 trong khai triển của
92
2
3 2
 
 
 
x
x
;
ĐS:
5 4
4 4
9
2 1
( 1)
3 2
C
   
    
   
(k=4)

k. Tìm số hạng không chứa x trong khai triển của
8
3 2
3
 
 
 
x
x
;
ĐS: 6 6 6 2
8( 1) 2 3C ;( 24 4 0 6k k    )
l. Tìm số hạng không chứa x trong khai triển của
7
3
3
2
7x
x
 
 
 
;
ĐS: (không có)    
7
21 6 0 (voâ lyù)
2
k k .
m. Tìm số hạng không chứa x trong khai triển của
6
6
3
5
2
 
 
 
x
x
;
ĐS: 4 4 2 4
6( 1) 2 5 C (k=4)
n. Tìm số hạng không chứa a trong khai triển của
82
6
3 2
7 5
 
 
 
a
a
;
ĐS:
6 2
2
8
3 2
7 5
   
   
   
C (k=2)
o. Tìm số hạng không chứa x trong khai triển của
18
2
4 2
5 11
 
 
 
x
x
;
ĐS:
12 6
6 6
18
4 2
( 1)
5 11
   
    
   
C (k=6).
 Vấn đề 3: [Nâng cao] Một số bài toán
nâng cao liên quan nhị thức Newton:
Bài 84:
a/ Chứng minh rằng với mọi số nguyên dƣơng n ta có:
0 1 2
... 2n n
n n n nC C C C    
b/ Chứng minh rằng với mọi số nguyên dƣơng n ta có:

0 2 4 2 1 3 3 2 1
2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1... ...n n
n n n n n n n nC C C C C C C C 
               
c/ Tìm hệ số của x5
trong khai triển của biểu thức:
(x + 1)4
+ (x + 1)5
+ (x + 1)6
+ (x + 1)7
.
d/ Tìm số nguyên dƣơng n sao cho:
   0 1 2 n n
n n n nC 2C 4C ... 2 C = 243.
e/ Khai triển đa thức: P(x) = (1+2x)12
thành dạng:
a0 + a1x + a2x2
+ … + a12x12
Tìm max(a1, a2, …, a12).
f/ Chứng minh: 
       0 n 1 n 1 n n 0 1 n
n n n n n nC 3 C 3 ... ( 1) C C C ... C
g/ Gọi a1, a2, …, a11 là các hệ số trong khai triển sau:
(x + 1)10
.(x + 2) = x11
+ a1x10
+ a2x9
+ … + a11.
Hãy tính hệ số a5.
h/ Chứng minh rằng với số nguyên dƣơng n, ta có:
    
     n 1 1 n 1 2 n 3 3 n 4 4 n n 1
n n n n n2 C 2 C 3.2 C 4.2 C ... nC n.3
CHỦ ĐỀ 3: XÁC SUẤT
 Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả SẼ
xảy ra của nó mặc dù ta đã biết được tập hợp tất cả các kết quả CÓ THỂ xảy
ra của nó.
Không gian mẫu: tập hợp tất cả các kết quả CÓ THỂ xảy ra của một phép
thử. Kí hiệu: 
Biến cố là một tập con của không gian mẫu. Kí hiệu bằng chữ in hoa A, B,
C….
Biến cố có thể được phát biểu dưới 2 dạng: dạng mệnh đề hoặc dạng tập
hợp
Tập  là biến cố không thể, tập  là biến cố chắc chắn
Phép toán trên các biến cố:
+ A gọi là biến cố đối của A kí hiệu A tức là A A 
+Tập A B là hợp của các biến cố A và B. Gọi là biến cố “A hoặc B”
+Tập A B là giao của các biến cố A và B. Gọi là biến cố :A và B” (còn
được kí hiệu là A.B)
+ A B = thì ta nói A và B xung khắc

Xác suất của biến cố A:
( )
( )
( )
n A
P A
n


CÁC TÍNH CHẤT:
   0; 1P P   
 0 1,P A A   là biến cố
     P A B P A P B   (nếu A và B xung khắc)
   1P A P A 
Định nghĩa: A và B độc lập ( . ) ( ). ( )P AB P A P B 
Các cặp biến cố đối
Biến cố A Biến cố đối của A là A
Có ít nhất 1 Không có cái nào
Không cùng (loại, màu, giới,…) Cùng (loại, màu, giới,…)
Ví dụ: Từ một hộp có 6 viên bi xanh, 5 viên bi vàng, lấy ngẫu nhiên 3 viên.
Tính xác suất sao cho lấy được:
a. 3 viên cùng màu xanh; b. không viên nào màu xanh;
c. 2 xanh+1 vàng; d. có ít nhất 2 vàng;
e. Có nhiều nhất 1 xanh; f. viên xanh không nhiều hơn 1;
g. Có ít nhất 1 bi xanh.
Giải:
Mỗi cách lấy 3 viên trong 11 viên là một tổ hợp chập 3 của 11 phần tử nên có
   3
11
11.10.9
( ) 165
3.2.1
n C (cách)
a. Gọi biến cố A: “3 viên cùng màu xanh”
3 viên màu xanh đƣợc lấy trong 6 viên màu xanh, vậy có
  3
6
6.5.4
( ) 20
3.2.1
n A C (cách)
Vậy   

( ) 20 4
( )
( ) 165 33
n A
P A
n
b. Gọi biến cố B: “không viên nào màu xanh”= “3 viên vàng”

3 viên màu vàng đƣợc lấy trong 5 viên màu vàng, vậy có
  3
5
5.4.3
( ) 10
3.2.1
n B C (cách)
Vậy   

( ) 10 2
( )
( ) 165 33
n B
P B
n
c. Gọi biến cố C: “2 xanh+ 1 vàng”
2 xanh:  2
6
6.5
15
2.1
C (cách)
1 vàng: 1
5
5C (cách)
Theo Qui tắc nhân  ( ) 15.5 75n C (cách)
Vậy   

( ) 75 15
( )
( ) 165 33
n C
P C
n
d. Gọi biến cố D: “có ít nhất 2 vàng”
TH1: 2 vàng+ 1 xanh:  2 1
5 6
5.4
. .6 60
2.1
C C (cách)
TH1: 3 vàng  3
5
5.4.3
10
3.2.1
C (cách)
Theo qui tắc cộng    ( ) 60 10 70n D (cách)
Vậy   

( ) 70 14
( )
( ) 165 33
n D
P D
n
. e. Gọi biến cố E: “có nhiều nhất 1 vàng”
TH1: 0 vàng+ 3 xanh:  3
6
6.5.4
20
3.2.1
C (cách)
TH1: 1 vàng+2 xanh:  1 2
5 6
6.5
. 5. 75
2.1
C C (cách)
Theo qui tắc cộng    ( ) 20 75 95n E (cách)

Vậy   

( ) 95 19
( )
( ) 165 33
n E
P E
n
. f. Gọi biến cố F: “viên xanh không nhiều hơn 1”
TH1: 3 vàng+ 0 xanh:  3
5
5.4.3
10
3.2.1
C (cách)
TH1: 2 vàng+1 xanh:  2 1
5 6
5.4
. .6 60
2.1
C C (cách)
Theo qui tắc cộng    ( ) 10 60 70n F (cách)
Vậy   

( ) 70 14
( )
( ) 165 33
n F
P F
n
g. Gọi biến cố G: “có ít nhất 1 xanh”
 G : “không có bi xanh nào”= “tất cả đều bi vàng”=B
  
2
( ) ( )
33
p G p B
Vậy     
2 31
( ) 1 ( ) 1
33 33
P G P G .
Bài 85:Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần.
a. Mô tả không gian mẫu;
b. Xác định các biến cố sau: A: “Tổng số chấm xuất hiện trong hai lần gieo
không bé hơn 10” và B: “Mặt 5 chấm xuất hiện ít nhất một lần”;
c. Tính P(A), P(B).
Bài 86: Có bốn tấm bìa đƣợc đánh số từ 1 đến 4. Rút ngẫu nhiên cùng lúc 3
tấm.
a. Xác định số phần tử của không gian mẫu;
b. Xác định các biến cố sau:A: “Tổng các số trên ba tấm bìa bằng 8”; B: “Các
số trên ba tấm bìa là 3 số tự nhiên liên tiếp”;
c.Tính P(A), P(B).
Bài 87: Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên hai ngƣời. Tìm xác suất
sao cho hai ngƣời đó:
a.Cả hai đều là nữ; b. Không có nữ nào;
c. Ít nhất một ngƣời là nữ; d.Có đúng một ngƣời là nữ.

Bài 88: Một nhóm học sinh có 15 nam và 10 nữ. Chọn ngẫu nhiên 7 ngƣời đi
dự Đại hội Đoàn trƣờng. Tính xác suất sao cho 7 ngƣời đƣợc chọn:
a. toàn là nam; b. có ít nhất một nữ; c. không cùng 1 giới;
d. 3 nam+4 nữ; e. Nhiều nhất 2 nữ; f. nam không ít hơn 5.
Bài 89: Một hộp chứa 10 quả cầu đỏ đƣợc đánh số từ 1 đến 10 và 20 quả cầu
xanh đƣợc đánh số từ 1 đến 20. Lấy ngẫu nhiên một quả. Tìm xác suất sao cho
quả đƣợc chọn:
a. ghi số chẵn; b. màu đỏ;
c. Màu đỏ và ghi số chẵn; d. màu xanh hoặc ghi số lẻ.
Bài 90: Trong một hộp chứa 13 bi vàng, 11 bi đỏ và 9 bi xanh. Lấy ngẫu
nhiên 5 bi. Tính xác suất sao cho:
a. Cả 5 bi đều màu xanh; b. Có ít nhất 3 bi vàng;
c.5 bi không cùng một màu; d.2 vàng+ 2 đỏ+1 xanh;
e. nhiều nhất 2 bi vàng; f. bi đỏ ít hơn 2;
g. bi xanh không nhiều hơn 2; h. 5 bi chỉ có hai loại màu.
Bài 91: Trong 1 tổ có 4 nam và 6 nữ. Chọn ngẫu nhiên 4 ngƣời. Tính xác suất
sao cho:
a. Cả bốn là nữ; b. Không có nữ; c.Ít nhất một nữ; d. Có đúng một nữ;
e. Số nữ không vƣợt quá 2; f. Nam không ít hơn 3; g. vừa có nam, vừa có nữ
Bài 92: Một hộp bút có 10 bút xanh và 7 bút đỏ. Lấy ngẫu nhiên 5 bút. Tính
xác suất sao cho trong 5 bút lấy ra:
a. có ít nhất một bút xanh ; b. không cùng một màu;
c. Nhiều nhất 3 bút đỏ; d. Ít nhất 4 bút xanh;
e. Số bút xanh không vƣợt quá 2; f. có đúng 3 bút đỏ.
Bài 93: Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất sao cho
a. Tổng số chấm hai lần gieo là 8; b. Ít nhất một lần gieo xuất hiện mặt 5
chấm;
c. hai lần gieo nhƣ nhau; d. tích số chấm hai lần gieo là lẻ.
Bài 94: Một lớp có 45 học sinh trong đó 30 học thêm Toán, 20 học thêm Lý,
10 em học cả Toán và Lý. Đọc tên ngẫu nhiên 1 em. Tính xác suất sao cho:
a. Em đó học thêm Toán; b. Em đó học thêm Lý; c. Em đó học thêm
cả Toán và Lý; d. Em đó học chỉ học thêm Toán (không học Lý); e.
Em đó chỉ học thêm Lý (không học Toán); f. Em đó học ít nhất một môn;
g. Em đó không học Toán cũng không học Lý.
Bài 95: Gieo đồng thời hai con súc sắc. Tính xác suất sao cho:
a. Hai con súc sắc đều xuất hiện mặt chẵn; b. Tích các số chấm trên hai con
súc sắc là số lẻ.

Bài 96: Xét phép thử “Tung một đồng xu ba lần”. Hãy mô tả không gian mẫu.
Sau đó tính xác suất sao cho ba lần tung:
a. đều mặt sấp; b. không lần nào sấp;
c. chỉ đúng một lần sấp; d. nhiều hơn một lần ngửa.
Bài 97: Gieo một con súc sắc ba lần. Tính xác suất sao cho mặt 6 chấm xuất
hiện ít nhất một lần.
Bài 98: Một lớp có 60 học sinh học thêm Anh hoặc Pháp. Sau khi đăng kí
GVCN nhận thấy có 40 em học Anh, 30 học Pháp, 10 em học cả Anh lẫn
Pháp. Chọn ngẫu nhiên một em. Tính xác suất sao cho:
a. Em đó học Anh; b. Em đó học Pháp; c. em đó học cả Anh và Pháp;
d. Em đó chỉ học Anh (không học Pháp); e. Em đó chỉ học Pháp (không
học Anh); f. Em đó học ít nhất một môn; g.Em đó không học cả Anh
lẫn Pháp.
Bài 99: Từ một cỗ bài tú lơ khơ có 52 con, rút ngẫu nhiên cùng lúc 4 con. Tính
xác suất sao cho:
a. cả 4 con đều là át; b. có ít nhất một con át; c. 2 át và 2 con K.
Bài 100: Từ một hộp có 7 viên bi xanh, 9 viên bi vàng, lấy ngẫu nhiên 4 viên.
Tính xác suất sao cho lấy đƣợc:
a. 4 viên cùng màu xanh; b. không viên nào màu xanh;
c. 3 xanh+1 vàng; d. có ít nhất 2 vàng;
e. Có nhiều nhất 3 xanh; f. viên xanh không nhiều hơn 3.
Bài 101: Gieo một con súc sắc cân đối, đồng chất và quan sát số chấm xuất
hiện:
a.Mô tả không gian mẫu?
b.Xác định các biến cố sau: A: " Xuất hiện mặt chấm chẵn" B: " Xuất hiện
mặt chấm lẻ"; C: " Xuất hiện mặt có chấm không nhỏ hơn 3"
c. Trong các biến cố trên, hãy tìm các biến cố xung khắc?
Bài 102: Từ một hộp chứa ba bi trắng, hai bi đỏ lấy đồng thời ngẫu nhiên 2 bi.
a.Hãy xây dựng không gian mẫu?
b.Xác định các biến cố sau: A: "Hai bi cùng màu trắng "; B: "Hai bi cùng
màu đỏ "; C: "Hai bi cùng màu "; D: "Hai bi khác màu ".
c.Trong các biến cố trên, hãy tìm các biến cố xung khắc, các biến cố đối nhau?
Bài 103: Gieo 1 đồng tiền 3 lần và xét sự xuất hiện mặt sấp (S), mặt ngửa (N)
a. Hãy xây dựng không gian mẫu?
b. Xác định các biến cố sau: A: "Gieo lần đầu xuất hiện mặt sấp "; B:
"Gieo ba lần xuất hiện các mặt nhƣ nhau "; C: "Đúng 2 lần xuất hiện mặt
sấp "; D: " Ít nhất 1 lần xuất hiện mặt sấp "
c.Trong các biến cố trên, hãy tìm các biến cố xung khắc, các biến cố đối nhau?
Bài 104: Một con súc sắc đƣợc gieo 3 lần. Quan sát số chấm xuất hiện.

a.Hãy xây dựng không gian mẫu?
b.Xác định các biến cố sau : A:" Tổng số chấm 3 lần gieo là 6"
B:" Số chấm lần gieo thứ nhất bằng tổng số chấm của lần gieo thứ 2 và 3";
C: “Số chấm là các số nguyên tố”;
D: “Số chấm gồm 3 số tự nhiện liên tiếp”.
Bài 105: Trong 1 tổ có 6 nam và 4 nữ. Chọn ngẫu nhiên 2 ngƣời. Tìm xác suất
sao cho 2 ngƣời đó:
a.Cả hai là nữ b.Không có nữ; c. Ít nhất một nữ d. Có đúng một nữ
Bài 106: Xếp ngẫu nhiên ba ngƣời đàn ông, hai ngƣời đàn bà và một đứa bé
vào ngồi trên 6 cái ghế hàng ngang. Tính xác xuất:
a.Đứa bé ngồi giữa hai ngƣời đàn ông; b.Đứa bé ngồi giữa hai ngƣời đàn bà.
Bài 107: Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 ngƣời. Tính xác suất
sao cho trong 2 ngƣời đó:
a.Cả hai đều là nam ? b. Không có nam nào?
c. Ít nhất 1 ngƣời là nam? d. Có đúng 1 ngƣời là nam ?
Bài 108: Có 2 hộp chứa các quả cầu. Hộp thứ nhất chứa 3 quả trắng và 2 quả
đen, hộp thứ hai chứa 4 quả trắng và 6 quả đen. Lấy ngẫu nhiên mỗi hộp 1 quả.
Tính xác suất sao cho:
a. Cả 2 quả đều trắng b. Cả 2 quả cùng màu c. Cả 2 quả khác màu.
Bài 109: Có 2 bi xanh, 5 bi đỏ và 4 bi vàng. Chọn ngẫu nhiên 4 bi. Tính xác
suất sao cho:
a. Có 1 bi xanh, 2 bi đỏ và 1 bi vàng;
b. Có nhiều nhất 1 bi đỏ c. Có đủ 3 màu
Bài 110: Một ngƣời chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày cỡ khác
nhau. Tính xác suất để hai chiếc đƣợc chọn tạo thành một đôi.

Chƣơng 3: DÃY SỐ- CẤP SỐ CỘNG-
CẤP SỐ NHÂN
CHỦ ĐỀ 1. PHƢƠNG PHÁP QUY NẠP
TOÁN HỌC
Các bƣớc của Phƣơng pháp qui nạp để chứng minh
mệnh đề ( )P n đúng với mọi 0 0
; ,n n n n N  :
Bước 1: Kiểm tra rằng mệnh đề đúng với 0
n n (tức 0
( )P n đúng).
Bước 2: (Giả thiết qui nạp) giả thiết rằng mệnh đề đúng với
 0
n k k n  bất kì (tức ta giả sử ( )P k đúng).
Bước 3: Chứng minh rằng mệnh đề đúng với 1n k  (tức chứng minh
( 1)P k  đúng).
Sơ đồ: 0
coù ( ) ñuùng
chöùng minh ( 1) ñuùng
giaû söû ( ) ñuùng
P n
P k
P k

 

Ví dụ 1: Chứng minh rằng với 2 *
1 3 5 .... (2 1) ,      n n n .
Giải:
Với n=1: 2
1
1
VT
VP
 


đẳng thức đúng
 Giải sử đẳng thức đúng với  ( 1)n k k , ta có 2
1 3 5 .... (2 1)     k k
Ta chứng minh đẳng thức cũng đúng với 1n k  tức là chứng minh
   
2
1 3 5 .... (2 1) 2 1 1 1k k k           
   
22
2 1 1 1k k k       
2 2
2 1 2 1k k k k      (đúng)
Vậy đẳng thức đúng với mọi *
n

Ví dụ 2: Chứng minh rằng
( 1)( 2)
1 2 3 ... ( 1) , , 2.
2
 
       
n n
n n n
Giải:
Với n=2:
1 2 3 6
(2 1)(2 2)
6
2
VT
VP
    

  
 

đẳng thức đúng
 Giải sử đẳng thức đúng với n k ( 2k  ), tức là
( 1)( 2)
1 2 3 ... ( 1) .
2
 
     
k k
k
Ta chứng minh đẳng thức cũng đúng với 1n k  tức là chứng minh
 
  ( 1) 1 ( 1) 2
1 2 3 ... ( 1) ( 1) 1
2
   
        
k k
k k
 
( 1)( 2) ( 2)( 3)
1 1
2 2
   
      
k k k k
k
 ( 1)( 2) 2 2 ( 2)( 3)       k k k k k
2 2
5 6 5 6     k k k k (đúng)
Vậy đẳng thức đúng với mọi , 2n n  .
Bài 1: Chứng minh các đẳng thức sau bằng phƣơng pháp qui nạp toán học:
a.
( 1)
1 2 3 ...
2

    
n n
n , *
 n
b. 2
1 3 5 ... (2 1)     n n , *
 n
c. 2 4 6 ........ 2 ( 1)n n n      ; *
 n
d.
(3 1)
2 5 8 ... (3 1) ,
2
n n
n

      *
 n
e.   2
1.2 2.5 3.8 ... . 3 1 ( 1),      n n n n *
 n
f. 2 2 2 2 ( 1)(2 1)
1 2 3 ... ;
6
 
    
n n n
n *
 n
g.
2 2
3 3 3 3 ( 1)
1 2 3 ... ;
4

    
n n
n *
 n

h.
( 1)( 2)
1.2 2.3 3.4 ... ( 1) ;
3
 
     
n n n
n n *
 n
i. 2
1.4 2.7 3.10 ... (3 1) ( 1) ;      n n n n *
 n
j.
1 1 1 1
... ;
1.2 2.3 3.4 ( 1) 1
    
 
n
n n n
*
 n
k.
1 1 1 1
... ;
1.5 5.9 9.13 (4 3)(4 1) 4 1
    
  
n
n n n
*
 n ;
l. 2 1
2 2 ... 2 2 2n n
     , *
 n N ;
m.
1 1 1 1
.......
1.3 3.5 5.7 (2 1)(2 1) 2 1
n
n n n
    
  
, *
 n ;
n.
 
1 1 1 1 ( 3)
... , , 4
1.2 2.3 3.4 ( 3) 2 2

      
  
n
n n
n n n
;
o.  
 2
22 2 2
4 1
1 3 5 ... 2 1
3
n n
n

     , *
n  ;
p.
(3 1)
1 4 7 ... (3 2)
2
n n
n

      , *
n  ;
q.    2 *
4.2 8.5 12.8 ... 4 3 1 4 4 ,        n n n n n ;
r.  11
3 9 27 ... 3 3 3
2
n n
      , *
n  ;
s.
5 ( 1)( 2)
5.2 10.3 15.4 ... [5 ( 1)]
3
n n n
n n
 
      , *
n  ;
t.  10 20 30 ... 10 20 ( 2)(5 5)n n n        , , 3  n n ;
u.
1 1 1 1 1
... 1
2 4 8 2 2n n
      *
n  ;
v.
1 2 3 2
... 2
2 4 8 2 2n n
n n 
      *
n  ;
w.  11
5 25 125 ... 5 5 5
4
n n
      , *
n  ;
x. 2
1 1 1 1
1 1 ... 1
4 9 2
n
nn
     
       
    
, *
n  .

Bài 2: Chứng minh rằng *
 n , ta có:
a.n(n+1)(n+2) 6 b. n(n + 1)(2n + 1) 6 c. (13n
1) 6
d. (32n+1
+ 2n+2
) 7 e. (4n
+15n - 1) 9 f. n3
+ 2n 3
Bài 3: Chứng minh rằng với mọi số tự nhiên n  2
a. 3n
> 3n + 1 b. 2n+1
> 2n + 3.
CHỦ ĐỀ 2. DÃY SỐ
 Vấn đề 1: Số hạng, số hạng tổng quát
của dãy số:
Bài 5: Cho dãy số (un): 2
2
1
n
n
u
n


a. Viết 5 số hạng đầu tiên; b.
9
41
là số hạng thứ mấy của dãy số?
Bài 6: Cho dãy số (un):
1
1
3
2n n
u
u u



a. Viết 5 số hạng đầu tiên; b.Tìm số hạng tổng quát của dãy số?
Bài 7: Cho dãy số
1
2 1
n
n
u
n



a.
8
15
là số hạng thứ mấy của dãy số? b.Tìm số hạng thứ 9 của dãy số?
Bài 8: Cho dãy số (un) có tổng Sn = 4n2
– 3n. Tìm số hạng tổng quát un ?
( Biết Sn = u1 + u2 + u3 + ………..+ un )
Bài 9: Viết số hạng tổng quát của dãy số tăng gồm các số nguyên dƣơng
biết mỗi số hạng của dãy chia cho 5 dƣ 2?
Bài 10: Tìm công thức tính số hạng tổng quát của các dãy số sau:
a.
1
1
1
, n 1
2n n
u
u u

 
 
; b.
1
1
3
, n 11
2
n n
u
u u


 

; c.
1
1
2
, n 1
n n
u
u u

 
 

 Vấn đề 2: Dãy số tăng, dãy số giảm:
Lập hiệu 1n n
u u
 hoặc thương 1n
n
u
u

tùy dãy số. Nếu hiệu >0, hoặc
thương >1 thì dãy tăng. Nếu hiệu <0, hoặc thương <1 thì dãy giảm.
Bài 11. Cho dãy số 2
3 1
5
n
n
u
n



a. Viết 5 số hạng đầu tiên; b.
22
54
là số hạng thứ mấy?
Bài 12. Xét tính tăng giảm của các dãy số sau:
a. 3 100n
u n  ; b. 5( 2) 19n
u n    ; c. 5( 2) 19n
u n    ;
d.
3 5
2n
n
u
n



; e.
2 10
5 5n
n
u
n
 


; f.
3
2
5
n
n
u

 
  
 
;
g. 1
( 1) 2n n
n
u 
  ; h. 3
17.5 n
n
u  
 ; i.
3.2 1
5.2 3
n
n n
u



.
 Vấn đề 3: Dãy số bị chặn:
Phƣơng pháp: Chứng minh: ,n
u M n   .
Bài 13: Xét tính bị chặn của dãy số (un) với:
a.
2
2
1
1
n
n n
u
n
 


b.
1
( 1)
nu
n n


c. 2
2 1nu n  d. 2 2 2
1 1 1
1 ...
2 3
nu
n
    
Bài 14: Xét tính đơn điệu và bị chặn của dãy số (un) với:
a.
2
2
1
1
n
n n
u
n
 


b. 1 1
( 1) .sinn
nu
n

 
c. un = sin n + cos n d.
1 *
1
2
, n N
2n n
u
u u
 

 

Chƣơng 4: PHÉP DỜI HÌNH- PHÉP
ĐỒNG DẠNG TRONG MẶT PHẲNG
PHÉP TỊNH TIẾN
Đặc trƣng Công thức
Tịnh tiến theo v . kí hiệu v
T : biến M thành
M‟ sao cho 'MM v
'
'
M M v
M M v
x x x
y y y
  

 
PHÉP ĐỐI XỨNG TRỤC
Đối xứng trục d. Kí
hiệu d
Ñ : biến M thành
M‟ sao cho d là trung
trực của MM‟
d Ox
'
'
M M
M M
x x
y y
 

 
d Oy
'
'
M M
M M
x x
y y
  


PHÉP ĐỐI XỨNG TÂM
Đối xứng tâm I .kí hiệu I
Ñ :
biến M thành M‟ sao cho I là
trung điểm của MM‟.
I là gốc O
'
'
M M
M M
x x
y y
  

 
I bất kỳ
'
'
2
2
M I M
M I M
x x x
y y y
  

 
PHÉP VỊ TỰ
Vị tự tâm I, tỉ số. Kí hiệu ( ; )I k
V :
biến M thành M‟ sao cho
'IM kIM
'
'
( )
( )
M I M I
M I M I
x x k x x
y y k y x
   

  
 '
'
( )
( )
M M I I
M M I I
x k x x x
y k y x y
   

  

CHỦ ĐỀ 1: PHÉP TỊNH TIẾN:
Ví dụ: Cho (3; 2); (5;4); ( 1;9)A B C  ,( ):2 3 7 0d x y   ,
2 2
( ):( 2) ( 5) 25C x y    .
a. Tìm tọa độ ảnh của A qua phép tịnh tiến theo ( 4;7)v  .
b. Viết phương trình ảnh của d qua AB
T .
c. Viết phương trình đường tròn 2
( ') (( ))BC
C T C
 .
Giải:
a.Gọi ' ( )v
A T A 
'
'
3 ( 4) 1
( 2) 7 5
A A v
A A v
x x x
y y y
       

     
'( 1;5)A  .
b. (5 3;4 ( 2)) (2;6)AB      .
 Lấy ( , )M M
M x y d 2 3 7 0M M
x y    (1).
 Gọi ' ( )AB
M T M  '
'
2
6
M M MAB
M M MAB
x x x x
y y y y
    

   
 '
'
2
(2)
6
M M
M M
x x
y y
  

 
Thay (2) vào (1) ta đƣợc: ' '
2( 2) 3( 6) 7 0M M
x y    
 ' '
2 3 21 0M M
x y  
 Gọi ' ( )AB
d T d  ' 'M d .
Vậy ':2 3 21 0d x y  
c. ( 6;5)BC   2 (12;10)BC  

taâm I(2; 5)
( ) coù
baùn kính R=5
C
 


Gọi 2
' ( )BC
I T I

' 2
' 2
2 12 14
5 10 5
I I BC
I I BC
x x x
y y y


     
 
     

taâm I'(14;5)
( ') coù
baùn kính R'=R=5
C



sVậy 2 2
( '):( 14) ( 5) 25C x y    .

Bài 1: a.Cho    2;3 , 1;5A v , tìm  ' v
A T A
b.Cho    3;6 , 0;8B v , tìm ảnh của B qua 2 v
T ;
c. Tìm ảnh của ( 3;7)C  qua phép tịnh tiến theo vector 5DE với
D(5; 2), (6;8)E
Bài 2: a.Cho  ( ): 2 3 6 0; 1; 1      d x y v , tìm  ' v
d T d
b.Cho  ( ):2 3 4 0; 2; 1    d x y v , viết p.t ảnh của d qua 5v
T .
c.Cho  ( ): 5 0; 2;6  d x v , tìm  ' 
 v
d T d
d.Cho  ( ): 5 4;A 2;3 ; (5;10) d y x B , viết  '  AB
d T d
e.Cho  ( ): 6 0; 3;4 ; ( 4;9)   d y A B , tìm  3
' 
 AB
d T d
Bài 3: a.Cho        
2 2
: 2 7 144; 3;8C x y v     , tìm     ' v
C T C
b.Cho      
22
: 5 25; 2; 5C x y v     , tìm     4
'  v
C T C
c. Cho   2 2
: 4 8 5 0; ( 3;1)      C x y x y v , viết    3
'  v
C T C
d.Cho      
2 2
: 4 16; 3;4 ; ( 4;9)    C x y A B , viết    2
' 
 AB
C T C
e.Cho    2 2
: 4 0; 2;2C x y y v    , tìm     ' v
C T C
f.Cho    2 2
: 16 144; A 2;3 ; (5;10)  C x y x B , viết pt     3
'  AB
C T C
Bài 4: Cho (2; 4); ( 7;6); ( 3;5)A B C   ,( ):5 2 15 0d x y   ,
2 2
( ): ( 7) 169C x y   .
a.Tìm tọa độ ảnh của B qua phép tịnh tiến theo AC .
b.Tìm ảnh của d qua AB
T
; c.Tìm 4
( ') (( ))BC
C T C .
Bài 5: Cho (3; 5); ( 8;2); ( 1;6)A B C   ,( ):3 8 12 0d x y   ,
2 2
( ): 6 40 0C x y x    .
a.Tìm tọa độ ảnh của C qua phép tịnh tiến theo vector 2AB.
b.Tìm ảnh của d qua AC
T
; c.Tìm 3
( ') (( ))CB
C T C
 .
Bài 6: Cho ABC gọi M là trung điểm BC.
a.Tìm ảnh của ABM qua phép tịnh tiến BC
T ?

b.Tìm điểm D sao cho BA
C = T ( )D ?
c.Tìm ảnh của đtròn đkính BM qua AC
T ?
Bài 7: Cho hình bình hành ABCD, tâm I.
a.Tìm ảnh của đoạn AC qua BD
T ?
b.Tìm ảnh của ABC qua phép tịnh tiến AD
T ?
Bài 8: Trong mp Oxy cho (2, 3)v   , A(–1, 2), B( - 3 , – 4) và
đƣờng thẳng (d): 2x + 3y – 1 = 0
a.Tìm A' là ảnh của A qua phép tịnh tiến v
T ?
b.Tìm B1 sao cho B là ảnh của B1 qua phép tịnh tiến v
T ?
c.Tìm ảnh của (d) qua phép tịnh tiến v
T ?
d.Tìm ảnh của đƣờng tròn (C): (x+1)2
+ (y – 2)2
= 9 qua 2v
T
?
Bài 9: Trong mp Oxy cho đtròn (C): x2
+ y2
– 2x + 4y – 4 = 0 và (3, 1)v   .
Tìm ảnh của (C) qua phép tịnh tiến v
T ?
Bài 10: Cho  2; 1v   , A(– 3, 2), B(5,-2), đƣờng thẳng d: 2x – 3y +1 = 0 &
đƣờng tròn (C): x2
+ y2
– 2x + 4y + 1 = 0. Tìm ảnh của:
a.Các điểm A ,B qua v
T ; b. Đƣờng thẳng d qua 3v
T
c. Đƣờng tròn (C) qua 5v
T
Bài 11: Cho A( 3, - 2), B(-5,2), đƣờng thẳng d: 3x – 2y +1 = 0 và đƣờng tròn
(C):    
2 2
1 2 9x y    .Tìm ảnh của:
a. Các điểm D( -1; -3), I ( tâm đƣờng tròn (C)) qua AB
T
b. Đƣờng thẳng d qua 4BA
T
c) Đƣờng tròn (C) qua 2AB
T
CHỦ ĐỀ 2: PHÉP ĐỐI XỨNG TRỤC:
Làm giống nhƣ phép tịnh tiến, chỉ thay công thức của phép đối xứng trục
cho phù hợp.
Bài 12: a.Cho  2;3A , tìm ' ( ) OxA Đ A ;
b.Cho  3;6B , tìm 'B  ĐOx  B

Bài 13: a.Cho( ): 2 3 6 0d x y    , tìm 'd  ĐOx  d
b.Cho ( ):2 3 4 0d x y   , tìm 'd  ĐOy  d
c.Cho( ): 5 0d x   , tìm 'd  ĐOx  d
d.Cho ( ): 5 4d y x  , tìm 'd  ĐOy  d
e.Cho( ): 6 0d y   , tìm 'd  ĐOx  d
Bài 14: a.Cho      
2 2
: 2 7 144C x y    , viết pt  'C  ĐOx   C
b.Cho    
22
: 5 25C x y   , tìm  'C  ĐOy   C
c. Cho   2 2
: 4 8 5 0    C x y x y viết pt  'C  ĐOx   C
d.Cho    
2 2
: 4 16C x y   , viết pt  'C  ĐOy   C
e.Cho   2 2
: 4 0C x y y   , tìm  'C  ĐOx   C
f.Cho   2 2
: 16 144C x y x   , viết pt  ' (( )) OyC Đ C .
Bài 15: Cho (2; 4)A  ,( ):5 2 15 0d x y   , 2 2
( ): ( 7) 169C x y   .
a.Tìm tọa độ ảnh của A qua phép đối xứng trục Ox .
b.Tìm ảnh của d qua Oy
Ñ .
c.Tìm( ') (( ))Ox
C Ñ C .
Bài 16: Cho ( 8;2)B  ,( ):3 8 12 0d x y   , 2 2
( ): 6 40 0C x y x    .
a.Tìm tọa độ ảnh của B qua Oy
Ñ .
b.Viết phƣơng trình đƣờng thẳng ' ( )Ox
d Ñ d .
c.Tìm( ')C của đƣờng tròn ( )C qua phép đối xứng trục Oy .
Bài 17: Cho ABC, AH là đƣờng cao
a.Tìm ảnh của ABH qua phép đối xứng trục ĐAC ?
b.Tìm điểm D sao cho C = ĐAB(D)?
c.Tìm ảnh của đtròn đƣờng kính CH qua phép đối xứng trục ĐAB ?
Bài 18: Trong mp Oxy cho A(–1, 2), B(4, 1), đt (d): x –y + 1= 0
và đƣờng tròn (C): x2
+ y2
–2x + 4y – 4 = 0.
a.Tìm ảnh của A, (d), (C) qua phép đối xứng trục Ox, Oy ?
b.Tìm ảnh của A, ảnh của đƣờng AB qua phép đxứng trục Đd?
c.Tìm ảnh của đtròn (C) qua phép đối xứng trục Đd?

d.Tìm M trên Ox để (MA + MB) bé nhất?
Bài 19: Trong mp Oxy cho A(–2, 3), B(4, -1), đt (d): 3x –2y + 1= 0
và đƣờng tròn (C):    
2 2
3 1 4x y    . Tìm ảnh của :
a.A, d qua phép đối xứng trục ĐOx; b.B , (C) qua phép đối xứng trục ĐOy
c.Đƣờng thẳng : 2 5 0x y    qua phép đối xứng trục Đd
CHỦ ĐỀ 3: PHÉP ĐỐI XỨNG TÂM:
Làm giống nhƣ phép tịnh tiến, chỉ thay công thức của phép đối xứng tâm
cho phù hợp.
Bài 20: a.Cho  2;3A , tìm 'A  ĐO  A
b.Cho    3;6 , 0;8B I , tìm 'B  ĐI  B
c.Cho  4;7C , tìm ảnh của C qua phép đối xứng gốc O.
d.Cho    11; 2 , 4;3  D I , tìm tọa độ điểm 'D  ĐI  D
Bài 21: a.Cho( ): 2 3 6 0d x y    , viết pt 'd  ĐO  d
b.Cho ( ):2 3 4 0d x y   ,  2;5I , viết pt 'd  ĐI  d
c.Cho( ): 5 0d x   , tìm pt 'd  ĐO  d
d.Cho ( ): 5 4d y x  ,  4; 1I   , tìm 'd  ĐI  d
e.Cho( ): 6 0d y   ,  2; 7I  , tìm pt 'd  ĐI  d
Bài 22: a.Cho      
2 2
: 2 7 144C x y    , tìm pt  'C  ĐO   C
b.Cho    
22
: 5 25C x y   ,  2;5I , viết pt 'C  ĐI   C
c.Cho    
2 2
: 4 16C x y   , tìm  'C  ĐO   C
d. Cho   2 2
: 4 8 5 0    C x y x y
Cho   2 2
: 4 0C x y y   ,  3;4I , tìm  'C  ĐI   C
e.Cho   2 2
: 16 144C x y x   ,  5; 3I  , viết pt  'C  ĐI   C
Bài 23: Cho (2; 4); ( 7;6); ( 3;5)A B C   ,( ):5 2 15 0d x y   ,
2 2
( ): ( 7) 169C x y   .

a.Tìm ảnh B‟của B lần lƣợt qua phép đối xứng tâm O(0;0) và tâm C.
b.Viết phƣơng trình ảnh của d qua A
Ñ ; c.Tìm 4
( ') (( ))BC
C T C .
Bài 24: Cho (3; 5); ( 8;2); ( 1;6)A B C   ,( ):3 8 12 0d x y   ,
2 2
( ): 6 40 0C x y x    .
a.Tìm ảnh của C qua phép A
Ñ ; b.Tìm ảnh của d qua B
Ñ .
c.Tìm( ') (( ))O
C Ñ C .
Bài 25: Cho hình bình hành ABCD, tâm O.
a.Tìm ảnh của ABO qua phép đối xứng tâm O ?
b.Tìm ảnh của ABC qua phép đối xứng tâm D ?
Bài 26: Trong mp Oxy cho A(1, 2), B(–2, 3),đt (d): 3x –y + 9= 0
và đƣờng tròn (C): x2
+ y2
+ 2x – 6y + 6 = 0.
a.Tìm ảnh của A, (d), (C) qua phép đối xứng tâm O ?
b.Tìm ảnh của B qua phép đối xứng tâm A ?
c.Tìm ảnh của (d), (C) qua phép đối xứng tâm B ?
Bài 27: Trong mp Oxy cho A(2,- 3 ), B(–1, 4),đt (d): 2x –y + 1= 0
và đƣờng tròn (C):    
2 2
3 1 9x y    .Tìm ảnh của :
a.A, d , (C) qua phép đối xứng ĐO; b.B, (C) qua phép đối xứng ĐA
c.A, d qua phép đối xứng ĐB
CHỦ ĐỀ 4: PHÉP VỊ TỰ:
Làm giống nhƣ phép tịnh tiến, chỉ thay công thức của phép vị tự cho phù
hợp.
Chú ý: bán kính đƣờng tròn ảnh bằng k lần bán kính đƣờng tròn ban
đầu (tức là ' .R k R )
Bài 28: a. Cho  2;3 , ( 4;7)A I , tìm ( ;3)' ( ) IA V A
b. Cho  3;6B , tìm ảnh của B qua phép vị tự tâm  0;8I , tỉ số 4 .
Bài 29: a.Cho( ): 2 3 6 0d x y    , tìm  ( ; 2)'  Bd V d với (4; 2)B  .
b. Cho( ):2 3 4 0d x y   ,  2;5C , tìm  ( ;5)'  Cd V d .
c. Cho( ): 5 0d x   , tìm ảnh của d qua phép vị tự tâm O(0;0), tỉ số k=3.

d. Cho( ): 5 4d y x  ,  4; 1I   , viết ( : 3)' ( ) Id V d .
e. Cho( ): 6 0d y   ,  2; 7I  , viết pt ảnh của d qua ( ; 4)I
V 
.
Bài 30: a.Cho      
2 2
: 2 7 144C x y    , viết pt  ( ; 3)' (( )) OC V C .
b.Cho    
22
: 5 25C x y   ,  2;5I , tìm   ( ; 1/2)' (( )) IC V C .
c.Cho    
2 2
: 4 16C x y   , viết pt ảnh của( )C qua ( ; 4)A
V 
, (2; 5)A 
d.Cho   2 2
: 4 0C x y y   ,  3;4B , tìm pt   ( ;3/2)' (( )) BC V C .
e.Cho   2 2
: 16 144C x y x   ,  5; 3D , viết  ( ; 3)' (( )) DC V C .
Bài 31: Cho (2; 4); ( 7;6); ( 3;5)A B C   ,( ):5 2 15 0d x y   ,
2 2
( ): ( 7) 169C x y   .
a.Tìm ảnh của A qua phép vị tự tâm C, tỉ số k=5.
b.Viết phƣơng trình ảnh của d qua ( ; 3)B
V 
.
c.Tìm ( ; 2)
( ') (( ))A
C V C
 .
Bài 32: Cho (3; 5); ( 8;2)A B  ,( ):3 8 12 0d x y   ,
2 2
( ): 6 40 0C x y x    .
a.Tìm ảnh của B qua ( ; 3)A
V 
b.Viết phƣơng trình đƣờng thẳng ảnh của d qua ( ;4)B
V .
c.Viết phƣơng trình của ( ; 7)
( ') (( ))A
C V C
 .
Bài 33: Trong mp Oxy cho đthẳng (d): 3x + 2y – 6 = 0.
a.Tìm ảnh của (d) qua phép V(O,–2) ?
b.Tìm ảnh của (d) qua phép V(O,3) ?
Bài 34: Trong mp Oxy cho (C): (x – 3)2
+ (y + 1)2
= 9. Tìm ảnh của (C) qua
phép vị tự V(I,2) với I(1,2).
Bài 35: Trong mặt phẳng Oxy cho B(1; -3), I(-1; -2), đƣờng thẳng d: 2x – y –
1= 0, đƣờng tròn (C) : 2 2
2x 4 1 0x y y     . Tìm ảnh của :
a. B, I , d, (C) qua V(O,2) ;b.B, d, (C) qua V(I,-2)
Bài 36: Trong mặt phẳng Oxy cho A(-1; 2), I(3; -1), đƣờng thẳng d: 2x + y –
1= 0, đƣờng tròn (C) :    
2 2
3 1 9x y    . Tìm ảnh của :

a. I , d, (C) qua V(O,-3); b .A, d, (C) qua V(I, 4)
CHỦ ĐỀ 5: PHÉP QUAY.
Bài 37: Cho lục giác đều ABCDEF, tâm O, I là trung điểm AB.
a.Tìm ảnh của AIF qua phép quay tâm O, góc 1200
?
b.Tìm ảnh của ABO qua phép quay tâm F, góc – 600
?
Bài 38: Trong mp Oxy cho A(3,3), B0,5), C(1,1) và đƣờng thẳng (d): 5x – 3y
+ 15 = 0. Hãy xác định tọa độ đỉnh của A'B'C' và phƣơng trình đƣờng thẳng
(d') theo thứ tự là ảnh của ABC và đƣờng thẳng (d) qua phép quay tâm O,
góc quay 900
?
Bài 39: Cho nửa đtròn tâm O, đkính BC. Điểm A chạy trên nửa đƣờng tròn đó.
Dựng phía ngoài ABC hình vuông ABEF. Chứng minh rằng: E chạy trên
nửa đƣờng tròn cố định ?
BÀI TỔNG HỢP:
Bài 40: Trong mp (Oxy), cho điểm (5; 4)A , đƣờng thẳng
  :3 5 7 0d x y , đƣờng tròn     2 2
( ): 2 4 4 0C x y x y .
a. Tìm phƣơng trình đƣờng thẳng 'd là ảnh của d qua phép đối xứng tâm A.
b. Tìm phƣơng trình đƣờng thẳng ( ')C là ảnh của ( )C qua phép đối xứng trục
Ox.
Bài 41: Cho A(–1, –3), B(–5, 2), M(3,4); đthẳng (d): 3x + 2y – 1 = 0 và
đƣờng tròn (C): x2
+ y2
– 10x + 2y + 1 = 0
a.Tìm tọa độ M' là ảnh của M qua 3AB
T
?
b.Tìm ảnh của (d), (C) qua AB
T ?
c.Tìm ảnh của A, (D): x + y = 0 qua ĐOx, Đd ?
d.Tìm ảnh của B, (d), (C) qua ĐO , ĐM ?
e.Tìm ảnh của A, (): 3x – 5y +12 = 0 qua Q(O,
2

 ) ?
f. Tìm N trên (d) để AN + BN bé nhất ?
Bài 42: Cho điểm A ( 1; -2) , B ( -3; 2), đƣờng thẳng d: 2x – 3y + 1 = 0 và
đƣờng tròn (C) : x2
+ y2
- 4x +2y – 4 = 0.Tìm ảnh của

a.Điểm A qua phép đối xứng tâm B
b.Đƣờng thẳng d qua phép đối xứng trục Ox
c.Đƣờng tròn (C) qua phép tịnh tiến AB
d.Đƣờng tròn (T) đƣờng kính AB qua phép vị tự tâm O tỉ số - 2 .

Chƣơng 5: QUAN HỆ SONG SONG
TRONG KHÔNG GIAN
1. Các đối tƣợng và quan hệ liên thuộc trong không gian.
Điểm Đƣờng thẳng Mặt phẳng
. A d
A mp (P)
Điểm A nằm trên d
(A thuộc d) ta
viết: A d
B nằm trong mp(P) ta viết ( )B P ,
d nằm trong (P) ta viết ( )d P hay
( )P d
2. Sự tƣơng giao giữa các đối tƣợng.
ST
T
Sự tƣơng giao giữa
Đƣờng thẳng và đƣờng thẳng
Sự tƣơng giao giữa
Mặt phẳng và mặt phẳng
1
Trùng nhau Trùng nhau
2 Song song
(Cùng mặt phẳng
và không có điểm
chung)
Song song
(Không có điểm
chung)
3 Cắt nhau
(Cùng mặt phẳng
và có điểm
chung)
Cắt nhau
(Có vô số điểm
chung lập thành
một đƣờng thẳng
gọi là giao tuyến)
4 Chéo nhau
(Không cùng nằm
trên một mặt
P
B d

phẳng nào cả)
STT Sự tƣơng giao giữa
Đƣờng thẳng và mặt phẳng
1 Đƣờng trong mặt- Mặt chứa
đƣờng.
2 Song song
(Không có điểm chung)
3 Cắt nhau
(có đúng 1 điểm chung)
3. Cách biểu diễn một hình không gian.
Nguyên tắc chung:
 Phần nào bị che khuất biểu diễn bằng nét đứt.
 Hai đƣờng thẳng song song vẫn đƣợc biểu diễn bởi hai đƣờng thẳng song
song
Cụ thể:
 Hình thang đƣợc biểu diễn bằng hình thang.
 Hình vuông, hình chữ nhật, hình thoi, hình bình hành đƣợc biểu diễn bằng
h.b.hành.
 Tam giác đều, vuông, cân, bất kì đƣợc biểu diễn bằng tam giác bất kì.
4. Một số hình cơ bản:
Hình chóp tứ giác bất kì Hình chóp đáy là hình thang
Hình chóp đáy là hình bình hành Hình chóp đáy tam giác (Tứ diện)

Hình lăng trụ (đáy tứ giác, tam
giác,..)
Hình hộp
Hình chóp cụt
5. Một số kí hiệu thể hiện đúng quan hệ liên thuộc :
Cho A, B là các điểm, a, b, d là các đƣờng thẳng, ( ),( )  là các mặt phẳng.
A a, ( )A ( )a 
 A a b  ( )A a
  ( ) ( )A   ( ) ( )a
6. Một số qui tắc trình bày.
1 2
( )
( ) ( )
( )
A
A
A

 

 
  

( )
( )
A a
A a
A


 
  

3 4
( ) ( )
( ) ( )
( ) ( )
A
AB
B
 
 
 
  
  
 
( )
( ) ( )
( )
d
d
d

 

 
  


CHỦ ĐỀ 1: GIAO TUYẾN, GIAO ĐIỂM
 Vấn đề 1: Giao tuyến của hai mặt phẳng:
Phƣơng pháp: Tìm 2 điểm ( ) ( )A P Q  , ( ) ( )B P Q  đƣợc giao tuyến
là AB.
Tuy nhiên: Nếu 2 mặt phẳng ( ),( )  có một điểm chung A và chứa 2
đƣờng thẳng a, b song song với nhau thì giao tuyến của chúng là đƣờng
thẳng x’Ax qua điểm A và song song với a, b.
Nhớ: Đi tìm giao tuyến em ơi/ Tìm 2 giao điểm được rồi là xong
Cách sau cũng dễ như không / 1 giao điểm với song song 2 đường.
Bài 1: (0k)Cho hình bình hành ABCD, và điểm S không thuộc (ABCD).
Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
Bài 2: (0k)Cho hình chóp S.ABCD có đáy là tứ giác có các cặp cạnh
đối không song song. M là điểm thuộc miền trong của tam giác SCD.
Tìm giao tuyến của các cặp mặt phẳng sau:
a.(SAD) và (SBC); b. (SAC) và (SBD); c. (SAB) và (SBC).
d. (SBM) và (SCD); e. (ABM) và (SCD); f*. (ABM) và (SAC).
Bài 3: Cho tứ diện ABCD. Gọi E, F là hai điểm trong đoạn AB và BC
sao cho EA = EB, 3BF FC . Tìm giao tuyến của mp (DEF) với các
mp sau:
a. (ABC), b.(BCD), c.(ABD), d.(ACD).
Bài 4: (0k)Cho hình chóp tứ giác S.ABCD với hai đƣờng thẳng AB và
CD cắt nhau. Gọi A‟ là một điểm nằm giữa hai điểm S và A. Hãy tìm
các giao tuyến của:
a. (A‟CD) và (ABCD); b. (A‟CD) và (SCD),
c.(A‟CD) và (SDA), d. (A‟CD) và (SAB), e*.(A‟CD) và (SBC).
Bài 5: (0k) ( Tìm phương giao tuyến) Cho hình chóp S.ABCD có đáy
ABCD là hình bình hành tâm O, M là trung điểm của SB. Tìm giao
tuyến của các cặp mặt phẳng sau:
a. (SAB) và (SDC); b. (SAD) và (SBC);
c. (DMC) và (SAC), d. (DMC) và (SDC);
e. (DMC) và (SAB); f. (DMC) và (SAD).

Bài 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,
N lần lƣợt là trung điểm của SB, SD. Gọi P là điểm trên SC sao cho
SP > PC. Tìm giao tuyến của (MNP) với các mặt phẳng:
a. (SAC), b.(SAB), c.(SAD), d.(ABCD);
e. Tìm thiết diện của (MNP) với hình chóp S.ABCD
(sẵn đây GV nói về thiết diện luôn)
Bài 8: Cho hình chóp S.ABCD, Tứ giác ABCD là hình thang tâm I đáy
lớn 2DC AB , F là trung điểm của SD. Tìm giao tuyến của các mặt
phẳng sau
a. (ABF) và (SAD); b.(ABF) và (SBD); c. (ABF) và (SAC);
d. (ABF) và (SBC); e. (ABF) và (SDC); f.(SAD) và (SBC).
Bài 9: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm
giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAD) và (SBC).
Bài 10: Cho tứ diện ABCD có M, N lần lƣợt thuộc đoạn AB, AC sao
cho
AM AN
AB AC
 . Xác định giao tuyến của (DBC) và (DMN).
Bài 11: Cho hình chóp tứ giác S.ABCD với hai đƣờng thẳng AB và CD
cắt nhau. Gọi A‟ là một điểm nằm giữa hai điểm S và A, C‟ là điểm nằm
giữa S và C sao cho
' 'SA SC
SA SC
 . Hãy tìm các giao tuyến của:
a. (SAB) và (SCD);b. (A‟C‟D) và (SDA), c.(A‟C‟D) và (ACD);
d. (A‟C‟D) và (SBD), e.(A‟C‟D) và (SBC).
Bài 12: Cho hình chóp S.ABCD, có đáy ABCD là hình thang tâm I đáy
lớn 2DC AB . Tìm giao tuyến của các cặp mặt phẳng sau:(SAB) và
(SDC); (SAD) và (SBC).
Bài 13: Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lƣợt
là trung điểm của AD và BC.
a.Xác định giao tuyến của (MBC) và (NAD)
b.Cho I, J lần lƣợt là hai điểm nằm trên đoạn AB, AC. Xác định giao
tuyến của (MBC) với (IJD).
Bài 14: Cho tứ diện ABCD. Trên AB lấy điểm I và lấy J, K thuộc miền
trong của tam giác BCD và ACD.
a Gọi L là giao điểm của JK với (ABC). Tìm L.
b.Tìm giao tuyến của (IJK) với các mặt của tứ diện ABCD.

Bài 15: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm
O. M là trung điểm của SB. Tìm thiết diện của m.phẳng (DMC) và hình
chóp.
Bài 16: Cho hình chóp S.ABCD, Tứ giác ABCD là hình thang tâm I
đáy lớn 2DC AB . F là trung điểm của SD. Tìm thiết diện của mặt
phẳng (ABF) với hình chóp.
Bài 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,
N lần lƣợt là trung điểm của AD, SB. Gọi K là điểm thuộc SC sao cho
SK>KC.
a.Tìm giao tuyến của (MNK) với (ABCD); suy ra giao tuyến của
(MNK) với (SCD);
b.Tìm giao tuyến của (MNK) với (SAB);
c.Xác định thiết diện của (MNK) với hình chóp.
 Vấn đề 2: Các bài tập tìm giao tuyến
bằng cách tìm phương giao tuyến:
Bài : Cho tứ diện ABCD. Gọi I, J lần lƣợt là trung điểm của BC, AC,
M AD . Tìm giao tuyến của (MIJ) và (ABD).
Bài: Cho hình chóp S.ABCD đáy là hình thang có đáy lớn AB. Gọi I, J
lần lƣợt là trung điểm AD, BC, G là trọng tâm tam giác SAB.
a. Tìm giao tuyến của (SIJ) và (SAB);
b. Xác định giao tuyến của (GIJ) và (SAB);
c. Xác đinh thiết diện của hình chóp với (GIJ). Thiết diện là hình gì?
Bài: Cho hình chóp S.ABCD đáy là hình vuông. Gọi I là trung điểm SB
và K là trung điểm SD.
a. Tìm ( ) ( )CDI SAB ; b. Tìm ( ) ( )AIK ABCD ;
c. Tìm ( ) ( )KBC SAD .
 Vấn đề 3: Giao điểm của đường thẳng
với mặt phẳng:
Phương pháp: Để xác định giao điểm của d với (Q).
1. Tìm mp (P) chứa đƣờng d; 2. Xác định giao tuyến ( ) ( )P Q   .
3. Xác định giao điểm M d  thì M là giao điểm cần tìm.
Nhớ: Tìm giao điểm của đường với mặt/ Ta đi tìm mặt khác chứa đường.

Rồi tìm giao tuyến bình thường/ Điểm giao là điểm hai đường cắt nhau.
Bài 17: (0k)Cho tứ diện ABCD. Gọi M, N lần lƣợt là trung điểm của
AC và BC, K BD sao cho K không là trung điểm của BD. Tìm giao
điểm của: a. CD với (MNK); b. AD với (MNK)
Bài 18: (0k)Cho tứ diện ABCD. Trên AB, AC lấy 2 điểm M, N sao cho
MN không song song với BC. Gọi O là một điểm trong tam giác BCD.
Xác định:
a. Giao tuyến của (OMN) với (BCD);
b. Giao điểm của BD với (OMN); c. Giao điểm của DC với (OMN)
Bài 19: (0k)Cho tứ diện SABC. Gọi M SA , ( )N SBC , ( )P ABC .
a. Xác định giao điểm của MN và (ABC), suy ra giao tuyến của (MNP)
và (ABC).
b. Tìm giao điểm của AB và (MNP);
c. Tìm giao điểm của NP và (SAB).
Bài 20: Cho hình chóp S.ABCD lấy M, N lần lƣợt thuộc các cạnh SC và
BC. Tìm giao điểm của SD và (AMN), biết AN không song song với
CD.
Bài 21: Cho tứ diện S.ABC, M SA , N SB sao cho MN cắt AB, O là
điểm thuộc miền trong của (ABC). Tìm:
a. Giao tuyến của (MNO) và (ABC);
b. Giao tuyến của (MNO) và (SBC);
c. Giao điểm của (MNO) với AB, BC, AC, SC;
d. Giao điểm của MO và (SBC).
Bài 22: Cho hình thang ABCD ( //AB CD ), ( )S ABCD , O là giao
điểm của hai đƣờng chéo, M SB .
a. Xác định giao tuyến của: (SAD) và (SBC), (SAC) và (SBD).
b. Tìm giao điểm của SO với (MDC), SA với (MDC).
Bài 23: Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lƣợt
là trung điểm của AC, BC. Trên BD lấy P sao cho BP=2PD.
a. Tìm giao điểm của CD với (NMP)
b. Tìm giao tuyến của (MNP) với (ABD).
Bài 24: Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi
M là điểm bất kì trên SB, N là điểm trong (SCD).Tìm giao điểm của:
a. MN và (ABCD); b. SC và (AMN) ;
c. SD và (AMN); d. SA và (CMN).

Bài 25: Cho tứ giác ABCD nằm trong mặt phẳng (P) sao cho AB và CD
không song song. S là điểm nằm ngoài (P), M là trung điểm của SC.
Tìm giao điểm của:
a. AM và (SBD); b. SD và (ABM).
Bài 26: Cho tứ diện SABC có I, J, K lần lƣợt là ba điểm nằm trong ba
mặt phẳng (SAB), (SBC), (ABC).
a.Tìm giao điểm của IJ và (ABC);
b. Tìm giao tuyến của (IJK) và (ABC) suy ra giao điểm của (IJK) với
AC, AB, BC.
Bài 27: Cho hình chóp S.ABCD có đáy là h.h.hành tâm O. Gọi M, N
lần lƣợt là trung điểm các cạnh SC, AB.
a. Tìm giao tuyến của các cặp mặt phẳng (SBD) và (SAC); (AMN) và
(SCD).
b. Tìm giao điểm P của AM và (SBD); giao điểm Q của MN và (SBD)
(Thi HK1 năm 2007-2008/ đề A).
Bài 28: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi
M, N lần lƣợt là trung điểm của các cạnh SD, BC.
a.Tìm giao tuyến của các cặp mặt phẳng (SBD) và (SAC), (BMN) và
(SAD).
b.Tìm giao điểm P của BM và (SAC), giao điểm Q của MN và (SAC).
(Thi HK1 năm 2007-2008/ đề B).
Bài 29: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi
M, N lần lƣợt là trung điểm của các cạnh SB, AB, K là điểm trên cạnh
CD (K không là trung điểm của CD)
a.Xác định giao tuyến của ( )MNK và ( )SBD ; ( )MNK và ( )SAC .
b.Tìm giao điểm của ( )MNK và BC; ( )MNK và SC.
c.Xác định thiết diện của hình chóp S.ABCD với ( )MNK .
(Thi HK1 năm 2008-2009/ đề A).
Bài 30: Cho hình chóp S.ABCD có ABCD là hình thang (AD đáy lớn).
Gọi M là trung điểm SD. Tìm:
a. (SAB)  (SCD) ; ( SAC)  ( SBD); (SAD)  (SBC);
b. BM  ( SAC) ; SA  ( BCM)
c. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (BCM).
(Thi HK1 năm 2009-2010/ đề A).

CHỦ ĐỀ 2: QUAN HỆ SONG SONG
 Vấn đề 1: Đường thẳng song song với
đường thẳng:
Phƣơng pháp: Để chứng minh a//b ta làm nhƣ sau:
Cách 1. Chứng minh a, b cùng thuộc một mặt phẳng (một mặt phẳng
tam giác nào đó) rồi chứng minh a, b không cắt nhau (dùng Talet đảo,
đƣờng trung bình, cặp cạnh đối hình bình hành,…);
Cách 2. Chứng minh chúng cùng song song với đƣờng thẳng thứ 3;
Cách 3: Dùng tính chất “Hai mặt phẳng phân biệt lần lƣợt chứa hai
đƣờng thẳng song song thì giao tuyến của chúng (nếu có) cũng song
song với hai đƣờng thẳng đó”;
Cách 4: Dùng định lí về giao tuyến của 3 mặt phẳng (3 giao tuyến hoặc
đôi một song song hoặc đồng qui).
Bài 31: Cho tứ diện ABCD có I, J lần lƣợt là trọng tâm của tam giác
ABC, ABD. Cmr: IJ//CD.
Bài 31: Cho hình chóp S.ABCD đáy là hình thang có đáy lớn là AB.
Gọi M, N lần lƣợt là trung điểm của SA, SB. Chứng minh: MN//CD.
Bài 31: Cho hình chóp S.ABCD đáy là hình bình hành. Gọi H, K lần
lƣợt là các điểm trên SA, SB sao cho
1
3
SH SK
SA SB
  .
a. Chứng minh HK//CD;
b.
Bài 32: Cho tứ diện ABCD. Lấy I, J lần lƣợt là trung điểm của BC, AC
với M là điểm tùy ý trên AD.
a.Xác định giao tuyến d của (MIJ) và (ABD).
b.Gọi N là giao điểm của BD với d, K là giao điểm của IN với JM. Tìm
giao tuyến của (ABK) và (MIJ).
Bài 33: Cho tứ diện ABCD, gọi M, N theo thứ tự là trung điểm của AB,
BC và Q là một điểm trên AD, ( )P CD MNQ  . CMR: PQ//MN,
PQ//AC.
Bài 34: Cho hình chóp tứ giác S.ABCD có đáy là tứ giác lồi. Gọi M, N,
E, F lần lƣợt là trung điểm của các cạnh bên SA, SB, SC, SD. CMR:
ME//AC, NF// BD.

 Vấn đề 2: Đường thẳng song song với
mặt phẳng:
Phƣơng pháp: Để chứng minh đƣờng thẳng a// ( )
Cách 1: Ta chứng minh a // b, b nằm trong mặt phẳng ( )
Bước 1: Chọn  b  Bước 2: Chứng minh a//b.
Cách 2: Ta chứng minh a nằm trong mặt phẳng ( ) , ( ) // ( )
Bước 1: Chọn   a  Bước 2: Chứng minh ( ) // ( ) .
Bài 35 (ok): Cho tứ diện ABCD, G là trọng tâm tam giác ABD. Trên
đoạn BC lấy M sao cho MB=2MC. Chứng minh rằng MG//(ACD).
Bài 36 (ok): Cho tứ diện ABCD với G1, G2 là trọng tâm tam giác ACD,
BCD. Cmr: G1G2// (ABC) và G1G2// (ABD).
Bài 4 (ok). Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M, N, P
lần lƣợt là trung điểm của AB, CD, SA. Chứng minh:
a. MN//(SBC); b. MN//(SAD);
c. SB//(MNP); d. SC//(MNP)
Bài 37 (ok): Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
G là trọng tâm SAB, I là trung điểm AB. Lấy M trong đoạn AD sao cho
AD=3AM.
a.Xác định giao tuyến của (SAD) và (SBC).
b.Đƣờng thẳng qua M song song với AB cắt CI tại N. Chứng minh rằng:
NG//(SCD),
c*. Chứng minh: MG//(SCD).
Bài 38 (ok): Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
G là trọng tâm SAB, I là trung điểm AB. Lấy M trong đoạn SA sao cho
MS=2MA. Lấy N thuộc đoạn IC sao cho IC=3IN.
a. Xác định giao tuyến của (SAD) và (SBC);
b.Chứng minh MG//(SCD); c. Chứng minh NG//(SBC);
d.Xác định giao tuyến của (MNG) và (SAC); (MNG) và (ABCD).
Bài 39: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là
AD, đáy nhỏ là BC và AD=2BC. Gọi O là giao điểm của AC và BD, G
là trọng tâm của tam giác SCD.

a. Chứng minh rằng OG//(SBC).
b. Gọi M là trung điểm của SD. Chứng minh rằng CM//(SAB).
c. Gọi I là điểm nằm trên SC sao cho IS=2IC. Cmr: SA//(BDI).
O. Gọi M là điểm thuộc đoạn SB sao cho MS=2MB, G là trọng tâm tam
giác SAC.
a. Chứng minh rằng MG//(ABCD);
b.Tìm giao tuyến của (AMG) với (ABCD);
c.Tìm giao điểm của SC với (AMG);
d. Xác định thiết diện của (AMG) với hình chóp.
Bài 40: Cho hình chóp S.ABCD có đáy là hình bình hành với O là giao
điểm của hai đƣờng chéo. Gọi M, N lần lƣợt là trung điểm của AB, AD.
Gọi I, J lần lƣợt thuộc cạnh SM, SN sao cho
2
3
SI SJ
SM SN
  .
a. Chứng minh: MN// (SBD); b. Chứng minh: IJ// (SBD);
c. Chứng minh: SC// (IJO);
 Vấn đề 3: Mặt phẳng song song với mặt
phẳng:
Phương pháp:
Cách 1. Để chứng minh ( ) //( ) ta chứng minh :
( ) ,
, caét nhau
// ( )
// ( )
a b
a b
a
b



 





 ( ) // ( )
Cách 2. Chứng minh chúng song song với mặt phẳng thứ 3.
Bài 42: Cho tứ diện ABCD có G1, G2, G3 lần lƣợt là trọng tâm của tam
giác ABC, ACD, ABD. Chứng minh rằng: (G1G2G3)//(BCD).
Bài 43: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M,N, P
lần lƣợt là trung điểm SA, SB, BC. Chứng minh: (MNP)//(ABC)
Bài 43: Cho hình chóp S.ABCD đáy là hình thang có đáy lớn AB. Gọi I,
J, K lần lƣợt là trung điểm của SA, AD, SD.

a. Chứng minh (IJK)//(SCD);
b. Gọi M là giao điểm của AC và JK. Chứng minh IM//(SBC).
Bài 4 (ok). Cho hai hình bình hành ABCD và ABEF không cùng nằm
trong một mặt phẳng. Gọi M ,M AC N BF  sao cho MC=2AM,
NF=2BN. Từ M, N lần lƣợt vẽ các đƣờng thẳng song song với AB, cắt
AD tại M‟, cắt AF tại N‟. Chứng minh rằng:
a. DF// (BCE); b. M‟N‟//(BCE); c. MN//(DEF).
Bài 41: Cho hình lăng trụ tam giác ABC.A‟B‟C‟ . Gọi I, J, K lần lƣợt là
tâm của các hình bình hành ACC‟A‟, BCC‟B‟; ABB‟A‟. Chứng minh
rằng:
a. IJ//(ABB‟A‟); b.JK//(ACC‟A‟);
c. IK//(BCC‟B‟); d. (IJK)//(ABC);
O. Gọi M, N, P lần lƣợt lad trung điểm của SA, SB, SD.
a. Chứng minh: (OMN)// (SCD); b. Chứng minh: (PMN)// (ABCD);
c. Gọi K, I lần lƣợt là trung điểm của BC, OM. Chứng minh: KI//(SCD)
Bài 44: Cho 2 hình vuông ABCD, ABEF ở trong hai mặt phẳng phân
biệt. Trên các đƣờng chéo AC và BF lần lƣợt lần lƣợt lấy M, N sao cho
AM=BN. Các đƣờng thẳng song song với AB vẽ từ M, N lần lƣợt cắt
AD, AF tại M‟, N‟. Chứng minh rằng:
a. (ADF)//(BCE); b. M‟N‟//DF;
c. (DEF)//(MM‟NN‟); d. MN//(DEF).
Bài 45: Cho hình lăng trụ tam giác ABC.A‟B‟C‟ . Gọi I, I‟ lần lƣợt là
trung điểm của BC, B‟C‟.
a. Chứng minh rằng: AI//A‟I‟; b. giao điểm của IA‟ với (AB‟C‟);
c. giao tuyến của (AB‟C‟) và (A‟BC).
Bài 46: Cho hình lăng trụ tam giác ABC.A‟B‟C‟ . Gọi H là trung điểm
của A‟B‟.
a. CMR: CB‟//(AHC‟); b. giao tuyến của (AB‟C‟) và (ABC).

CHỦ ĐỀ 3: THIẾT DIỆN CỦA HÌNH
CHÓP VỚI MỘT MẶT PHẲNG
Thiết diện của một hình chóp với mặt phẳng ( ) là phần chung của
hình chóp với mặt phẳng ( ) .
Phương pháp: Để dựng thiết diện của một hình chóp với mặt phẳng
( ) ta lần lƣợt làm nhƣ sau
Bƣớc 1: Dựng giao tuyến của ( ) với một mặt nào đó của hình
chóp
Bƣớc 2: Giới hạn đoạn giao tuyến là phần của giao tuyến nằm
trong mặt đang xét của hình chóp
Tiếp tục hai bƣớc trên với các mặt khác của hình chóp cho đến khi
các đoạn giao tuyến khép kín tạo thành một đa giác, đa giác ấy là thiết
diện.
Bài 47: Cho tứ diện ABCD.Trên các cạnh BC,CD,AD lấy các điểm
M,N,P.Dựng thiết diện của ABCD với mặt phẳng(MNP).
Bài 48: Cho hình chóp S.ABCD có AD không song song với BC.Trên
cạnh SD lấy điểm M. Dựng thiết diện của hình chóp với mặt phẳng
(BCM).
Bài 49: Cho hình chóp S.ABCD có AD song song với BC.Trên cạnh
SD lấy điểm M. Dựng thiết diện của hình chóp với mặt phẳng (BCM).
Bài 50: Cho tứ diện ABCD.Trên các cạnh AB,AC lấy 2 điểm M, N;
trong tam giác BCD lấy điểm I. Dựng thiết diện của hình chóp với mặt
phẳng (MNI).
Bài 51: Cho hình chóp S.ABCD trên các cạnh SA,AB,BC lấy các điểm
M, N, P.Dựng thiết diện của hình chóp với mặt phẳng (MNP).
Bài 52: Cho hình chóp S.ABCD trên các cạnh SA,SB,SC lấy các điểm
M,N,P.
a.Tìm giao điểm MN  (ABCD) ; b.Tìm giao điểm NP  (ABCD)
c. Dựng thiết diện của hình chóp với mặt phẳng(MNP)
Bài 53: Cho tứ diện ABCD.Trong 3 tam giác ABC ,ACD và BCD lần
lƣợt lấy 3 điểm M, N, P.
a.Tìm giao điểm MN  (BCD) ; b. Dựng thiết diện của tứ diện với mặt
phẳng(MNP).

Bài 54: Cho hình chóp S.ABCD có đáy là hình thang ABCD đáy lớn
AB. Gọi M, N là trung điểm của SB và SC.
a.Tìm giao tuyến (SAD)  (SBC);
b.Tìm giao điểm SD  (AMN);
c. Dựng thiết diện của hình chóp với mặt phẳng (AMN)
Bài 55: Cho hình chóp S.ABCD. Trong tam giác SCD ta lấy điểm M
a. Tìm giao tuyến (SBM)  (SAC);
b.Tìm giao điểm của BM với (SAC)
c. Dựng thiết diện của hình chóp với mặt phẳng(ABM)
Bài 56: Cho hình chóp S.ABCD có đáy là hình thang ABCD với AB là đáy
lớn. Gọi M và N lần lƣợt là trung điểm của các cạnh SB và SC.
a. Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC);
b.Tìm giao điểm của đƣờng thẳng SD với mặt phẳng (AMN);
c. Dựng thiết diện của hình chóp với mặt phẳng (AMN).
Bài 57: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi
H và K lần lƣợt là trung điểm các cạnh CB và CD, M là điểm bất kỳ
trên cạnh SA. Dựng thiết diện của hình chóp với mặt phẳng (MHK)
Bài 58: Cho tứ diện đều ABCD có cạnh bằng a. Gọi I là trung điểm của
AD, J là điểm đối xứng với D qua C, K là điểm đối xứng với D qua B
a. Xác định thiết diện của tứ diện với mặt phẳng (IJK);
b. Tính diện tích của thiết diện ấy.
 BÀI TỔNG HỢP
Bài 59 (ok): Cho hình chóp S.ABCD, đáy ABCD là h.bình hành tâm O.
Gọi M, N lần lƣợt là trung điểm của SC và AB.
a. Tìm giao tuyến của (MNO) và (SBC);
b. Tìm giao tuyến của (MNO) và (SAB),
c. Tìm giao tuyến của (MNO) và (SCD).
d. Xác định thiết diện của (MNO) với hình chop S.ABCD.
e. Tìm giao tuyến của (AMB) và (SBD), từ đó tìm giao điểm của M N
với (SBD);
d. Chứng minh SD//(MNO).

Bài 60 (ok): Cho tứ diện ABCD, M là trọng tâm tam giác ABC, N là
trung điểm của AD, P là trung điểm của CD.
a. Tìm giao tuyến của (AMN) và (BCD).
b. Tìm giao tuyến của (ABC) và (MNP).
c. Tìm giao tuyến của (AMP) và(BCD).
d.Tìm giao điểm của AB và mp(MNP). Suy ra thiết diện (MNP) với tứ
diện ABCD. Thiết diện là hình gì?
e. Gọi I, J lần lƣợt là trung điểm AB, BC. Chứng minh IJ//(MNP).
Bài 61Cho hình chóp S.ABCD đáy là hình thang, đáy lớn là AD và
AD=2 BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam
giác SDC, N là trung điểm của SC, M là trung điểm SD,O‟ là giao điểm
của AB và CD.
a.Tìm giao tuyến của (SAB) và (SCD)
b. Tìm giao tuyến của (SAD) và (SBC).
b. Chứng minh:OG//BN suy ra OG//(SBC)
c. Chứng minh C là trung điểm của O‟D. Từ đó chứng minh
CM//(SAB).
Bài 62: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi
M, N lần lƣợt là trung điểm của SB và AB, K là điểm trên cạnh CD
(K không là trung điểm của CD).
a.Xác định giao tuyến của: (MNK) và (SBD); (MNK) và (SAC);
b. Tìm giao điểm của (MNK) và BC; (MNK) và SC;
c. Xác định thiết diện của hình chóp S.ABCD và (MNK).
Bài 63: (ok) Cho hình chóp SABCD, đáy ABCD là hình bình hành tâm
O. Gọi M, N lần lƣợt là trung điểm của SC và AB.
a. Chứng minh NO// (SBC); suy ra ( ) ( )MNO SBC ;
b.Tìm( ) ( )AMB SBD ;
c. Tìm giao điểm của MN với (SBD),
d. Tìm giao điểm của SD với (AMB);
e. Tìm giao tuyến của (AMB) và (SCD);
f. Xác định thiết diện của (AMB) với hình chóp S.ABCD.
Bài 64: Cho tứ diện ABCD, M là một điểm thuộc miền trong tam giác
BCD, N là trung điểm của AD, K là trung điểm của CD.
a.Tìm giao tuyến của (BCN) và (ADM);

b. Tìm giao tuyến của (ABC) và (MNK).
c. Tìm giao điểm của AM và mp(BCN);
d. Xác định thiết diện của (CMN) với tứ diện.
Bài 65: Cho tứ diện ABCD, M, N lần lƣợt là trung điểm của CD, BC và
G là trọng tâm của tam giác ABC.
a. Chứng minh NM// BD rồi tìm giao tuyến của (AMG) và (ABD);
b. Tìm giao tuyến của (ADG) và (BCD).
c. Tìm giao điểm của DG và mp(ABM);
d. Xác định thiết diện của (DGM) với tứ diện ABCD.
Bài 66: (ok) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành
tâm O. Gọi M là điểm thuộc đoạn SB sao cho MS=2MB, G là trọng tâm
tam giác SAC.
b. Tìm giao tuyến của (AMG) với (ABCD);
c. Tìm giao điểm của SC với (AMG);
d. Tìm giao điểm của SD với (AMG);
e. Tìm giao điểm của CD với (AMG);
f. Xác định thiết diện của (AMG) với hình chóp.
Bài 67: Cho hình chóp S.ABCD, có đáy ABCD là hình thang, AB là
đáy lớn. Gọi M, N lần lƣợt là trung điểm của SB và SC.
a. Tìm giao tuyến của (SAD) và (SBC); (SAB) và (SCD);
b. Tìm giao điểm của SD và (AMN).
c. Giao tuyến của (BCD) và (AMN); d. Xác định thiết diện của (AMN)
với hình chóp. Thiết diện là hình gì?
Bài 68 (ok): Cho hình chóp S.ABC. Gọi D là trọng tâm tam giác SBC,
E là trung điểm của BC, F là trung điểm của SC.
a. Tìm giao tuyến của (SAD) và (ABC);
b. Tìm giao tuyến của (SAB) và (AEF);
c. Tìm giao điểm của GF và (SAE) với G là trung điểm của AB;
d. Gọi H là giao điểm của AE và GC. Chứng minh: DH//(SAB);
e. Gọi I là trọng tâm tam giác SAB. Chứng minh: (DHI)//(SAC).
Bài 69 (ok): Cho hình chóp S.ABCD, đáy ABCD là hình thang có đáy
lớn là AB. Gọi M, N, P lần lƣợt là trung điểm của SA, AD, BC.
a. Tìm giao tuyến của (SAD) và (SBC)

b. Chứng minh (MNP)// (SCD);
c. Tìm giao tuyến của (MNP) và (SPD);
d. Tìm giao điểm của MC và (SBD);
Bài 70: (ok) Cho hình chóp S.ABCD đáy ABCD là hình thang, AD là
đáy lớn. Gọi H là điểm nằm trên đoạn SA sao cho 2SH HA , và G là
trọng tâm tam giác SCD.
a. Tìm giao tuyến của (SAB) và (SCD);
b. Tìm giao tuyến của (SGH) và (ABCD);
c. Chứng minh GH // (ABCD), suy ra giao tuyến của (BGH) và
(ABCD);
d. Chứng minh (GHK) // (ABCD) với K là điểm trên đoạn SB, sao cho
2SK KB ;
e. Tìm giao điểm của SB với (ADG), giao điểm của CH với (SBD).

PHỤ LỤC
Phụ lục 1:ĐỀ ÔN THI GIỮA HK1
TÓM TẮT.
1. Chú ý các dạng phƣơng trình lƣợng giác:
 Phƣơng trình cơ bản:
sin sin ,cos cos ,tan tan ,cot cotu v u v u v u v    ;
sin ,cos ,tan ,cotu a u b u c u d    .
 Phƣơng trình “Làm mất dấu trừ”:
sin sin 0,cos cos 0u v u v    ;
tan tan 0,cot cot 0u v u v    .
 Phƣơng trình “Phụ chéo”:
sin cos 0,tan cot 0u v u v    .
 Phƣơng trình dùng cả “Làm mất dấu trừ” và Phụ chéo”:
sin cos 0,tan cot 0u v u v    .
 Phƣơng trình đƣa về bậc hai theo một hàm số lƣợng giác:….(tự
xem lại).
 Phƣơng trình bậc nhất sin, cos:
sin cosa u b u c 
 Phƣơng trình đẳng cấp:
2 2
sin sin cos cosa u b u u c s u d  
 Phƣơng trình tích:
0
. 0
0
A
A B
B
 
  

 Ghi nhớ:
sin sin( )A A   , cos cos( )A A  
tan tan( )A A   , cot cot( )A A  
2. Các phép biến hình:
 Phép tịnh tiến:
/
/
/
( ) ' ;
M vM
v
M vM
x x x
M T M MM v
y y y
  
    
 

 Phép đối xứng tâm:
/
/
/
2
( ) I laø trung ñieåm MM' ;
2
I MM
I
I MM
x x x
M Ñ M
y y y
  
   
 
 Phép đối xứng trục:
Trục Ox:
/
/
/
( ) ;
MM
Ox
MM
x x
M Ñ M
y y
 
  
 
Trục Oy:
/
/
/
( ) ;
MM
Oy
MM
x x
M Ñ M
y y
  
  

 Phép vị tự:
/
/
/ /
( ; )
( )
( ) ;
( )
I M IM
I k
I M IM
x x k x x
M V M IM kIM
y y k y y
   
    
  
Đề số 1
Bài 1.Giải các phƣơng trình sau:
a.   3 2
7 cos3 1 tan (4 ) 0
3

   x x ;
b. sin2 os 3 0
3
 
   
 
x c x ;
c. 2 6sin cos 2 cos 2
2 2
   
x x
x ;
d.
2 2
4sin 3 3sin3 cos3 3cos 3 4 0x x x x    ;
e.    2
cos4 5 4sin2 cos 2x x x ;
f. 4 4
cos sin sin4x x x  .
Bài 2. Cho ( 9; 4), (6;16), ( 4;5)  A B C , đƣờng thẳng
:7 5 10 0  d x y và đƣờng tròn 2 2
( ): ( 28) 256  C x y .
a. Tìm ảnh của A qua phép tịnh tiến theo
3
5
AB;
b. Tìm ảnh của d qua phép đối xứng tâm C;

c. Tìm ảnh của d qua phép đối xứng trục Ox;
d. Tìm ảnh của (C) qua phép vị tự tâm B tỉ số là
7
2
 .
Bài 3. Tìm ảnh của (5; 13)N qua phép Đd với :3 4 7 0  d x y .
Đề số 2
a. 5 5
os ( ) 0
6

  c x ;
b. sin3 cos7 0 x x ;
c. 2 3sin2 cos2 2 cos4 0   x x x ;
d.
2 2
5sin 3 3sin3 .cos3 2cos 3 cos6 4   x x x x x ;
e.
2
cos 6sin 7 cos
2 2
x x
x     ;
f. sin2 cos 1 sin .cos2 x x x x.
Bài 2. Cho (13;4), (9; 8), ( 4;10) A B C , đƣờng thẳng :3 7 5 0  d x y .
a. Tìm ảnh của B qua phép tịnh tiến theo 10 AC ;
b. Tìm ảnh của d qua phép đối xứng tâm B;
c. Tìm ảnh của đƣờng tròn đƣờng kính AB qua phép vị tự tâm C tỉ số là 5 ;
d. Tìm ảnh của đƣờng tròn (T) tâm A, qua C qua phép 3
4
a
T với  (1; 3)a .
Bài 3. Tìm ảnh của 2 2
( ):( 2) ( 1) 9   C x y qua Đd với : 5 0d x y  
Đề số 3
a. 2
3sin (2 ) 0
4

  x ;

b. tan3 tan7 0 x x ;
c. 0 0
3sin(2 60 ) 2 cos(2 60 ) 0     x x ;
d.
2 2
3sin 3sin2 3cos cos2 2 0    x x x x ;
e.
2
cos4 2 cos2 sin 2x x x    ;
f. sin4 2sin2x x.
Bài 2. Cho ( 6;10), (11;7), (5;17)A B C ,đƣờng thẳng :7 4 5 0  d x y
và đƣờng tròn 2 2
( ): 14 6 6   C x y x y .
a. Tìm ảnh của A qua phép tịnh tiến theo 2BC ;
b. Tìm ảnh của (C) qua phép vị tự tâm B, tỉ số là 3;
c. Tìm ảnh của d qua phép đối xứng tâm C.
Bài 3. Tìm ảnh của ( 13;8)N qua phép Đd với :2 5 7 0  d x y .
Đề số 4
a. 3
2 os (3 ) 0
3
c x

  ;
b. tan3 cot 4 0 x x ;
c. 0 0
2 3sin(30 3 ) 2 cos(30 3 ) 0    x x ;
d.
2 2
3sin 2 3sin4 5cos 2 3 0x x x    ;
e.    2
cos4 cos2 2 sin 2x x x ;
f. 8sin cos cos2 – 2x x x .
Bài 2. Cho ( 9;8), (11;7), (6; 14) A B D , đƣờng thẳng :3 4 5 0d x y   .
a. Tìm ảnh của A qua phép tịnh tiến theo 8BC ;
b. Cho đƣờng tròn (C) có tâm A, qua điểm B. Hãy tìm ảnh của (C) qua phép vị
tự tâm D tỉ số là 5 ;
c. Tìm ảnh của d qua phép đối xứng tâm B.
Bài 3. Tìm ảnh của 2 2
( ):( 13) ( 5) 49   C x y qua phép Đd
với: :2 10 0  d x y

Đề số 5
Bài 1: Giải các phƣơng trình sau:
a. cos 5 sin2 0
3
x x
 
   
 
;
b. cos6 9sin3 5 0x x   ;
c. 2 2
sin 2sin2 cos 2 0   x x x ;
d. 2 sin 6 cos 2
4 4
x x
    
      
   
.
Bài 2: Trong mặt phẳng Oxy cho điểm (1; 2); ( 3;2)A B  , (2; 4)v   , đƣờng
thẳng :3 2 1 0d x y   và đƣờng tròn 2 2
( ): 4 2 4C x y x y    .
a.Tìm ảnh của điểm A qua phép đối xứng tâm B?
b.Tìm ảnh của đƣờng thẳng d qua phép 3vT ?
c.Tìm ảnh của đƣờng tròn (C) qua phép đối xứng trục Ox?
d. Tìm ảnh của đƣờng tròn (T) có đƣờng kính AB qua phép vị tự tâm
(2; 7)I  , tỉ số 3k   .
Đề số 6
Bài 1. Giải các phƣơng trình sau:
a.
2
2cos 3 3 0
3
x
 
   
 
;
b. cos 4 cos2 0
5
x x
 
   
 
;
c. 2 sin4 6 cos4 2x x   ;
d. 2 2
5sin 3sin .cos 2cos 5x x x x     ;
e. 2
3cos sin cos2 4 0x x x    ;
f. sin7 .sin5 cos3 .cosx x x x .
Bài 2. Cho điểm (2;7)M , (3; 4)N  , đƣờng thẳng :3 6 9 0d x y   ,
2 2
( ): 16 6 9 0C x y x y    

a.Tìm tọa độ 1M  ĐOx ( )M , 1N  ĐOy ( )N .
b.Tìm tọa độ 2M sao cho M  ĐK 2( )M với K(5;6).
c.Tìm ảnh của d qua phép tịnh tiến theo vectơ MN .
d.Tìm ảnh của (C) qua phép vị tự ( , 3)PV  với  4; 5P   .
Phụ lục 2: ĐỀ THI GIỮA HK1 các năm
trƣớc
Đề giữa Hk1 năm 2008- 2009 (đề A)
a. 2 sin 6 cos 2
4 4
x x
    
      
   
;
b. sin 2 cos 2 0
3 6
x x
    
      
   
;
c. 2
2sin 4sin2 cos2 3 0   x x x ;
d. cos6 3sin3 4x x  
Bài 2: Trong mặt phẳng Oxy cho điểm (1; 2); ( 3;2)A B  đƣờng thẳng
:2 3 1 0d x y   và phƣơng trình đƣờng tròn
2 2
( ): 4 2 4 0C x y x y     .
a. Tìm ảnh của điểm A qua phép đối xứng tâm B?
b. Tìm ảnh của d qua phép đối xứng trục Oy.
c. Tìm ảnh của (C) qua phép tịnh tiến theo AB
d. Tìm ảnh của đƣờng tròn (T) đƣờng kính AB qua phép vị tự tâm O, tỉ số 2 .
Đề giữa Hk1 2009- 2010 (đề A)
a. 2
3cos 3 2sin3 2 0  x x ; b. 6 cos2 2sin2 2  x x ;
c. 2 2
cos sin2 3sin 3  x x x ;

Bài 2: Trong mp (Oxy) cho (2; 1); (1;3)A B , đƣờng thẳng : 2 1 0  d x y
( ): 2 4 1 0    C x y x y .
a. Tìm ảnh của A qua phép đối xứng tâm B;
b. Tìm ảnh của B qua phép tịnh tiến theo 2v với (1; 1)v   ;
c. Tìm ảnh của đƣờng tròn (C) qua phép đối xứng trục Oy;
d. Tìm ảnh của B qua phép vị tự tâm A, tỉ số 2.
Đề giữa Hk1 2011- 2012 (đề A)
Bài 1 ( 6 điểm ) : Giải các phƣơng trình sau :
a/ sin 4 cos2 0
5
x x b/ 2cos4 5sin2 3 0x x
c/ sin 3 0
2
x
x sin d/ sin4 cos5 sin6 0x x x
Bài 2 ( 4 điểm ) : Trong mặt phẳng Oxy cho 1,3 , 4, 2A B , đƣờng
thẳng :2 1 0d x y
: 2 6 6 0C x y x y
a/ (1đ) Tìm ảnh của điểm B qua phép vị tự tâm A , tỉ số - 2
b/ (1,5đ) Tìm ảnh của đƣờng tròn ( C) qua phép vị tự tâm B , tỉ số
1
2
c/ (1,5đ) Tìm ảnh của đƣờng thẳng d qua phép tịnh tiến theo OA .
Phụ lục 3: BỘ ĐỀ ÔN THI HK1
Đề số 1
Bài 1. Cho nhị thức 2 6
4
2
(9 )x
x
. Tìm
a. số hạng không chứa x; b. hệ số của 12
x
;
c. hệ số của số hạng chính giữa; d. số hạng cuối;
e. số hạng đầu; f. hệ số của số hạng thứ 6.

Bài 2. Một tổ có 10 nam và 7 nữ. Chọn ngẫu nhiên đồng thời 5 bạn. Tính xác
suất sao cho:
a. nam nữ tùy ý; b.5 bạn đều là nam; c. 5 bạn đều là nữ; d. không cùng một
giới; e. có ít nhất 1 nam; f. có nhiều nhất (không quá) 2 nam; g. có ít nhất 4 nữ;
h. không nhiều hơn 2 nữ; i. không ít hơn 3 nam; j. nhiều hơn 3 nữ.
Bài 3. Chứng minh rằng *
n N  ta có:
2
2.4 4.7 6.10 ... 2 (3 1) 2 ( 1)n n n n      
Bài 4. Cho hình chóp S.ABCD, đáy ABCD là hình bình hành tâm O. Gọi M, N
lần lƣợt là trung điểm của SC và AB.
a.Chứng minh NO// (SBC); suy ra ( ) ( )MNO SBC .
b.Tìm( ) ( )AMB SBD
c. Tìm giao điểm của MN với (SBD),
d. Tìm giao điểm của SD với (AMB);
e. Tìm giao tuyến của (AMB) và (SCD);
f. Xác định thiết diện của (AMB) với h.chóp S.ABCD.
Đề số 2
Bài 1. Trong khai triển của nhị thức 2 5
3
2
( 3 )x
x
 , hãy tìm:
x .
c. 2 số hạng chính giữa; d. hệ số của số hạng cuối;
e. hệ số của số hạng đầu; f. số hạng thứ 5.
Bài 2. Từ 1 hộp bi có 6 bi vàng, 7 đỏ và 8 xanh, lấy ngẫu nhiên 4 bi. Tính xác
suất sao cho 4 bi lấy đƣợc:
a. có màu sắc tùy ý; b.nhiều nhất 2 bi vàng; c. cùng màu; d. không cùng một
màu; e. không có bi xanh nào; f. có ít nhất 1 bi xanh; g. nhiều hơn 2 bi vàng;
h.không quá 2 bi đỏ.
Bài 3. Chứng minh rằng , 2  n N n ta có:
1.6 2.9 3.12 ... ( 1)3 ( 1) ( 1)n n n n n       
Bài 4. Cho tứ diện ABCD, M là một điểm thuộc miền trong tam giác BCD (giả
sử MK không song song với BC), N là trung điểm của AD, K là trung điểm
của CD.
a.Tìm giao tuyến của (BCN) và (ADM).

b. Tìm giao tuyến của (ABC) và (MNK).
c. Tìm giao điểm của AM và (BCN).
d. Xác định thiết diện của (CMN) với tứ diện.
Đề số 3
Bài 1.Trong khai triển 2 52
(4 )
3
x
x
. Tìm
a. số hạng không chứa x; b. hệ số của số hạng chứa 4
x
c. 2 số hạng chính giữa; d.hệ số của số hạng cuối;
e. Số hạng đầu; f. hệ số của số hạng thứ 2.
Bài 2. Từ các số 1, 2, 3, 4, 5, 6, 7 lập các số tự nhiên có 3 chữ số. Tính xác
suất biến cố sau:
a. A:”số lập đƣợc lẻ”; b. B: “số lập đƣợc chia hết cho 5”;
c.
Bài 3. Chứng minh rằng , 3n N n   ta có:
 
   
2 2
33 3 3 2 1
1 2 3 ... 2
4
n n
n
 
     
Bài 4. Cho tứ diện ABCD. Gọi M, N lần lƣợt là trung điểm của CD, BC và G
là trọng tâm của tam giác ABC.
a. Chứng minh: NM// BD rồi tìm giao tuyến của (AMG) và (ABD)
b. Tìm giao tuyến của (ADG) và (BCD).
c. Tìm giao điểm của DG và mp(ABM).
d. Xác định thiết diện của (DGM) với tứ diện ABCD.
Đề số 4
Bài 1. Trong khai triển
2
7
2
2 5
( )
3 2
x
x
 . Tìm:
a. số hạng không chứa x; b. số hạng chứa 6
x ;
c. hệ số của 2 số hạng chính giữa; d. số hạng cuối;
e. số hạng đầu; f. hệ số của số hạng thứ ba.
Bài 2. Từ một hộp có 5 bút xanh, 6 bút tím, 4 bút đỏ, lấy ngẫu nhiên 4 bút.
Tính xác suất sao cho 4 bút lấy đƣợc :

a. cùng màu đỏ; b. không bút nào màu xanh; c. có 2 bút tím; d. có ít nhất 1 bút
tím; e. Có nhiều nhất là 3 bút xanh; f. bút đỏ không nhiều hơn 3 bút.
Bài 3. Chứng minh rằng , 2n N n   ta có:
( 1)(3 2)
2 5 8 ... 3 4
2
 
     
n n
n .
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M
là điểm thuộc đoạn SB sao cho 2MS MB , G là trọng tâm tam giác SAC.
b. Tìm giao tuyến của (AMG) với (ABCD);
c. Tìm giao điểm của SC với (AMG);
d. Xác định thiết diện của (AMG) với hình chóp.
Đề số 5
Bài 1. Cho nhị thức:
3
6
3
1
( )
2 3

x
x
. Tìm
x
c. số hạng chính giữa; d. hệ số của số hạng cuối;
e. số hạng đầu; f. hệ số của số hạng thứ 5.
Bài 2. Từ các chữ số 1,2,3,4,5, 6 lập các số tự nhiên gồm 4 chữ số đôi một
khác nhau. Chọn ngẫu nhiên một trong số các số tự nhiên đó. Tính xác suất sao
cho:
a. số đƣợc chọn là số lẻ; b. số đƣợc chọn là số chia hết cho 5;
c. Số đƣợc chọn bắt đầu bằng 5; d. Số đƣợc chọn không bắt đầu bằng 6;
d. Số đƣợc chọn bắt đầu bằng 24; e.Số đƣợc chọn không bắt đầu bằng 13;
f. Số đƣợc chọn không chứa chữ số 5;g. Số đƣợc chọn có ít nhất một chữ số 3
n N  ta có:
3 3 3 3 3
...
1.2 2.3 3.4 ( 1) 1
    
 
n
n n n
.
Bài 4. Cho hình chóp SABCD, có đáy ABCD là hình thang, AB là đáy lớn.
Gọi M, N lần lƣợt là trung điểm của SB và SC.
a. Tìm giao tuyến của (SAD) và (SBC); (SAB) và (SCD).
b. Tìm giao điểm của SD và (AMN).
c. Giao tuyến của (BCD) và (AMN).
d. Xác định thiết diện của (AMN) với hình chóp. Thiết diện là hình gì?

Đề số 6
Bài 1. Trong khai triển 5 45
(3 )
2
x
x
 . Tìm
a. số hạng không chứa x; b. Hệ số của 2
x
c. số hạng chính giữa; d. số hạng cuối;
e. số hạng đầu; f. số hạng thứ 2.
Bài 2. Từ 1 hộp có 13 bóng đèn, trong đó có 6 bóng hỏng, lấy ngẫu nhiên 5
bóng ra khỏi hộp, Tính xác suất sao cho:
a. nhiều nhất 2 bóng hỏng; b. có ít nhất 1 bóng tốt.
n N  ta có:
1 1 1 1
...
1.5 5.9 9.13 (4 3)(4 1) 4 1
n
n n n
    
  
.
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Goi M, N lần
lƣợt là trung điểm của AD, SB. Gọi K là điểm thuộc SC sao cho SK>KC.
a.Tìm giao tuyến của (MNK) với (ABCD); suy ra giao tuyến của (MNK) với
(SCD);
b.Tìm giao điểm của (MNK) với SA;
c. Tìm giao điểm của (MNK) với SD;
d.Xác định thiết diện của (MNK) với hình chóp.
Đề số 7
Bài 1. Trong khai triển:
4
5
3
2 1
( )
7 3

x
x
tìm
a. số hạng chứa 8
x
; b. số hạng không chứa x;
c. 2 số hạng chính giữa; d. hệ số của số hạng cuối;
e. số hạng đầu; f. hệ số của số hạng thứ 5
Bài 2. Lan có 8 cái áo=5 sơmi+3 thun và 7 quần=3 quần jean+ 4 quần tây.
a. Có bao nhiêu cách tạo thành một bộ quần áo?
b. Tính xác suất sao cho chọn đƣợc một bộ thỏa yêu cầu: “nếu chọn áo sơ mi
thì không được chọn quần jean”.
, 3  n N n ta có:

( 2)( 1)
1 2 3 ... ( 2)
2
 
     
n n
n .
Bài 4. Cho hình chóp SABCD, đáy ABCD là hình chữ nhật tâm I. Gọi M, N
lần lƣợt là trung điểm của ABvà SC.
a.Tìm giao tuyến của (DMN) và (SBC). Suy ra thiết diện của (DMN) với hình
chóp.
b.Tìm giao điểm của MN và (SBD).
c. Gọi P là trung điểm của SB. Xác định giao tuyến của (INP) và (ABCD).
d.Xác định thiết diện của (INP) với hình chóp. Thiết diện là hình gì?
Đề số 8
Bài 1. Trong khai triển:
4
8
3
2
( )
3 2

x
x
, tìm
x ;
c. hệ số của số hạng chính giữa; d. số hạng cuối;
e. hệ số của số hạng đầu; f. số hạng thứ nhất.
Bài 2. Từ một cỗ bài tú lơ khơ, rút ngẫu nhiên cùng lúc 4 con. Tính xác suất
sao cho:
a. cả 4 con đều là K; b. đƣợc ít nhất một con 10;
c. đƣợc 2 con J, 1 con 8, 1 con Q.
n N  ta có
 11
3 9 27 ... 3 3 3
2
n n
     
Bài 4. Cho hình chóp S.ABCD, đáy ABCD là hình thang với AB là đáy lớn.
Gọi M, N, P lần lƣợt là trung điểm của SB, SC, SA. O là giao điểm của AC và
BD. a.Tìm giao tuyến của (SAB) và (SDC), (SAD) và (MBC). b.Tìm giao
điểm của SD và (AMN). Suy ra thiết diện của (AMN) với hình chóp.
c. Xác định thiết diện của (OMP) với hình chóp. Thiết diện là hình gì?
Đề số 9
Bài 1. Cho nhị thức: 5 62
(3 )x
x

a.Tìm số hạng không chứa x trong khai triển

b.Tìm số hạng thứ 4 trong khai triển
c. Tìm hệ số của số hạng chính giữa.
Bài 2. Một hộp bút có 10 bút mực, 7 bút bi và 5 bút chì. Chọn ngẫu nhiên 6
bút tính xác suất sao cho:
a.6 bút tùy ý; b.6 bút cùng loại
c. trong 6 bút có ít nhất một bút chì; d. 6 bút không cùng một loại.
n N  , ta có:
2
3.4 6.7 9.10 ... 3 (3 1) 3 ( 1)n n n n      
Bài 4. Cho hình chóp SABCD, đáy ABCD là hình bình hành tâm O. Gọi M, N
lần lƣợt là trung điểm của SC và AB.
a.Tìm giao tuyến của (MNO) và (SBC); (MNO) và (SAB), (MNO) và (SCD).
b. Xác định thiết diện của (MNO) với hình chóp S.ABCD.
c.Tìm giao tuyến của (AMB) và (SBD), từ đó tìm giao điểm của M N với
(SBD).
d. Chứng minh SD//(MNO).
Đề số 10
Bài 1. Cho nhị thức:
103
2
3 2
2
x
x
 
 
 
a.Tìm số hạng không chứa x trong khai triển
b.Tìm hệ số của x7
trong khai triển.
c. Tìm hệ số của số hạng cuối của khai triển.
Bài 2. Từ 1 hộp bi có 6 bi vàng, 7 đỏ và 8 xanh. Lấy ngẫu nhiên 4 bi. Tính xác
suất biến cố:
a.Lấy 4 bi có đúng 1 viên đỏ.
b.Lấy 4 có ít nhất 1 bi khác màu
Bài 3. *
n N  chứng minh:
5 ( 1)( 2)
5.2 10.3 15.4 ... [5 ( 1)]
3
n n n
n n
 
     
Bài 4. Cho tứ diện ABCD, M là trọng tâm tam giác ABC, N là trung điểm của
AD, P là trung điểm của CD.
a.Tìm giao tuyến của (AMN) và (BCD).
b. Tìm giao tuyến của (ABC) và (MNP).

c. Tìm giao tuyến của (AMP) và(BCD).
d.Tìm giao điểm của AB và mp(MNP). Suy ra thiết diện (MNP) với tứ diện
ABCD.
e. Gọi I, J lần lƣợt là trung điểm AB, BC. Chứng minh IJ//(MNP).
Đề số 11
Bài 1. Hệ số của x2
trong khai triển (1 3 )n
x là 90. Tìm n và tìm hệ số của x5
.
Bài 2. Gieo 1 đồng xu 4 lần:
a.Mô tả không gian mẫu:
b.Tính xác suất để kết quả gieo sau 4 lần có ít nhất một mặt sấp.
c. Tính xác suất để 4 lần gieo không cùng một loại mặt xuất hiện.
Bài 3. , 3n N n   , chứng minh:
 10 20 30 ... 10 20 ( 2)(5 5)n n n       
Bài 4.Cho hình chóp SABCD, tứ giác ABCD có các cặp cạnh đối không song
song. Gọi M, N lần lƣợt là trung điểm của SC và AB.
a.Tìm giao tuyến của (SAB) và (SCD); b.Tìm giao điểm của AM và (SBD)
c.Tìm giao điểm J của MN với (SBD).
Phụ lục 4: ĐỀ THI HK1 các năm trƣớc
Đề thi HK 1 năm 2008- 2009
Bài 1. Cho nhị thức
6
2
3
2x
x
 
 
 
a.Tìm số hạng không chứa x trong khai triển;
b.Tìm hệ số của số hạng chính giữa trong khai triển;
Bài 2. Từ một hộp chứa 15 viên bi gồm 3 bi màu vàng, 5 bi đỏ và 7 bi xanh,
lấy ngẫu nhiên đồng thời 3 viên bi. Tính xác suất sao cho 3 viên bi:
a.3 viên bi cùng màu; b. Có ít nhất 1 bi vàng.
Bài 3. Chứng minh rằng với mọi *n N ta có:
2
1.4 2.7 3.10 ... (3 1) ( 1)n n n n      

Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần
lƣợt là trung điểm của SB và AB, K là điểm trên cạnh CD (K không là trung
điểm của CD).
a.Xác định giao tuyến của: (MNK) và (SBD); (MNK) và (SAC);
b. Tìm giao điểm của (MNK) và BC; (MNK) và SC;
c. Xác định thiết diện của hình chóp S.ABCD và (MNK).
Đề thi HK 1 năm 2009- 2010 (đề A)
Bài 1. Cho khai triển nhị thức 9
2
3
( )x
x
 .
a.Tìm số hạng không chứa x; b.Tìm hệ số của số hạng chứa 3
x
.
Bài 2. Trên một kệ sách có 7 quyển sách Toán, 5 quyển sách Lý và 3 quyển
sách Hóa. Lấy ngẫu nhiên đồng thời 3 quyển sách.
a.Tính số phần tử của không gian mẫu.
b.Tính xác suất các biến cố:
A: “Có đúng 2 quyển sách Toán” „; B: “Có ít nhất một quyển sách Lý”.
Bài 3. Chứng minh *
n N  ta có :
(3 1)
1 4 7 ... (3 2)
2
n n
n

      .
Bài 4. Cho tứ diện ABCD. GỌi M, N lần lƣợt là trung điểm của AC và BC, P
là trung điểm trên cạnh BD sao cho BP>PD.
a. Xác định giao điểm I của (MNP) và đƣờng thẳng CD.
b. Chứng minh AB//(MNP) ;
c. (MNP) cắt AD tại Q. Tứ giác MNPQ là hình gì?
Đề thi HK 1 năm 2010- 2011 (đề A)
Bài 1 ( 2đ ) : Cho nhị thức
8
3
2
x
x
 
 
 
a.Tìm số hạng không chứa x; b. Tìm hệ số của số hạng chính giữa
Bài 2 ( 2đ ) : Chứng minh với *
n N  ,ta có
  
4 4 4 4
......
1.5 5.9 4 3 4 1 4 1
n
n n n
   
  

Bài 3 ( 2đ ) : Có 5 học sinh nữ và 7 học sinh nam .Chọn ngẫu nhiên một tổ lao
động gồm 3 học sinh . Tính xác suất sao cho 3 học sinh đƣợc chọn
a.có ít nhất một học sinh nữ; b. cùng giới tính
Bài 4 ( 4đ ): Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O,
M là trung điểm của cạnh SB
a.Tìm giao tuyến của ( SAC) và (SBD) ; ( SBC) và ( SAD)
b.Chứng minh OM // mp ( SCD)
c.Tìm giao điểm của DM và mp ( SAC)
d.Thiết diện của mặt phẳng ( ADM) và hình chóp S.ABCD là hình gì ?
Đề thi HK 1 năm 2011- 2012 (đề A)
Câu 1 ( 2 đ ) : Cho nhị thức
10
3
2
2
x
x
 
 
 
a/ Tìm số hạng không chứa x ; b/ Tìm hệ số của số hạng chính giữa
Câu 2 ( 3 đ ) : Từ một hộp chứa 7 bi đỏ , 3 bi xanh , 5 bi vàng lấy ngẫu nhiên
đồng thời 4 bi . Tính xác suất sao cho 4 bi đƣợc chọn :
a/ cùng màu b/ có ít nhất 1 bi đỏ c/ có nhiều nhất 1 bi xanh
Câu 3 ( 1 đ ) : Chứng minh với mọi n N
 ta có :
  
1 1 1 1
.......
1.5 5.9 9.13 4 3 4 1 4 1
n
n n n
    
  
Câu 4 ( 4 đ ) : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm
O. Gọi M ,N lần lƣợt là trung diểm của SA , SB . Tìm :
a/ Tìm giao tuyến của  SAC và  SBD ;  SAD và  SBC
b/ Chứng minh mp  OMN // mp  SCD
c/ Tìm giao điểm của DN và mp  SAC
d/ Xác định thiết diện của hình chóp S.ABCD và mp  OMN .
-HẾT-
Chúc các
em thi
tốt!

Chuanhk1

More Related Content

What's hot

Similar to Chuanhk1

More from Võ Tâm Long

Recently uploaded

Chuanhk1