This document discusses chemical kinetics and reaction rates. It begins by defining key terms like reaction rate, rate laws, half-life, and the Arrhenius equation. It then discusses methods for determining the order of reactions, such as zero-order, first-order, and second-order reactions. Specific equations are provided for calculating rate constants and half-lives for each reaction order. The document emphasizes the importance of understanding reaction kinetics for applications like predicting drug stability and dissolution.

1. Chemical kinetics

2. Basics….
1) Reaction rate How we measure rate
2) Rate laws How the rate depend on amount of factors
3) Half life (𝑡1/2) How long it takes to react 50% of its reactants.
4) Arrhenius equation How rate constants changes with T.
5) Mechanisms Link between rate and molecular scale
processes

3. Basics…..
• Molarity refers to the concentration of a compound or ion in a
solution, normality refers to the molar concentration only of the
acid component or only of the base component of the solution.
M= Moles/Lit of solvent used in solution
N= Eq/V
Eq- No. of gm equivalents of solute
V- Volume of solvent in Lit.
• The relation between normality and molarity is N = M x n where
N refers to normality, M is molarity, and n denotes the number of
equivalents.

4. Need of Chemical Kinetics
• To study, understand and interpret conditions of instability of
p’ceutical product as well as to be able to offer
• Recognize alterations in stability may occur when a drug is combined
with other ingredients.
• Knowing the rate at which a drug deteriorates at various hydrogen ion
concentrations allows one to choose a vehicle that will retard or
prevent the degradation.
• The pharmacist is able to assist the physician & patient regarding
storage & use of medicinal agents.
• Molecularity of reactions
Unimolecular, Bimolecular & Termolecular reactions

5. Rates, Order and Molecularity of Reactions
Law of Mass Action:
The rate of chemical reaction is proportional to the product of the
molar concentration of the of the reactants each raised to a power
usually equal to the number of molecules, a and b, respectively,
a A + b B+……= Products (1)
Rate/velocity/Speed of reaction
dc/dt

6. APPLICATIONS
1) Drug stability: help to predict shelf life of drug.
2) Dissolution: Drug is expected to release from solid dosage form and
immediately get into molecular solutions.
3) Drug release: prodrugs (agents who don’t have therapeutic activity
but converted back in vivo to their parent compounds)
Eg. Levodopa is prodrug of Dopamine.
4) Pharmacokinetics: ADME mechanism
5) Drug action: Interaction of drugs with bio membranes or receptors

7. Order of reaction
• Zero order reaction
−
𝑑𝑐
𝑑𝑡
= 𝑘𝑜
Ko= Specific rate constant
m+n=0
Eg.: 1) Colour loss of liquid multisulphonamide preparation.
2) Oxidation of vitamin A in an oily solution.
3)Photochemical degradation of chlorpromazine in aqueous solution.

8. Derivation
−
𝑑𝐴
𝑑𝑡
= 𝑘𝑜
A=absorbance of preparation
- ve sign= colour is fading
Integrating above equation between initial absorbance ,Ao at t=0 time
& absorbance, 𝐴𝑡 at t=t gives
𝐴𝑜
𝐴𝑡
𝑑𝐴 = −𝑘𝑜
0
𝑡
𝑑𝑡 − 𝑘𝑜
0
𝑡
𝑑𝑡
𝐴𝑡−𝐴0= -k0𝑡
Or 𝑘0= 𝐴0- 𝐴𝑡/t
An integral equation for zero order reaction. Also permits us to
calculate the con. Of drug remain undecomposed after time t.

9. Type equation here. Initial con. = ‘a’ & con. at any time t, is ‘c’. Then
equation becomes
𝑘𝑜 = (𝑎 − 𝑐)/𝑡
It may be written as 𝑐 = 𝑎 − 𝑘𝑜𝑡
Half life: 𝑐 =
𝑎
2
, 𝑡 = 𝑡1/2

10. Substituting values in rearranged equation
𝑡1
2
=
𝑎 − 𝑐
𝑘𝑜
= 𝑎 −
𝑎
2
𝑘𝑜
=
1
2
𝑘𝑜
=
𝑎
2𝑘𝑜
Unit is time scale, i.e., sec/con, min/con, h/con
According to equation half life period od zero order is directly
proportional to the initial concentration of reactant.
SHELF LIFE : 𝑐 =
90𝑎
100
t=𝑡90
Substituting values in rearranged equation
𝑡90 =
𝑎 − 0.9
𝑘𝑜
=
0.1𝑎
𝑘𝑜

11. APPARENT ZERO ORDER - SUSPENSIONS
 It may be first order but
behaves like a zero order,
depending on the
experimental conditions.
 Degradation is possible only
when drug is available in
solution form.
 As the drug in solutions starts
to degrade suspended
particles act as reservoir &
continuously release drug in
solution. Thus con. Remains
constant throughout the
process.
 In case of no reservoir; −
𝑑 𝐴
𝑑𝑡
=
𝑘1[𝐴]
]

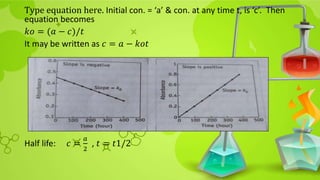
12. FIRST ORDER REACTION
• −
𝑑𝑐
𝑑𝑡
∝ 𝑐 or −
𝑑𝑐
𝑑𝑡
= 𝑘1𝑐
Derivation
A Products
According to definition of 1st order,
−
𝑑𝑐
𝑑𝑡
= 𝑘1𝑐
𝑐0
𝑐1
𝑑𝑐
𝑐
= −𝑘1
𝑜
𝑡
𝑑𝑡
[𝐼𝑛 𝑐]𝑐𝑜
𝑐𝑡
=-k1[𝑡]0
𝑡

13. 𝐼𝑛 𝑐1 − 𝐼𝑛 𝑐0 = −𝑘1(𝑡 − 𝑜)
𝐼𝑛 𝑐𝑡 = 𝐼𝑛 𝑐𝑜 − 𝑘1𝑡
Converting equation to the base 10
log 𝑐1 = log 𝑐0 −
𝑘1𝑡
2.303
Rearranging gives,
𝑘1 =
2.303
𝑡
log
𝑐𝑜
𝑐𝑡
K1 value explains the fraction of the reactant consumed per unit time

14. HALF LIFE
𝑐𝑡 =
𝑐𝑜
2
Or 𝑡 = 𝑡
1
2
Substituting in equation
𝑘1 =
2.303
𝑡1
2
log
𝑐𝑜
𝑐𝑜
2
𝑡1
2
=
2.303
𝑘1
log 2 = 2.3003 ∗
0.3010
𝑘1
=
0.693
𝑘1
SHELF LIFE
𝑐𝑡 =
90
100
𝑐𝑜 𝑡 = 𝑡90

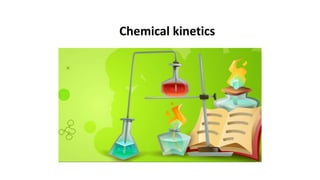
15. Substituting in rearranged equation
𝑡90 =
2.303
𝑘1
log
𝑐𝑜
0.9𝑐0
𝑡90 =
2.303
𝑘1
log
10
9
= 2.303 ∗
0.04575
𝑘1
=
0.105
𝑘1
Pseudo first Order Reaction
−
𝑑𝑐
𝑑𝑡
= 𝑘2[𝐴][𝐵]
A& B= reactants, K2= 2nd order rate constant
Reaction conditions are maintained such that B present in excess
amount compared to A. That’s why equation changes to
−
𝑑𝑐
𝑑𝑡
= 𝑘2 𝐴 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 = 𝑘1[𝐴]

16. SECOND ORDER REACTION
A+B=Products
Rate equation can be written as:
−
𝑑𝐴
𝑑𝑡
= −
𝑑𝐵
𝑑𝑡
= 𝑘2[𝐴]1[𝐵]1
[A] & [B]= concentration of A & B respectively
K2= Specific rate constant for 2nd order.
i.e. Rate of reaction is 1st order W.R.T. A & again 1st order W.R.T B.
Therefore, m+n=2
For identification/evidence purpose; Plot graph of log con. Vs. time.
Straight line indicating 1st order w.r.t A & again 1st order w.r.t B.

17. DERIVATION
−
𝑑𝐴
𝑑𝑡
= −
𝑑𝐵
𝑑𝑡
= 𝑘2[𝐴][𝐵]
Let ‘a’ & ‘b’ be the initial con. Of A&B, and ‘x’ be the con. Of each
species reacting in time t. On substituting these gives,
𝑑𝑥
𝑑𝑡
= 𝑘2 𝑎 − 𝑥 (𝑏 − 𝑥)
By considering case in which a=b i.e. (both having same con.) then the
equation will be
𝑑𝑥
𝑑𝑡
= 𝑘2(𝑎 − 𝑥)2
Integrating above equation on employing the conditions x=0 at t=0 &
x=x at t=t, gives
0
𝑥
𝑑𝑥/(𝑎 − 𝑥)2 = 𝑘2
0
𝑡
𝑑𝑡

18. 1
(1−𝑥)
−
1
(𝑎−0)
= 𝑘2(𝑡 − 0)
𝑎−𝑎+𝑥
𝑎(𝑎−𝑥)
=𝑘2 𝑡 − 0
𝑥
𝑎 𝑎−𝑥
= 𝑘2𝑡
Or
𝑘2 =
1
𝑎𝑡
∗
𝑥
𝑎−𝑥
(a=b)
𝑘2 = 2.303/𝑡 𝑎 − 𝑏 log
𝑏 𝑎−𝑥
𝑎 𝑏−𝑥
(a≠b)

19. Half life
𝑎 − 𝑥 =
𝑎
2
, t=𝑡1/2; x=a/2
𝑘2 =
1
𝑎𝑡
.
𝑥
𝑎 − 𝑥
=
1
𝑎𝑡1
2
.
𝑎
2
𝑎
2
𝑘2 = 1/𝑎𝑡1/2
Or 𝑡1/2 =
1
𝑎𝑘2
(a=b)
Shelf life
𝑡90% = 0.11/𝑎𝑘2

20. Determination Of Order
1) Graphic method :
More reliable coz deviation from best fit line can be easily observed.
A straight line that gives better fit is identified, & reaction is
considered to be that order.
2) Substitution method:
From kinetic expt. Data are collected on time course of change in con.
Of reactants.
Data are substituted in the integral equations of zero, first, & second
order reactions to get k values.
Zero order: 𝑘𝑜 =
𝐴𝑜−𝐴𝑡
𝑡
First order: 𝑘1 =
2.303
𝑡
log
𝑐0
𝑐𝑡

21. Second order: 𝑘2 =
1
𝑎𝑡
.
𝑥
(𝑎−𝑥)

22. 3) Half life method
Average k value is calculated using the data for zero, first and second
orders as given in substitution method or graphic method. Followed by
it half life are calculated for each time period in kinetic study.
Zero order:
𝑡1
2
=
𝑎
2𝑘0
First order:
𝑡1
2
=
0.693
𝑘1
Second order:
𝑡1
2
=
1
𝑎𝑘2
(where a=b)
From above equations we may consider that