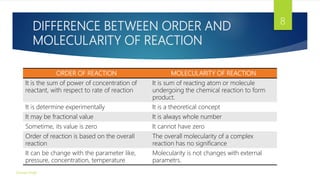
1) The document discusses various topics related to chemical kinetics including reaction order, molecularity, and rate laws for zero-order, first-order, and second-order reactions. 2) It provides examples and characteristics of zero-order reactions where the rate is independent of concentration and the rate law is equal to the rate constant. It also discusses calculating half-life and shelf life for zero-order reactions. 3) First-order reactions are described where the rate is directly proportional to the concentration of one reactant and the integrated rate law results in an exponential decay of concentration over time. Half-life calculations for first-order reactions are also covered. 4) Second-order reactions have the rate directly proportional

1. CHEMICAL KINETICS
PRESENTED BY
GOURAV SINGH
B-PHARMACY- 4TH SEMESTER (NEW PCI SYLLABUS)
Gourav
Singh
1

2. INTRODUCTION
1) Reactions kinetics also known as Chemical kinetics.
2) Chemical kinetics describe the mechanism of a chemical reaction.
3) This give an ideas of an activation energy of a chemical reaction.
4) Many properties such as the order of a chemical reaction, the rate of reaction or the
concentration of the component can be easily calculated from the study of chemical
kinetics.
5) Rate of reaction is the speed at which chemical reaction take place and it is
measured by change in concentration (dc) with respect to time (dt). It is expressed as
Rate of reaction = ±
𝑑𝑐
𝑑𝑡
Gourav Singh
2

3. INTRODUCTION
Where,
Positive (+) sign- Increase in concentration over a period of time.
Negative (-) sign – Decrease in concentration with respect to time.
 In general, a chemical reaction for kinetic study is written as
cC + dD Products
Rate =−
1
𝑐
𝑑[𝐶]
𝑑𝑡
Rate =−
1
𝑑
𝑑[𝐷]
𝑑𝑡
Gourav Singh
3

4. INTRODUCTION
Rate = 𝑘[𝐶]𝑐
[𝐷]𝑑
Where
K- rate constant or specific constant
[C]and [D] – molar concentration of C and D respectively.
 Rate constant express the relationship between the rate of chemical reaction
and the concentration of the reacting substances.
Gourav Singh
4

5. MOLECULARITY REACTION
1) It is defined as number of reactant molecules or atoms that take part in
chemical reaction to give the products.
2) If number of reacting particle is one, then the reaction is considered to be
Unimolecular.
For example:- 𝐵𝑟2 → 2𝐵𝑟
OR 𝑃𝐶𝑙5 → 𝑃𝐶𝑙3 + 𝐶𝑙2
3) When two reactant molecules are involved to carry out the reaction, this
reaction are called bimolecular reaction.
For example- 2𝐻𝐼 → 𝐻2 + 𝐼2
Gourav Singh
5

6. MOLECULARITY REACTION
4) When three reactant molecules are involved to carry out the reaction, this
reaction are called trimolecular reaction.
For example- 2𝑁𝑂 + 𝑂2 → 2𝑁𝑂2
Gourav Singh
6

7. ORDER OF REACTION
1) The sum of exponents or power of concentration term in the rate equation is
known as order of reaction.
2) Let us consider a general reaction.
𝑅𝑎𝑡𝑒 = 𝐾[𝐶]𝑐
[𝐷]𝑑
Thus the above order reaction is (c+d)
a) If the value of (c+d) is 0, then it is called zero order reactions.
b) If the value of (c+d) is 1, then it is called first order reactions.
c) If the value of (c+d) is 2, then it is called second order reactions.
Gourav Singh
7

8. DIFFERENCE BETWEEN ORDER AND
MOLECULARITY OF REACTION
ORDER OF REACTION MOLECULARITY OF REACTION
It is the sum of power of concentration of
reactant, with respect to rate of reaction
It is sum of reacting atom or molecule
undergoing the chemical reaction to form
product.
It is determine experimentally It is a theoretical concept
It may be fractional value It is always whole number
Sometime, its value is zero It cannot have zero
Order of reaction is based on the overall
reaction
The overall molecularity of a complex
reaction has no significance
It can be change with the parameter like,
pressure, concentration, temperature
Molecularity is not changes with external
parametrs.
Gourav Singh
8

9. ZERO ORDER REACTION
 When rate is independent of the reactant concentration, then it is called zero order
reaction.
 Let us consider a reaction:
𝐴 → 𝐵
For this Zero order reaction, x=0
Therefore rate =k
Rate =−𝑑𝐴
𝑑𝑡
Where,
−𝑑𝐴
𝑑𝑡 = change in concentration with respect to time negative (-) indicate decrease
in concentration.
K = specific rate constant for zero order.
Gourav Singh
9

10. ZERO ORDER REACTION
 Derivatives
The rate of zero order reaction is expressed as
−𝑑𝐴
𝑑𝑡
On integrate equation
= − 𝐴0
𝐴𝑡
𝑑𝐴 = 𝐾 0
𝑡
𝑑𝑡
= − 𝐴0
𝐴𝑡
𝐴 = 𝐾 0
𝑡
[𝑡]
Gourav Singh
10

11. ZERO ORDER REACTION
= 𝐴0 − 𝐴𝑡 = 𝑘(𝑡 − 0)
= 𝐴0 − 𝐴𝑡 = 𝑘𝑡
Or 𝑘 =
𝐴0−𝐴𝑡
𝑡
This is integrated rate of equation
t= 0 time (t)
Slope = -k
Concentration [A]
Plot of concentration vs time
Gourav Singh
11

12. ZERO ORDER REACTION
 Characteristics
1) Half life (𝒕𝟏/𝟐): It is the time required to reduce initial concentration of the
reactant to become half of its value during the progress of the reaction.
Initial concentration = 𝐴0
Final concentration = 𝐴0/2
By putting this value in equation [𝐴0 − 𝐴𝑡 = 𝑘𝑡] , we get:
𝑘𝑡1/2 = 𝐴0 −
𝐴0
2
𝑘𝑡1/2 =
𝐴0
2
Gourav Singh
12

13. ZERO ORDER REACTION
𝑡1/2 =
𝐴0
2𝑘
Half life is directly proportional to the initial concentration of reactant.
2) Shelf life: It is a time required for reactant concentration to decrease to 90% of
the initial concentration.
𝐴𝑡 = 0.9 𝐴0
By putting this value in equation [𝐴0 − 𝐴𝑡 = 𝑘𝑡] , we get:
𝑡0.9 =
𝐴0 −0.9 𝐴0
𝑘
Gourav Singh
13

14. ZERO ORDER REACTION
𝑡0.9 =
0.1 𝐴0
𝑘
This unit of k for zero order reaction is moles/litre/second
 Example
1. Photochemical reaction between hydrogen and chlorine.
𝐻2 𝑔 + 𝐶𝑙2 𝑔
ℎ𝑣
2𝐻𝐶𝐿 (𝑔)
2. Decomposition of 𝑵𝟐𝑶 on a hot platinum surface.
𝑁2𝑂 → 𝑁2 +
1
2
𝑂2
𝑅𝑎𝑡𝑒 ∝ [𝑁2𝑂]0
= 𝑘[𝑁2𝑂]0
= 𝑘
Gourav Singh
14

15. ZERO ORDER REACTION
𝑑[𝑁2𝑂]
𝑑𝑡
= 𝑘
3. Decomposition of 𝑵𝑯𝟑 in the presence of molybdenum or tungsten.
2𝑁𝐻3
[𝑀𝑜]
𝑁2 + 3𝐻2
 Problems
I. What is the value of rate constant if [𝐴0] = 2.30M and half life is 7.30 min.
Ans:- 𝑡1/2 = 𝐴0/2𝑘
k=2.3 M/2 (7.3min)
k = 0.157 mol/1.min
Gourav Singh
15

16. ZERO ORDER REACTION
II. The amount of vitamin A oxidized in a certain period of time is 300 unit for a
given dose of 3000 IU/ml. It mean that the decrease in potency is 10 percent. If
the dose of the vitamin is 3,00,000, IU/ml, then shelf life = 𝑡90 = ?
Ans: - 𝑡90 =
0.1𝐴0
𝑘0
=
0.1 𝑥 2.5
2.2 𝑥 10−7
= 1136363.64 sec or 315.66 hrs or 13.15 days
Self study—
At 400
𝐶, the intensity of colour of drug preparation is reduced from 1.345 to 1.335
in 90 days. Estimate the reaction rate if colour fading follow zero order reaction?
Answer – 0.011𝑑𝑎𝑦𝑠−1
.
Gourav Singh
16

17. PSEUDO ORDER REACTION
 An order of a chemical reaction that appears to be less than the true order due to
experimental conditions; when a one reactant is in large excess.
 There are two types of reaction
1) Pseudo first order reaction
2) Pseudo second order reaction
FIRST ORDER REACTION SECOND ORDER REACTION
Pseudo first order kinetics 2nd order rate law
= k [A] or [B]
Pseudo second order kinetic 3rd order rate
law = 𝑘[𝑎]2[𝐵]
Reduce to first Pseudo first order if either [a]
or [B] in large excess
Reduce to pseudo first order if [A] is in
excess, Pseudo second order if [B] is in
Gourav Singh
17

18. FIRST-ORDER REACTION
 First order reaction is defined as a reaction in which the rate of reaction
depends on the concentration of one reactant.
Let us consider
𝐴 → 𝑝𝑟𝑜𝑑𝑢𝑐𝑡𝑠
Rate =𝑘[𝐴]1
Rate = -d[A]/dt
equate both above equation, we get
k[A] = -d[A]/dt
or k dt = -d[A]/[A]
Gourav Singh
18

19. FIRST-ORDER REACTION
Integrating the above equation
On integration
 𝑘 0
𝑡
𝑑𝑡 = − 𝐴0
𝐴 𝑑𝐴
𝐴
 𝑘0
𝑡
𝑡 = −𝐴0
𝐴𝑡
[𝑙𝑜𝑔𝑒 𝐴]
 𝑘𝑡 = −[𝑙𝑜𝑔𝑒𝐴𝑡 − log 𝐴0]
 𝑘𝑡 = − log
𝐴𝑡
𝐴0
As we know
 log 𝑋𝑛 = 𝑛𝑙𝑜𝑔 𝑥
Gourav Singh
19

20. FIRST-ORDER REACTION
𝑠𝑜 𝑘𝑡 = log
𝐴0
𝐴𝑡
= 𝑘𝑡 = 2.303 𝑙𝑜𝑔10
𝐴0
𝐴𝑡
Or k =
2.303
𝑡
log
𝐴0
𝐴𝑡
This equation is integrated rate law of equation
In exponential form, the equation becomes,
𝑘𝑡 = 𝑙𝑜𝑔𝑒
𝐴0
𝐴𝑡
𝑒𝑘𝑡
=
𝐴0
𝐴𝑡
Gourav Singh
20

21. FIRST-ORDER REACTION
Or 𝐴𝑡 = 𝐴0𝑒−𝑘𝑡
For first order equation, when we plot concentration against time, a curve is
obtained.
The curve shows that concentration decrease exponentially with time.
The 𝑘 =
2.303
𝑡
log[
𝐴0
𝐴𝑡
] can be written as-
Gourav Singh
21

22. FIRST-ORDER REACTION
𝑘 =
2.303
𝑡
log
𝑎
𝑎 − 𝑥
Where,
a is initial concentration and equal to 𝐴0
X is decrease in concentration with time
a-x is the concentration remained at time t and equal to 𝐴𝑡
The unit of k for first order reaction is 𝑡𝑖𝑚𝑒−1
𝑖. 𝑒. 𝑆𝑒𝑐−1
, 𝑚𝑖𝑛𝑢𝑡𝑒−1
ℎ𝑜𝑢𝑟−1
Gourav Singh
22

23. FIRST-ORDER REACTION
 Half life:
To calculate half life
𝐴𝑡 =
𝐴0
2
As we know rate equation for first order reaction is
𝑘𝑡 = 2.303 log[
𝐴0
𝐴𝑡
]
By putting value of 𝐴𝑡 into above equation, we get
𝑘𝑡1/2 = 2.303 log[
𝐴0
𝐴0/2
]
Or 𝑘𝑡1/2 = 2.303 𝑙𝑜𝑔2
𝑡1/2 = 0.693/k
Gourav Singh
23

24. FIRST-ORDER REACTION
This equation shows that in first order reaction the half life is independent of the initial
concentration
 Shelf life:
As per definition
𝐴𝑡 = 0.9 𝐴0
By putting these value in equation {𝑘𝑡 = 2.303 log
𝐴0
𝐴𝑡
}, we get
𝑡90 =
2.303
𝑘
𝑙𝑜𝑔
𝐴0
0.9𝐴0
𝑡90 =
2.303
𝑘
𝑙𝑜𝑔
10
9
𝑡90 =
0.105
𝑘
Gourav Singh
24

25. FIRST-ORDER REACTION
 Problems
I. The half life of drug which decompose according to first order kinetics, is 75
days. Calculate shelf life and K
Ans:- 𝑡1/2 = 0.693/k
75 = 0.693/k
k = 0.0092𝑑𝑎𝑦−1 shelf life
𝑡90 =
0.105
𝑘
=
𝟎.𝟏𝟎𝟓
𝟎.𝟎𝟎𝟗𝟐
= 11.41 𝑑𝑎𝑦𝑠.
Gourav Singh
25

26. FIRST-ORDER REACTION
II. The initial concentration of drug was found to be 0.075 M. The concentration
after 12 hours was 0.055 M. Calculate the reaction rate constant if
decomposition of drug follows first order reaction.
Solution:- The first order reactions is
𝑘𝑡 = 2.303 log[
𝐴0
𝐴𝑡
]
𝑘 =
2.303
12
𝑙𝑜𝑔
0.075
0.055
k = 0.02527ℎ𝑟−1
Gourav Singh
26

27. SECOND-ORDER REACTION
 The reaction is said to be second order when rate of reaction is directly
proportional to the concentration of two reactants.
 In second order reaction two condition are possible
1) When
A Products
𝑑𝑥
𝑑𝑡 𝛼 [𝐴]2
2) When
A + B Products
𝑑𝑥
𝑑𝑡 𝛼 𝐴 𝐵
Gourav Singh
27

28. SECOND-ORDER REACTION
Case 1
When there is one reactant or concentration of both reactants are same
A + A products
At time = 0, initial concentration a a 0
At time = t, Concentration (a-x)(a-x) x
𝑟𝑎𝑡𝑒 =
𝑑𝑥
𝑑𝑡
𝛼( 𝑎 − 𝑥 )2
𝑑𝑥
𝑑𝑡
= 𝑘 ( 𝑎 − 𝑥 )2
Where K is second order rate constant.
Gourav Singh
28

29. SECOND-ORDER REACTION
On integrating between x=0 at t=0 and x=dx at t=t, we obtain
0
𝑥 𝑑𝑥
( 𝑎 −𝑥)2 = 𝑘 0
𝑡
𝑑𝑡
=
1
(𝑎 − 𝑥)
−
1
𝑎 − 0
= 𝑘𝑡
𝑜𝑟 𝑘𝑡 =
1
𝑎
𝑥
(𝑎 − 𝑥)
𝑜𝑟 𝑘 =
1
𝑎𝑡
𝑥
(𝑎 − 𝑥)
Gourav Singh
29

30. SECOND-ORDER REACTION
The plot of x/a(a-x) versus time give straight line having slope = k
Plot of x/a(a - x) vs time in case of second order reaction
𝑥
𝑎(𝑎 − 𝑥)
Time
Slope = k
Gourav Singh
30

31. SECOND-ORDER REACTION
 Half life = 𝑥 =
𝑎
2
𝑎𝑛𝑑 𝑡 = 𝑡1/2
By putting these value in above equation, we get
𝑘 =
1
𝑎𝑡1/2
𝑥
𝑎/2
(𝑎−𝑎/2)
𝑘 =
1
𝑎𝑡1/2
or 𝑡1/2 =
1
𝑘𝑎
According to this equation half life is inversely proportional to initial
concentration.
Gourav Singh
31

32. SECOND-ORDER REACTION
Case 2
When concentration of both reactant are different or not same
A + B Product
At time = 0, initial Concentration A B 0
At time = t, Concentration (a - x)(b - x) X
Where a and b are initial concentrations of A and B respectively and x is amount of
each of A and B reacting in time t, (a - x) and (b – x ) represent concentration of A
and B remaining unreacted at time t.
𝑑𝑥
𝑑𝑡
𝛼 (𝑎 − 𝑥)(𝑏 − 𝑥)
Gourav Singh
32

33. SECOND-ORDER REACTION
Or
𝑑𝑥
𝑑𝑡
= 𝑘 (𝑎 − 𝑥 )(𝑏 − 𝑥)
Rearrange the equation
𝑑𝑥
(𝑎 −𝑥)(𝑏 −𝑥)
= 𝑘𝑑𝑡
On integration
𝑑𝑥
(𝑎 − 𝑥)(𝑏 − 𝑥)
= 𝑘𝑑𝑡
By using partial fraction of
1
(𝑎 −𝑥)(𝑏 −𝑥)
, we get
Gourav Singh
33

34. SECOND-ORDER REACTION
1
𝑎 − 𝑥 𝑏 − 𝑥
=
1
𝑎 − 𝑏
1
𝑏 − 𝑥
−
1
𝑎 − 𝑥
Put this value of partial fraction into above equation, we get
𝑑𝑥
(𝑎 − 𝑥)(𝑏 − 𝑥)
=
1
(𝑎 − 𝑏)
𝑑𝑥
𝑏 − 𝑥
−
𝑑𝑥
𝑎 − 𝑥
= 𝑘. 𝑑𝑡
1
(𝑎 − 𝑏)
− ln 𝑏 − 𝑥 − − ln 𝑎 − 𝑥 = 𝑘𝑡 + 𝐶
By putting t = 0 and x = 0 in above equation, the value of C will be
𝐶 =
1
(𝑎 − 𝑏)
𝑙𝑛
𝑎
𝑏
Gourav Singh
34

35. SECOND-ORDER REACTION
Put the value of C in above equation, we get

1
(𝑎 −𝑏)
ln 𝑎 − 𝑥 − 𝑏 − 𝑥 = 𝑘𝑡 +
1
(𝑎 −𝑏)
𝑙𝑛
𝑎
𝑏

1
(𝑎 −𝑏)
ln
𝑎 −𝑥
𝑏 −𝑥
− ln
𝑎
𝑏
= 𝑘𝑡
 𝑘 =
1
𝑎 −𝑏 𝑡
ln
𝑎 −𝑥
𝑏 −𝑥
− ln
𝑎
𝑏
 𝑘 =
1
𝑎 −𝑏 𝑡
ln
𝑏(𝑎 −𝑥)
𝑎(𝑏 −𝑥)
 𝑘 =
2.303
𝑎 −𝑏 𝑡
log
𝑏(𝑎 −𝑥)
𝑎(𝑏 −𝑥)
The unit of rate constant for second order reaction is litre.mole−1
sec−1
Gourav Singh
35

36. SECOND-ORDER REACTION
 In the saponification of methylacetate at 250
𝐶, the concentration of sodium
hydroxide remaining after 75 minutes was 0.00552 M. The initial concentration of
ester and the base was 0.01 molar. Calculate the second order rate constant and
half life of the reaction.
Solution:- Given:- a = 0.01 molar; (a - x) = 0.00552; t= 75 min;
To find:- 𝑘2= ?
x = a – (a - x) = 0.01 – 0.00552
x = 0.00448
𝑘2 =
1
𝑎𝑡
.
𝑥
(𝑎 −𝑥)
=
1
0.01 𝑥 75
.
0.00448
0.00552
= 1.082
𝑙𝑖𝑡𝑟𝑒
𝑚𝑜𝑙
. 𝑚𝑖𝑛
Gourav Singh
36

37. SECOND-ORDER REACTION
Half life = ?
𝑡1/2 =
1
𝑎 𝑥 𝑘2
=
1
1.082 𝑥 0.01
= 92.42 𝑚𝑖𝑛
Examples:
1) Hydrolysis of ester by an alkali (saponification)
𝐶𝐻3𝐶𝑂𝑂𝐶2𝐻5 + 𝑁𝑎𝑂𝐻 → 𝐶𝐻3𝐶𝑂𝑂𝑁𝑎 + 𝐶2𝐻5𝑂𝐻
2) Decomposition of 𝑵𝒐𝟐 into NO and 𝑶𝟐
2𝑁𝑂2 → 2𝑁𝑂 + 𝑂2
3) Conversion of ozone into oxygen at 𝟏𝟎𝟎𝟎
𝒄
2𝑂3 → 3𝑂2
4) Thermal Decomposition of choline monoxide.
2𝐶𝑙2𝑂 → 2𝐶𝑙2 + 𝑂2
Gourav Singh
37

38. DETRMINATION OF REACTION ORDER
 Order of a reaction can be determine by any one of the following methods:
1) Substitution Method: In this method, the data obtained from a kinetic
experiment is substituted in the appropriate rate equation. The equation gives a
fairly constant value of k and indicates the order of a reaction. The rate and
half-life equation for different order reaction are given in table:-
Order Rate Law
0 Rate=k
1 Rate=k[A]
2 Rate=k[𝐴]2
Gourav Singh
38

39. DETRMINATION OF REACTION ORDER
2) Graphical Method: In this method,, the data obtained from a kinetics
experiment is plotted in the appropriate form for determining the order of a
reaction. For Example,
i. If a plot of concentration versus time (t) yield a straight line, the reaction is of
zero-order.
ii. If a plot of log (a - x)versus t yield a straight line, the reaction is of first –order.
iii. If a plot of
𝑥
[𝑎 𝑎 −𝑥 ]
versus t yields a straight line (provided the initial
concentration are equal), the reaction is of second-order.
Gourav Singh
39

40. DETRMINATION OF REACTION ORDER
3) Half-Life Method: by calculating value of k by above method,𝑡1/2 value can be
estimate for each time period in Kinetic study.
Order of reaction 𝒕𝟏/𝟐
0 𝒕𝟏/𝟐 = 𝐴0/2𝑘
1 𝒕𝟏/𝟐 = 0.693/𝑘
2 𝒕𝟏/𝟐 = 1/𝑎𝑘
Gourav Singh
40

41. DETRMINATION OF REACTION ORDER
 A general expression for the determination of the half –life of a reaction can be
given as:
𝑇1/2 𝛼
1
𝑎𝑛−1
Where,
n= Order of the reaction.
 If two reactions are initiated with two different initial concentrations (𝑎1 and 𝑎2,
respectively), the half-lives are determined as:
𝑡1/2 1 𝛼
1
𝑎1
𝑛−1
Gourav Singh
41

42. DETRMINATION OF REACTION ORDER
And, 𝑡 1
2
2 𝛼
1
𝑎2
𝑛−1
On dividing 𝑡 1
2
(1) with 𝑡 1
2
(2):
𝑡 1
2
(1)
𝑡 1
2
(2)
=
1
𝑎1
𝑛 −1
1
𝑎2
𝑛−1
= (𝑎2
𝑎1)𝑛−1
On taking log:
log
𝑡1
2
(1)
𝑡1
2
(2)
= 𝑛 − 1 log
𝑎2
𝑎1
.𝑛−1
Gourav Singh
42

43. DETRMINATION OF REACTION ORDER
𝑜𝑟, 𝑛 =
log 𝑡1
2
1 /𝑡1/2 (2)
log( 𝑎2/𝑎1)
+ 1
Where, n = order of reaction.
Half- lives are calculated by plotting a graph between ‘a’ and ‘t’ at two different
initial concentration (a1 and a2). The half- life times are then read at 1/2 a1 and 1/2
a2 respectively from the graph. The values of half life and the initial concentration
are then substituted in the above equation and the order of reaction (n) is
calculated directly.
Gourav Singh
43

44. IMPORTANT DEFINITIONS
1) Chemical Kinetics- It include the study of the speed or rate of chemical
processes that occur during chemical reactions.
2) Rate of reaction- It is a speed at which chemical reaction take place.
3) Molecularity of reaction- It is defines as number of reactant molecules or atom
that take part in chemical reactions to give the products.
4) Unimolecular reaction- When only one reactant molecule participate to carry
out the reaction, this reaction are called Unimolecular reaction.
5) Bimolecular reaction- When two reactants molecules are involved to carry out
the reaction these reactions are called Bimolecular reaction.
Gourav Singh
44

45. IMPORTANT DEFINITIONS
6) Order of reaction- The sum of exponents or power of concentration terms in
the rate equation is known as order of reactions.
7) Zero order reactions- When rate is independent of the reactant concentration,
that is called as Zero order reactions.
8) Half life- It is the time required to reduce initial concentration of the reactant to
become half of its value during the progress of the reaction.
9) Shelf life- It is the time required for reactant concentration to decrease to 90%
of the initial concentrations.
Gourav Singh
45

46. SUMMARY OF THE KINETICS
Order Rate Law Concentration-
time
Equation
Half –Life M/t Unit of k
0 Rate=k [A] = [𝐴]0 - kt
𝑡1
2
=
[𝐴]0
2𝑘
k m/s, m/min,
m/hrs, etc
1 Rate=k[A] In[A] = In[𝐴]0 -
kt
𝑡1
2
=
𝐼𝑛2
𝑘
kM 𝑠−1, 𝑚𝑖𝑛−1, ℎ𝑟−1,
𝑒𝑡𝑐.
2 Rate=k[𝐴]2 1
[𝐴]
=
1
[𝐴]0
+ 𝑘𝑡 𝑡1
2
=
1
𝑘 𝐴 0
𝑘𝑀2
𝑚−1
𝑠−1
, 𝑚−1𝑚𝑖𝑛−1
𝑚−2
ℎ𝑟−1
, 𝑒𝑡𝑐.
Gourav Singh
46

47. Reference
1) Subramanyam C.V.S, First edition, “Chemical Kinetics” Text Book of Physical
Pharmaceutics, Page No. 13 – 49
2) Martin Physical Pharmacy and Pharmaceutical Science, Sixth edition, “Chemical
Kinetics and Stability” Text Book of Physical Pharmaceutics, Page No. 328 -- 354
Gourav Singh
47