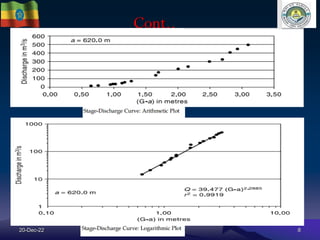
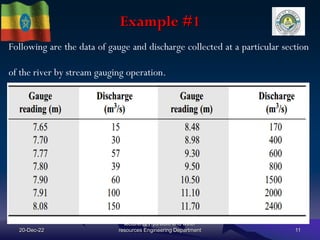
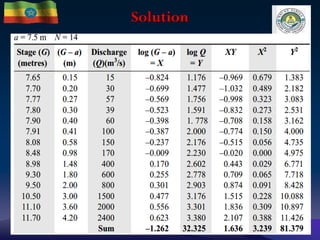
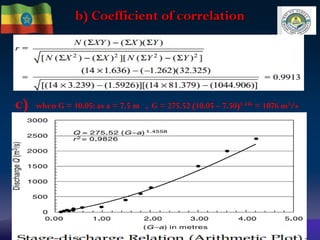
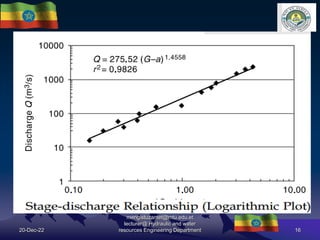
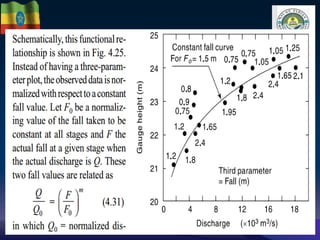
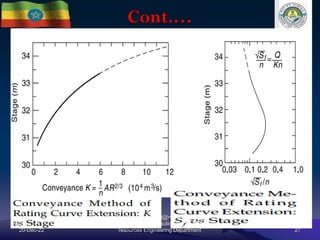
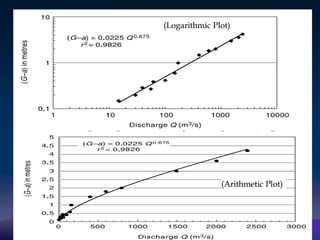
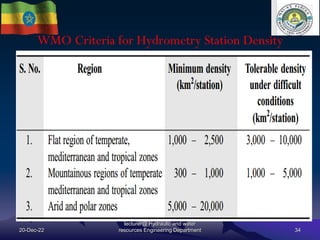
The document discusses techniques for developing discharge-stage relationships (rating curves) at hydrometry stations. It covers permanent and shifting control rating curves, methods for extending rating curves like conveyance and logarithmic plotting, and considerations for siting hydrometry stations according to World Meteorological Organization criteria. Examples are provided to illustrate calculating rating curves and addressing shifting control due to backwater effects. The overall aim is to accurately measure stream discharge, a key parameter in hydrologic studies.