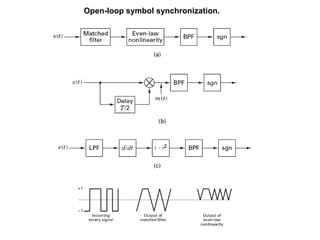
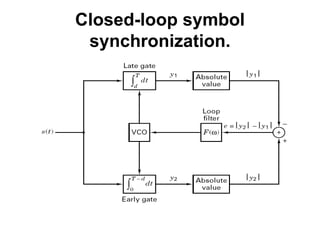
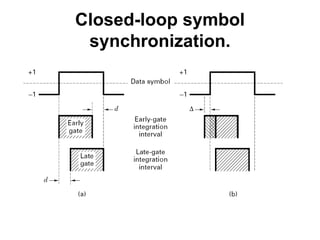
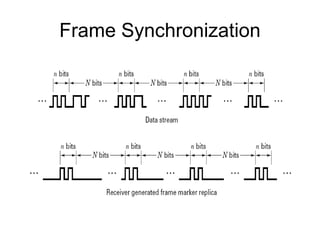
This document discusses various aspects of synchronization in digital communication systems. It covers receiver synchronization techniques like frequency and phase synchronization using phase-locked loops. It also discusses symbol synchronization, both data-aided and non-data-aided approaches. Network synchronization techniques like open-loop and closed-loop transmitter synchronization are introduced as well. The document provides detailed explanations of concepts like acquisition, tracking performance in noise, and steady-state tracking characteristics of phase-locked loops.

1. EEE4026F Digital
Communication Engineering
with
Mqhele E. Dlodlo and Emmanuel O. Bejide
backed by
Bernard Sklar and Kamilo Feher

2. Chapter 10 Synchronisation
• Lecture 21: Introduction & Receiver
Synchronisation
– Introduction
• Definition
• Cost-Benefit Issues
• Approach & Assumptions
– Receiver Synch
• Frequency & Phase Synch
• Lecture 22: Receiver Synch (cont’d)
– Costas Loops
– High-Order Suppressed Carrier
Loops
– Acquisition
– Phase Tracking Errors &
Performance
– Spectrum Analysis Techniques
– Symbol Synch – Discrete Case
• Lecture 23: Receiver Synch (cont’d)
– Synch with CPM
– Data-Aided Synch
– Non-Data-Aided Synch
– Frame Synch
• Lecture 24: Network Synch
– Open-Loop Transmitter
Synch
– Closed-Loop Transmitter
Synch
– Conclusion

3. Synchronization Defined
• Phase synchronization.
• Symbol Synchronization.
• Frame Synchronization.
• Frequency Synchronization.
• Network Synchronization.

4. Tradeoff
• There are added cost to receiver design due to
the implementation of acquisition and tracking
circuits.
• Time required for synchronization to be
achieved.
• Energy expended, for instance on pilot signals,
for the purpose of synchronization.
• Complexity due to error control.
– Frame, block, message synchronization.
• Complexity due to spread spectrum technique.
– PN sequence synchronization.

5. Receiver Synchronization.
• All digital communication receivers require
some degree of synchronization to the
incoming signal.

6. Frequency and Phase
Synchronization.
• A Phase-Locked-Loop (PLL) is at the heart
of nearly all synchronization circuits.

7. Frequency and Phase
Synchronization.
• PLL are servo-control loops, whose
controlled parameter is the phase of a
locally generated replica of the incoming
carrier signal.
• Components of a PLL:
– A phase detector
– A loop filter
– A voltage-controlled oscillator (VCO).

8. Frequency and Phase
Synchronization.
• A phase detector determines the difference in phase
between the incoming signal and the reference signal.
• The loop filter controls the response of the PLL to the
error signal.
• The VCO is an oscillator whose output frequency is a
linear function of its voltage over some range of input
and output.
– +ve signal increase frequency beyond the uncontrolled value.
– -ve signal  reduce frequency below the uncontrolled value.

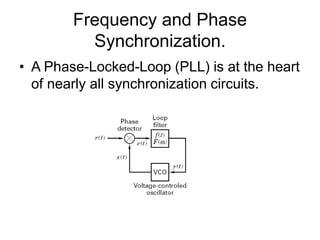
9. Frequency and Phase
Synchronization.
• For a normalized
input signal of the
form:
• Consider a
normalized VCO
output of the form:
)]
(
cos[
)
( 0 t
t
w
t
r 


)]
(
ˆ
sin[
2
)
( 0 t
t
w
t
x 




10. Frequency and Phase
Synchronization.
• Output error signal at
the phase detector
output:
• If the filter output is
low-pass, we will
have
)]
(
ˆ
)
(
2
sin[
)]
(
ˆ
)
(
sin[
)]
(
cos[
)]
(
ˆ
sin[
2
)
(
)
(
)
(
0
0
0
t
t
t
w
t
t
t
t
w
t
t
w
t
r
t
x
t
e















)]
(
ˆ
)
(
sin[
)
( t
t
t
y 
 


11. Frequency and Phase
Synchronization.
• The low pass filter produces an output that is
solely the function of difference in phase between
the two signals.
• The VCO output will be a linear function of y(t).
• Deviation in frequency is given as
)
(
*
)]
(
ˆ
)
(
[
)
(
*
)
(
)
(
)]
(
ˆ
[
)
(
t
f
t
t
K
t
f
t
e
K
t
y
K
dt
t
d
t
o
o
o










Gain of the VCO Loop filter impulse response

12. Frequency and Phase
Synchronization.
• The Fourier transform of the difference equation
leads to
Reorganizing, we have
)
(
*
)]
(
ˆ
)
(
[
)
(
*
)
(
)
(
)]
(
ˆ
[
)
(
t
f
t
t
K
t
f
t
e
K
t
y
K
dt
t
d
t
o
o
o










)
(
)]
(
ˆ
)
(
[
)
( w
F
K
j o 


 




)
(
)
(
)
(
)
(
)
(
ˆ




H
w
F
K
j
w
F
K
o
o





Closed-loop transfer function

13. Frequency and Phase
Synchronization.
• The order of the PLL is the order of the
highest term in jwin the denominator of
H(w).

14. Steady state tracking Characteristic
of the PLL.
• The expression for the Fourier transform of the
phase error can be given as:
• The steady-state error is the residual error after all
transients have died away.
)
(
)
(
)
(
))
(
1
(
)
(
ˆ
)
(
)}
(
{
)
(
w
F
K
j
j
H
t
e
F
E
o



















)
(
)
(
)
(
)}
(
{
)
(
2
0
lim
lim w
F
K
j
j
t
e
F
j
t
e
o
j
t 





 





15. Performance in noise
• The input might be noisy, as is the case in many
communication systems.
• n(t) can be expanded into quadrature
components.
)
(
]
cos[
)
( 0 t
n
t
w
t
r 

 
t
w
t
n
t
w
t
n
t
n s
c 0
0 sin
)
(
cos
)
(
)
( 


16. Performance in noise
• The output of the phase detector can be written as
• The loop filter eliminates the high-frequency components. We
are then left with
• Let us denote the variance of n/(t) by σn.
• It can be shown that the variance of the output phase is:
• For the special case of white noise
• This is related to the
frequency)
carrier
the
at twice
terms
(
]
ˆ
cos[
)
(
]
ˆ
sin[
)
(
]
ˆ
sin[
)
(
)
(
)
( 




 


 t
n
t
n
t
r
t
x
t
e c
s
]
ˆ
cos[
)
(
]
ˆ
sin[
)
(
]
ˆ
sin[
)
( 


 t
n
t
n
t
n c
s 









d
H
G 2
2
ˆ |
)
(
|
)
(
2
1









d
H
No 2
2
ˆ |
)
(
|
2 




L
oB
N
2
2
ˆ 



17. Acqusition.
• Acquisition is the process of getting the
PLL to lock with the incoming signal.
– Aided acquisition
• With the aid of external circuits.
– Self-acqusition
• Without the aid of extrnal signals

18. Symbol synchronization.
• Symbol synchronization is needed in order to achieve
optimum demodulation.
– Non-Data Aided (NDA).
– Data Aided (DA).

19. Open-loop symbol synchronization.

20. Closed-loop symbol
synchronization.

21. Closed-loop symbol
synchronization.

22. Frame Synchronization