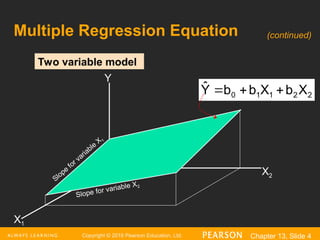
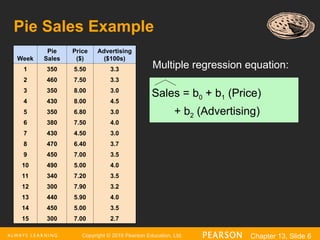
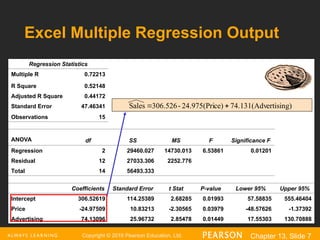
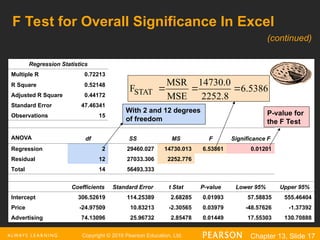
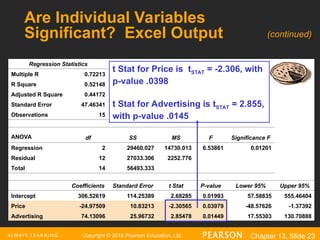
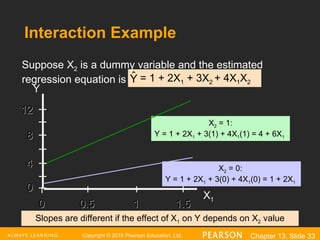
The document explains the concept of multiple regression, emphasizing the examination of the linear relationship between one dependent variable and multiple independent variables. It includes examples, regression statistics, and an analysis of factors such as price and advertising on pie sales, along with how to interpret coefficients, R^2, and significance tests. The importance of residual plots and assumptions for regression analysis is also discussed.