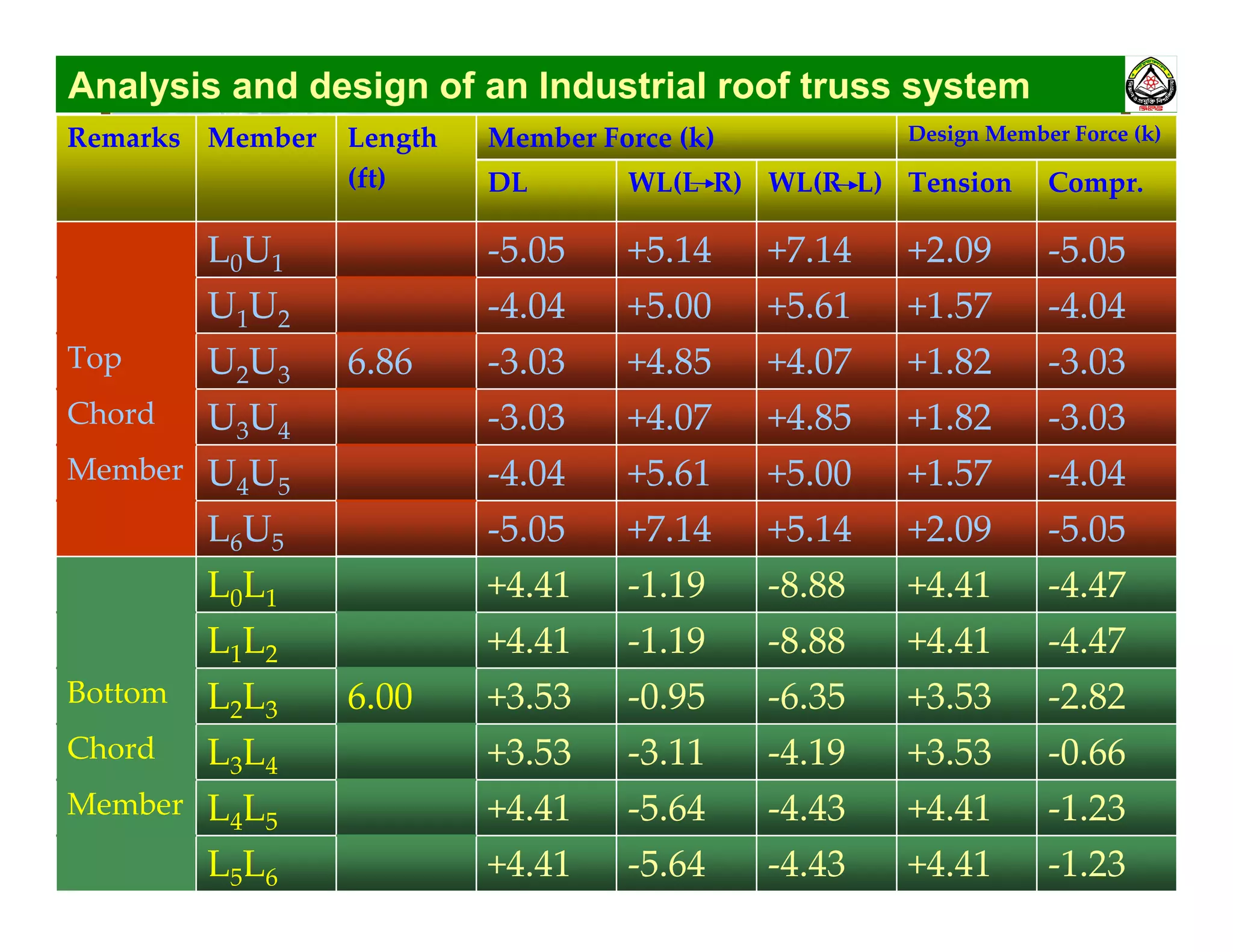
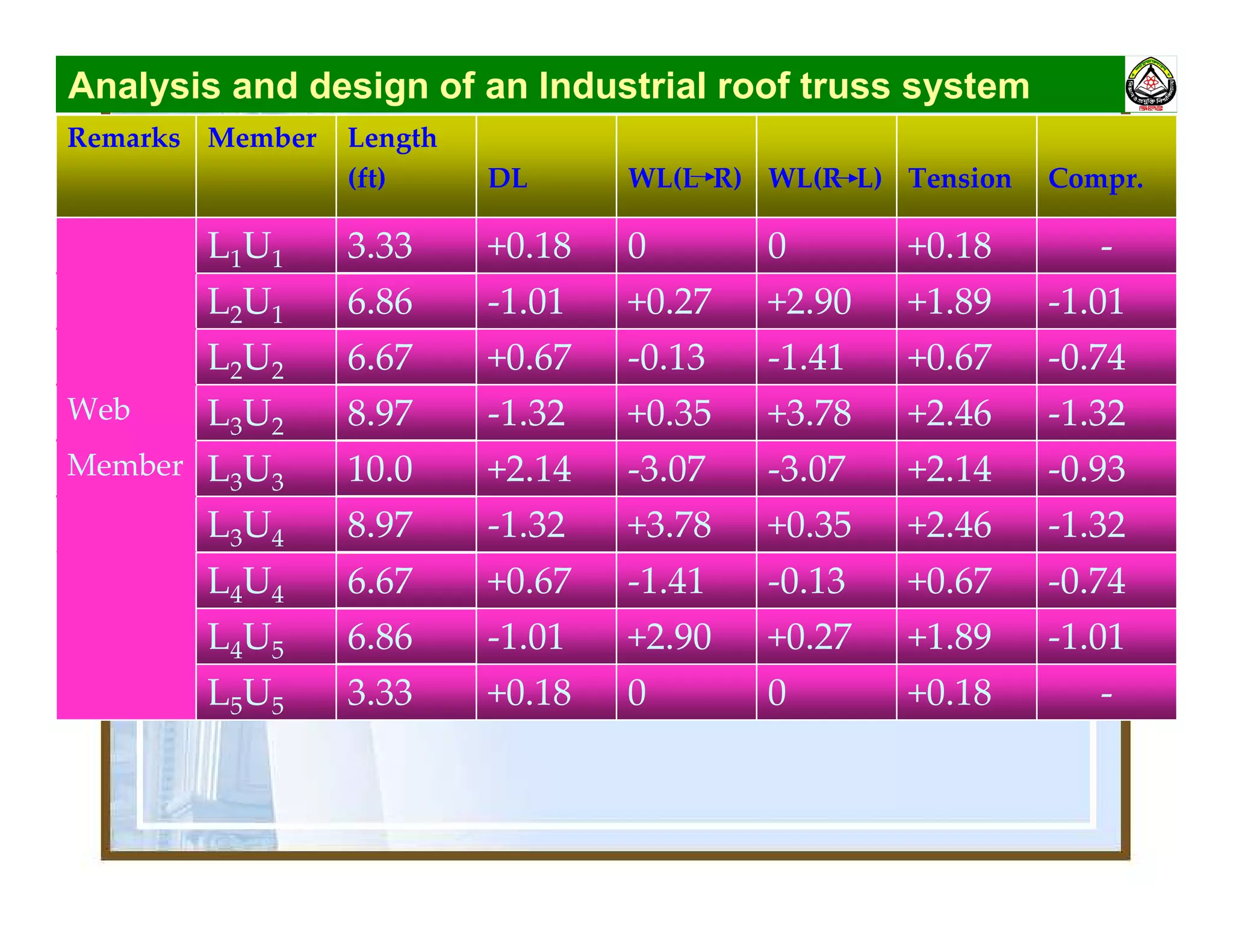
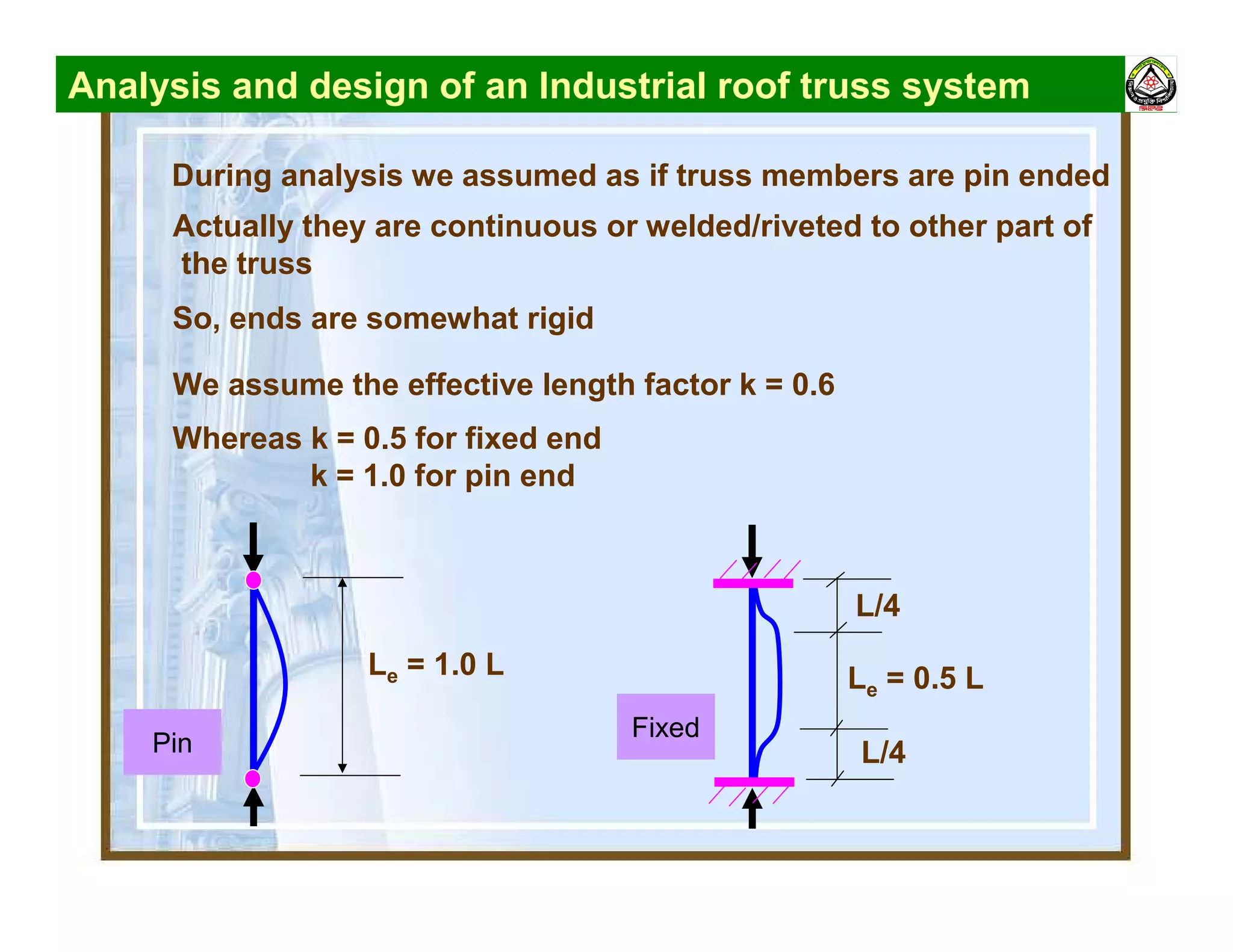
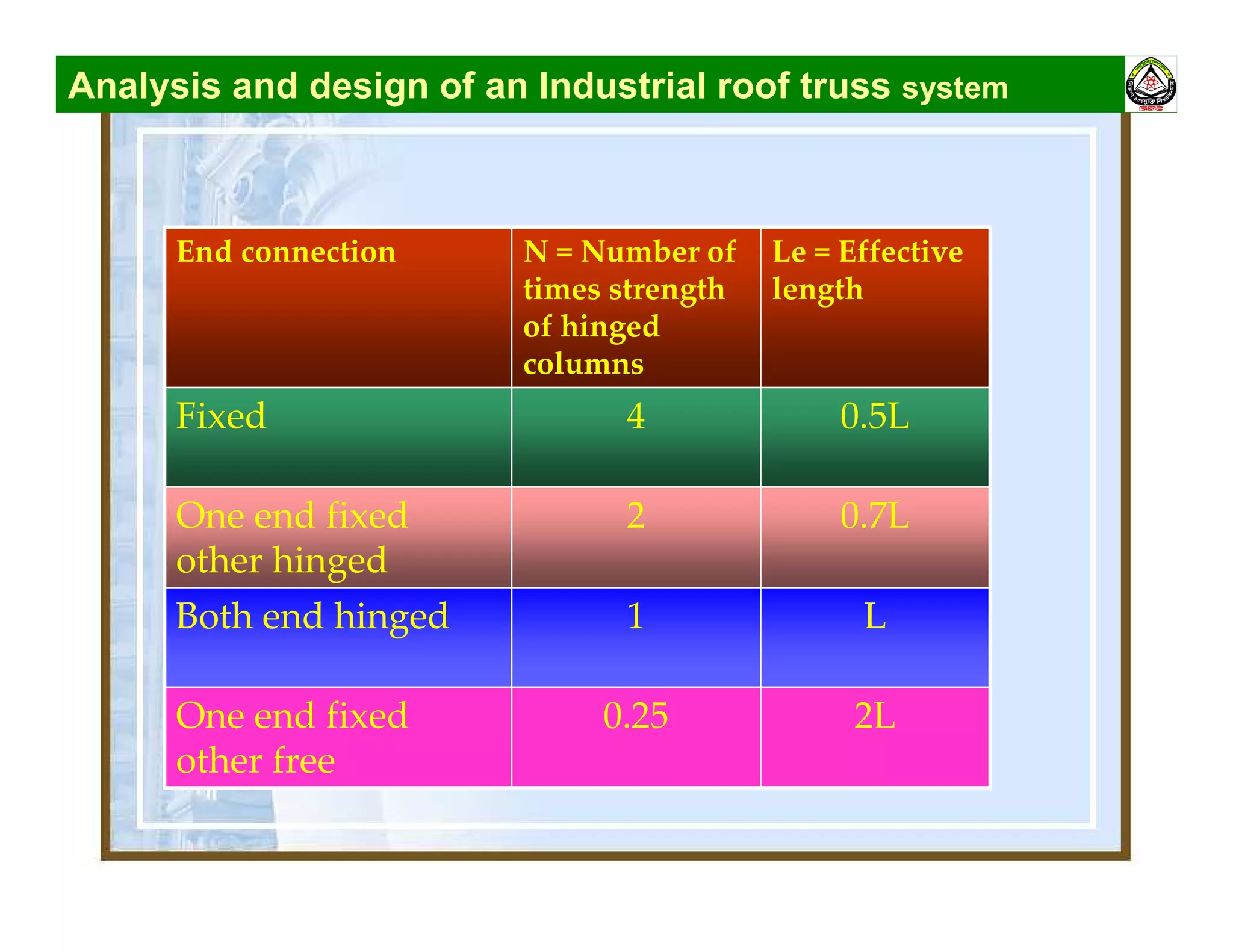
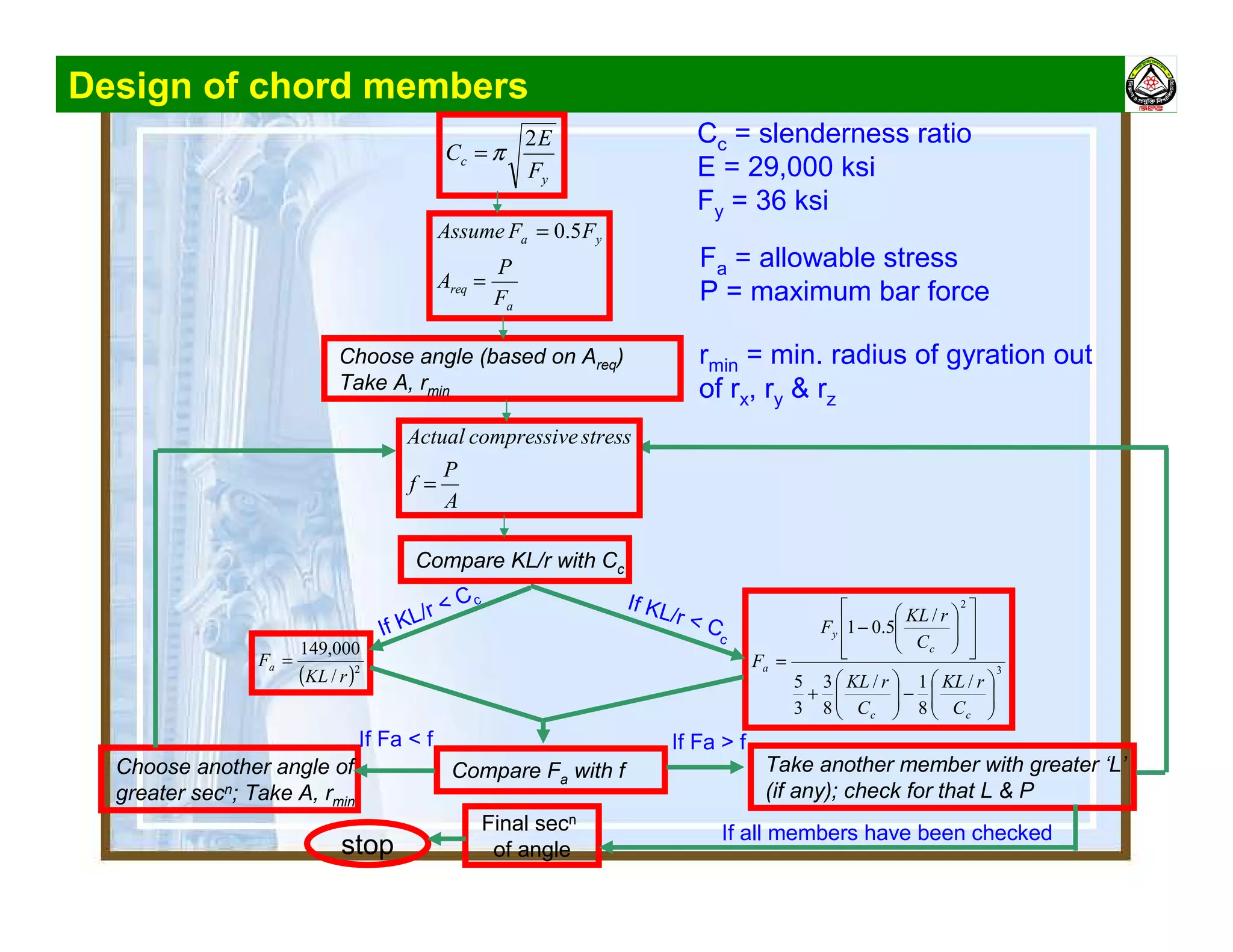
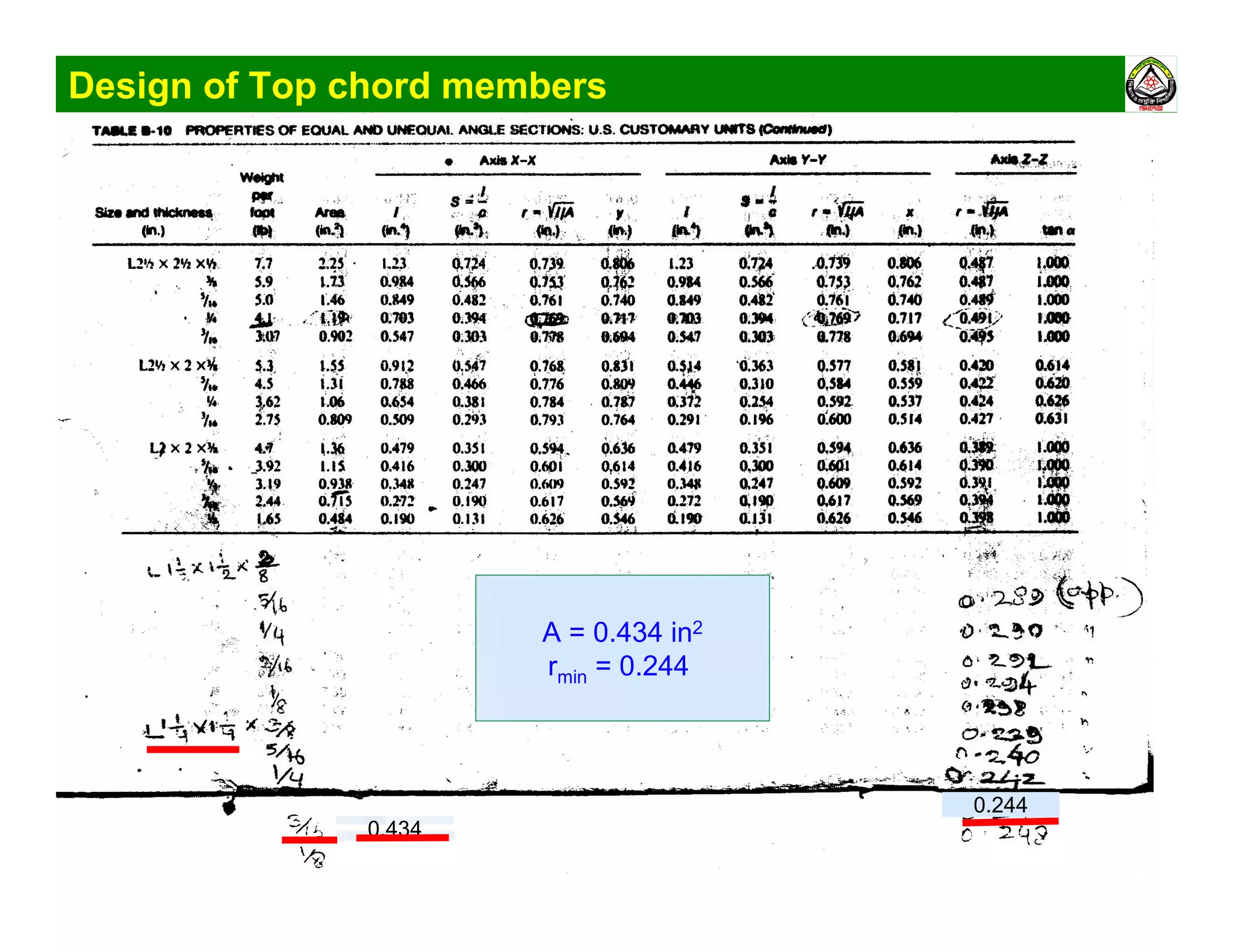
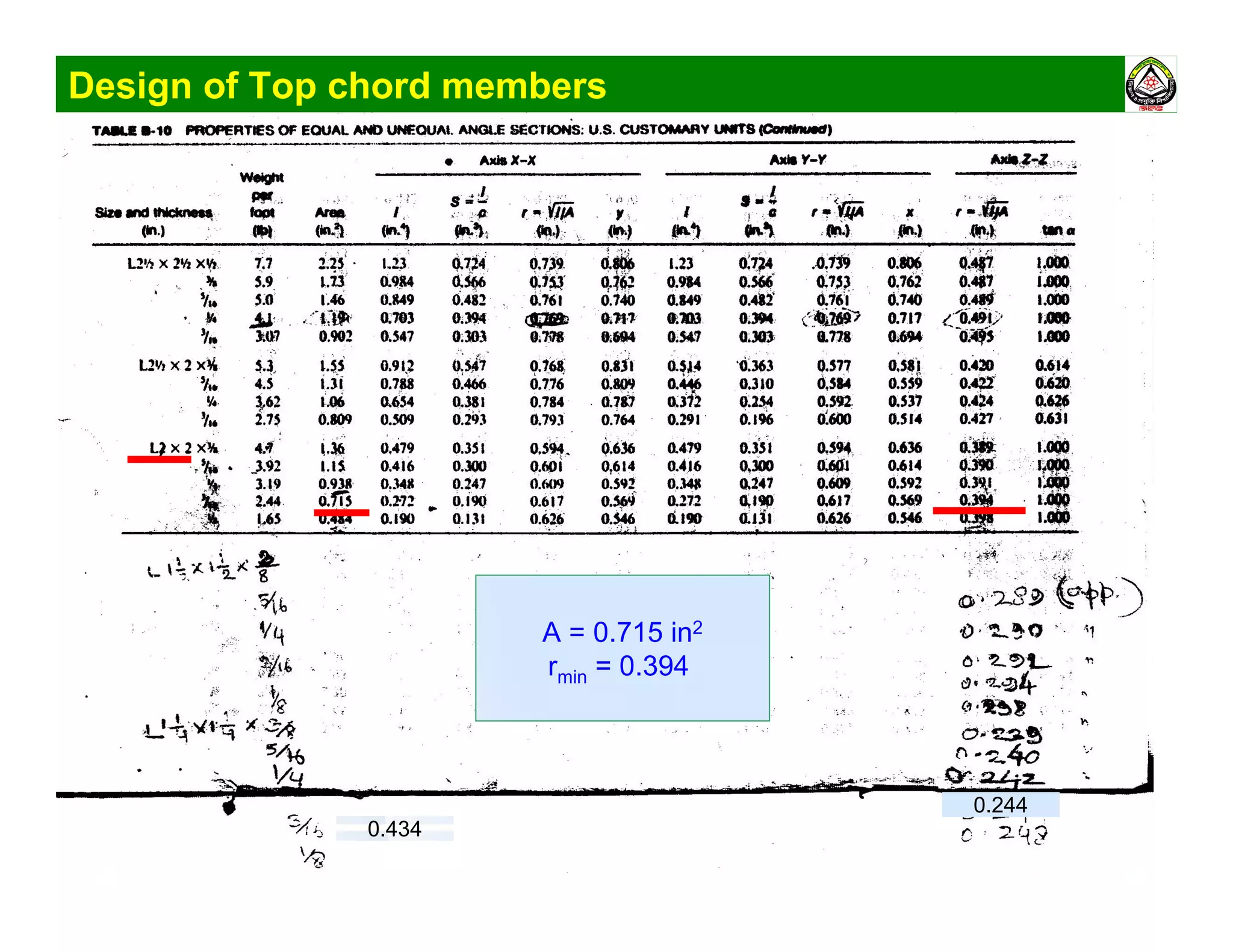
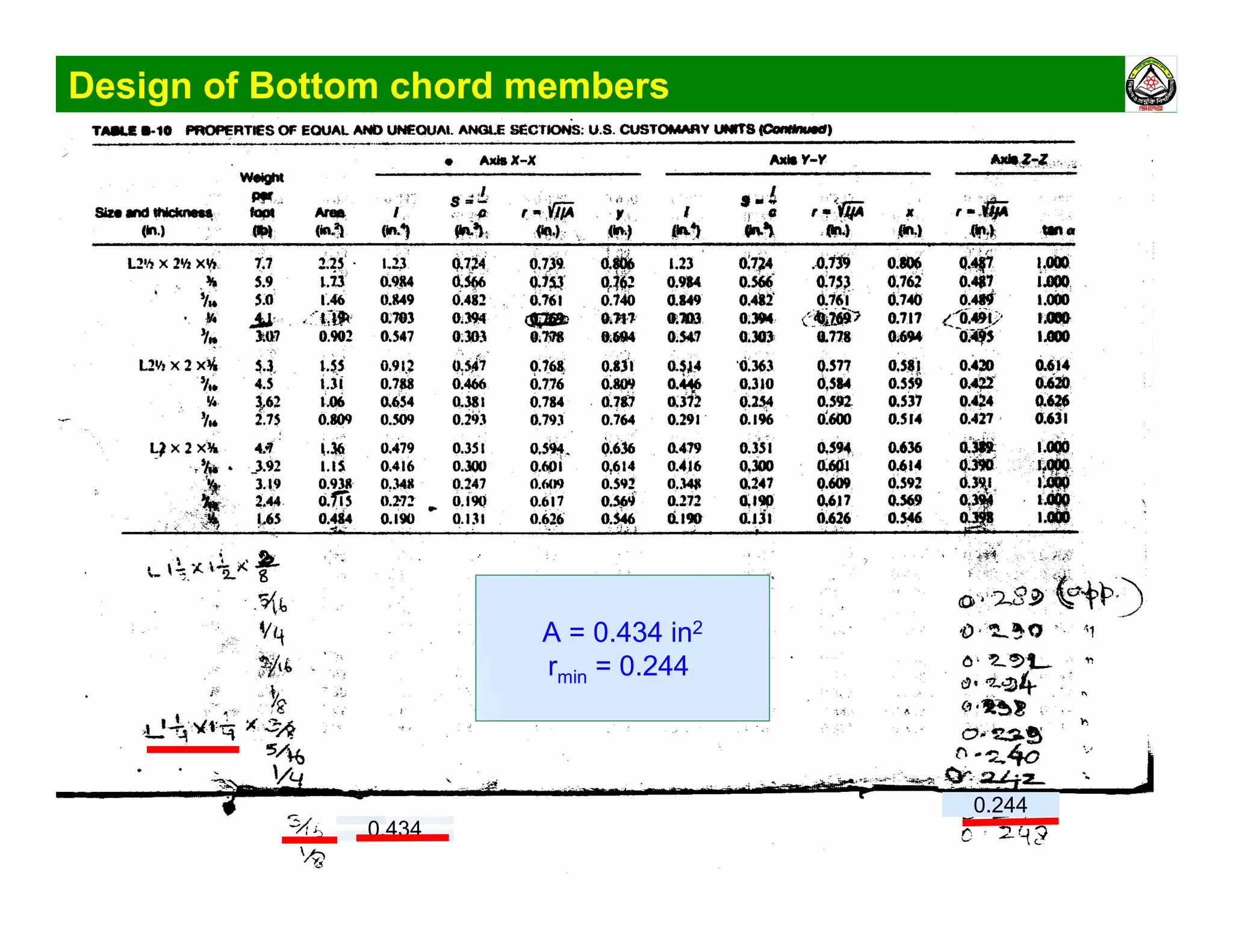
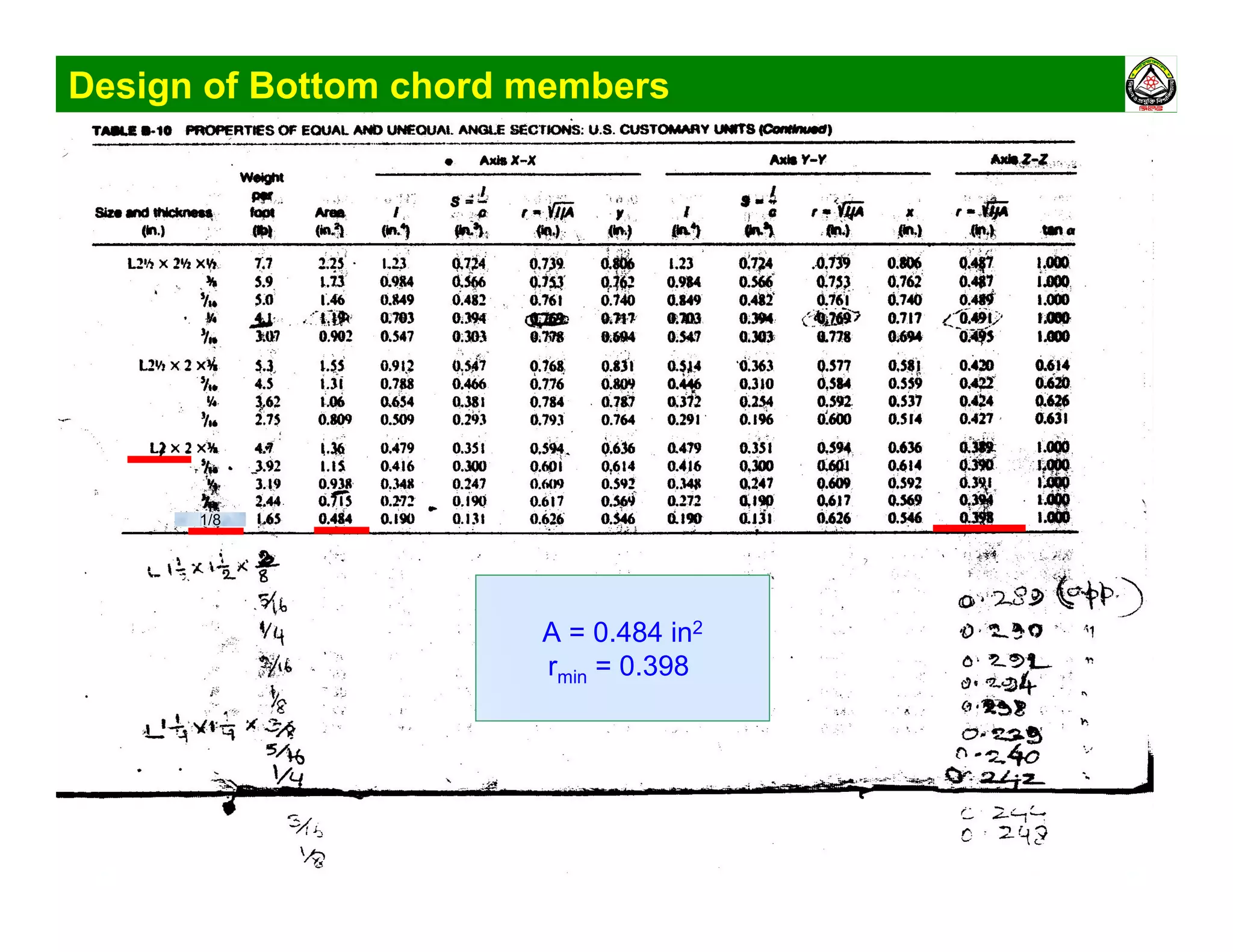
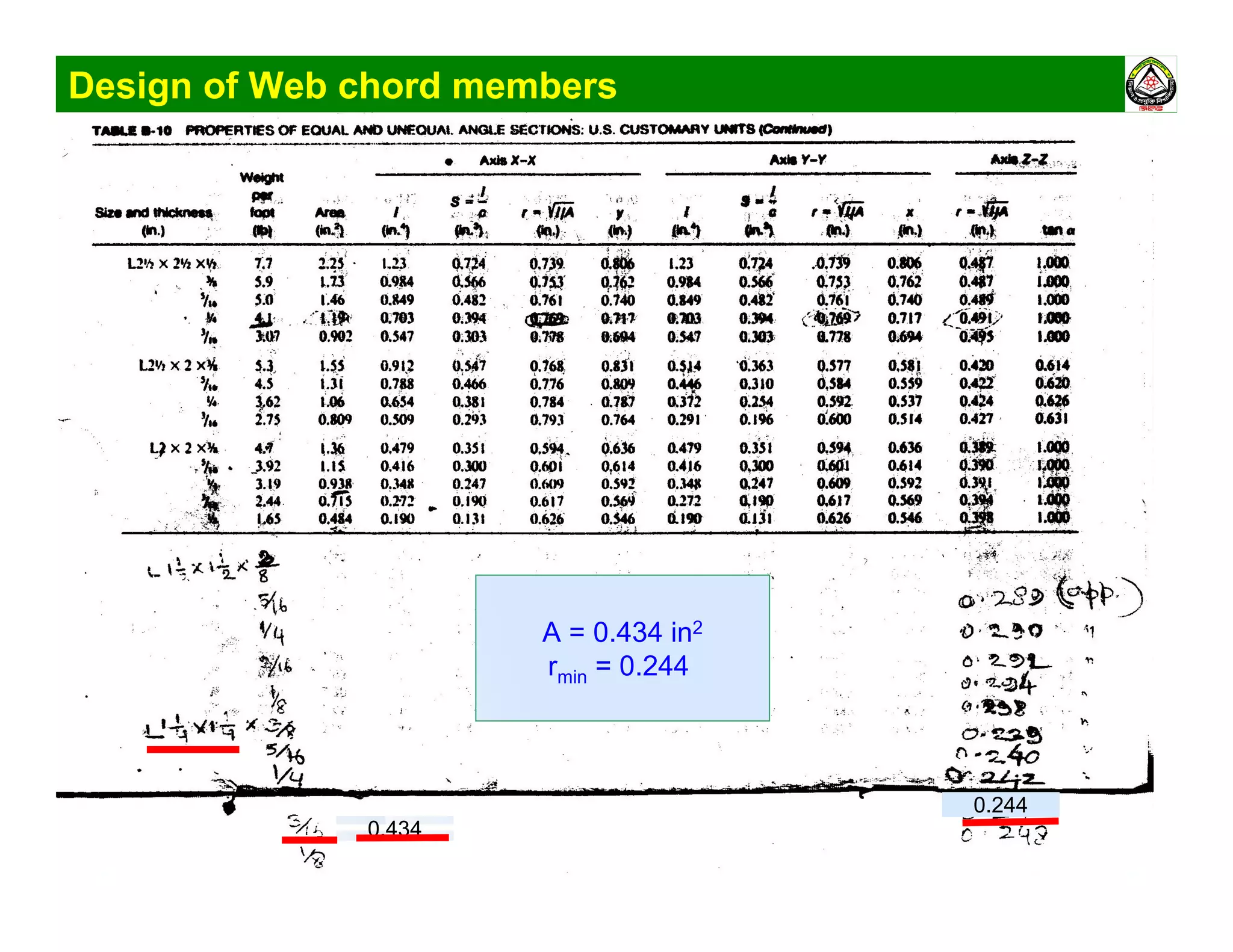
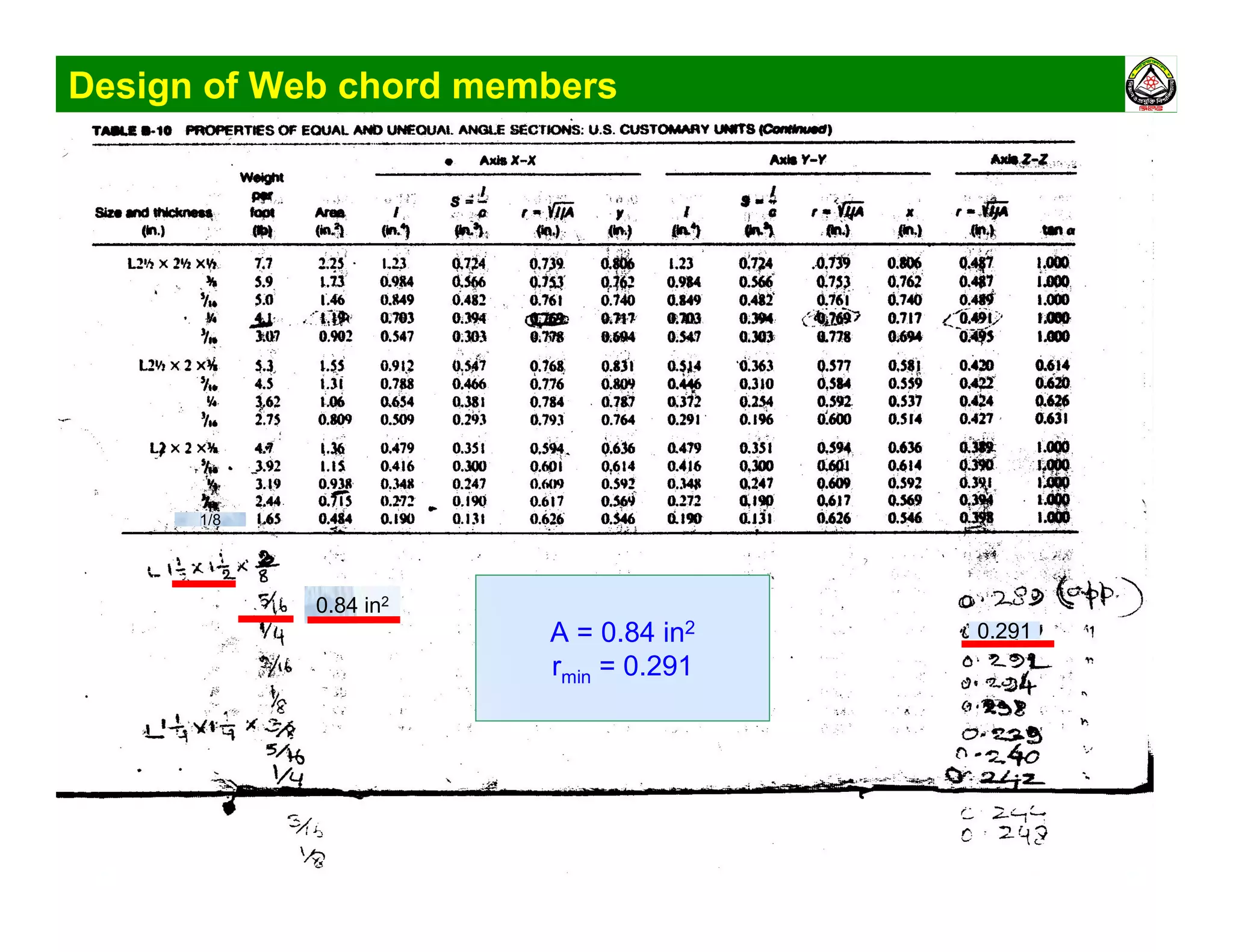
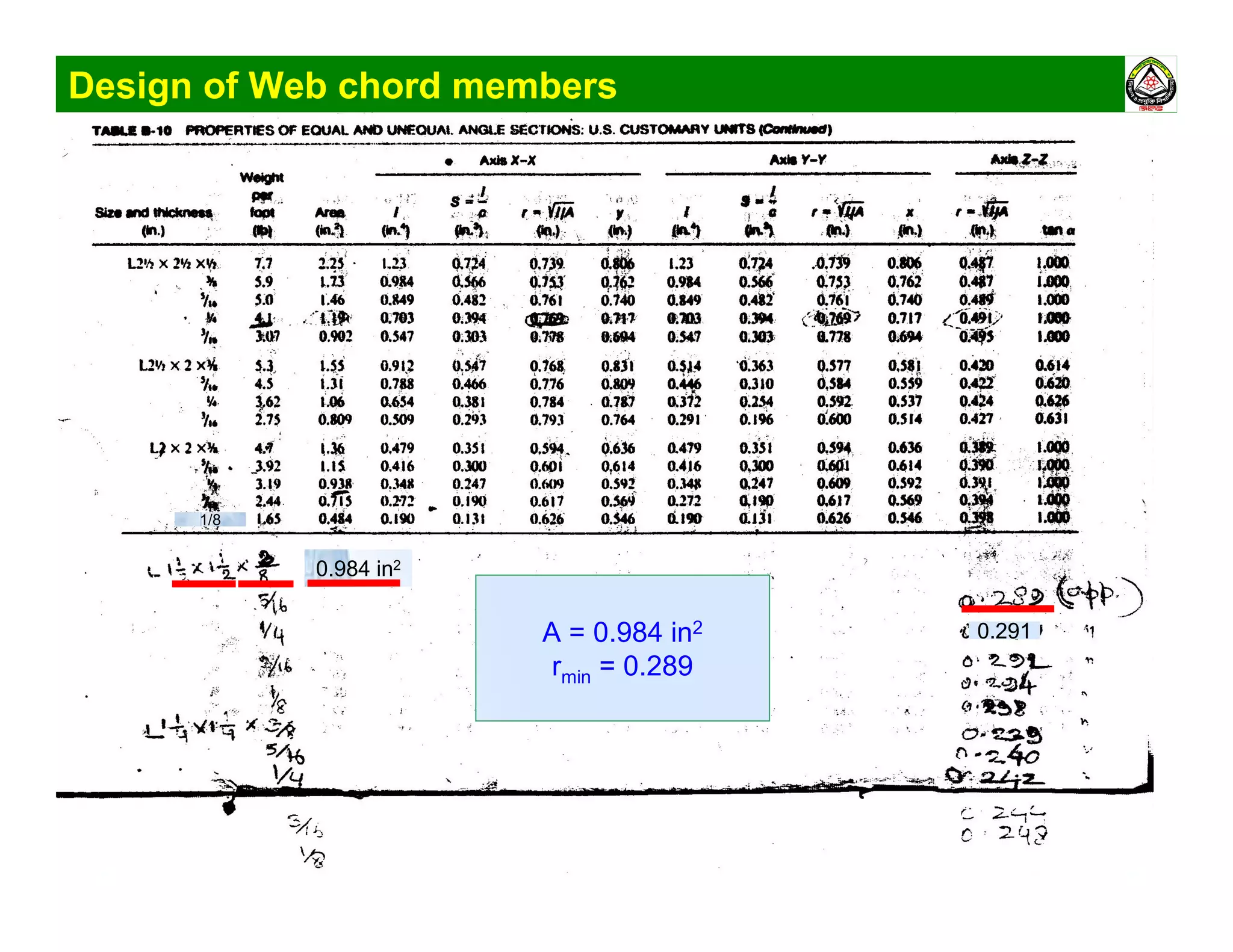
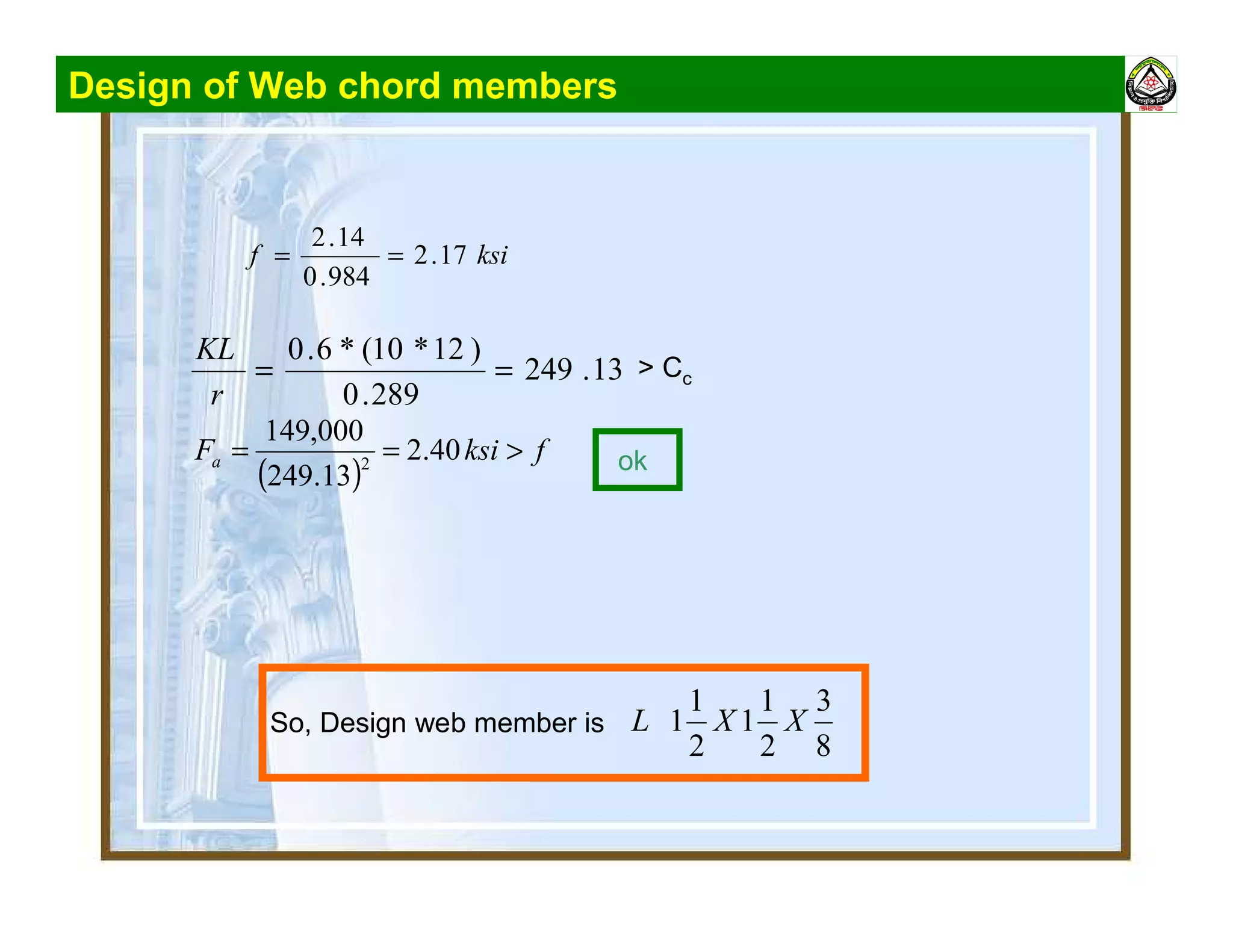
The document summarizes the structural analysis and design of an industrial roof truss system. It includes analysis of the truss under different load combinations, calculation of member forces, and design of the chord and web members. Key steps shown are determination of effective length factors, selection of member sections based on required area, and checking slenderness ratios and allowable stresses.

1. CEE-312
Structural Analysis and Design Sessional-I
(1.0 credit)
Lecture: 6
Bijit Kumar Banik
Assistant Professor, CEE, SUST
Room No.: 115 (“C” building)
bijit_sustbd@yahoo.com
Department of Civil and Environmental Engineering

2. Analysis and design of an Industrial roof truss system
R L
(- 8.88) (-8.88) (-6.35) (-4.19) (-4.43) (-4.43)
(7.14) (5.61) (4.07) (4.85) (5.00) (5.14)
6@6 ft = 36 ft
L0 L1 L2 L3 L4 L5
L6
U1
U2
U3
U4
U5
2.60 k4.54 k
(0)
(-0.13)
(-1.41)
(0)
(-3.07)
(3.78)
(2.90)
(0.35)
(0.27)
3.24k
L→R
6@6 ft = 36 ft
L0 L1 L2 L3 L4 L5
L6
U1
U2
U3
U4
U5
4.54 k2.60 k
(- 1.19) (-1.19) (-0.95) (-3.11) (-5.64) (-5.64)
(5.14) (5.00) (4.85) (4.07) (5.61) (7.14)
(0)
(-0.13)
(-1.41)
(0)
(-3.07)
(0.35)
(0.27)
(3.78)
(2.90)
3.24k
(4.41) (4.41) (3.53) (3.53) (4.41) (4.41)
(- 5.05) (- 4.04) (- 3.03) (- 3.03) (- 4.04) (- 5.05)
6@6 ft = 36 ft
L0 L1 L2 L3 L4 L5
L6
U1
U2
U3
U4
U5
2.94 k2.94 k
(.18)
(0.67)
(0.67)
(.18)
(2.14)
(-1.32)
(- 1.01)
(-1.32)
(- 1.01)
Dead Load

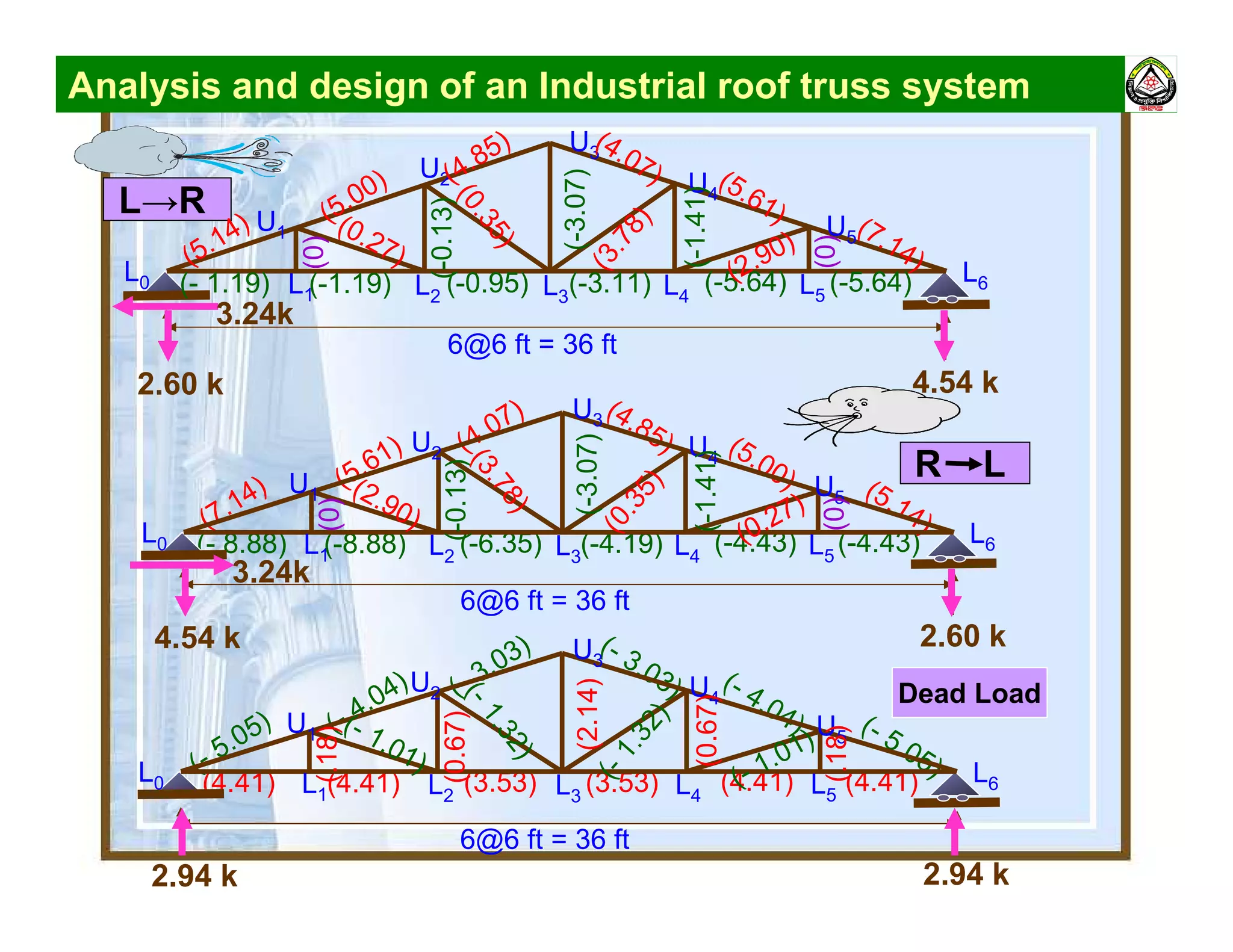
3. Analysis and design of an Industrial roof truss system
Load combinations
Condition 1: F1 = DL [No wind]
Condition 2: F2 = DL + WL (L→R)
Dead Load →DL
Wind Load →WL
Condition 3: F3 = DL + WL (R→L)
For design compressive force → Minimum of F1, F2 & F3 (If
positive leave it !)
For design tensile force → Maximum of F1, F2 & F3 (If
negative leave it !)

4. Analysis and design of an Industrial roof truss system
Compr.TensionWL(R L)WL(L R)DL
-1.23+4.41-4.43-5.64+4.41L5L6
-1.23+4.41-4.43-5.64+4.41L4L5
Member
-0.66+3.53-4.19-3.11+3.53L3L4
Chord
-2.82+3.53-6.35-0.95+3.536.00L2L3
Bottom
-4.47+4.41-8.88-1.19+4.41L1L2
-4.47+4.41-8.88-1.19+4.41L0L1
-5.05+2.09+5.14+7.14-5.05L6U5
-4.04+1.57+5.00+5.61-4.04U4U5
Member
-3.03+1.82+4.85+4.07-3.03U3U4
Chord
-3.03+1.82+4.07+4.85-3.036.86U2U3
Top
-4.04+1.57+5.61+5.00-4.04U1U2
-5.05+2.09+7.14+5.14-5.05L0U1
Design Member Force (k)Member Force (k)Length
(ft)
MemberRemarks

5. Analysis and design of an Industrial roof truss system
-1.32+2.46+0.35+3.78-1.328.97L3U4
-0.93+2.14-3.07-3.07+2.1410.0L3U3
Member
-1.32+2.46+3.78+0.35-1.328.97L3U2
Web
-0.74+0.67-1.41-0.13+0.676.67L2U2
-1.01+1.89+2.90+0.27-1.016.86L2U1
-+0.1800+0.183.33L1U1
Compr.TensionWL(R L)WL(L R)DL
Length
(ft)
MemberRemarks
-+0.1800+0.183.33L5U5
-1.01+1.89+0.27+2.90-1.016.86L4U5
-0.74+0.67-0.13-1.41+0.676.67L4U4

6. Analysis and design of an Industrial roof truss system
During analysis we assumed as if truss members are pin ended
Actually they are continuous or welded/riveted to other part of
the truss
So, ends are somewhat rigid
We assume the effective length factor k = 0.6
Whereas k = 0.5 for fixed end
k = 1.0 for pin end
Le = 1.0 L Le = 0.5 L
L/4
L/4Pin
Fixed

7. Analysis and design of an Industrial roof truss system
2L0.25One end fixed
other free
L1Both end hinged
0.7L2One end fixed
other hinged
0.5L4Fixed
Le = Effective
length
N = Number of
times strength
of hinged
columns
End connection

8. Design of chord members
y
c
F
E
C
2
π=
Cc = slenderness ratio
E = 29,000 ksi
Fy = 36 ksi
Fa = allowable stress
P = maximum bar force
Choose angle (based on Areq)
Take A, rmin
rmin = min. radius of gyration out
of rx, ry & rz
3
2
/
8
1/
8
3
3
5
/
5.01






−





+














−
=
cc
c
y
a
C
rKL
C
rKL
C
rKL
F
F
( )2
/
000,149
rKL
Fa =
If KL/r < CcIf KL/r < Cc
Compare Fa with f Take another member with greater ‘L’
(if any); check for that L & P
Choose another angle of
greater secn; Take A, rmin
If Fa < f If Fa > f
Final secn
of anglestop If all members have been checked
a
req
ya
F
P
A
FFAssume
=
= 5.0
A
P
f
stressecompressivActual
=
Compare KL/r with Cc

9. Design of Top chord members
Maximum compressive force found on L0U1 , having L = 6.86 ft ; P = 5.05 k
y
c
F
E
C
2
π=
36
000,29*2
π= 1.126=
Fa = 0.5Fy = 0.5*36 = 18 ksi
a
req
F
P
A =
18
05.5
= = 0.281 in2
From AISC chart, select
16
3
4
1
1
4
1
1 XXL

10. Design of Top chord members
0.244
0.434
A = 0.434 in2
rmin = 0.244

11. Design of Top chord members
ksif 64.11
434.0
05.5
==
4.202
244.0
)12*86.6(*6.0
==
r
KL
> Cc
From AISC chart, now select
16
3
22 XXL
( )
fksiFa <== 64.3
4.202
000,149
2 Not ok

12. Design of Top chord members
0.244
0.434
A = 0.715 in2
rmin = 0.394

13. Design of Top chord members
ksif 06.7
715.0
05.5
==
36.125
394.0
)12*86.6(*6.0
==
r
KL
< Cc
So, Design Top chord is
16
3
22 XXL
ok
3
2
/
8
1/
8
3
3
5
/
5.01






−





+














−
=
cc
c
y
a
C
rKL
C
rKL
C
rKL
F
F
3
2
1.126
36.125
8
1
1.126
36.125
8
3
3
5
1.126
36.125
5.0136






−





+














−
=
= 9.50 ksi > f

14. Design of Bottom chord members
Maximum compressive force found on L0L1 , having L = 6 ft ; P = 4.47 k
y
c
F
E
C
2
π=
36
000,29*2
π= 1.126=
Fa = 0.5Fy = 0.5*36 = 18 ksi
a
req
F
P
A =
18
47.4
= = 0.248 in2
From AISC chart, select
16
3
4
1
1
4
1
1 XXL

15. Design of Bottom chord members
0.244
0.434
A = 0.434 in2
rmin = 0.244

16. Design of Bottom chord members
ksif 3.10
434.0
47.4
==
05.177
244.0
)12*6(*6.0
==
r
KL
> Cc
From AISC chart, now select
8
1
22 XXL
( )
fksiFa <== 75.4
05.177
000,149
2 Not ok

17. Design of Bottom chord members
A = 0.484 in2
rmin = 0.398
1/8

18. Design of Bottom chord members
ksif 24.9
484.0
47.4
==
54.108
398.0
)12*6(*6.0
==
r
KL
< Cc
So, Design Bottom chord is
8
1
22 XXL
ok
3
2
/
8
1/
8
3
3
5
/
5.01






−





+














−
=
cc
c
y
a
C
rKL
C
rKL
C
rKL
F
F
3
2
1.126
54.108
8
1
1.126
54.108
8
3
3
5
1.126
54.108
5.0136






−





+














−
=
= 11.88 ksi > f

19. Design of Web members
Maximum tensile force found on U2L3 , having L = 8.97 ft ; P = 2.46 k
y
c
F
E
C
2
π=
36
000,29*2
π= 1.126=
Fa = 0.5Fy = 0.5*36 = 18 ksi
a
req
F
P
A =
18
46.2
= = 0.137 in2
From AISC chart, select
16
3
4
1
1
4
1
1 XXL

20. Design of Web chord members
0.244
0.434
A = 0.434 in2
rmin = 0.244

21. Design of Web chord members
ksif 67.5
434.0
46.2
==
69.264
244.0
)12*97.8(*6.0
==
r
KL
> Cc
From AISC chart, now select
16
5
2
1
1
2
1
1 XXL
( )
fksiFa <== 13.2
69.264
000,149
2 Not ok

22. Design of Web chord members
A = 0.84 in2
rmin = 0.291
1/8
0.291
0.84 in2

23. Design of Web chord members
ksif 93.2
84.0
46.2
==
94.221
291.0
)12*97.8(*6.0
==
r
KL
> Cc
ok
( )
fksiFa >== 02.3
94.221
000,149
2
But we have a member U3L3 of length 10 ft with P = 2.14 k
Now check the section for this member
ksif 55.2
84.0
14.2
==
42.247
291.0
)12*10(*6.0
==
r
KL
> Cc
( )
fksiFa <== 43.2
42.247
000,149
2 Not ok

24. Design of Web chord members
A = 0.984 in2
rmin = 0.289
1/8
0.291
0.984 in2

25. Design of Web chord members
ksif 17.2
984.0
14.2
==
13.249
289.0
)12*10(*6.0
==
r
KL
> Cc
( )
fksiFa >== 40.2
13.249
000,149
2 ok
So, Design web member is
8
3
2
1
1
2
1
1 XXL

26. Design summery of members
Design web member
8
3
2
1
1
2
1
1 XXL
Design Bottom chord member
8
1
22 XXL
Design Top chord member
16
3
22 XXL