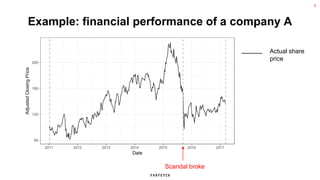
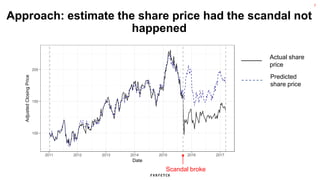
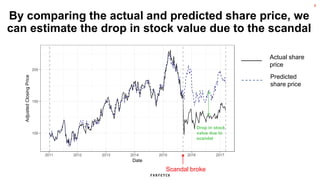
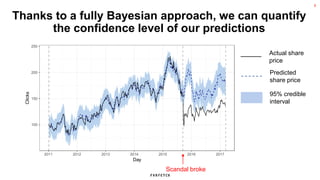
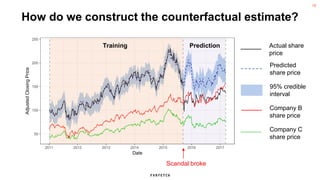
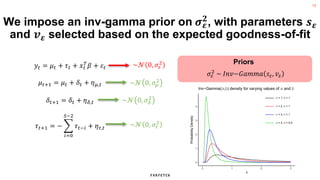
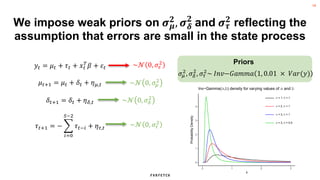
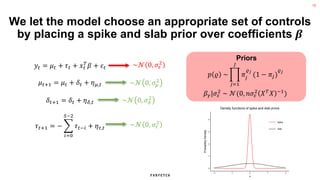
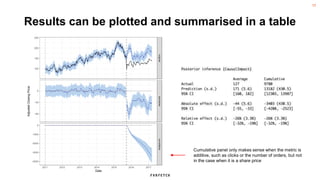
The document discusses the methodology for estimating causal effects in marketing, particularly when traditional A/B testing is unfeasible. It outlines a Bayesian structural time series model to analyze the impact of events, illustrated by an example involving stock price predictions following a scandal. The process includes specifications for model parameters and emphasizes the importance of proper covariate selection and validation techniques.