The document contains calculations of areas and volumes for various geometric shapes using integrals. These include: 1) The area of a cardioid curve defined by r = a(1 - cosθ). 2) The area between the circles defined by r = acosθ and r = bsenθ, where b > a. 3) The area of the Bernoulli lemniscate defined by r^2 = a^2cos^2θ. 4) Calculations also include volumes of spheres, solids of revolution, and regions bounded by cylinders.

1. a) Calcular el área del cardiode: 𝑟 = 𝑎(1 − 𝑐𝑜𝑠𝜃). Representar
gráficamente.
Trabajamos en y positivo
𝐴𝑅𝐸𝐴 = ∬ 𝑑𝐴
𝐷
𝑅 = {(𝑟, 𝜃) / 0 ≤ 𝜃 ≤ 𝜋 , 0 ≤ 𝑟 ≤ 𝑎(1 − 𝑐𝑜𝑠𝜃)}
𝐴𝑅𝐸𝐴 = 2 ∫ ∫ 𝑟𝑑𝑟𝑑𝜃
𝑎(1−𝑐𝑜𝑠𝜃)
0
𝜋
0

2. 𝐴𝑅𝐸𝐴 = 2 ∫ [
𝑟2
2
]
𝑎(1 − 𝑐𝑜𝑠𝜃)
0
𝜋
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 2 ∫ 𝑎2
𝜋
0
(1 − 𝑐𝑜𝑠𝜃)2
2
𝑑𝜃
𝐴𝑅𝐸𝐴 =
2𝑎2
2
∫(1 − 𝑐𝑜𝑠𝜃)2
𝜋
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 𝑎2
∫ 1 − 2𝑐𝑜𝑠𝜃 + 𝑐𝑜𝑠2
𝜃
𝜋
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 𝑎2
∫ 1 − 2𝑐𝑜𝑠𝜃 +
1
2
+
𝑐𝑜𝑠2𝜃
2
𝜋
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 𝑎2
[
3
2
𝜃 − 2𝑠𝑒𝑛𝜃 +
𝑠𝑒𝑛2𝜃
4
]
𝜋
0
𝐴𝑅𝐸𝐴 = 𝑎2
[
3
2
𝜋 − 0 + 0 − 0 − 0 + 0]
𝐴𝑅𝐸𝐴 =
3𝜋𝑎2
2
b) Calcular el área comprendida entre los círculos: 𝑟 = 𝑎𝑐𝑜𝑠𝜃; 𝑟 =
𝑏𝑠𝑒𝑛𝜃 𝑐𝑜𝑛 𝑏 > 𝑎.
c) Calcular el área de la lemniscata de Bernoulli 𝑟2
= 𝑎2
𝑐𝑜𝑠2𝜃.

3. 𝐴𝑅𝐸𝐴 = ∬ 𝑑𝐴
𝐷
𝑅 = {(𝑟, 𝜃)/ 0 ≤ 𝜃 ≤
𝜋
4
, 0 ≤ 𝑟 ≤ 𝑎√𝑐𝑜𝑠2𝜃}
𝐴𝑅𝐸𝐴 = 4 ∫ ∫ 𝑟𝑑𝑟𝑑𝜃
𝑎√𝑐𝑜𝑠2𝜃
0
𝜋
4
0
𝐴𝑅𝐸𝐴 = 4 ∫ [
𝑟2
2
]
𝑎√𝑐𝑜𝑠2𝜃
0
𝜋
4
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 2 ∫[𝑎√𝑐𝑜𝑠2𝜃]
2
𝜋
4
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 2𝑎2
∫ 𝑐𝑜𝑠2𝜃
𝜋
4
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 2𝑎2
[
𝑠𝑒𝑛2𝜃
2
]
𝜋
4
0
𝐴𝑅𝐸𝐴 = 𝑎2
d) Calcular el área interior a la curva 𝑟 = 2𝑠𝑒𝑛3𝜃 y exterior a 𝑟 = 1 en el
primer cuadrante.

4. 𝐴𝑅𝐸𝐴 = ∬ 𝑑𝐴
𝐷
𝑅 = {(𝑟, 𝜃)/ 0 ≤ 𝜃 ≤
𝜋
3
, 0 ≤ 𝑟 ≤ 2𝑠𝑒𝑛3𝜃}
𝐴𝑅𝐸𝐴 = ∫ ∫ 𝑟𝑑𝑟𝑑𝜃
2𝑠𝑒𝑛3𝜃
0
𝜋
3
0
𝐴𝑅𝐸𝐴 = ∫ [
𝑟2
2
]
2𝑠𝑒𝑛3𝜃
0
𝜋
3
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = ∫ [
(2𝑠𝑒𝑛3𝜃)2
2
]
𝜋
3
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = ∫ 2𝑠𝑒𝑛2
3𝜃
𝜋
3
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 2 ∫
1
2
−
𝑐𝑜𝑠6𝜃
2
𝜋
3
0
𝑑𝜃
𝐴𝑅𝐸𝐴 = 2 [
𝜃
2
−
𝑠𝑒𝑛6𝜃
12
]
𝜋
3
0
𝐴𝑅𝐸𝐴 =
2𝜋
6
=
𝜋
3

5. e) Calcular el volumen de la esfera de ecuación: 𝑥2
+ 𝑦2
+ 𝑧2
= 𝑎2
.
a
a

6. 𝑉𝑂𝐿𝑈𝑀𝐸𝑁 = ∬ 𝑑𝐴
𝐷
𝑅 = {(𝑟, 𝜃)/ 0 ≤ 𝜃 ≤ 2𝜋 , 0 ≤ 𝑟 ≤ 𝑎}
𝑥2
+ 𝑦2
+ 𝑧2
= 𝑎2
𝑧 = √𝑎2 − 𝑥2 − 𝑦2 = √𝑎2 − 𝑟2
𝑉 = 2 ∫ ∫ √𝑎2 − 𝑟2𝑟𝑑𝑟𝑑𝜃
𝑎
0
𝑐𝑎𝑚𝑏𝑖𝑜 𝑑𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 {𝑢 = 𝑎2
− 𝑟2
𝑑𝑢 = −2𝑟𝑑𝑟
2𝜋
0
𝑉 = 2 ∫ [
√𝑢
−2
]
𝑎
0
𝑑𝑢
2𝜋
0
𝑑𝜃
𝑉 = − ∫ [
2𝑢
3
2
3
]
𝑎
0
2𝜋
0
𝑑𝜃 = − ∫ [
2(𝑎2
− 𝑟2)
3
2
3
]
𝑎
0
2𝜋
0
𝑑𝜃
𝑉 = −
2
3
∫ [(𝑎2
− 𝑟2
)
3
2 ]
𝑎
0
2𝜋
0
𝑑𝜃
𝑉 = −
2
3
∫ 0 − 𝑎3
2𝜋
0
𝑑𝜃
𝑉 =
2
3
𝑎3
[𝜃]
2𝜋
0
𝑉 =
2
3
𝑎3
2𝜋
𝑉 =
4𝜋
3
𝑎3
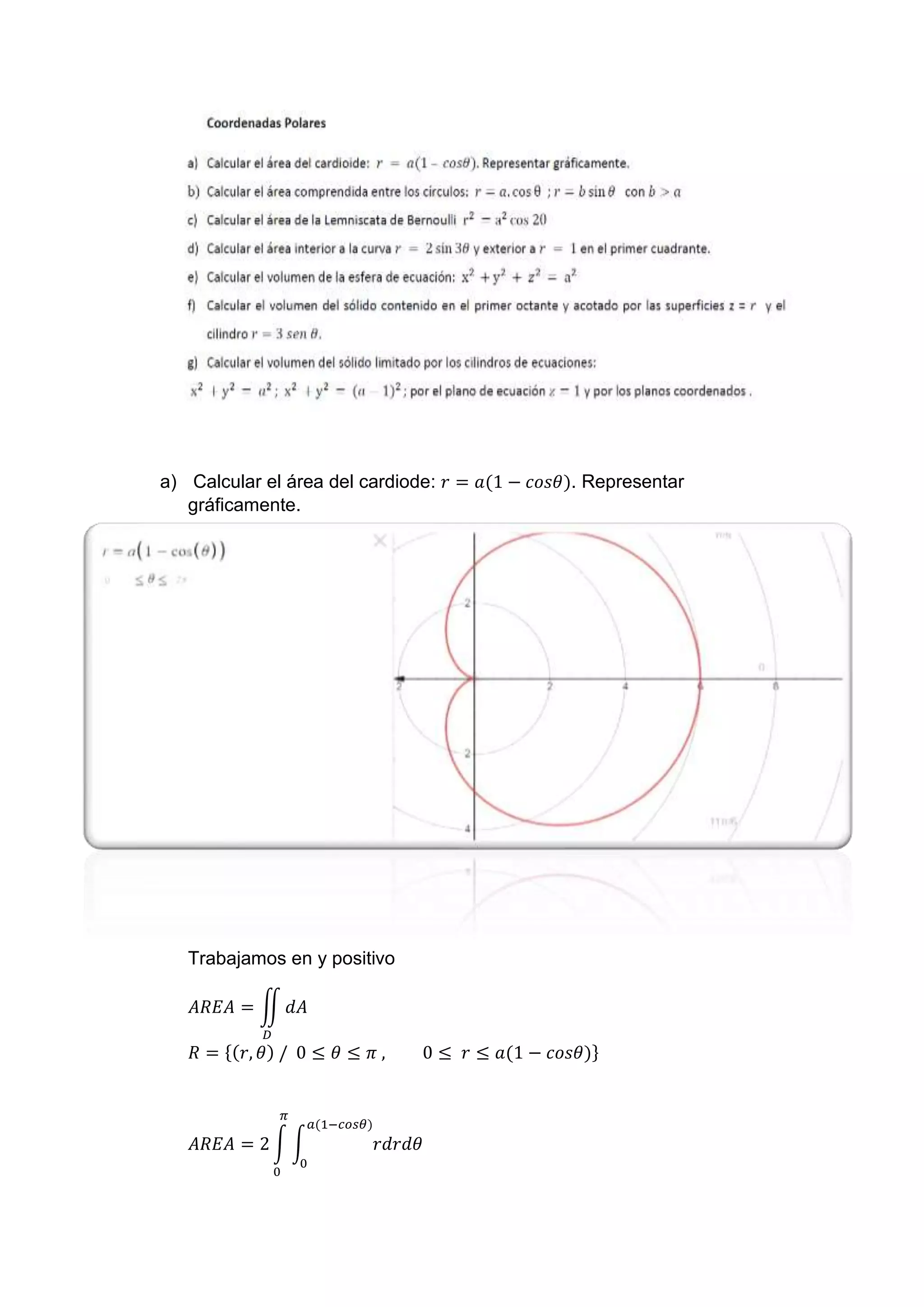
f) Calcular el volumen del solido contenido en el primer octante y acotado
por las superficies 𝑧 = 𝑟 y el cilindro 𝑟 = 3𝑠𝑒𝑛𝜃.

7. 𝑉𝑂𝐿𝑈𝑀𝐸𝑁 = ∬ 𝑑𝐴
𝐷
𝑅 = {(𝑟, 𝜃)/ 0 ≤ 𝜃 ≤
𝜋
2
, 0 ≤ 𝑟 ≤ 3𝑠𝑒𝑛𝜃}
𝑧 = 𝑟 y el cilindro 𝑟 = 3𝑠𝑒𝑛𝜃.

8. 𝑉 = ∫ ∫ (𝑟 − 0)𝑟𝑑𝑟𝑑𝜃
3𝑠𝑒𝑛𝜃
0
𝜋/2
0
𝑉 = ∫ ∫ (𝑟 − 0)𝑟𝑑𝑟𝑑𝜃
3𝑠𝑒𝑛𝜃
0
𝜋/2
0
𝑉 = ∫ ∫ 𝑟2
𝑑𝑟𝑑𝜃
3𝑠𝑒𝑛𝜃
0
𝜋/2
0
𝑉 = ∫
27𝑠𝑒𝑛3
𝜃
3
𝑑𝜃
𝜋/2
0
𝑉 = 9 ∫ 𝑠𝑒𝑛𝜃(1 − 𝑐𝑜𝑠2
𝜃)𝑑𝜃
𝜋/2
0
𝑉 = 9 ∫ (𝑠𝑒𝑛𝜃 − 𝑠𝑒𝑛𝜃𝑐𝑜𝑠2
𝜃)𝑑𝜃 𝑐𝑎𝑚𝑏𝑖𝑜 𝑑𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 {
𝑢 = 𝑐𝑜𝑠𝜃
𝑑𝑢 = −𝑠𝑒𝑛𝜃
𝜋/2
0
𝑉 = 9 ∫ 𝑠𝑒𝑛𝜃𝑑𝜃 − 9 ∫ 𝑠𝑒𝑛𝜃𝑐𝑜𝑠2
𝜃
𝜋/2
0
𝑑𝜃
𝜋/2
0
𝑉 = 9 ∫ 𝑠𝑒𝑛𝜃𝑑𝜃 + 9 ∫ 𝑢2
𝜋/2
0
𝑑𝜃
𝜋/2
0
𝑉 = 9 [ −cos𝜃 +
𝑐𝑜𝑠3
𝜃
3
]
𝜋
2
0
𝑉 = 9 (0 + 0 + 1 −
1
3
)
𝑉 = 6𝑢3
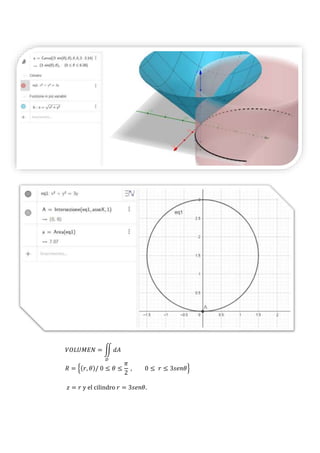
g) Calcular el volumen del solido limitado por los cilindros de ecuaciones:
𝑥2
+ 𝑦2
= 𝑎2
; 𝑥2
+ 𝑦2
= (𝑎 − 1)2
; por el plano 𝑧 = 1 y por los planos
coordenados.

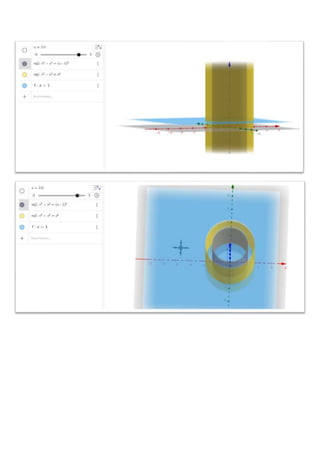
10. 𝑉𝑂𝐿𝑈𝑀𝐸𝑁 = ∬ 𝑑𝐴
𝐷
𝑅 = {(𝑟, 𝜃)/ 0 ≤ 𝜃 ≤ 2𝜋 , 𝑎 − 1 ≤ 𝑟 ≤ 𝑎}
𝑥2
+ 𝑦2
= 𝑎2
; 𝑥2
+ 𝑦2
= (𝑎 − 1)2
; por el plano 𝑧 = 1 y z=0
𝑉 = ∫ ∫ (1 − 0)𝑟𝑑𝑟𝑑𝜃
𝑎
𝑎−1
2𝜋
0
𝑉 =
1
2
∫ [𝑟2
]
𝑎
𝑎 − 1
𝑑𝜃
2𝜋
0
𝑉 =
1
2
∫ 𝑎2
−(𝑎 − 1)2
𝑑𝜃
2𝜋
0
𝑉 =
1
2
(𝑎2
−(𝑎 − 1)2) [𝜃]
𝜋
2
0
𝑉 =
2𝜋
2
(𝑎2
−(𝑎 − 1)2
)
𝑉 = 𝜋(𝑎2
−(𝑎 − 1)2
)
𝑉 = 𝜋(2𝑎 − 1)