BOAC - Intelligent reasoning

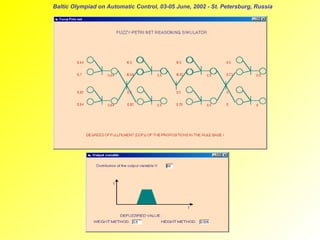
Baltic Olympiad on Automatic Control, 03-05 June, 2002 - St. Petersburg, Russia

Republic of Macedonia
Military Academy - Skopje

EXPERT DECISION AND CONTROL:
FUZZY-PETRI NET REASONING SIMULATOR (FUPERS)

Zoran M.Gacovski

Stojce Deskovski
Georgi Dimirovski



1. Introduction
2. Fuzzy production systems
3. Petri-net model of fuzzy production system
4. Fuzzy-Petri net reasoning components
5. Reasoning algorithm
6. Fupers software tool
7. Conclusions and application


1. INTRODUCTION
1. INTRODUCTION
- Intelligent Control = multi-level structure obeying the Principle of Increasing Precision
with Decreasing Intelligence (original theory of G. N. Saridis ).
- Probabilistic models = uncertainty of reasoning, planning decision making at the
organization level, assignment of tasks at the coordination level, and control activities at
the execution level.
- The Intelligent Machine uses entropies as measures of the execution of various
commands and they serve for the optimal decision-making. reformulation of the
organizing controller as a fuzzy-Petri net production system.
- Petri net (PN) formalism = great power for representation and modeling of parallel and
concurrent processes + modeling fuzzy-rule based systems directly.
- Some of the elements (marking function) and features (places and transitions) of Petri’s
formalism correspond to elements of a fuzzy knowledge base (KB) (propositions, degree
of truth and implication relationships).
- Formal separation between the representational scheme (the FPN itself) and the
associated dynamic process (data driven evaluation algorithm), is established using
elements defined in the formalism.
- We propose more adequate handling of multi-propositional rules. The degree of truth
of the rules is still a numerical value, and the chaining is still done at the value level and
thus the drawbacks are still present.


2. FUZZY PRODUCTION SYSTEMS
2. FUZZY PRODUCTION SYSTEMS
Rr: IF X1r IS A1r AND ... AND XMrr IS AMrr THEN
XMr+1r IS B1r AND ... AND XMr+Nrr IS BNrr , (τr),

(1)

Amrr = { amrr,i }, r=1,...,R, mr =1,...,Mr , i=1,...,I

(2)

Bmr r = { bmrr,i }, r=1,...,R, mr =1,...,Mr , i=1,...,I

(3)

"Xmrr IS Amrr ", => DOFmrr = V amrr,i / amrr,i

(4)

Degree of fulfilment for rule r:
DOF r = / DOF rmr, r=1,...,R

(5)

Possibility distribution for XMr+Nrr :
bnr,ir = τr (DOF r / bnr,ir ), nr=1,...,Nr, i=1,...,I

(6)

Aggregation:
/ bnr,i r , nr=1,...,Nr, i=1,...,I

(7)


Linguistic variables: low(t) = 1 - ( t / 10 ); high(t) = t / 10

rule 1: if x is low and y is low then z is high
rule 2: if x is low and y is high then z is low

LOW

HIGH

rule 3: if x is high and y is low then z is low
rule 4: if x is high and y is high then z is high

0

10

- In the fuzzification sub-process, the membership functions defined on the input
variables are applied to their actual values, to determine the degree of truth for each rule
premise.
- In the inference sub-process, the truth-value for the premise of each rule is computed,
and applied to the conclusion part of each rule.
- In MIN inference, the output membership function is clipped off at a height
corresponding to the rule premise's computed degree of truth. In PRODUCT inference,
the output membership function is scaled by the rule premise's computed degree of truth.
- In MAX composition, the combined output fuzzy subset is constructed by taking the
point wise maximum over all of the fuzzy subsets assigned to the output variable by the
inference rule. In SUM composition, the combined output fuzzy subset is constructed by
taking the point wise sum over all of the fuzzy subsets assigned to the output variable by
the inference rule.


Inputs: x=0, y=3.2
MIN - INFERENCE :
rule1(z) = { z / 10, if z <= 6.8;

0.68, if z >= 6.8};

rule3(z) = 0.0

rule2(z) = { 0.32, if z <= 6.8;

1 - z / 10, if z >= 6.8}; rule4(z) = 0.0

MAX - COMPOSITION :
fuzzy(z) = { 0.32, if z <= 3.2 ;

α(x)=1

α(y)=0.68

z / 10, if 3.2 <= z <= 6.8 ;
Rule1(z)
6.8

α(x)=1

α(y)=0.32

0.68, if z >= 6.8 }

Rule2(z)

0.68

Comp(z)

Defuzz.(aver. of MAX)= 8.4

Fig. 1 – MIN inference / MAX composition for the given example.


Inputs: x=0, y=3.2
PRODUCT - INFERENCE :
rule1(z) = 0.068 * z; rule2(z) = 0.32 - 0.032 * z; rule3(z) = 0.0; rule4(z) = 0.0
SUM - COMPOSITION :
fuzzy(z) = 0.32 + 0.036 * z

α(x)=1

α(y)=0.68

Rule1(z)

10

α(x)=1

α(y)=0.32

Rule2(z)

0.68

Comp(z)

Defuzz.(centroid)= 5.6

Fig. 2 – PRODUCT inference / SUM composition for the given example.


3. PETRI-NET MODEL OF FUZZY PRODUCTION SYSTEM
3. PETRI-NET MODEL OF FUZZY PRODUCTION SYSTEM
Rr: IF X1r IS A1r AND ... AND XMrr IS AMrr THEN
XMr+1r IS B1r AND ... AND XMr+Nrr IS BNrr , (τr),

α: P -> PR, pk -> α(pk)=prk, k=1,...,K,

(8)

T = TR U TC = { t1,...,tR,tR+1,...,tR+C}
If tj ∈ TR, ∀ pi ∈P, pi ∈ I(tj) <=> a(pi) ∈ Antecedent part of Rj

(9)

If tj ∈ TR, ∀ pi ∈ P, pi∈ O(tj) <=> a(pi) ∈ Consequent part of Rj

(10)

If tj ∈ TC, pi ∈ I(tj) , pk ∈ O(tj) <=> a(pi) is linked with α ((pk))

(11)

g(p) = DOF(α(p))

(12)

M : p ---> { 0,1 }, pi ---> M(pi)= { 0, if g(pi) is unknown; 1, otherwise}
tf: M x T ---> M, (M,tj) ---> M'
M'(pi)={ 0, if pi ∈ I(tj); 1, if pi ∈ O(tj); M(pi ), otherwise}

(13)
(14)
(15)


4. FUZZY-PETRI NET REASONING COMPONENTS
4. FUZZY-PETRI NET REASONING COMPONENTS
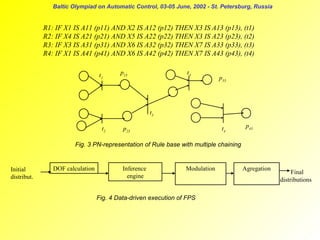
RS: IF X1S IS A1S AND ... AND XMsS IS AMsS THEN XMs+1S IS B1S AND ...AND XMs+NsS IS BNsS (τΣ)
RT: IF X1T IS A1T AND...AND XMTT IS AMTT THEN XMT+1T IS B1T AND...AND XMT+NTT IS BNTT (τT)

(16)
which are linked by :

XMs+1S = X1T

(17)

P= { prmr | mr = 1, ... ,Mr+Nr, r=S,T }

(18)

PR=prrmr = { "Xrmr IS Armr", mr<= Mr; "Xrmr IS Brmr-Mr", mr>Mr}

(19)

TR= { tS, tT}
TC = { t3 }
p 1S

pMsS

tS

pMs+1S

pMs+NsS

(20)
(21)

t3

p1T

tT

pMtT

pMt+1T

pMt+NtT

bS1,i = τS(g(pMs+1 s) Λ bS1,i), i=1,...,I

(22)

g(p1T) = V [ τS(g(pMs+1 s) Λ bS1,i) Λ aT1,i ]

(23)

g(p1T) = τS(g(pMs+1 s)) Λ V [τS(bS1,i) Λ aT1,i ]

(24)


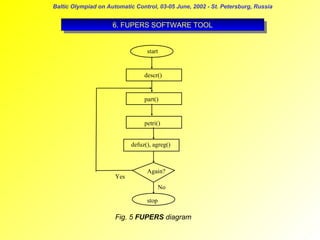
5. REASONING ALGORITHM
5. REASONING ALGORITHM
Step 1

Initial marking function will be:
M(pi) = { 0, if pi ∉ IP; 1, if pi ∈ IP }

Step 2

(25)

We fire the active transitions and calculate DOF-s.

∃ tj∈ T | ∀ pk ∈ I(tj), M(pk)=1

(26)

If tj ∈ TR, g(pi) = Λ g(pk) , ∀pi∈ O(tj), pk∈ I(tj)
If tj ∈ TC, g(pi) = V [τrk( g(pk)) Λ µpk,pi] , ∀pi ∈ O(tj), pk ∈ I(tj)
Step 3:

(27)
(28)

Go back to step 2, while:

∃ tj∈ T | M(pi) = 1, ∀ pi ∈ I(tj)
Step 4:

(29)

For each output variable X, its associated possibility distribution B={bi}, i=1,...,I, is:
bi= V τr(g(pnr)) Λ τr(brn,i), pnr∈ Px

(30)

Px = { pnr ∈ P | α(pnr) = "X IS Bnr”}

(31)


R1: IF X1 IS A11 (p11) AND X2 IS A12 (p12) THEN X3 IS A13 (p13), (t1)
t1

p13

t3

p33

t5
t2

p23

t4

p43

Fig. 3 PN-representation of Rule base with multiple chaining

Initial
distribut.

DOF calculation

Inference
engine

Modulation

Fig. 4 Data-driven execution of FPS

Agregation

Final
distributions


6. FUPERS SOFTWARE TOOL
6. FUPERS SOFTWARE TOOL
start

descr()

part()

petri()
defuz(), agreg()

Yes

Again?
No
stop

Fig. 5 FUPERS diagram


FUPERS – reasoning tool based on fuzzy-Petri net


Application – mobile robot avoiding obstacle

If no obstacle – go straight;
If obstacle is close left, go more right;
If obstacle is far left, go little right;
If obstacle is close right, go more left;
If obstacle is far right, go little left;


7. C O N C LLU S I IO N S
7. C O N C U S O N S

- Petri net formalism as a model of FPS as a model for inference and conclusion chaining,
which is compatible with well-structured algorithms for data-driven execution of a fuzzified
KB.
- KB execution through the compositional rule of inference, transfers most of the
computational load to the design, and not execution stage.
- The complexity of the execution algorithms is independent of the discretization of the
discourse universes over which the linguistic variables to be manipulated in the fuzzy
production systems are defined.
- Algorithms are carried out for a sub-min compositional rule of inference; the same results
are valid for the sub-prod rule. With Petri net formalism we have obtained a formal structure
that permits the definition of algorithms for carrying out inferences in different situations.
- FUPERS software tool is surpassing the limitations of computational demands, because of
the developing of a priori chained FPS compilation process. The execution time takes only
few milliseconds on a PC, so it is useful for real-time application.

BOAC - Intelligent reasoning

More Related Content

What's hot

Viewers also liked

Similar to BOAC - Intelligent reasoning

Recently uploaded

BOAC - Intelligent reasoning