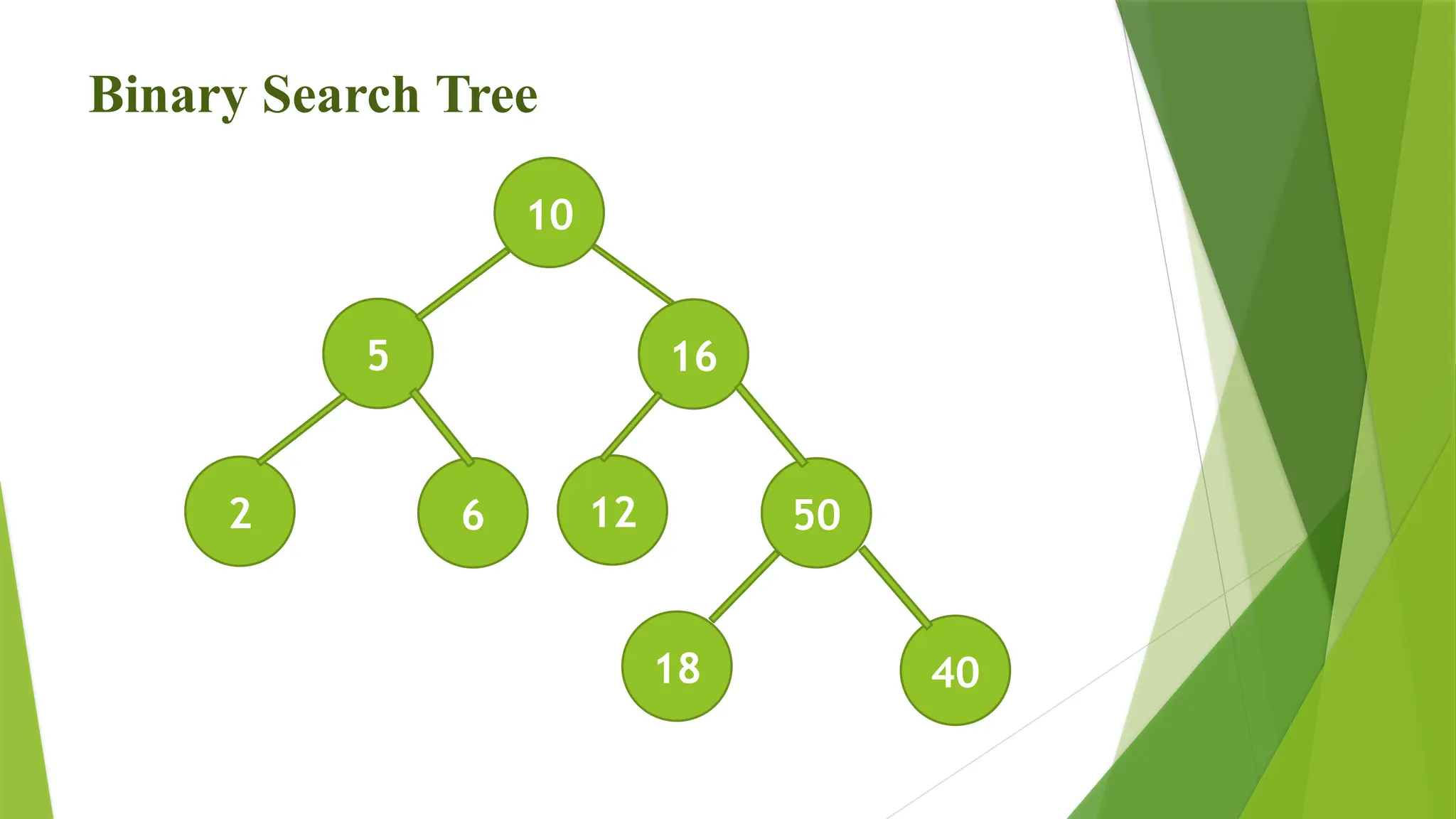
Binary Search Tree (BST) - A Complete Description 1. Introduction to BST A Binary Search Tree (BST) is a special type of binary tree that maintains its elements in a sorted manner. It is a hierarchical data structure where each node has at most two children: a left child and a right child. The key characteristic of a BST is the following property: For every node in the tree: All elements in the left subtree are less than the node. All elements in the right subtree are greater than the node. This structure makes searching, insertion, and deletion operations much more efficient compared to linear data structures like arrays and linked lists. Why Use BST? BSTs are useful in scenarios where fast data retrieval, insertion, and deletion are important. They provide: Faster search (on average, O(log n) time). Dynamic memory usage (no need to allocate a fixed size). Ordered data storage (can be used for sorting and searching simultaneously). 2. 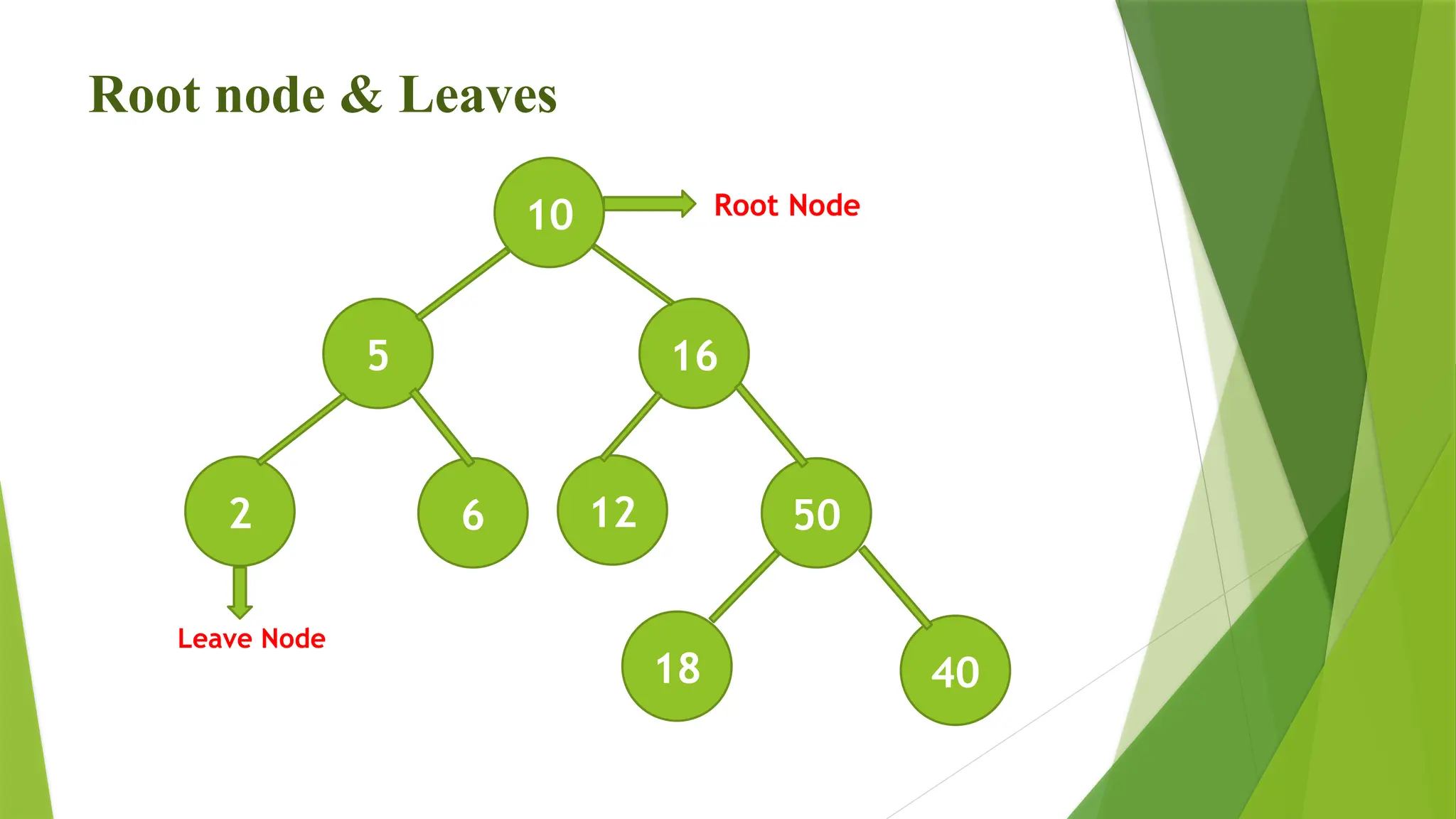Basic Terminologies Before diving deeper, it's important to understand some basic terminologies related to trees: Node: Each element in the tree. Root: The topmost node in the tree. Parent: A node that has one or more child nodes. Child: A node that descends from another node. Leaf: A node with no children. Subtree: A tree entirely contained within another tree. 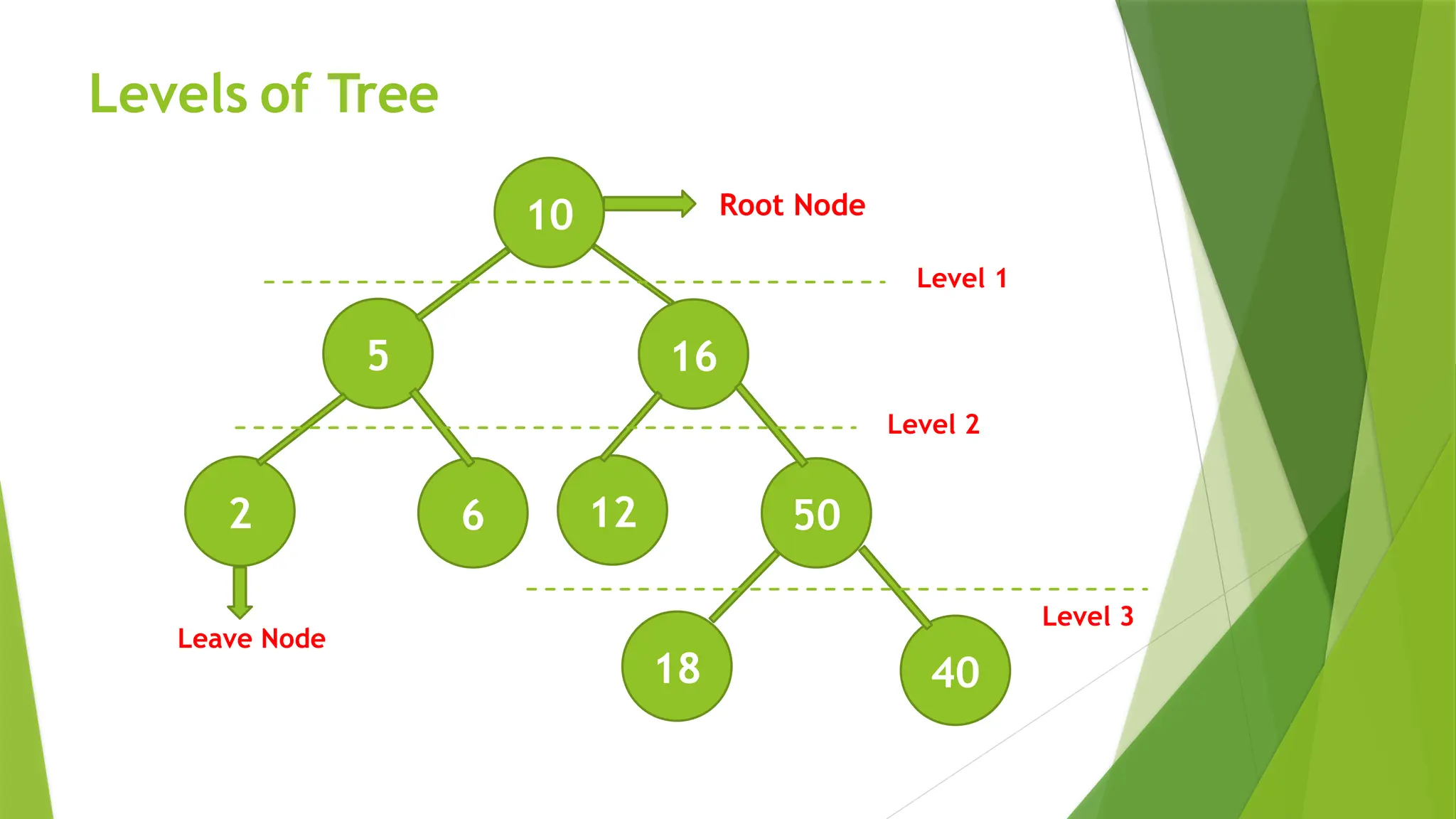Height: The number of edges on the longest path from a node to a leaf. Depth: The number of edges from the root to a particular node. 4. BST Operations a) Insertion To insert a new node: Compare it with the root. If smaller, go to the left subtree. If larger, go to the right subtree. Repeat until a null position is found, and insert the node there. Example: Insert 50, 30, 70, 20, 40, 60, 80 Resulting BST: markdown Copy Edit 50 / \ 30 70 / \ / \ 20 40 60 80 b) Searching Search operation follows the same rule as insertion: Start at root. If the key equals the node value, found. If the key is less, go left. If the key is more, go right. c) Deletion Deleting a node in BST has three cases: Leaf node: Just delete it. One child: Replace the node with its child. Two children: Find the inorder successor (smallest value in right subtree), copy its value to the node, then delete the successor. 5. BST Traversals Tree traversal is the process of visiting all the nodes in some order. a) Inorder Traversal (Left - Root - Right) This traversal returns values in sorted order for BST. Example: cpp Copy Edit void inorder(Node* root) { if (root != nullptr) { inorder(root->left); cout << root->data << " "; inorder(root->right); } } b) Preorder Traversal (Root - Left - Right) Useful for copying the tree or expression trees. c) Postorder Traversal (Left - Right - Root) Used for deleting the tree or evaluating expressions. 6. Time Complexity of BST Operations Operation Best Case Average Case Worst Case Search O(log n) O(log n) O(n) Insertion O(log n) O(log n)

1. ‫ال‬
ُ‫م‬ ‫اَل‬َّ‫س‬
ْ
‫م‬ُ
‫ك‬ْ‫ي‬َ‫ل‬َ
‫ع‬

2. BST
BINARY
SEARCH TREE
Syed Hasnat Ali and Hassan Butt

3. Agenda
 Binary Search Tree
 Insertion
 Deletion
 Tree Traversal Types
 Time Complexity

4. BST properties
• Maximum 2 child nodes.
• Smaller values on the left side.
• Bigger values on the right side.
• Leaves have no further nodes.
• Levels define the height of the tree.
• Balanced tree has equal elements on both sides.

5. Binary Search Tree
10
16
5
6
2 50
12
40
18

6. Root node & Leaves
10
16
5
6
2 50
12
40
18
Root Node
Leave Node

7. Levels of Tree
10
16
5
6
2 50
12
40
18
Root Node
Leave Node
Level 1
Level 2
Level 3

8. 10,13,17,18,20,25
10
13
17
18
20
25

9. 99,53,23,13,7,6
99
53
23
13
7
6

10. Insertion

11. Search Code

12. Deletion
Search for the Node
•Start at the root.
•Move left if d is less than current node.
•Move right if d is greater.
•Keep going until you find the node or reach nullptr.
Time Complexity: O(h) → height of tree

13. Handle Deletion Cases
Case 1: Node has no children (leaf)
•Simply remove the node by setting
its parent's pointer to nullptr.
Time Complexity: O(1)

14. Handle Deletion Cases
Case 2: Node has one child
•Replace the node with its child.
•Update the parent's pointer.
Time Complexity: O(1)

15. Handle Deletion Cases
Case 3: Node has two children
•Find the in-order successor (smallest node in right subtree).
•Copy successor's data into the current node.
•Delete the successor node (which has at most one child).
Time Complexity: O(h) → finding successor takes height of
tree

16. Time Complexity
Operation Time Complexity
Search node O(h) (height of tree)
Delete node O(h)
Overall
O(h) = O(log n) for balanced BST,
O(n) for skewed BST

17. Time Complexity of Insertion in BST
Case Explanation Time Complexity
Best Case
Inserting at root or near
root (very small tree)
O(1)
Average Case
Tree is balanced. Height
is log (n)
₂
O(log n)
Worst Case
Tree is skewed (like linked
list: all left or all right) O(n)

18. Time Complexity of Search in BST
Case Explanation Time
Complexity
Best Case Element is at the root O(1)
Average Case
Tree is balanced, and we
go down log (n)
₂ levels
O(log n)
Worst Case
Tree is skewed, we
check every node
O(n)

19. Binary Search TreeTraversal Types
 Inorder
 Pre order
 Post order

20. Inorder Traversal in BST
• Explore Left side
Traverse the left subtree recursively.
• Print
Visit and print the current node's data.
• Explore Right side
Traverse the right subtree recursively.

21. Preorder Traversal in BST
•Print
Visit and print the current node's data.
•Explore Left side
Traverse the left subtree recursively.
•Explore Right side
Traverse the right subtree recursively.

22. Postorder Traversal in BST
• Explore Left side
Traverse the left subtree recursively.
• Explore Right side
Traverse the right subtree recursively.
• Print
Visit and print the current node's data.

23. Time Complexity of Tree Traversals
Traversal
Type
Best Case
Average
Case
Worst Case
Time
Complexity
Inorder O(n) O(n) O(n) O(n)
Preorder O(n) O(n) O(n) O(n)
Postorder O(n) O(n) O(n) O(n)