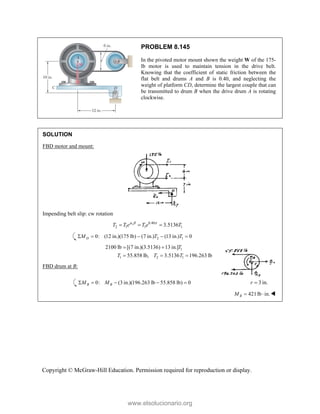
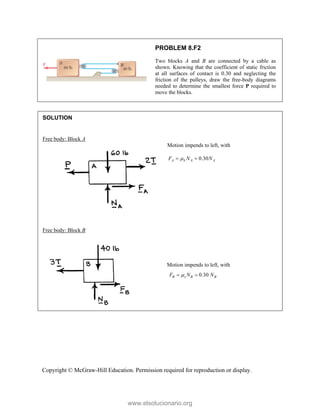
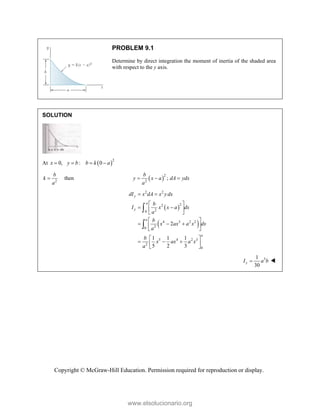
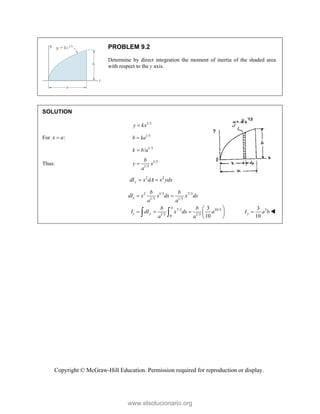
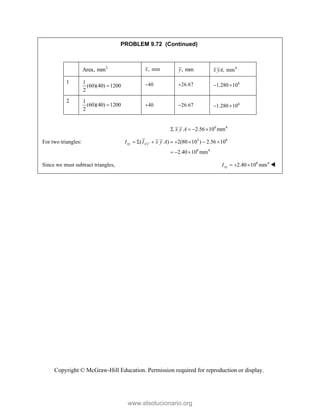
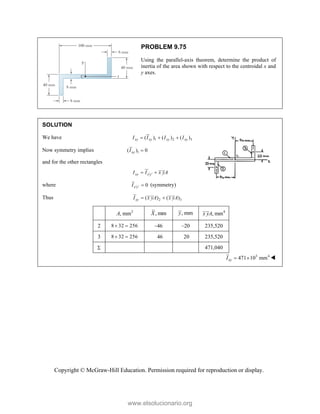
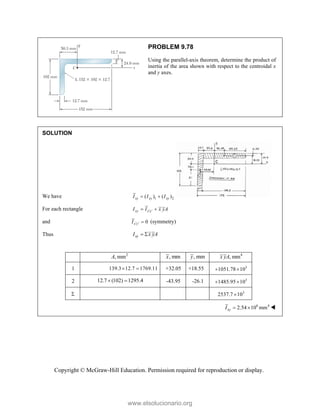
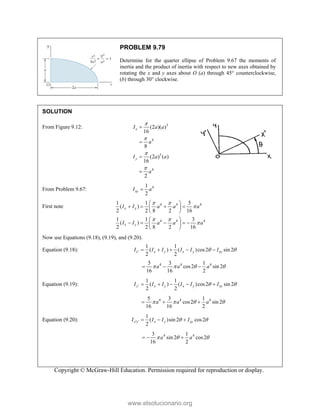
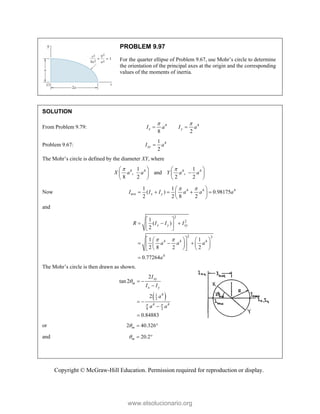
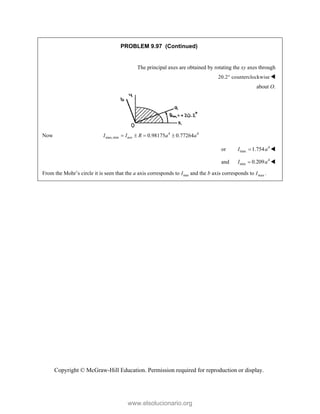
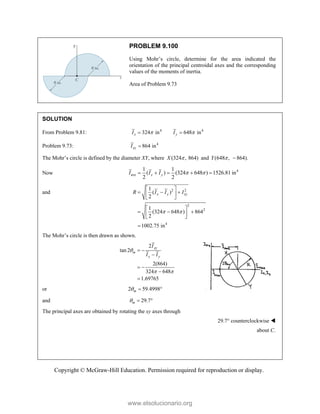
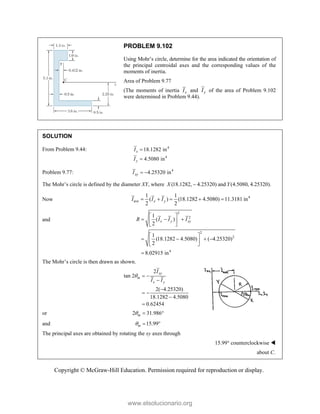
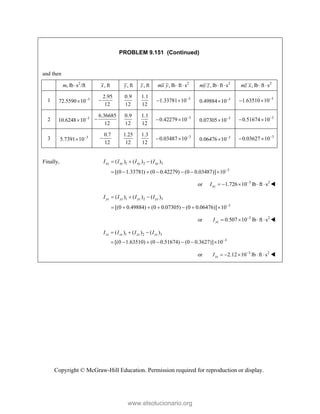
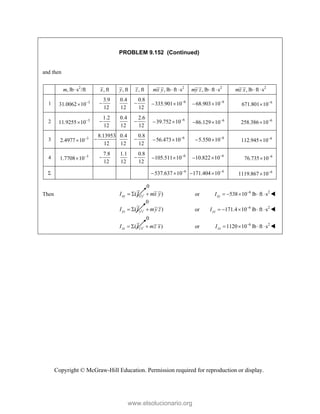
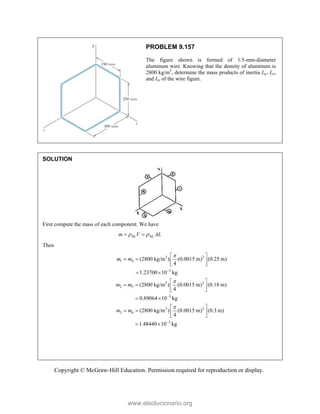
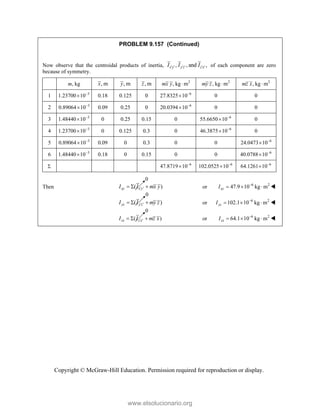
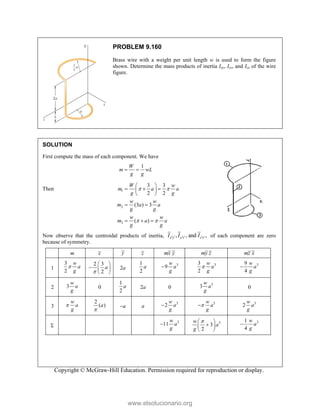
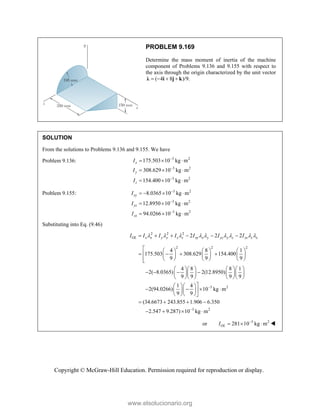
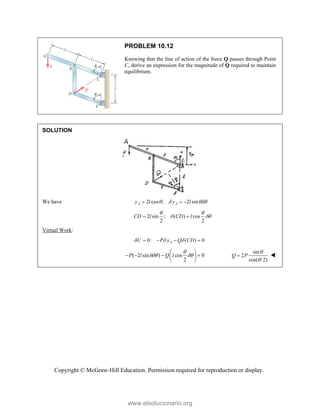
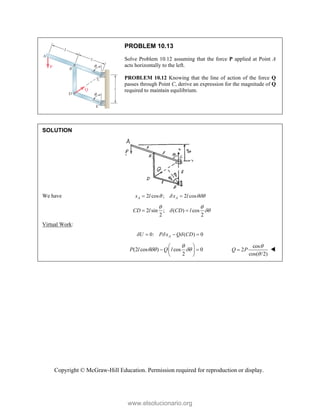
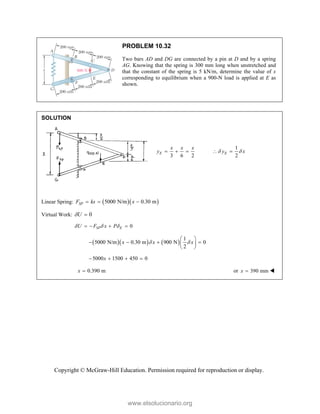
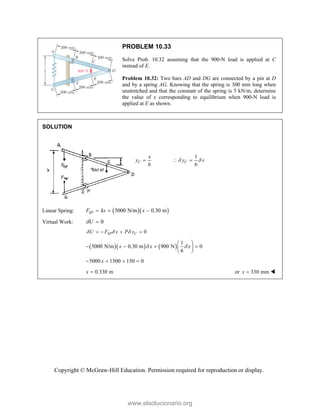
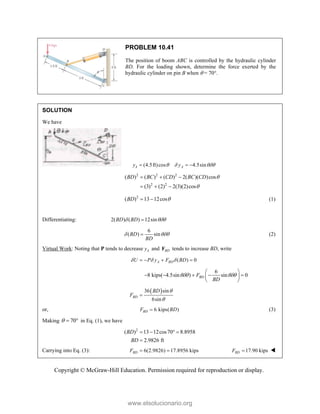
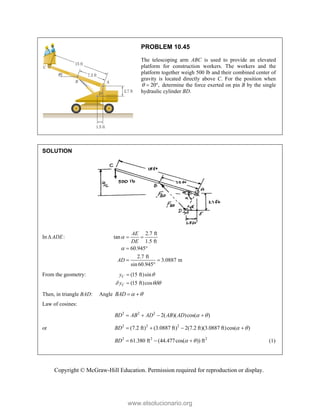
This document provides an instructor's manual for Vector Mechanics for Engineers: Statics, 11th Edition. It describes the content and organization of the textbook, provides suggested schedules and assignments, and offers guidance on teaching key concepts. Tables outline topics, assign minimum and maximum class periods for coverage, and provide sample homework assignments with problems in both SI and U.S. customary units. The manual aims to help instructors effectively structure their statics course based on the level and preparation of their students.


























































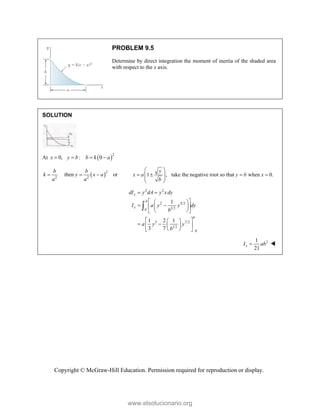
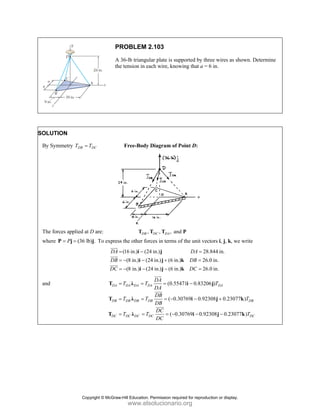
![SOLUT
Resolvin
Substitu
In the y-
Thus,
In the x-
Thus,
TION
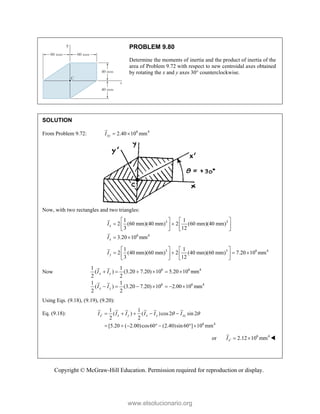
ng the forces i
uting compone
-direction (one
-direction:
into x- and y-d
=
R
ents: =
R
e unknown for
−
(65
P
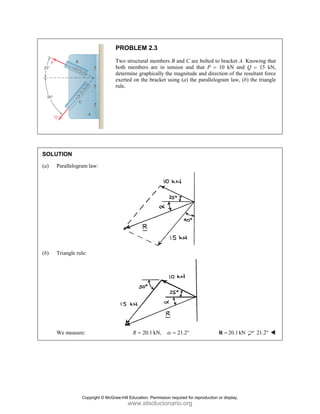
Tw
co
an
m
directions:
A
= + + +
P Q F
(500 lb)
[(650 lb)si
( c
B A
F F
= − +
−
+ −
j
i
rce):
500 lb (650
− −
500 lb
A
F
+
=
1302.70
=
50 lb)cos50° +
cos50
(1302.70
B A
F F
=
=
419.55 lb
=
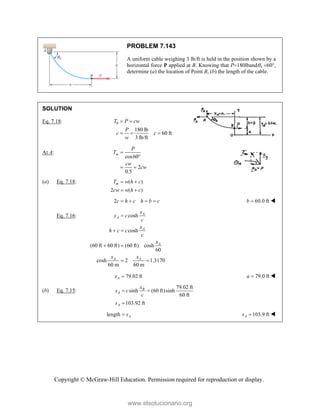
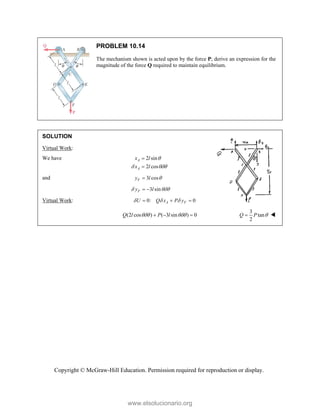
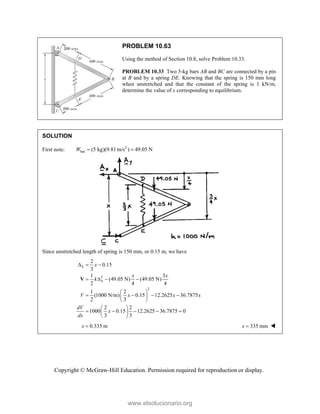
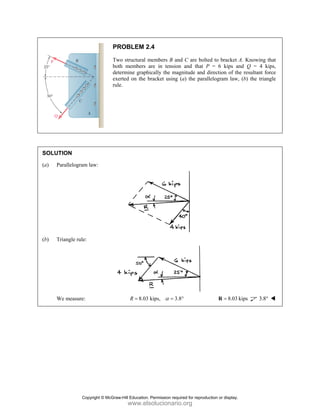
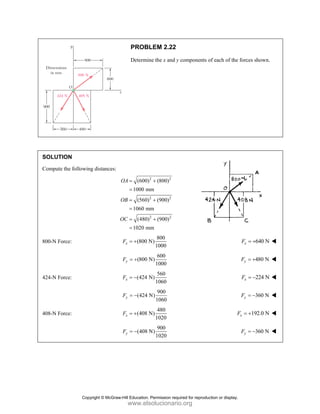
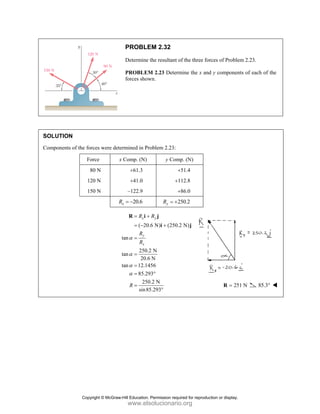
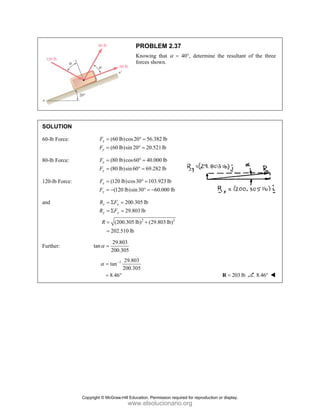
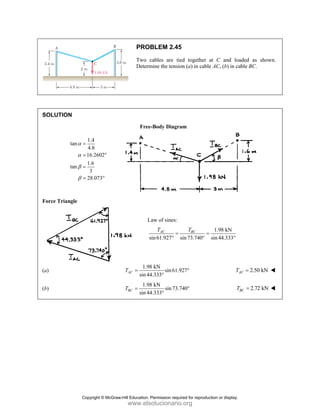
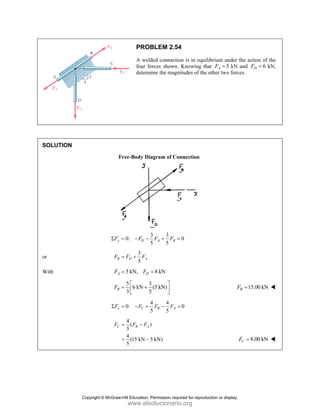
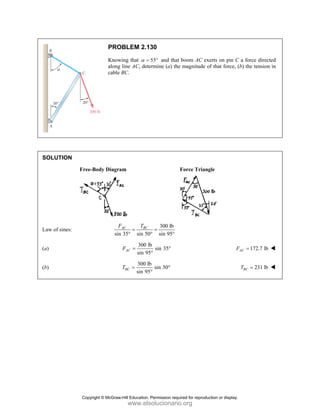
PROBLEM 2
wo forces P a
onnection. Kn
nd that P =
magnitudes of t
0
B
+ =
F
[(650 lb)cos5
in50 ]
cos50 ) ( A
F
°
° +
j
i
lb)sin50 F
° +
(650 lb)sin50
sin50
+
°
lb
cos5
B A
F F
+ −
0 (650 lb)c
0 lb)cos50
° −
° −
b
2.51
and Q are ap
nowing that th
500
= lb and
the forces exer
50 ]
sin50 ) 0
A
°
° =
i
j
sin50 0
A
F ° =
0°
50 0
° =
cos50
(650 lb)cos50
°
pplied as show
e connection i
650
Q = lb,
rted on the rod
Free
0°
wn to an aircr
is in equilibriu
determine
ds A and B.
e-Body Diagr
1303lb
A
F =
420 lb
B
F =
raft
um
the
ram
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-81-320.jpg)
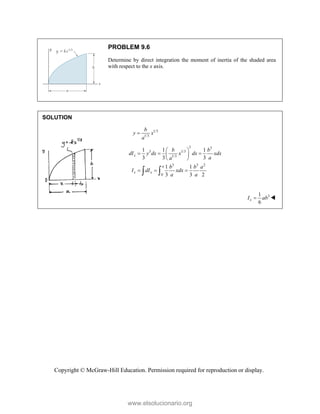
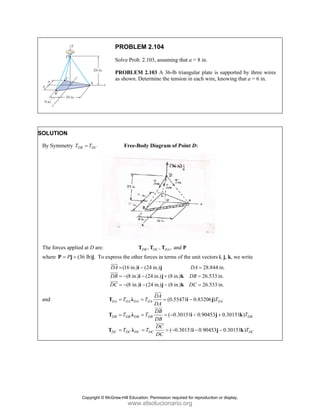
![SOLUT
Resolvin
Substitu
In the x-
In the y-
TION
ng the forces i
uting compone
-direction (one
-direction:
into x- and y-d
=
R P
ents: = −
−
+
R
e unknown for
cos 5
Q
P
− −
P =
=
=
P
T
c
e
o
d
directions:
A
+ + +
P Q F F
cos 50
[(750 lb)cos
[(750 lb)sin
P Q
− +
−
+
j
rce):
50 [(750 lb)
° −
(750 lb
127.710
Q =
=
sin 50
Q
− ° +
sin 50
(127.710 lb
476.70 lb
Q
= − ° +
= −
=
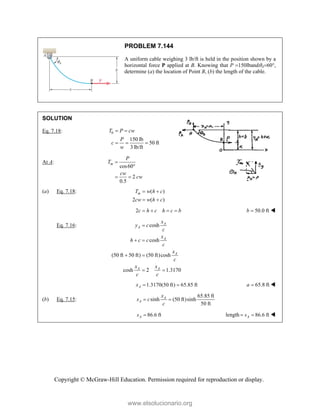
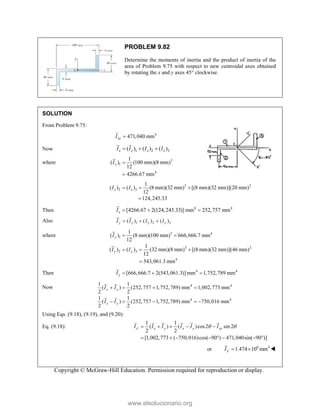
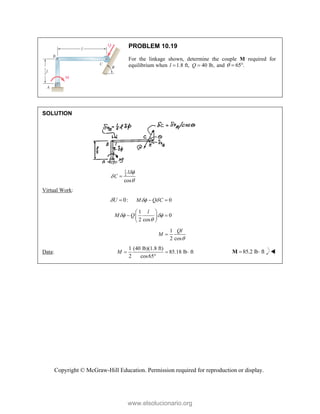
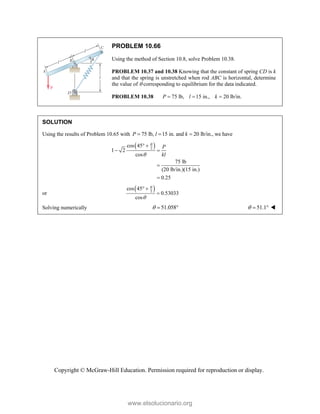
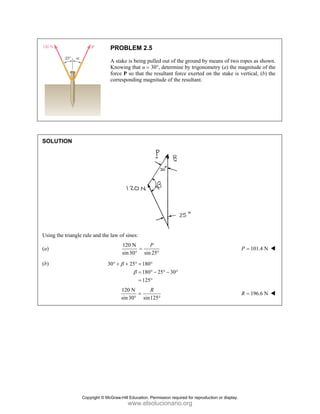
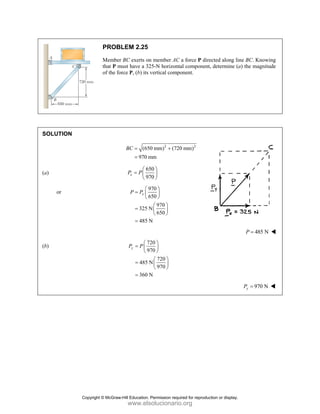
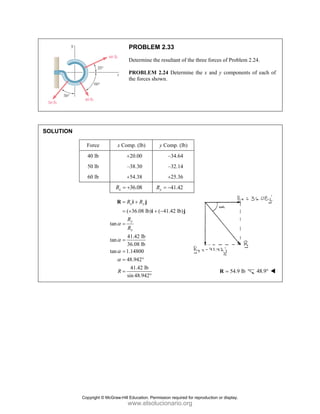
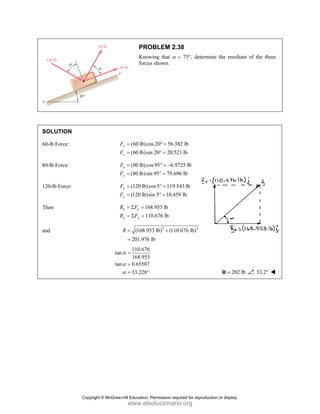
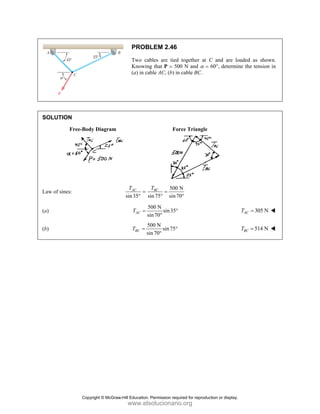
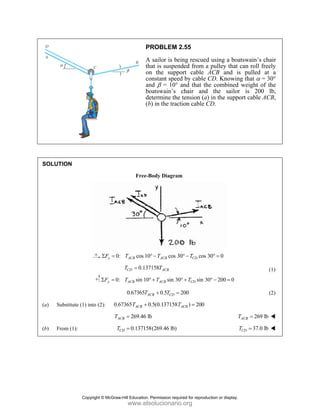
PROBLEM
Two forces P
connection.
equilibrium an
on rods A a
determine the
0
B =
F
0 sin 50
50 ]
50 ] (400 lb
Q
° − °
°
° +
i
i
j
cos 50 ] 400
° +
b)cos 50 40
cos 50
0 lb
° −
°
(750 lb)sin 5
(750 lb)sin 5
b)sin 50 (75
+
° +
M 2.52
and Q are ap
Knowing th
nd that the ma
and B are F
magnitudes o
b)
°j
i
0 lb 0
=
00 lb
0 0
° =
50
50 lb)sin 50
°
°
pplied as show
hat the con
agnitudes of th
750
A
F = lb an
of P and Q.
Free-Bo
477 lb;
P =
wn to an aircr
nnection is
he forces exer
nd 400
B
F =
ody Diagram
127.7 lb
Q =
raft
in
rted
lb,
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-82-320.jpg)
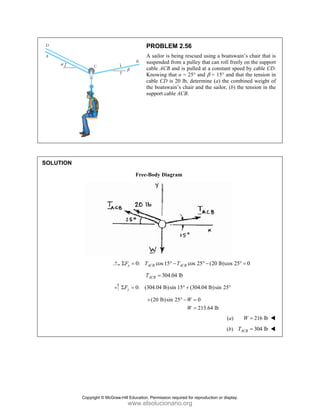























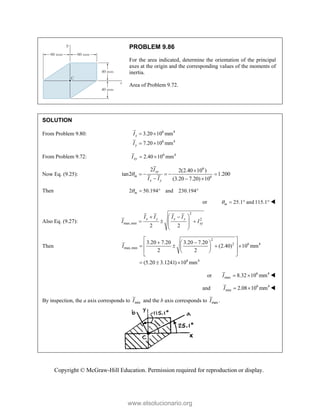
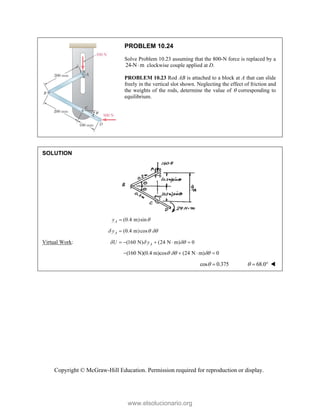
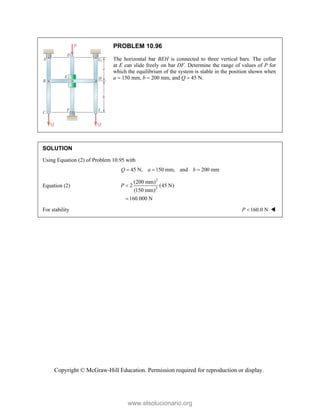
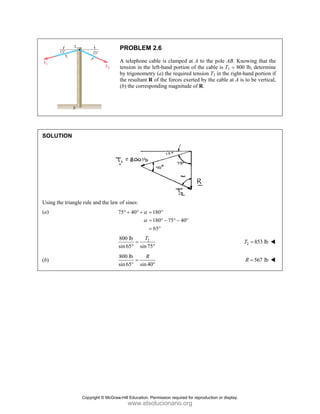
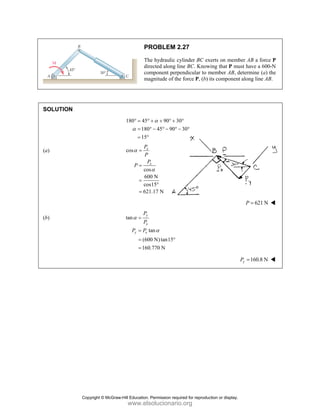
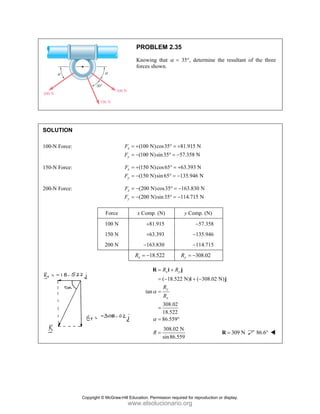
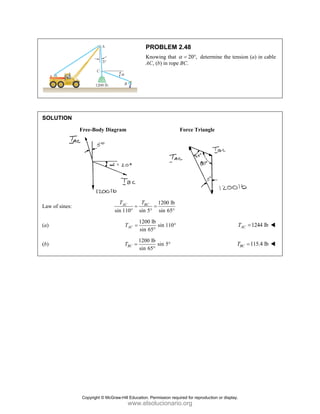
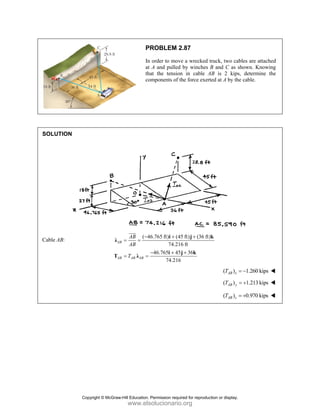
![PROBLEM 2.85
A frame ABC is supported in part by cable DBE that
passes through a frictionless ring at B. Knowing that the
tension in the cable is 385 N, determine the components
of the force exerted by the cable on the support at D.
SOLUTION
2 2 2
(480 mm) (510 mm) (320 mm)
(480 mm) (510 mm ) (320 mm)
770 mm
385 N
[(480 mm) (510 mm) (320 mm) ]
770 mm
(240 N) (255 N) (160 N)
DB
DB
DB
F
DB
F
DB
= − +
= + +
=
=
=
= − +
= − +
i j k
F λ
i j k
i j k
JJJ
G
JJJ
G
240 N, 255 N, 160.0 N
x y z
F F F
= + = − = +
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-115-320.jpg)
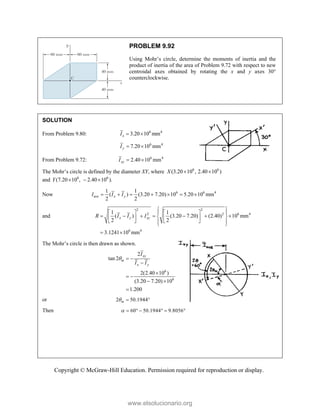
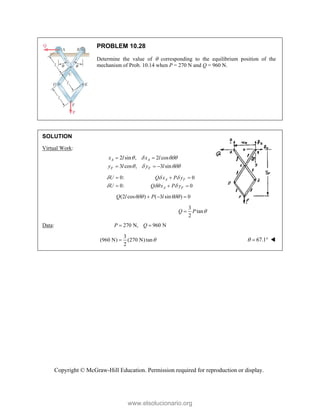
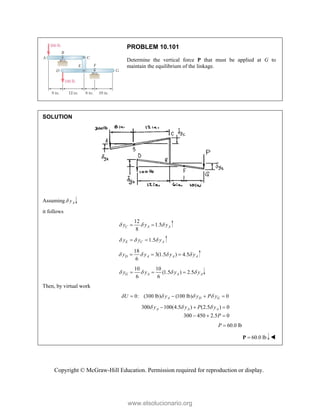
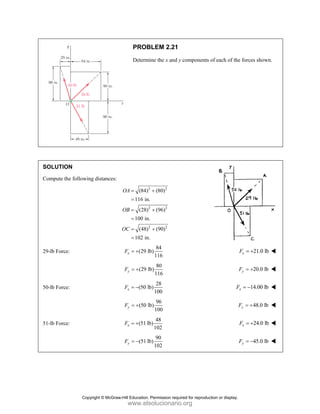
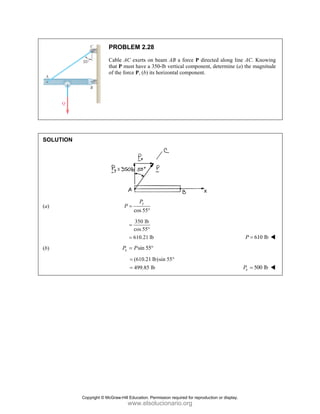
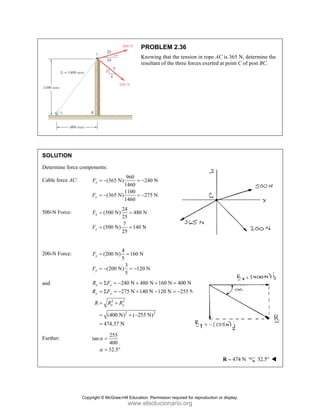
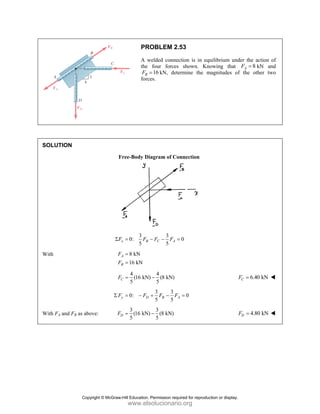
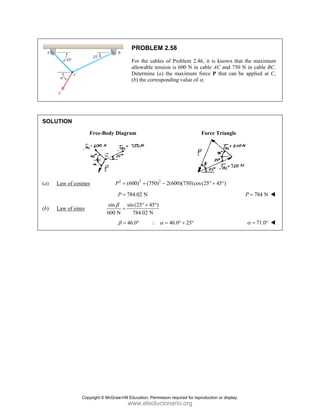
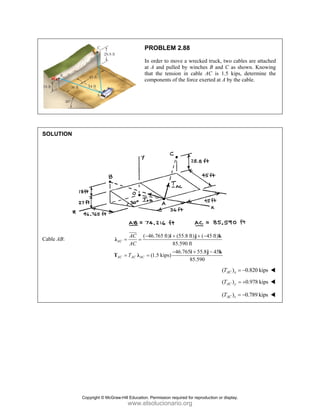
![PROBLEM 2.86
For the frame and cable of Problem 2.85, determine the
components of the force exerted by the cable on the
support at E.
PROBLEM 2.85 A frame ABC is supported in part by
cable DBE that passes through a frictionless ring at B.
Knowing that the tension in the cable is 385 N, determine
the components of the force exerted by the cable on the
support at D.
SOLUTION
2 2 2
(270 mm) (400 mm) (600 mm)
(270 mm) (400 mm) (600 mm)
770 mm
385 N
[(270 mm) (400 mm) (600 mm) ]
770 mm
(135 N) (200 N) (300 N)
EB
EB
EB
F
EB
F
EB
= − +
= + +
=
=
=
= − +
= − +
i j k
F λ
i j k
F i j k
JJJ
G
JJJ
G
135.0 N, 200 N, 300 N
x y z
F F F
= + = − = +
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-116-320.jpg)


![PROBLEM 2.91
Find the magnitude and direction of the resultant of the two forces
shown knowing that P = 300 N and Q = 400 N.
SOLUTION
(300 N)[ cos30 sin15 sin30 cos30 cos15 ]
(67.243 N) (150 N) (250.95 N)
(400 N)[cos50 cos20 sin50 cos50 sin 20 ]
(400 N)[0.60402 0.76604 0.21985]
(241.61 N) (306.42 N) (87.939 N)
(174.
= − ° ° + ° + ° °
= − + +
= ° ° + ° − ° °
= + −
= + −
= +
=
P i j k
i j k
Q i j k
i j
i j k
R P Q
2 2 2
367 N) (456.42 N) (163.011 N)
(174.367 N) (456.42 N) (163.011 N)
515.07 N
R
+ +
= + +
=
i j k
515 N
R =
174.367 N
cos 0.33853
515.07 N
x
x
R
R
θ = = = 70.2
x
θ = °
456.42 N
cos 0.88613
515.07 N
y
y
R
R
θ = = = 27.6
y
θ = °
163.011 N
cos 0.31648
515.07 N
z
z
R
R
θ = = = 71.5
z
θ = °
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-121-320.jpg)
![PROBLEM 2.92
Find the magnitude and direction of the resultant of the two forces
shown knowing that P = 400 N and Q = 300 N.
SOLUTION
(400 N)[ cos30 sin15 sin30 cos30 cos15 ]
(89.678 N) (200 N) (334.61 N)
(300 N)[cos50 cos20 sin50 cos50 sin 20 ]
(181.21 N) (229.81 N) (65.954 N)
(91.532 N) (429.81 N) (268.66 N)
(91.5
R
= − ° ° + ° + ° °
= − + +
= ° ° + ° − ° °
= + −
= +
= + +
=
P i j k
i j k
Q i j k
i j k
R P Q
i j k
2 2 2
32 N) (429.81 N) (268.66 N)
515.07 N
+ +
= 515 N
R =
91.532 N
cos 0.177708
515.07 N
x
x
R
R
θ = = = 79.8
x
θ = °
429.81 N
cos 0.83447
515.07 N
y
y
R
R
θ = = = 33.4
y
θ = °
268.66 N
cos 0.52160
515.07 N
z
z
R
R
θ = = = 58.6
z
θ = °
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-122-320.jpg)


![PROBLEM 2.95
For the frame of Problem 2.85, determine the magnitude and
direction of the resultant of the forces exerted by the cable at B
knowing that the tension in the cable is 385 N.
PROBLEM 2.85 A frame ABC is supported in part by cable
DBE that passes through a frictionless ring at B. Knowing that
the tension in the cable is 385 N, determine the components of
the force exerted by the cable on the support at D.
SOLUTION
2 2 2
(480 mm) (510 mm) (320 mm)
(480 mm) (510 mm) (320 mm) 770 mm
BD
BD
= − + −
= + + =
i j k
JJJG
(385 N)
[ (480 mm) (510 mm) (320 mm) ]
(770 mm)
(240 N) (255 N) (160 N)
BD BD BD BD
BD
T T
BD
= =
= − + −
= − + −
F λ
i j k
i j k
JJJ
G
2 2 2
(270 mm) (400 mm) (600 mm)
(270 mm) (400 mm) (600 mm) 770 mm
BE
BE
= − + −
= + + =
i j k
JJJ
G
(385 N)
[ (270 mm) (400 mm) (600 mm) ]
(770 mm)
(135 N) (200 N) (300 N)
BE BE BE BE
BE
T T
BE
= =
= − + −
= − + −
F λ
i j k
i j k
JJJ
G
(375 N) (455 N) (460 N)
BD BE
= + = − + −
R F F i j k
2 2 2
(375 N) (455 N) (460 N) 747.83 N
R = + + = 748 N
R =
375 N
cos
747.83 N
x
θ
−
= 120.1
x
θ = °
455 N
cos
747.83 N
y
θ = 52.5
y
θ = °
460 N
cos
747.83 N
z
θ
−
= 128.0
z
θ = °
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-125-320.jpg)














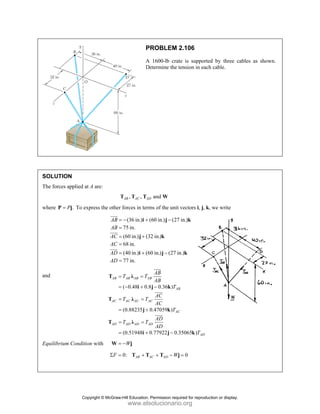

![PROBLEM 2.107
Three cables are connected at A, where the forces P and Q are
applied as shown. Knowing that 0,
Q = find the value of P for
which the tension in cable AD is 305 N.
SOLUTION
0: 0
A AB AC AD
Σ = + + + =
F T T T P where P
=
P i
(960 mm) (240 mm) (380 mm) 1060 mm
(960 mm) (240 mm) (320 mm) 1040 mm
(960 mm) (720 mm) (220 mm) 1220 mm
AB AB
AC AC
AD AD
= − − + =
= − − − =
= − + − =
i j k
i j k
i j k
JJJ
G
JJJG
JJJG
48 12 19
53 53 53
12 3 4
13 13 13
305 N
[( 960 mm) (720 mm) (220 mm) ]
1220 mm
(240 N) (180 N) (55 N)
AB AB AB AB AB
AC AC AC AC AC
AD AD AD
AB
T T T
AB
AC
T T T
AC
T
⎛ ⎞
= = = − − +
⎜ ⎟
⎝ ⎠
⎛ ⎞
= = = − − −
⎜ ⎟
⎝ ⎠
= = − + −
= − + −
T λ i j k
T λ i j k
T λ i j k
i j k
JJJ
G
JJJG
Substituting into 0,
A
Σ =
F factoring , , ,
i j k and setting each coefficient equal to φ gives:
48 12
: 240 N
53 13
AB AC
P T T
= + +
i (1)
:
j
12 3
180 N
53 13
AB AC
T T
+ = (2)
:
k
19 4
55 N
53 13
AB AC
T T
− = (3)
Solving the system of linear equations using conventional algorithms gives:
446.71 N
341.71 N
AB
AC
T
T
=
= 960 N
P =
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-144-320.jpg)






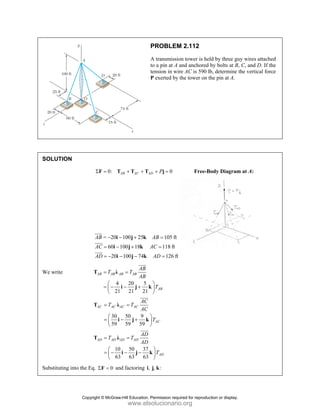










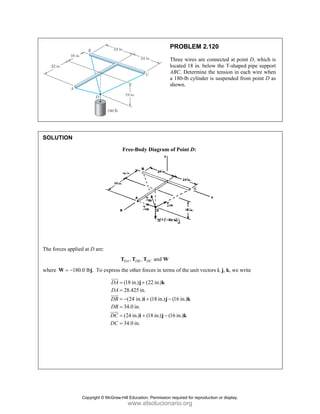

![PROBLEM 2.121
A container of weight W is suspended from ring
A, to which cables AC and AE are attached. A
force P is applied to the end F of a third cable
that passes over a pulley at B and through ring A
and that is attached to a support at D. Knowing
that 1000 N,
W = determine the magnitude of P.
(Hint: The tension is the same in all portions of
cable FBAD.)
SOLUTION
The (vector) force in each cable can be written as the product of the (scalar) force and the unit vector
along the cable. That is, with
2 2 2
(0.78 m) (1.6 m) (0 m)
( 0.78 m) (1.6 m) (0)
1.78 m
[ (0.78 m) (1.6 m) (0 m) ]
1.78 m
( 0.4382 0.8989 0 )
AB AB AB
AB
AB AB
AB
AB
AB
T T
AB
T
T
= − + +
= − + +
=
= =
= − + +
= − + +
i j k
T λ
i j k
T i j k
JJJ
G
JJJ
G
and
2 2 2
(0) (1.6 m) (1.2 m)
(0 m) (1.6 m) (1.2 m) 2 m
[(0) (1.6 m) (1.2 m) ]
2 m
(0.8 0.6 )
AC
AC AC AC
AC AC
AC
AC
T
AC
T T
AC
T
= + +
= + + =
= = = + +
= +
i j k
T λ i j k
T j k
JJJG
JJJG
and
2 2 2
(1.3 m) (1.6 m) (0.4 m)
(1.3 m) (1.6 m) (0.4 m) 2.1 m
[(1.3 m) (1.6 m) (0.4 m) ]
2.1 m
(0.6190 0.7619 0.1905 )
AD
AD AD AD
AD AD
AD
AD
T
AD
T T
AD
T
= + +
= + + =
= = = + +
= + +
i j k
T λ i j k
T i j k
JJJG
JJJG
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-164-320.jpg)
![PROBLEM 2.121 (Continued)
Finally,
2 2 2
(0.4 m) (1.6 m) (0.86 m)
( 0.4 m) (1.6 m) ( 0.86 m) 1.86 m
[ (0.4 m) (1.6 m) (0.86 m) ]
1.86 m
( 0.2151 0.8602 0.4624 )
AE AE AE
AE
AE AE
AE
AE
AE
T T
AE
T
T
= − + −
= − + + − =
= =
= − + −
= − + −
i j k
T λ
i j k
T i j k
JJJ
G
JJJ
G
With the weight of the container ,
W
= −
W j at A we have:
0: 0
AB AC AD W
Σ = + + − =
F T T T j
Equating the factors of i, j, and k to zero, we obtain the following linear algebraic equations:
0.4382 0.6190 0.2151 0
AB AD AE
T T T
− + − = (1)
0.8989 0.8 0.7619 0.8602 0
AB AC AD AE
T T T T W
+ + + − = (2)
0.6 0.1905 0.4624 0
AC AD AE
T T T
+ − = (3)
Knowing that 1000 N
W = and that because of the pulley system at B ,
AB AD
T T P
= = where P is the
externally applied (unknown) force, we can solve the system of linear Equations (1), (2) and (3) uniquely
for P.
378 N
P =
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-165-320.jpg)






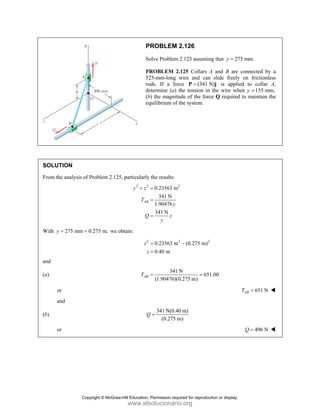






![PROBLEM 2.134
Knowing that the tension in cable AC is 2130 N, determine
the components of the force exerted on the plate at C.
SOLUTION
2 2 2
(900 mm) (600 mm) (920 mm)
(900 mm) (600 mm) (920 mm)
1420 mm
2130 N
[ (900 mm) (600 mm) (920 mm) ]
1420 mm
(1350 N) (900 N) (1380 N)
CA CA CA
CA
CA
CA
CA
T
CA
T
CA
= − + −
= + +
=
=
=
= − + −
= − + −
i j k
T λ
T i j k
i j k
JJJ
G
JJJ
G
( ) 1350 N, ( ) 900 N, ( ) 1380 N
CA x CA y CA z
T T T
= − = = −
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-180-320.jpg)
![PROBLEM 2.135
Find the magnitude and direction of the resultant of the two forces
shown knowing that P = 600 N and Q = 450 N.
SOLUTION
(600 N)[sin 40 sin 25 cos40 sin 40 cos25 ]
(162.992 N) (459.63 N) (349.54 N)
(450 N)[cos55 cos30 sin55 cos55 sin30 ]
(223.53 N) (368.62 N) (129.055 N)
(386.52 N) (828.25 N) (220.49 N)
(3
R
= ° ° + ° + ° °
= + +
= ° ° + ° − ° °
= + −
= +
= + +
=
P i j k
i j k
Q i j k
i j k
R P Q
i j k
2 2 2
86.52 N) (828.25 N) (220.49 N)
940.22 N
+ +
= 940 N
R =
386.52 N
cos
940.22 N
x
x
R
R
θ = = 65.7
x
θ = °
828.25 N
cos
940.22 N
y
y
R
R
θ = = 28.2
y
θ = °
220.49 N
cos
940.22 N
z
z
R
R
θ = = 76.4
z
θ = °
Copyright © McGraw-Hill Education. Permission required for reproduction or display.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-181-320.jpg)














![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.4
A 300-N force is applied at A as shown. Determine
(a) the moment of the 300-N force about D, (b) the
smallest force applied at B that creates the same moment
about D.
SOLUTION
(a) (300 N)cos 25
271.89 N
(300 N)sin 25
126.785 N
(271.89 N) (126.785 N)
x
y
F
F
F i j
(0.1m) (0.2 m)
[ (0.1m) (0.2 m) ] [(271.89 N) (126.785 N) ]
(12.6785 N m) (54.378 N m)
(41.700 N m)
D
D
DA
r i j
M r F
M i j i j
k k
k
41.7 N m
D
M
(b) The smallest force Q at B must be perpendicular to
DB
at 45°
( )
41.700 N m (0.28284 m)
D Q DB
Q
M
147.4 N
Q 45.0°
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-199-320.jpg)




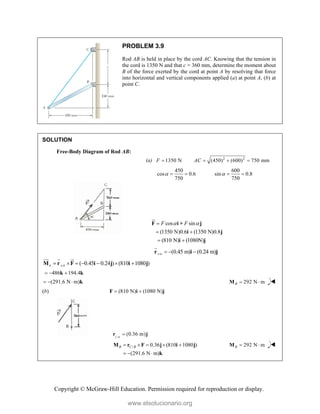
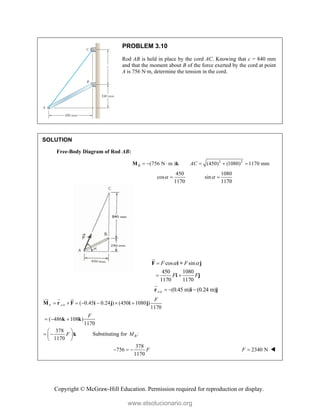
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.11
The tailgate of a car is supported by the hydraulic lift BC. If
the lift exerts a 125-lb force directed along its centerline on
the ball and socket at B, determine the moment of the force
about A.
SOLUTION
First note 2 2
(12.0 in.) (2.33 in.)
12.2241in.
CB
d
Then
12.0 in.
cos
12.2241in.
2.33 in.
sin
12.2241in.
and cos sin
125 lb
[(12.0 in.) (2.33 in.) ]
12.2241in.
CB CB CB
F F
F i j
i j
Now /
A B A CB
M r F
where / (15.3 in.) (12.0 in. 2.33 in.)
(15.3 in.) (14.33 in.)
B A
r i j
i j
Then
125 lb
[(15.3 in.) (14.33 in.) ] (12.0 2.33 )
12.2241in.
(1393.87 lb in.)
A
M i j i j
k
(116.156 lb ft)
k or 116.2 lb ft
A
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-206-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.12
The tailgate of a car is supported by the hydraulic lift BC. If
the lift exerts a 125-lb force directed along its centerline on
the ball and socket at B, determine the moment of the force
about A.
SOLUTION
First note 2 2
(17.2 in.) (7.62 in.)
18.8123 in.
CB
d
Then
17.2 in.
cos
18.8123 in.
7.62 in.
sin
18.8123 in.
and ( cos ) ( sin )
125 lb
[(17.2 in.) (7.62 in.) ]
18.8123 in.
CB CB CB
F F
F i j
i j
Now /
A B A CB
M r F
where / (20.5 in.) (4.38 in.)
B A
r i j
Then
125 lb
[(20.5 in.) (4.38 in.) ] (17.2 7.62 )
18.8123 in.
A
M i j i j
(1538.53 lb in.)
(128.2 lb ft)
k
k or 128.2 lb ft
A
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-207-320.jpg)
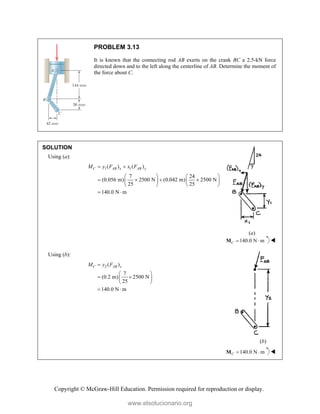
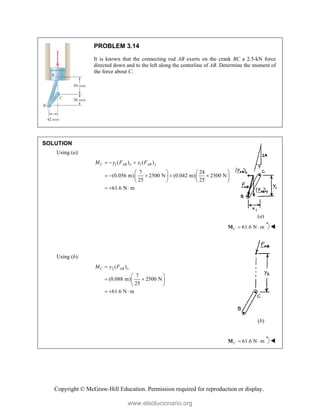

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.16
The vectors P and Q are two adjacent sides of a parallelogram. Determine the area of the parallelogram
when (a) P = –8i + 4j – 4k and Q = 3i + 3j + 6k, (b) P = 7i – 6j – 3k and Q = –3i + 6j – 2k
SOLUTION
(a) We have | |
A
P Q
where 8 4 4
P i j k
3 3 6
Q i j k
Then 8 4 4
3 3 6
[(24 12) ( 12 48) ( 24 12) ]
(36) (36) ( 36)
i j k
P Q
i j k
i j k
2 2 2
(36) (36) ( 36)
A or 62.4
A
(b) We have | |
A
P Q
where 7 6 3
P i j k
3 6 2
Q i j k
Then 7 6 3
3 6 2
[(12 18) (9 14) (42 18) ]
(30) (23) (24)
i j k
P Q
i j k
i j k
2 2 2
(30) (23) (24)
A or 44.8
A
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-211-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.18
A line passes through the points (12 m, 8 m) and (–3 m, –5 m). Determine the perpendicular distance d from
the line to the origin O of the system of coordinates.
SOLUTION
2 2
[12 m ( 3 m)] [8 m ( 5 m)]
394 m
AB
d
Assume that a force F, or magnitude F(N), acts at Point A and is
directed from A to B.
Then AB
F
F
where
1
(15 13 )
394
B A
AB
AB
d
r r
i j
By definition, | |
O A dF
M r F
where ( 3 m) ( 5 m)
A
r i + j
Then [( 3 m) ( 5 m) ] [(15 m) (13 m) ]
394m
[ 39 75 ] N m
394
36
N m
394
O
F
F
F
M i + j i j
k k
k
Finally,
36
( )
394
F d F
36
m
394
d 1.184 m
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-213-320.jpg)


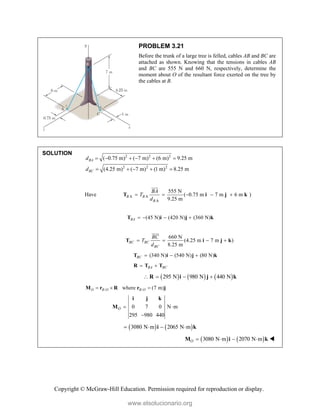

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.23
A 200-N force is applied as shown to the bracket ABC.
Determine the moment of the force about A.
SOLUTION
We have /
A C A C
M r F
where / (0.06 m) (0.075 m)
(200 N)cos 30 (200 N)sin 30
C A
C
r i j
F j k
Then 200 0.06 0.075 0
0 cos30 sin 30
200[(0.075sin 30 ) (0.06sin 30 ) (0.06cos 30 ) ]
A
i j k
M
i j k
or (7.50 N m) (6.00 N m) (10.39 N m)
A
M i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-218-320.jpg)










![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.34
Determine the value of a that minimizes the
perpendicular distance from Point C to a
section of pipeline that passes through Points
A and B.
SOLUTION
Assuming a force F acts along AB,
/
| | | | ( )
C A C F d
M r F
where d perpendicular distance from C to line AB
2 2 2
/
(24 ft) (24 ft) (28 ft)
(24) (24) (28) ft
(6) (6) (7)
11
(3 ft) (10 ft) ( 10 ft)
3 10 10
11
6 6 7
[(10 6 ) (81 6 ) 78 ]
11
AB
A C
C
F
F
F
a
F
a
F
a a
F λ
i j k
i j k
r i j k
i j k
M
i j k
Since 2 2 2
/ /
| | | | or | | ( )
C A C A C dF
M r F r F
2 2 2 2
1
(10 6 ) (81 6 ) (78)
121
a a d
Setting 2
( ) 0
d
da
d to find a to minimize d:
1
[2(6)(10 6 ) 2( 6)(81 6 )] 0
121
a a
Solving 5.92 ft
a or 5.92 ft
a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-229-320.jpg)

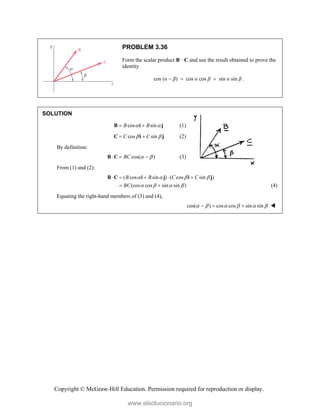

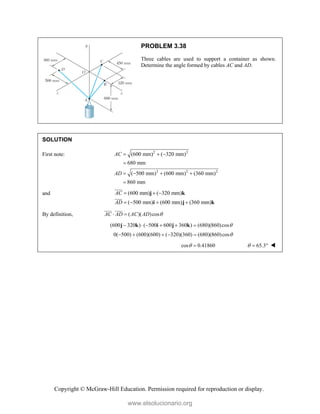


![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.41
Ropes AB and BC are two of the ropes used to
support a tent. The two ropes are attached to a
stake at B. If the tension in rope AB is 540 N,
determine (a) the angle between rope AB and
the stake, (b) the projection on the stake of the
force exerted by rope AB at Point B.
SOLUTION
First note: 2 2 2
2 2 2
( 3) (3) ( 1.5) 4.5 m
( 0.08) (0.38) (0.16) 0.42 m
BA
BD
Then ( 3 3 1.5 )
4.5
( 2 2 )
3
1
( 0.08 0.38 0.16 )
0.42
1
( 4 19 8 )
21
BA
BA
BA
BD
T
T
BD
BD
T i j k
i j k
i j k
i j k
(a) We have cos
BA BD BA
T
T
or
1
( 2 2 ) ( 4 19 8 ) cos
3 21
BA
BA
T
T
i j k i j k
or
1
cos [( 2)( 4) (2)(19) ( 1)(8)]
63
0.60317
or 52.9
(b) We have ( )
cos
(540 N)(0.60317)
BA BD BA BD
BA
T
T
T
or ( ) 326 N
BA BD
T
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-236-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.42
Ropes AB and BC are two of the ropes used to
support a tent. The two ropes are attached to a
stake at B. If the tension in rope BC is 490 N,
determine (a) the angle between rope BC and
the stake, (b) the projection on the stake of the
force exerted by rope BC at Point B.
SOLUTION
First note: 2 2 2
2 2 2
(1) (3) ( 1.5) 3.5 m
( 0.08) (0.38) (0.16) 0.42 m
BC
BD
( 3 1.5 )
3.5
(2 6 3 )
7
1
( 0.08 0.38 0.16 )
0.42
1
( 4 19 8 )
21
BC
BC
BC
BD
T
T
BD
BD
T i j k
i j k
i j k
i j k
(a) cos
BC BD BC
T
T
1
(2 6 3 ) ( 4 19 8 ) cos
7 21
BC
BC
T
T
i j k i j k
1
cos [(2)( 4) (6)(19) ( 3)(8)]
147
0.55782
56.1
(b) ( )
cos
(490 N)(0.55782)
BC BD BC BD
BC
T
T
T
( ) 273 N
BC BD
T
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-237-320.jpg)






![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.49
To loosen a frozen valve, a force F of magnitude 70 lb is
applied to the handle of the valve. Knowing that 25 ,
Mx 61lb ft,
and 43 lb ft,
z
M determine and d.
SOLUTION
We have /
:
O A O O
M r F M
where / (4 in.) (11in.) ( )
(cos cos sin cos sin )
A O d
F
r i j k
F i j k
For 70 lb, 25
F
(70 lb)[(0.90631cos ) 0.42262 (0.90631sin ) ]
(70 lb) 4 11 in.
0.90631cos 0.42262 0.90631sin
(70 lb)[(9.9694sin 0.42262 ) ( 0.90631 cos 3.6252sin )
(1.69048 9.9694cos ) ] in.
O d
d d
F i j k
i j k
M
i j
k
and (70 lb)(9.9694sin 0.42262 ) in. (61lb ft)(12 in./ft)
x
M d
(1)
(70 lb)( 0.90631 cos 3.6252sin ) in.
y
M d
(2)
(70 lb)(1.69048 9.9694cos ) in. 43 lb ft(12 in./ft)
z
M
(3)
From Equation (3): 1 634.33
cos 24.636
697.86
or 24.6
From Equation (1):
1022.90
34.577 in.
29.583
d
or 34.6 in.
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-244-320.jpg)

O F
F
i j k
M
i
j
k
and (11cos sin 27sin )(lb in.)
x
M F
(1)
( 27cos cos 4cos sin ) (lb in.)
y
M F
(2)
(4sin 11cos cos ) (lb in.)
z
M F
(3)
Now, Equation (1)
1
cos sin 27sin
11
x
M
F
(4)
and Equation (3)
1
cos cos 4sin
11
z
M
F
(5)
Substituting Equations (4) and (5) into Equation (2),
1 1
27 4sin 4 27sin
11 11
x
z
y
M
M
M F
F F
or
1
(27 4 )
11
y z x
M M M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-245-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.51
To lift a heavy crate, a man uses a block and tackle attached to the
bottom of an I-beam at hook B. Knowing that the moments about
the y and the z axes of the force exerted at B by portion AB of the
rope are, respectively, 120 N m and 460 N m, determine the
distance a.
SOLUTION
First note (2.2 m) (3.2 m) ( m)
BA a
i j k
Now /
D A D BA
M r T
where / (2.2 m) (1.6 m)
(2.2 3.2 ) (N)
A D
BA
BA
BA
T
a
d
r i j
T i j k
Then 2.2 1.6 0
2.2 3.2
{ 1.6 2.2 [(2.2)( 3.2) (1.6)(2.2)] }
BA
D
BA
BA
BA
T
d
a
T
a a
d
i j k
M
i j k
Thus 2.2 (N m)
10.56 (N m)
BA
y
BA
BA
z
BA
T
M a
d
T
M
d
Then forming the ratio
y
z
M
M
2.2 (N m)
120 N m
460 N m 10.56 (N m)
BA
BA
BA
BA
T
d
T
d
or 1.252 m
a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-247-320.jpg)



![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.55
The 23-in. vertical rod CD is welded to the midpoint C of
the 50-in. rod AB. Determine the moment about AB of the
235-lb force P.
SOLUTION
(32 in.) (30 in.) (24 in.)
AB
i j k
2 2 2
(32) ( 30) ( 24) 50 in.
AB
0.64 0.60 0.48
AB
AB
AB
i k
We shall apply the force P at Point G:
/ (5 in.) (30 in.)
G B
r i k
(21 in.) (38 in.) (18 in.)
DG
i j k
2 2 2
(21) ( 38) (18) 47 in.
DG
21 38 18
(235 lb)
47
DG
P
DG
i j k
P
(105 lb) (190 lb) (90 lb)
P i j k
The moment of P about AB is given by Eq. (3.46):
/
0.64 0.60 0.48
( ) 5 in. 0 30 in.
105 lb 190 lb 90 lb
AB AB G B P
M r
0.64[0 (30 in.)( 190 lb)]
0.60[(30 in.)(105 lb) (5 in.)(90 lb)]
0.48[(5 in.)( 190 lb) 0]
2484 lb in.
AB
M
207 lb ft
AB
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-251-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.56
The 23-in. vertical rod CD is welded to the midpoint C of
the 50-in. rod AB. Determine the moment about AB of the
174-lb force Q.
SOLUTION
(32 in.) (30 in.) (24 in.)
AB
i j k
2 2 2
(32) ( 30) ( 24) 50 in.
AB
0.64 0.60 0.48
AB
AB
AB
i j k
We shall apply the force Q at Point H:
/ (32 in.) (17 in.)
H B
r i j
(16 in.) (21 in.) (12 in.)
DH
i j k
2 2 2
(16) ( 21) ( 12) 29 in.
DH
16 21 12
(174 lb)
29
DH
DH
i j k
Q
(96 lb) (126 lb) (72 lb)
Q
i j k
The moment of Q about AB is given by Eq. (3.46):
/
0.64 0.60 0.48
( ) 32 in. 17 in. 0
96 lb 126 lb 72 lb
AB AB H B
M r Q
0.64[(17 in.)( 72 lb) 0]
0.60[(0 ( 32 in.)( 72 lb)]
0.48[( 32 in.)( 126 lb) (17 in.)( 96 lb)]
2119.7 lb in.
AB
M
176.6 lb ft
AB
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-252-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.57
The frame ACD is hinged at A and D and is supported by a
cable that passes through a ring at B and is attached to
hooks at G and H. Knowing that the tension in the cable is
450 N, determine the moment about the diagonal AD of
the force exerted on the frame by portion BH of the cable.
SOLUTION
/
( )
AD AD B A BH
M
r T
Where
/
1
(4 3 )
5
(0.5 m)
AD
B A
i k
r i
and 2 2 2
(0.375) (0.75) ( 0.75)
1.125 m
BH
d
Then
450 N
(0.375 0.75 0.75 )
1.125
(150 N) (300 N) (300 N)
BH
T i j k
i j k
Finally,
4 0 3
1
0.5 0 0
5
150 300 300
1
[( 3)(0.5)(300)]
5
AD
M
or 90.0 N m
AD
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-253-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.58
In Problem 3.57, determine the moment about the diagonal
AD of the force exerted on the frame by portion BG of the
cable.
PROBLEM 3.57 The frame ACD is hinged at A and D
and is supported by a cable that passes through a ring at B
and is attached to hooks at G and H. Knowing that the
tension in the cable is 450 N, determine the moment about
the diagonal AD of the force exerted on the frame by
portion BH of the cable.
SOLUTION
/
( )
AD AD B A BG
M
r T
Where
/
1
(4 3 )
5
(0.5 m)
AD
B A
i k
r j
and 2 2 2
( 0.5) (0.925) ( 0.4)
1.125 m
BG
Then
450 N
( 0.5 0.925 0.4 )
1.125
(200 N) (370 N) (160 N)
BG
T i j k
i j k
Finally,
4 0 3
1
0.5 0 0
5
200 370 160
AD
M
1
[( 3)(0.5)(370)]
5
111.0 N m
AD
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-254-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.59
The triangular plate ABC is supported by ball-and-socket
joints at B and D and is held in the position shown by
cables AE and CF. If the force exerted by cable AE at A is
55 N, determine the moment of that force about the line
joining Points D and B.
SOLUTION
First note: AE AE
AE
T
AE
T
2 2 2
(0.9) ( 0.6) (0.2) 1.1 m
AE
Then
55 N
(0.9 0.6 0.2 )
1.1
5[(9 N) (6 N) (2 N) ]
AE
T i j k
i j k
Also, 2 2 2
(1.2) ( 0.35) (0)
1.25 m
DB
Then
1
(1.2 0.35 )
1.25
1
(24 7 )
25
DB
DB
DB
i j
i j
Now /
( )
DB DB A D AE
M
r T
where / (0.1 m) (0.2 m)
A D
r j k
Then
24 7 0
1
(5) 0 0.1 0.2
25
9 6 2
1
( 4.8 12.6 28.8)
5
DB
M
or 2.28 N m
DB
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-255-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.60
The triangular plate ABC is supported by ball-and-socket
joints at B and D and is held in the position shown by
cables AE and CF. If the force exerted by cable CF at C is
33 N, determine the moment of that force about the line
joining Points D and B.
SOLUTION
First note: CF CF
CF
T
CF
T
2 2 2
(0.6) ( 0.9) ( 0.2) 1.1 m
CF
Then
33 N
(0.6 0.9 0.2 )
1.1
3[(6 N) (9 N) (2 N) ]
CF
T i j k
i j k
Also, 2 2 2
(1.2) ( 0.35) (0)
1.25 m
DB
Then
1
(1.2 0.35 )
1.25
1
(24 7 )
25
DB
DB
DB
i j
i j
Now /
( )
DB DB C D CF
M
r T
where / (0.2 m) (0.4 m)
C D
r j k
Then
24 7 0
1
(3) 0 0.2 0.4
25
6 9 2
3
( 9.6 16.8 86.4)
25
DB
M
or 9.50 N m
DB
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-256-320.jpg)
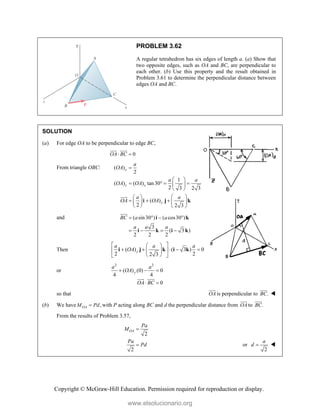



![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.66
In Problem 3.57, determine the perpendicular distance
between portion BH of the cable and the diagonal AD.
PROBLEM 3.57 The frame ACD is hinged at A and D
and is supported by a cable that passes through a ring at B
and is attached to hooks at G and H. Knowing that the
tension in the cable is 450 N, determine the moment about
the diagonal AD of the force exerted on the frame by
portion BH of the cable.
SOLUTION
From the solution to Problem 3.57: 450 N
(150 N) (300 N) (300 N)
BH
BH
T
T i j k
| | 90.0 N m
AD
M
1
(4 3 )
5
AD
i k
Based on the discussion of Section 3.11, it follows that only the perpendicular component of TBH will
contribute to the moment of TBH about line .
AD
Now parallel
( )
1
(150 300 300 ) (4 3 )
5
1
[(150)(4) ( 300)( 3)]
5
300 N
BH BH AD
T
T
i j k i k
Also, parallel perpendicular
( ) ( )
BH BH BH
T T T
so that 2 2
perpendicular
( ) (450) (300) 335.41 N
BH
T
Since AD
and perpendicular
( )
BH
T are perpendicular, it follows that
perpendicular
( )
AD BH
M d T
or 90.0 N m (335.41 N)
d
0.26833 m
d 0.268 m
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-262-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.67
In Problem 3.58, determine the perpendicular distance
between portion BG of the cable and the diagonal AD.
PROBLEM 3.58 In Problem 3.57, determine the moment
about the diagonal AD of the force exerted on the frame by
portion BG of the cable.
PROBLEM 3.57 The frame ACD is hinged at A and D
and is supported by a cable that passes through a ring at B
and is attached to hooks at G and H. Knowing that the
tension in the cable is 450 N, determine the moment about
the diagonal AD of the force exerted on the frame by
portion BH of the cable.
SOLUTION
From the solution to Problem 3.58: 450 N
(200 N) (370 N) (160 N)
BG
BG
T i j k
| | 111 N m
AD
M
1
(4 3 )
5
AD
i k
Based on the discussion of Section 3.11, it follows that only the perpendicular component of TBG will
contribute to the moment of TBG about line .
AD
Now parallel
( )
1
( 200 370 160 ) (4 3 )
5
1
[( 200)(4) ( 160)( 3)]
5
64 N
BG BG AD
T
T
i j k i k
Also, parallel perpendicular
( ) ( )
BG BG BG
T T T
so that 2 2
perpendicular
( ) (450) ( 64) 445.43 N
BG
T
Since AD
and perpendicular
( )
BG
T are perpendicular, it follows that
perpendicular
( )
AD BG
M d T
or 111 N m (445.43 N)
d
0.24920 m
d 0.249 m
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-263-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.68
In Problem 3.59, determine the perpendicular distance
between cable AE and the line joining Points D and B.
PROBLEM 3.59 The triangular plate ABC is supported by
ball-and-socket joints at B and D and is held in the position
shown by cables AE and CF. If the force exerted by cable
AE at A is 55 N, determine the moment of that force about
the line joining Points D and B.
SOLUTION
From the solution to Problem 3.59: 55 N
5[(9 N) (6 N) (2 N) ]
AE
AE
T i j k
| | 2.28 N m
DB
M
1
(24 7 )
25
DB
i j
Based on the discussion of Section 3.11, it follows that only the perpendicular component of TAE will
contribute to the moment of TAE about line .
DB
Now parallel
( )
1
5(9 6 2 ) (24 7 )
25
1
[(9)(24) ( 6)( 7)]
5
51.6 N
AE AE DB
T
T
i j k i j
Also, parallel perpendicular
( ) ( )
AE AE AE
T T T
so that 2 2
perpendicular
( ) (55) (51.6) 19.0379 N
AE
T
Since DB
and perpendicular
( )
AE
T are perpendicular, it follows that
perpendicular
( )
DB AE
M d T
or 2.28 N m (19.0379 N)
d
0.119761
d 0.1198 m
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-264-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.69
In Problem 3.60, determine the perpendicular distance
between cable CF and the line joining Points D and B.
PROBLEM 3.60 The triangular plate ABC is supported by
ball-and-socket joints at B and D and is held in the position
shown by cables AE and CF. If the force exerted by cable
CF at C is 33 N, determine the moment of that force about
the line joining Points D and B.
SOLUTION
From the solution to Problem 3.60: 33 N
3[(6 N) (9 N) (2 N) ]
CF
CF
T i j k
| | 9.50 N m
DB
M
1
(24 7 )
25
DB
i j
Based on the discussion of Section 3.11, it follows that only the perpendicular component of TCF will
contribute to the moment of TCF about line .
DB
Now parallel
( )
1
3(6 9 2 ) (24 7 )
25
3
[(6)(24) ( 9)( 7)]
25
24.84 N
CF CF DB
T T
i j k i j
Also, parallel perpendicular
( ) ( )
CF CF CF
T T T
so that 2 2
perpendicular
( ) (33) (24.84)
21.725 N
CF
T
Since DB
and perpendicular
( )
CF
T are perpendicular, it follows that
perpendicular
| | ( )
DB CF
M d T
or 9.50 N m 21.725 N
d
or 0.437 m
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-265-320.jpg)
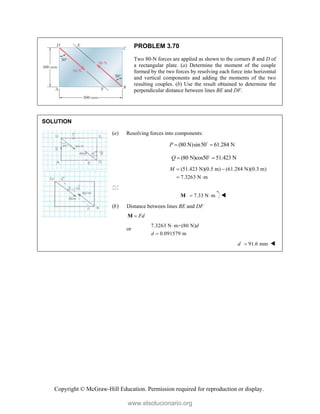

Fd
M k
k
(6.1946 N m)
k or 6.19 N m
M
(c) We have / /
: ( )
A A B A B C A C
M r F r F r F M
(0.390 m)(40 N) cos55 sin55 0
cos20 sin 20 0
(0.660 m)(40 N) cos55 sin55 0
cos20 sin 20 0
(8.9478 N m 15.1424 N m)
(6.1946 N m)
M
i j k
i j k
k
k or 6.19 N m
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-267-320.jpg)

 [(12 ) in.](40 lb)
AD AD BC BC
M d F d F
d d
1.125 in.
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-269-320.jpg)


![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.76
If 0,
P replace the two remaining couples with a single
equivalent couple, specifying its magnitude and the
direction of its axis.
SOLUTION
1 2 1 2
1
/ 2 /
2 2 2
2
2
; 16 lb, 40 lb
(30 in.) [ (16 lb) ] (480 lb in.)
; (15 in.) (5 in.)
(0) (5) (10) 5 5 in.
40 lb
(5 10 )
5 5
8 5[(1 lb) (2 lb) ]
8 5 15 5 0
0 1 2
8 5[(10 lb in.)
C
E B E B
DE
F F
d
F
1
2
M M M
M r F i j k
M r F r i j
j k
j k
i j k
M
i (30 lb in.) (15 lb in.) ]
(480 lb in.) 8 5[(10 lb in.) (30 lb in.) (15 lb in.) ]
(178.885 lb in.) (536.66 lb in.) (211.67 lb in.)
j k
M k i j k
i j k
2 2 2
(178.885) (536.66) ( 211.67)
603.99 lb in
M
604 lb in.
M
axis
z
0.29617 0.88852 0.35045
cos 0.29617
cos 0.88852
cos 0.35045
x
y
M
M
i j k
z
72.8 27.3 110.5
x y
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-272-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.77
If 20 lb,
P replace the three couples with a single
equivalent couple, specifying its magnitude and the
direction of its axis.
SOLUTION
From the solution to Problem. 3.78:
16-lb force: 1 (480 lb in.)
M k
40-lb force: 2 8 5[(10 lb in.) (30 lb in.) (15 lb in.) ]
M
i j k
P 20 lb
3
(30 in.) (20 lb)
(600 lb in.)
C
M P
r
i k
j
1 2 3
2 2 2
(480) 8 5 (10 30 15 ) 600
(178.885 lb in.) (1136.66 lb in.) (211.67 lb in.)
(178.885) (113.66) (211.67)
1169.96 lb in.
M
M M M M
k i j k j
i j k
1170 lb in.
M
axis 0.152898 0.97154 0.180921
cos 0.152898
cos 0.97154
cos 0.180921
x
y
z
M
M
i j k
81.2 13.70 100.4
x y z
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-273-320.jpg)





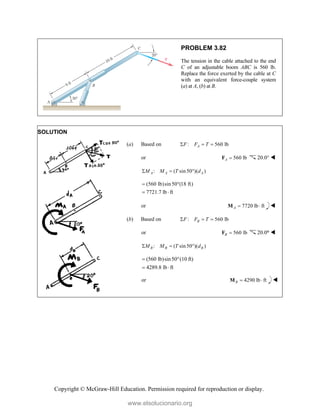
 ( cos30 )(10.7 m)
C A
M F
388.79 N
A
F
or 389 N
A
F 60.0°
Based on
: [(1040 N)cos30 ](6.7 m) ( cos30 )(10.7 m)
A C
M F
651.21 N
C
F
or 651 N
C
F 60.0°
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-280-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.85
A worker tries to move a rock by applying a 360-N
force to a steel bar as shown. (a) Replace that force
with an equivalent force-couple system at D. (b) Two
workers attempt to move the same rock by applying a
vertical force at A and another force at D. Determine
these two forces if they are to be equivalent to the
single force of Part a.
SOLUTION
(a) We have : 360 N( sin 40° cos40 ) (231.40 N) (275.78 N)
F i j i j F
or 360 N
F 50°
We have /
:
D B D
M r R M
where / [(0.65 m)cos30 ] [(0.65 m)sin30 ]
(0.56292 m) (0.32500 m)
0.56292 0.32500 0 N m
231.40 275.78 0
[155.240 75.206)N m]
B D
r i j
i j
i j k
M
k
(230.45 N m)
k or 230 N m
M
(b) We have /
:
D A D A
M M r F
where / [(1.05 m)cos30 ] [(1.05 m)sin30 ]
(0.90933 m) (0.52500 m)
0.90933 0.52500 0 N m
0 1 0
[230.45 N m]
B D
A
F
r i j
i j
i j k
k
(a) (b)
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-282-320.jpg)



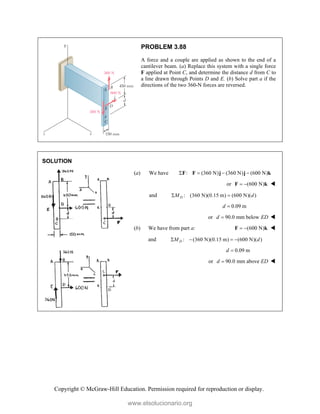
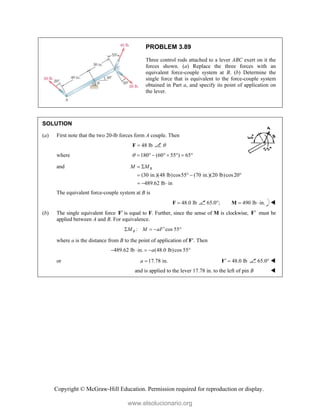

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.91
While tapping a hole, a machinist applies the horizontal
forces shown to the handle of the tap wrench. Show that
these forces are equivalent to a single force, and specify, if
possible, the point of application of the single force on the
handle.
SOLUTION
Since the forces at A and B are parallel, the force at B can be replaced with the sum of two forces with one
of the forces equal in magnitude to the force at A except with an opposite sense, resulting in a force-
couple.
We have 2.9 lb 2.65 lb 0.25 lb,
B
F where the 2.65-lb force is part of the couple. Combining the two
parallel forces,
couple (2.65 lb)[(3.2 in. 2.8 in.)cos25 ]
14.4103 lb in.
M
and couple 14.4103 lb in.
M
A single equivalent force will be located in the negative z direction.
Based on : 14.4103 lb in. [(0.25 lb)cos 25 ]( )
B
M a
63.600 in.
a
F (0.25 lb)(cos 25 sin 25 )
i k
F (0.227 lb) (0.1057 lb)
i k and is applied on an extension of handle BD at a
distance of 63.6 in. to the right of B.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-289-320.jpg)

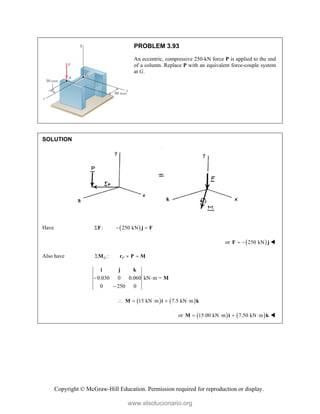

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.95
Replace the 150-N force with an equivalent force-couple
system at A.
SOLUTION
Equivalence requires : (150 N)( cos 35 sin 35 )
(122.873 N) (86.036 N)
F F j k
j k
/
:
A D A
M M r F
where / (0.18 m) (0.12 m) (0.1 m)
D A
r i j k
Then 0.18 0.12 0.1 N m
0 122.873 86.036
[( 0.12)( 86.036) (0.1)( 122.873)]
[ (0.18)( 86.036)]
[(0.18)( 122.873)]
(22.6 N m) (15.49 N m) (22.1 N m)
i j k
M
i
j
k
i j k
The equivalent force-couple system at A is
(122.9 N) (86.0 N)
F j k
(22.6 N m) (15.49 N m) (22.1 N m)
M i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-293-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.96
To keep a door closed, a wooden stick is wedged between the
floor and the doorknob. The stick exerts at B a 175-N force
directed along line AB. Replace that force with an equivalent
force-couple system at C.
SOLUTION
We have
: AB C
F P F
where
(33 mm) (990 mm) (594 mm)
(175 N)
1155.00 mm
AB AB AB
P
P λ
i j k
or (5.00 N) (150.0 N) (90.0 N)
C
F i j k
We have /
:
C B C AB C
M r P M
5 0.683 0.860 0 N m
1 30 18
(5){( 0.860)( 18) (0.683)( 18)
[(0.683)(30) (0.860)(1)] }
C
i j k
M
i j
k
or (77.4 N m) (61.5 N m) (106.8 N m)
C
M i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-294-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.97
A 46-lb force F and a 2120-lbin. couple
M are applied to corner A of the block
shown. Replace the given force-couple
system with an equivalent force-couple
system at corner H.
SOLUTION
We have 2 2 2
(18) ( 14) ( 3) 23 in.
AJ
d
Then
46 lb
(18 14 3 )
23
(36 lb) (28 lb) (6 lb)
F i j k
i j k
Also 2 2 2
( 45) (0) ( 28) 53 in.
AC
d
Then
2120 lb in.
( 45 28 )
53
(1800 lb in.) (1120 lb in.)
M i k
i k
Now /
A H
M M r F
where / (45 in.) (14 in.)
A H
r i j
Then ( 1800 1120 ) 45 14 0
36 28 6
i j k
M i k
( 1800 1120 ) {[(14)( 6)] [ (45)( 6)] [(45)( 28) (14)(36)] }
( 1800 84) (270) ( 1120 1764)
(1884 lb in.) (270 lb in.) (2884 lb in.)
(157 lb ft) (22.5 lb ft) (240 lb ft)
i k i j k
i j k
i j k
i j k
The equivalent force-couple system at H is (36.0 lb) (28.0 lb) (6.00 lb)
F i j k
(157.0 lb ft) (22.5 lb ft) (240 lb ft)
M i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-295-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.98
A 110-N force acting in a vertical plane parallel to the yz-
plane is applied to the 220-mm-long horizontal handle AB
of a socket wrench. Replace the force with an equivalent
force-couple system at the origin O of the coordinate
system.
SOLUTION
We have : B
F P F
where 110 N[ (sin15 ) (cos15 ) ]
(28.470 N) (106.252 N)
B
P j k
j k
or (28.5 N) (106.3 N)
F j k
We have /
:
O B O B O
M
r P M
where / [(0.22cos35 ) (0.15) (0.22sin35 ) ] m
(0.180213 m) (0.15 m) (0.126187 m)
B O
r i j k
i j k
0.180213 0.15 0.126187 N m
0 28.5 106.3
O
i j k
M
[(12.3487) (19.1566) (5.1361) ] N m
O
M i j k
or (12.35 N m) (19.16 N m) (5.13 N m)
O
M i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-296-320.jpg)





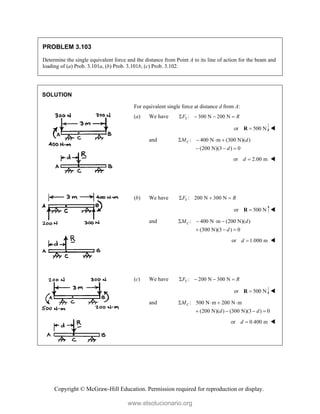
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.104
Five separate force-couple systems act at the corners of a piece of sheet metal, which has been bent into
the shape shown. Determine which of these systems is equivalent to a force F (10 lb)i and a couple of
moment M (15 lb ft)j (15 lb ft)k located at the origin.
SOLUTION
First note that the force-couple system at F cannot be equivalent because of the direction of the force [The
force of the other four systems is (10 lb)i]. Next, move each of the systems to the origin O; the forces
remain unchanged.
: (5 lb ft) (15 lb ft) (2 ft) (10 lb)
A O
A
M M j k k i
(25 lb ft) (15 lb ft)
j k
: (5 lb ft) (25 lb ft)
[(4.5 ft) (1 ft) (2 ft) ] 10 lb)
(15 lb ft) (15 lb ft)
D O
D
M M j k
i j k i
i k
: (15 lb ft) (15 lb ft)
: (15 lb ft) (5 lb ft)
[(4.5 ft) (1 ft) ] (10 lb)
G O
I I
G
I
M M i j
M M j k
i j j
(15 lb ft) (15 lb ft)
j k
The equivalent force-couple system is the system at corner D.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-303-320.jpg)

 ( in.)(11.7 lb)
D
F
d L
or 375.4 3.5 11.7 ( , in in.)
d L d L
(a) 25 in.
d
We have 375.4 3.5(25) 11.7 or 39.6 in.
L L
The resultant passes through a Point 39.6 in. to the right of D.
(b) 42 in.
L
We have 375.4 3.5 11.7(42)
d
or 33.1 in.
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-305-320.jpg)
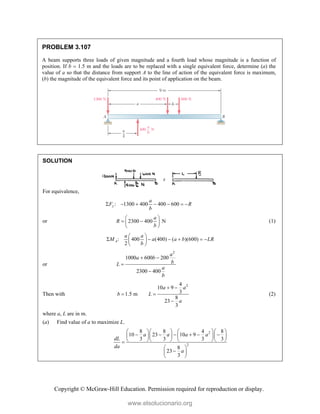

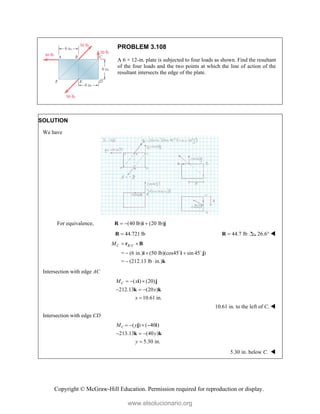
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.109
A 32-lb motor is mounted on the floor. Find the resultant of
the weight and the forces exerted on the belt, and determine
where the line of action of the resultant intersects the floor.
SOLUTION
We have
: (60 lb) (32 lb) (140 lb)(cos30 sin30 )
F i j i j R
(181.244 lb) (38.0 lb)
R i j
or 185.2 lb
R 11.84°
We have :
O O y
M M xR
[(140 lb)cos30 ][(4 2cos30 )in.] [(140 lb)sin30 ][(2 in.)sin30 ]
(60 lb)(2 in.) (38.0 lb)
x
1
( 694.97 70.0 120) in.
38.0
x
and 23.289 in.
x
Or resultant intersects the base (x-axis) 23.3 in. to the left of
the vertical centerline (y-axis) of the motor.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-309-320.jpg)
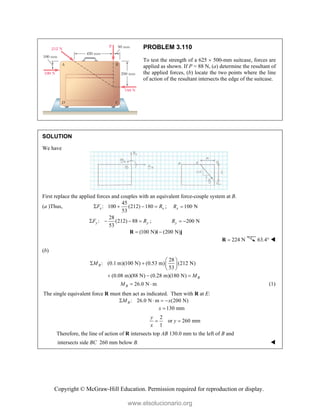
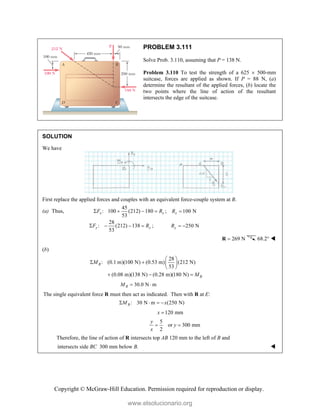


[(360 lb)sin 25 ](12 in.) 90 lb in.
(350.56 lb in.)
F
M k
To determine where a single resultant force will intersect line FE,
350.56 lb in.
127 857 lb
2.7418 in.
F y
F
y
M dR
M
d
R
or 2.74 in.
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-313-320.jpg)
 [240 lbsin 70 ](4 ft)
(160 lb)(12 ft) [300 lbcos40 ](6 ft)
[300 lbsin 40 ](20 ft) (180 lb)(8 ft)
7232.5 lb ft
A
M
7232.5 lb ft
758.36 lb
9.5370 ft
d
or 9.54 ft to the right of
d A
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-314-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.115
A couple M and the three forces shown are applied to an angle
bracket. Find the moment of the couple if the line of action of the
resultant of the force system is to pass through (a) point A, (b) point
B, (c) point C.
SOLUTION
In each case, we must have 1 0
R
M
(a) (12 in.)[(25 lb)sin 60 ] (8 in.)(40 lb) 0
B
A A
M M M
60.192 lb in.
M 60.2 lb in.
M
(b) (12 in.)(10 lb) (8 in.)(40 lb) 0
R
B B
M M M
200 lb in.
M 200 lb in.
M
(c) (12 in.)(10 lb) (8 in.)[(25 lb)cos60 ] 0
R
C C
M M M
20.0 lb in.
M 20.0 lb in.
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-316-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.117
Solve Problem 3.116, assuming that P 60 N.
PROBLEM 3.116 A machine component is subjected to
the forces and couples shown. The component is to be held
in place by a single rivet that can resist a force but not a
couple. For P 0, determine the location of the rivet hole
if it is to be located (a) on line FG, (b) on line GH.
SOLUTION
See the solution to Problem 3.116 leading to the development of Equation (1):
and
(55.544 0.13 ) N m
(152.142 ) N
G
x
M P
R P
For 60 N
P
we have (152.142 60)
212.14 N
[55.544 0.13(60)]
63.344 N m
x
G
R
M
Then with R at I, : 63.344 N m (244.53 N)
G
M a
or 0.259 m
a
and with R at J, : 63.344 N m (212.14 N)
G
M b
or 0.299 m
b
(a) The rivet hole is 0.299 m above G.
(b) The rivet hole is 0.259 m to the right of G.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-318-320.jpg)
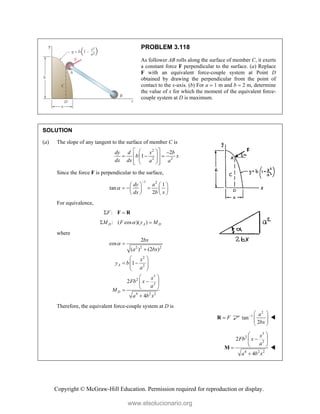


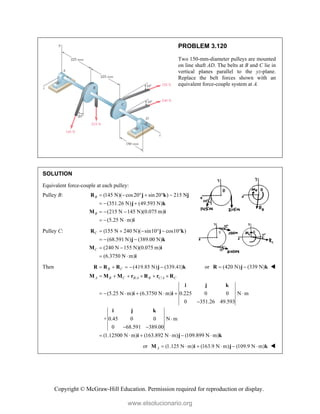

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.122
In order to unscrew the tapped faucet A, a
plumber uses two pipe wrenches as shown.
By exerting a 40-lb force on each wrench, at
a distance of 10 in. from the axis of the pipe
and in a direction perpendicular to the pipe
and to the wrench, he prevents the pipe from
rotating, and thus avoids loosening or further
tightening the joint between the pipe and the
tapped elbow C. Determine (a) the angle θ
that the wrench at A should form with the
vertical if elbow C is not to rotate about the
vertical, (b) the force-couple system at C
equivalent to the two 40-lb forces when this
condition is satisfied.
SOLUTION
We first reduce the given forces to force-couple systems at A and B, noting that
| | | | (40 lb)(10 in.)
400 lb in.
A B
M M
We now determine the equivalent force-couple system at C.
(40 lb)(1 cos ) (40 lb)sin
R i j (1)
(15 in.) [ (40 lb)cos (40 lb)sin ]
(7.5 in.) (40 lb)
400 400 600cos 600sin 300
(600 lb in.)sin (300 lb in.)(1 2cos )
R
C A B
M M M k i j
k i
j i j
i j (2)
(a) For no rotation about vertical, y component of R
C
M must be zero.
1 2cos 0
cos 1/2
60.0
(b) For 60.0
in Eqs. (1) and (2),
(20.0 lb) (34.641 lb) ; (519.62 lb in.)
R
C
R i j M i
(20.0 lb) (34.6 lb) ; (520 lb in.)
R
C
R i j M i
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-324-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.123
Assuming θ 60° in Prob. 3.122, replace the
two 40-lb forces with an equivalent force-
couple system at D and determine whether
the plumber’s action tends to tighten or
loosen the joint between (a) pipe CD and
elbow D, (b) elbow D and pipe DE.
Assume all threads to be right-handed.
PROBLEM 3.122 In order to unscrew the
tapped faucet A, a plumber uses two pipe
wrenches as shown. By exerting a 40-lb
force on each wrench, at a distance of 10 in.
from the axis of the pipe and in a direction
perpendicular to the pipe and to the wrench,
he prevents the pipe from rotating, and thus
avoids loosening or further tightening the
joint between the pipe and the tapped elbow
C. Determine (a) the angle θ that the
wrench at A should form with the vertical if
elbow C is not to rotate about the vertical,
(b) the force-couple system at C equivalent
to the two 40-lb forces when this condition
is satisfied.
SOLUTION
The equivalent force-couple system at C for 60
was obtained in the solution to Prob. 3.122:
(20.0 lb) (34.641 lb)
(519.62 lb in.)
R
C
R i j
M i
The equivalent force-couple system at D is made of R and R
D
M where
/
(519.62 lb in.) (25.0 in.) [(20.0 lb) (34.641 lb) ]
(519.62 lb in.) (500 lb in.)
R R
D C C D
M M r R
i j i j
i k
Equivalent force-couple at D:
(20.0 lb) (34.6 lb) ; (520 lb in.) (500 lb in.)
R
C
R i j M i k
(a) Since R
D
M has no component along the y-axis, the plumber’s action will neither loosen
nor tighten the joint between pipe CD and elbow.
(b) Since the x component of R
D
M is , the plumber’s action will tend to tighten
the joint between elbow and pipe DE.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-325-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.124
Four forces are applied to the machine component
ABDE as shown. Replace these forces with an
equivalent force-couple system at A.
SOLUTION
(50 N) (300 N) (120 N) (250 N)
(420 N) (50 N) (250 N)
(0.2 m)
(0.2 m) (0.16 m)
(0.2 m) (0.1 m) (0.16 m)
B
D
E
R j i i k
R i j k
r i
r k
i
r i j k
[ (300 N) (50 N) ]
( 250 N) ( 120 N)
0.2 m 0 0 0.2 m 0 0.16 m
300 N 50 N 0 0 0 250 N
0.2 m 0.1 m 0.16 m
120 N 0 0
(10 N m) (50 N m) (19.2 N m) (12 N m)
R
A B
D
M r i j
r k r i
i j k i j k
i j k
k j j k
Force-couple system at A is
(420 N) (50 N) (250 N) (30.8 N m) (22.0 N m)
R
A
R i j k M j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-326-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.125
A blade held in a brace is used to tighten a screw at
A. (a) Determine the forces exerted at B and C,
knowing that these forces are equivalent to a force-
couple system at A consisting of R = (25 N)i + Ryj
+ Rzk and M R
A = – (13.5 N·m)i. (b) Find the
corresponding values of Ry and Rz. (c) What is the
orientation of the slot in the head of the screw for
which the blade is least likely to slip when the brace
is in the position shown?
SOLUTION
(a) Equivalence requires :
F R B C
or (25 N) ( )
y z x y z
R R B C C C
i j k k i j k
Equating the i coefficients: : 25 N or 25 N
x x
C C
i
Also, / /
: R
A A B A C A
M M r B r C
or (13.5 N m) [(0.2 m) (0.15 m) ] ( )
(0.4 m) [ (25 N) ]
y z
B
C C
i i j k
i i j k
Equating coefficients: : 13.5 N m (0.15 m) or 75 N
: 0 (0.4 m) or 0
: 0 (0.2 m)(75 N) (0.4 m) or 37.5 N
y y
z z
B B
C C
C C
i
k
j
(75.0 N) (25.0 N) (37.5 N)
B k C i k
(b) Now we have for the equivalence of forces
(25 N) (75 N) [( 25 N) (37.5 N) ]
y z
R R
i j k k i k
Equating coefficients: : 0
y
R
j 0
y
R
: 75 37.5
z
R
k or 37.5 N
z
R
(c) First note that (25 N) (37.5 N) .
R i k Thus, the screw is best able to resist the lateral force z
R
when the slot in the head of the screw is vertical.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-327-320.jpg)
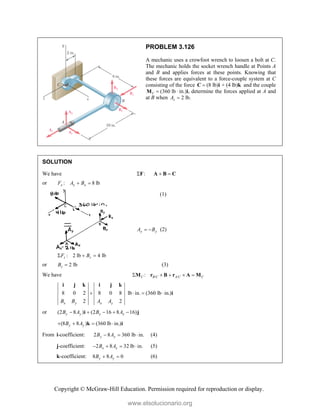

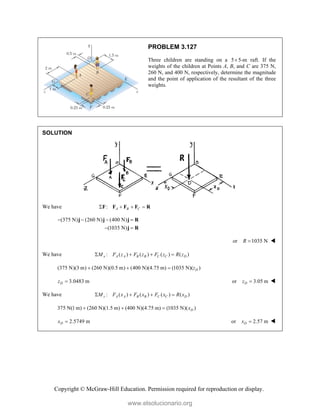
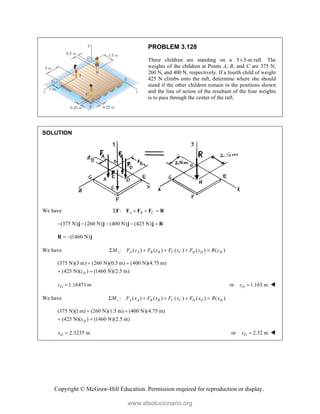





![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.135*
The forces and couples shown are applied to two screws
as a piece of sheet metal is fastened to a block of wood.
Reduce the forces and the couples to an equivalent
wrench and determine (a) the resultant force R, (b) the
pitch of the wrench, (c) the point where the axis of the
wrench intersects the xz-plane.
SOLUTION
First, reduce the given force system to a force-couple system.
We have : (20 N) (15 N) 25 N
R
F i j R
We have : ( ) R
O O C O
M r F M M
20 N(0.1 m) (4 N m) (1 N m)
(4 N m) (3 N m)
R
O
M j i j
i j
(a) (20.0 N) (15.00 N)
R i j
(b) We have 1
( 0.8 0.6 ) [ (4 N m) (3 N m) ]
5 N m
R
R O
M
R
R
M
i j i j
Pitch: 1 5 N m
0.200 m
25 N
M
p
R
or 0.200 m
p
(c) From above, note that
1
R
O
M M
Therefore, the axis of the wrench goes through the origin. The line of action of the wrench lies in
the xy-plane with a slope of
3
4
y x
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-339-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.136*
The forces and couples shown are applied to two screws as a
piece of sheet metal is fastened to a block of wood. Reduce the
forces and the couples to an equivalent wrench and determine
(a) the resultant force R, (b) the pitch of the wrench, (c) the point
where the axis of the wrench intersects the xz-plane.
SOLUTION
First, reduce the given force system to a force-couple at the origin.
We have : (10 lb) (11lb)
F j j R
(21lb)
R j
We have : ( ) R
O O C O
M r F M M
0 0 20 lb in. 0 0 15 lb in. (12 lb in)
0 10 0 0 11 0
(35 lb in.) (12 lb in.)
R
O
i j k i j k
M j
i j
(a) (21lb)
R j or (21.0 lb)
R j
(b) We have 1
1
( ) [(35 lb in.) (12 lb in.) ]
12 lb in. and (12 lb in.)
R
R O R
M
R
R
λ M λ
j i j
M j
and pitch 1 12 lb in.
0.57143 in.
21lb
M
p
R
or 0.571in.
p
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-340-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.136* (Continued)
(c) We have 1 2
2 1 (35 lb in.)
R
O
R
O
M M M
M M M i
We require 2 /
(35 lb in.) ( ) [ (21lb) ]
35 (21 ) (21 )
Q O
x z
x z
M r R
i i k j
i k i
From i: 35 21
1.66667 in.
z
z
From k: 0 21
0
x
z
The axis of the wrench is parallel to the y-axis and intersects the xz-plane at 0, 1.667 in.
x z
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-341-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.137*
Two bolts at A and B are tightened by applying the forces
and couples shown. Replace the two wrenches with a
single equivalent wrench and determine (a) the resultant
R, (b) the pitch of the single equivalent wrench, (c) the
point where the axis of the wrench intersects the xz-plane.
SOLUTION
First, reduce the given force system to a force-couple at the origin.
We have : (84 N) (80 N) 116 N
R
F j k R
and : ( ) R
O O C O
M r F M M
0.6 0 0.1 0.4 0.3 0 ( 30 32 ) N m
0 84 0 0 0 80
R
O
i j k i j k
j k M
(15.6 N m) (2 N m) (82.4 N m)
R
O
M i j k
(a) (84.0 N) (80.0 N)
R j k
(b) We have 1
84 80
[ (15.6 N m) (2 N m) (82.4 N m) ]
116
55.379 N m
R
R O R
M
R
R
λ M λ
j k
i j k
and 1 1 (40.102 N m) (38.192 N m)
R
M
M j k
Then pitch 1 55.379 N m
0.47741m
116 N
M
p
R
or 0.477 m
p
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-342-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.137* (Continued)
(c) We have 1 2
2 1 [( 15.6 2 82.4 ) (40.102 38.192 )] N m
(15.6 N m) (42.102 N m) (44.208 N m)
R
O
R
O
M M M
M M M i j k j k
i j k
We require 2 /
( 15.6 42.102 44.208 ) ( ) (84 80 )
(84 ) (80 ) (84 )
Q O
x z
z x x
M r R
i j k i k j k
i j k
From i: 15.6 84
0.185714 m
z
z
or 0.1857 m
z
From k: 44.208 84
0.52629 m
x
x
or 0.526 m
x
The axis of the wrench intersects the xz-plane at
0.526 m 0 0.1857 m
x y z
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-343-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.138*
Two bolts at A and B are tightened by applying the forces
and couples shown. Replace the two wrenches with a single
equivalent wrench and determine (a) the resultant R,
(b) the pitch of the single equivalent wrench, (c) the point
where the axis of the wrench intersects the xz-plane.
SOLUTION
First, reduce the given force system to a force-couple at the origin at B.
(a) We have
8 15
: (26.4 lb) (17 lb)
17 17
F k i j R
(8.00 lb) (15.00 lb) (26.4 lb)
R i j k
and 31.4 lb
R
We have /
: R
B A B A A B B
M r F M M M
8 15
0 10 0 220 238 264 220 14(8 15 )
17 17
0 0 26.4
(152 lb in.) (210 lb in.) (220 lb in.)
R
B
R
B
i j k
M k i j i k i j
M i j k
(b) We have 1
8.00 15.00 26.4
[(152 lb in.) (210 lb in.) (220 lb in.) ]
31.4
246.56 lb in.
R
R O R
M
R
R
λ M λ
i j k
i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-344-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.139*
Two ropes attached at A and B are used to move the trunk
of a fallen tree. Replace the forces exerted by the ropes
with an equivalent wrench and determine (a) the resultant
force R, (b) the pitch of the wrench, (c) the point where the
axis of the wrench intersects the yz-plane.
SOLUTION
(a) First replace the given forces with an equivalent force-couple system
, R
O
R M at the origin.
We have
2 2 2
2 2 2
(6) (2) (9) 11 m
(14) (2) (5) 15 m
AC
BD
d
d
Then
1650 N
(6 2 9 )
11
(900 N) (300 N) (1350 N)
AC
T
i j k
i j k
and
1500 N
(14 2 5 )
15
(1400 N) (200 N) (500 N)
BD
T
i j k
i j k
Equivalence then requires
:
(900 300 1350 )
(1400 200 500 )
(2300 N) (500 N) (1850 N)
AC BD
F R T T
i j k
i j k
i j k
: R
O O A AC B BD
M M r T r T
(12 m) [(900 N) (300 N) (1350 N) ]
(9 m) [(1400 N) (200 N) (500 N) ]
(3600) (10,800 4500) (1800)
(3600 N m) (6300 N m) (1800 N m)
k i j k
i i j k
i j k
i j k
The components of the wrench are 1
( , ),
R M where
(2300 N) (500 N) (1850 N)
R i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-346-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.139* (Continued)
(b) We have
2 2 2
100 (23) (5) (18.5) 2993.7 N
R
Let
axis
1
(23 5 18.5 )
29.937
R
R
i j k
Then 1 axis
1
(23 5 18.5 ) ( 3600 6300 1800 )
29.937
1
[(23)( 36) (5)(63) (18.5)(18)]
0.29937
601.26 N m
R
O
M
M
i j k i j k
Finally, 1 601.26 N m
2993.7 N
M
P
R
or 0.201 m
P
(c) We have 1 1 axis
1
( 601.26 N m) (23 5 18.5 )
29.937
M M
λ
i j k
or 1 (461.93 N m) (100.421 N m) (371.56 N m)
M i j k
Now 2 1
( 3600 6300 1800 )
( 461.93 100.421 371.56 )
(3138.1 N m) (6400.4 N m) (2171.6 N m)
R
O
M M M
i j k
i j k
i j k
For equivalence:
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-347-320.jpg)


![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.140* (Continued)
(b) We have 1
R
R O
M M
where
3 25 1
(2 20 ) (2 20 )
25 27 5 9 5
R
P
R P
R
i j k i j k
Then 1
1 24 8
(2 20 ) ( )
5
9 5 15 5
Pa Pa
M
i j k i k
and pitch 1 8 25 8
81
15 5 27 5
M Pa a
p
R P
or 0.0988
p a
(c) 1 1
8 1 8
(2 20 ) ( 2 20 )
675
15 5 9 5
R
Pa Pa
M
M i j k i j k
Then 2 1
24 8 8
( ) ( 2 20 ) ( 430 20 406 )
5 675 675
R
O
Pa Pa Pa
M M M i k i j k i j k
We require 2 /
Q O
M r R
8 3
( 403 20 406 ) ( ) (2 20 )
675 25
3
[20 ( 2 ) 20 ]
25
Pa P
x z
P
z x z x
i j k i k i j k
i j k
From i:
3
8( 403) 20 1.99012
675 25
Pa P
z z a
From k:
3
8( 406) 20 2.0049
675 25
Pa P
x x a
The axis of the wrench intersects the xz-plane at
2.00 , 1.990
x a z a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-350-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.141*
Determine whether the force-and-couple system shown can
be reduced to a single equivalent force R. If it can,
determine R and the point where the line of action of R
intersects the yz-plane. If it cannot be so reduced, replace
the given system with an equivalent wrench and determine
its resultant, its pitch, and the point where its axis intersects
the yz-plane.
SOLUTION
First, reduce the given force system to a force-couple at the origin.
We have : A G
F F F R
(40 mm) (60 mm) (120 mm)
(50 N) 70 N
140 mm
(20 N) (30 N) (10 N)
i j k
R k
i j k
and 37.417 N
R
We have : ( ) R
O O C O
M r F M M
0
[(0.12 m) (50 N) ] {(0.16 m) [(20 N) (30 N) (60 N) ]}
(160 mm) (120 mm)
(10 N m)
200 mm
(40 mm) (120 mm) (60 mm)
(14 N m)
140 mm
(18 N m) (8.4 N m) (10.8 N m)
R
O
R
M j k i i j k
i j
i j k
M i j k
To be able to reduce the original forces and couples to a single equivalent force, R and M must be
perpendicular. Thus, 0.
R M
Substituting
?
(20 30 10 ) (18 8.4 10.8 ) 0
i j k i j k
or
?
(20)(18) (30)( 8.4) ( 10)(10.8) 0
or 0 0
R and M are perpendicular so that the given system can be reduced to the single equivalent force.
(20.0 N) (30.0 N) (10.00 N)
R i j k
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-351-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.142*
Determine whether the force-and-couple system shown
can be reduced to a single equivalent force R. If it can,
determine R and the point where the line of action of R
intersects the yz-plane. If it cannot be so reduced, replace
the given system with an equivalent wrench and
determine its resultant, its pitch, and the point where its
axis intersects the yz-plane.
SOLUTION
First determine the resultant of the forces at D. We have
2 2 2
2 2 2
( 12) (9) (8) 17 in.
( 6) (0) ( 8) 10 in.
DA
ED
d
d
Then
34 lb
( 12 9 8 )
17
(24 lb) (18 lb) (16 lb)
DA
F i j k
i j k
and
30 lb
( 6 8 )
10
(18 lb) (24 lb)
ED
F i k
i k
Then
: DA ED
F R F F
( 24 18 16 ( 18 24 )
(42 lb) (18 lb) (8 lb)
i j k i k
i j k
For the applied couple
2 2 2
( 6) ( 6) (18) 6 11 in.
AK
d
Then
160 lb in.
( 6 6 18 )
6 11
160
[ (1 lb in.) (1 lb in.) (3 lb in.) ]
11
M i j k
i j k
To be able to reduce the original forces and couple to a single equivalent force, R and M
must be perpendicular. Thus
?
0
R M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-353-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 3.142* (Continued)
Substituting
?
160
( 42 18 8 ) ( 3 ) 0
11
i j k i j k
or
?
160
[( 42)( 1) (18)( 1) ( 8)(3)] 0
11
or 0 0
R and M are perpendicular so that the given system can be reduced to the single equivalent force.
(42.0 lb) (18.00 lb) (8.00 lb)
R i j k
Then for equivalence,
Thus, we require /
P D
M r R
where / (12 in.) [( 3)in.] ( in.)
P D y z
r i j k
Substituting:
160
( 3 ) 12 ( 3)
11
42 18 8
[( 3)( 8) ( )(18)]
[( )( 42) ( 12)( 8)]
[( 12)(18) ( 3)( 42)]
y z
y z
z
y
i j k
i j k
i
j
k
Equating coefficients:
160
: 42 96 or 1.137 in.
11
480
: 216 42( 3) or 11.59 in.
11
z z
y y
j
k
The line of action of R intersects the yz-plane at 0 11.59 in. 1.137 in.
x y z
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-354-320.jpg)









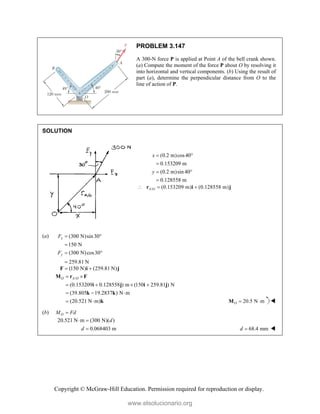
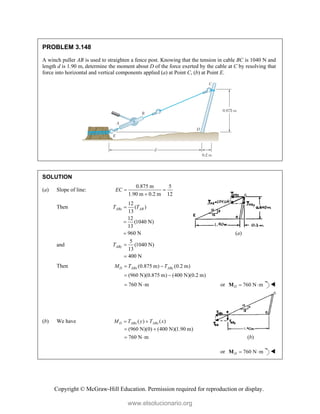

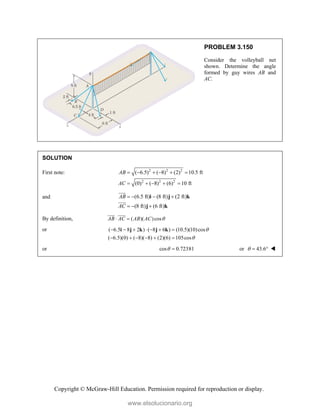








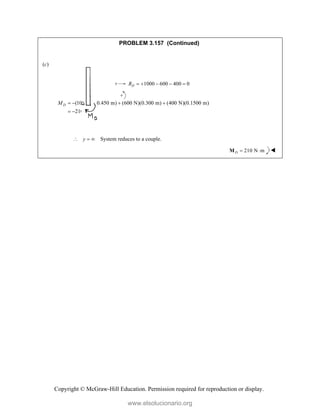















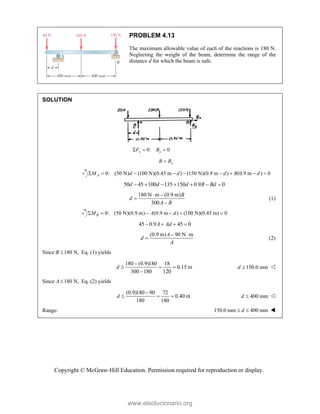
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 4.14
For the beam and loading shown, determine the range of
the distance a for which the reaction at B does not exceed
100 lb downward or 200 lb upward.
SOLUTION
Assume B is positive when directed .
Sketch showing distance from D to forces.
0: (300 lb)(8 in. ) (300 lb)( 2 in.) (50 lb)(4 in.) 16 0
D
M a a B
600 2800 16 0
a B
(2800 16 )
600
B
a
(1)
For 100 lb
B 100 lb,
Eq. (1) yields:
[2800 16( 100)] 1200
2 in.
600 600
a
2.00 in.
a
For 200
B 200 lb,
Eq. (1) yields:
[2800 16(200)] 6000
10 in.
600 600
a
10.00 in.
a
Required range: 2.00 in. 10.00 in.
a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-393-320.jpg)




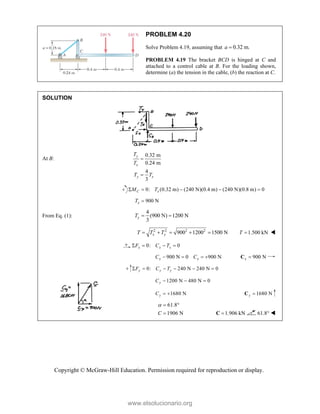


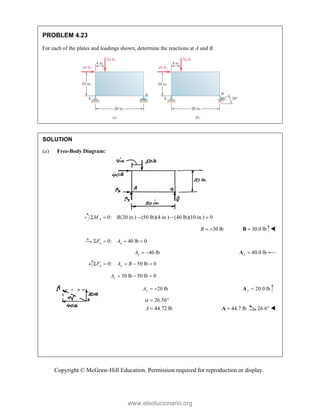
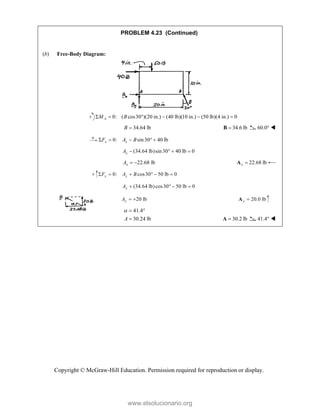
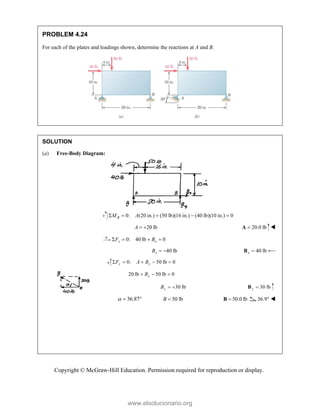
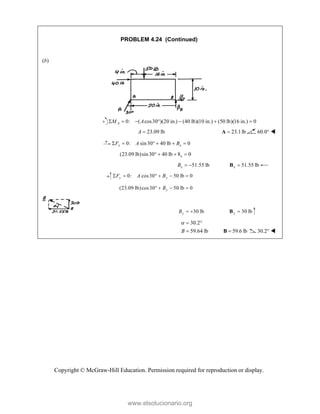


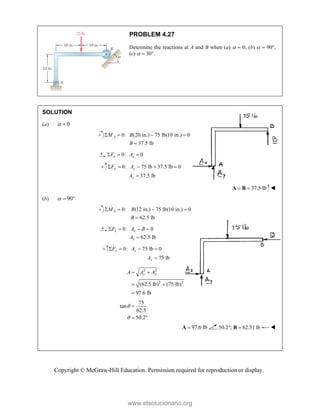
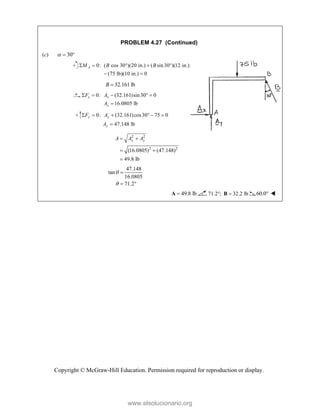













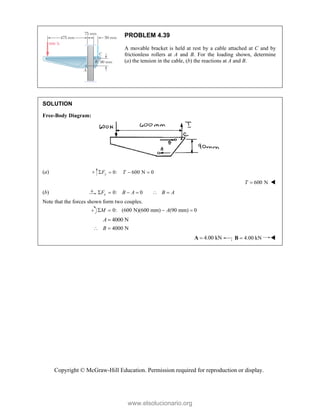
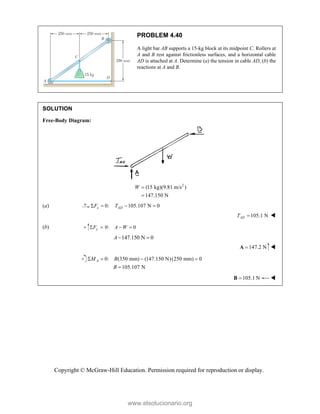


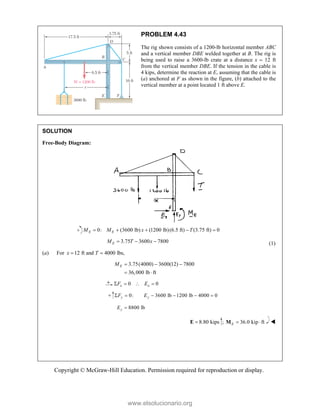

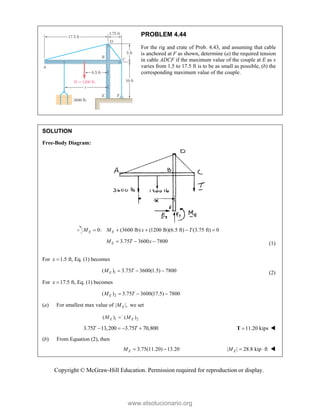
 + max
1.5
3.90
T
(3.6 m) 0
Tmax 2244.7 N or Tmax 2240 N
With MA 500 N m
counter-clockwise: (i.e. corresponding to Tmin )
0:
A
M
500 N m
– [(600 N) cos 15o
](4.5 m) + min
1.5
3.90
T
(3.6 m) 0
Tmin 1522.44 N or Tmin 1522 N
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-430-320.jpg)







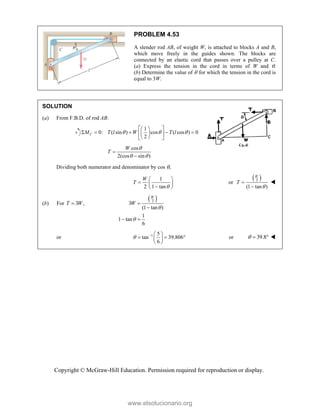



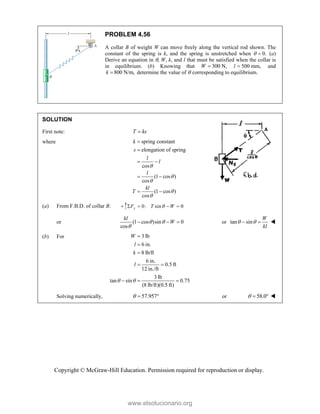









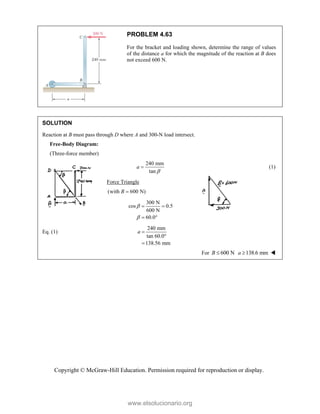


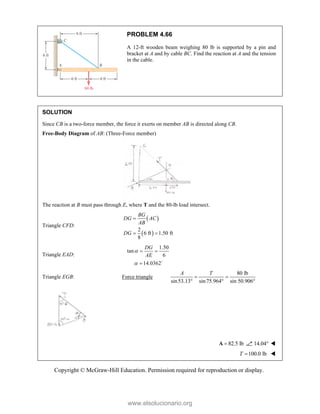


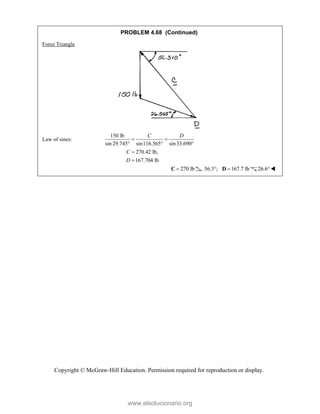
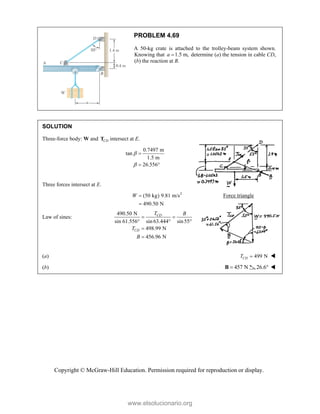
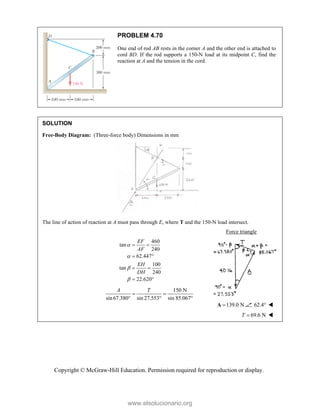





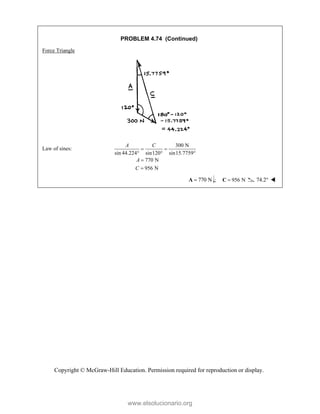

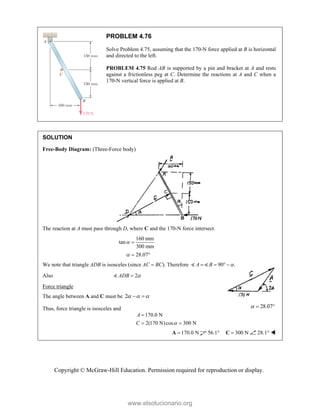
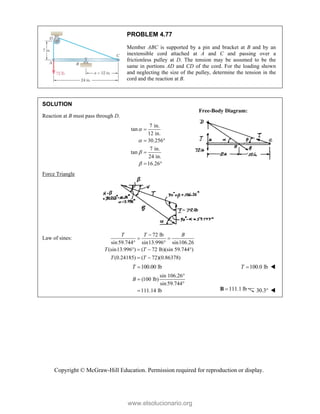



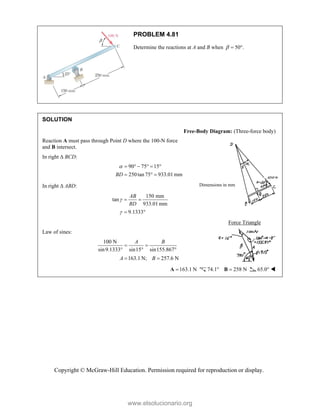
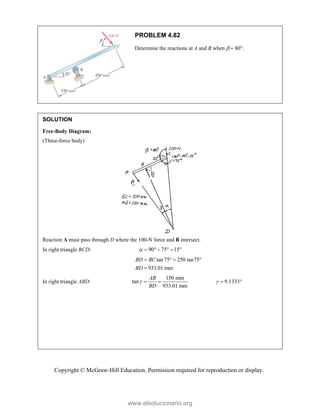
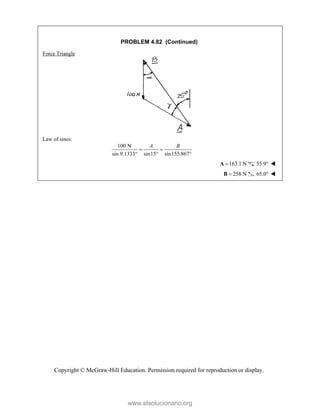
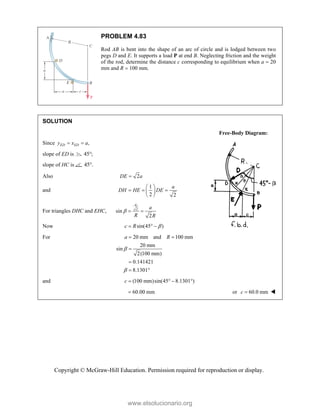










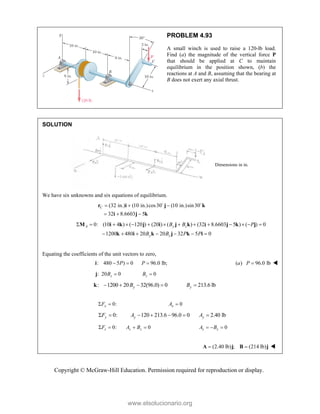



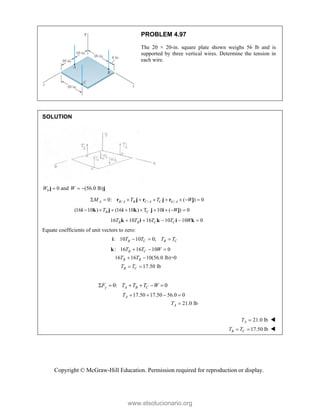



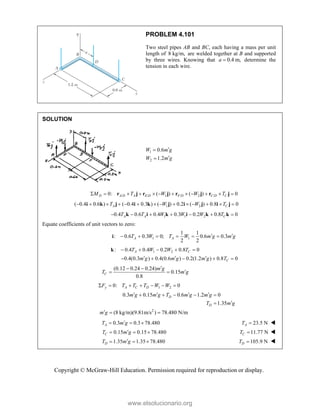
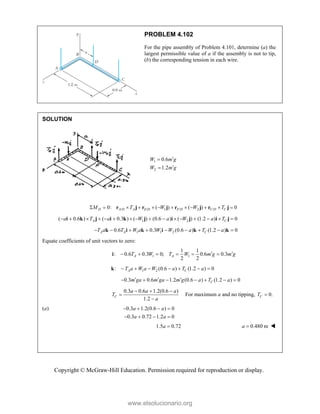



![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 4.104
The table shown weighs 30 lb and has a diameter of 4 ft. It is supported
by three legs equally spaced around the edge. A vertical load P of
magnitude 100 lb is applied to the top of the table at D. Determine the
maximum value of a if the table is not to tip over. Show, on a sketch,
the area of the table over which P can act without tipping the table.
SOLUTION
2 ft sin30 1ft
r b r
We shall sum moments about AB.
( ) ( ) 0
b r C a b P bW
(1 2) ( 1)100 (1)30 0
C a
1
[30 ( 1)100]
3
C a
If table is not to tip, 0.
C
[30 ( 1)100] 0
30 ( 1)100
a
a
1 0.3 1.3 ft 1.300 ft
a a a
Only distance from P to AB matters. Same condition must be satisfied for each leg. P must be located
in shaded area for no tipping.
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-500-320.jpg)






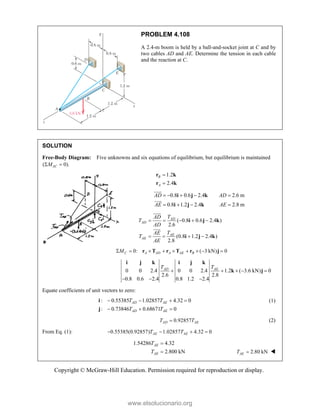











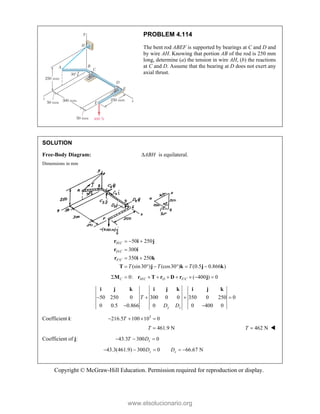













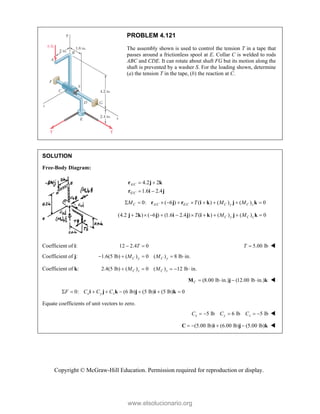
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 4.122
The assembly shown is welded to collar A that fits on the
vertical pin shown. The pin can exert couples about the x
and z axes but does not prevent motion about or along the y-
axis. For the loading shown, determine the tension in each
cable and the reaction at A.
SOLUTION
Free-Body Diagram:
First note:
2 2
2 2
(0.08 m) (0.06 m)
(0.08) (0.06) m
( 0.8 0.6 )
(0.12 m) (0.09 m)
(0.12) (0.09) m
(0.8 0.6 )
CF CF CF CF
CF
DE DE DE DE
DE
T T
T
T T
T
i j
T λ
i j
j k
T λ
j k
(a) From F.B.D. of assembly:
0: 0.6 0.8 480 N 0
y CF DE
F T T
or 0.6 0.8 480 N
CF DE
T T
(1)
0: (0.8 )(0.135 m) (0.6 )(0.08 m) 0
y CF DE
M T T
or 2.25
DE CF
T T
(2)
Substituting Equation (2) into Equation (1),
0.6 0.8[(2.25) ] 480 N
CF CF
T T
200.00 N
CF
T
or 200 N
CF
T
and from Equation (2): 2.25(200.00 N) 450.00
DE
T
or 450 N
DE
T
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-534-320.jpg)

[(450 N)(0.8)](0.09 m) 0
x
x A
M M
16.2000 N m
x
A
M
0: (480 N)(0.08 m) [(200.00 N)(0.6)](0.08 m)
[(450 N)(0.8)](0.08 m) 0
z
z A
M M
0
z
A
M
or (16.20 N m)
A
M i
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-535-320.jpg)
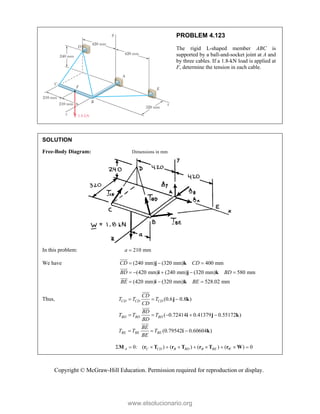




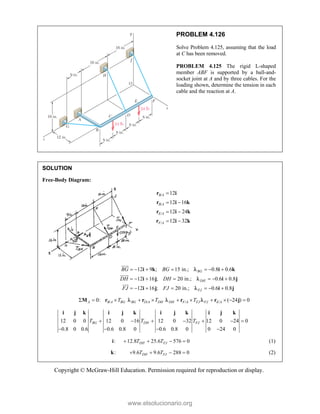





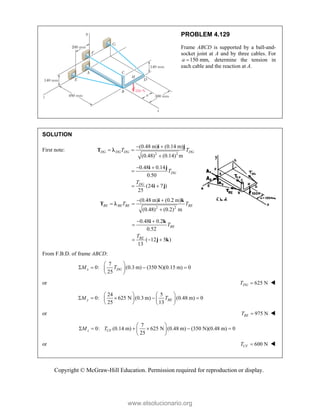

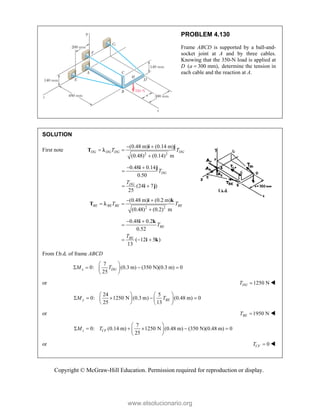

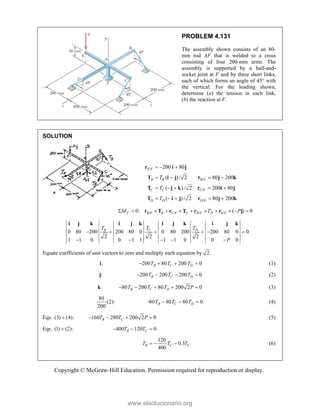



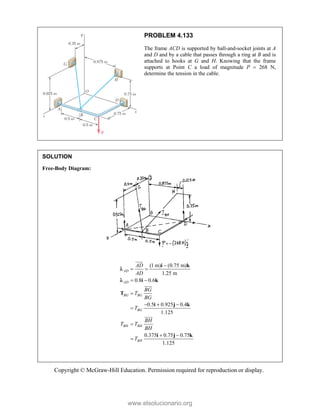

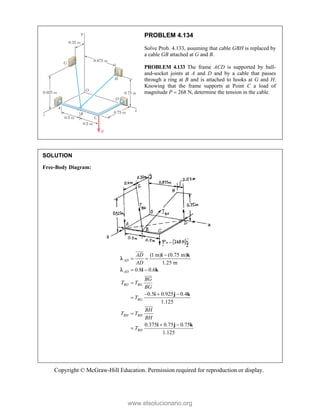

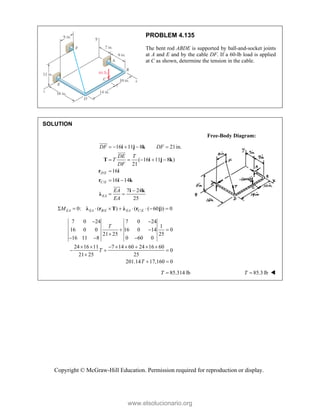



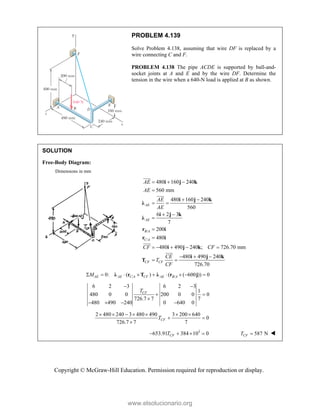
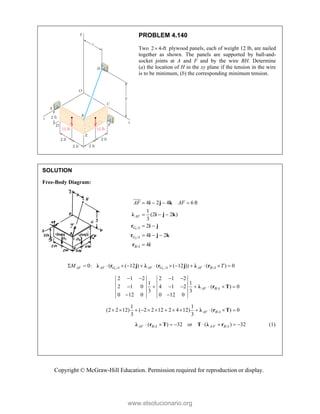



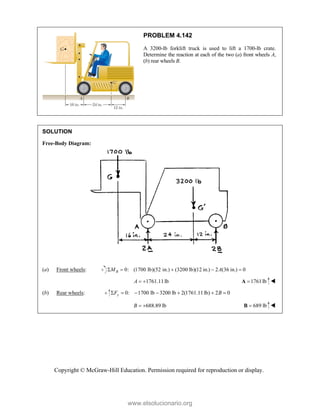

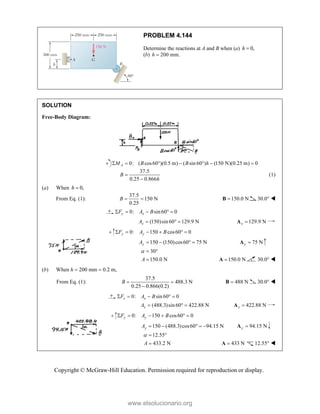
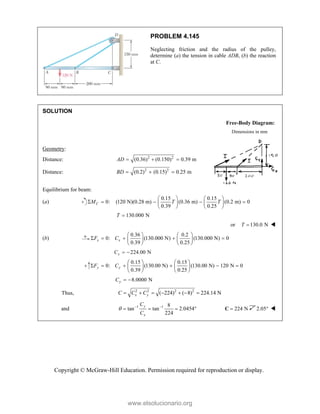


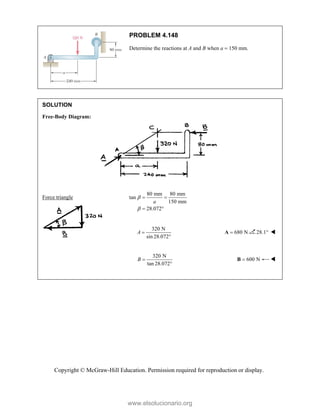

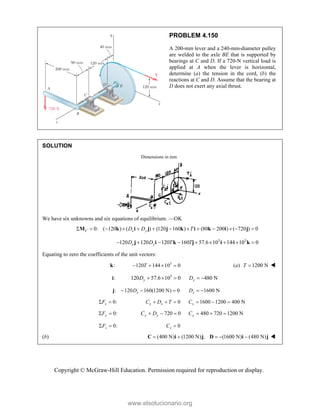
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 4.151
The 45-lb square plate shown is supported by three vertical
wires. Determine the tension in each wire.
SOLUTION
Free-Body Diagram:
/ / /
0: ( 45 lb) 0
B C B C A B A G B
M T T
r j r j r j
[ (20 in.) (15 in.) ] (20 in.)
C A
T T
i k j k j
[ (10 in.) (10 in.) ] [ (45 lb) ] 0
i k j
20 15 20 450 450 0
C C A
T T T
k i i k i
Equating to zero the coefficients of the unit vectors,
:
k 20 450 0
C
T
; 22.5 lb
C
T
:
i 15(22.5) 20 450 0
A
T
; 5.625 lb
A
T
0:
y
F
45 lb 0
A B C
T T T
5.625 lb 22.5 lb 45 lb 0
B
T
; 16.875 lb
B
T
5.63 lb; 16.88 lb; 22.5 lb
A B C
T T T
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-577-320.jpg)








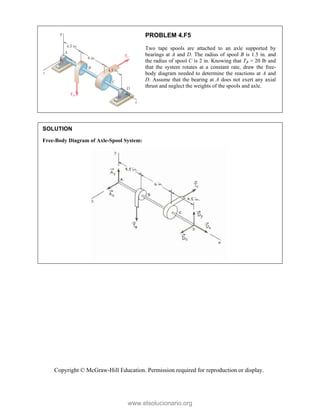

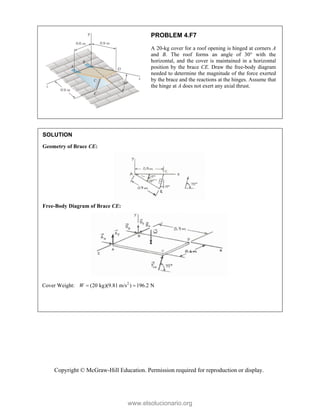


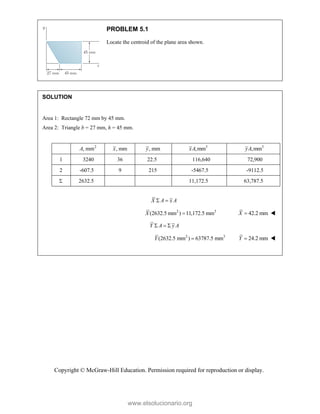
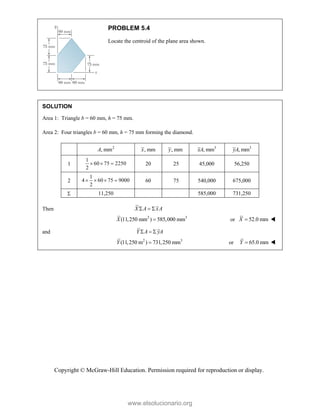
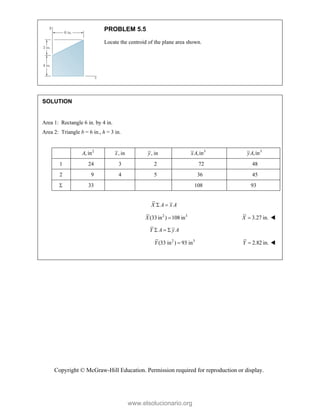

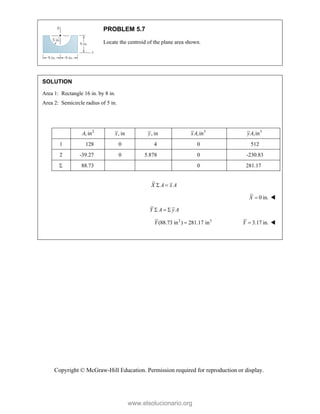

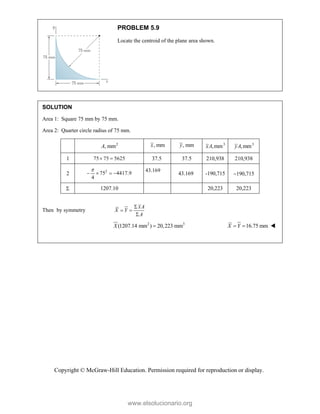
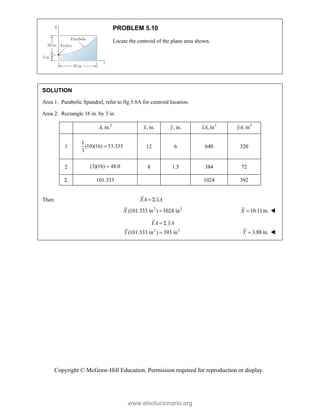
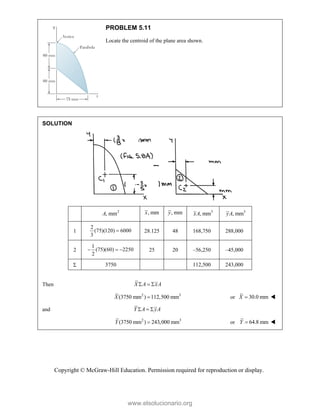

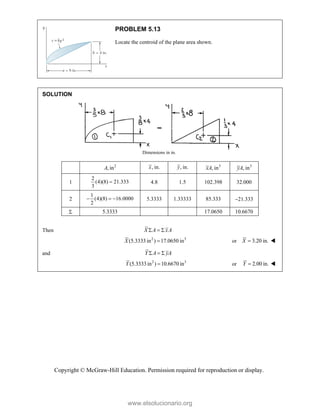

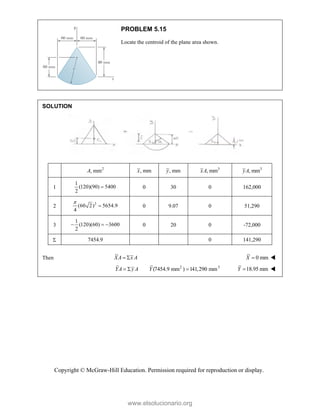







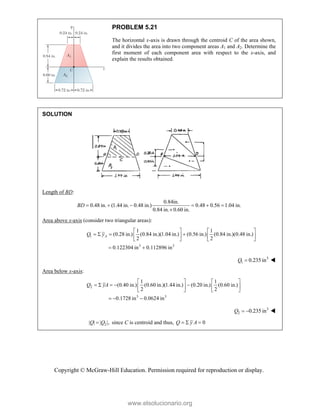

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.23
The first moment of the shaded area with respect to the x-axis is denoted by
Qx. (a) Express Qx in terms of b, c, and the distance y from the base of the
shaded area to the x-axis. (b) For what value of y is x
Q maximum, and what is
that maximum value?
SOLUTION
Shaded area:
( )
1
( )[ ( )]
2
x
A b c y
Q yA
c y b c y
(a) 2 2
1
( )
2
x
Q b c y
(b) For max,
Q
1
0 or ( 2 ) 0
2
dQ
b y
dy
0
y
For 0,
y 2
1
( )
2
x
Q bc
2
1
( )
2
x
Q bc
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-615-320.jpg)
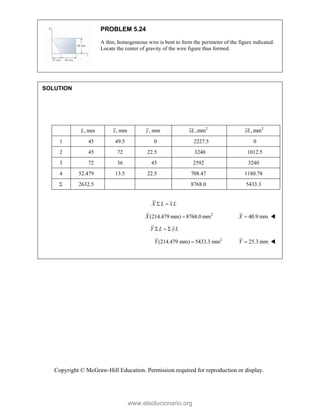
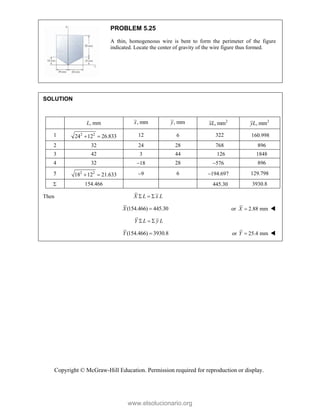
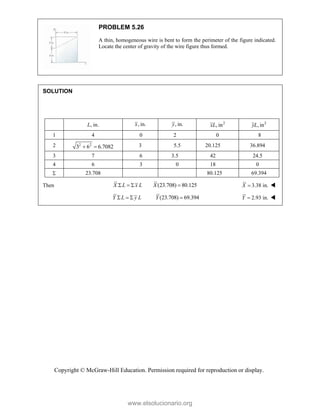





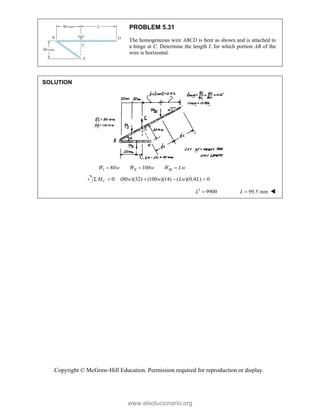




![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.35
Determine by direct integration the centroid of the area shown.
Express your answer in terms of a and h.
SOLUTION
At ( , ),
a h 2
1 :
y h ka
or 2
h
k
a
2 :
y h ma
or
h
m
a
Now
1 2
1
( )
2
EL
EL
x x
y y y
and 2
2 1 2
2
2
( )
( )
h h
dA y y dx x x dx
a a
h
ax x dx
a
Then 2 2 3
2 2
0
0
1 1
( )
2 3 6
a
a h h a
A dA ax x dx x x ah
a a
and
2 3 4 2
2 2
0
0
2 2
1 2 2 1 2 1
1 1
( )
3 4 12
1 1
( )[( ) ]
2 2
a
a
EL
EL
h h a
x dA x ax x dx x x a h
a a
y dA y y y y dx y y dx
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-629-320.jpg)

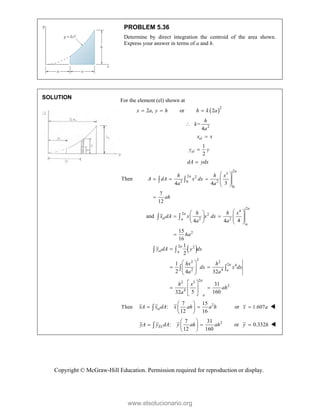
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.37
Determine by direct integration the centroid of the area shown.
SOLUTION
First note that symmetry implies 0
y
EL
dA adx
x x
1
( )
2
2
cos
3
EL
dA a ad
x a
Then
2
0
2
2
0
1
2
[ ] [ ] (1 )
2
a
a
A dA adx a d
a
a x a
and
2
0
2
3
0
3
2 1
( ) cos
3 2
1
[sin ]
2 3
1 2
sin
2 3
a
EL
a
x dA x adx a a d
x
a a
a
2 3 1 2
: [ (1 )] sin
2 3
EL
xA x dA x a a
or
3 4sin
6(1 )
x a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-632-320.jpg)



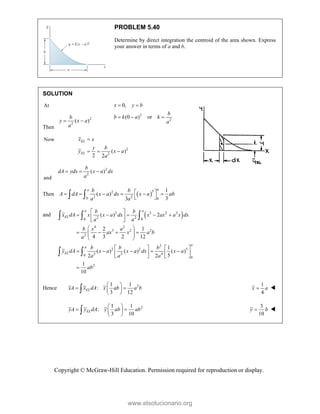
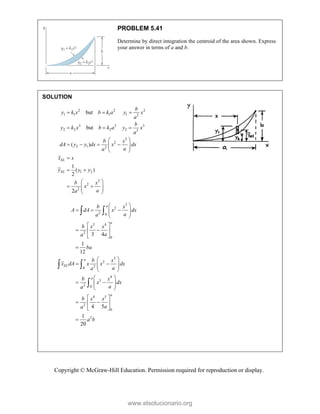




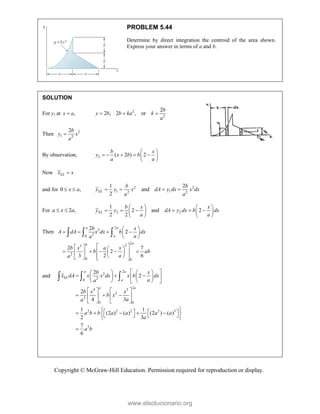

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.45
A homogeneous wire is bent into the shape shown. Determine by direct
integration the x coordinate of its centroid.
SOLUTION
First note that because the wire is homogeneous, its center of gravity coincides with the centroid of the
corresponding line.
Now 3 2 2
cos and
EL
x a dL dx dy
where
3 2
3 2
cos : 3 cos sin
sin : 3 sin cos
x a dx a d
y a dy a d
Then 2 2 2 2 1/2
2 2 1/2
/2
/2
2
0
0
[( 3 cos sin ) (3 sin cos ) ]
3 cos sin (cos sin )
3 cos sin
1
3 cos sin 3 sin
2
3
2
dL a d a d
a d
a d
L dL a d a
a
and
/2
3
0
/2
2 5 2
0
cos (3 cos sin )
1 3
3 cos
5 5
EL
x dL a a d
a a
Hence, 2
3 3
:
2 5
EL
xL x dL x a a
2
5
x a
Alternative Solution:
2/3
3 2
2/3
3 2
cos cos
sin sin
x
x a
a
y
y a
a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-644-320.jpg)

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.46
A homogeneous wire is bent into the shape shown. Determine by direct
integration the x coordinate of its centroid.
SOLUTION
First note that because the wire is homogeneous, its center of gravity coincides with the centroid of the
corresponding line.
Now cos and
EL
x r dL rd
Then
7 /4
7 /4
/4
/4
3
[ ]
2
L dL r d r r
and
7 /4
/4
7 /4
2
/4
2
2
cos ( )
[sin ]
1 1
2 2
2
EL
x dL r rd
r
r
r
Thus 2
3
: 2
2
xL xdL x r r
2 2
3
x r
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-646-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.47*
A homogeneous wire is bent into the shape shown. Determine by direct
integration the x coordinate of its centroid. Express your answer in terms of a.
SOLUTION
First note that because the wire is homogeneous, its center of gravity will coincide with the centroid of the
corresponding line.
We have at ,
x a
3/2 1
, , or
y a a ka k
a
Then 3/2
1
y x
a
and 1/2
3
2
dy
x
dx a
Now EL
x x
and
2
1/2
2
1/2
1
3
1
2
1
4 9
2
dy
dL dx
dx
x dx
a
a x dx
a
Then
0
3/2
0
3/2
1
4 9
2
1 2 1
(4 9 )
3 9
2
[(13) 8]
27
1.43971
a
a
L dL a x dx
a
a x
a
a
a
and
0
1
4 9
2
a
EL
x dL x a x dx
a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-647-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.47* (Continued)
Use integration by parts with
3/2
4 9
2
(4 9 )
27
u x dv a x dx
du dx v a x
Then 3/2 3/2
0
0
3/2
2 5/2
0
2
3/2 5/2
2
1 2 2
(4 9 ) (4 9 )
27 27
2
(13) 1 2
(4 9 )
27 45
27
2
(13) [(13) 32]
27 45
0.78566
a
a
EL
a
x dL x a x a x dx
a
a a x
a
a
a
2
: (1.43971 ) 0.78566
EL
xL x dL x a a
or 0.546
x a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-648-320.jpg)


![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.49*
Determine by direct integration the centroid of the area shown.
SOLUTION
/2 /2
0 0
/2
0
sin
1
, ,
2
sin
cos
EL EL
L L
L
x
y a
L
x x y y dA y dx
x
A y dx a dx
L
L x aL
A a
L
/2 /2
0 0
sin
L L
EL
x
x dA xydx xa dx
L
Setting ,
x
u
L
we have ,
L
x u
,
L
dx du
2
/2 /2
0 0
sin sin
EL
L L L
x dA u a u du a u x du
Integrating by parts,
2 2
/2
/2
0 2
0
2
/2 /2 /2
2 2 2 2
0 0 0
/2
2 2
/2
2
2 0
0
[ cos ] cos
1 1
sin sin
2 2 2
1 1 1
(1 cos2 ) sin 2
2 4 2 8
2
EL
L L
EL
L aL
x dA a u u u du
x a L
y dA y dx a dx u du
L
a L a L
u du u u a L
2
2
:
EL
aL aL
xA x dA x
L
x
2
1
:
8
EL
aL
yA y dA y a L
8
y a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-651-320.jpg)
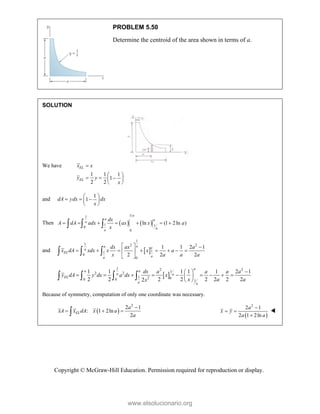
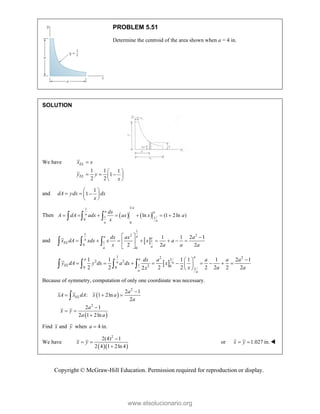
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.52
Determine the volume and the surface area of the solid obtained by rotating
the area of Prob. 5.1 about (a) the x axis, (b) the line x = 72 mm.
SOLUTION
From the solution of Problem 5.1, we have
2
3
3
2632.5 mm
111,172.5 mm
63,787.5 mm
A
xA
yA
Applying the theorems of Pappus-Guldinus, we have
(a) Rotation about the x-axis:
area
3
Volume 2 2
2 (63,787.5 mm )
y A yA
or 3 3
Volume 401 10 mm
line line
2 2 3 3 4 4
2 2
Area 2 2 ( )
2 ( )
2 [(22.5) 45 (45)(72) (22.5) 27 45 ]
y L y L
y L y L y L
or 3 2
Area 34.1 10 mm
(b) Rotation about the line x=72 mm:
area
2 3
Volume 2 (72 ) 2 (72 )
2 72 mm 2632.5 mm 111,172.5 mm
x A A xA
or 3 3
Volume 492 10 mm
line line 1 3 4
1 1 3 3 4 4
2 2
Area 2 2 ( ) where , and are measured wrt 72 mm
2 ( )
45 72
2 [(22.5)(45) (36)(72) 27 45 ]
2
x L x L x x x x
x L x L x L
or 3 2
Area 41.9 10 mm
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-654-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.53
Determine the volume and the surface area of the solid obtained by rotating the
area of Problem 5.2 about (a) the x-axis, (b) the y-axis.
SOLUTION
From the solution of Problem 5.2, we have
2
3
3
11in
11.5 in
39.5 in
A
xA
yA
Applying the theorems of Pappus-Guldinus, we have
(a) Rotation about the x-axis:
area
3
Volume 2 2
2 (39.5 in )
y A yA
or 3
Volume 248 in
line line
2 2 3 3 4 4 5 5 6 6 7 7 8 8
Area 2 2 ( )
2 ( )
2 [(1)(2) (2)(3) (2.5)(1) (3)(3) (5.5)(5) (8)(1) (4)(8)]
y L y L
y L y L y L y L y L y L y L
or 2
Area 547 in
(b) Rotation about the y-axis:
area
3
Volume 2 2
2 (11.5 in )
x A xA
or 3
Volume 72.3in
line line
1 1 2 2 3 3 4 4 5 5 6 6 7 7
Area 2 2 ( )
2 ( )
2 [(0.5)(1) (1)(2) (2.5)(3) (4)(1) (2.5)(3) (1)(5) (0.5)(1)]
x L x L
x L x L x L x L x L x L x L
or 2
Area 169.6 in
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-655-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.54
Determine the volume and the surface area of the solid obtained by rotating the
area of Problem 5.6 about (a) the line x 60 mm, (b) the line y 120 mm.
SOLUTION
From the solution of Problem 5.6, we have
2
3 3
3 3
7200 mm
72 10 mm
629.83 10 mm
A
x A
y A
Applying the theorems of Pappus-Guldinus, we have
(a) Rotation about line 60 mm:
x
3
Volume 2 ( 60) 2 ( 60 )
2 [ 72 10 60(7200)]
x A xA A
6 3
Volume 2.26 10 mm
line line
1 1 2 2 3 3
Area 2 2 ( )
2 ( )
2(60) (60) 2(60) (60)
2 60 60 (60)(120)
2 2
x L x L
x L x L x L
where 1 2 3
, ,
x x x are measured with respect to line 60 mm.
x 3 2
Area 116.3 10 mm
(b) Rotation about line 120 mm:
y
3
Volume 2 (120 ) 2 (120 )
2 [120(7200) 629.83 10 ]
y A A yA
6 3
Volume 1.471 10 mm
line line
1 1 2 2 4 4
Area 2 2 ( )
2 ( )
y L y L
y L y L y L
where 1 2 4
, ,
y y y are measured with respect to line 120 mm.
y
2(60) (60) 2(60) (60)
Area 2 120 (60)(120)
2 2
3 2
Area 116.3 10 mm
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-656-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.55
Determine the volume and the surface area of the chain link
shown, which is made from a 6-mm-diameter bar, if R 10 mm
and L 30 mm.
SOLUTION
The area A and circumference C of the cross section of the bar are
2
and .
4
A d C d
Also, the semicircular ends of the link can be obtained by rotating the cross section through a horizontal
semicircular arc of radius R. Now, applying the theorems of Pappus-Guldinus, we have for the volume V,
side end
2( ) 2( )
2( ) 2( )
2( )
V V V
AL RA
L R A
or 2
2[30 mm (10 mm)] (6 mm)
4
V
3
3470 mm
3
or 3470 mm
V
For the area A, side end
2( ) 2( )
2( ) 2( )
2( )
A A A
CL RC
L R C
or 2[30 mm (10 mm)][ (6 mm)]
A
2
2320 mm
2
or 2320 mm
A
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-657-320.jpg)
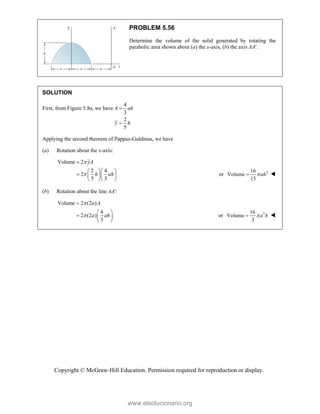


![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.59
Three different drive belt profiles are to be
studied. If at any given time each belt
makes contact with one-half of the
circumference of its pulley, determine the
contact area between the belt and the
pulley for each design.
SOLUTION
Applying the first theorem of Pappus-Guldinus, the contact area C
A of a
belt is given by
C
A yL yL
where the individual lengths are the lengths of the belt cross section that
are in contact with the pulley.
(a)
1 1 2 2
[2( ) ]
0.125 0.125 in.
2 3 in. [(3 0.125) in.](0.625 in.)
2 cos20
C
A y L y L
or 2
8.10 in
C
A
(b) 1 1
[2( )]
0.375 0.375 in.
2 3 0.08 in.
2 cos20
C
A y L
or 2
6.85 in
C
A
(c) 1 1
[2( )]
2(0.25)
3 in. [ (0.25 in.)]
C
A y L
or 2
7.01in
C
A
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-661-320.jpg)






![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.65*
The shade for a wall-mounted light is formed from a thin
sheet of translucent plastic. Determine the surface area of the
outside of the shade, knowing that it has the parabolic cross
section shown.
SOLUTION
First note that the required surface area A can be generated by rotating the parabolic cross section through
radians about the y-axis. Applying the first theorem of Pappus-Guldinus, we have
A xL
Now at
2 1
100 mm, 250 mm
250 (100) or 0.025 mm
x y
k k
and
2
1
EL
x x
dy
dL dx
dx
where 2
dy
kx
dx
Then 2 2
1 4
dL k x dx
We have
100
2 2
0
1 4
EL
xL x dL x k x dx
100
2 2 3/2
2
0
2 2 3/2 3/2
2
2
1 1
(1 4 )
3 4
1 1
[1 4(0.025) (100) ] (1)
12 (0.025)
17,543.3 mm
xL k x
k
Finally, 2
(17,543.3 mm )
A
or 3 2
55.1 10 mm
A
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-668-320.jpg)








 300(4 ) N
2
R a a
R a a
Then 0: 900 300(4 ) 0
y y y
F A a a B
or 1200 600
y y
A B a
Now 600 300 (N)
y y y y
A B A B a
(1)
Also, 0: (4 m) 4 m [(900 ) N]
3
B y
a
M A a
1
(4 ) m [300(4 ) N] 0
3
a a
or 2
400 700 50
y
A a a
(2)
Equating Eqs. (1) and (2), 2
600 300 400 700 50
a a a
or 2
8 4 0
a a
Then
2
8 ( 8) 4(1)(4)
2
a
or 0.53590 m
a 7.4641m
a Now 4 m
a 0.536 m
a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-677-320.jpg)

 300(4 ) N
2
R a a
R a a
Then
8
0: m (900 N) m [300(4 )N] (4 m) 0
3 3
A y
a a
M a a B
or 2
50 100 800
y
B a a
(1)
Then 100 100 0
y
dB
a
da
or 1.000 m
a
(b) From Eq. (1): 2
50(1) 100(1) 800 750 N
y
B 750 N
B
and 0: 0
x x
F A
0: 900(1) N 300(4 1) N 750 N 0
y y
F A
or 1050 N
y
A 1050 N
A
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-679-320.jpg)


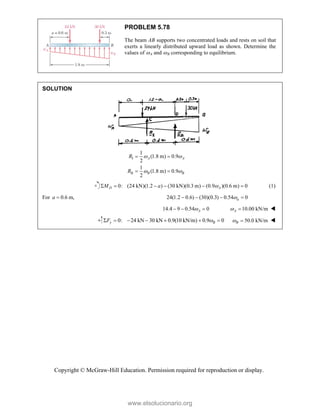
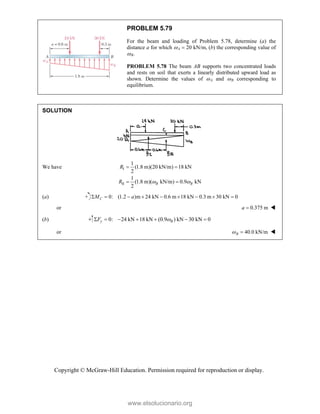
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.80
The cross section of a concrete dam is as shown. For a 1-ft-wide
dam section determine (a) the resultant of the reaction forces exerted
by the ground on the base AB of the dam, (b) the point of application
of the resultant of part a, (c) the resultant of the pressure forces
exerted by the water on the face BC of the dam.
SOLUTION
The free body shown consists of a 1-ft thick section of the dam and the triangular section of water above
the dam.
Note:
1
2
3
4
6 ft
(9 3)ft 12 ft
15 2 ft 17 ft
15 4 ft 19 ft
x
x
x
x
(a) Now W V
So that
3
1
3
2
3
3
3
4
1
(150 lb/ft ) (9 ft) 15 ft (1 ft) 10,125 lb
2
(150 lb/ft )[(6 ft)(18 ft)(1 ft)] 16,200 lb
1
(150 lb/ft ) 6 ft 18 ft (1 ft) 8100 lb
2
1
(62.4 lb/ft ) (6 ft) 18 ft (1 ft) 3369.6 lb
2
W
W
W
W
Also 3
1 1
[(18 ft)(1 ft)][(62.4 lb/ft )(18 ft)] 10,108.8 lb
2 2
P Ap
Then 0: 10,108.8 lb 0
x
F H
or 10.11 kips
H
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-684-320.jpg)



![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.82
The dam for a lake is designed to withstand the additional force caused by
silt that has settled on the lake bottom. Assuming that silt is equivalent to
a liquid of density 3 3
1.76 10 kg/m
s
and considering a 1-m-wide
section of dam, determine the percentage increase in the force acting on
the dam face for a silt accumulation of depth 2 m.
SOLUTION
First, determine the force on the dam face without the silt.
We have
3 3 2
1 1
( )
2 2
1
[(6.6 m)(1 m)][(10 kg/m )(9.81 m/s )(6.6 m)]
2
213.66 kN
w w
P Ap A gh
Next, determine the force on the dam face with silt
We have 3 3 2
3 3 2
I
3 3 2
II
1
[(4.6 m)(1 m)][(10 kg/m )(9.81m/s )(4.6 m)]
2
103.790 kN
( ) [(2.0 m)(1 m)][(10 kg/m )(9.81m/s )(4.6 m)]
90.252 kN
1
( ) [(2.0 m)(1 m)][(1.76 10 kg/m )(9.81 m/s )(2.0 m)]
2
34.531 kN
w
s
s
P
P
P
Then I II
( ) ( ) 228.57 kN
w s s
P P P P
The percentage increase, % inc., is then given by
% inc. 100%
(228.57 213.66)
100%
213.66
6.9874%
w
w
P P
P
% inc. 6.98%
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-688-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.83
The base of a dam for a lake is designed to resist up to 120 percent of the
horizontal force of the water. After construction, it is found that silt (that is
equivalent to a liquid of density 3 3
1.76 10 kg/m )
s
is settling on the
lake bottom at the rate of 12 mm/year. Considering a 1-m-wide section of
dam, determine the number of years until the dam becomes unsafe.
SOLUTION
First determine force on dam without the silt,
3 3 2
allow
1 1
( )
2 2
1
[(6.6 m)(1m)][(10 kg/m )(9.81m/s )(6.6 m)]
2
213.66 kN
1.2 (1.5)(213.66 kN) 256.39 kN
w
w p
w
P A A gh
P P
Next determine the force Pon the dam face after a depth d of silt has settled.
We have 3 3 2
2
3 3 2
I
2
3 3 2
II
2
1
[(6.6 ) m (1m)][(10 kg/m )(9.81m/s )(6.6 ) m]
2
4.905(6.6 ) kN
( ) [ (1m)][(10 kg/m )(9.81m/s )(6.6 ) m]
9.81(6.6 ) kN
1
( ) [ (1m)][(1.76 10 kg/m )(9.81m/s )( ) m]
2
8.6328 kN
w
s
s
P d d
d
P d d
d d
P d d
d
2
I II
2 2
2
( ) ( ) [4.905(43.560 13.2000 )
9.81(6.6 ) 8.6328 ] kN
[3.7278 213.66] kN
w s s
P P P P d d
d d d
d
Now it’s required that allow
P P
to determine the maximum value of d.
2
(3.7278 213.66) kN 256.39 kN
d
or 3.3856 m
d
Finally, 3 m
3.3856 m 12 10 N
year
or 282 years
N
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-689-320.jpg)



![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.87
The 3 4-m side of an open tank is hinged at its bottom A and is held in place by
a thin rod BC. The tank is to be filled with glycerine, whose density is 1263
kg/m3
. Determine the force T in the rod and the reactions at the hinge after the
tank is filled to a depth of 2.9 m.
SOLUTION
Consider the free-body diagram of the side.
We have
3 2
1 1
( )
2 2
1
[(2.9 m)(4 m)] [(1263 kg/m )(9.81 m/s )(2.9 m)]
2
= 208.40 kN
P Ap A gd
Then 0: 0
y y
F A
2.9
0: (3 m) m (208.4 kN) 0
3
A
M T
or 67.151 kN
T 67.2 kN
T
0: 208.40 kN 67.151 kN 0
x x
F A
or 141.249 kN
x
A 141.2 kN
A
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-693-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.88
A 0.5 0.8-m gate AB is located at the bottom of a tank filled with
water. The gate is hinged along its top edge A and rests on a
frictionless stop at B. Determine the reactions at A and B when cable
BCD is slack.
SOLUTION
First consider the force of the water on the gate.
We have
1 1
( )
2 2
P Ap A gh
so that 3 3 2
I
1
[(0.5 m)(0.8 m)] [(10 kg/m )(9.81 m/s )(0.45 m)]
2
882.9 N
P
3 3 2
II
1
[(0.5 m)(0.8 m)] [(10 kg/m )(9.81 m/s )(0.93 m)]
2
1824.66 N
P
Reactions at A and B when T 0:
We have
1 2
0: (0.8 m)(882.9 N) + (0.8 m)(1824.66 N) (0.8 m) 0
3 3
A
M B
or 1510.74 N
B
or 1511 N
B 53.1
0: 1510.74 N 882.9 N 1824.66 N 0
F A
or 1197 N
A 53.1
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-694-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.89
A 0.5 0.8-m gate AB is located at the bottom of a tank filled with
water. The gate is hinged along its top edge A and rests on a
frictionless stop at B. Determine the minimum tension required in
cable BCD to open the gate.
SOLUTION
First consider the force of the water on the gate.
We have
1 1
( )
2 2
P Ap A gh
so that 3 3 2
I
1
[(0.5 m)(0.8 m)] [(10 kg/m )(9.81 m/s )(0.45 m)]
2
882.9 N
P
3 3 2
II
1
[(0.5 m)(0.8 m)] [(10 kg/m )(9.81 m/s )(0.93 m)]
2
1824.66 N
P
T to open gate:
First note that when the gate begins to open, the reaction at B 0.
Then
1 2
0: (0.8 m)(882.9 N)+ (0.8 m)(1824.66 N)
3 3
8
(0.45 0.27)m 0
17
A
M
T
or 235.44 973.152 0.33882 0
T
or 3570 N
T
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-695-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.90
A 4 2-ft
gate is hinged at A and is held in position by rod CD. End
D rests against a spring whose constant is 828 lb/ft. The spring is
undeformed when the gate is vertical. Assuming that the force
exerted by rod CD on the gate remains horizontal, determine the
minimum depth of water d for which the bottom B of the gate will
move to the end of the cylindrical portion of the floor.
SOLUTION
First determine the forces exerted on the gate by the spring and the water when B is at the end of the
cylindrical portion of the floor.
We have
2
sin 30
4
Then (3 ft)tan30
SP
x
and
828 lb/ft 3 ft tan30°
1434.14 lb
SP SP
F kx
Assume 4 ft
d
We have
1 1
( )
2 2
P Ap A h
Then 3
I
1
[(4 ft)(2 ft)] [(62.4 lb/ft )( 4) ft]
2
249.6( 4) lb
P d
d
3
II
1
[(4 ft)(2 ft)] [(62.4 lb/ft )( 4 4cos30 )]
2
249.6( 0.53590 ) lb
P d
d
For min
d so that the gate opens, 0
W
Using the above free-body diagrams of the gate, we have
4 8
0: ft [249.6( 4) lb] ft [249.6( 0.53590) lb]
3 3
A
M d d
(3 ft)(1434.14 lb) 0
or (332.8 1331.2) (665.6 356.70) 4302.4 0
d d
or 6.00 ft
d
4 ft
d assumption correct 6.00 ft
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-696-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.91
Solve Problem 5.90 if the gate weighs 1000 lb.
PROBLEM 5.90 A 4 2-ft
gate is hinged at A and is held in
position by rod CD. End D rests against a spring whose constant is
828 lb/ft. The spring is undeformed when the gate is vertical.
Assuming that the force exerted by rod CD on the gate remains
horizontal, determine the minimum depth of water d for which the
bottom B of the gate will move to the end of the cylindrical portion
of the floor.
SOLUTION
First determine the forces exerted on the gate by the spring and the water when B is at the end of the
cylindrical portion of the floor.
We have
2
sin 30
4
Then (3 ft)tan30
SP
x
and 828 lb/ft 3 ft tan30°
1434.14 lb
SP SP
F kx
Assume 4 ft
d
We have
1 1
( )
2 2
P Ap A h
Then 3
I
1
[(4 ft)(2 ft)] [(62.4 lb/ft )( 4) ft]
2
249.6( 4) lb
P d
d
3
II
1
[(4 ft)(2 ft)] [(62.4 lb/ft )( 4 4cos30 )]
2
249.6( 0.53590 ) lb
P d
d
For min
d so that the gate opens, 1000 lb
W
Using the above free-body diagrams of the gate, we have
4 8
0: ft [249.6( 4) lb] ft [249.6( 0.53590) lb]
3 3
(3 ft)(1434.14 lb) (1ft)(1000 lb) 0
A
M d d
or (332.8 1331.2) (665.6 356.70) 4302.4 1000 0
d d
or 7.00 ft
d
4 ft
d assumption correct 7.00 ft
d
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-697-320.jpg)









![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.97 (Continued)
(b) For 2.5 ,
h b
2 2
1
(2.5 ) 1.8333
3
V a b b a b
2 2 2
2 2
2 2
1 1 1
(2.5 ) (2.5 )
2 3 12
[0.5 0.8333 0.52083]
1.85416
xV a b b b b
a b
a b
2 2 2
: (1.8333 ) 1.85416 1.01136
XV xV X a b a b X b
Centroid is 0.01136b to the right of base of cone.
Note: Centroid is at base of cone for 6 2.449 .
h b b
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-707-320.jpg)


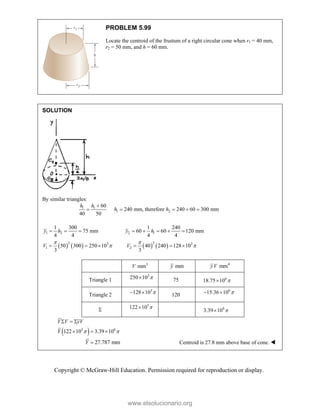
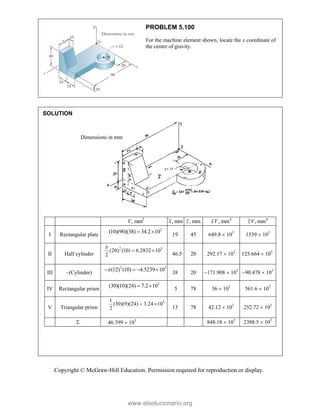

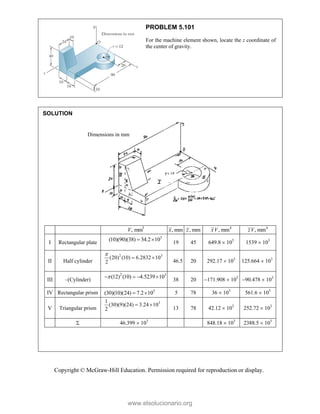

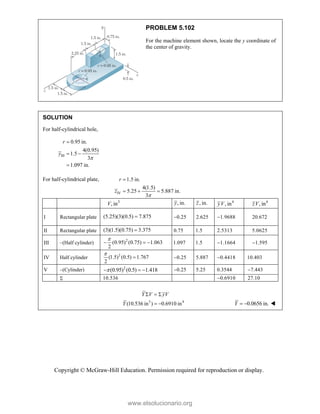
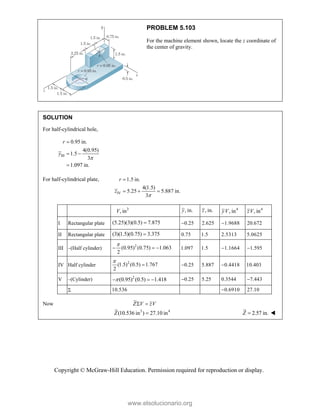
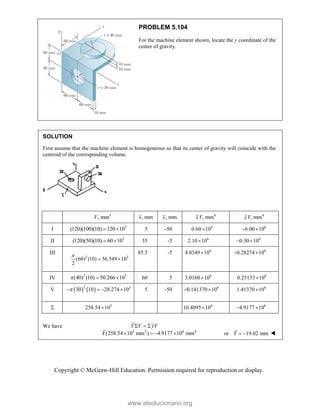
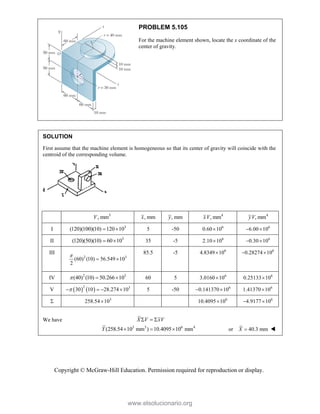
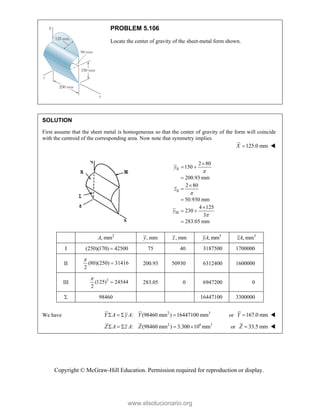
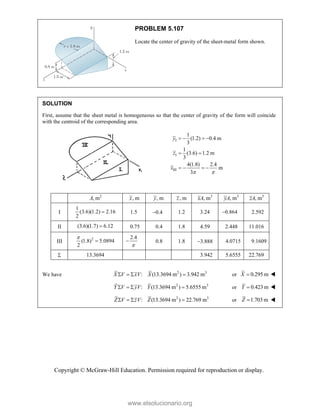


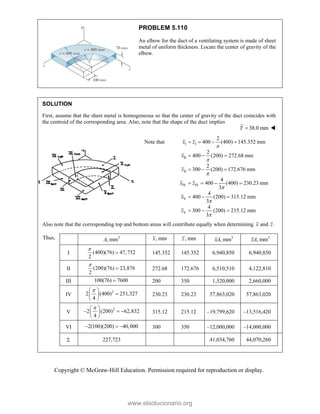



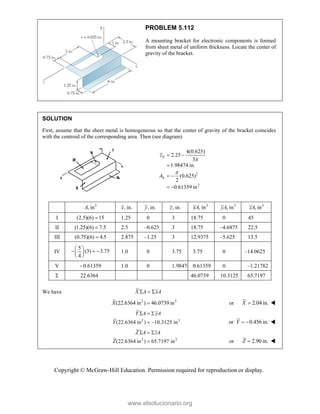

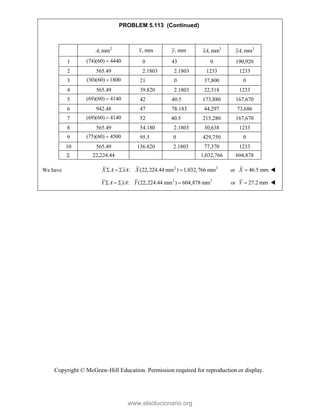
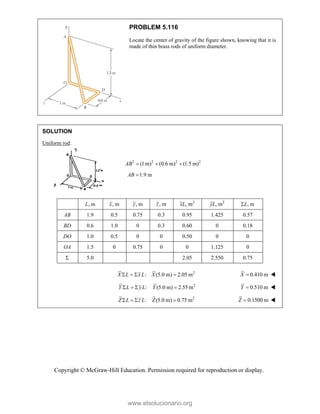
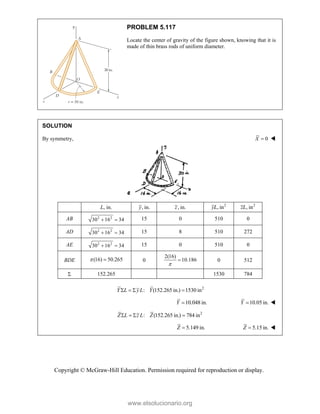

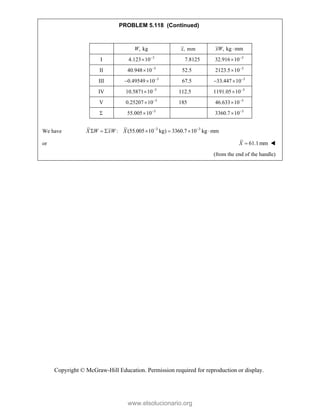
 0.23889 lb
4
0.90 in. (0.284 lb/in ) [(1.125 0.75 ) in ](1in.) 0.156834 lb
4
0.70 in. (0.318 lb/in ) [(0.75 0
4
y W
y W
y W
2 2
.5 ) in ](1.4 in.) 0.109269 lb
We have
(0.20 in.)(0.23889 lb) (0.90 in.)(0.156834 lb) (0.70 in.)(0.109269 lb)
0.23889 lb 0.156834 lb 0.109269 lb
Y W yW
Y
or 0.526 in.
Y
(above base)
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-736-320.jpg)

4
3.8693 lb
W V
Component W(lb) (in.)
y (lb in.)
yW
Rod 0.81229 2 1.62458
Collar 3.8693 1.25 4.8366
4.6816 6.4612
: (4.6816 lb) 6.4612 lb in.
Y W yW Y
1.38013in.
Y 1.380 in.
Y
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-737-320.jpg)








![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.126
Locate the centroid of the volume obtained by rotating the shaded area
about the x-axis.
SOLUTION
First note that symmetry implies 0
y
and 0
z
We have 2
( )
y k X h
At 0, ,
x y a
2
( )
a k h
or 2
a
k
h
Choose as the element of volume a disk of radius r and thickness dx. Then
2
, EL
dV r dx X x
Now 2
2
( )
a
r x h
h
so that
2
4
4
( )
a
dV x h dx
h
Then
2 2
4 5
0
4 4
0
2
( ) [( ) ]
5
1
5
h
h
a a
V x h dx x h
h h
a h
and
2
4
4
0
2
5 4 2 3 3 2 4
4 0
2
6 5 2 4 3 3 4 2
4
0
2 2
( )
( 4 6 4 )
1 4 3 4 1
6 5 2 3 2
1
30
h
EL
h
h
a
x dV x x h dx
h
a
x hx h x h x h x dx
h
a
x hx h x h x h x
h
a h
Now 2 2 2
:
5 30
EL
xV x dV x a h a h
1
or
6
x h
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-746-320.jpg)


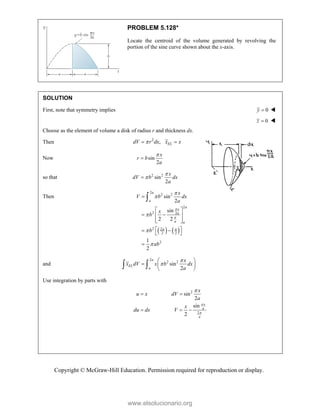




![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.131
Determine by direct integration the location of the centroid of one-half of
a thin, uniform hemispherical shell of radius R.
SOLUTION
First note that symmetry implies 0
x
The element of area dA of the shell shown is obtained by cutting the shell with two planes parallel to the
xy plane. Now
( )( )
2
EL
dA r Rd
r
y
where sin
r R
so that 2
sin
2
sin
EL
dA R d
R
y
Then
/2
2 2 /2
0
0
2
sin [ cos ]
A R d R
R
and
/2
2
0
/2
3
0
3
2
sin ( sin )
sin 2
2
2 4
2
EL
R
y dA R d
R
R
Now 2 3
: ( )
2
EL
yA y dA y R R
or
1
2
y R
Symmetry implies z y
1
2
z R
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-754-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.132
The sides and the base of a punch bowl are of
uniform thickness t. If t R
and R 250 mm,
determine the location of the center of gravity of
(a) the bowl, (b) the punch.
SOLUTION
(a) Bowl:
First note that symmetry implies 0
x
0
z
for the coordinate axes shown below. Now assume that the bowl may be treated as a shell; the
center of gravity of the bowl will coincide with the centroid of the shell. For the walls of the bowl,
an element of area is obtained by rotating the arc ds about the y-axis. Then
wall (2 sin )( )
dA R R d
and wall
( ) cos
EL
y R
Then
/2
2
wall
/6
/2
2
/6
2
2 sin
2 [ cos ]
3
A R d
R
R
and wall wall wall
/2
2
/6
/2
3 2
/6
3
( )
( cos )(2 sin )
[cos ]
3
4
EL
y A y dA
R R d
R
R
By observation, 2
base base
3
,
4 2
A R y R
Now y A yA
or 2 2 3 2
3 3
3
4 4 4 2
y R R R R R
or 0.48763 250 mm
y R R
121.9 mm
y
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-755-320.jpg)


![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.133 (Continued)
Then 0
0
2 (1 cos ) [ sin ]
2
aht
V d aht
aht
and
0
2
2
0
2
0
2
2 (5 cos ) (1 cos )
12 2
(5 6cos cos )
12
sin 2
5 6sin
12 2 4
11
24
EL
h aht
y dV d
ah t
d
ah t
ah t
0
2
0
2
2 cos (1 cos )
2
sin 2
sin
2 4
1
2
EL
aht
z dV a d
a ht
a ht
Now 2
11
: ( )
24
EL
yV y dV y aht ah t
or
11
24
y h
and 2
1
: ( )
2
EL
zV z dV z aht a ht or
1
2
z a
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-758-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.134*
Locate the centroid of the section shown, which was cut from an
elliptical cylinder by an oblique plane.
SOLUTION
First note that symmetry implies 0
x
Choose as the element of volume a vertical slice of width zx, thickness dz, and height y. Then
1
2 , ,
24
EL EL
dV xy dz y z z
Now 2 2
a
x b z
b
and
/2
( )
2 2
h h h
y z b z
b b
Then 2 2
2 ( )
2
b
b
a h
V b z b z dz
b b
Let sin cos
z b dz b d
Then
/2
2 /2
/2
2 2
/2
/2
3
/2
( cos )[ (1 sin )] cos
(cos sin cos )
sin 2 1
cos
2 4 3
1
2
ah
V b b b d
b
abh d
abh
V abh
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-759-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.134* (Continued)
and 2 2
2
2 2 2
3
1
( ) 2 ( )
2 2 2
1
( )
4
b
EL
b
b
b
h a h
y dV b z b z b z dz
b b b
ah
b z b z dz
b
Let sin cos
z b dz b d
Then
2 /2
2
3 /2
/2
2 2 2 2 2
/2
1
[ (1 sin )] ( cos ) ( cos )
4
1
(cos 2sin cos sin cos )
4
EL
ah
y dV b b b d
b
abh d
Now 2 2
1 1
sin (1 cos2 ) cos (1 cos2 )
2 2
so that 2 2 2
1
sin cos (1 cos 2 )
4
Then
/2
2 2 2 2
/2
/2
2 3
/2
2
1 1
cos 2sin cos (1 cos 2 )
4 4
1 sin 2 1 1 1 sin 4
cos
4 2 4 3 4 4 2 8
5
32
EL
y dV abh d
abh
abh
Also, 2 2
2 2
2
2 ( )
2
( )
b
EL
b
b
b
a h
z dV z a z b z dz
b b
ah
z b z b z dz
b
Let sin cos
z b dz b d
Then
/2
2 /2
/2
2 2 2 2
/2
( sin )[ (1 sin )]( cos ) ( cos )
(sin cos sin cos )
EL
ah
z dV b b b b d
b
ab h d
Using 2 2 2
1
sin cos (1 cos 2 )
4
from above,
/2
2 2 2
/2
1
sin cos (1 cos 2 )
4
EL
z dV ab h d
/2
2 3 2
/2
1 1 1 sin 4 1
cos
3 4 4 2 8 8
ab h ab h
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-760-320.jpg)





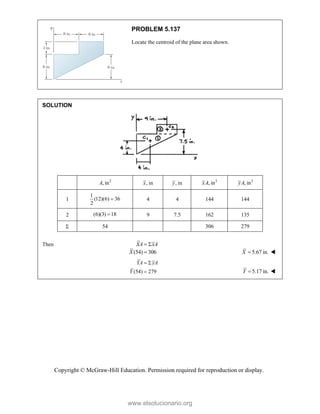
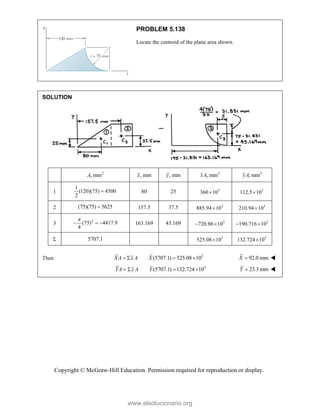
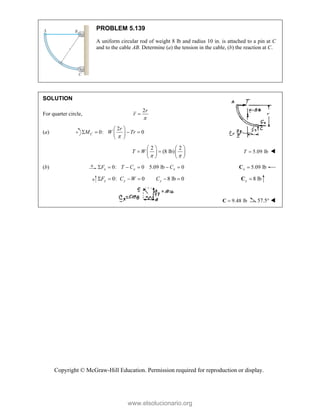

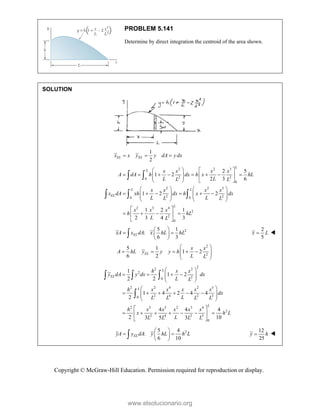
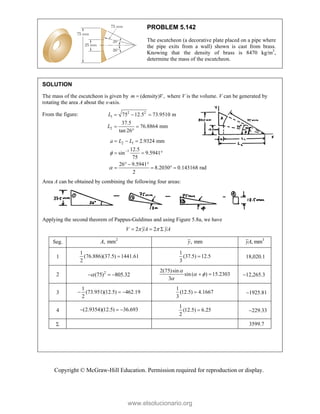



![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 5.145
A tank is divided into two sections by a 1 1-m square gate that is
hinged at A. A couple of magnitude 490 N · m is required for the
gate to rotate. If one side of the tank is filled with water at the rate of
0.1 m3
/min and the other side is filled simultaneously with methyl
alcohol (density ma 789 kg/m3
) at the rate of 0.2 m3
/min,
determine at what time and in which direction the gate will rotate.
SOLUTION
Consider the free-body diagram of the gate.
First note base
V A d
and .
V rt
Then
3
3
0.1m / min (min)
0.25 (m)
(0.4 m)(1m)
0.2 m / min (min)
(m)
(0.2 m)(1m)
W
MA
t
d t
t
d t
Now
1 1
( )
2 2
P Ap A gh
so that
3 3 2
2
3 2
2
1
[(0.25 ) m (1 m)][(10 kg/m )(9.81 m/s )(0.25 ) m]
2
306.56 N
1
[( ) m (1 m)][(789 kg/m )(9.81m/s )( ) m]
2
3870 N
W
MA
P t t
t
P t t
t
Now assume that the gate will rotate clockwise and when 0.6 m.
MA
d When rotation of the gate is
impending, we require
1 1
: 0.6 m 0.6 m
3 3
A R MA MA W W
M M d P d P
Substituting
2 2
1 1
490 N m 0.6 m (3870 ) N 0.6 0.25 m (306.56 ) N
3 3
t t t t
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-775-320.jpg)


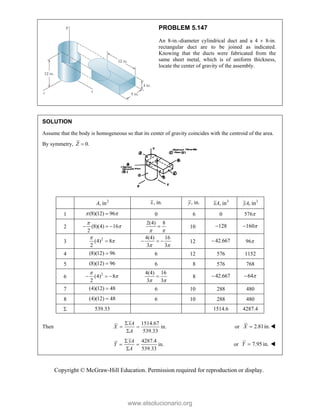

4
270.22 10 m
(7860 kg/m )(270.22 10 m )
2.1239 kg
V
m V
Each brass plate: 6 3
3 6 3
1
(0.096 m)(0.192 m)(0.006 m) 55.296 10 m
2
(8470 kg/m )(55.296 10 m ) 0.46836 kg
V
m V
Flagpole base:
2.1239 kg 3(0.46836 kg) 3.5290 kg
(0.096 m)(2.1239 kg) 3[(0.064 m)(0.46836 kg)] 0.29382 kg m
: (3.5290 kg) 0.29382 kg m
m
ym
Y m ym Y
0.083259 m
Y 83.3 mm
Y above the base
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-779-320.jpg)


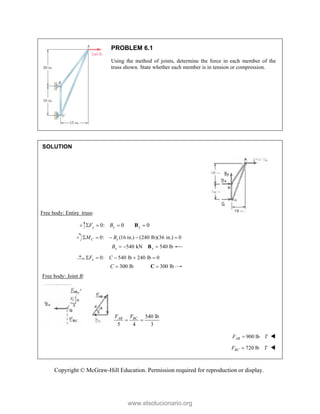







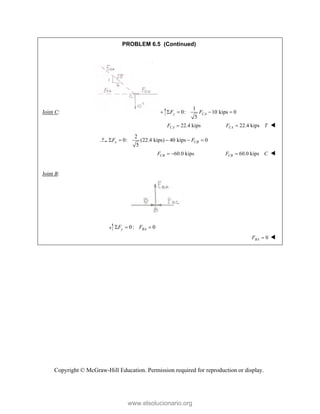












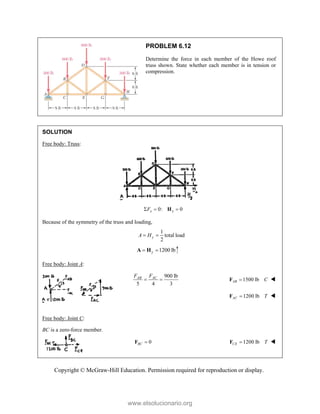

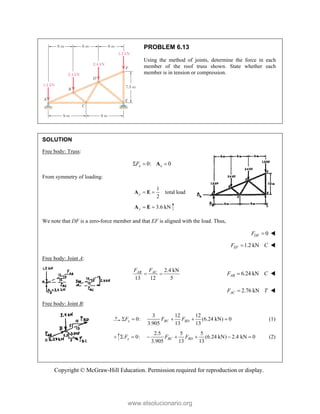



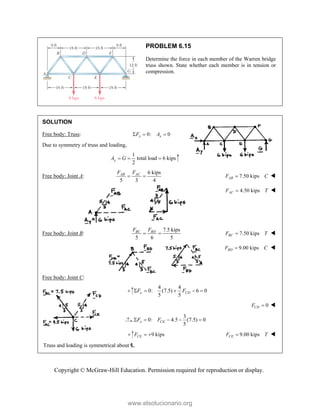
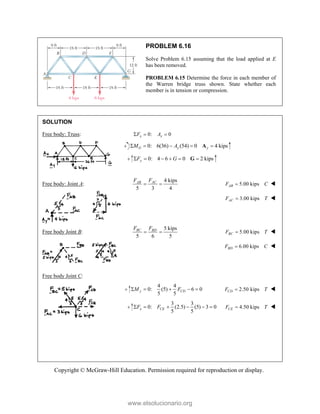
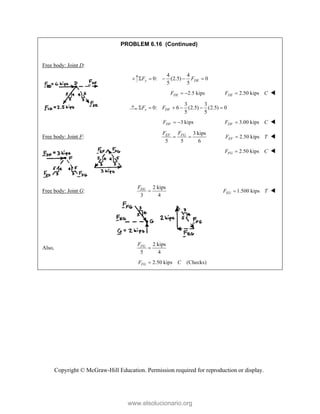








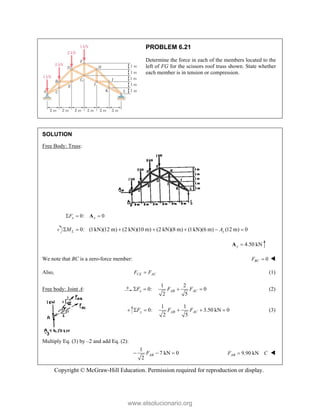

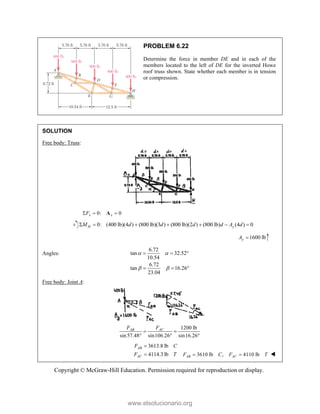

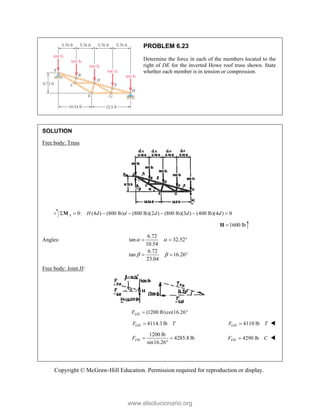

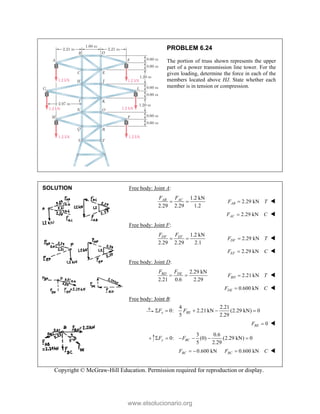

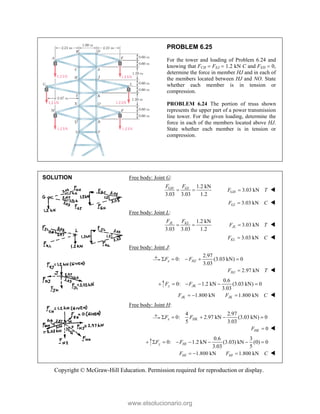








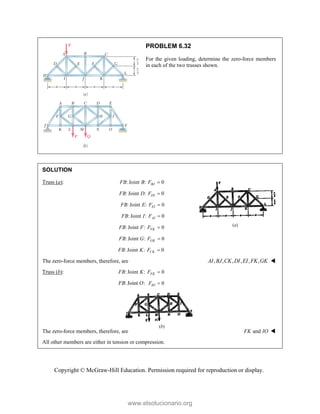

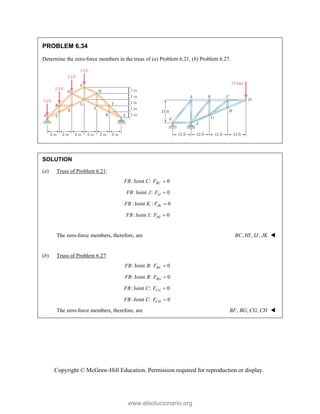
















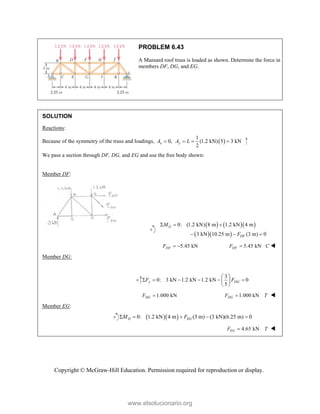
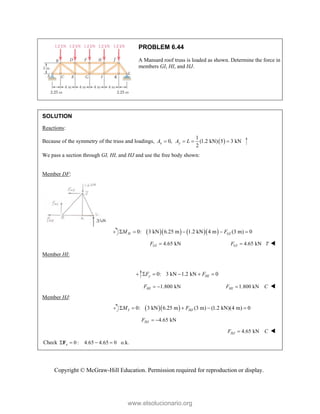
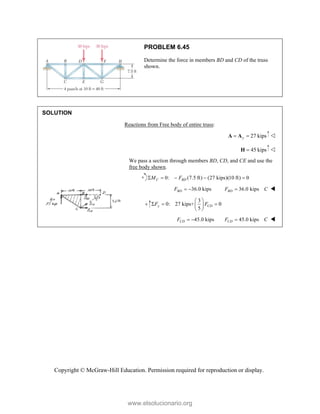
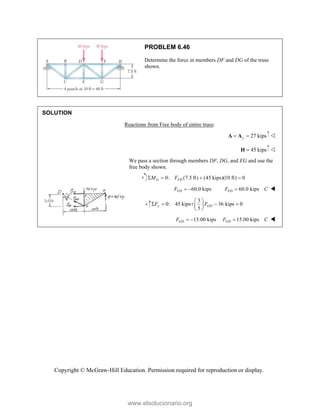

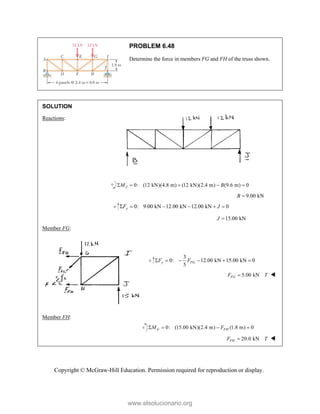
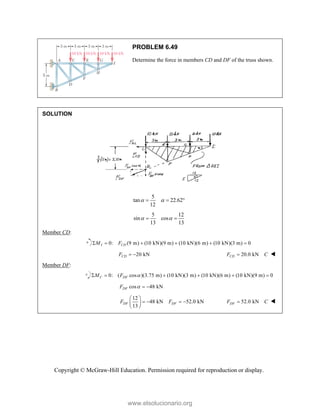
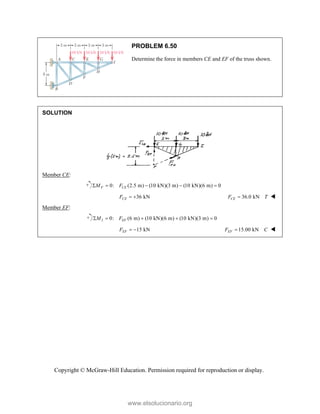
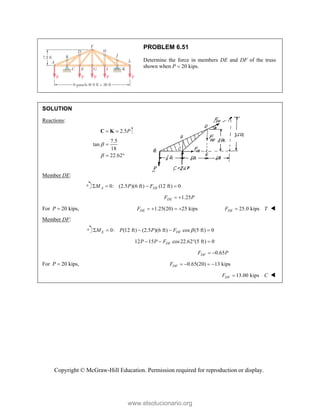
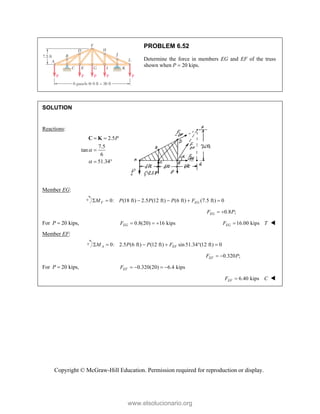
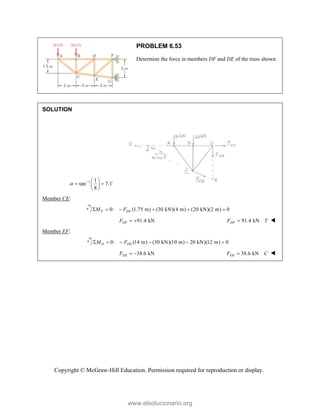
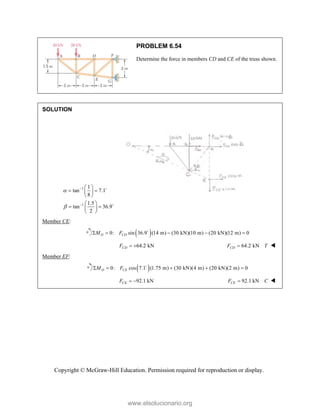
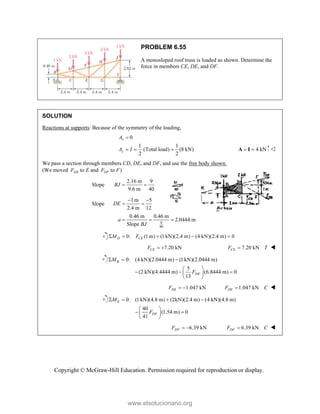
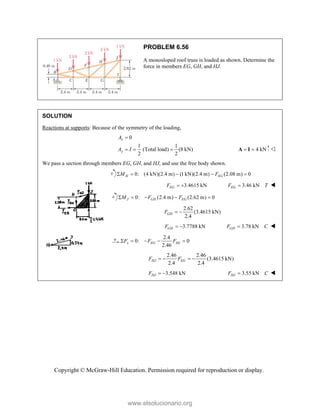




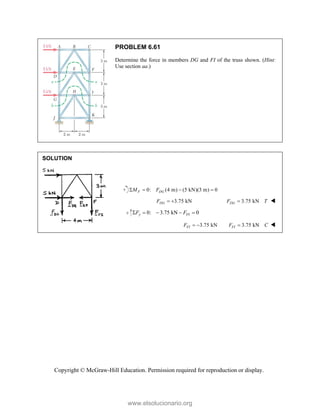
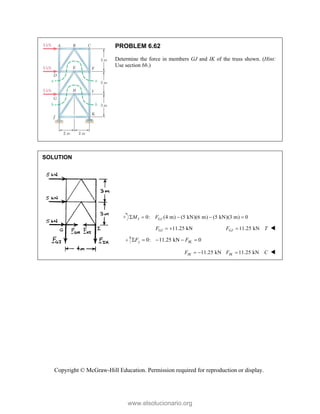
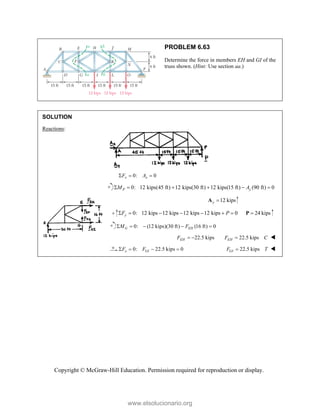











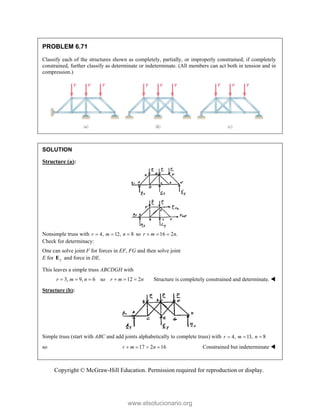

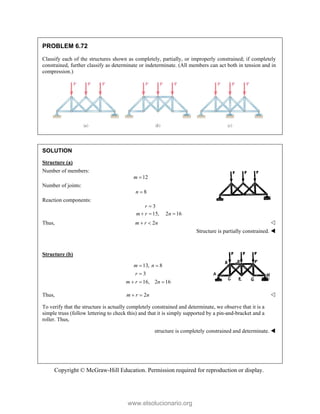


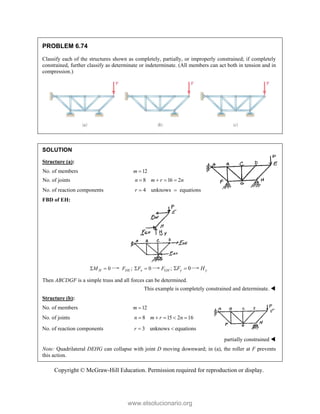


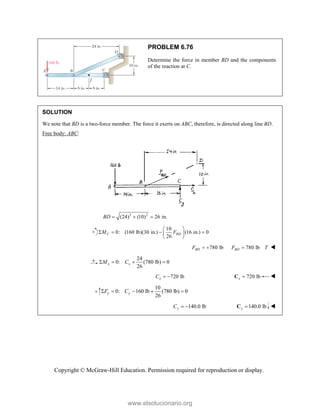


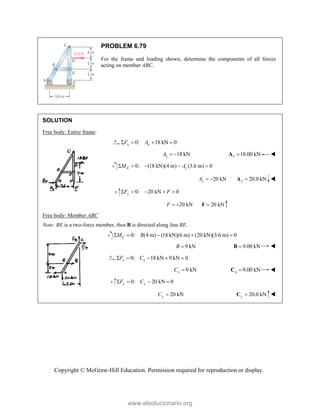
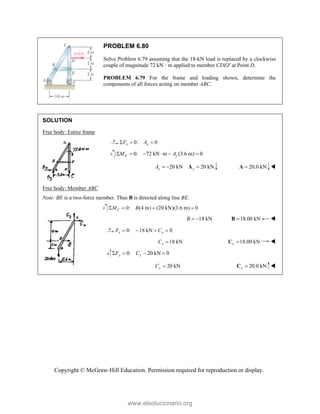

















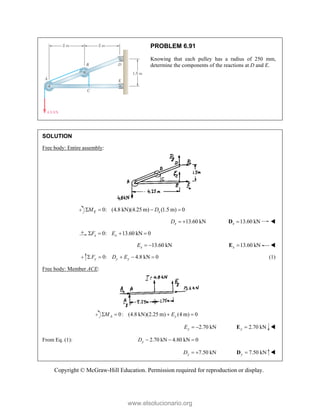

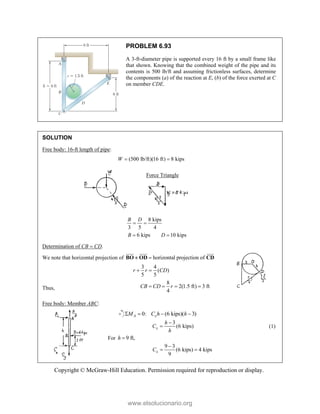






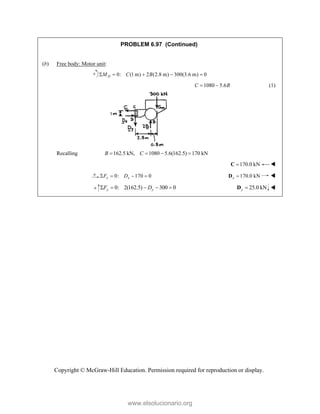








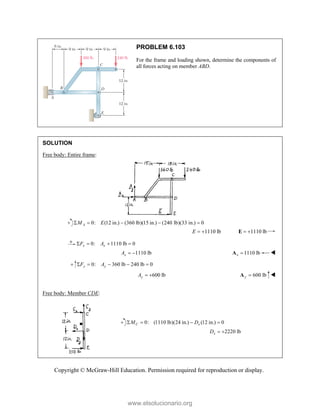




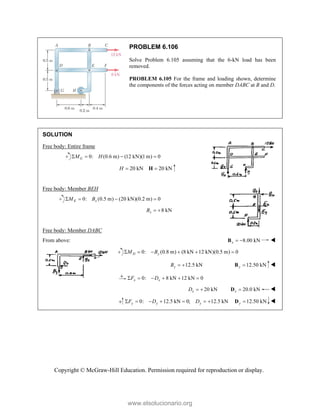




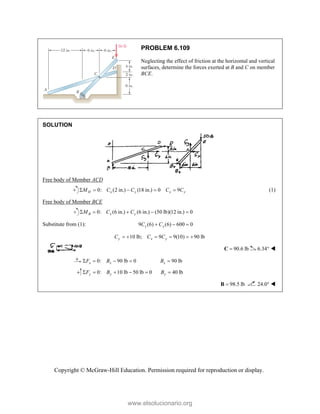

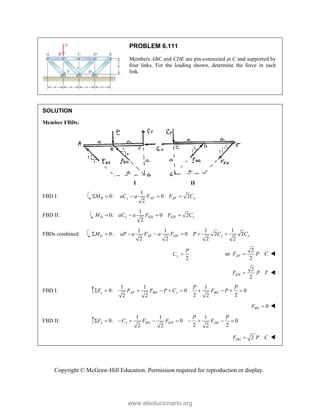
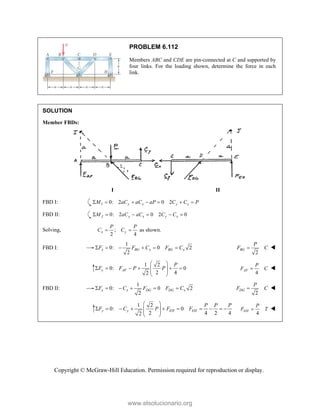
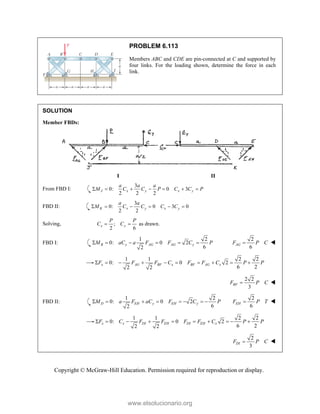









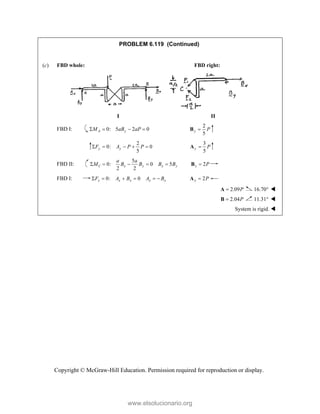







![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 6.125
The control rod CE passes through a
horizontal hole in the body of the toggle
system shown. Knowing that link BD is 250
mm long, determine the force Q required to
hold the system in equilibrium when 20.
SOLUTION
We note that BD is a two-force member.
Free body: Member ABC:
Since 250,
BD 1 33.404
sin ; 7.679
250
0: ( sin )187.94 ( cos )68.404 (100 N)328.89 0
C BD BD
M F F
[187.94sin7.679 68.404cos7.679 ] 32,889
770.6 N
BD
BD
F
F
0: (770.6 N)cos7.679 0
x x
F C
763.7 N
x
C
Member CQ:
0: 763.7 N
x x
F Q C
764 N
Q
Dimensions in mm
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-971-320.jpg)
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 6.126 (Continued)
0: ( sin )198.90 ( cos )20.906 (100 N)348.08 0
C BD BD
M F F
[198.90sin3.232 20.906cos3.232 ] 34808
1084.8 N
BD
BD
F
F
0: cos 0
x BD x
F F C
(1084.8 N)cos3.232 0
x
C
1083.1 N
x
C
Member DE: 0:
x x
F Q C
1083.1 N
Q 1083 N
Q
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-973-320.jpg)
 0
793.64 N
BD
F C
and, from above,
(793.64 N)cos20
E
(a) 746 N
E
0: (793.64 N)sin20 0
x x
F A
271.44 N
x
A
0: (793.64 N)cos20 250 N 0
y y
F A
495.78 N
y
A
(b) 565 N
A 61.3°
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-974-320.jpg)
cos20 [(0.2 m)(cos30 )](957.76 N)sin 20
A
M
[(0.2 m)sin30 (0.4 m)cos15 ] 0
P
301.70 N,
P 302 N
P
(b) 0: (957.76 N)sin20 0
x x
F A
327.57 N
x
A
0: (957.76 N)cos20 301.70 N 0
y y
F A
598.30 N
y
A
682 N
A 61.3°
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-975-320.jpg)


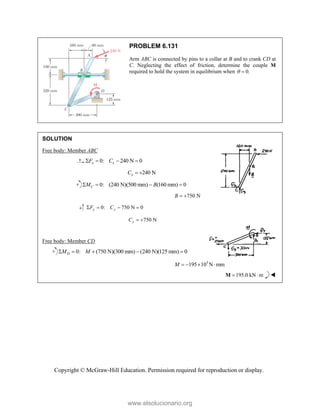
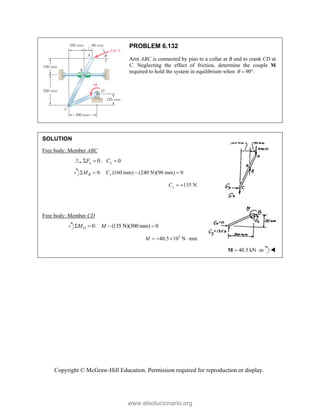
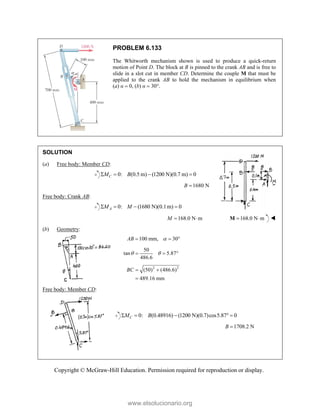

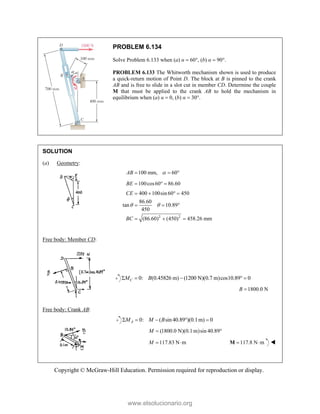




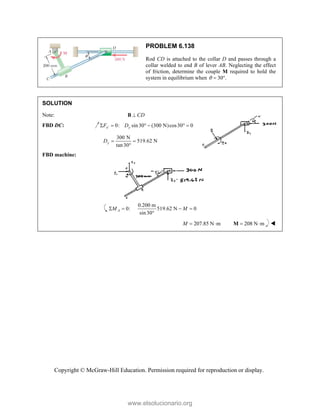
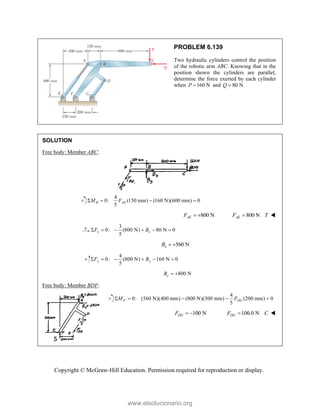
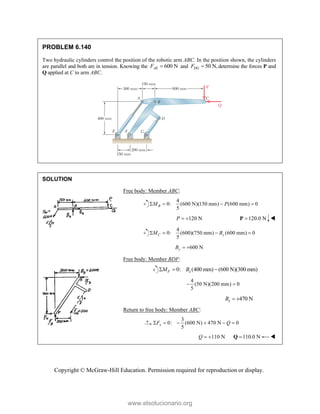

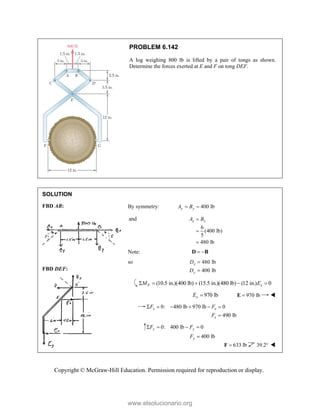
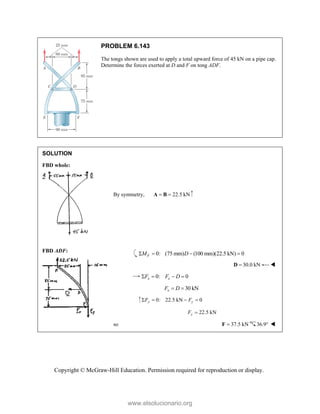
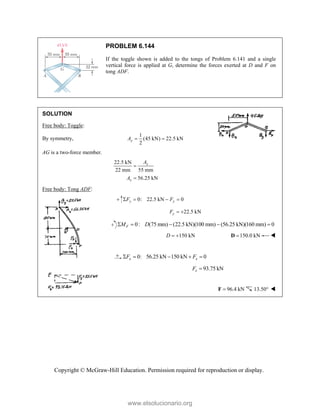
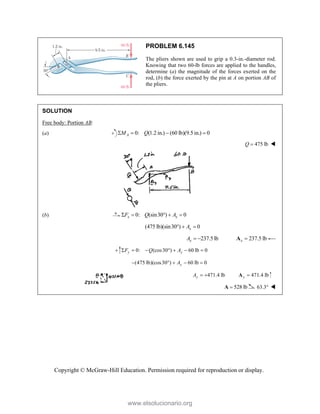

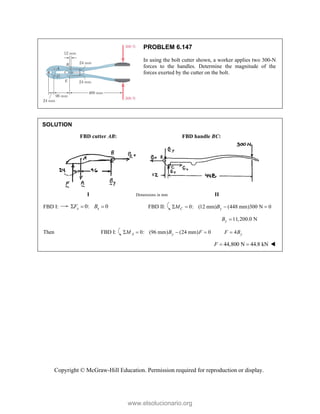
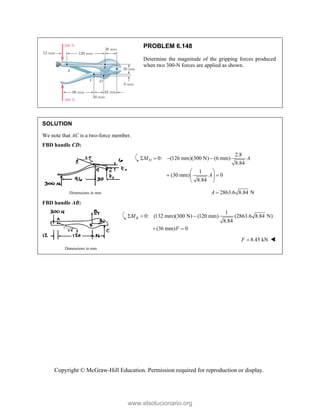









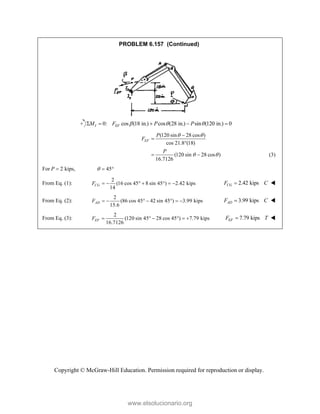

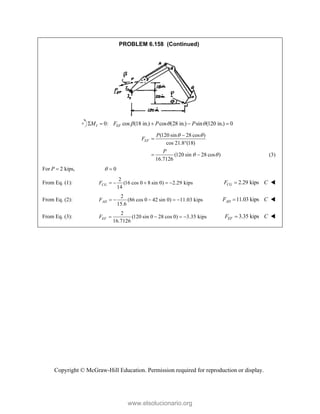
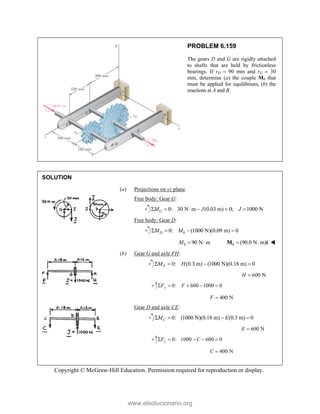
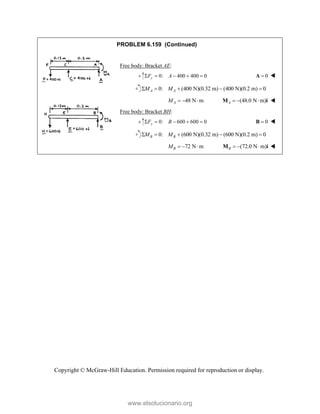









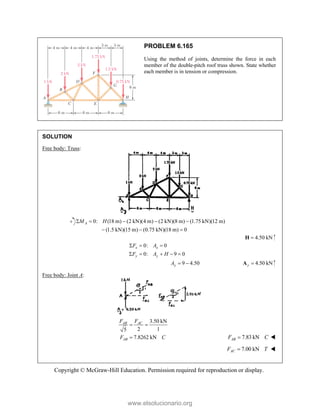
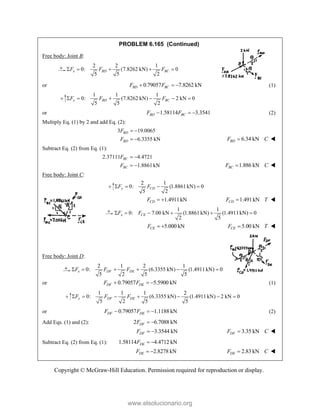
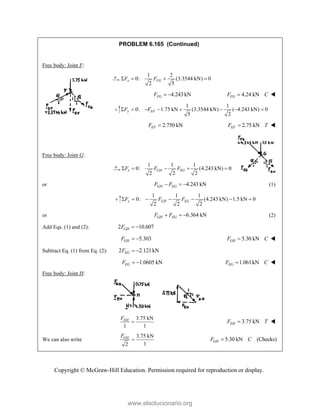
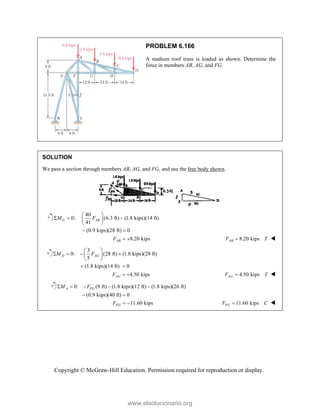
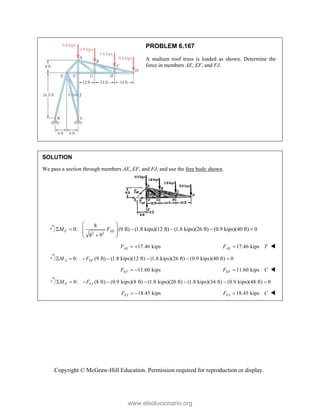
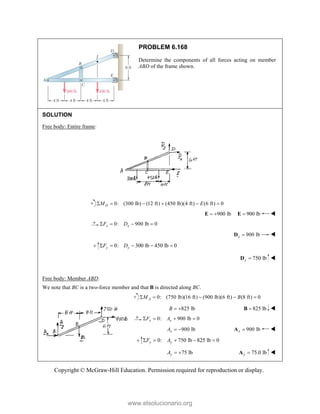





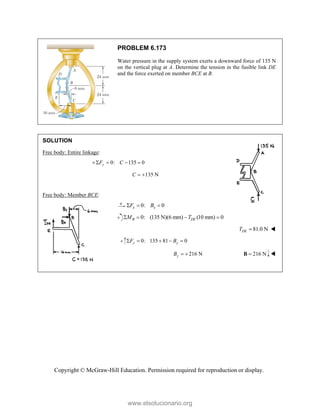









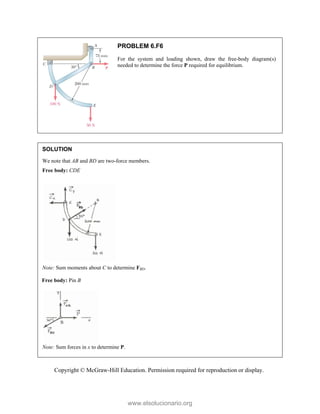

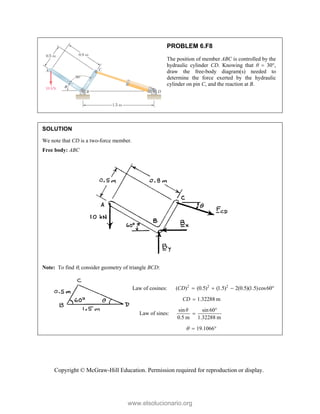

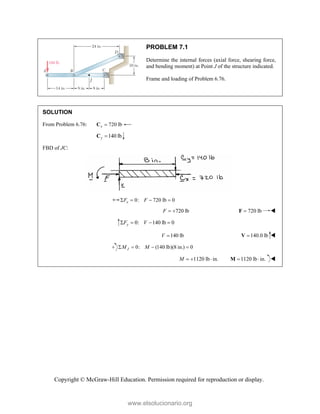

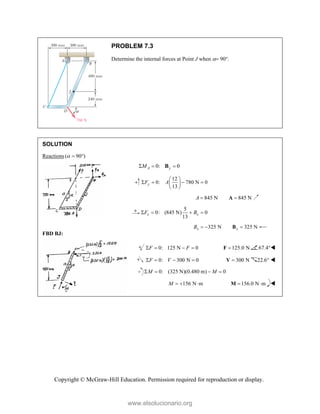

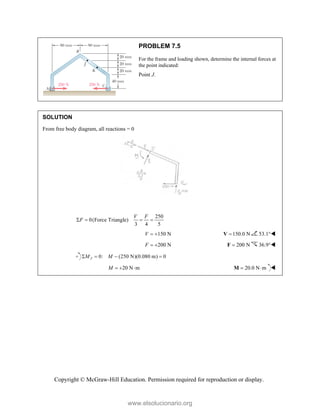
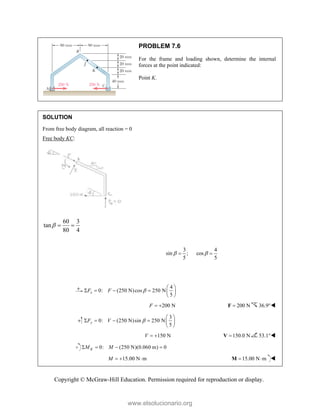

![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 7.7 (Continued)
0: (37.5 lb)sin (39.094 ) 0
y
F F
23.647
F 23.6 lb
F 76.0°
3 4
0: (16 in.) (37.5 lb) [(8 2) in.] (37.5 lb) 0
5 5
J
M M
540 lb in.
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-1053-320.jpg)


 0
J
M M
18.7061
M
18.71
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-1056-320.jpg)
 0
K
M M
10.80 N m
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-1057-320.jpg)
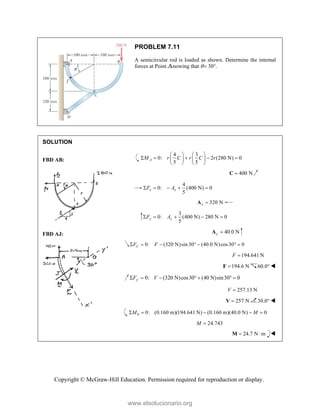
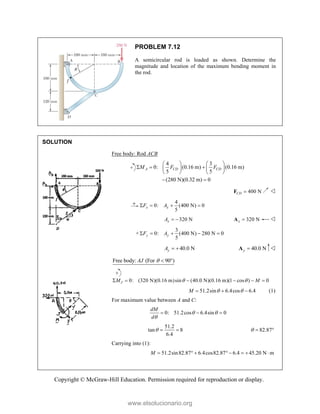



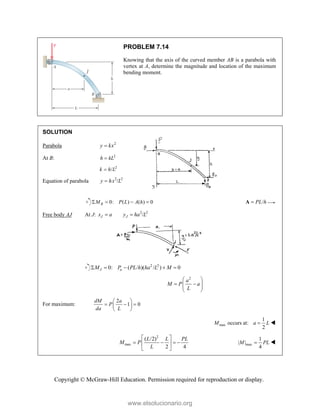



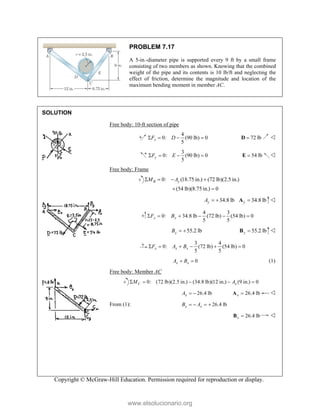





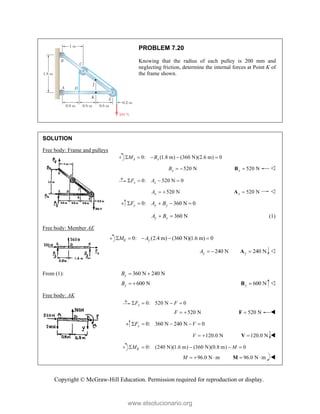





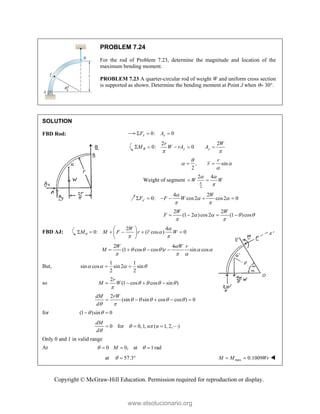













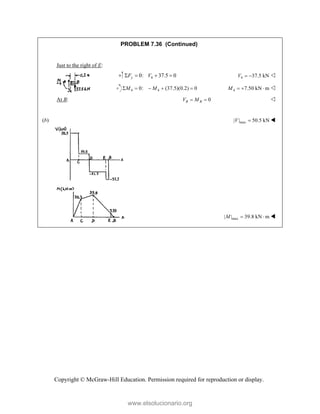


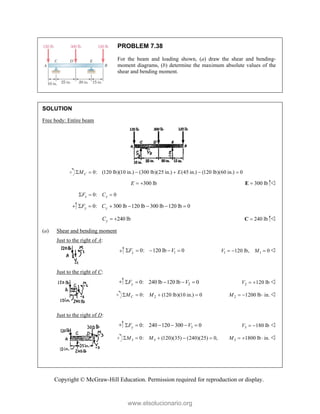
















![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 7.47
Assuming the upward reaction of the ground on beam AB to be
uniformly distributed, (a) draw the shear and bending-moment
diagrams,(b) determine the maximum absolute values of the shear and
bending moment.
SOLUTION
For equilibrium,
0: (6 m) (8 kN/m)(3 m) 0
y g
F w
4 kN/m
g
w
(a) Shear and bending-moment diagrams from A to C:
0: 4 0 (4 ) kN
y
F x V V x
0: (4 )
2
J
x
M M x
2
(2 ) kN m
M x
For 0:
x 0
A A
V M
For 1.5 m: 6 kN,
C
x V
4.5 kN m
C
M
From C to D:
0: 4 8( 1.5) 0
y
F x x V
(12 4 ) kN
V x
1.5
0: 8( 1.5) (4 ) 0
2 2
J
x x
M M x x
2 2
[2 4( 1.5) ]kN m
M x x
2
9 12 2
M x x
For 3 m: 0,
x V
c
L 9 kN m
M
For 4.5 m: 6 kN,
D
x V
4.5 kN m
D
M
At B: 0
B B
V M
(b) max
| | 6.00 kN
V
max
| | 9.00 kN m
M
Bending-moment diagram consists or three distinct arcs of
parabola, all located above the x axis.
Thus: 0 everywhere
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-1113-320.jpg)



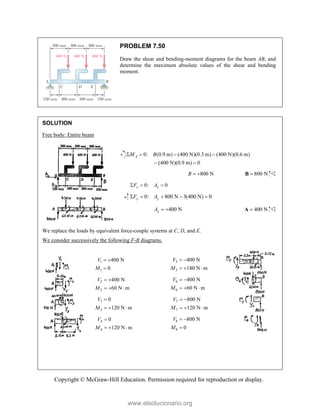
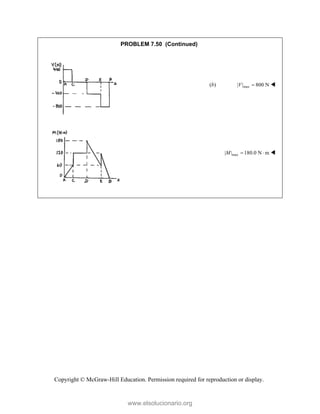



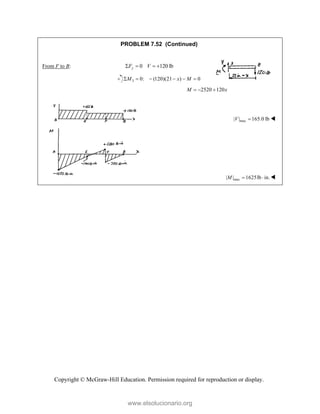

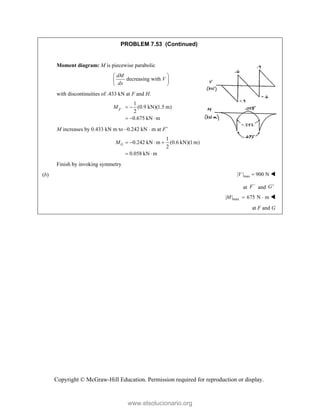

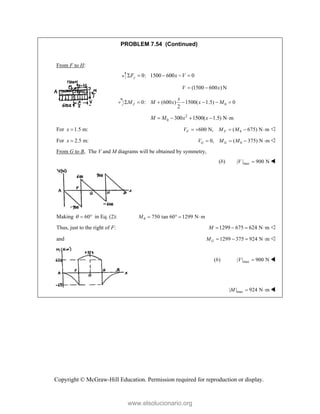
![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 7.55
For the structural member of Problem 7.53, determine
(a) the angle for which the maximum absolute value of
the bending moment in beam AB is as small as possible,
(b) the corresponding value of max
| | .
M (Hint: Draw the
bending-moment diagram and then equate the absolute
values of the largest positive and negative bending
moments obtained.)
PROBLEM 7.53 Two small channel sections DF and EH
have been welded to the uniform beam AB of weight
W 3 kN to form the rigid structural member shown. This
member is being lifted by two cables attached at D and E.
Knowing that 30 and neglecting the weight of the
channel sections, (a) draw the shear and bending-moment
diagrams for beam AB, (b) determine the maximum absolute
values of the shear and bending moment in the beam.
SOLUTION
See solution of Problem 7.50 for reduction of loading or beam AB to the following:
where 0 (750 N m) tan
M
[Equation (2)]
The largest negative bending moment occurs Just to the left of F:
1 1
1.5 m
0: (900 N) 0
2
M M
1 675 N m
M
The largest positive bending moment occurs
At G:
2 2 0
0: (1500 N)(1.25 m 1 m) 0
M M M
2 0 375 N m
M M
Equating 2
M and 1 :
M
0 375 675
M
0 1050 N m
M
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-1127-320.jpg)





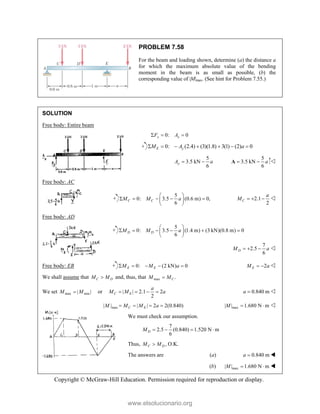














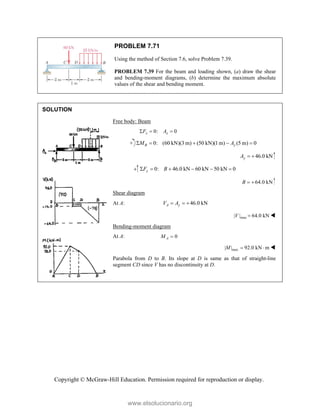



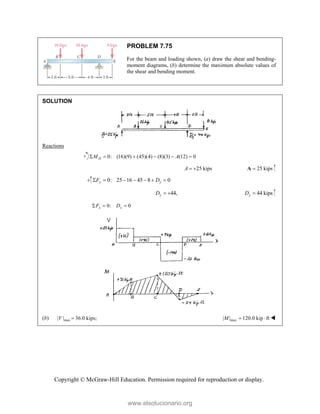



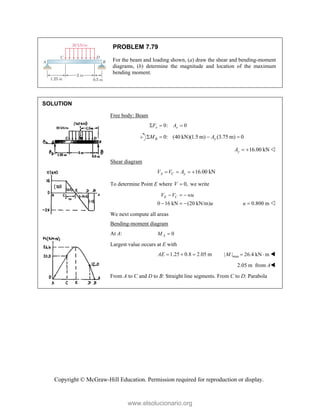
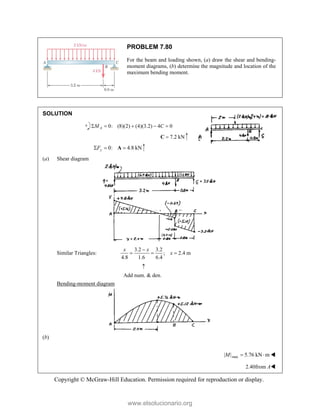

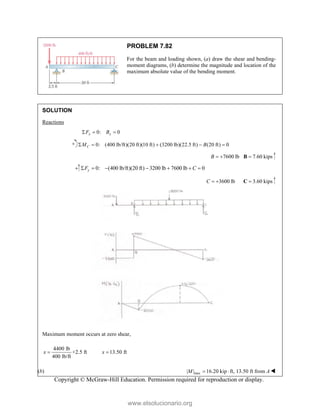



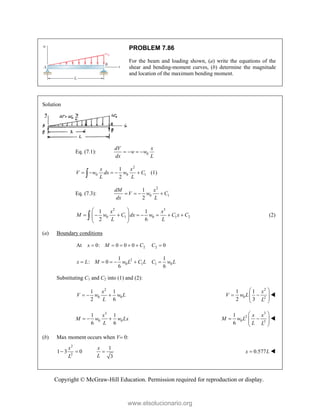

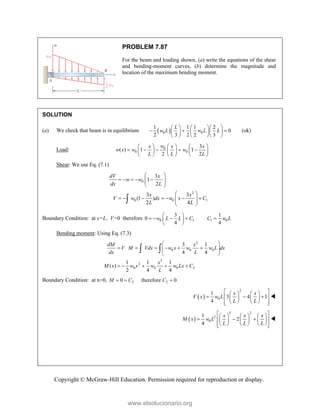


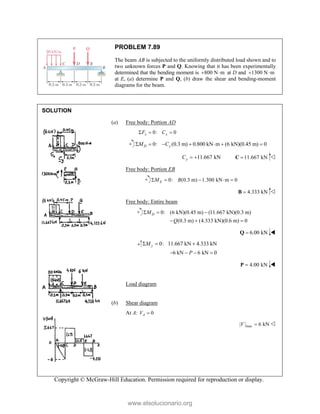
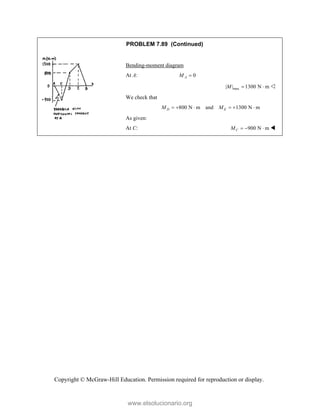
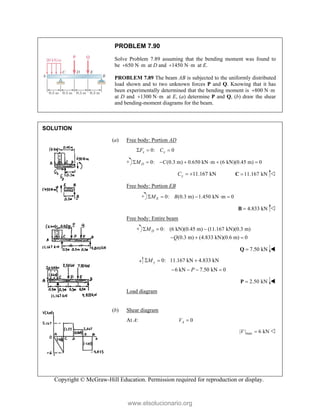

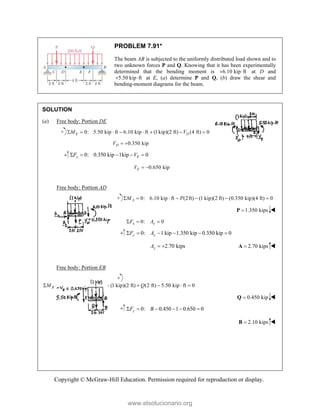
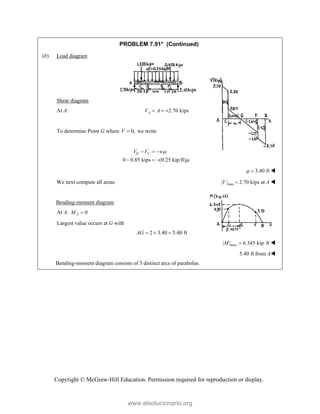


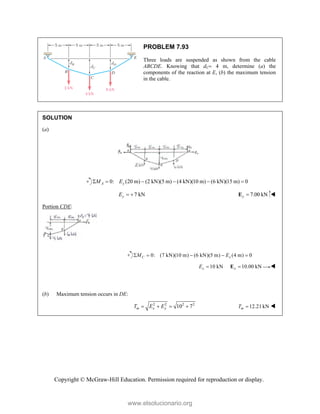
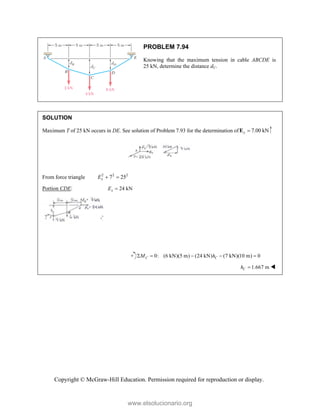


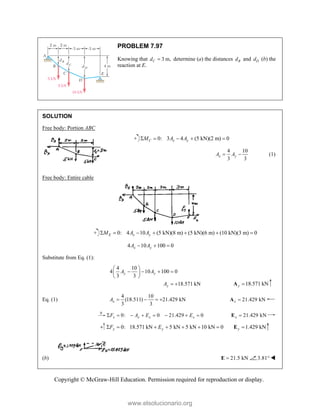
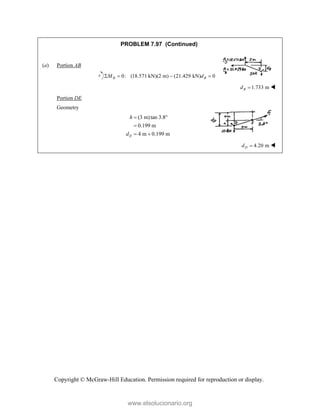



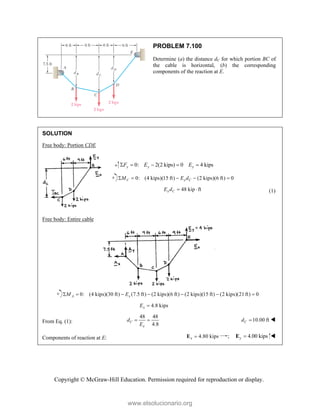




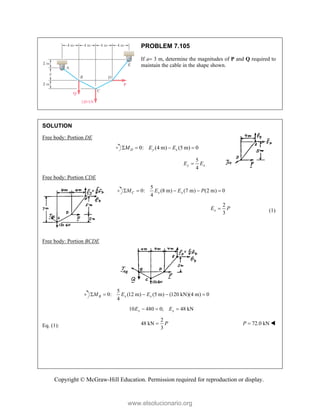

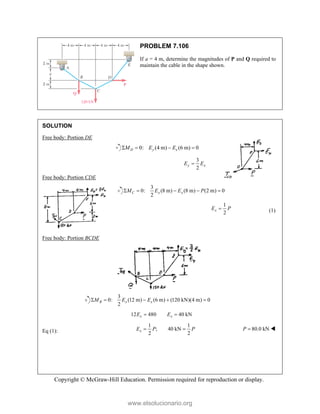


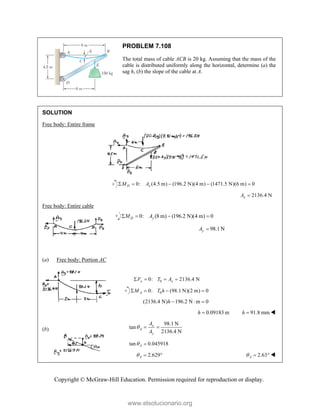





![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 7.113
A 76-m length of wire having a mass per unit length of 2.2 kg/m is used to span a horizontal distance of
75 m. Determine (a) the approximate sag of the wire, (b) the maximum tension in the wire. [Hint: Use
only the first two terms of Eq. (7.10).]
SOLUTION
First two terms of Eq. 7.10
(a)
2
1
(76 m) 38 m,
2
1
(75 m) 37.5 m
2
2
1
3
B
B
B
B
B B
B
s
x
y h
y
s x
x
2
2
2
38 m 37.5 m 1
3
0.02
0.141421
0.141421
37.5m
B
B
B
B
B
B
y
x
y
x
y
x
h
5.3033 m
h 5.30 m
h
(b) Free body: Portion CB
(2.2 kg/m)(9.81m) 21.582 N/m
(38 m)(21.582 N/m)
820.12 N
B
w
W s w
W
2
2
2
0
0
0
2.2 kg/m 9.81 m/s 37.5 m
:
2 2 5.3033 m
2861.6 N
2861.6 N
B
B
B
x
wx
y T
y
T
B T
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-1201-320.jpg)












![Copyright © McGraw-Hill Education. Permission required for reproduction or display.
PROBLEM 7.125*
Using the property indicated in Problem 7.124, determine the curve assumed by a cable of span L and sag
h carrying a distributed load ww0 cos (x/L), where x is measured from mid-span. Also determine the
maximum and minimum values of the tension in the cable.
PROBLEM 7.124 Show that the curve assumed by a cable that carries a distributed load w(x) is defined
by the differential equation d2
y/dx2
w(x)/T0, where T0is the tension at the lowest point.
SOLUTION
0
( ) cos
x
w x w
L
From Problem 7.124
2
0
2
0 0
( )
cos
w
d y w x x
T T L
dx
So 0
0 0
sin using 0
W L
dy x dy
dx T L dx
2
0
2
0
1 cos [using (0) 0]
w L x
y y
L
T
But
2 2
0 0
0
2 2
0
1 cos so
2 2
w L w L
L
y h T
T h
And 0 min
T T
so
2
0
min 2
w L
T
h
0
max
0 0
/2
:
By
A B
x L
T w L
dy
T T T
T dx T
0
By
w L
T
2
2 2 0
max 0 1
By
w L L
T T T
h
www.elsolucionario.org](https://image.slidesharecdn.com/beerjohnstonstatics11-solutionmanual-221206002834-f2e2ab83/85/Beer-johnston-Statics-11-Solution-Manual-pdf-1215-320.jpg)