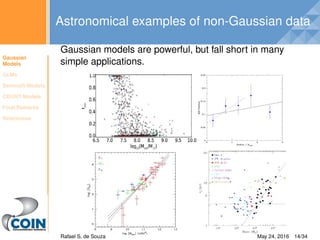
This document is a slide presentation on Bayesian models for astronomy. It introduces Gaussian, Bernoulli, and Poisson/negative binomial count models. It provides examples of fitting these models to astronomical data using the JAGS software. The presentation covers linear regression, logistic regression for binary outcomes, and models for count data like the number of globular clusters in galaxies. Real astronomical applications discussed include modeling Hubble residuals, star formation activity, and globular cluster populations.






![Gaussian
Models
GLMs
Bernoulli Models
COUNT Models
Final Remarks
References
JAGS: Just Another Gibbs Sampler
An intuitive program for analysis of Bayesian hierarchical
models using MCMC.
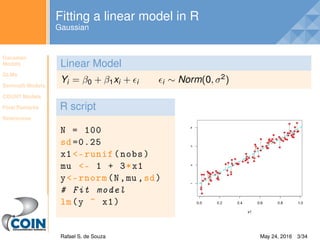
Normal Model JAGS syntax
Likelihood
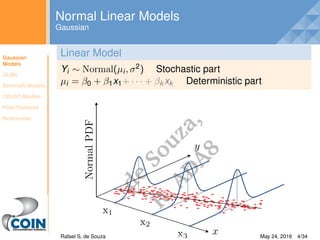
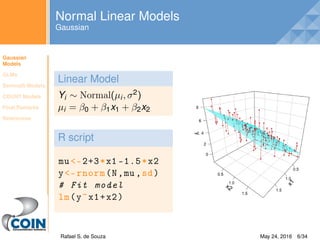
Yi ∼ N(µi, σ2) Y[i] ∼ dnorm(mu[i], pow(sigma, −2)
µi = β1 + β2 × Xi mu[i] < −inprod(beta[], X[i, ])
Priors
βi ∼ N(0, 104) beta[i] ∼ dnorm(0, 0.001)
σ ∼ U(0, 100) sigma ∼ dunif(0, 100)
Rafael S. de Souza Bayesian Models for Astronomy May 24, 2016 10/34](https://image.slidesharecdn.com/ada-tutorial-160525091357/85/Bayesian-Models-for-Astronomy-10-320.jpg)






![Gaussian
Models
GLMs
Bernoulli Models
COUNT Models
Final Remarks
References
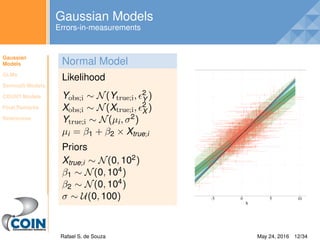
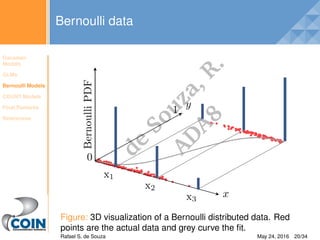
Normal vs Bernoulli model
Figure: Linear regression predicts fractional (or probability)
values outside the [0, 1] range.
Rafael S. de Souza Bayesian Models for Astronomy May 24, 2016 21/34](https://image.slidesharecdn.com/ada-tutorial-160525091357/85/Bayesian-Models-for-Astronomy-21-320.jpg)
![Gaussian
Models
GLMs
Bernoulli Models
COUNT Models
Final Remarks
References
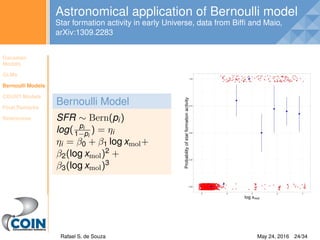
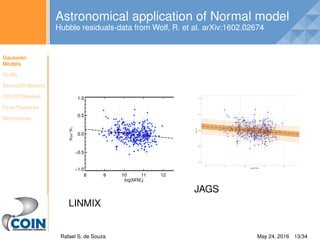
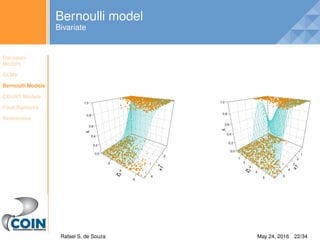
Bernoulli model in JAGS
Bernoulli Model
Yi ∼ Bern(pi)
log( pi
1−pi
) = ηi
ηi = β0 + β1Xi
JAGS
Y[i] ∼ Bern(p[i])
logit(p[i]) = η[i]
η[i] = β[1] + β[2] ∗ X[i]
Rafael S. de Souza Bayesian Models for Astronomy May 24, 2016 23/34](https://image.slidesharecdn.com/ada-tutorial-160525091357/85/Bayesian-Models-for-Astronomy-23-320.jpg)