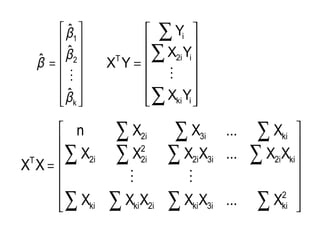
Tài liệu trình bày mô hình hồi quy bội với các biến độc lập, bao gồm giả thiết, ước lượng tham số và kiểm định giả thiết. Mô hình hồi quy này sử dụng phương pháp OLS để xác định các hệ số hồi quy và phân tích các vấn đề liên quan đến đa cộng tuyến. Đồng thời, nó cũng đề cập đến việc dự báo giá trị trung bình và cá biệt dựa trên mô hình đã thiết lập.

1. BÀI 7B: HỒI QUY BỘI
1. Mô hình :
Mô hình hồi qui tuyến tính k biến (PRF) :
E(Y/X2i,…,Xki) = β1+ β2X2i +…+ βkXki
Yi = β1+ β2X2i + …+ βkXki+ Ui
Trong đó :
Y - biến phụ thuộc
X2,…,Xk- các biến độc lập

2. β1 là hệ số tự do
βj là các hệ số hồi qui riêng,
βj cho biết khi Xj tăng 1 đvị thì trung bình
của Y sẽ thay đổi βj đvị trong trường
hợp các yếu tố khác không đổi (j=2,
…,k).
Khi k = 3 thì ta có mô hình hồi qui tuyến
tính ba biến :
E(Y/X2, X3) = β1+ β2X2 + β3X3 (PRF)
Yi = β1+ β2X2i + β3X3i+ Ui

3. 2. Các giả thiết của mô hình
• Giả thiết 1: Các biến độc lập phi ngẫu
nhiên, giá trị được xác định trước.
• Giả thiết 2 : E(Ui) = 0 ∀i
• Giả thiết 3 : Var(Ui) =σ2
∀i
• Giả thiết 4 : Cov(Ui, Uj) = 0 i ≠j
• Giả thiết 5 : Cov(Xi, Ui) = 0 ∀i
• Giả thiết 6 : Ui ~ N (0, σ2
) ∀i
• Giả thiết 7 : Không có hiện tượng cộng
tuyến giữa các biến độc lập.

4. 3. Ước lượng các tham số
a. Mô hình hồi qui ba biến :
Yi = β1+ β2X2i + β3X3i+ Ui (PRF)
Hàm hồi qui mẫu :
ii33i221iii eXˆXˆˆeYˆY +++=+= βββ
j
ˆβ
mine2
i →∑
Giả sử có một mẫu gồm n quan sát các giá
trị (Yi, X2i, X3i). Theo phương pháp OLS,
(j= 1,2,3) phải thoả mãn :

5. Tức là :
i33i221ii XˆXˆˆYe βββ −−−=







=−−−−
=−−−−
=−−−−











=
∂
∂
⇔=
∂
∂
=
∂
∂
∑
∑
∑
∑
∑
∑
0)X)(XˆXˆˆY(2
0)X)(XˆXˆˆY(2
0)1)(XˆXˆˆY(2
0
ˆ
e
0
ˆ
e
0
ˆ
e
i3i33i221i
i2i33i221i
i33i221i
3
2
i
2
2
i
1
2
i
βββ
βββ
βββ
β
β
β
Do

6. Giải hệ ta có :
33221
3
2
XˆXˆYˆ
ˆ
ˆ
βββ
β
β
−−=
−
−
=
−
−
=
∑ ∑ ∑
∑ ∑ ∑ ∑
∑ ∑ ∑
∑ ∑ ∑ ∑
2
3i2i
2
3i
2
2i
i2i3i2i
2
2ii3i
2
3i2i
2
3i
2
2i
i3i3i2i
2
3ii2i
)xx(xx
yxxxxyx
)xx(xx
yxxxxyx

7. * Phương sai của các hệ số ước lượng
( )
2
3
2
2
2
2
32
1
)ˆ(Var
)ˆ(Var
XX
n
1
)ˆ(Var
σβ
σβ
σβ
×
−
=
×
−
=
×








−
−
+=
∑ ∑ ∑
∑
∑ ∑ ∑
∑
∑ ∑ ∑
∑
2
3i2i
2
3i
2
2i
2
2i
2
3i2i
2
3i
2
2i
2
3i
2
3i2i
2
3i
2
2i
2i3i
)xx(xx
x
)xx(xx
x
)xx(xx
xx

8. Trong đó : σ2
= Var(Ui)
σ2
chưa biết nên dùng ước lượng của nó là :
3n
e
ˆ
2
i2
−
=
∑σ
Với :
i3i2
2
i
ˆˆESSTSSe yxyxy 3i2i
2
i ∑∑∑∑ −−=−= ββ

9. b. Mô hình hồi qui tuyến tính k biến
Yi = β1+ β2X2i + …+ βkXki+Ui (PRF)
(i = 1,…, n)
Hàm hồi qui mẫu :
ikiki221iii eXˆ...XˆˆeYˆY ++++=+= βββ
j
ˆβ
∑ → mine2
i
Theo phương pháp OLS,
(j= 1,2,…,k) phải thoả mãn :

10. Tức là :
⇔









=
∂
∂
=
∂
∂
∑
∑
0
ˆ
e
0
ˆ
e
k
2
i
1
2
i
β
β







=−−−−−
=−−−−−
∑
∑
0)X)(Xˆ...XˆˆY(2
0)1)(Xˆ...XˆˆY(2
kikiki221i
kiki221i
βββ
βββ

Viết hệ dưới dạng ma trận : ( ) YXˆXX TT
=β
( ) ( )YXXXˆ T1T −
=⇒ β

11. 













=
∑∑∑∑
∑∑∑∑
∑∑∑
2
kii3kii2kiki
kii2i3i2
2
i2i2
kii3i2
T
X...XXXXX
XX...XXXX
X...XXn
XX















=
k
2
1
ˆ
ˆ
ˆ
ˆ
β
β
β
β















=
∑
∑
∑
iki
ii2
i
T
YX
YX
Y
YX


12. 4. Hệ số xác định
* Chú ý : Khi tăng số biến độc lập trong
mô hình thì R2
cũng tăng cho dù các biến
độc lập thêm vào có ảnh hưởng mô hình
hay không . Do đó không thể dùng R2
để
quyết định có hay không nên thêm
∑
∑−=−== 2
iy
2
i2 e
1
TSS
RSS
1
TSS
ESS
R
∑∑∑
∑
−−−=
−==
ikii2i
2
i yxyxy k2
2
i
ˆ...ˆ
ESSTSSRSSe
ββ

13. ∑
∑
−
−
−=
)1n/(
)kn/(e
1R
2
i2
2
iy
Hay:
kn
1n
)R1(1R 22
−
−
−−=
Tính chất của :2
R
2
R
1RR 22
≤≤- Khi k > 1,
- có thể âm, trong trường hợp âm, ta coi
giá trị của nó bằng 0.
biến vào mô hình mà thay vào đó có thể sử
dụng hệ số xác định được hiệu chỉnh :

14. * Cách sử dụng để quyết định đưa
thêm biến vào mô hình :
Mô hình hai biến Mô hình ba biến
2
2
2
1 RR >
tức là không cần đưa thêm biến X3 vào
mô hình. Ngược lại, ta chọn mô hình (2).
)1(XˆˆYˆ i221i ββ +=
2
1R
2
1R
)2(XˆXˆˆYˆ i33i221i βββ ++=
2
2R
2
2R
2
R
- Nếu thì chọn mô hình (1) ,

15. • So sánh hai giá trị R2
:
Nguyên tắc so sánh :
- Cùng cỡ mẫu n .
- Cùng các biến độc lập.
- Biến phụ thuộc phải ở dạng giống
nhau. Biến độc lập có thể ở bất cứ dạng
nào.
Ví dụ :

16. 5. Ma trận tương quan
kiki221i Xˆ...XˆˆYˆ βββ +++=












1...rr
......
r...1r
r...r1
2k1k
k221
k112
Gọi rtj là hệ số tương quan tuyến tính
giữa biến thứ t và thứ j. Trong đó Y
được xem là biến thứ 1.
Ma trận tương quan tuyến tính có dạng :
Xét mô hình :

17. 6. Ma trận hiệp phương sai














=
)ˆvar(...)ˆ,ˆcov()ˆ,ˆcov(
......
)ˆ,ˆcov(...)ˆvar()ˆ,ˆcov(
)ˆ,ˆcov(...)ˆ,ˆcov()ˆvar(
)ˆcov(
k2k1k
k2212
k1211
βββββ
βββββ
βββββ
β
21T
)XX()ˆcov( σβ −
=
Để tính ma trận hiệp phương sai của các hệ
số, áp dụng công thức :
với
kn
RSS
ˆ 2
−
=σ
Trong đó, k là số tham số trong mô hình.

18. 7. Khoảng tin cậy của các hệ số hồi qui
Khoảng tin cậy của βj (j =1,2, …, k) là :
)kn(t)ˆ(eˆsˆ
2/jj −± αββ
Trong đó, k là số tham số trong mô hình.

19. 8. Kiểm định giả thiết
a. Kiểm định H0 : βj= a (=const)
( j = 1, 2, …, k)
Phần này hoàn toàn tương tự như ở mô
hình hồi qui hai biến, khác duy nhất ở chỗ
bậc tự do của thống kê t là (n-k).

20. Nếu p(F* > F) ≤ α
Nếu F > Fα(k-1, n-k)
)kn/()R1(
)1k/(R
F 2
2
−−
−
=
b. Kiểm định giả thiết đồng thời :
H0 : β2 = β3 =…= βk = 0 ⇔ H0 : R2
= 0
H1: ∃ βj ≠ 0 (2 ≤ j ≤ k) ⇔ H1 : R2
≠ 0
Cách kiểm định :
-Tính
⇒ bác bỏ H0,
Tức là các hệ số hồi qui không đồng thời
bằng 0 hay hàm hồi qui phù hợp.

21. c. Kiểm định Wald
Xét mô hình (U) sau đây :
Yi = β1+ β2X2i + β3X3i+ β4X4i+ β5X5i+Ui
(U) được xem là mô hình không hạn chế.
Ví dụ 1 : Với mô hình (U), cần kiểm định
H0 : β3= β5= 0
Áp đặt giả thiết H0 lên mô hình (U), ta có
mô hình hạn chế (R) như sau :
Yi = β1+ β2X2i + β4X4i+Ui (R)
Để kiểm định H0, ta dùng kiểm định Wald.

22. Các bước kiểm định Wald :
- Hồi qui mô hình (U)  thu được RSSU.
- Hồi qui mô hình (R)  thu được RSSR.
- Tính
- Nếu p (F* > F) ≤ α
Nếu F > Fα(dfR- dfU, dfU)
⇒ bác bỏ H0,
UU
URuR
df/RSS
)dfdf/()RSSRSS(
F
−−
=
dfU : bậc tự do của (U)
dfR : bậc tự do của (R)

23. Ví dụ 2 : VớI mô hình (U), kiểm định
H0 : β2= β3= β4
Áp đặt H0 lên (U), ta có mô hình (R):
Yi = β1+ β2X2i + β2X3i+ β2X4i+ β5X5i+Ui
hay
Yi =β1+ β2(X2i+X3i+X4i) + β5X5i+Ui
Đến đây, áp dụng các bước kiểm định Wald
cho giả thiết H0.

24. Ví dụ 3 : VớI mô hình (U), kiểm định
H0 : β2+ β3= 1
Thực hiện tương tự như các ví dụ trên, bằng
các áp đặt H0 lên (U), ta có mô hình hạn
chế (R) :
Yi= β1+ β2X2i+(1- β2)X3i+ β4X4i+ β5X5i+Ui
(Yi-X3i)= β1+ β2(X2i-X3i)+ β4X4i+ β5X5i+Ui
* Chú ý : Trong Eviews, thủ tục kiểm định
Wald được viết sẵn, bạn chỉ cần gõ vào giả

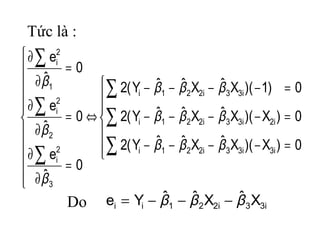
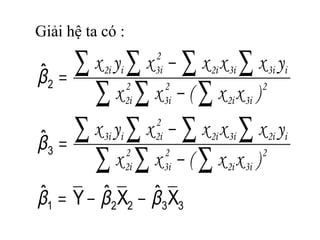
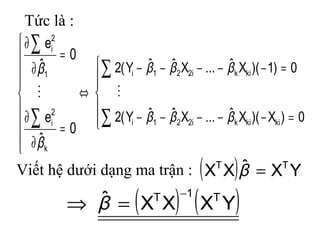
25. 9. Dự báo :
a. Dự báo giá trị trung bình
Cho X2
0
, X3
0
, …, Xk
0
. Dự báo E(Y).
0
kk
0
2210 Xˆ...XˆˆYˆ βββ +++=
)]kn(t)Yˆ(eˆsYˆ;)kn(t)Yˆ(eˆsYˆ[ 2/002/00 −+−− αα
- Dự báo điểm của E(Y) là :
- Dự báo khoảng của E(Y) :

26. Trong đó :
Var( ) = X0T
(XT
X)-1
X0
σ2
0Yˆ












=
0
k
0
20
X
X
1
X

)]kn(t)YˆY(eˆsYˆ;)kn(t)YˆY(eˆsYˆ[ 2/0002/000 −−+−−− αα
2
000 )Yˆ(Var)YˆY(Var σ+=−
b. Dự báo giá trị cá biệt của Y khi X=X0
.
Trong đó :

27. I. Bản chất của đa cộng tuyến
Đa cộng tuyến là tồn tại mối quan hệ
tuyến tính giữa một số hoặc tất cả
các biến độc lập trong mô hình.
Xét hàm hồi qui k biến :
Yi = β1+ β2X2i + …+ βkXki + Ui
- Nếu tồn tại các số λ2, λ3,…,λk không
đồng thời bằng 0 sao cho :
Đa cộng tuyến

28. λ2X2i + λ3X3i +…+ λkXki + a = 0
(a : hằng số)
Thì giữa các biến độc lập xảy ra hiện
tượng đa cộng tuyến hoàn hảo.
- Nếu tồn tại các số λ2, λ3,…,λk không
đồng thời bằng 0 sao cho :
λ2X2i + λ3X3i +…+ λkXki + Vi = 0
(Vi : sai số ngẫu nhiên)
Thì giữa các biến độc lập xảy ra hiện
tượng đa cộng tuyến không hoàn hảo.

29. Ta có : X3i = 5X2i có hiện tượng cộng
tuyến hoàn hảo giữa X2 và X3và r23 =1
X4i = 5X2i + Vi  có hiện tượng
cộng tuyến không hoàn hảo giữa X2 và
X3 , có thể tính được r24 = 0.9959.
X2 10 15 18 24 30
X3 50 75 90 120 150
X4 52 75 97 129 152
Ví dụ : Yi = β1+β2X2i+β3X3i+ β4X4i + Ui
Với số liệu của các biến độc lập :

30. Hậu quả của đa cộng tuyến
1. Phương sai và hiệp phương sai của các ước lượng
OLS lớn.
2. Khoảng tin cậy rộng hơn
3. Thống kê t nhỏ nên tăng khả năng các hệ số ước
lượng không có ý nghĩa
4. R2
cao nhưng thống kê t nhỏ.
5. Dấu của các ước lượng có thể sai.
6. Các ước lượng OLS và sai số chuẩn của chúng trở
nên rất nhạy với những thay đổi nhỏ trong dữ
liệu.
7. Thêm vào hay bớt đi các biến cộng tuyến với các
biến khác, mô hình sẽ thay đổi về dấu hoặc độ
lớn của các ước lượng.

31. Dấu hiệu nhận dạng đa cộng tuyến
1. Hệ số R2
lớn nhưng thống kê t nhỏ.
2. Tương quan cặp giữa các biến giải thích
(độc lập) cao. Tuy nhiên điều ngược lại
không đúng, nếu các r nhỏ thì chưa biết
có đa cộng tuyến hay không.
3. Sử dụng mô hình hồi qui phụ (hồi quy
từng cặp biến độc lập)

32. 4. Sử dụng nhân tử phóng đại phương sai
là hệ số xác định của mô hình hồi qui
phụ Xj theo các biến độc lập khác.
Nếu có đa cộng tuyến thì VIF lớn.
VIFj > 5 thì Xj có đa cộng tuyến cao với
các biến khác.
* Với mô hình 3 biến thì
2
j
j
R1
1
VIF
−
=
2
23r1
1
VIF
−
=
2
jR

33. Phương sai thay đổi
Phương sai có điều kiện của Ui không
giống nhau ở mọi quan sát.
Var (Ui) =
2
iσ
Nguyên nhân :
- Do bản chất của các mối quan hệ trong
kinh tế chứa đựng hiện tượng này.
(i=1,2,…,n)

34. - Do kỹ thuật thu thập số liệu được cải
tiến, sai lầm phạm phải càng ít hơn.
- Do con người học được hành vi trong
quá khứ.
- Do trong mẫu có các giá trị bất thường
(hoặc rất lớn hoặc rất nhỏ so với các
giá trị khác).
Hiện tượng phương sai không đồng đều
thường gặp đối với số liệu chéo.

35. Hậu quả của phương sai thay đổi
1. Các ước lượng OLS vẫn là các ước
lượng tuyến tính, không chệch nhưng
không còn hiệu quả nữa.
2. Ước lượng phương sai của các ước
lượng OLS bị chệch nên các kiểm định
t và F không còn đáng tin cậy nữa.
3. Kết quả dự báo không hiệu quả khi sử
dụng các ước lượng OLS.

36. Dấu hiệu nhận dạng phương sai thay đổi
1. Phương pháp đồ thị
Xét mô hình : Yi = β1+ β2Xi +Ui (1)
- Hồi qui (1)  thu được các phần dư ei.
- Vẽ đồ thị phân tán của e theo X.
- Nếu độ rộng của biểu đồ rải tăng hoặc giảm khi X
tăng thì mô hình (1) có thể có hiện tượng phương
sai thay đổi.
• Chú ý : Với mô hình hồi qui bội, cần vẽ đồ thị
phần dư theo từng biến độc lập hoặc theo
2. Kiểm định Park
3. Kiểm định Glejser
4. Kiểm định White
Yˆ

37. Tự tương quan
Tự tương quan: Là sự tương quan giữa
các thành phần của chuỗi các quan
sát theo thời gian hay không gian.
Nếu có tự tương quan giữa các sai số
ngẫu nhiên thì :
Cov(Ui, Uj) ≠ 0 (i ≠ j)

38. Hậu quả của việc sử dụng phương
pháp OLS khi có tự tương quan
1. Các ước lượng OLS vẫn là các ước lượng
tuyến tính, không chệch nhưng không
còn hiệu quả nữa.
2. Ước lượng của các phương sai bị chệch
(thường thấp hơn giá trị thực) nên các
kiểm định t và F không còn hiệu lực nữa.
3. Thường R2
được ước lượng quá cao so với
giá trị thực.
4. Sai số chuẩn của các giá trị dự báo không
còn tin cậy nữa.

39. Dấu hiệu nhận dạng tự tương quan
1. Phương pháp đồ thị
- Hồi qui mô hình gốc  thu phần dư et.
- Vẽ đồ thị phần dư et theo thời gian.
- Nếu phần dư phân bố ngẫu nhiên xung quanh
trung bình của chúng, không biểu thị một kiểu
mẫu nào khi thời gian tăng  mô hình gốc không
có tự tương quan.
2. Kiểm định d của Durbin-Watson
3. Kiểm định Breusch-Godfrey (BG)

40. Hồi qui với biến giả (xét mô hình hồi
qui có biến định lượng và biến định tính)
Ví dụ : Lập mô hình quan hệ giữa chi tiêu cá nhân với
thu nhập và giới tính của cá nhân đó.
Yi = β1+ βXi + β3Zi + Ui (1)
Y – chi tiêu (triệu/tháng)
X – thu nhập (triệu/tháng)
Zi = 1 : nam giới
0 : nữ giới.
• Mở rộng mô hình : Với mô hình trên, khi thu nhập
cá nhân tăng 1 triệu đồng thì chi tiêu tăng β triệu
đồng bất kể là nam hay nữ.

41. Nhưng với giả thiết cho rằng nếu thu nhập
tăng 1 triệu đồng thì mức chi tiêu tăng
thêm của nam và nữ khác nhau thì β phải là
β = β2+ β4Zi
Lúc này mô hình (1) được viết :
Yi = β1+ (β2+ β4Zi)Xi + β3Zi + Ui
Hay :
Yi = β1+ β2Xi + β3Zi + β4XiZi + Ui (2)
Trong đó : XiZi được gọi là biến tương tác
giữa X và Z.

42. - Khi Zi =1 : Yi = (β1 +β3) + (β2+ β4)Xi +Ui
Đây là hồi qui chi tiêu-thu nhập của nam.
- Khi Zi =0 : Yi = β1+ β2 Xi +Ui
Đây là hồi qui chi tiêu-thu nhập của nữ.
Ý nghĩa của các hệ số :
− β1: Khi không có thu nhập thì chi tiêu
trung bình của một người nữ là β1 triệu.
− β2: Khi thu nhập của một người nữ tăng 1
triệu đồng thì chi tiêu của họ tăng β2 triệu
đồng.

43. − β3: Khi không có thu nhập thì chi tiêu trung
bình của một người nam chênh lệch so với
của một người nữ là β3 triệu (hay chênh
lệch về hệ số tung độ gốc giữa hàm hồi qui
cho nam và hàm hồi qui cho nữ).
− β4: Khi thu nhập của một người nam tăng 1
triệu đồng thì chi tiêu của họ tăng nhiều
hơn của nữ β4 triệu đồng (nếu β4 > 0) hay
tăng ít hơn của nữ β4 triệu đồng (nếu β4< 0)
(Hay chênh lệch về hệ số độ dốc giữa hàm
hồi qui cho nam và hàm hồi qui cho nữ).

44. − β3: Khi không có thu nhập thì chi tiêu trung
bình của một người nam chênh lệch so với
của một người nữ là β3 triệu (hay chênh
lệch về hệ số tung độ gốc giữa hàm hồi qui
cho nam và hàm hồi qui cho nữ).
− β4: Khi thu nhập của một người nam tăng 1
triệu đồng thì chi tiêu của họ tăng nhiều
hơn của nữ β4 triệu đồng (nếu β4 > 0) hay
tăng ít hơn của nữ β4 triệu đồng (nếu β4< 0)
(Hay chênh lệch về hệ số độ dốc giữa hàm
hồi qui cho nam và hàm hồi qui cho nữ).

45. Chọn mô hình và kiểm định
việc chọn mô hình
I. Các thuộc tính của một mô hình tốt
1. Tính tiết kiệm
2. Tính đồng nhất
3. Tính thích hợp
4. Tính bền vững về mặt lý thuyết
5. Có khả năng dự báo tốt

46. Các sai lầm thường gặp khi chọn mô hình
• Bỏ sót biến thích hợp
2. Đưa vào mô hình các biến không
thích hợp (mô hình thừa biến)
3. Chọn dạng hàm không đúng
Phát hiện những sai lầm
1. Phát hiện sự có mặt của biến không cần thiết:Nếu lý
thuyết cho rằng tất cả biến độc lập trên đều quyết
định Y thì phải giữ chúng trong mô hình dù hệ số
của chúng không có ý nghĩa thống kê.
2. Kiểm định các biến bị bỏ sót
3. Kiểm định phân phối chuẩn của U