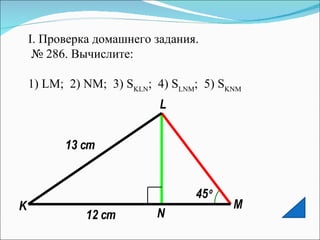
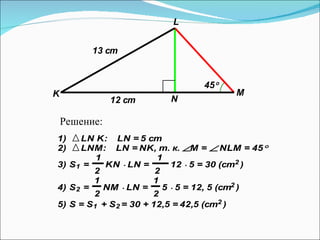
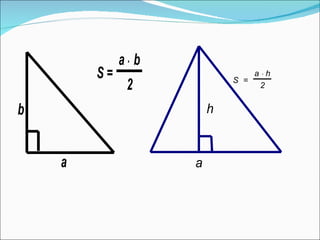
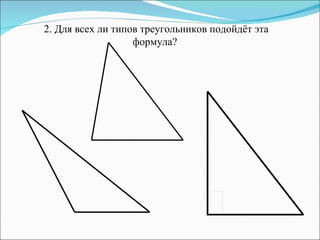
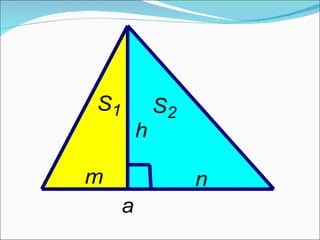
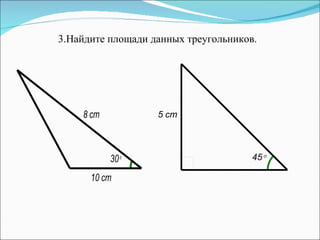
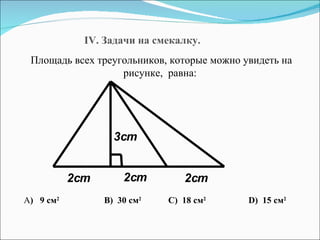
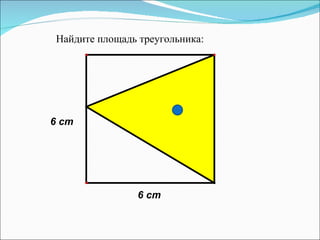
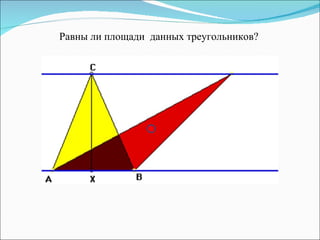
Документ описывает методы обучения геометрическим задачам на нахождение площади треугольника, включая использование формул и развитие логического мышления. Также представлены примеры задач, теоремы, тесты и рекомендации для домашних заданий. Основная цель - укрепить понимание студентов о площади треугольников и их практическом применении.

1. Три пути ведут к знанию: путь размышления – путь самый благородный, путь подражания – это путь самый лёгкий и путь опыта – это путь самый горький. Конфуций.

2. Задачи : закрепить умение решать геометрические задачи на нахождение площади произвольного треугольника, используя формулу; развивать логическое, аналитическое и пространственное мышление, умение делать выводы на основе наблюдений за учебным материалом.

3. I. Проверка домашнего задания. № 286. Вычислите: 1) LM ; 2) NM ; 3) S KLN ; 4) S LNM ; 5) S KNM

4. Решение:

5. При решении геометрических задач, почти в каждой из них мы решаем задачи на решение треугольника. И очень часто при этом используем формулы нахождения площади треугольника. Мы научились с вами строить высоты треугольников, находить периметры треугольников, а сейчас продолжаем вычислять их площади. 1 . Клумба для цветов имеет форму прямоугольного треугольника с катетами 3 м и 4 м. Сколько понадобиться кустов роз, если на 1 м 2 надо посадить 5 кустов ?

7. 2. Для всех ли типов треугольников подойдёт эта формула?

8. II. Убедимся, что площадь, записанная на доске правильная

10. 1) m + n = a 2) S 1 = 3) S 2 = Доказательство: 4 ) S 1 + S 2 = + = Вывод: площадь любого треугольника равна половине произведения его основания на высоту, проведённую к нему.

12. 3.Найдите площади данных треугольников.

15. 4. Как с помощью веревки, разделенной на 12 равных частей построить прямоугольный треугольник

17. Площадь всех треугольников, которые можно увидеть на рисунке , равна : А ) 9 см 2 B ) 30 см 2 C) 18 см 2 D ) 15 см 2 IV. Задачи на смекалку .

18. Найдите площадь треугольника:

19. Равны ли площади данных треугольников?

20. V. Математический тест. 1. Как переводится слово «геометрия»? А) Наука B ) Измерение C ) Изучение D ) Землемерие 2. Расположите в порядке убывания: А ) Ар B) Квадратный метр С ) Гектар D ) Квадратный дециметр. 3. Многоугольник с наименьшим числом сторон называется ... A) Квадратом. B ) Треугольником C ) Прямоугольником D ) Ромбом 4. Площадь квадрата равна 49 см 2 Чему равен его периметр? A ) 14 см B ) 49см C ) 28см D ) 21см 5. Кто ввел прямоугольную систему координат? A) Пифагор B )Декарт C )Ньютон D )Виет 6. Периметр прямоугольника равен 24см. Чему равна площадь квадрата с тем же периметром? A ) см 2 B) 6 см 2 C ) 8 см 2 D ) 36 см 2

21. YI . Рефлексия. Что мы выяснили сегодня на уроке? Где нам пригодятся эти знания? Что удалось, а на что надо обратить внимание? Домашнее задание: составить две задачи на нахождение площади треугольника.

22. Справочная страничка. 1.Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2. 3. В прямоугольном треугольнике, катет лежащий против угла в , в два раза меньше гипотенузы. 4.Если один из углов прямоугольного треугольника равен , то второй угол также равен . При этом треугольник является равнобедренным . 5. c a b

23. Прогнозируемые результаты знать определения треугольника, квадрата, прямоугольника, уметь вычислять их площади; продемонстрировать осведомленность о практическом применении площадей этих фигур; знать сведения вычисления площадей в древности; получать навыки анализа и систематизации полученных ранее знаний;