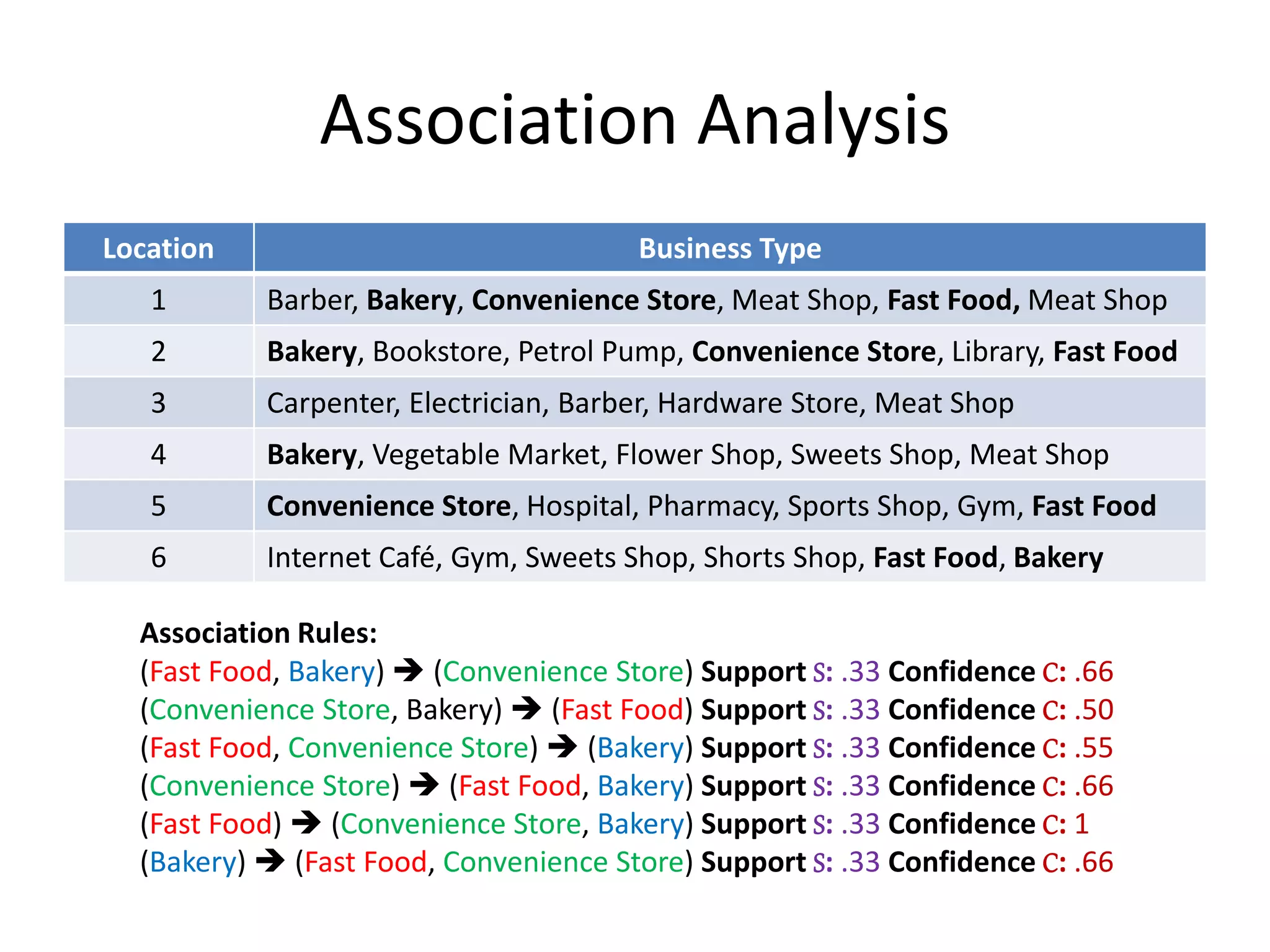
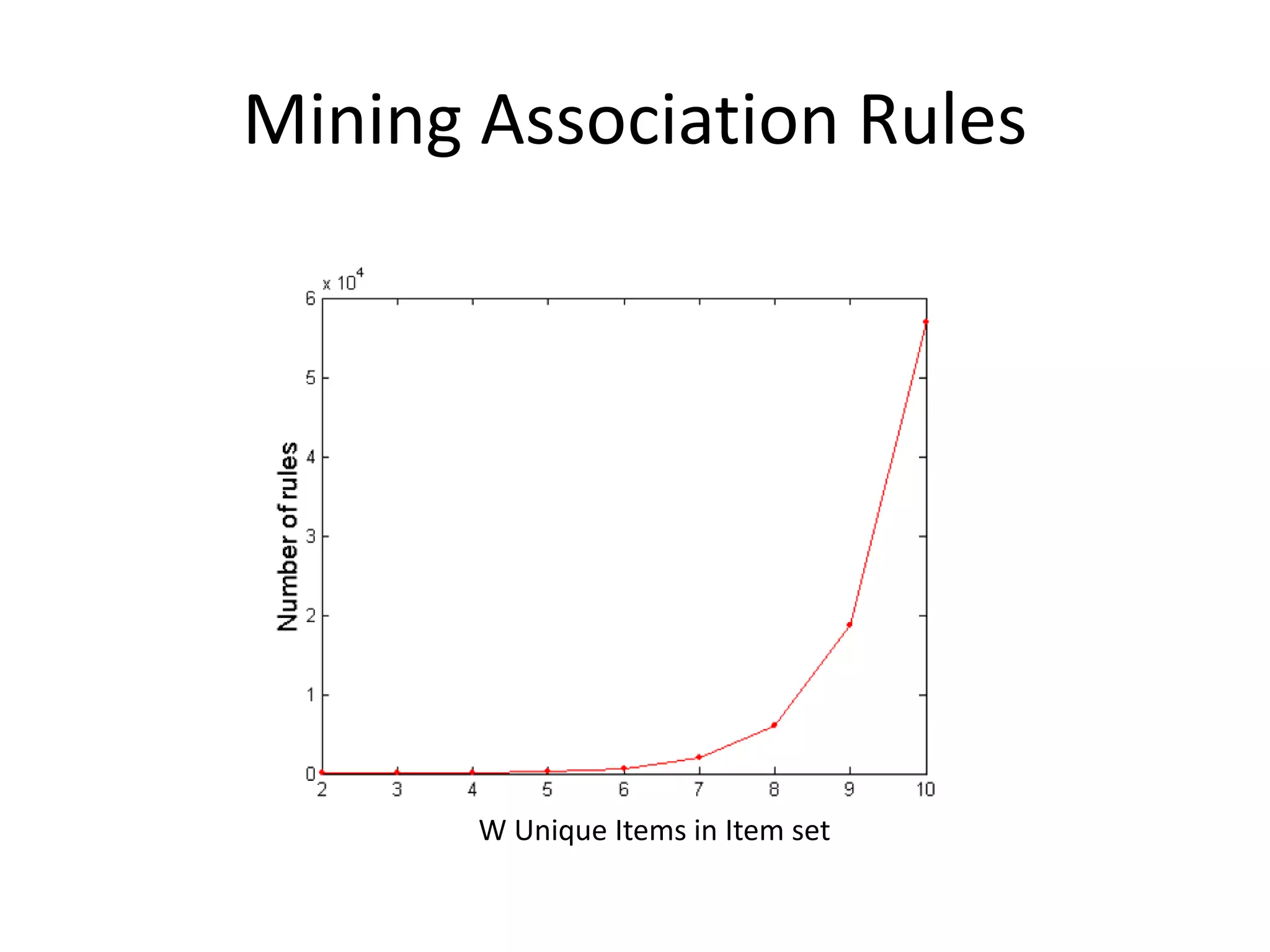
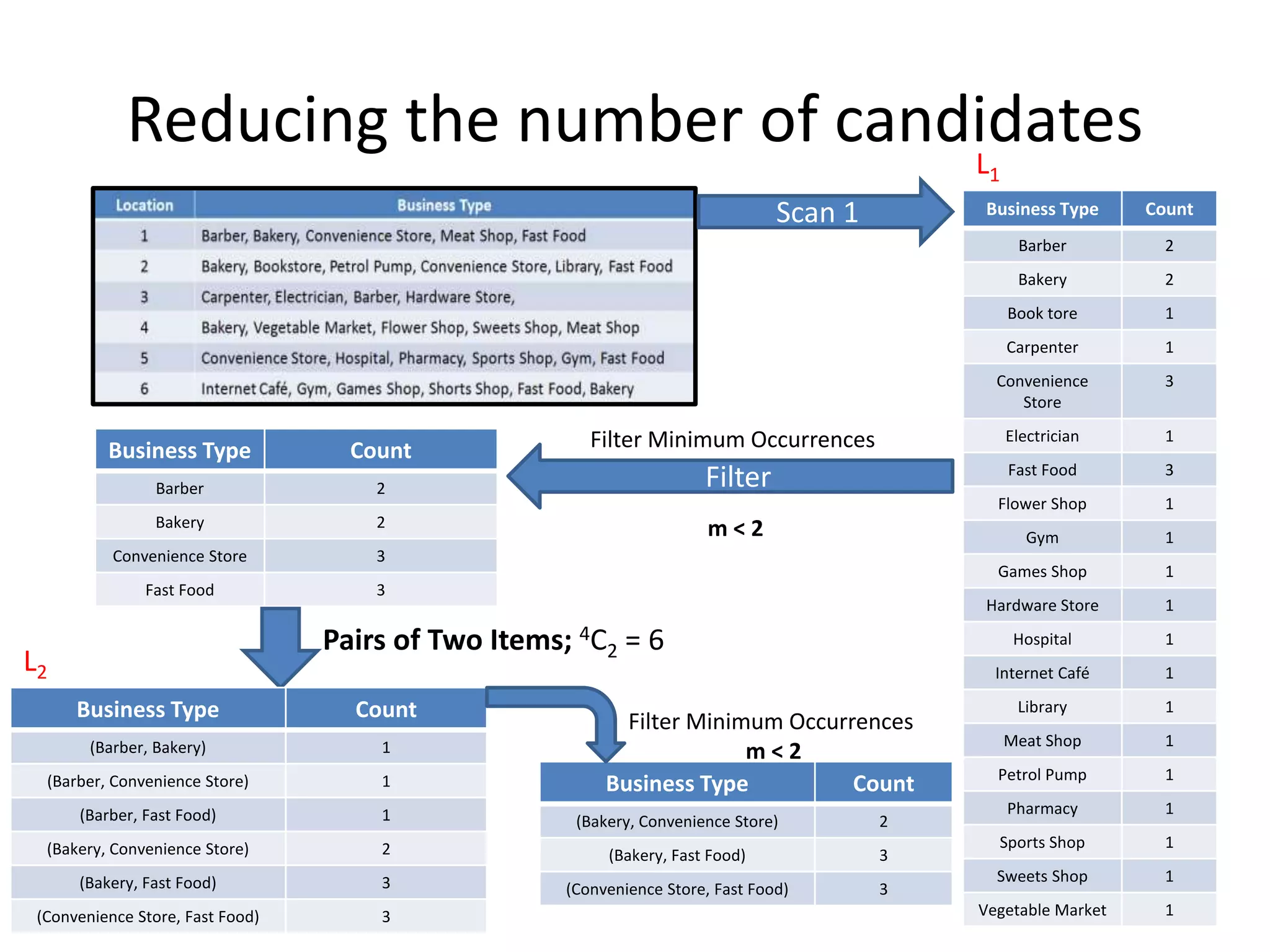
The document discusses association rule mining to discover relationships between data items in large datasets. It describes how association rules have the form of X → Y, showing items that frequently occur together. The key steps are: (1) generating frequent itemsets whose support is above a minimum threshold; (2) extracting high-confidence rules from each frequent itemset. It proposes using the Apriori algorithm to efficiently find frequent itemsets by pruning the search space based on the antimonotonicity of support.

1. Association Rule Mining
Ayesha Ali

2. Association Analysis
• Discovery of Association Rules
– showing attribute-value conditions that occur
frequently together in a set of data, e.g. market
basket
– Given a set of data, find rules that will predict the
occurrence of a data item based on the
occurrences of other items in the data
• A rule has the form body ⇒head
– buys(Omar, “milk”) ⇒ buys(Omar, “sugar”)

3. Association Analysis

4. Association Analysis
Location Business Type
1 Barber, Bakery, Convenience Store, Meat Shop, Fast Food
2 Bakery, Bookstore, Petrol Pump, Convenience Store, Library, Fast Food
3 Carpenter, Electrician, Barber, Hardware Store,
4 Bakery, Vegetable Market, Flower Shop, Sweets Shop, Meat Shop
5 Convenience Store, Hospital, Pharmacy, Sports Shop, Gym, Fast Food
6 Internet Café, Gym, Games Shop, Shorts Shop, Fast Food, Bakery
Association Rule: X Y ; (Fast Food, Bakery)  (Convenience Store)
Support S: Fraction of items that contain both X and Y = P(X U Y)
S(Fast Food, Bakery, Convenience Store) = 2/6 = .33
Confidence C: how often items in Y appear in locations that contain X = P(X U Y)
C[(Fast Food, Bakery)  (Convenience Store)] = P(X U Y) / P(X)
= 0.33/0.50 = .66

5. Association Analysis
• Given a set of transactions T, the goal of
association rule mining is to find all rules having
– support ≥ minsup threshold
– confidence ≥ minconf threshold
• Brute-force approach:
– List all possible association rules
– Compute the support and confidence for each rule
– Prune rules that fail the minsup and minconf
thresholds
⇒ Computationally prohibitive!

6. Association Analysis
Location Business Type
1 Barber, Bakery, Convenience Store, Meat Shop, Fast Food, Meat Shop
2 Bakery, Bookstore, Petrol Pump, Convenience Store, Library, Fast Food
3 Carpenter, Electrician, Barber, Hardware Store, Meat Shop
4 Bakery, Vegetable Market, Flower Shop, Sweets Shop, Meat Shop
5 Convenience Store, Hospital, Pharmacy, Sports Shop, Gym, Fast Food
6 Internet Café, Gym, Sweets Shop, Shorts Shop, Fast Food, Bakery
Association Rules:
(Fast Food, Bakery)  (Convenience Store) Support S: .33 Confidence C: .66
(Convenience Store, Bakery)  (Fast Food) Support S: .33 Confidence C: .50
(Fast Food, Convenience Store)  (Bakery) Support S: .33 Confidence C: .55
(Convenience Store)  (Fast Food, Bakery) Support S: .33 Confidence C: .66
(Fast Food)  (Convenience Store, Bakery) Support S: .33 Confidence C: 1
(Bakery)  (Fast Food, Convenience Store) Support S: .33 Confidence C: .66

7. Association Analysis
Association Rules:
(Fast Food, Bakery)  (Convenience Store) Support S: .33 Confidence C: .66
(Convenience Store, Bakery)  (Fast Food) Support S: .33 Confidence C: .50
(Fast Food, Convenience Store)  (Bakery) Support S: .33 Confidence C: .66
(Convenience Store)  (Fast Food, Bakery) Support S: .33 Confidence C: .66
(Fast Food)  (Convenience Store, Bakery) Support S: .33 Confidence C: 1
(Bakery)  (Fast Food, Convenience Store) Support S: .33 Confidence C: .66
Observations
 Above rules are binary partitions of given item set
 Identical Support but different Confidence
 Support and Confidence thresholds may be different

8. Mining Association Rules
• Two-step approach:
Step 1. Frequent Itemset Generation
Generate all itemsets whose support ≥ minsup
Step 2. Rule Generation
Generate high confidence rules from each frequent itemset,
where each rule is a binary partitioning of a frequent itemset
Note: Frequent itemset generation is still computationally expensive

9. Mining Association Rules
• Frequent Item Generation
Lattice Graph of possible item sets

10. Mining Association Rules
• Brute-force approach:
– Each node in the lattice graphs is a candidate frequent itemset
– Count the support of each candidate by scanning the database
– N = 6
– w = (Barber, Bakery, Convenience Store, Meat Shop, Fast Food, Bookstore, Petrol Pump, Library,
Carpenter, Electrician, Hardware Store, Vegetable Market, Flower Shop, Sweets Shop, Meat Shop,
Hospital, Pharmacy, Sports Shop, Gym, Internet Café) = 20
– M = 220 = 1048576
– Complexity ~ O (NMw)

11. Mining Association Rules
W Unique Items in Item set

12. Mining Association Rules
• Frequent Itemset Generation
– Reduce the number of candidates (M)
– Reduce the number of transactions/locations (N)
– Reduce the number of comparisons (NM)
• Use efficient data structures to store the candidates
• No need to match every candidate against every
transaction/location

13. Reducing the number of candidates
• Apriori principle:
– If an itemset is frequent, then all of its subsets must
also be frequent
• Important Support property:
– Support of an itemset never exceeds the support of its
subsets
– This is known as the anti-monotone property of
support

14. Reducing the number of candidates
Applying Apriori principle

15. Reducing the number of candidates
• N = 20
• All Possible candidate sets;
– NC1 + NC2 + NC3 + … + NCN
• Minimum Occurrence Based Filtering
Set m= 2 and L = 1
While (L < N){
Scan DB:
List = Create Occurrence Frequency Table of candidate sets of Length L
If no candidate in List then Break;
Filter all candidate sets with Occurrence Frequency < m
Create new candidate set of Length (L=L+1) from List
}

16. Filter Minimum Occurrences
m < 2
Reducing the number of candidates
Business Type Count
Barber 2
Bakery 2
Book tore 1
Carpenter 1
Convenience
Store
3
Electrician 1
Fast Food 3
Flower Shop 1
Gym 1
Games Shop 1
Hardware Store 1
Hospital 1
Internet Café 1
Library 1
Meat Shop 1
Petrol Pump 1
Pharmacy 1
Sports Shop 1
Sweets Shop 1
Vegetable Market 1
Business Type Count
Barber 2
Bakery 2
Convenience Store 3
Fast Food 3
Filter
Scan 1
Business Type Count
(Barber, Bakery) 1
(Barber, Convenience Store) 1
(Barber, Fast Food) 1
(Bakery, Convenience Store) 2
(Bakery, Fast Food) 3
(Convenience Store, Fast Food) 3
Pairs of Two Items; 4C2 = 6
Business Type Count
(Bakery, Convenience Store) 2
(Bakery, Fast Food) 3
(Convenience Store, Fast Food) 3
Filter Minimum Occurrences
m < 2
L1
L2