1. Lecture Notes On
Algo-Design
Lecturer: Ulf-Peter Schroeder
February 16, 2006
written by:
Braun, Rudolf
Brune, Philipp
Piepmeyer, Meik
Please send corrections - including [AlgoDesign-Script] in the subject line -
to: meikp <KLAMMERAFFE> upb <PUNKT> de
1
3. 1 GREEDY ALGORITHMS 3
18.10.2005
1 Greedy Algorithms
• builds of a solution in ”small” steps
• choosing a irreversible decision at each step ??? to optimize some underlying criterion
Questions
1. When did a greedy algorithm succeed in solving a mentioned problem optimally?
2. How to proof that a greedy algorithm produces an optimal solution to a problem?
1.1 Interval Scheduling
Def.: Set of requests {1, 2, .., m}
The ith request corresponds to an interval of time starting at s(i) and finishing at f (i). We’ll
say that a subset of the request is compatible if no two of them overlap in time.
Our goal is to accept as long a compatible subset as possible. Compatible set of maximum
size will be called optimal.
Idea: The basic idea is to use a simple route to select the first request i1 . We reject all requests
that are not compatible with i1 . Repeat this procedure until we run out of requests.
Rule 1: ”Select the available request that starts earliest.”
Rule 2: ”Select the request that requires the smallest interval of time.”
Rule 3: ”Select the request that has the fewest number of non-compatible requests.”
Rule 4: ”Select first the request that finishes first, that is the request i for which f (i) is as small as
possible.”
Algo.: Initially let R be a set of requests and let A be empty.
while R is not yet empty
choose a request i ∈ R that has the smallest finishing time.
add request i to A.
delete all requests from R that are not compatible with request i.
end while
return A.
Analyzing the Algorithm
√
Part 1: A is a compatible set of requests.
Is the solution A optimal?
Let O be an optimal set of intervals.
| A |=| O | is to prove!
Let i1,..,k be the set of requests in A in the order they were added to A. | A |= k
Let j1,..,m be the requests in O.
Our goal is to prove that k = m.
Part 2: For all indices r ≤ k we have f (ir ) ≤ f (jr ).
4. 1 GREEDY ALGORITHMS 4
Proof: r=1 Our Greedy Rule guaranties that f (i1 ) ≤ f (j1 ).
I.H.: The statement is true for r − 1.
I.S.: We know that f (jr−1 ) ≤ s(jr ). Combining this with the I.H: f (ir−1 ) ≤ f (jr−1 )
we get f (ir−1 ) ≤ s(jr ). Since interval jr is one of available interests at the time when the
greedy algorithm selects ir , we have f (ir ) ≤ f (jr ).
Part 3: The greedy algorithm returns an optimal set A.
Proof: ( given by contradiction )
If A is not optimal then an optimal set 0 must have more requests, that is, we must have
m > k. Applying Part 2 with r = k, then is f (ik ) ≤ f (jk ). Since m > k, there is a request
jk+1 in O.
This request starts after request jk ends, and ends after ik ends. But the greedy algorithm
stops with request ik , and it is only supposed to stop when R is empty. `
25.10.2005
1.2 Scheduling to Minimize Lateness
Definition of the Problem
A single ressource, a set of n requests to use the ressource for an interval of time, ressource is
available starting at time S, the request i has a deadline di , and it requires a continuous time
interval of length ti . Each request must be assigned non overlapping intervals.
Objective function
We will assign each request i an interval of time of length ti , let us denote this interval [s(i), f (i)]
with f (i) = s(i) + ti .
We say that a request i is late if it misses the deadline, that is if di < f (i).
li = f (i) − di . We say that li = 0 if request i is not late.
maximum lateness L = max li
i∈{1,..,n}
Idea 1: ”Schedule the jobs in order of increasing length ti .”
Idea 2: ”Schedule the jobs in order of increasing slacktime di − ti ”.
Idea 3: ”Earliest Deadline First”
Analyzing the ”Earliest Deadline First” - Greedy Algorithm
We start with an optimized schedule O.
Our plan we have is to gradually modify O, perserving its optimality at each step, but transforming
it into a schedule that is indicated to the schedule A formed by our algorithm.
Fact 1: There is an optimal schedule with no idle time.
Def.: A schedule A′ has an inversion if a job i with deadline di is scheduled before another job j
with earlier deadline dj < di .
Fact 2: All schedules with no inversions and no idle time have the same maximum lateness.
Fact 3: There is an optimal schedule that has no inversions and no idle time.
Proof of Fact 3: By Fact 1 there is an optimal schedule with no idle time.
5. 1 GREEDY ALGORITHMS 5
1. If O has an inversion, then there is a pair of jobs i and j and that j is immediately
after i and has dj < di .
2. After swapping i and j, we get a schedule with one less inversion.
√
3. The new swapped schedule has a maximum lateness no longer then that of O.
Proof of (3.): All jobs other then jobs i and j finish at the same time in the two schedules.
˜i = f (i) − di = f (j) − di < f (j) − dj = l′
l ˜
j
⇐⇒ ˜i < lj
l ′
Notation
Optimal schedule O: each request r is scheduled [s(r), f (r)]
′
and has lateness lr
L′ = max lr
′
r
swapped schedule O : s(r), f (r), ˜r , L
˜ ˜ ˜ l ˜
1.3 ( Huffman Codes and Data Compressions )
1.4 Theoretical foundations for the greedy method
Def.: A matroid is a pair M = (S, I) satisfying the following conditions:
1. S is a finite non-empty set
1
2. I is a non-empty family of subsets of S such that: B ∈ I and A ⊂ B implies A ∈ I.
3. If A ∈ I, B ∈ I and |A| < |B|, then there exists some element x ∈ B A such that
A ∪ [x] ∈ I. 2
Examples: 1. Matrix Matroid
Def.: S = set of n-vectors
I consists of all subsets of linear independent vectors from S.
1 1 1 0
A = 0 0 1 1
1 0 1 1
1
1 1 0
S = 0, 0, 1, 1
1
0 1 1
e1 e2 e3 e4
I = {∅, {e1 }, {e2}, {e3 }, {e4 }, {e1 , e2 }, {e1, e3 }, {e1 , e4 }, {e2 , e3 }, {e2, e4 },
{e3 , e4 }, {e1, e2 , e3 }, {e1 , e2 , e4 }, {e1, e3 , e4 }}
2. Graphic Matroid
Def.: Let G = (V, E) be a continued, undirected graph.
MG = (SG , IG ) is defined by SG = E. I consists of all subset A ⊂ E such that
(V, A) is acyclic.
1 hereditary
2 exchange property
6. 1 GREEDY ALGORITHMS 6
1. and 2. trivial.
3. exchange property?
Let A and B belong to I with |A| < |B|, i.e. A and B are forests. Let V (A), V (B)
be sets of vertices incident to edges from A and B, resp.
(a) If b ∈ V (B) V (A), then exists some e ∈ V (B) such that [b, e] ∈ B.
A ∪ {(b, c)} is acyclic.
(b) Now we can assume that V (B) ⊂ V (A)
( Theorem: Forest with k edges contains exactly |V | − k trees. )
A consists of τ1 = |V (A)| − |A| trees and
B consists of τ2 = |V (B)| − |B| trees.
|V (B)| ≤ |V (A)| and |A| < |B| implies τ2 < τ1 .
=⇒ ∃ some edge e ∈ B connecting 2 trees from A
=⇒ A ∪ {e} is acyclic.
3. ”counter example”
Interval Scheduling
S = {1, .., n} be the set of requests.
U ⊂ S belongs to I if its requests are mutually compatible.
Def.: Let M = [S, I] be a matroid.
A ∈ I is called maximal, if there exists no x ∈ S A such that A ∪ {x} ∈ I.
Lemma: All maximum independent subsets in a matroid have the same size.
Proof: Suppose the contrary:
There exist two maximum independent subsets A, B with |A| < |B|.
` to the exchange property.
3
Example: 1. A is maximal ⇔ |A| = rank(S)
4
2. A is maximal ⇔ A is spanning tree of G ⇔ |A| = |V | − 1
Def.: A Matroid M = (S, I) is called weighted if there is a weight w(x) > 0 to each x ∈ S.
For A ⊂ S we set w(A) = x⊂A w(x).
The maximum weight independent subset problem: Find a maximum weight independent
subset in a weighted matroid.
Greedy(M,w)
A=∅
sort S[M ] into nonincreasing order by weight w
for each x ∈ S[M ] take in nonincreasing order by weight w do
if A ∪ {x} ∈ I(M ) then
A := A ∪ {x}
return A
MST: Define the matroid MG = (SG , IG ) with SG = E. IS consists of all subsets A ⊂ E such that
(V, A) is acyclic.
We define w′ (e) = (wmax + 1) − w(e) with wmax = max{w(e)}.
e∈E
It holds w′ (e) > 0 ∀e ∈ E and Greedy(MI , w′ ) computes an optimal subset5 which is a MST
in the original graph.
3 rank means rank for the Matrix Matroid.
4 |V | means vertices for the Graphire Matroid.
5 that means a maximum weight independent subset
7. 1 GREEDY ALGORITHMS 7
Lemma: Suppose that M = (S, I) is a weighted matroid with weight function w and that S is
sorted into nonincreasing order by weight. Let x be the first element of S such that {x} is
independent. Then there exists an optimal subset A of S that contains x.
Proof: Let B ∈ I be an optimal subset.
If x ∈ B, then the proof is done.
So now let x ∈ B hold.
/
Construct the set A as follows:
Begin with A = {x}
By the choice of x, A is independent and w(x) ≥ w(y) for any y ∈ B.
Using the exchange property, find an element x1 ∈ B such that A = {x1 , x} is indepen-
dent .
Repeat this procedure until |A| = |B|.
Then, A = (B {y}) ∪ {x} for some y ∈ B and B is independent ⇒ {y} is independent.
w(x) ≥ w(y) by the choice of x ⇒ w(A) ≥ w(B).
Since B is optimal A must also be optimal, and since x ∈ A, the Lemma is proofed.
Theorem: If M = (S, I) is a weighted matroid with weight function w, then the call Greedy(M,w)
returns an optimal independent subset.
Proof: We show the so called ”optimal-substructure property”.
Let x be the first element chosen by Greedy.
If x is chosen to be the element of the solution, then this defines the problem to find a
maximum weight independent subset in the matroid
M ′ = (S ′ , I ′ ) with S ′ = {y ∈ S : {x, y} ∈ I}
I ′ = {B ⊂ (S {x}) : B ∪ {x}) ∈ I}
Proof of this property: If A is any maximum-weighted independent subset containing x, then A′ = a {x} is an
optimal subset for M ′ .
Conversely, any optimal subset A′ in M ′ yields a subset A = A′ ∪ {x} which has optimal
weight among all subset from I containing x.
From the previous Lemma we have that there exists an optimal solution containing x. This
shows the optimality of Greedy by induction on |S|.
Conclusion
Here, we have learned three techniques to proof the function of a Greedy Al-
gorithm.
8. 2 DIVIDE AND CONQUER 8
08.11.2005
2 Divide and Conquer
Principle:
• break the input into several parts
• solves the problem in each part recursively
• combines the solutions of the subproblems into an overall solution
Running time: T (n) ≤ aT ( n ) + f (n)
b
• a is the number of subsolutions
• b specifies the size of the subsolutions
Example: Sorting with Quick-Sort
The function ”Partition” establishes an element x:
... x ...
≥x x≥
• Best case, Partition always finds the element in the middle:
T (n) ≤ 2T ( n ) + cn =⇒ O(n ∗ log(n))
2
• Worst case, Partition always finds a marginal element:
T (n) ≤ T (n − 1) + cn =⇒ O(n2 )
2.1 Finding Closest Pair of Points
Definition of the Problem
Given n points in the plane. Find the pair that is closest together. Let P = {p1 , ..., pn } be the set
of points where pi has coordinates (xi , yi ). For two points pi , pj ∈ P , we use d(pi , pj ) to denote
the Euclidian distance between them. Our goal is to find a pair of points pi , pj that minimizes
d(pi , pj ).
Idea
q
Q R
q q
q
q
q
q
q q
q q
q
A: Setting up the recursion:
(1) We sort all the points in P by x-coordinate and again by y-coordinate producing lists
Px and Py .
9. 2 DIVIDE AND CONQUER 9
(2) We define Q to be the set of points in the n positions of the list Px and R to be the
2
set of points in the final n positions of the list Px .
2
(3) By a single pass through each of Px and Py , we can create the following four lists:
Qx : consisting of the points in Q sorted by increasing x-coordinate
Qy : consisting of the points in Q sorted by increasing y-coordinate
Rx : consisting of the points in R sorted by increasing x-coordinate
Ry : consisting of the points in R sorted by increasing y-coordinate
x x
(4) We now recursively determine a closest pair of points in Q. Suppose q0 and q1 are
returned as a pair of points in Q. Similarly we determine a closest pair of points in R,
x x
obtaining r0 and r1 .
B: Combining the solutions:
Let δ be the minimum of d(q0 , q1 ) and d(r0 , r1 ). Let x∗ denote the x-coordinate of the
x x x x
rightmost point in Q, and let L denote the vertical line described by the equation x = x∗ .
Fact 1: If there exists q ∈ Q and r ∈ R for which d(q, r) < δ, then each of q and r lies within a
distance δ of L.
q
Q R
q ' E' E q
δ δ
q
q
q
q
q q
q q
q
L
Proof: Suppose such q and r exist. We write q = (qx , qy ) and r = (rx , ry ). We know
qx ≤ x∗ ≤ rx =⇒
x∗ − qx ≤ rx − qx ≤ d(q, r) < δ and
√
rx − x∗ ≤ rx − qx ≤ d(q, r) < δ
We know that we can restrict our search to the narrow band consisting of only points in P
within δ of L.
Let S ⊆ P denote this set and let Sy denote the list consisting of the points in S sorted by
increasing y-coordinate.
=⇒ There exist q ∈ Q and r ∈ R for which d(q, r) < δ if and only if there exist s, s′ ∈ S for
which d(s, s′ ) < δ.
Fact 2: If s, s′ ∈ S have the property that d(s, s′ ) < δ, then s and s′ are within 15 positions of each
other in the sorted list Sy .
10. 2 DIVIDE AND CONQUER 10
Proof: Consider the subset Z of the plane consists of all points within distance δ of L. We partition
Z into boxes,
Z
' δ E' δ E
q
Q R
q q
′
s
q12 13 q
14 15
q
δ
3∗ 2
q
8 9 10 11
q
q
4 5 6 7
q s 1 2 3 q
q
L
δ
squares with horizontal and vertical size of length
√ 2. It holds: each box contains at most
one point of S.
Now suppose that s, s′ ∈ S have the property that d(s, s′ ) < δ and that they are at least
16 positions apart in Sy . Assume w.l.o.g. that s has the smaller y-coordinate. Then, since
there can be at most one point per box, there are at least three ”rows” of Z lying between
s and s′ . But any two points in Z separated by at least three ”rows” must be a distance of
δ
at least 3 ∗ 2 apart. `
We can conclude the algorithm as following:
We make one pass through Sy and for each s ∈ Sy , we compute its distance to each of the
next 15 points in Sy .
Running time: T (n) ≤ 2 ∗ T ( n ) + O(n) = O(n ∗ log(n))
2
2.2 Convolutions at the Fast Fourier Transformation
Definition of the problem:
Given two vectors
a = (a0 , . . . , an−1 )
b = (b0 , . . . , bn−1 ).
The convolution of the two vectors of length n is a vector with 2n − 1 coordinates, where co-
ordinate k is equal to
ai ∗ bj =⇒
(i,j):i+j=k∧i,j<n
a ∗ b = (a0 ∗ b0 , a1 ∗ b0 + a0 ∗ b1 , a0 ∗ b2 + a1 ∗ b1 + a2 ∗ b0 , . . .)
b0 b1 b2 b3 ... bn−1
¨ ¨
¨ ¨¨ ¨¨ ¨¨ ¨
a0 a¨0 a0 b1 a0 b2 a0 b3 ... a0 bn−1
¨ 0 b¨¨ ¨¨ ¨¨
a1 a¨0 a¨1 a¨2 a1 b3 ... a1 bn−1
¨ 1b ¨ 1b ¨ 1b
¨ ¨
a2 a¨0 a¨1 a2 b2 a2 b3 ...
¨ 2 b¨¨ 2 b a2 bn−1
a3 a¨0 a3 b1 a3 b2 a3 b3 ... a3 bn−1
. ¨ 3.b
. . .
. .
. .
. .
.
. . . . . .
an−1an−1 b0 an−1 b1 an−1 b2 an−1 b3 . . . an−1 bn−1
11. 2 DIVIDE AND CONQUER 11
Motivation
Example 1: ”Polynomial Multiplication”
Representation
2 m−1
A(x) = a0 + a1 x + a2 x + . . . + am−1 x −→ (a0 , a1 , a2 , . . . , am−1 )
B(x) = b0 + b1 x + b2 x2 + . . . + bn−1 xn−1 −→ (b0 , b1 , b2 , . . . , bn−1 )
C(x) = A(x) ∗ B(x) −→ (c0 , c1 , c2 , . . . , cm+n−2 )
ck = ai b j
(i,j):i+j=k
Example 2: ”Signal Processing”
Suppose we have a vector a = (a0 , a1 , . . . , am−1 ) representing a sequence of measurements,
sampled at m consecutive points in time.
A common operation is to ”smooth” the measurements by averaging each ai with a weighted
sum of its neighbors within k steps to the left and right in the sequence. We define a ”mask”
w = (w−k , w−(k−1) , . . . , w−1 , w0 , w1 , . . . , wk−1 , wk ) consisting of the weights we want to use
for averaging each point with its neighbor.
k
We replace ai with a′ =
i ws ai+s
s=−k
Let’s define b = (b0 , b1 , . . . , b2k ) by setting bl = wk−l :
a′ =
i b l aj
(j,l):j+l=i+k
Example 3: ”Combining Histograms”
15.11.2005
Aim: Running time of O(n log n)
Explanation : Complex roots of Unity Complex number reω∗i
where eΠ∗i = −1 and e2∗Π∗i = 1
The polynomial equitation xk = 1 has k distinct complex roots
2∗Π∗j∗i
wjk = e k for j = 0, 1, ..., k − 1 called k th roots of unity.
12. 2 DIVIDE AND CONQUER 12
k=8 Imaginary Axis
T
ω2,8 i
r
ω3,8 r r ω1,8
-1 ω4,8 ω0,8 1
r r E
Real Axis
r r
ω5,8 ω6,8 ω7,8
r
-i
Idea : We are given the vectors a = (a1 , a2 , ..., an−1 ) and b = (b1 , b2 , ..., bn−1 ).
We will view them as the polynomial A(x) = a0 + a1 x + a2 x2 + ... + an−1 xn−1
B(x) = b0 + b1 x + b2 x2 + ... + bn−1 xn−1 . We will seek to compute their product C(x) =
A(x)∗ B(x) in (O(nlog(n)) time. The vector C = (c0 , c1 , ..., c2n−2 ) is exactly the convolution
a ∗ b. Now, rather than multiplying A and B symbolically, we can treat them as functions
of the variable x and multiply them as follows :
(i) Polynomial Evaluation : We chose 2n values x1 , ..., x2n and evaluate A(xj ),B(xj ) for
each j = 1, 2, .., 2n.
(ii) Compute C(xj ) for each j = 1, ..., 2n
(iii) Polynomial Interpolation : Recover C from its values on x1 , ..., x2n
For our numbers x1 , ..., x2n on which to evaluate A and B we will choose the (2n)th roots of
unity. The representation of a degree-d polynomial P by its values on the (d + 1)th roots of
unity is referred to as the ”‘Discrete Fourier transform of P ”’.
n−2
(A) A(x) = Aeven (x2 ) + x ∗ Aodd (x2 ) with Aeven (x) = a0 + a2 x + a4 x2 + ... + an−2 x 2
n−2
Aodd (x) = a1 + a3 x + a5 x2 + ... + an−1 x 2 . Suppose that we evaluate each of the Aeven
and Aodd on the (n)th roots of unity. This is exactly a version of the problem we face
with A and the (2n)th roots of unity, except that the input is half as large. We have
just to produce the evaluation of A on the (2n)th roots of unity using O(n) additional
2Πji
operations. Consider one of these roots of unity ωj2n = ǫ 2n
2Πji 2Πij
(ωj2n )2 = (ǫ 2n )2 = ǫ n and hence (ωj2n )2 is a (n)th root of unity ⇒ T (n) ≤
2T ( n ) + O(n)
2
(B) The construction of C can be achieved by defining an appropriate polynomial (P ) and
evaluating it at the (2n)th roots of unity.
2n−1
Consider a polynomial C(x) = cs ∗ x2 that we want to reconstruct from its values
s=0
C(ωs2n ) at the (2n)th roots of unity.
2n−1
Define a new polynomial D(x) = ds ∗ xs where ds = C(ωs2n ).
s=0
2n−1
D(ωj2n ) = C(ωs2n ) ∗ ωj2n s
s=0
13. 2 DIVIDE AND CONQUER 13
2n−1 2n−1
= ( ct ∗ ωs2n t ) ∗ ωj2n s
s=0 t=0
2n−1 2n−1
= ct ∗ ( ωs2n t ∗ ωj2n s )
t=0 s=0
2n−1 2n−1 2Πi 2Πi
= ct ∗ ( ((e 2n )s )t ∗ ((e 2n )j )s )
t=0 s=0
2n−1 2n−1 (2Πi)∗(st+js)
= ct ∗ ( e 2n )
t=0 s=0
2n−1 2n−1 (2Πi)∗(t+j)
= ct ∗ ( (e 2n )s )
t=0 s=0
2n−1 2n−1
= ct ∗ ( ωt+j2n s )
t=0 s=0
The only form of the last lines outer sum that is not equal to 0 is for ct such that
ωt+j2n = 1.
Explanation :
2n−1
For any (2n)th root of unity ω = 1, we have ω s = 0 x2n = 1 ⇔ x2n − 1 = 0 ⇔
s=0
2n−1
x2n − 1 = (x − 1) ∗ ( xt ) → This happens if t + j is a multiple of 2n, that is, if
t=0
2n−1 2n−1
s
t = 2n − j For this value, ωt+j2n = 2n So we get that D(ωj,2n ) = 2n ∗ c2n−1
s=0 s=0
2n−1
Fact: For any polynomial C(x) = cs ∗ xs and corresponding polynomial D(X) =
s=0
2n−1
1
C(ωs2n ) ∗ xs we have that cs = 2n ∗ D(ω2n−s,2n )
s=0
14. 3 DYNAMIC PROGRAMMING 14
3 Dynamic Programming
Basic Idea
One implicitly explores this space of all possible solutions, by carefully decomposing things in a
series of sub solutions, and then building up correct solutions to large and larger subproblems.
3.1 Weighted Interval Scheduling
Definition of the Problem
We have n requests labeled 1, . . . , n, with each request i specifying start time si and finishing
time fi . Each interval i has a weight vi . Two intervals are compatible if they do not overlap. The
Goal is to select S ⊆ {1, . . . , n} of mutually compatible intervals, so as to maximize the sum the
values of the selected intervals, vi .
i∈S
Lets suppose that the requests are sorted in order of nondecreasing finishing time:
f1 ≤ f2 ≤ . . . ≤ fn .
Well say a request i comes before request j if i < j.
Example:
v1 = 2
1 p(1) = 0
v2 = 4 p(2) = 0
2
v3 = 4
3 p(3) = 1
v4 = 7 p(4) = 0
4
v5 = 2
5 p(5) = 3
v6 = 1
6 p(6) = 3
We define p(j) for an interval j to be the largest index i < j such that intervals i and j
are disjoint. We define p(j) = 0 if no request i < j is disjoint from j. For any j between
1 and n let vj denote the optimal solution of the problem consisting of requests {1, . . . , j},
and let OP T (j) denote the value of this solution. For the optimal solution vj it holds,
that either j ∈ Oj in which case OP T (j) = vj + OP T (p(j)), or j ∈ Oj in which case
/
OP T (j) = OP T (j − 1).
Fact 1: OP T (j) = max{vj + OP T (p(j)), OP T (j − 1)}
Fact 2: Request j belongs to an optimal solution on the set {1, . . . , j} if and only if
vj + OP T (p(j)) ≥ OP T (j − 1)
Remark 1: These facts form the first crucial component on which dynamic programming solution is
based: recurrence equation that expresses the optimal solution in terms of the optimal
solutions to smaller subproblems.
15. 3 DYNAMIC PROGRAMMING 15
OP T (6)
OP T (5) OP T (3)
OP T (4) OP T (3) OP T (2) OP T (1)
OP T (3) OP T (0) OP T (2) OP T (1) OP T (1) OP T (0)
OP T (2) OP T (1) OP T (1) OP T (0)
OP T (1) OP T (0)
Example:
Remark 2: A fundamental observation, which forms the second crucial component of a dynamic pro-
gramming solution, is that our recursive algorithm is really only solving n + 1 different sub
solutions.
How could we eliminate the redundancy?
=⇒ ”Memorization”
22.11.2005
”Memorization”
M [0..n]: M [j] will start with the value ”empty” but will hold the value of OP T (j) as soon as it is
first determined.
M-OPT(j)
if j=0 then
return 0
else
if M[j] is not empty then
return M[j]
else
M[j] = max(vj + M-OPT(p(j)), M-OPT(j − 1))
return M[j]
Iterative-M-OPT(j)
16. 3 DYNAMIC PROGRAMMING 16
M[0] = 0
for j=1,..,n
M[j] = max(vj + M − (p(j)), M (j − 1))
return M[j]
So far we have simply computed the value of an optimal solution. What we want is the full
optimal set of intervals as well. We know from Fact 2 that j belongs to an optimal solution for
the set of intervals {1, .., j} iff 6 vj + OP T (p(j)) ≥ OP T (j − 1).
Find Solution(j)
if j=0 then
Output nothing
else
if vj + M [p(j)] ≥ M [j − 1] then
Output j together with the result of Find Solution(p(j))
else
Output the result of Find Solution(j-1)
”Informal Guidelines”
1. There are only a polynomial number of subproblems
2. The solution to the original problem can be easily computed from the solutions to the
subproblems.
3. There is a natural ordering on subproblems from ”smallest” to ”largest” together with an
easy to compute recurrence that allows one to determine the solution to a subproblem from
the solutions to some number of smaller subproblems
3.2 Segmented Least Squares
y
T
r
d
d d
rd
d dr
d
r
d d
d
dr
r
d d
d
dr
E
x
6 ”iff” means ”if and only if”
17. 3 DYNAMIC PROGRAMMING 17
Problem description
Suppose our data consists of a set P of n points in the plane, denote (x1 , y1 ), (x2 , y2 ), .., (xn , yn ).
Suppose x1 < x2 < .. < xn .
Given a line L defined by the equation y = ax + b, we say that the error of L with respect to P is
the sum of its squared ”distances” to the points in P .
n
Error(L, P ) = (yi − axi − b)2
i−1
The line of minimal error is y = ax + b, where
n∗ i xi yi − ( i xi )( i yi )
a= n 2 2
n∗ i xi − ( i xi )
i xi − a ∗ i xi
b=
n
y
T
r
@ r r @@
@@@
r
r r
r
r
E
x
Formulating the Problem
We are given a set of points P = {(x1 , y1 ), (x2 , y2 ), .., (xn , yn )} with x1 < x2 < .. < xn . We will
use pi to donate the point (xi , yi ). We must first partition P into some number of segments. Each
segment is a subset of P that represents a continuous set of x-coordinates, that is, it is a subset
of the form {pi , pi+1 , .., pj−1 , pj } for some indices i ≤ j.
Then, for each segment S in our partition of P , we compute the line minimizing the error with
respect to the points in S. The penalty of a partition is defined to be a sum of the following terms:
1. The number of segments into which we partition P , times a fixed given multiple C > 0.
2. For each segment, the error value of the optimal line though that segment.
Our goal in the ”Segmented Least Squares” is to find a partition of minimum penalty.
y
T
r
n
r @
i @@r
r
@
@@
r
r
r
r
r
E
1 i-1 x
18. 3 DYNAMIC PROGRAMMING 18
Observation: The last point pn belongs to a single segment in the optimal partition. If we knew the
identity of the last segment pi , .., pn , then we could remove these points from consideration
and recursively solve the problem on the remaining points p1 , .., pi .
Suppose we let OP T (i) denote the optimal solution for the points p1 , .., pi , and we let eij
denote the minimum error of any line with respect to pi , .., pj .
Fact 1: If the last segment of the optimal partition is pi , .., pn then the value of the optimal solution
is
OP T (n) = ein + C + OP T (i − 1)
Fact 2: For the subproblems on the points p1 , .., pj
OP T (j) = min {eij + C + OP T (i − 1)}
1≤i≤j
and the segment pi , .., pj is used in an optimal solution for the subproblem iff the minimum
is obtained using index i.
3.3 Subset Sum / Knapsack
16.12.2005
Subset Sum Problem
We are given n items {1, .., n} and each has a given nonnegative weight wi (for i = 1, .., n). We
are also given a bound W .
We would like to select a subset S of the items so that i∈S wi ≤ W and, subject to this restriction
i∈S wi is as large as possible.
0 W
W1
W2
Knapsack: each item has both a value vi and a weight wi ,
i∈S wi ≤ W and i∈S vi is as large as possible.
OPT(n)
n ∈ O:
/ OPT(n) = OPT(n-1)
n ∈ O: OPT(n) = ?
OPT(n) can not solve the problem as it has only one parameter, n. Suppose we take more than
one parameter:
OPT(n,W)
n ∈ O:
/ OPT(n,W) = OPT(n-1,W)
n ∈ O: OPT(n,W) = wn + OP T (n − 1, W − wn )
19. 3 DYNAMIC PROGRAMMING 19
OPT(i,W) = max{OP T (i − 1, W ), wi + OP T (i − 1, W − wi )}
SubsetSum(n, W)
Array M[0..n,0..W]
Initialize M[0,w] = 0 ∀w ∈ {0, .., w}
For i=1 to n
For j=0 to w
compute M[i,j] = max{M [i − 1, j], wi + M [i − 1, j − vi ]}
return M[m,W]
n
i
i-1
.
.
.
1
0
0 1 2 ... j ... W
Fact 1: The SubsetSum(n, W) Algorithm correctly computes the optimal value if the problem and
runs in O(n ∗ W ) time.
Note 1: The running time is a polynomial function of n and W , the largest integer involved in defining
the problem. We call such algorithms ”pseudo-polynomial”.
Extension to the Knapsack problem
n ∈ O:
/ OPT(n,W) = OPT(n-1,W)
n ∈ O: OPT(n,W) = wn + OP T (n − 1, W − wn )
Fact 2: If w < vi , then OP T (i, W ) = OP T (i − 1, W )
else n ∈ O: OPT(i,W) = max{OP T (i − 1, W ), vi + OP T (i − 1, W − wi )}
3.4 Sequence Alignment
Motivation
1. ”Online dictionaries”
Input: o c c u r r a n c e
Output: Do you mean o c c u r r e n c e ?
o currance o curr ance
occurrence occurre nce
costmism + costgap < 3 ∗ costgap ?
20. 3 DYNAMIC PROGRAMMING 20
Goal: We want a model in which similarity is determined roughly by the number of gaps
and mismatches we have when we line up the two words.
2. ”Computational biology”
Organism’s genome is divided into giant linear DNA molecules known as chromosomes.
We can think of it as an linear tape, containing a string over the alphabet {A, C, G, T}.
Definition
Suppose we are given two strings x and y, where x consists of the sequence of symbols x1 x2 x3 ...xm
and y consists of the sequence of symbols y1 y2 y3 ...yn . Consider the sets {1, ..., m} and {1, ..., n}
are representing the different positions on the string x and y. Consider a matching of these sets,
that is a set of ordered pairs with the property that each item occurs in at most one pair. We say
that a matching M of these two sets is an alignment if there are no ”crossing” pairs:
if (i, j), (i′ , j ′ ) ∈ M and i < i′ ⇒ j < j ′
Example: s t o p
tops
Corresponding alignments: (2, 1), (3, 2), (4, 3)
Problem: Suppose M is a given alignment between x and y:
(1) There is a parameter δ > 0 that defines a gap penalty.
(2) For each pair of letters p, q in our alphabet, there is a mismatch cost of αpq for lining
up p with q.
(3) The cost of M is the sum of its gaps and mismatch costs, and we seek for an alignment
of minimum costs.
Fact 1: Let M be any alignment of x and y. If (m, n) ∈ M , then either the mth position of x or the
/
nth position of y is not matched in M .
Proof: Suppose by way of contradiction, that (m, n) ∈ M and there are numbers i < m and j < n
/
so that (m, j) ∈ M and (i, n) ∈ M . This contradicts our definition of alignments: we have
(i, n), (m, j) ∈ M with i < m, but n > i so that the pairs (i, n) and (m, j) cross. `
Fact 2: In an optimal alignment M , at least one of the following is true:
(i) (m, n) ∈ M
(ii) the mth position of x is not matched or
(iii) the nth position of y is not matched
Let OP T (i, j) denote the minimum cost of an alignment between x1 x2 x3 ...xi and y1 y2 y3 ...yj .
In case (i), we pay αxm yn and then align x1 x2 ...xm−1 as well as possible with y1 y2 ...yn−1 .
OP T (m, n) = αxm yn + OP T (m − 1, n − 1)
In case (ii), we pay gap costs of δ since the mth position of x is not matched, and then we
align x1 ...xm−1 as well as possible with y1 ...yn .
OP T (m, n) = δ + OP T (m − 1, n)
In case (iii), we pay gap costs of δ since the nth position of y is not matched, and then we
align x1 ...xm as well as possible with y1 ...yn−1 .
OP T (m, n) = δ + OP T (m, n − 1)
Fact 3: The minimum alignment costs satisfy the following recurrence for i ≥ 1, j ≥ 1:
OP T (i, j) = min{αxi ,yj + OP T (i − 1, j − 1), δ + OP T (i − 1, j), δ + OP T (i, j − 1)}
21. 3 DYNAMIC PROGRAMMING 21
Formulation of the sequence alignment algorithm as graph theoretical problem
Suppose we build a two-dimensional grid graph Gx,y , with the rows labeled by symbols in the
string x and the columns labeled by the symbols in y. We number the rows from 0 to m and the
columns from 0 to n.
We put costs on edges of Gx,y :
• each horizontal and vertical edge get cost δ.
• the diagonal edge from (i − 1, j − 1) to (i, j) get cost αxi ,yj .
x3 iE iE iE iE i
T
T
T
T
T
x2 i
E i
E i
E i
E i
T
T
T
T
T
x1 i
E i
E i
E i
E i
T
T
T
T
T
0 i
E i
E i
E i
E i
0 y1 y2 y3 y4
Fact 4: Let f (i, j) denote the minimum cost of a path from (0, 0) to (i, j) in Gx,y . Then for all i, j,
we have f (i, j) = OP T (i, j).
22. 4 APPROXIMATION ALGORITHM 22
20.12.2005
4 Approximation Algorithm
Informal Definition
”Algorithm, which run in polynomial time and find solutions that are guaranteed to be close to
optimal.”
Techniques
(1) Greedy Algorithm
(2) Pricing Method (primal-dual technique)
(3) Linear Programming and Rounding
(4) Polynomial-time Approximation Scheme
4.1 Load-Balancing Problem
Definition
We are given a set of m machines M1 , ..., Mm and a set of n jobs; each job j has a processing time
tj . Let A(i) be the set of jobs assigned to machine Mi . Under this assignment, machine Mi needs
to work for a total time of
Ti = tj
j∈A(i)
and we declare this to be load on the machine Mi .
We seek to minimize a quantity known as the makespan; it is simply the maximum load on any
machine, T = max{T1 , ..., Tm }
Greedy Balance
Start with no jobs assigned.
Set Ti = 0 and A(i) = ∅ for all machines Mi .
For j = 1 to n
Let Mi be a machine that achieves the minimum min{T1, ..., Tm }
Assign job j to machine Mi .
Set A(i) ← A(i) ∪ {j}
Set T (i) ← Ti + tj
Example: m = 3; n = 6; ti = {2, 3, 4, 6, 2, 2}
time
9 T
8
7
6
5 6 2
4 2 makespan = 8
3
2 4
3
1 2
0
M1 M2 M3
23. 4 APPROXIMATION ALGORITHM 23
Fact 1: The optimal makespan T ∗ is at least
n
1
T∗ ≥ ∗ tj
m j=1
Fact 2: The optimal makespant T ∗ is at least
T ∗ ≥ max{t1 , ..., tn }
Fact 3: Algorithm Greedy-Balance produces an assignment of jobs to machines with makespan
T ≥ 2 ∗ T∗
Proof: We consider a machine Mi that attains the maximum load T in our assignment and we ask:
What was the last job j to be placed on Mi ?
When we assigned job j to Mi , the machine Mi had the smallest load of any machines. Its
load before this assignment was Ti − tj .
It follows that every machine had load at least Ti − tj . We have
m
Tk ≥ m ∗ (Ti − tj )
k=1
n
1
⇔ (Ti − tj ) ≤ ∗ tj ≤ T ∗
m j=1
F act1
T := Ti = (Ti − tj ) + tj ≤ 2 ∗ T ∗
≤T ∗ ≤T ∗
T
Approximation ratio: T∗ ≤2
Worst case example: We have m machines and we have n = m ∗ (m − 1) + 1 jobs. The first m ∗ (m − 1) = n − 1
jobs require time tj = 1. The last job requires time tn = m.
Greedy makespan: 2m − 1
Optimal makespan: m
2m−1 1
=⇒ m =2− m −→ 2
An improved Greedy Algorithm
Sorted Greedy Balance
Sort the list of jobs not ascending by the processing time
Start with no jobs assigned.
Set Ti = 0 and A(i) = ∅ for all machines Mi .
For j = 1 to n
Let Mi be a machine that achieves the minimum min{T1, ..., Tm }
Assign job j to machine Mi .
Set A(i) ← A(i) ∪ {j}
Set T (i) ← Ti + tj
25. 4 APPROXIMATION ALGORITHM 25
Further Definition
Set U of n elements. A list of S subsets S1 , ..., Sm of U. Each set Si has an associated weight
wi ≥ 0. Goal is to minimize si ∈e wi . It holds:
wi wi
−→
|Si | |Si ∩ R|
Greedy Set Cover
Start with R = U
while R = ∅
wi
Select set Si that minimizes |Si ∩R|
Delete set Si from R
return the selected sets
Example:
n
s n S6
s
S5
given weights:
s s
S2
' s $
w1 = 1, w2 = 1
w3 = 1 + ǫ, w4 = 1 + ǫ s
w5 = 1, w6 = 1
s s
%
S1
choosing order:
S4 S3
S1 , S2 , S5 , S6
Let the cost paid for an element s be described by the quantity cs :
wi
cs = |Si ∩R| for all s ∈ Si ∩ R.
Fact 1: If C is the set cover obtained by Greedy Set Cover, then si ∈C wi = s∈U Cs .
n
1
Fact 2: For every Sk , the sum s∈Sk Cs is at most H(|Sk |) ∗ Wk whereas H(n) := i = Θ(ln n).
i=1
Proof: We assume that the element of Sk are the first d = |Sk | of the set U . That is Sk = s1 , ...sd .
Further, let us assume that these element are labelled in the order in which they are assigned
a cost csj by the Greedy algorithm. Now consider the iteration in which element sj is covered
by the greedy algo for some j ≤ d. At the start of this iteration , sj , sj+1 , ..., sd ∈ R by our
labeling of the elements. This implies that |Sk ∩ R| is at least d − j + 1, and so the average
wk Wk
cost of the set Sk is at most |Sk ∩R| ≤ d−j+1 . In this iteration, the greedy algorithm selected
a set Si of minimum average cost, so this set Si has average cost at most that of Sk . Thus
wi wk wk
csj = ≤ ≤ .
|Si ∩ R| |Sk ∩ R| d−j+1
d
wk wk wk wk 1 1
cs = j = 1d csj ≤ = + +...+ = wk ( + +...+1) = wk H(d)
j=1
d−j−1 d d−1 1 d d−1
s∈Sk
Fact 3: The set cover C selected by Greedy-Set-Cover has weight at most H(d∗ ) times the optimal
weight w∗ whereas d∗ = maxi |Si |.
26. 4 APPROXIMATION ALGORITHM 26
Proof: Let C ∗ denote the optimum set cover, so that w∗ = wi . For each of the sets in C ∗ ,
Si ∈C ∗
Fact 2 implies:
1
wi ≥ ∗ Cs (∗)
H(d∗ )
s∈Si
Cs ≥ Cs (∗∗)
si ∈C ∗ s∈Si s∈U
1 1 1
w∗ =(Def.) wi ≥(∗) Cs ≥(∗∗) Cs =F act1 wi
H(d∗ ) H(d∗ ) H(d∗ )
Si ∈C ∗ Si ∈C ∗ s∈Si s∈U Si ∈C
4.3 Vertex Cover (Pricing Method)
Definition
A vertex cover in a graph G = (V, E) is a set S ⊆ V so that each edge has at least one end in S.
We consider have, each vertex i ∈ V has a weight wi ≥ 0. We would like to find a vertex cover S
for which w(S) is minimum.
It holds: Vertex Cover ≤p Set Cover and Independent Set ≤p Vertex Cover.
The ”Pricing Method”
The pricing method (also known as primal-dual method) is motivated by an economic perspective.
For the vertex cover problem, we will think of the weights on the nodes as costs, and we will think
of each edge as having to pay for its “share” of the cost of the vertex cover we find.
More precisely: We will think of the weight wi of the vertex i as the cost for wing i in the
cover. We will think of each edge e as an “agent” who is willing to pay something to the node
that covers it.
The algorithm will not only find a vertex cover S, but also determine prices pe ≥ 0 for each
edge e ∈ E, so that if each edge e ∈ E pays the price pe , this will in total approximately cover the
cost of S. Selecting vertex i covers all edges incident to i, so it would be “unfair” to change these
incident edges in total more then the cost of vertex i. We call prices pe fair, if for each vertex i,
the edges adjacent to i do not have to pay more than the cost of the vertex:
pe ≤ wi
e=(i,j)
Fact 1: For any vertex cover S ∗ and any nonnegative and fair prices pe , we have pe ≤ w(S∗).
e∈E
Proof: By the definition of fairness, we have e=(i,j) pe ≤ wi for all nodes i ∈ S ∗ . e∈E pe ≤
∗
i∈S ∗ pe ≤ i∈S ∗ wi = w(S ).
Algorithm:
Def.: We say that a node i is tight (or ”‘paid for”’) if pe = wi
e=(i,j)
VertexCoverApprox(G, w)
Set pe = 0 for all e ∈ E
while ∃e = (i, j) such that neither i nor j is tight
select such an edge e
increase pe without violating fairness
27. 4 APPROXIMATION ALGORITHM 27
end while
Let S be the set of all tight nodes.
return S
Example:
a 4 SELECT(a,b) 4 a payment ≤ 3
t t
t t pay = 3
t t
t t ⇒ b is tight
t t
p=0 t p=0 3 t 0
t t
p=0 t 0 t
t t
t t
t t
t
t
3 5 3 3 5 3
p = 0 p = 0 0 0
b c d b c d
SELECT(a,d) a 4 payment ≤ 1 SELECT(c,d) a 4 payment ≤ 2
t t
t pay = 1 t pay = 2
t t
t ⇒ a is tight t ⇒ d is tight
t t
3 t 1 3 t 1
t t
0 t 0 t
t t
t t
t t
t
t
3 5 3 3 5 3
0 0 0 2
b c d b c d
⇒ S = {a, b, d}, w(S) = 10
Fact 2: The Set S and the prices p returned by the algorithm satisfy the inequality w(S) ≤ 2 ∗
e∈E pe .
Proof : All Nodes in S are tight, so we have e=(i,j) pe = wi for all i ∈ Si w(S) = i∈S wi =
i∈S e=(i,j) pe ≤ 2 ∗ e∈E pe
Fact 3: The Set S returned by the algorithm is a vertex cover, and its cost is at most twice the
minimum cost of any vertex cover.
Proof : Suppose by contradiction, that S does not cover edge e = (i, j). This implies that neither
i nor j is tight, and this contradicts that the while-loop of the algorithm terminated. Let
p be the prices set by the algorithm, and let S ∗ be an optimal vertex cover. By Fact 2
we have 2 ∗ e∈E pe ≥ w(S) and we have by Fact 1 that e∈Epe ≤ w(S ∗ ) =⇒ w(S) ≤
2 ∗ e∈E pe ≤ 2 ∗ w(S ∗ )
28. 4 APPROXIMATION ALGORITHM 28
4.4 Linear Programming and Rounding
The basic linear programming problem can be viewed as a complex version of the problem of si-
multaneous linear equations with inequalities in place of equations. Specially consider the problem
of determining a vector x that satisfies Ax ≥ b.
x1
Example: x1 ≥ 0, x2 ≥ 0 (1.5, 1) ∗ (x2 )
x1 + 2 ∗ x2 ≥ 6
2 ∗ x1 + x2 ≥ 6
→
cT ∗ x → M in
6
5
4
3
2
1
0
0 1 2 3 4 5 6
Definition: Given an m × n Matrix A, and vector b ∈ Rm and vector e ∈ Rn , find a vector x ∈ Rn to
solve the following optimization problem :
min( cT ∗ x , such that x ≥ 0, Ax ≥ b)
ObjectiveF unction Constraints
Vertex cover as an Integer Program
Choose a decision variable xi for each node i ∈ V
xi = 1 will indicate that node i is in the vertex cover
xi = 0 will indicate that node i is not in the vertex cover
For each edge (i, j) ∈ E, we write the inequality xi + xj ≥ 1
→
Objective function : wT ∗ x → min
VC-IP M in i∈V wi ∗ xi
xi + xj ≥ 1∀(i, j) ∈ E
xi ∈ {0, 1}∀i ∈ V
Fact 1: S is a vertex cover in G if and only if the vector x defined as xi = 1 for i ∈ S, and xi = 0
for i ∈ S satisfies the constraints in VC-IP. Further we have w(S) = wT ∗ x
/
Fact 2: Vertex Cover ≤p Integer Programming.
Using linear programming for vertex cover
Modify the VC-IP by dropping the requirement that each xi ∈ {0, 1} and reverting to the
constraint that each xi is an arbitrary real number between 0 and 1.
֒→ VC-LP.
29. 4 APPROXIMATION ALGORITHM 29
Fact 3: Let S ∗ denote a vertex cover of minimum weight. Then WLP ≤ w(S ∗ ).
1
w(S ∗ ) = |V C| = 2 x1 = x2 = x3 =
2
1
d
d WLP = 3
d 2
1 1
Given a fractional solution (x∗ ), we define S = {i ∈ V : x∗ ≥ 1 }
i i 2
1
Fact 4: The set S defined in this way is a vertex cover, and 2 ∗ w(S) ≤ WLP
Proof : Consider an edge e = (i, j). Recall that one inequality xi + xj ≥ 1 ⇒ in any solution x∗
that satisfies this inequality either x∗ ≥ 2 or x∗ ≥ 1 . Thus at least one of these two will be
i
1
j 2
rounded up, and i or j will be placed in S. Therefore S is a vertex cover.
WLP = wT ∗ x∗ = i wi ∗ x∗ ≥ i∈S wi ∗ x∗ ≥ 1 ∗ i∈S wi = 1 ∗ w(S).
i i 2 2
Fact 5: The algorithm produces a vertex cover S of at most twice the minimum possible weight.
27.01.2006
4.5 A more advanced LP-Application: Load Balancing
Definition of the problem
Each job j has a fixed given size tj ≥ 0 and a set of machines Mj ⊆ M that it may be assigned to.
We call an assignment of jobs to machines feasible i each job j is assigned to a machine i ∈ MJ .
The goal is still to minimize the maximum load on any machine: Using Ji ⊆ J to denote the jobs
assigned to a machine i ∈ M in a feasible assignment, and using Li = j∈Ji tj to denote the
resulting load, we seek to minimize maxi Li .
”Generalized Load Balancing Problem”
GL-IP: xij to each pair (i, j) of a machine i ∈ M , job j ∈ J:
Setting xij = 0 will indicate that job j is not assigned to machine i,
setting xij = tj will indicate that job j is assigned to machine i.
For each job we require i xij = tj . We require xij = 0 whenever i ∈ Mj . The load of a
/
machine i can be expressed as Li = j xij . We use one more variable L. We use inequalities
j xij ≤ L∀i ∈ M .
min L
xij = tj ∀j ∈ J
i
GL-IP: xij ≤ L ∀i ∈ M
j
(∗) xij ∈ {0, tj } ∀j ∈ J, i ∈ Mj
xij = 0 ∀j ∈ J, i ∈ Mj
/
30. 4 APPROXIMATION ALGORITHM 30
Fact 1: An assignment of jobs to machines has load at most L if and only if the vector x satisfies
constraints in GL-IP, with L set to the maximum load of the assignment.
xij ≥ 0 ∀j ∈ J, i ∈ Mj
GL-IL:
instead of (*)
Fact 2: If the optimum value of GL-LP is L, then the optimum load is at least L∗ ≥ L.
Fact 3: The optimum load is at least L∗ ≥ maxj tj .
We’ll consider the following bipartite graph G(x) = (V (x), E(x))
V (x) = M ∪ J
(i, j) ∈ E(x) if and only if xij 0
Fact 4: Given a solution (X, L) of GL-LP such that the graph G(X) has no cycles, we can use the
solution X to obtain a feasible assignment of jobs to machines with load at most L + L∗ .
Proof: Since the graph G(X) has no cycles, each of its connected components is a tree. First, root
the tree at an arbitrary node.
.
.
.
Consider a job j:
1. If the node corresponding to job j is a leaf of the tree, let machine node i be its parent.
Since j has degree 1 in G(X) machine i is the only machine that has been assigned any
part of job j and hence xij = tj .
2. For a job j whose corresponding node is not a leaf in G(X) we assign j to an arbitrary
child of the corresponding node in the rooted tree.
Let i be any machine, and let Ji be the set of jobs assigned to machine i. The set Ji contains
those children of node i that are leaves, plus possibly the parent p(i) of node i.
For all jobs j = p(i) assigned to i, we have xij = tj .
tj = xij ≤ xij ≤ L
j∈Ji ,j=p(i) j∈Ji ,j=p(i) j∈Ji
For the parent j = p(i) of node i, we use Fact 3 tj ≤ L∗
=⇒ ≤ L + L∗
j∈Ji
31. 4 APPROXIMATION ALGORITHM 31
Jobs Machines
∞
∞ L
∞ L
tj j i
V
L
∞
∞
Fact 5: Solution of this flow problem with capacity L are in one-to-one correspondence with the
solution of GL-LP with value along edge (j, i) and the flow value on edge (i, v) is the load
j xij on machine i.
Fact 6: Let X, L) be any solution to GL-LP and C be a cycle in G(X). We can modify the solution
X to eliminate at lest one edge from G(X) without increasing the load or introducing any
→
←
V
←
→
new edges.
Proof idea: We modify the solution by augmenting the flow along the cycle C. Assume that the nodes
along the cycle are i1 j1 i2 j2 ...ik jk where il is a machine node and jl is a job node. We’ll flow
along all edges and increasing the flow on the edge (jl , il+1 ) for all l = 1, ..., k (where k + 1
is used to denote 1), by the same amount δ with
δ = min xil jl
l=1,...,k
31.01.2006
4.6 Arbitrarily Good Approximations - Knapsack Problem
Goal: “Produce a solution within a small percentage of the optimal solution.”
Definition: Suppose we have n items. Each item i = 1, ..., n has two integer parameters: weight wi ,
value vi . Given a knapsack capacity W, the goal of the Knapsack problem is to find a subset
S of items of maximum value subject to the restriction that the total weight of the set should
not exceed W . vi →max under the condition wi ≤ W .
i∈S i∈S
Our algorithm will take as input the weights and values defining the problem and will also
take an extra parameter ǫ, the desired precision. It will find a subset S whose total weight
does not exceed W , with value vi at most a (1 + ǫ) factor below the maximum possible
i∈S
solution.
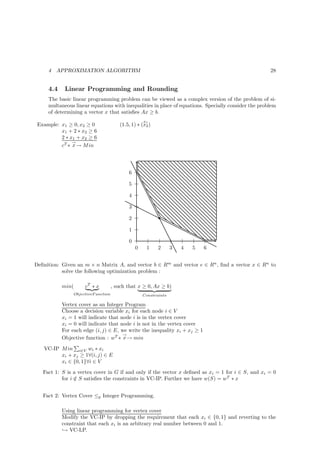
32. 4 APPROXIMATION ALGORITHM 32
The algorithm will run in polynomial time for any fixed choice ǫ 0 however, the dependence
on ǫ will not be polynomial. We call such an algorithm a “Polynomial-time approximation
scheme” (PTAS).
We already know an dynamic programming algorithm that run in O(n · W ).
“Old”: OP T (i, W )
“New”: OP T (i, V ) is the smallest knapsack weight W so that one can obtain a solution using a
subset of items 1, ..., i with values at least V .
i
We will have a subproblem for all i = 0, ..., n and values V = 0, ..., vj .
j=1
i
vj ≤ n · (max vi ) = n · v ∗ ⇒ O(n2 · v ∗ ) subproblems.
j=1 i
v∗
Recurrence for solving these subproblems:
n−1
if V vi then OP T (n, V ) = wn + OP T (n − 1, V − vn )
i=1
else OP T (n, V ) = min{OP T (n − 1, v), wn + OP T (n − 1, max(0, V − vn ))}
Knapsack (n)
Array M [0...n, 0...v]
For i = 0...n do M [i, 0] = 0
For i = 1, ..., n do
i
For v = 1, ..., vj do
j=1
i−1
if v vj then
j=1
M [i, v] = wi + M [i − 1, v]
else
M [i, v] = minM [i − 1, v], wi + M [i − 1, max0, v − vi ]
return the maximum value V such that M [n, V ] ≤ W
Idea for a PTAS:
If the values are small integers, then v ∗ is small and the problem can be solved in polynomial
time already. On the other hand, we will use a rounding parameter b and will consider the values
rounded to an integer multiple of b. More precisely, for each item i, let its rounded value be
vi = vi · b.
˜ b
We will use our dynamic programming algorithm to solve the problem with the rounded values.
Fact 1: For each item i we have vi ≤ vi ≤ vi + b. The rounded values are all integers multiples of a
˜
common value b. Instead of solving the problem with the rounded values vi , we can change
˜
˜
the units; we can divide all values by b and get an equivalent problem. vi = vi = vi for
ˆ b b
all i = 1, ..., n .
33. 4 APPROXIMATION ALGORITHM 33
Fact 2: The Knapsack problem with values vi and the scaled problem with values vi have the same
˜ ˆ
set of optimum solutions, the optimum values differ exactly by a factor of b, and the scaled
values are integers.
Knapsack-Approx(ǫ)
ǫ
set b = n ∗ (max vi )
i
solve the Knapsack Problem with values vi (with the help of our dyn.
ˆ Prog. Algo.)
return the set S of items found by this algorithm
Fact 3: The set of items S returned by the algorithm has total weight at most W , that is wi ≤ W .
i∈S
Fact 4: The algorithm Knapsack-Approx runs in polynomial time for any fixed ǫ 0.
Proof: The Dyn. Prog. Algo. runs in time O(n2 · v ∗ ) with v ∗ = max vi .
i
Determine max vi : The item j with maximum value vj = max vi has also maximum value
ˆ
i i
vj
in the rounded problem. So, max vi = vi =
ˆ ˆ b = n · ǫ−1 . ⇒ The overall running time:
i
O(n3 · ǫ−1 ).
Fact 5: If S is the solution found by the Knapsack-Approx algorithm, and S ∗ is any other solution
satisfying wi ≤ W , then we have (1 + ǫ) · vi ≥ vi .
i∈S ∗ i∈S i∈S ∗
Proof: Let S ∗ be any set satisfying wi ≤ W . Our algorithm finds the optimal solution with
i∈S ∗
values vi :
˜
vi ≥
˜ vi
˜ (∗)
i∈S i∈S ∗
vi ≤ vi ≤
˜ vi ≤
˜ (vi + b) ≤ n · b + vi
F act1 (∗)
i∈S ∗ i∈S ∗ i∈S i∈S i∈S
We get:
vi ≥ vj := max vi
˜ ˜
i
i∈S
ǫ
b= · (max vi ) ⇒ n · b = ǫ(max vi ) ≤ ǫ · vi
n i i
i∈S
Thus, we get:
√
vi ≤ (ǫ · vi ) + ( vi ) = (ǫ + 1) · vi
i∈S ∗ i∈S i∈S i∈S
![Lecture Notes On
Algo-Design
Lecturer: Ulf-Peter Schroeder
February 16, 2006
written by:
Braun, Rudolf
Brune, Philipp
Piepmeyer, Meik
Please send corrections - including [AlgoDesign-Script] in the subject line -
to: meikp <KLAMMERAFFE> upb <PUNKT> de
1](https://image.slidesharecdn.com/script-mda1-101011070309-phpapp01/85/script-md-a1-1-320.jpg)
