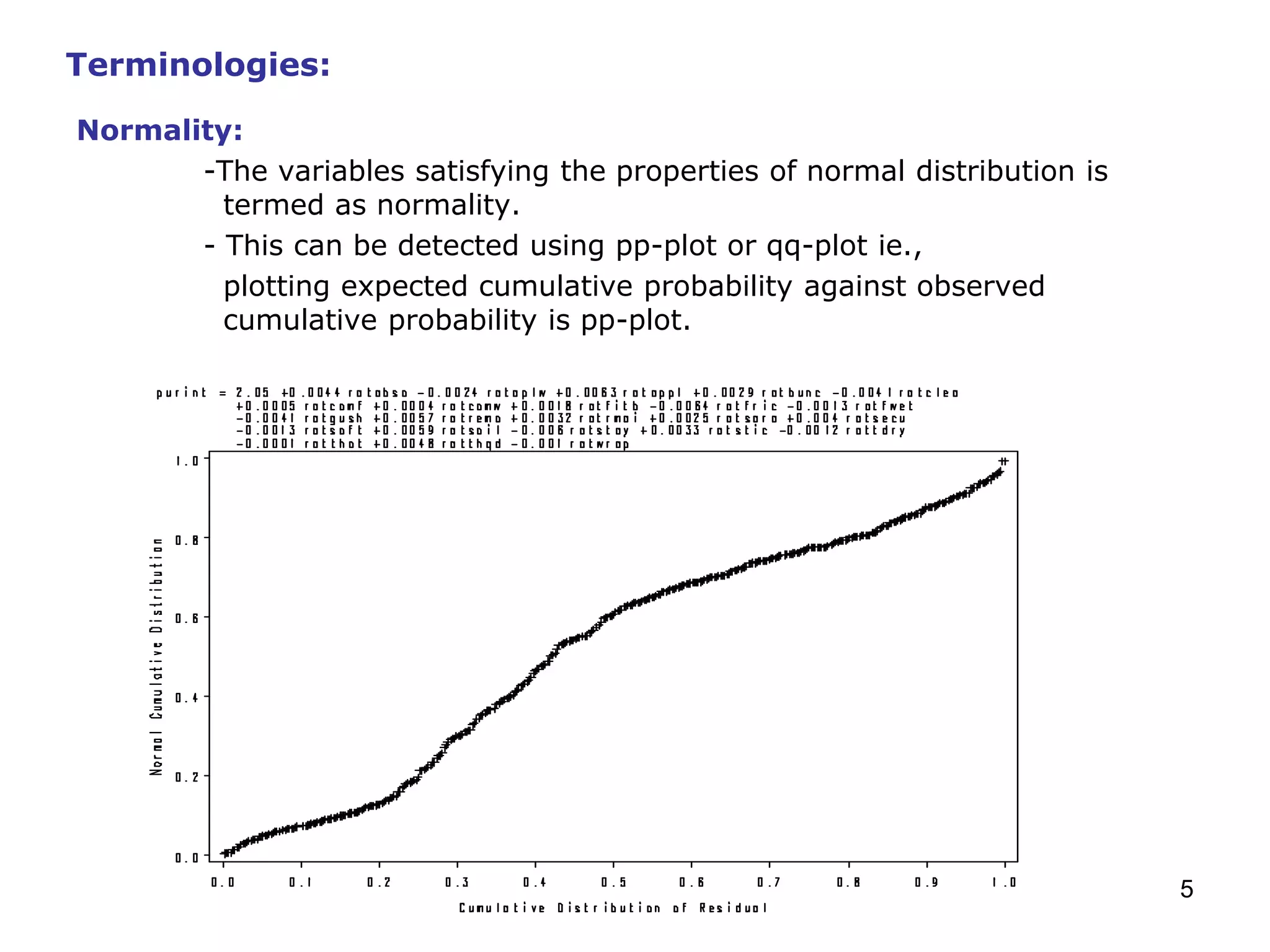
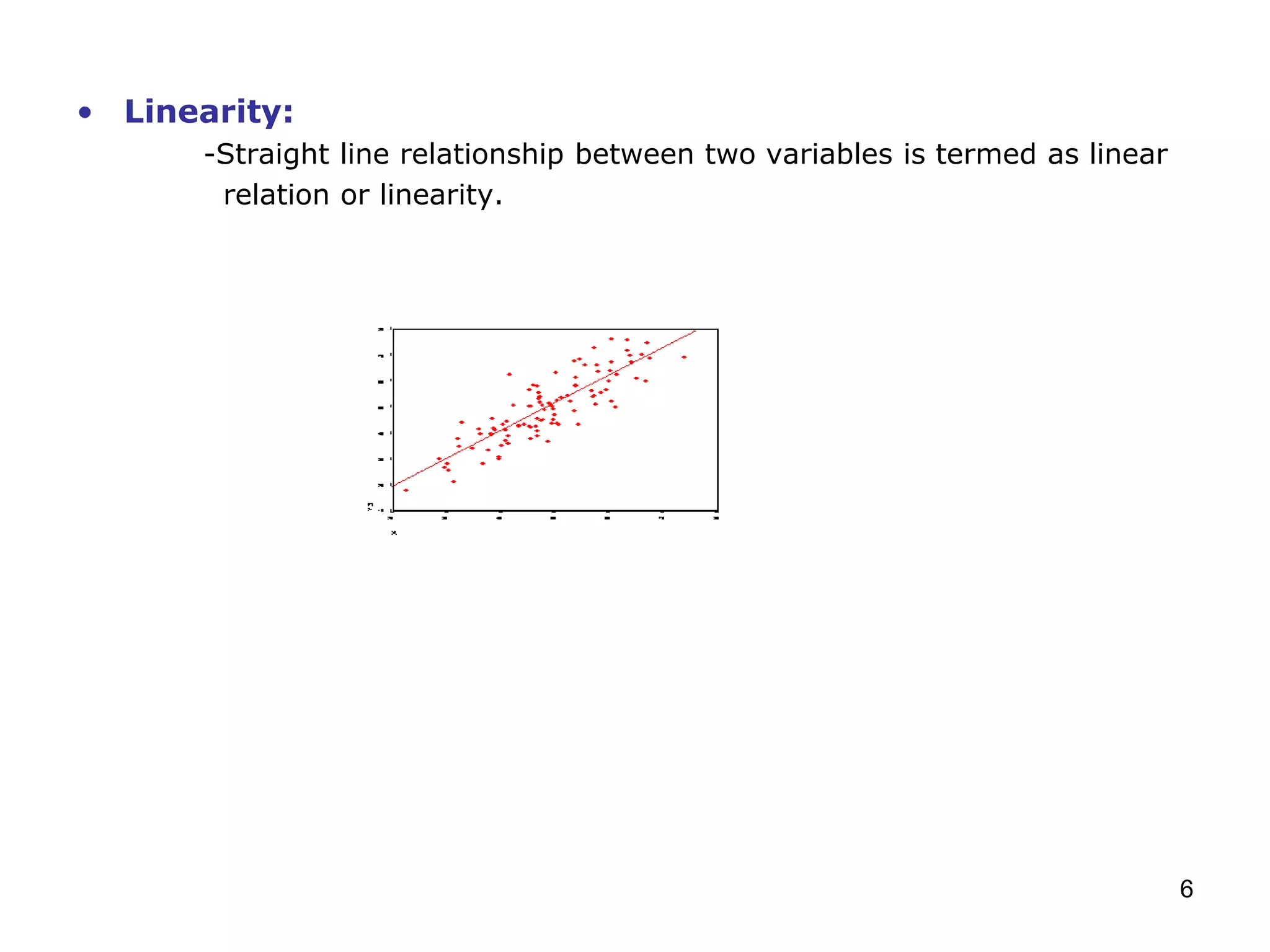
This document provides an overview of regression analysis, including simple and multiple regression models. Simple regression involves one dependent and one independent variable, while multiple regression has one dependent variable and more than one independent variable. Regression is used to identify factors that influence metrics like brand preference, demand, and sales. Key aspects discussed include assumptions of linearity, normality, absence of outliers and multicollinearity. Metrics like R-square, adjusted R-square, residuals, and variance inflation factor (VIF) are defined.

1. 1
Regression Analysis

2. 2
Regression – Basic Concepts
• What is regression analysis?
- It is multivariate dependence technique used to find linear
relationship between one metric dependent variable and more metric
independent variables
• When is regression analaysis used?
- Identifies factors which contribute to take up that brand.
- Identifies the factor which influences a consumer's impression on a
brand
- Identifies the features which make it more likely to buy that brand.
• Regression model:
- The two types of regression model are
Simple regression
Multiple regression

3. 3
Simple Regression:
In Simple Regression only one dependent variable and only
one independent variable is present in the analysis.
Y = a + bX
Where ‘a’ is intercept, ‘b’ is regression coefficient.
Multiple Regression:
In multiple Regression there are one dependent variable and
more than one independent variables present in the analysis.
Y = a + b1 X1 + b2 X2 +…+ bn Xn
a is intercept, represents the amount of dependent Y when all independents
are “0” & b’s are regression coefficients

4. 4
Data Types:
Variables in the regression analysis must be metric.
Variables used for regression analysis are
•Price
•Cost
•Demand
•Supply
•Income
•Taste and Preferences

5. 5
Normality:
-The variables satisfying the properties of normal distribution is
termed as normality.
- This can be detected using pp-plot or qq-plot ie.,
plotting expected cumulative probability against observed
cumulative probability is pp-plot.
Terminologies:

6. 6
• Linearity:
-Straight line relationship between two variables is termed as linear
relation or linearity.

7. 7
Outliers:
-Extreme values of a predictor or outcome variable that appear
discrepant from the other values .
Predicted values:
-Also called fitted values, substituting the regression coefficient
and the independent variables in the model we get the predicted
values for each case.
Residuals:
-Residuals are the difference between the observed values and
predicted values of the dependent variables.

8. 8
Beta weights:
-Standardization of regression coefficient are called Beta Weights.
Ratio of Beta weights are the ratio of relative predictive power of the
independent variable.
R-Square :
-Proportion of the variation of dependent variable explained by
the independent variable.
Adjusted R-Square:
-Proportion of the variation of dependent variable explained by the
independent variable after adding or deletion of the variables.
Multicollinearity:
-Inter correlation among the independent variables.

9. 9
VIF (Variance Inflation factor):
-It is a measure, used to find the amount of multicollinearity.
-VIF= 1/tolerance=1/1-R2
-Higher the VIF indicates higher the multicollinearity.
F Test:
-F Test is used to test the R square and it is same as to testing the
significance of the regression model.
-Null hypothesis: The data doesn’t fit the model i.e., we have to
reject the null hypothesis.

10. 10
Assumptions:
• The variables should be metric variables.
• The sample size should be adequate i.e., each variable should have at
least ten observation.
• Linearity among the dependent and independent should be satisfied.
• Multicollinearity should be absent.
• Residuals should be normally distributed.
• Residuals should satisfy homoscedasticity property.
• Residuals should be independent.
• Multivariate normality for variables should be satisfied.
• No outliers.

11. 11
Expected output:
• Model should be significant i.e., (Pr>F) ≤ 0.05.
• VIF should be ≤2.
• Condition index should be ≤ 15.
• Independent variable should be significant (Pr >t) ≤0.05.
• Standard estimates tells us the amount of variance of dependent variable
explained by that independent variable (tested using significance t test).
• R square tells the amount of variance explained by the model on the
whole (tested using significance F test).
• Parameter estimates can be negative or positive.

12. 12
Thank
you 