This document presents a nonlinear finite element analysis of a notched unreinforced concrete beam tested by Petersson in 1981. A medium mesh model from an Abaqus example was used to model the beam in MSC/Marc. The analysis found the load-deflection curve computed in MSC/Marc was stiffer than the experimental results, similar to results from Abaqus/Standard which also uses a linear tension softening assumption. The document provides details on the beam geometry, material properties, and compares the load-deflection curves from the analysis to the experimental test data.

1. Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 1 of 9
Analysis of Notched Unreinforced Concrete Beam
Using Nonlinear Finite Element Techniques
Prepared By:
David R. Dearth, P.E.
Applied Analysis & Technology, Inc.
16731 Sea Witch Lane
Huntington Beach, CA 92649
Telephone (714) 846-4235
E-Mail AppliedAT@aol.com
Web Site www.AppliedAnalysisAndTech.com

2. Introduction
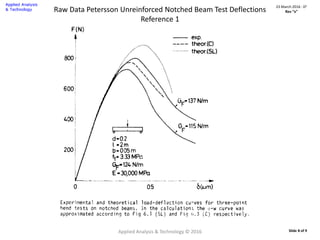
 Petersson, P.E (1.) tested an unreinforced notched concrete beam in 1981.
[Ref. Figure 8.16 Experimental and theoretical load-deflection curves for three-point bend tests on
notched beams.] See Slide 8.
 The purpose of this summary is to present results of addressing this Notched
Unreinforced Concrete Beam and computing the load deflection curve using MSC/Marc
for comparison to the experimental test data at the nominal fracture toughness, Gf = 124
N/m.
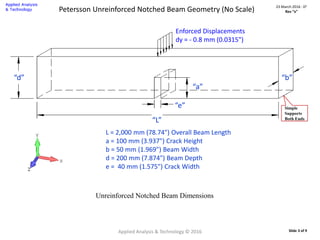
 For purposes of this analysis a medium mesh model definition was borrowed from an
Abaqus example problem “3.2.11 Notched unreinforced concrete beam under 3-point
bending”. (2.)
 Since Marc uses a linear tension softening modulus, Es, results from Abaqus/Standard
with linear tension softening are used for comparison. [Ref. Figure 3.2.11-6 Plane stress
Abaqus/Standard mesh refinement study – medium mesh.]
 Note: As noted in the Abaqus example, when linear tension softening is assumed in the
Abaqus solution, this leads to a response that is overly stiff compared with the
experimental observations of Petersson.
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 2 of 9

3. Petersson Unreinforced Notched Beam Geometry (No Scale)
Unreinforced Notched Beam Dimensions
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 3 of 9
Simple
Supports
Both Ends
“L”
“a”
“e”
“d”
Enforced Displacements
dy = - 0.8 mm (0.0315")
“b”
L = 2,000 mm (78.74") Overall Beam Length
a = 100 mm (3.937") Crack Height
b = 50 mm (1.969") Beam Width
d = 200 mm (7.874") Beam Depth
e = 40 mm (1.575") Crack Width

4. Half Symmetric Unreinforced Notched Concrete Beam with Boundary
Conditions & Loading
Y-Z Symmetric
Plane, BC = Tx
Enforced Displacements at Beam Mid-
Span, Δy = -0.8 mm (-0.0315 inch)
Corner Vertical
Reaction, BC=Ty
Mesh size for the half symmetric model is
280 plane stress elements (medium mesh)
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 4 of 9
Symmetric Half Section Unreinforced Notched beam Mesh Sizing
(Reference Abaqus Examples Manual Figure 3.2.11-2)
Concrete Material Properties
Ec= 4.350 x 106 psi ν =0.20
Critical Cracking Stress (Rupture Stress) fr = 482.96 psi(1.)
Tension Softening Strain at Failure, ε = 0.00197 in/in(2.)

5. Concrete : Isotropic Linear Tension Softening Properties
Note: Abaqus input is “strain at failure”.
Marc input is “tension softening slope”.
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 5 of 9

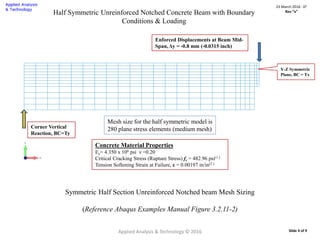
6. Concrete : Isotropic Properties
The concrete is idealized using 2D Plane Stress elements. Young’s modulus of elasticity for the concrete is given as:
Concrete Material Properties
Elastic : Ec= 4.35 x106 psi ν = 0.20
Cracking : Critical Cracking Stress (Rupture Stress) fr = 482.96 psi
Softening Modulus, Es= 259,410 psi [Failure Strain = 0.00197 in/in]
Crushing Strain, εc = 0.005 in/in, Shear Retention : 7.5%
Concrete Isotropic Material Input Dialog
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 6 of 9

7. Petersson Unreinforced Notched Beam Test Deflections
MSC/Marc vs Abaqus/Standard
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 7 of 9

8. Raw Data Petersson Unreinforced Notched Beam Test Deflections
Reference 1
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 8 of 9

9. References
1) Petersson, P. E., “Crack Growth and Development of Fracture Zones in Plain
Concrete and Similar Materials” Report No. TVBM-1006, Division of Building
Materials, University of Lund, Sweden, 1981
http://www.iaea.org/inis/collection/NCLCollectionStore/_Public/13/668/13668228.pdf
2) Dassault Systems, 3.2.11 Notched unreinforced concrete beam under 3-point bending
Abaqus 6.13 Abaqus Benchmarks Guide, 2013
http://129.97.46.200:2080/v6.13/books/bmk/default.htm
3) MSC/Marc Reference Manuals & Finite Element Analysis System: Volumes A, B, C, D"
MSC Software Corporation, 2 MacArthur Place, Santa Ana, California 92707
Applied Analysis & Technology © 2016
23 March 2016 : D2
Rev “x”
Slide 9 of 9