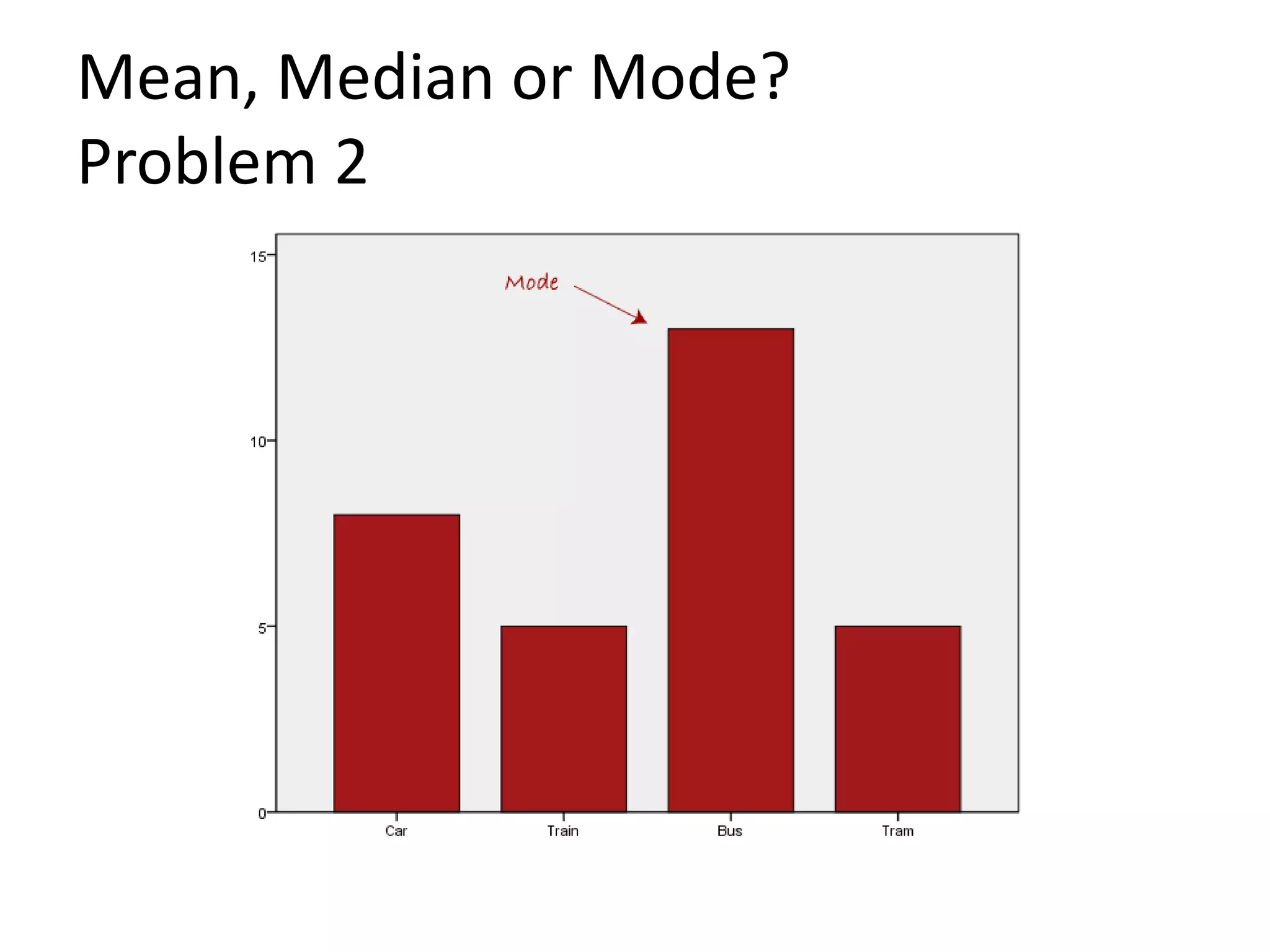
This document discusses analyzing test results and different statistical measures including mean, median, mode, and range. It provides examples of calculating each measure and explains when each might be the best measure to use depending on the data set. It discusses situations where the mean could be skewed by outliers and how the median is not affected by outliers. It also includes examples of using a spreadsheet to calculate the mean of a large data set. Finally, it discusses measuring health and fitness through different tests and examples of questions that could be investigated by analyzing class test results data.

1. Analysing Our Results From
Our Tests
Looking at our data!

2. What is
Mean, Median,
Mode and
Range?
Give examples

3. Which is the best
average
Mean, Median
and Mode? Why?

4. The mean
The mean is the most commonly used average.
To calculate the mean of a set of values we add
together the values and divide by the total number of
values.
Sum of values
Mean = Number of values
For example, the mean of 3, 6, 7, 9 and 9 is
3+6+7+9+9 34
= = 6.8
5 5

5. Finding the mode
The mode or modal value in a set of
data is the data value that appears the
most often.
For example, the number of goals scored
by the local football team in the last ten
games is:
2, 1, 2, 0, 0, 2, 3, 1, 2, 1.
The modal score is 2.
Is it possible to have more than one modal value? Yes.
Is it possible to have no modal value? Yes.

6. Finding the median
The median is the middle value of a set of numbers
arranged in order. For example:
Find the median of
10, 7, 9, 12, 7, 8, 6,
Write the values in order:
6, 7, 7, 8, 9, 10, 12.
The median is the middle value.

7. Finding the median
When there is an even number of values, there will be
two values in the middle.
In this case, we have to find the mean of the two middle
values.
Find the median of 56, 42, 47, 51, 65 and 43.
The values in order are:
42, 43, 47, 51, 56, 65.
There are two middle values, 47 and 51.

8. Rogue values
The median is often used when there is a rogue value –
that is, a value that is much smaller or larger than the
rest.
What is the rogue value in the following data set:
192, 183, 201, 177, 193, 197, 4, 186, 179?
The median of this data set is:
4, 177, 179, 183, 186, 192, 193, 197, 201.
The median of the data set is not affected by the rogue value, 4.
The mean of the data set is 168. This is not representative of the set because it is lower
than almost all the data values.

9. Finding the range
The range of a set of data is a measure of how
the data is spread across the distribution.
To find the range we subtract the lowest value in the set
from the highest value.
Range = highest value – lowest value
If the range is small, it tells us that the values are
similar in size.
If the range is large, it tells us that the values vary
widely in size.

10. Mean or median?
Would it be better to use the median or the mean to represent the following
data sets?
34.2, 36.8, 29.7, 356, 42.5, 37.1? median
0.4, 0.5, 0.3, 0.8, 0.7, 1.0? mean
892, 954, 1026, 908, 871, 930? mean
3.12, 3.15, 3.23, 9.34, 3.16, 3.20? median
97.85, 95.43, 102.45, 98.02, 97.92, 99.38? mean
87634, 9321, 78265, 83493, 91574, 90046? median

11. Mean, Median or Mode?
Transport Car Train Bus Tram
Number of 8 5 13 5
people

12. Mean, Median or Mode?
Problem 2

13. Calculating the mean using a spreadsheet
When processing large amounts of data it is often helpful to use a spreadsheet to
help us calculate the mean.
For example, 500 households were asked how many children under the age of 16
lived in the home. The results were collected in a spreadsheet.

14. How do we Measure Health and
Fitness?

15. The tests
Beep test
Ruler Drop test
Vertical Jump test
Sit & Reach test
Standing Broad Jump test

16. What kind of information would you
like to find out about the class?
• Some suggestions
• Are girls fitter than boys?
• Is 7R fitter than 7N?
Are 10 year olds fitter than 11 year olds? Go
back to your classrooms to discuss what you
would like to find out about.
• Present

17. Questions?
• DOES height affect flexibility?
• Are tall people fitter than short people?
• Is 7R fitter than 7N?
• Do boys have more stamina girls?
• Is 7R sporty than 7N?
• Is 7R fitter than the rest of year 7