This document provides an introduction and overview to the textbook "An Introduction to Numerical Methods Using Mathcad" by Khyruddin Akbar Ansari. The textbook is designed as a guide for teaching numerical methods using Mathcad software. It covers topics such as root-finding, matrices, interpolation, curve-fitting, differentiation, integration, and solving differential equations. The author has many years of experience in engineering education and research.

1. AN INTRODUCTION TO NUMERICAL
METHODS USING MATHCAD
Mathcad Release 14
Khyruddin Akbar Ansari, Ph.D., P.E.
Professor of Mechanical Engineering
School of Engineering and Applied Science
Gonzaga University
Spokane, Washington

2. Copyright 2007 Khyruddin Akbar Ansari.
All rights reserved
No part of this book may be used or reproduced or distributed in any form , or by any means or
stored in a database or retrieval system, without the prior written permission of the author .
Mathcad screenshots are reprinted by permission of Parametric Technology Corporation (PTC).
Mathcad is a registered trademark of PTC, 140 Kendrick Street, Needham, MA 02494. All rights
reserved

3. Dedicated to my dear wife, Fatima

4. ABOUT THE AUTHOR
Khyruddin Akbar Ansari, who has been a professor of mechanical engineering at Gonzaga
University in Spokane, Washington, since 1986, received his bachelor’s degree in electrical
engineering from Osmania University, Hyderabad, India in 1964, his master’s degree in mechanical
engineering from the University of California at Berkeley in 1965 and his Ph.D. degree in
engineering mechanics from the University of Texas at Arlington in 1972. He did his doctoral
thesis work in the area of nonlinear vibrations of rotating blades under the guidance of the late
Professor Nils O. Myklestad. Professor Ansari has many years of varied industrial , teaching and
research experience, having been associated in the past with such organizations as Bell Helicopter,
Westinghouse Electric , Bell Aerospace, Brown and Root, King Fahd’s University of Petroleum
and Minerals and Battelle Pacific Northwest Laboratories .
At Gonzaga University, Professor Ansari is currently involved in the teaching of courses in the
areas ofengineeringmechanics,numerical methods,advancedengineeringmathematics,vibrations,
system dynamics and controls , and machine design. His research, which has been varied, has
resulted in several published articles and contributions to books including chapters in the
Encyclopedia of Fluid Mechanics and Developments in Offshore Engineering.
Professor Ansari is a member of the American Society of Mechanical Engineers and the American
Society for Engineering Education. He is also a registered professional engineer.

5. TABLE OF CONTENTS
Preface v
1. Basics of Mathcad. 1
1.1 Introduction 1
1.2 The Mathcad Screen 1
1.3 Exact Answers 3
1.4 Variables, Functions and Live math. 3
1.5 Feedback 4
1.6 Graphics 5
1.7 Graphing of Functions and Plotting of Data 5
1.8 Animations 7
1.9 The Mathcad Tutorials 7
1.10 Advantages of Mathcad 7
1.11 Computations in Mathcad 10
1.12 The Mathcad Window, Toolbars and Palettes 13
1.13 Mathcad Regions 15
1.14 Entering Math and Text 16
1.15 Mathcad Worksheets,Templates and Styles 17
1.16 Defining Variables 18
1.17 Defining Functions in Mathcad 19
1.18 Building and Editing Mathematical Expressions 21
1.19 Defining Range Variables 23
1.20 Defining Vectors and Matrices 24
1.21 Creating Graphs 28
1.22 Formatting Math, Text and Results 35
1.23 Using Units 39
2. Introduction to Numerical Methods. 43
2.1 The Use of Numerical Methods in Science and Engineering 43
2.2 Comparison of Numerical Methods with Analytical Methods 43
2.3 Sources of Numerical Errors and their Computation 44
2.4 Taylor Series Expansion 44
Problems 49
3. Roots of Equations. 53
3.1 Introduction 53
3.2 Methods Available 53
3.3 Bisection Method 53
3.4. The Regula Falsi or the False Position Method 58
3.5 Newton-Raphson Method 65
3.6 Use of Mathcad’s root and polyroots Functions 71
Table of Contents: i

6. 3.7 Secant Method 72
3.8. Method of Successive Substitution 78
3.9 Multiple Roots and Difficulties in Computation 80
3.10. Solution of Systems of Nonlinear Equations 84
3.11 Solving Systems of Equations using Mathcad's
Given and Find Functions 86
3.12 Applications in Root-Finding 87
3.12.1 Maximum Design Load for a Column 87
3.12.2 Natural frequencies of Vibration of a Uniform Beam 89
3.12.3 Solving the Characteristic Equation in Control
Systems Engineering 91
3.12.4 Horizontal Tension in a Uniform Cable 93
Problems 96
4. Matrices and Linear Algebra. 103
4.1 Basic Matrix Operations 103
4.2 Use of Mathcad in Performing Matrix Operations 105
4.3 Solution of Linear Algebraic Equations by Using the Inverse 108
4.4 Solution of Linear Algebraic Equations by Cramer’s Rule 110
4.5 Solution of Linear Algebraic Equations Using the Function lsolve 112
4.6 The Eigenvalue Problem 114
4.7 Solving the Eigenvalue Problem with Mathcad 116
4.8 Application of the Eigenvalue Problem to Vibration Engineering 117
4.9 Application of the Eigenvalue Problem to Stress Analysis-
Determination of Principal Stresses and Principal Directions 125
4.10 Repeated Roots in the Determinantal Equation 128
4.11 Solution of Nonlinear Simultaneous Equations 131
Problems 134
5. Numerical Interpolation. 141
5.1 Linear Interpolation 141
5.2 The Method of Undetermined Coefficients 141
5.3 The Gregory-Newton Interpolating Polynomial 144
5.4 Interpolation Using Finite Differences 149
5.5 Newton’s Method Utilizing Finite Differences 151
5.6 The Lagrange Interpolating Polynomial 155
5.7 Interpolation Using Linear, Quadratic and Cubic Splines 158
5.8 Interpolation with Mathcad 159
5.9 Applications in Numerical Interpolation 168
5.9.1 Stress-Strain data for Titanium 168
5.9.2 Notch Sensitivity of Aluminum 169
5.9.3 Speech Interference Level 172
5.9.4 Load-Deflection Data for Elastomeric Mounts 175
Problems 177
ii AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

7. 6. Curve-Fitting. 183
6.1 The Need to Fit a Function to Measured Data 183
6.2 The Method of Least Squares. 184
6.3 Straight Line Regression 185
6.4 Curve-Fitting with a Quadratic Function 188
6.5 Curve-Fit with a Power Function 191
6.6 Curve-Fitting with an Exponential Function 194
6.7 Curve-Fitting with a Linear Combination of Known Functions 199
6.8 Curve-Fitting with Polynomials. 203
6.9 Use of Mathcad's Regression Functions for Curve-Fitting 207
6.9.1 Linear Regression with Mathcad 207
6.9.2 Nonlinear Regression with Mathcad 209
6.9.3 Use of the Function linfit 211
6.9.4 Use of the Function genfit 213
6.9.5 Use of the Mathcad Functions logfit, lnfit, pwrfit and expfit 215
6.9.6 More Examples with Mathcad 220
6.10 Applications in Curve-Fitting 236
6.10.1 Fatigue Failure Curve for Loading in the Finite Life Range 236
6.10.2 Temperature Response of an Object Placed in a
Hot Stream of Air 239
6.10.3 The Effect of Operating Temperature on the Strength of a
Mechanical Element 242
6.10.4 Drop-Testing of Packaged Articles 245
Problems 248
7. Numerical Differentiation 255
7.1 Introduction to Numerical Differentiation and
the Use of the Mathcad Derivative Operators 255
7.2 Method of Finite Differences 255
7.3 Interpolating Polynomial Method 259
7.4 Applications in Numerical Differentiation 262
7.4.1 Determination of Velocities and Accelerations
from Given Displacement Data 262
7.4.2 Determination of Shock Absorber Parameters, and Damper
and Spring Restoring Forces from Given Vehicle Displacement Data 266
Problems 271
8. Numerical Integration 277
8.1 Introduction to Numerical Integration and
the Use of the Mathcad Integral Operator 277
8.2 The Interpolating Polynomial Method 279
8.3 Trapezoidal Rule 280
8.4 Simpson’s Rules 283
Table of Contents: iii

8. 8.4.1 Simpson’s One-Third Rule 283
8.4.2 Simpson’s Three-Eighth Rule 286
8.4.3 Limitations of Simpson’s Rules 287
8.5 Romberg Integration 288
8.6 Applications in Numerical Integration 301
8.6.1 Centroid of a Rod Bent into the Shape of A Parabola 301
8.6.2 Moment of Inertia of a Beam of Semi-Elliptic Cross Section 302
8.6.3 Launch of a Projectile 303
8.6.4 Large Oscillations of a Simple Pendulum 304
Problems 306
9. Numerical Solution of Ordinary Differential Equations. 311
9.1 Introduction 311
9.2 Taylor Series Method 312
9.3 Euler’s Method 317
9.4 Modified Euler’s Method 323
9.5 Runge- Kutta Methods 329
9.5.1 Fourth-Order Runge-Kutta Method 329
9.5.2 Mathcad Solutions to a First-Order Differential Equation 335
9.6 Systems of Ordinary Differential Equations 341
9.7 Solution of Higher-Order Ordinary Differential Equations 349
9.8 Boundary-Value Problems and the Shooting Method 358
9.9 Applications in Numerical Solution of Ordinary Differential Equations 363
9.9.1 Response of an Electric R-L Circuit to a Unit-Step Voltage Input 363
9.9.2 Deflection Curve of a Cantilevered Beam with a Uniformly
Distributed Load 364
9.9.3 Temperature Response of a Solid Steel Ball Placed in a Hot
Stream of Air 366
9.9.4 Nonlinear Vibration of a Simple Pendulum 367
9.9.5 Transient Vibration of a Spring-Mass-Damper System
Excited by a Pulse Function 370
9.9.6 Nonlinear Vibration of a Damped System with a
Hardening Spring 373
9.9.7 Temperature Distribution in the Wall of a Pipe
Carrying a Hot Fluid 378
9.9.8 Response of an R-L Circuit with a Nonlinear Resistor 382
9.9.9 The Effect of Damping on the Step Response of a
Second-Order Control System 384
Problems 386
Bibliography 399
Index 401
iv AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

9. PREFACE
This book, which is designed to be used in a first numerical methods course in a computer science,
mathematics, science , engineering or engineering technology curriculum, has been developed from
notes that I generated over several years in the process of teaching a one- semester / three-credit
sophomore level course in computer methods at Gonzaga University. It should also provide a
reliable source of reference material to practicing engineers and scientists and in other junior and
senior-level courses such as machine design, vibrations, system dynamics and controls, where
Mathcad can be effectively utilized as a software tool in problem solving. A principal goal of this
book , then, is to furnish the background needed to create Mathcad documents for the generation
of solutions to a variety of problems. Specific applications involving root-finding, interpolation,
curve-fitting, matrices, derivatives, integrals and differential equations are discussed and the broad
applicability of Mathcad demonstrated. The material contained herein should be easily grasped by
students with a background in calculus, elementary differential equations and some linear algebra,
and when utilized in a mathematics, science, engineering, computer science or engineering
technology course sequence, it should give a good basic coverage of numerical methods while
simultaneously demonstrating the general applicability of Mathcad to problem- solving and
solution documentation.
The first chapter discusses Mathcad basics while the second gives a general introduction to
numerical methods in science and engineering and presents the computation of numerical errors
along with the Taylor series as a basis of approximation in numerical analysis. Chapter 3 offers a
coverage of the popular methods of finding roots of equations such as Bisection, Regula-Falsi,
Newton-Raphson, Secant and Iteration . Solutions to systems of nonlinear algebraic equations
obtained by the iteration method are also presented. The applicability of root-finding to practical
problems such as those that occur in column design, vibration analysis and control systems
engineering is demonstrated. In the fourth chapter, matrices and linear algebra are dealt with along
with the solution of eigenvalue problems. Applications to the field of vibration engineering and
stress analysis are also discussed. Chapters 5 and 6 focus on numerical interpolation and curve-
fitting respectively. The common techniques of interpolation and the functions generally resorted
to for curve-fitting of data are covered quite thoroughly. The applicability of these to the analysis
of scientific and engineering data such as stress-strain, load-deflection and fatigue failure is
presented. Chapters 7 and 8 address numerical differentiation and integration. The concept of finite
differences is introduced and the common methods of differentiation and integration , such as the
interpolating polynomial method, trapezoidal and Simpson’s rules and Romberg integration are
covered. Applications of numerical differentiation and integration such as determination of
velocities and accelerations from given displacement data and computation of the moment of inertia
of a cross section are included. The last chapter, which is the ninth one, deals with coverage of
numericalsolutionofordinarydifferentialequations,andalthough it does not discuss each and every
technique that is available, it does focus on the popular ones such as Taylor series method, Euler,
modified Euler and Runge-Kutta methods. A variety of practical applications of numerical
procedures are included in this chapter, ranging from the response of an electric circuit to an input
Preface: v

10. voltage to the effect of damping on the response of a control system. Partial differential equations
is a topic that is typically dealt with in detail only in graduate level courses and , therefore, I did not
think it very appropriate to introduce it in this book which is really aimed at the needs of
undergraduate students. Mathcad documents are generated and examples showing the applicability
and use of Mathcad are presented throughout the book. Wherever appropriate, the use of Mathcad
functions offering shortcuts and alternatives to otherwise long and tedious numerical solutions is
also demonstrated. At the end of every chapter is included a set of problems to be solved covering
the material presented. A solutions manual that provides solutions to these exercises can be made
available to instructors.
Although Mathcad is a very powerful and versatile tool that combines text, graphics and equations
in a single worksheet, several figures and sketches in the book had to be done using AutoCad. The
help provided by Carlos G. Alfaro earlier in generating these figures and Ryan Lambert later in
making some additions and modifications to them is gratefully acknowledged. I am also thankful
to those of my students who have so kindly made useful suggestions and pointed out errors and
mistakes in the manuscript. Their input and feedback have certainly been helpful. Last but not least,
I am indebted to my wife, Fatima , for her patience, support and understanding during the
preparation of this book. Without her encouragement, its completion would still be wishful thinking.
Users of this book are welcome to e-mail any comments and suggestions to me at
ansari@gonzaga.edu , and, of course, I will be pleased to address these in subsequent versions /
editions.
Khyruddin . Akbar Ansari
October 2007
vi: AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

11. C H A P T E R 1
BASICS OF MATHCAD
1.1 INTRODUCTION
Mathcad 14 is the first global release of Mathcad presented by Parametric Technology
Corporation (PTC) with many significant enhancements since it acquired Mathsoft in April 2006.
This is a very powerful software that offers a wide variety of tools in the solution of problems
requiring the use of numerical analysis. New ways of using Mathcad are constantly being found
leading to overwhelming possibilities. The sections that follow give an overview of the features in
Mathcad 14 and will help the novice to get introduced to its problem-solving capabilities.
Mathcad 14 has a number of improvements and added capabilities designed to increase the
productivity of the user as well as Web connectivity. There is a wealth of information that can
be found by clicking on "Help" and going to "Tutorials" , where you can get an overview and a
quick tour of Mathcad , see the new features available in Mathcad 14, learn the fundamental
skills for working in Mathcad, and obtain on-line help if needed. By clicking on "Help", the
Mathcad Quicksheets can be accessed, which are ready-made recipes for performing a variety
of tasks in Mathcad. E-books and Reference Tables, user-contributed files, samples,
animations and graphs along with other example files for using and extending Mathcad can also
be accessed. By choosing "User Forums" under the "Help" menu, questions can be posted
for other Mathcad users. The Mathcad web site can always be accessed for updates, technical
support information and user files , and Mathcad documents can now be saved on the Web or
in Microsoft Word using Rich Text Format (RTF).
1.2 THE MATHCAD SCREEN
Mathcad has a full screen numerical and symbolic calculator, which is essentially a blank
workspace that you see when you open up a new Mathcad document. To use Mathcad's
calculating capabilities, type the expression you want to evaluate and then type an equals sign
to get the result:
435
57
24
+ 437.375
=
As shown in Figure 1.1. the palette buttons open up palettes that include a host of math
operations . An expression such as the following can be assembled quite easily.
sin
π
8
⎛
⎜
⎝
⎞
⎟
⎠
ln 76.5
( )
e
95.2
⋅ 1.952 10
40
×
=
Chapter 1: Basics of Mathcad 1

12. Figure 1.1 The Math palettes
2 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

13. Matrix arithmetic, calculus operations such as differentiation and integration, and essentially all
of the mathematical operations normally required in engineering and scientific analysis can be
easily done in Mathcad. Some examples are given below.
2
7
x
e
2x
sin 4 x
⋅
( )
⋅
⌠
⎮
⌡
d 2.641 10
5
×
=
7 9i
+
13 7i
−
0.128 0.761i
+
=
5
4
7
2
8
3
7
9
6
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
1
− 0.168
−
0.312
−
0.352
0.072
−
0.152
8 10
3
−
×
0.304
0.136
0.256
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
1.3 EXACT ANSWERS
If exact answers are needed in terms of fractions and radicals instead of decimals, the
"symbolic equals sign" (-->) on the fourth math palette can be used to obtain exact answers.
Some examples are given below.
546
59
17
+
9341
17
→
sin
π
16
⎛
⎜
⎝
⎞
⎟
⎠
ln 75.6
( )
e
90.5
⋅ 9.0751625112586372168e37
→
5
4
9
2
8
3
3
9
5
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
1
−
13
7
61
7
60
7
−
1
7
−
2
7
−
3
7
6
7
−
33
7
−
32
7
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
→
2
7
x
e
2 x
⋅
sin 4 x
⋅
( )
⋅
⌠
⎮
⌡
d
cos 8
( ) e
4
⋅
5
cos 28
( ) e
14
⋅
5
−
e
4
sin 8
( )
⋅
10
−
e
14
sin 28
( )
⋅
10
+
→
1.4 VARIABLES, FUNCTIONS AND LIVE MATH
When there is a need to evaluate an expression for several different inputs, the desired
variables and functions can be defined and calculated like built-in constants and functions.
This computational feature in Mathcad is called live math.
Chapter 1: Basics of Mathcad 3

14. For example, if the area of a circle for various values of the radius is to be calculated, define a
radius variable r and give it a value.
r 8
:=
The := symbol can be inserted by typing a colon. Evaluate the area as
π r
2
⋅ 201.062
=
The numerical value of r can now be changed to some other number . Click anywhere outside
the definition to recalculate the area . . This is live math .
If this area computation is to be usable in other parts of the worksheet, an area function must
be defined.
area r
( ) π r
2
⋅
:=
Use this function as needed to calculate an area . Length units for the radius can also be
assigned as shown..
area 60 cm
⋅
( ) 1.131 m
2
=
Live math works for symbolic answers as well. Put in a function , obtain the derivative of the
function, and then change the function to some other function. Click outside the definition to
see how Mathcad redoes the derivative symbolically.
1.5 FEEDBACK
There is continuous feedback in Mathcad. As you edit math expressions, the status line will
provide advice and information . When Mathcad cannot understand something, it will color the
expression red. Clicking on this red expression will give an error message indicating what is
wrong. To see an example, click on the expression below.
p q
+ =
p
In the above, variables p and q were not defined. Therefore, Mathcad tells us so. Also,
Mathcad calculates from top to bottom and left to right.
p 5
:= q 9
:= <--This works ---> p q
+ 14
=
4 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

15. F 4
( ) =
F <-This does not work
F x
( ) x
2
4
−
:=
1.6 GRAPHICS
It has been demonstrated that Mathcad can be used as a calculator and as an equation solver.
It can also be used as a versatile visualization tool that supports a full set of plot types, an
animation facility, as well as simple image processing.
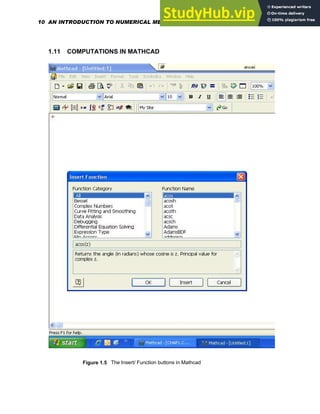
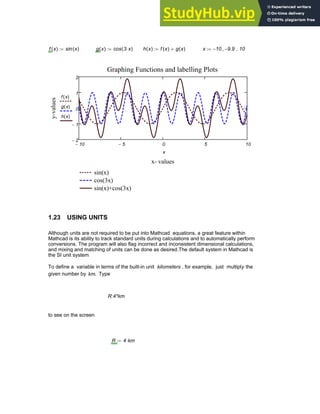
1.7 GRAPHING OF FUNCTIONS AND PLOTTING OF DATA
To create a plot in Mathcad, type the expression you would like to plot, say t
9
. Then click the
graphing button on your palette bar (See Figure 1.2 ) to bring up the graphing palette and click
the upper left button for an XY plot. Click outside the graph or press [Enter] to see the result:
4
− 2
− 0 2 4
1
− 10
5
×
5
− 10
4
×
0
5 10
4
×
1 10
5
×
t
9
t
Parametric plots can also be done easily . .
1
− 0.5
− 0 0.5 1
1
−
0.5
−
0
0.5
1
sin 5 t
⋅
( )
cos 7 t
⋅
( )
Chapter 1: Basics of Mathcad 5

16. Figure 1.2 The graph palette
6 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

17. . . . and like all Mathcad calculations, plots are also live, which means that changes can be
easily made.
1.8 ANIMATIONS
Mathcad can create and play short animation clips by using the built-in variable FRAME and
the Animation dialog box. Choose Animation, and then Record from the Tools menu to bring
up this dialog box Plots as well as numerical results can be animated, and the animation
played back at different speeds.
1.9 THE MATHCAD TUTURIALS
The Mathcad tutorials offer a step-by-step guide to building and editing expressions, creating
and formatting graphs, using Mathcad's wordprocessing capability to enter and format text,
working with units and utilizing Mathcad's built-in functions and operators. For a Mathcad
novice, this is a good place to begin. The Mathcad tutorials can be accessed as indicated in
Figure 1.3 by choosing Help and then Tutorials .
1.10 ADVANTAGES OF MATHCAD
Mathcad offers a great way to work with equations, numbers, text, and graphs. Unlike other
programs, Mathcad uses the language of mathematics and does mathematics in a very natural
way. It works like a scratchpad and pencil combination . Mathcad's on-screen interface is a
blank worksheet on which equations, graph data or functions can be entered and combined
with text -- anywhere on the page.
In Mathcad, an equation looks exactly as in a textbook :
x
b
− b
2
4 a
⋅ c
⋅
−
+
2 a
⋅
=
Mathcad's equations and graphs are live, which means that any data, variable, or equation can
be changed with Mathcad doing an instant recalculation and redrawing of the graphs.
Mathcad can solve a wide range of problems, numerically as well as symbolically, and
equations and data can be evaluated with 2D and 3D plots.
Mathcad Quicksheets are full-featured worksheets that offer ready-made Mathcad templates
that can be customized to perform a wide range of mathematical tasks from solving equations
to graphing and calculus. They also demonstrate how some of Mathcad's special features like
programming and animation can be used. Choose Help and then QuickSheets to use this
capability.
Chapter 1: Basics of Mathcad 7

18. Figure 1.3 Accessing the Mathcad tutorials
8 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

19. Mathcad's Electronic Books have a wealth of mathematical knowledge and reference
material -- all live - which can be dragged and dropped into your worksheets. In order to do
this, choose Help and then E-books .
Mathcad has proven to be an extremely remarkable , effective and powerful tool for the
solution of problems. A wide range of problems can indeed be explored, formulated,
analyzed and optimized, after which the best solution can be documented and presented.
By choosing Help and then User Forums, users can connect with and share their work
with colleagues and other professionals around the world , and collaboration is easy . A
host of forums can be accessed as shown in Figure 1.4.
Figure 1.4 Accessing the Mathcad Collaboratory
Chapter 1: Basics of Mathcad 9

20. 1.11 COMPUTATIONS IN MATHCAD
Figure 1.5 The Insert/ Function buttons in Mathcad
10 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

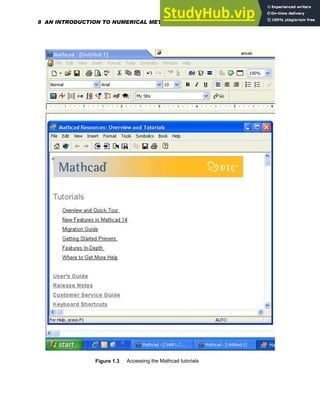
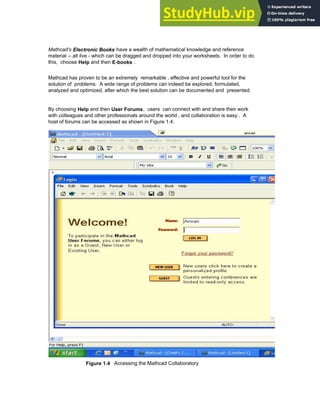
21. Several mathcad palettes can be found on the palette strip at the top of the window that give
access to Mathcad's mathematical operators. A click in your worksheet will place a red
crosshair cursor. Math operators can now be placed in the worksheet via these palettes. To
access Mathcad's built-in functions, go to the Insert menu as shown in Figure 1.5, and
select Function , or click on the Insert Function button on the toolbar
.
EXAMPLES
In the following examples, the number of decimal places required may be put in by choosing
Result from the Format menu and then selecting Number Format.
The red crosshair
Use the Arithmetic Palette (See Figure 1.1)
, and type = to obtain the answer. The basic
operations are +, -, *, and / which are
available on the keyboard .
2.645 10
8
⋅
30007
5
5
6
+
1.0426928428 10
7
−
×
= <--
<- Examples of built-in functions (See
Figure 1.5)
log 1768.985
( ) sin
4
79
π
⋅
⎛
⎜
⎝
⎞
⎟
⎠
⋅ 0.514
=
14.95 5.7i
( )
+
[ ]
3
e
6 5i
−
+ 1.999 10
3
× 4.024i 10
3
×
+
= <-- Complex numbers.
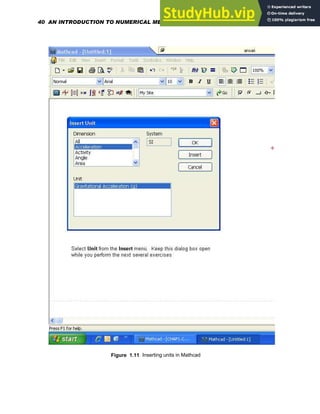
Use of units- Choose Unit from
the Insert menu (See Figure 1.5)
<--- .
7600 km
⋅
1 hr
⋅
2.11 10
3
× m s
1
−
⋅
=
Use of := by typing a colon
character or using the
Arithmetic Palette
a 8
:= a
3 a
4
+ 513.414
= <----
f x
( )
sin x
( )
a
x
6
+
:= f 37
( ) 0.045
−
= <-- Use of a defined function
Chapter 1: Basics of Mathcad 11

22. Use of the range operator in the
Arithmetic Palette. You can also use
a semicolon (;). This will evaluate
any function of z for z values from
zero to 1 in increments of 0.2
z 0 .2
, 1
..
:= <--
z
0
0.2
0.4
0.6
0.8
1
= f z
( )
0
0.025
0.048
0.07
0.088
0.103
= cos f z
( )
( ) z
⋅
0
0.2
0.4
0.599
0.797
0.995
=
<-- Create these tables by
typing z=, f(z)=, etc.
x 0 0.2
, 20
..
:= <-- Define a range of values for the plot.
0 5 10 15 20
0.2
−
0.1
−
0
0.1
0.2
f x
( )
cos x
( ) f x
( )
x
Use the X-Y Plot button in
the Graph Palette, and type
expressions to be plotted in the middle
placeholders on the x and y axes.
Several expressions separated by a
comma (,) can be entered in these
placeholders.
<--
0
100
n
1
n! cos 2 n
⋅
( )
⋅
∑
=
2.28758499
−
=
Use the Calculus Palette (See
Figure 1.1) to do sums, derivatives
and integrals. Click in your worksheet
to position the red crosshair, click on
the proper button in the palette, then
fill in each placeholder as appropriate .
<--
0
25
x
1
1 x
3
e
x
⋅
+
⌠
⎮
⎮
⎮
⌡
d 0.842
=
x 5
:=
x
e
x
sin x
( )
⋅
( )
d
d
100.218
−
=
12 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

23. Matrices can be entered using the
Vector and Matrix palette or by going
to the Insert menu and choosing
Matrix .
A
3
1
1
7
5
10
1
6
2
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= <--
A
1
−
0.427
0.034
−
0.043
−
0.034
0.043
−
0.197
0.316
−
0.145
0.068
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= <-- Type A ^-1= to obtain the inverse
A 117
−
= <-- Use the Vector and Matrix Palette to
obtain the determinant.
t 2.5
:= root t
4
cos 3 t
⋅
( )
− t
,
( ) 0.502
= <-- Find the root of an
expression using the root
function, starting with the guess
of t =2.5
1.12 THE MATHCAD WINDOW, TOOLBARS AND PALETTES
The Mathcad Window and the Main Menu
This does math, graphics and symbolic algebra besides handling the editing and management
of a worksheet. The array of computational and formatting capabilities available can be seen by
clicking on each of the menus.
The Math Toolbar
This is below the main menu. It opens up palettes of math operators as described below.
Chapter 1: Basics of Mathcad 13

24. Calculator toolbar Boolean toolbar
Graph toolbar Programming toolbar
Matrix toolbar Greek toolbar
Evaluation toolbar Symbolic toolbar
Calculus toolbar
Just click on one of these as appropriate and start inserting math symbols into the
worksheet.
The Standard Toolbar
This provides shortcuts for many common tasks from opening and saving files, cutting and
deleting to spell checking and bringing up lists of built-in functions and units. Hover over each
button to see tooltips with a brief description.
The Formatting Toolbar
This formats your text and math at the click of a button. In case the Format Bar does not
show, go to the View Menu, select Toolbars and then Formatting.
The Resources Window and E- books
If you seek examples, want information that can be utilized in your Mathcad worksheets or wish to
access web information from within Mathcad, go to the Help menu, and then open Tutorials,
QuickSheets , Reference Tables or E-books. Tutorials includes Getting Started Primers,
Migration Guide and Features In-Depth, while Quicksheets are live examples showing the use of
Mathcad functions, graphs and programming features. Information on physical constants,
chemical and physical data and mathematical formulas in Mathcad format can be found in
Reference tables . Mathcad E-books can be accessed by opening E-books. These E-books
have the advantage that all equations are live in them and you can change the values of variables,
constants etc. to test and evaluate different results. A number of Mathcad E-books and articles are
also available in the Resources section on http://www.ptc.com/go/mathsoft/mathcad/.
14 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

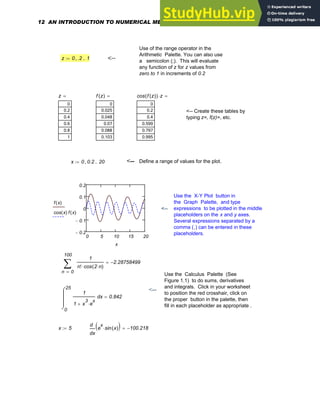
25. Controlling Calculation and The Status Line
The calculation mode, whether manual or automatic, is a property saved in your worksheet and
template files. Mathcad starts in the automatic mode and all calculations and results are updated
automatically. The word " Auto " can be seen in the message line at the bottom of the Mathcad
window. This line provides status alerts, tips, keyboard shortcuts, and other helpful information
along with the calculation status of the worksheet . Here, "auto" refers to the automatic
mode , in which Mathcad automatically recalculates any math expressions when changes in the
worksheet are made. When "WAIT" appears on the status line, the cursor changes to a flashing
lightbulb, indicating that Mathcad is still completing computations. Besides giving the page
number of the current worksheet, the message line will also indicate whether the Caps Lock or
the Num Lock key is depressed on your keyboard. In manual mode, Mathcad does not
compute or show results until recalculation is specifically requested. However, while in manual
mode, Mathcad does keep track of pending computations . Once a change is made that requires
recalculation, the word " Calc " appears on the status line to indicate to the user that the results
being displayed are not correct and that recalculation is necessary to ensure accuracy. The
screen can then be updated by going to the Tools menu and choosing Calculate and then
Calculate Now . Alternatively, click = on the Standard toolbar or press [F9]. To force
Mathcad to recalculate all equations in the worksheet, go to the Tools menu and choose
Calculate and then Calculate Worksheet .
1.13 MATHCAD REGIONS
Mathcad allows you to enter equations, text and graphs as separate objects anywhere in the
worksheet and each equation, text paragraph or plot is considered a region. A region can be
selected by clicking in math or text in your worksheet, after which it is indicated by a thin
rectangle around it. Moving the cursor to one of the edges of the region, will change it to a
small hand with which the region can be moved to anywhere in the worksheet. While clicking
in the math region will bring blue selecting lines under the material selected, clicking in a text
region will bring black boxes to each corner and the middle of each line. With these boxes
text regions can be resized as needed. To add a border around a region or regions, select the
region(s), then right-click and choose Properties from the menu. Then click on the Display tab
and check the box next to " Show Border ".
A math region looks like: A text region looks like:
x 1535.56
:= What is shown on the left was
created by typing
x:1535.56
Chapter 1: Basics of Mathcad 15

26. Moving Regions in the Worksheet
This can be accomplished by clicking in a region and drag-selecting it to put it in a dashed
selection box and then moving the cursor to the edge where it shows up as a small black
hand. Now, use the mouse to move the region as necessary by holding down the left
mouse button and dragging it. Once the regions are positioned in the desired manner, the
mouse button may be released . Then, an empty part of the screen may be clicked on to
deselect the regions. Alternatively, choose Regions from the View menu, which will
highlight the boundaries of the region against a contrasting background. Cut and Paste
can also be used to move regions. Once regions are inserted in the worksheet, they can
be aligned horizontally or vertically by going to the Format menu and choosing Align
Regions.
How Mathcad Reads Your Document
Mathcad reads your document from left to right and top to bottom . For example, if the value of
a function , ln(y) is desired for y= 67, either of the following setups will work.
(a) y 67
:= ln y
( ) 4.205
=
(b) y 67
:=
ln y
( ) 4.205
=
Deleting Selected Regions
Selected regions in dashed line boxes can be deleted by choosing Cut from the Edit menu.
Copying and Pasting Selected Regions
Selected regions can also be copied and put into any place within a document or into another
document by choosing the Copy and Paste commands from the Edit menu .
1.14 ENTERING MATH AND TEXT
Entering Math
Math can be entered by clicking the mouse in a blank space to see a red crosshair cursor.
Type
1+
which will get you
16 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

27. on the screen. The little black box delimited by blue editing lines that you see is called a
placeholder . Continue typing. Type 6 in the placeholder and press the equals key (=) to see
the result.
1 6
+ 7
=
The Arithmetic Palette can be seen by clicking on the Math Palette. This is shown below
Math Palette button
Operation Keystroke Button
Addition +
Subtraction -
Multiplication *
Division /
Powers ^
Entering Text
A text region can be created by clicking in a blank space to see the red crosshair cursor.
Then choose Text Region from the Insert menu or type the double quote (") . The
crosshair transforms to an insertion point with a black text box around it.
1.15 MATHCAD WORKSHEETS, TEMPLATES AND STYLES
Creating and Using Templates
Mathcad styles and templates are similar to those of any word-processing software. When
you create a new worksheet in Mathcad, you can start with Mathcad's default choices, or you
Chapter 1: Basics of Mathcad 17

28. can use a template containing customized formats. Several predefined templates are available
each with a variety of styles, and if necessary, new templates can also be created. Any
Mathcad worksheet can be saved as a new template. To create a new worksheet based on a
template, choose File/New , and then select a template from the list, or browse to your own
template directory. In the placeholders, substitute your own text or bitmaps in any of the
placeholders, or use the built-in styles. You can also revise them if needed. When you create
a worksheet based on a template, all of the formatting information, and any math, text and
image regions are copied into the new worksheet. By creating a new template or revising
another template , a customized format can be generated. Text styles and number formats
can be created, number formats, fonts and sizes can be set, bitmaps can be added , and also,
page numbers, filenames and dates can be inserted . Thus, by using templates, you maintain
consistency across multiple worksheets through definition of math styles, text styles, printing
margins, numerical result formats, units etc. To save a template, choose Save As from the
File menu and use the file extension .mct. The settings, styles and bitmaps saved will be
available for the next file you may want to create, leading to greater consistency in your files.
Using Styles
The use of Text Styles allows you to create a consistent appearance in your worksheets.
Styles in each template are available by choosing Style from the Format menu. Any specific
style with a defined font, size, etc. can be applied to a text region. To create or modify a style,
again choose Style from the Format menu . To save your styles for use in new files, you
must make a template file. Math Styles can be used to assign specific fonts, font sizes etc. to
mathematical expressions. There are predefined ones but additional styles can be defined and
applied. This can be accomplished by going to the Format menu and choosing Equation.
1.16 DEFINING VARIABLES
There are times when the value of a number may need to be changed several times in a
document . Such a number is termed a variable . Let Apples be, then, a variable . Type
Apples:50
to see on the screen
Apples 50
:=
By doing the above, we have given the value of 50 to the variable Apples . Similarly, another
variable Unitprice can be defined
18 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

29. Unitprice 0.35
:=
A third variable can also be defined as
Totprice Apples Unitprice
⋅
:=
Type
Totprice=
to see on the screen
Totprice 17.5
=
Now, if new values need to be given to Apples and to Unitprice, change the numbers
above as necessary and the result which is Totprice will also change accordingly as
shown below.
Apples 75
:= Unitprice 0.40
:= Totprice Apples Unitprice
⋅
:=
Totprice 30
=
1.17 DEFINING FUNCTIONS IN MATHCAD
The value of a function depends on the values assigned to its arguments. For example, to
define a function f(x), type
f(x):x^7
to see on the screen
f x
( ) x
7
:=
Putting in a numerical value of 6 as the argument of f(x) will give
Chapter 1: Basics of Mathcad 19

30. f 6
( ) 2.799 10
5
×
=
This can also be accomplished by doing
x 6
:= f x
( ) 2.799 10
5
×
=
If a range of values for the argument is given
x 1 6
..
:=
f(x) will yield a table of numbers as shown below
x
1
2
3
4
5
6
= f x
( )
1
128
3
2.187·10
4
1.638·10
4
7.813·10
5
2.799·10
=
In addition to defining a customized function, Mathcad's library of built-in functions can
also be utilized. To do this, select Function from the Insert menu, or click on the
function button on the toolbar
The Insert Function dialog box, shown below, will allow insertion of a function name
directly into the placeholder
Built-in functions can also be inserted directly from the keyboard. Some examples are given
below.
Trigonometry and Logarithms
ln 56
( ) 4.025
= cos 50 deg
⋅
( ) 0.455 2
⋅
= asinh 0.95
( ) 0.846
=
20 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

31. Matrix Functions
identity 6
( )
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= cols identity 6
( )
( ) 6
=
1.18 BUILDING AND EDITING MATHEMATICAL EXPRESSIONS
Building Mathematical Expressions
In Mathcad, various parts of an expression are assembled by observing the rules of precedence
and some additional procedures that enable entering denominators, exponents and expressions
inside of radicals. The following examples will illustrate the process.
Example 1
To create
Chapter 1: Basics of Mathcad 21

32. f x
( ) x 6
+
( ) x
3
5
−
( )
⋅
:=
Type
f(x):x+6[Spacebar]*(x^3[Spacebar]-5)
Example 2
To create
f x
( ) x 765 x
6 4
−
( )
⋅
+
:=
Type
f(x):x+765*(x^6-4)
The exponent operator is called a sticky operator because unless you get out by pressing
[Spacebar] , your keystrokes will "stick" to the exponent . This stickiness applies to
exponents, square roots, subscripts, and division.
Example 3
To create the expression
x
7
675
+
780
Type
x^7[Spacebar] <-- Puts x 7 in blue editing lines
+675[Spacebar] <-- Puts the whole equation in the editing lines
/780[Enter] <-- Expression is complete
Example 4
To create
22 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

33. x
7 675
780
+
do the same as above but without pressing the spacebar after +675
Example 5
To create
x
17
t
7
450
type
x^17/t^7[Spacebar][Spacebar][Spacebar]/450
Editing Expressions
The equation editor functions very much like a text editor and goes from left to right. Most
problems dealing with editing equations stem from working with operators. Although Mathcad
automatically inserts parentheses wherever necessary, the Mathcad user must put in
parentheses himself in accordance with his own judgement to give clarity to expressions .
When expressions become complicated, it is definitely preferable to work with smaller and
more manageable subexpressions within them. The reader is referred to Chapter 4 of the
Mathcad 14 User's Guide for a detailed discussion on Editing Expressions. This can be
accessed by choosing Tutorials from the Help menu.
1.19 DEFINING RANGE VARIABLES
To assign a range of values to a variable x going from 0 to 30, say, with an increment
of 3, type
x:0,3;30
The result on the screen will be
x 0 3
, 30
..
:=
To evaluate a function f(x) for x= 0 to 7 with an increment of 1, type
x:0;7 f(x):x^5[Spacebar]-6*x^3[Spacebar]+9
Chapter 1: Basics of Mathcad 23

34. to see on the screen
x 0 7
..
:= f x
( ) x
5
6 x
3
⋅
− 9
+
:=
Now, typing x= and f(x)= will give the following output table on the screen
x
0
1
2
3
4
5
6
7
= f x
( )
9
4
-7
90
649
3
2.384·10
3
6.489·10
4
1.476·10
=
If the range is to have increments other than 1, which is the default value, the next value in the
range must be entered. The following will provide a range of x values going from 2 to 4 with
increments of 0.5 and the corresponding f(x) values.
x 2 2.5
, 4
..
:=
x
2
2.5
3
3.5
4
= f x
( )
-7
12.906
90
276.969
649
=
1.20 DEFINING VECTORS AND MATRICES
To create a vector or a matrix in Mathcad, the dimensions of the array must be chosen and the
placeholders must be filled in.
24 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

35. Figure 1.6 Inserting matrices in Mathcad
Chapter 1: Basics of Mathcad 25

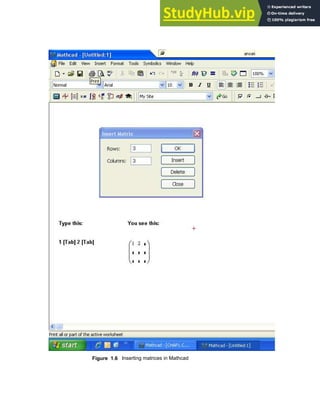
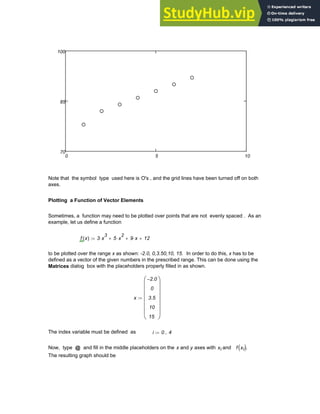
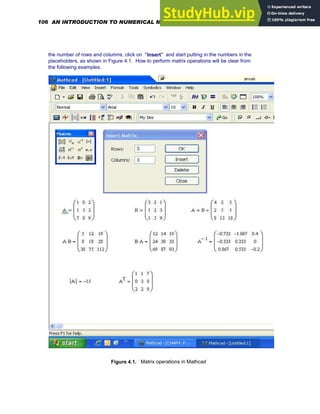
36. To create a vector V , click in a blank space, Choose Matrix from the Insert menu (See
Figure 1.6 ) or click on the button inside the Vector and Matrix Palette . Then, fill in the
appropriate number of rows and columns, click on Insert and finally fill in the placeholders with
given values. To move from placeholder to placeholder inside the vector, use [Tab] or click on
the appropriate placeholder to select it
V
7
8
9
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
To access a particular element of a vector, use the subscript operator , which can be
created by typing a left square bracket ( [ ), or by using the Xn button in the Matrix
Palette .
In Mathcad , by default the first element has the index 0. Type
V[0=
to see on the screen
V0 7
=
The next two elements will have indices 1 and 2 Thus typing V[1= and V[2= will
produce on the screen
V1 8
= V2 9
=
In order to obtain all the elements of the vector at the same time, the index can be defined
as a range variable as shown below::
i 0 2
..
:= giving Vi
7
8
9
=
<--- Type V[i=
The elements of a vector can also be used as the arguments of a function as shown below.
Define a function f(x) as.
f x
( ) sin 2 x
⋅
( ) cos 3 x
⋅
( )
+
:=
Let a vector V be a three-element vector as given below
26 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

37. v
1.3
2.6
−
7.9
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Then, typing i:0;2 and then f(v[i)= will show the following on the screen
i 0 2
..
:= f vi
( )
-0.21
0.937
0.046
=
The Vector and Matrix Palette contains most of the common matrix and vector operators.
These are listed below.
Operation Keystroke
Palette
Button Display
Dot product [Shift]8 v w
⋅ Displays like scalar
multiplication.
Cross product [Ctrl]8 v w
×
Determinant | M
Column [Ctrl]6 M
2
〈 〉
Returns the 2nd
column of M.
There is also a wide range of built-in functions in Mathcad that return information about the
size of an array and its elements. For a given matrix [M], various pieces of information can
be generated as shown below.
M
9
4
12
10
5
13
11
7
14
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Chapter 1: Basics of Mathcad 27

38. Number of columns: cols M
( ) 3
= Number of rows: rows M
( ) 3
=
Largest value in matrix: max M
( ) 14
= Determinant of matrix: M 3
=
Eigenvalues of a matrix: eigenvals M
( )
28.768
0.176
−
0.592
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
1.21 CREATING GRAPHS
To create an x-y plot, choose Graph/ X-Y Plot from the Insert Menu as shown in Figure
1.7. Press [Enter] and fill in the placeholders on the x and y axes. Alternatively, type an
expression depending on one variable such as: sin(x) + cos (3x) and click on the X-Y Plot
button on the Graph toolbar . The resulting plot will be
x 10
− 9.9
−
, 10
..
:=
10
− 5
− 0 5 10
2
−
1
−
1
2
sin x
( ) cos 3 x
⋅
( )
+
x
28 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

39. Figure 1.7 Creating graphs in Mathcad
X-Y Plot Button
Chapter 1: Basics of Mathcad 29

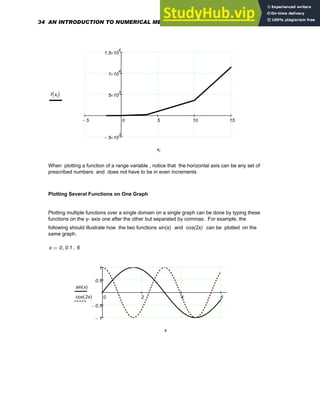
40. Using Range Variables to Plot a Function
The range of values being plotted on the x-axis must, in general, be specified. If this range is
not prescibed by you, Mathcad will choose a default range for the dependent variable. For
example, let us plot
f x
( ) x
3
8 x
2
⋅
+ 9 x
⋅
+ 14
+
:=
The graph of this function over the range x= 0 to x= 6 can be accomplished as follows.
x 0 1
, 6
..
:= f x
( ) x
3
8 x
2
⋅
+ 9 x
⋅
+ 14
+
:=
Now create the plot by clicking in the worksheet window. Type @ to create the x-y plot, type
x in the middle placeholder on the horizontal axis and type f(x) in the middle placeholder
on the vertical axis. Press [Enter] . The following graph should then appear on the screen.
0 2 4 6
0
200
400
600
f x
( )
x
The plot generated above does not seem to be very smooth. In order to obtain a smoother
trace, change the definition of x to x 0 0.1
, 6
..
:= . The smaller step enables Mathcad to
calculate more points. This will make the plot a lot smoother (see graph below ) because now
there are more points or dots being connected together.
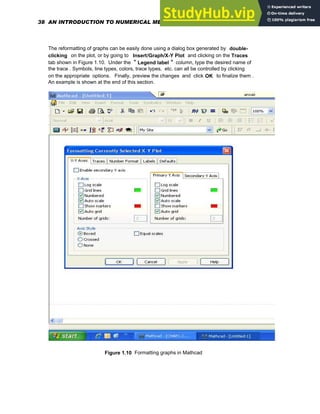
Formatting of an x-y plot can be accomplished as follows. Double-click on it or choose Graph
from the Format menu to open up a dialog box. This dialog box will allow several options in
terms of grid lines, legends, trace types, markers, colors, axis limits etc.
30 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

41. x 0 0.1
, 6
..
:=
0 2 4 6
200
400
600
f x
( )
x
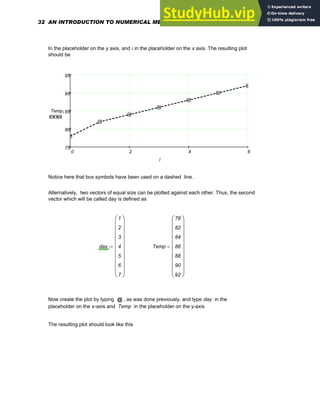
Plotting a Vector of Data Points
Let us say that we need to plot a vector of data points called Temp , which is the rising
outside temperature on different days of a week in a summer month. This vector which will
have 7 rows and 1 column can be created using the Matrix command on the Insert menu.
Temp
78
82
84
86
88
90
92
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
This data can be graphed by making the horizontal axis an index variable or a vector with
the same number of elements as the vector Temp . Define the index i as:
i 0 6
..
:=
Create your plot by typing [@] and typing in
Temp[i
Chapter 1: Basics of Mathcad 31

42. In the placeholder on the y axis, and i in the placeholder on the x axis. The resulting plot
should be
0 2 4 6
75
80
85
90
95
Tempi
i
Notice here that box symbols have been used on a dashed line.
Alternatively, two vectors of equal size can be plotted against each other. Thus, the second
vector which will be called day is defined as
day
1
2
3
4
5
6
7
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Temp
78
82
84
86
88
90
92
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Now create the plot by typing @ , as was done previously, and type day in the
placeholder on the x-axis and Temp in the placeholder on the y-axis
The resulting plot should look like this
32 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

43. 0 5 10
70
85
100
Note that the symbol type used here is O's , and the grid lines have been turned off on both
axes.
Plotting a Function of Vector Elements
Sometimes, a function may need to be plotted over points that are not evenly spaced . As an
example, let us define a function
f x
( ) 3 x
3
⋅ 5 x
2
⋅
+ 9 x
⋅
+ 12
+
:=
to be plotted over the range x as shown: -2.0, 0,3.50,10, 15. In order to do this, x has to be
defined as a vector of the given numbers in the prescribed range. This can be done using the
Matrices dialog box with the placeholders properly filled in as shown.
x
2.0
−
0
3.5
10
15
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
The index variable must be defined as i 0 4
..
:=
Now, type @ and fill in the middle placeholders on the x and y axes with xi and f xi
( ).
The resulting graph should be
Chapter 1: Basics of Mathcad 33

44. 5
− 0 5 10 15
5
− 10
3
×
5 10
3
×
1 10
4
×
1.5 10
4
×
f xi
( )
xi
When plotting a function of a range variable , notice that the horizontal axis can be any set of
prescribed numbers and does not have to be in even increments
Plotting Several Functions on One Graph
Plotting multiple functions over a single domain on a single graph can be done by typing these
functions on the y- axis one after the other but separated by commas. For example, the
following should illustrate how the two functions sin(x) and cos(2x) can be plotted on the
same graph.
x 0 0.1
, 6
..
:=
0 2 4 6
1
−
0.5
−
0.5
1
sin x
( )
cos 2x
( )
x
34 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

45. 1.22 FORMATTING MATH, TEXT AND RESULTS
Using the Format Bar in the Mathcad window, the appearance of the text as well as the
math can be altered quite easily, and different fonts, sizes and styles can be readily selected.
If the Format Bar is hidden, ensure that the Formatting bar on the View/Toolbars menu
is checked.
Formatting Text
Using the drop-down lists in the Format Bar, different fonts as well as point sizes can be
selected . Appropriate buttons must be clicked to generate special effects like boldface,
italics, etc. Several options become available upon choosing Text from the Format menu .
(See Figure 1.8).
Text Styles and Templates
Text styles provide consistency in the appearance of worksheets and enable the application of
text formatting to the text regions. Available text styles depend on the template used to create
a worksheet. To examine the different templates and text styles provided in Mathcad, choose
New from the File menu and modify them or create new ones.
Formatting Math
In Mathcad different font tags can be applied to variables and to constants. To make
changes in the font, click on a variable or constant in a math region and use the Format Bar.
Alternatively, you can choose Equation from the Format menu.
Highlighting of equations can also be done in Mathcad. To do this, click on an equation and
choose Properties/Highlight Region from the Format menu in the main worksheet
window. Below is shown an example of a highlighted equation.
S
1
n
i
ai xi
⋅
( )
∑
=
=
In Mathcad, you can specify how answers can be displayed in terms of the desired decimal
places, precision etc. Also, fonts and their sizes can be controlled and highlighting of
equations can be done as desired.
Chapter 1: Basics of Mathcad 35

46. Figure 1.8 Formatting text in Mathcad
Formatting Results and Graphs
To control the format of a result, double-click on the result , or click on the result and
choose Result from the Format menu . In the Number Format dialog box that shows
up, change the Exponential Threshold , and Number of decimal places as necessary
and click on OK . This will set the format only for this particular result. (See Figure 1.9 ).
However, if this needs to be done for the entire worksheet, click on a blank part of the
worksheet, and do the above .
36 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

47. Figure 1.9 Formatting results in Mathcad
Chapter 1: Basics of Mathcad 37

48. The reformatting of graphs can be easily done using a dialog box generated by double-
clicking on the plot, or by going to Insert/Graph/X-Y Plot and clicking on the Traces
tab shown in Figure 1.10. Under the " Legend label " column, type the desired name of
the trace . Symbols, line types, colors, trace types, etc. can all be controlled by clicking
on the appropriate options. Finally, preview the changes and click OK to finalize them .
An example is shown at the end of this section.
Figure 1.10 Formatting graphs in Mathcad
38 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

49. f x
( ) sin x
( )
:= g x
( ) cos 3 x
⋅
( )
:= h x
( ) f x
( ) g x
( )
+
:= x 10
− 9.9
−
, 10
..
:=
10
− 5
− 0 5 10
2
−
1
−
0
1
2
sin(x)
cos(3x)
sin(x)+cos(3x)
Graphing Functions and labelling Plots
x- values
y-values
f x
( )
g x
( )
h x
( )
x
1.23 USING UNITS
Although units are not required to be put into Mathcad equations, a great feature within
Mathcad is its ability to track standard units during calculations and to automatically perform
conversions. The program will also flag incorrect and inconsistent dimensional calculations,
and mixing and matching of units can be done as desired.The default system in Mathcad is
the SI unit system
To define a variable in terms of the built-in unit kilometers , for example, just multiply the
given number by km. Type
R:4*km
to see on the screen
R 4 km
⋅
:=
Chapter 1: Basics of Mathcad 39

50. Figure 1.11 Inserting units in Mathcad
40 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

51. The equation for a circular area of radius R now will automatically generate the result in terms
of the appropriate units
A π R
2
⋅
:= A 5.027 10
7
× m
2
=
Note that the above result is automatically shown in terms of the base units of the default
unit system, which, in this case, is SI. To change this result to feet , for example, click in
the name of the unit that you want to replace, then drag-select it and type in the new desired
unit in its place. Finally click outside the equation to see the new result. Alternatively, click
in the placeholder next to the unit name , go to Insert/Unit (See Figure 1.11) , click on the
appropriate Dimension name, then double-click on the unit name desired , and finally click
outside the equation to see the desired result.
R 1.312 10
4
× ft
⋅
=
To see a list of buit-in units in Mathcad, go to the Insert menu . The following equivalents can
be easily generated using the procedures described above.
Work 14000. J
⋅
:= Work 1.4 10
4
× m
2
kg s
2
−
⋅
⋅
= Work 13.269 BTU
⋅
=
Power 2000 kW
⋅
:= Power 2.682 10
3
× hp
⋅
=
Force 1500lbf
:= Force 6.672 10
3
× N
⋅
=
A calculation involving mixing of units is shown below. Although each term in the calculation is
expressed in a different unit of length, the result is calculated in the base SI unit for length,
namely, meters
6 ft
⋅ 30 in
⋅
+ 1.4 m
⋅
+ 0.8 yd
⋅
+ 4.722 m
=
The following calculation, obviously, cannot be completed and Mathcad indicates the same.
7 ft
⋅ 6 sec
⋅
+ =
6 sec
⋅
Click on the expression to see the error message,which is:
This value has units: Time, but must have units: Length
Chapter 1: Basics of Mathcad 41

52. To change the unit system of the worksheet from SI to U.S. units, select Worksheet
Options from the Tools menu. Then, click the Unit System tab, and select U.S. This
option gives you results in "English System" measures.
In the following calculation, a mass is multiplied by an acceleration to give force in proper
units. The result should be in Newtons or an equivalent force unit.
mass 5 kg
⋅
:= acc 20
m
sec
2
⋅
:=
Force mass acc
⋅
:= Force 100 m kg s
2
−
⋅
⋅
=
To display units, choose Result from the Format menu. Then, go to Unit Display and
check Format Units and Simplify units when possible, and results will display as shown
below.
g 9.807 s
2
−
⋅ m
⋅
:= 60 N
⋅ 20
⋅ m
⋅ 1.2 10
3
× J
=
8 kg
⋅ 6
⋅
m
sec
2
⋅ 48 N
=
42 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

53. C H A P T E R 2
INTRODUCTION TO NUMERICAL METHODS
2.1 THE USE OF NUMERICAL METHODS IN SCIENCE AND
ENGINEERING
Analysis of problems in engineering and the physical sciences typically involves four steps as
follows.
(1) Development of a suitable mathematical model that realistically represents a given physical
system.
(2) Derivation of the system governing equations using physical laws such as Newton's laws of
motion, conservation of energy, the laws governing electrical circuits etc.
(3) Solution of the governing equations, and
(4) Interpretation of the results.
Because real world problems are generally quite complex with the generation of closed-form
analytical solutions becoming impossible in many situations, there exists, most definitely, a
need for the proper utilization of computer-based techniques in the solution of practical
problems. The advancement of computer technology has made the effective use of numerical
methods and computer-based techniques very feasible, and thus, solutions can now be
obtained much faster than ever before and with much better than acceptable accuracy.
However, there are advantages as well as disadvantages associated with any numerical
procedure that is resorted to , and these must be kept in mind when using it.
2.2 COMPARISON OF NUMERICAL METHODS WITH ANALYTICAL
METHODS
While an analytical solution will be exact if it exists, a numerical method , on the other hand,
will generally require iterations to generate a solution, which is only an approximation and
which certainly cannot be considered exact by any means.
A disadvantage associated with analytical solution techniques is that they are generally
applicable only to very special cases of problems. Numerical solutions, on the contrary, will
solve complex situations as well.
While numerical techniques have several advantages including easy programming on a
computer and the convenience with which they handle complex problems, the initial
estimate of the solution along with the many number of iterations that are sometimes required
to generate a solution can be looked upon as disadvantages.
Chapter 2: Introduction to Numerical Methods 43

54. 2.3 SOURCES OF NUMERICAL ERRORS AND THEIR COMPUTATION
It is indeed possible for miscalculations to creep into a numerical solution because of various
sources of error. These include inaccurate mathematical modeling, wrong programming, wrong
input, rounding off of numbers and truncation of an infinite series. Round-off error is the general
name given to inaccuracies that affect the calculation scene when a finite number of digits are
assigned to represent an actual number. In a long sequence of calculations, this round-off error
can accumulate, then propagate through the process of calculation and finally grow very rapidly
to a significant number. A truncation error results when an infinite series is approximated by a
finite number of terms, and, typically, upper bounds are placed on the size of this error.
The true error is defined as the difference between the computed value and the true value of a
number.
ETrue XComp XTrue
−
=
(2.1)
while the relative true error is the error relative to the true value
(2.2)
er
XComp XTrue
−
XTrue
=
Expressed as a percentage, the relative true error is written as
er
XComp XTrue
−
XTrue
100
⋅
= (%) (2.3)
2.4 TAYLOR SERIES EXPANSION
The Taylor series is considered as a basis of approximation in numerical analysis. If the
value of a function of x is provided at " x 0", then the Taylor series provides a means of
evaluating the function at " x 0 + h", where " x 0" is the starting value of the independent
variable and " h " is the difference between the starting value and the new value at which
the function is to be approximated
f x0 h
+
( ) f x0
( ) h
x
f x0
( )
⎡
⎣ ⎤
⎦
d
d
⎡
⎢
⎣
⎤
⎥
⎦
⋅
+
h
2
2! 2
x
f x0
( )
d
d
2
⋅
+
h
3
3! 3
x
f x0
( )
d
d
3
⋅
+ .....................
+
= (2.4)
This equation can be used for generating various orders of approximations as shown
below. The order of approximation is defined by the highest derivative included in the
series. For example, If only terms up to the second derivative are retained in the series,
the result is a second order approximation.
44 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

55. First order approximation:
f x0 h
+
( ) f x0
( ) h
x
f x0
( )
d
d
⋅
+
=
(2.5)
Second order approximation:
f x0 h
+
( ) f x0
( ) h
x
f x0
( )
d
d
⋅
2
x
f x0
( )
d
d
2
⋅
+
= (2.6)
Third order approximation:
f x0 h
+
( ) f x0
( ) h
x
f x0
( )
d
d
⋅
+
h
2
2! 2
x
f x0
( )
d
d
2
⋅
+
h
3
3! 3
x
f x0
( )
d
d
3
⋅
+ ...........................
+
= (2.7)
It is to noted that the significance of the higher order terms in the Taylor series increases with
the nonlinearity of the function involved as well as the difference between the " starting x" value
and the "x" value at which the function is to be approximated. Thus , the fewer the terms that
are included in the series, the larger will be the error associated with the computation of the
function value. If the function is linear , however, only terms up to the first derivative term need
to be included.
Example 2.1
Using the Taylor series expansion for
f(x) = - 0.15 x4 - 0.17 x 3 - 0.25 x 2 -0.25 x + 1.25
determine the zeroth, first, second, third, fourth and fifth order approximations of
f(x0 + h ) where x0 = 0 and h = 1,2, 3, 4,5 and compare these with the exact solutions.
h=1.0: Put in the function and generate its derivatives:
f x
( ) 0.15
− x
4
⋅ 0.17 x
3
⋅
− 0.25 x
2
⋅
− 0.25x
− 1.25
+
:= x0 0
:= h 1.
:=
fprime x
( ) 0.60
− x
3
⋅ 0.51 x
2
⋅
− 0.50 x
⋅
− 0.25
−
:= <--Generate
derivatives
f2prime x
( ) 1.8
− x
2
⋅ 1.02 x
⋅
− 0.50
−
:=
f3prime x
( ) 3.6
− x
⋅ 1.02
−
:= f4prime x
( ) 3.6
−
:= f5prime x
( ) 0.
:=
Chapter 2: Introduction to Numerical Methods 45

56. term1 f x0
( )
:= term2 h fprime x0
( )
⋅
:= term3
h
2
2
f2prime x0
( )
⋅
:=
term4
h
3
6
f3prime x0
( )
⋅
:= term5
h
4
24
f4prime x0
( )
⋅
:= term6
h
5
120
f5prime x0
( )
⋅
:=
ftaylor0 term1
:= <---- one-term or zero-order approximation
ftaylor1 term1 term2
+
:= <---- first order approximation with two terms
ftaylor2 term1 term2
+ term3
+
:= <---second order approximation with 3 terms
ftaylor3 term1 term2
+ term3
+ term4
+
:= <---third order approximation with 4 terms
ftaylor4 term1 term2
+ term3
+ term4
+ term5
+
:= <---fourth order approximation with 5 terms
fifth order approximation
with 6 terms
ftaylor5 term1 term2
+ term3
+ term4
+ term5
+ term6
+
:= <-----
x x0 h
+
:= x 1
=
These are the zero- fifth order
approximations of the given
function f(x) using the Taylor
series.
ftaylor0 1.25
= ftaylor1 1
= ftaylor2 0.75
=
<--
ftaylor3 0.58
= ftaylor4 0.43
= ftaylor5 0.43
=
f 1
( ) 0.43
= <---EXACT ANSWER USING FUNCTION GIVEN.
err0 f x
( ) ftaylor0
−
:= err0 0.82
−
=
err1 f x
( ) ftaylor1
−
:= err1 0.57
−
=
err2 f x
( ) ftaylor2
−
:= err2 0.32
−
= These are errors ( differences between exact
values and approximations ) for the above
zero - fifth order approximations.
<--
err3 f x
( ) ftaylor3
−
:= err3 0.15
−
=
err4 f x
( ) ftaylor4
−
:= err4 0
=
err5 f x
( ) ftaylor5
−
:= err5 0
=
Similarly, by using h= 2, 3, 4, 5 , the zeroth- fifth order approximations for f(2), f(3), f(4),
f(5) and the associated errors can be determined. These are given in Tables 2.1 and 2.2
Plots of the various Taylor series approximations of the given function and associated errors
are generated below and are presented in Figs. 2.1 and 2.2
46 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

57. x0 0
:= x 0 0.01
, 5
..
:=
ftaylor0 x
( ) f x0
( )
:= <-- zeroth-order approximation
ftaylor1 x
( ) ftaylor0 x
( ) x x0
−
( ) fprime x0
( )
⋅
+
:= <---first-order approximation
ftaylor2 x
( ) ftaylor1 x
( )
x x0
−
( )
2
2
f2prime x0
( )
⋅
+
:= <--second-order approximation
ftaylor3 x
( ) ftaylor2 x
( )
x x0
−
( )
3
6
f3prime x0
( )
⋅
+
:= <---third-order approximation
ftaylor4 x
( ) ftaylor3 x
( )
x x0
−
( )
4
24
f4prime x0
( )
⋅
+
:= <---fourth-order approximation
ftaylor5 x
( ) ftaylor4 x
( )
x x0
−
( )
5
120
f5prime x0
( )
⋅
+
:= <---fifth- order approximation
Errors generated with the various approximations are as follows
Zero order approximation: err0 x
( ) f x
( ) ftaylor0 x
( )
−
:=
First order approximation: err1 x
( ) f x
( ) ftaylor1 x
( )
−
:=
Second order approximation: err2 x
( ) f x
( ) ftaylor2 x
( )
−
:=
Third order approximation: err3 x
( ) f x
( ) ftaylor3 x
( )
−
:=
Fourth order approximation: err4 x
( ) f x
( ) ftaylor4 x
( )
−
:=
Fifth order approximation: err5 x
( ) f x
( ) ftaylor5 x
( )
−
:=
The various approximations generated by the above calculations and the associated errors
are compared in the Table 2.1.
Chapter 2: Introduction to Numerical Methods 47

58. 0 1 2 3 4 5
150
100
50
0
50
Zeroth order approx
Third order approx
Fifth order approx/ given function
Zeroth order approx
Third order approx
Fifth order approx/ given function
Taylor series approx of given function
x- value
Function
approximated
by
Taylor
series
ftaylor0 x
( )
ftaylor3 x
( )
ftaylor5 x
( )
x
Figure 2.1. Taylor series approximation of given function
x 0 0.01
, 5
..
:=
0 1 2 3 4 5
150
100
50
0
50
Zero order approx
Third order approx
Fifth order approx
Zero order approx
Third order approx
Fifth order approx
Errors gen due to Taylor-series approx
x- value
errors
as
function
of
x
err0 x
( )
err3 x
( )
err5 x
( )
x
Figure 2.2. Errors associated with the various Taylor series approximations
48 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

59. The various approximations generated by the above calculations and the associated errors are
compared in the following tables.
Table 2.1
h 1 5
..
:=
Various orders of approximation generated by Taylor series
approach versus true values of given function
x 0 1
, 5
..
:=
zeroth
order
first
order
second
order
third
order
fourth
order
fifth
order
True
Value
x
0
1
2
3
4
5
= ftaylor0 x
( )
1.25
1.25
1.25
1.25
1.25
1.25
=
ftaylor1 x
( )
1.25
1
0.75
0.5
0.25
0
=ftaylor2 x
( )
1.25
0.75
-0.25
-1.75
-3.75
-6.25
=
ftaylor3 x
( )
1.25
0.58
-1.61
-6.34
-14.63
-27.5
=ftaylor4 x
( )
1.25
0.43
-4.01
-18.49
-53.03
-121.25
=ftaylor5 x
( )
1.25
0.43
-4.01
-18.49
-53.03
-121.25
=f x
( )
1.25
0.43
-4.01
-18.49
-53.03
-121.25
=
h
1
2
3
4
5
=
Table 2.2
Errors associated with the different orders of approximation
zeroth
order
first
order
second
order
third
order
fourth
order
fifth
order
x
0
1
2
3
4
5
= err0 x
( )
0
-0.82
-5.26
-19.74
-54.28
-122.5
= err1 x
( )
0
-0.57
-4.76
-18.99
-53.28
-121.25
= err2 x
( )
0
-0.32
-3.76
-16.74
-49.28
-115
= err3 x
( )
0
-0.15
-2.4
-12.15
-38.4
-93.75
= err4 x
( )
0
0
0
0
0
0
= err5 x
( )
0
0
0
0
0
0
=
h
1
2
3
4
5
=
PROBLEMS
2.1. Using the Taylor series expansion for cos x, which is given as
f(x) = cos x = 1- x 2 / 2 + x 4 / 24 ,
determine the one-term, two-term and three-term approximations of f(x0 + h ) , where x0 = 0
Chapter 2: Introduction to Numerical Methods 49

60. rad and h = 0. 1, 0.2 ....1.0 rad , and compare these with the exact solution. Using Mathcad,
generate plots of the various Taylor series approximations and associated errors as functions of
the independent variable x.
2.2 Develop a Taylor series expansion of the following function:
f(x) = x 5 - 6 x 4 + 3x 2 + 9 .
Use x =3 as the base and h as the increment. Using Mathcad, evaluate the series for h= 0.1,
0.2....1.0, adding terms incrementally as in Problem 2.1. Compare the various Taylor series
approximations obtained with true values in a table. Generate plots of the approximations and
associated errors as functions of x .
2.3 Given the following function:
f(x) = x 3 - 3 x 2 + 5 x + 10 ,
determine f ( x0 + h ) with the help of a Taylor series expansion, where x 0 = 2 and h = 0.4.
Compare the true value of f ( 2.4 ) with estimates obtained by resorting to (a) one term only (b)
two terms (c) three terms and (d) four terms of the series.
2.4 Given the following function
f x
( ) 3 x
3
⋅ 6 x
2
⋅
− 15 x
⋅
+ 25
+
=
use a Taylor series expansion to determine the zeroth, first, second and third order
approximations of f(x0+h) where x 0 = 2 and h = 0.5. Compare these with the exact
solution.
2.5 By developing a Taylor series expansion for
f(x) = e x
about x = 0 , determine the fourth-order approximation of e 2.5 and compare it with the exact
solution.
2.6. By developing a Taylor series expansion for
f(x) = ln(2-x)
about x = 0, determine the fourth-order approximation of ln (0.5) and compare it with the exact
solution
50 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

61. 2.7. By developing a Taylor series expansion for
f(x) = x3 e - 5x
about x = 1, determine the third-order approximation of f(1.2) and compare it with the exact
solution.
2.8. By developing a Taylor series expansion for
f(x) = e cos x
about x =0 , determine the fourth- order approximation of f (2π) and compare it with the exact
solution. .
2.9. By developing a Taylor series expansion for
f(x) = (x - 2) 1/2
about x = 2, determine the third-order approximation of f (2.2), that is, (0.2) 1/2 , and compare it
with the exact solution.
2.10. Given the function
f(x) = x2 - 5 x 0.5 + 6 ,
use a Taylor series expansion to determine the first, second , third and fourth order
approximations of f (2.5 ) by resorting to x 0 = 2 and h = 0.5 . Compare these with the exact
solution.
2.11. Given the function
f(x) = 6 x3 - 9 x2 +25 x + 40 ,
use a Taylor series expansion to determine the zeroth, first, second and third order
approximations of f (x0 + h ) where x 0 = 3 and h = 1 . Compare these with the exact solution.
2.12. Given the function
f(x) = 4 x4 - 7 x3 + 5 x2 - 6 x + 90
use a Taylor series expansion to determine the zeroth, first, second , third and fourth order
Chapter 2: Introduction to Numerical Methods 51

62. approximations of f (x0 + h ) ) where x 0 = 3 and h = 0.5 . Compare these with the exact
solution. Calculate errors abnd generate calculations to three decimal places.
2.13. Given the function
f(x) = 8 x3 - 10 x2 + 25 x + 45 ,
use a Taylor series expansion to determine the zeroth, first, second and third order
approximations of f (x0 + h ) where x 0 = 2 and h = 1 . Compare these with the exact solution.
2.14. Given the function
f(x) = 1 + x + x2 / 2! + x3 / 3! +x4 / 4!
use a Taylor series expansion to determine the zeroth, first, second , third and fourth order
approximations of f (x0 + h ) where x 0 = 0 and h = 0.5 . Compare these with the exact
solution. Generate answers correct to four decimal places.
2.15. Given the function
f(x) = x + x3 / 3 + 2 x5 / 15
use a Taylor series expansion to determine the zeroth, first, second , third and fourth order
approximations of f (x0 + h ) where x 0 = 0 and h = 0.8 . Compare these with the exact solution
by computing percentage errors. Generate answers correct to four decimal places.
2.16. Given the function
f(x) = sin (x)
use a Taylor series expansion to determine the fifth order approximation of f (x0 + h ) where x 0
= 0 and h = 0.2 radians . Compare your answer with the true value. Generate answers correct
to four decimal places.
2.17. Given the function
f(x) = 3 x2 - 6 x 0.5 + 9 ,
use a Taylor series expansion to determine the zeroth, first, second , third and fourth order
approximations of f (x0 + h ) whereo x 0 = 3 and h = 1 . Compare these with the exact
solution by computing percentage errors. Generate answers correct to four decimal places.
52 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

63. C H A P T E R 3
ROOTS OF EQUATIONS
3.1 INTRODUCTION
In many problems occurring in science and engineering, it is often necessary to find roots
or zeros of equations that are nonlinear. Nonlinear equations have no closed-form solutions
except in some very special cases, and thus, computer methods are indispensable in their
solution. Some examples of equations whose roots may need to be found are:
1 4 x
⋅
+ 16 x
2
⋅
− 3 x
3
⋅
+ 3 x
4
⋅
+ 0
= <-- a polynomial, a characteristic equation,
for instance
f x
( ) α
− 0
= <-- α is a number and f(x) is a function of x
tan α
( ) tanh 2 x
⋅
( )
= <-- a transcendental equation
3.2 METHODS AVAILABLE
There are several methods available for finding roots of equations. Some of these are:
(1) Direct Search, which is not a very efficient technique, (2) Bisection (3) False Position
(4) Newton-Raphson (5) Secant Method (6) Bairstow's Method, which is applicable only
to polynomials and (6) Successive Iteration or Fixed Point Iteration method . In this
chapter, however, only the Bisection, False Position, Newton-Raphson, Secant and
Successive Iteration methods will be addressed along with the functions used in Mathcad
to find roots.
3.3 BISECTION METHOD
This method can be resorted to when there is only one root occurring in a given range
of x. The method involves investigating a given range to seek a root and then bisecting
the region successively until a root is found. Other names for this technique are Interval
halving, Binary Chopping and Bolzano's Method.
Procedure for Finding Roots
1. Choose starting and end points xstart and xend
2. Compute: f(xstart) and f(xend)
3. Compute: f(xstart) times f(xend)
Chapter 3: Roots of Equations 53

64. 4. If the above product is negative, then the root lies between xstart and xend. If this
product is positive, reselect xstart and xend.
5. If f(xtart)* f(xend) < 0, compute the mid-point of the xstart-xend
range. Call it "xmid1" and repeat above steps, i.e., compute
f xstart
( ) f xmid1
( )
⋅ and f xmid1
( ) f xend
( )
⋅
6. If f(xstart)*f(xmid1) < 0, the root lies between xstart and xmid1.
If (xmid1)*f(xend) < 0, then the root lies between xmid1 and xend.
7. Repeat the above procedure until convergence at a root value occurs.
Figure 3.1. Bisection Method
Computation of Error and Convergence Criterion
A convergence criterion has to be followed in order to determine if a root has indeed been
found. This is expressed in terms of the error ε or the percentage relative error
ε rel which are defined as
54 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

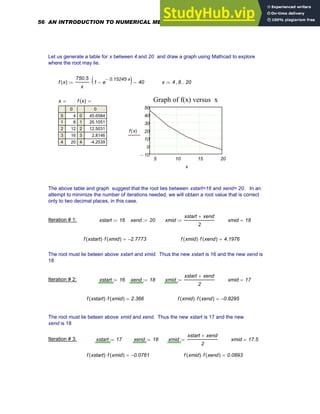
65. ε xmidi 1
+ xmidi
−
= (3.1)
(3.2)
εrel
xmidi 1
+ xmidi
−
xmidi 1
+
100
⋅
= percent
where xmid i+1 and xmid i are the midpoints in the current and previous iterations. While,
in general, the relative error should not be greater than 5 %, an error of 0.01 % is the
largest that is tolerable for some classes of problems, that require immense precision.
The true error , ε True , is an indicator of the real accuracy of a solution and can be
evaluated only if the true solution, x True , is known. It is defined as
εTrue
xTrue xmidi
−
xTrue
100
⋅
= (3.3)
Calculation of the true error clearly requires knowledge of the true solution, which, in general,
will not be known to us. Therefore, the quantity ε rel may have to be mostly used to
determine the error associated with a solution process.
Advantages and Disadvantages of Bisection
While Bisection is a simple, robust technique for finding one root in a given interval, when
the root is known to exist and it works even for non-analytic functions, its convergence
process is generally slow, making it a somewhat inefficient procedure.
Sometimes, a singularity may be identified as if it were a root, since the method does not
distinguish between roots and singularities, at which the function would go to infinity.
Therefore, as the method proceeds, a check must be made to see if the absolute value of
[f(xend)-f(xstart)], in fact, converges to zero. If this quantity diverges, the method is chasing
a singularity rather than a root .
When there are multiple roots, Bisection is not a desirable technique to use, since the
function may not change signs at points on either side of the roots. Therefore, a graph of
the function must first be drawn before proceeding to do the calculations.
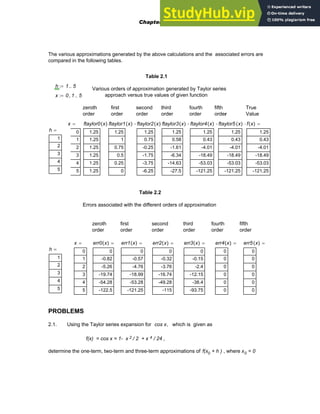
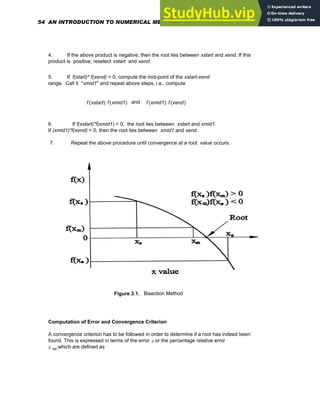
Example 3.1
Obtain a root of f(x) in the range of 4 < x < 20
f(x)= ( 750.5 / x ) [ 1 - exp( -0.15245x) ] - 40
Chapter 3: Roots of Equations 55

66. Let us generate a table for x between 4 and 20 and draw a graph using Mathcad to explore
where the root may lie.
f x
( )
750.5
x
1 e
0.15245
− x
⋅
−
( )
⋅ 40
−
:= x 4 8
, 20
..
:=
5 10 15 20
10
−
0
10
20
30
40
50
Graph of f(x) versus x
f x
( )
x
x
0
0
1
2
3
4
4
8
12
16
20
= f x
( )
0
0
1
2
3
4
45.6584
26.1051
12.5031
2.8146
-4.2539
=
The above table and graph suggest that the root lies between xstart=16 and xend= 20. In an
attempt to minimize the number of iterations needed, we will obtain a root value that is correct
only to two decimal places, in this case.
Iteration # 1: xstart 16
:= xend 20
:= xmid
xstart xend
+
2
:= xmid 18
=
f xstart
( ) f xmid
( )
⋅ 2.7773
−
= f xmid
( ) f xend
( )
⋅ 4.1976
=
The root must lie beteen above xstart and xmid. Thus the new xstart is 16 and the new xend is
18
Iteration # 2: xstart 16
:= xend 18
:= xmid
xstart xend
+
2
:= xmid 17
=
f xstart
( ) f xmid
( )
⋅ 2.366
= f xmid
( ) f xend
( )
⋅ 0.8295
−
=
The root must lie beteen above xmid and xend. Thus the new xstart is 17 and the new
xend is 18
Iteration # 3: xstart 17
:= xend 18
:= xmid
xstart xend
+
2
:= xmid 17.5
=
f xstart
( ) f xmid
( )
⋅ 0.0761
−
= f xmid
( ) f xend
( )
⋅ 0.0893
=
56 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

67. The root must lie beteen above xstart and xmid. Thus the new xstart is 17 and the new xend
is 17.5
Iteration # 4: xstart 17.
:= xend 17.5
:= xmid
xstart xend
+
2
:= xmid 17.25
=
f xstart
( ) f xmid
( )
⋅ 0.3115
= f xmid
( ) f xend
( )
⋅ 0.0335
−
=
The root must lie beteen above xmid and xend. Thus the new xstart is 17.25 and the new
xend is 17.5
Iteration # 5: xstart 17.25
:= xend 17.5
:= xmid
xstart xend
+
2
:= xmid 17.375
=
f xstart
( ) f xmid
( )
⋅ 0.0515
= f xmid
( ) f xend
( )
⋅ 0.0126
−
=
The root must lie beteen above xmid and xend. Thus the new xstart is 17.38 and the new xend is
17.5
Iteration # 6: xstart 17.38
:= xend 17.5
:= xmid
xstart xend
+
2
:= xmid 17.44
=
f xstart
( ) f xmid
( )
⋅ 2.5064 10
3
−
×
= f xmid
( ) f xend
( )
⋅ 1.7497
− 10
3
−
×
=
The root must lie beteen above xmid and xend. Thus the new xstart is 17.44 and the new
xend is 17.5
Iteration # 7: xstart 17.44
:= xend 17.5
:= xmid
xstart xend
+
2
:= xmid 17.47
=
f xstart
( ) f xmid
( )
⋅ 6.893
− 10
4
−
×
= f xmid
( ) f xend
( )
⋅ 3.2291 10
3
−
×
=
The root must lie beteen above xstart and xmid. Thus the new xstart is 17.44 and the new
xend is 17.47
Iteration # 8: xstart 17.44
:= xend 17.47
:= xmid
xstart xend
+
2
:= xmid 17.455
=
f xstart
( ) f xmid
( )
⋅ 1.5821
− 10
4
−
×
= f xmid
( ) f xend
( )
⋅ 2.9199 10
4
−
×
=
Chapter 3: Roots of Equations 57

68. The root must lie beteen above xstart and xmid. Thus the new xstart is 17.44 and the new
xend is 17.455
Iteration # 9: xstart 17.44
:= xend 17.455
:= xmid
xstart xend
+
2
:= xmid 17.447
=
f xstart
( ) f xmid
( )
⋅ 1.0756 10
4
−
×
= f xmid
( ) f xend
( )
⋅ 4.5564
− 10
5
−
×
=
a check to see if this is
small
f xstart
( ) 0.0193
= f xmid
( ) 5.5657 10
3
−
×
= <--
Since f(xmid) is a very small quantitity, it is reasonable to assume that the xmid obtained
in iteration # 9 is, in fact, the required root. The % error in this case is, then
error
17.447 17.455
−
17.447
100
⋅
:= error 0.0459
−
= (percent)
Thus, the solution which has been obtained after 9 iterations is : x = 17.447
3.4 THE REGULA FALSI OR THE FALSE POSITION METHOD
The False Position method is similar to the Bisection method in that the size of the interval
containing the root is reduced with every step of the iteration process until the root is found.
The main difference is that while the interval size in the Bisection method is reduced by
bisecting it in each step of the iteration , this reduction of interval size is achieved by a
linear interpolation fitting the two end points. While the Bisection method is reliable, it is
slower than the False Position method in achieving convergence.
The equation of a straight line connecting two points (xstart,ystart) and (xend, yend) is
y yend
yend ystart
−
xend xstart
−
x xend
−
( )
⋅
+
= (3.4)
58 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

69. f(xstart)
f(xend)
f(x)
x
xstart
xnew
Root
xend
(xstart, f(xstart))
(xend, f(xend))
Figure 3.2. Regula Falsi method
The procedure for finding roots then is as follows. ( See Figure 3.2 )
1. Choose the starting and ending points xstart and xend as in the Bisection
method.
2. Compute f(xstart) and f(xend). Make sure that f(xstart) times f(xend) is still
a negative product. If it is not, then there is no root between xstart and xend.
3. The new end point xnew is located by setting y = 0 in Equation 3.4 and solving for x.
xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
= (3.5)
4. If f(xstart)*f(xnew) < 0, the root lies between xstart and xnew. However, if f(xnew)*f(xend) <
0, the root lies between xnew and xend.
5. Repeat the above procedure until convergence takes place.
Chapter 3: Roots of Equations 59

70. A disadvantage of this method is that sometimes a root is approached from only one side and,
thus, one end of the interval does not change at all in successive iterations. This is called
stagnation of an end point. This is not desirable since it slows down the convergence process
especially when the initial interval is very large or when the function is highly nonlinear. Examples
3.2 and 3.3 show the occurrence of stagnation.
Example 3.2
Obtain the required root for the function of Example 3.1 by the False Position method
correct to four decimal places. The starting and ending points were 16 and 20 respectively.
f x
( )
750.5
x
1 e
0.15245
− x
⋅
−
( )
⋅ 40
−
:=
Iteration # 1: xstart 16
:= xend 20
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 2.8146
= yend 4.2539
−
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 17.5927
=
f xstart
( ) f xnew
( )
⋅ 0.73
−
= f xnew
( ) f xend
( )
⋅ 1.1033
=
The root must lie beteen above xstart and xnew. Thus the new xstart is 16 and the new
xend is 17.5927
Iteration # 2: xstart 16
:= xend 17.5927
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 2.8146
= yend 0.2593
−
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 17.4584
=
f xstart
( ) f xnew
( )
⋅ 0.0404
−
= f xnew
( ) f xend
( )
⋅ 3.7171 10
3
−
×
=
The root must lie between above xstart and xnew. Thus the new xstart is 16 and the new
xend is 17.4584
Iteration # 3: xstart 16
:= xend 17.4584
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 2.8146
= yend 0.0144
−
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 17.451
=
f xstart
( ) f xnew
( )
⋅ 2.2312
− 10
3
−
×
= f xnew
( ) f xend
( )
⋅ 1.143 10
5
−
×
=
The root must lie beteen above xstart and xnew. Thus the new xstart is 16 and the new xend
is 17.451
60 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

71. Iteration # 4: xstart 16
:= xend 17.451
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 2.8146
= yend 8.5304
− 10
4
−
×
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:=
xnew 17.4506
= f xstart
( ) f xnew
( )
⋅ 1.3196
− 10
4
−
×
= f xnew
( ) f xend
( )
⋅ 3.9995 10
8
−
×
=
The root must lie beteen above xstart and xnew. Thus the new xstart is 16 and the new xend
is 17.4506
Iteration # 5: xstart 16
:= xend 17.4506
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 2.8146
= yend 1.1956
− 10
4
−
×
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:=
xnew 17.4505
= f xstart
( ) f xnew
( )
⋅ 1.8496
− 10
5
−
×
= f xnew
( ) f xend
( )
⋅ 7.8568 10
10
−
×
=
The root must lie beteen above xstart and xnew. Thus the new xstart is 16 and the new xend
is 17.4505
Iteration # 6: xstart 16
:= xend 17.4505
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 2.8146
= yend 6.3811 10
5
−
×
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:=
xnew 17.4505
= f xstart
( ) f xnew
( )
⋅ 9.8712 10
6
−
×
= f xnew
( ) f xend
( )
⋅ 2.238 10
10
−
×
=
f xnew
( ) 3.5072 10
6
−
×
=
The above process indicates that in this case, the root is being approached only from the
side of the original starting point and therefore stagnation has occurred. Since the xnew
computed in the sixth iteration is the same as the one in the fifth, and f(xnew) is a very
small quantitity, it is reasonable to say that the xnew (=17.4505) computed above is, in
fact, the required root.
Example 3.3
Obtain a root of f(x) by the False Position method in the range of 0 < x < 10 correct to
three decimal places.
f x
( ) x
3
9 x
⋅
+ 200
−
:=
Iteration # 1: xstart 0
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
Chapter 3: Roots of Equations 61

72. ystart 200
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 1.8349
=
f xstart
( ) f xnew
( )
⋅ 3.5462 10
4
×
= f xnew
( ) f xend
( )
⋅ 1.578
− 10
5
×
=
The root must lie beteen above xnew and xend. Thus the new xstart is 1.835 and the new
xend is 10
Iteration # 2: xstart 1.835
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 177.3061
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 3.1914
=
f xstart
( ) f xnew
( )
⋅ 2.4605 10
4
×
= f xnew
( ) f xend
( )
⋅ 1.2351
− 10
5
×
=
The root must lie between above xnew and xend. Thus the new xstart is 3.191 and the new
xend is 10
Iteration # 3: xstart 3.191
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 138.7887
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 4.1096
=
f xstart
( ) f xnew
( )
⋅ 1.2992 10
4
×
= f xnew
( ) f xend
( )
⋅ 8.3312
− 10
4
×
=
The root must lie beteen above xnew and xend. Thus the new xstart is 4.11 and the new
xend is 10
Iteration # 4: xstart 4.11
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 93.5835
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 4.6704
=
f xstart
( ) f xnew
( )
⋅ 5.2493 10
3
×
= f xnew
( ) f xend
( )
⋅ 4.9922
− 10
4
×
=
The root must lie beteen above xnew and xstart. Thus the new xstart is 4.67 and the new
xend is 10
Iteration # 5: xstart 4.67
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
62 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

73. ystart 56.1224
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 4.9862
=
f xstart
( ) f xnew
( )
⋅ 1.7487 10
3
×
= f xnew
( ) f xend
( )
⋅ 2.7732
− 10
4
×
=
The root must lie beteen above xnew and xend. Thus the new xstart is 4.986 and the new
xend is 10
Iteration # 6: xstart 4.986
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 31.1731
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.1557
=
f xstart
( ) f xnew
( )
⋅ 516.0963
= f xnew
( ) f xend
( )
⋅ 1.4735
− 10
4
×
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.156 and the new
xend is 10
Iteration # 7: xstart 5.156
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 16.5272
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.2443
=
f xstart
( ) f xnew
( )
⋅ 141.6022
= f xnew
( ) f xend
( )
⋅ 7.6254
− 10
3
×
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.244 and the new
xend is 10
Iteration # 8: xstart 5.244
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 8.5964
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.2895
=
f xstart
( ) f xnew
( )
⋅ 37.8307
= f xnew
( ) f xend
( )
⋅ 3.9167
− 10
3
×
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.290 and the new
xend is 10
Iteration # 9: xstart 5.290
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
Chapter 3: Roots of Equations 63

74. ystart 4.3541
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.3129
=
f xstart
( ) f xnew
( )
⋅ 9.6414
= f xnew
( ) f xend
( )
⋅ 1.9707
− 10
3
×
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.313 and the new
xend is 10
Iteration # 10: xstart 5.313
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 2.2078
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.3246
=
f xstart
( ) f xnew
( )
⋅ 2.4707
= f xnew
( ) f xend
( )
⋅ 995.9944
−
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.325 and the new
xend is 10
Iteration # 11: xstart 5.325
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 1.0813
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.3307
=
f xstart
( ) f xnew
( )
⋅ 0.5916
= f xnew
( ) f xend
( )
⋅ 486.9595
−
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.331 and the new xend
is 10
Iteration # 12: xstart 5.331
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 0.5163
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.3337
=
f xstart
( ) f xnew
( )
⋅ 0.1348
= f xnew
( ) f xend
( )
⋅ 232.3231
−
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.334 and the new
xend is 10
Iteration # 13: xstart 5.334
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
64 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

75. ystart 0.2334
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.3352
=
f xstart
( ) f xnew
( )
⋅ 0.0275
= f xnew
( ) f xend
( )
⋅ 104.9753
−
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.335 and the new
xend is 10
Iteration # 14: xstart 5.335
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 0.139
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.3357
=
f xstart
( ) f xnew
( )
⋅ 9.7667 10
3
−
×
= f xnew
( ) f xend
( )
⋅ 62.5217
−
=
The root must lie beteen above xnew and xend. Thus the new xstart is 5.336 and the new
xend is 10
Iteration # 15: xstart 5.336
:= xend 10
:= ystart f xstart
( )
:= yend f xend
( )
:=
ystart 0.0446
−
= yend 890
= xnew xend
xend xstart
−
yend ystart
−
yend
⋅
−
:= xnew 5.3362
=
f xstart
( ) f xnew
( )
⋅ 1.0062 10
3
−
×
= f xnew
( ) f xend
( )
⋅ 20.0659
−
= f xnew
( ) 0.0225
−
=
The above process indicates that in this case, stagnation occurs as well, but the root is
being approached only from the side of the original ending point. Since the xnew computed
in the fifteenth iteration is about the same as the one in the fourteenth, it is reasonable to say
that the xnew ( = 5.336 ) computed above is, in fact, the required root.
3.5 NEWTON-RAPHSON METHOD
This is the most widely used iterative method for locating roots. In this method, an initial
approximation of the root must be assumed, and calculations are started with a "good
initial guess" . If this initial guess is not a good one, then divergence may occur.
By starting with an approximation of the root value , x i , and constructing a tangent to the
function curve at x i , an improved guess x i+1 can be determined as shown in Figure 3.3.
From Figure 3.3, the slope of the function f(x) at x i can be seen to be
Chapter 3: Roots of Equations 65

76. fprime xi
( )
f xi
( )
−
xi 1
+ xi
−
= (3.6)
which gives the new improved value of the guess as
xi 1
+ xi
f xi
( )
fprime xi
( )
−
= g xi
( )
= (3.7)
where fprime( x i ) is the slope of the function at x i
Figure 3.3. Newton-Raphson method
Procedure for Finding Roots
1. Make a good initial guess. Call it X Old.
2. Improve the guess using
XNew XOld
f XOld
( )
fprime XOld
( )
−
= g XOld
( )
= (3.8)
66 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

77. 3. Keep improving the guess using Equation (3.8).
4. Solution is done when a new improved value X New is almost equal to the
previous value X Old
Advantages and Disadvantages of the Method
While the Newton-Raphson method is faster than the Bisection method, is applicable to the
complex domain as well and can be extended to simultaneous nonlinear equations, it may
not converge in some situations. The solution may oscillate about a local maximum or
minimum, and if an initial estimate is chosen such that the derivative becomes zero at some
point in the iteration process, then a division by zero takes place and convergence will never
occur. Although convergence will occur quite rapidly if the initial estimate is sufficiently
close to the root, it is possible for it to be be slow when it is far from the root. Also, if the
roots are complex, they will never be generated with real initial guesses.
A worthwhile feature of the Newton-Raphson method is that the numerical process will
correct itself automatically for minor errors. Thus, any errors that are made in computing the
next guess will simply generate a different point for drawing the tangent line and will not have
any effect on the final answer.
Convergence Criterion for the Newton-Raphson Method
It can be mathematically shown that in order for the Newton-Raphson method to converge
to a real root, the absolute value of the derivative of the g(xi) of Equation (3.7) must
always be less than 1 , that is,
g xi
( ) 1
<
This condition must be satisfied if convergence is to be attained. However, in some cases, it
may not hold for the initial guess.
Example 3.4
Using the Newton- Raphson method, solve : f(x)= x3 - 4.2 x -8.5 =0 for a real root between 2
and 3.
Let us first draw a graph of the function in the given range
f x
( ) x
3
4.2 x
⋅
− 8.5
−
:= x 2 2.1
, 3
..
:=
Chapter 3: Roots of Equations 67

78. 2 2.2 2.4 2.6 2.8
10
−
5
−
0
5
10
f x
( )
x
The derivative of the given function is fprime x
( ) 3 x
2
⋅ 4.2
−
:= , and thus,
fdblprime x
( ) 6 x
⋅
:= , g x
( ) x
f x
( )
fprime x
( )
−
:= , gprime x
( ) 1
fprime x
( )
2
f x
( ) fdblprime x
( )
⋅
−
fprime x
( )
2
−
:=
where fdblprime(x) is the second derivative of f(x) and gprime(x) is the derivative of g(x). Start
with an initial estimate of 2.5
xold 2.5
:= xnew g xold
( )
:= xnew 2.732
= gprime xnew
( ) 0.0206
=
xold xnew
:= xnew g xold
( )
:= xnew 2.7091
= gprime xnew
( ) 2.1887 10
4
−
×
=
xold xnew
:= xnew g xold
( )
:= xnew 2.7088
= gprime xnew
( ) 2.3959 10
8
−
×
=
xold xnew
:= xnew g xold
( )
:= xnew 2.7088
= gprime xnew
( ) 0
=
Clearly, the root is the converged value 2.7088, and convergence has been established with the
absolute value of the slope of g(x) being less than 1 in all the iterations.
Example 3.5
Using the Newton- Raphson method, solve : f(x)= x3 +7x2+19x+13 = 0 for all roots, real as
well as complex.
Let us first draw a graph of the function
68 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

79. f x
( ) x
3
7 x
2
⋅
+ 19 x
⋅
+ 13
+
:=
which suggests that there is a real root between 0 and -2.5
x 5
− 4.999
−
, 0
..
:=
4
− 2
− 0
40
−
30
−
20
−
10
−
0
10
20
f x
( )
x
The derivative of the given function is fprime x
( ) 3 x
2
⋅ 14 x
⋅
+ 19
+
:= with
fdblprime x
( ) 6 x
⋅
:= , g x
( ) x
f x
( )
fprime x
( )
−
:= , gprime x
( ) 1
fprime x
( )
2
f x
( ) fdblprime x
( )
⋅
−
fprime x
( )
2
−
:=
where fdblprime(x) is the second derivative of f(x) and gprime(x) is the first derivative of g(x).
Let us start with an initial estimate of -2.5 in an attempt to find the real root.
xold 2.5
−
:= xnew g xold
( )
:= xnew 0.1818
−
= gprime xnew
( ) 0.0389
=
xold xnew
:= xnew g xold
( )
:= xnew 0.7721
−
= gprime xnew
( ) 0.095
=
xold xnew
:= xnew g xold
( )
:= xnew 0.9768
−
= gprime xnew
( ) 0.0164
=
xold xnew
:= xnew g xold
( )
:= xnew 0.9997
−
= gprime xnew
( ) 1.9933 10
4
−
×
=
Chapter 3: Roots of Equations 69

80. xold xnew
:= xnew g xold
( )
:= xnew 1
−
= gprime xnew
( ) 2.6521 10
8
−
×
=
xold xnew
:= xnew g xold
( )
:= xnew 1
−
= gprime xnew
( ) 0
=
From the above calculations, it is clear that the real root is the converged value of (-1).
Let us now determine the complex roots by starting with an initial estimate of (-4+i)
xold 4
− i
+
:= xnew g xold
( )
:= xnew 2.9024
− 1.122i
+
=
xold xnew
:= xnew g xold
( )
:= xnew 2.2579
− 2.5753i
+
=
xold xnew
:= xnew g xold
( )
:= xnew 2.636
− 1.9589i
+
=
xold xnew
:= xnew g xold
( )
:=
xnew 3.0346
− 1.9196i
+
=
xold xnew
:= xnew g xold
( )
:= xnew 2.9957
− 2.001i
+
=
xold xnew
:= xnew g xold
( )
:= xnew 3
− 2i
+
=
xold xnew
:= xnew g xold
( )
:= xnew 3
− 2i
+
= <-- Converged
Clearly, if we had started with an initial estimate of (-4-i ), we would have obtained the
complex conjugate of the above complex root, as demonstrated below. However, there is no
need to do this every time, since a complex root will always have a complex conjugate
associated with it.
xold 4
− i
−
:= xnew 3
− 2i
+
=
xnew g xold
( )
:=
xold xnew
:= xnew g xold
( )
:= xnew 2.2579
− 2.5753i
−
=
70 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

81. xold xnew
:= xnew g xold
( )
:= xnew 2.636
− 1.9589i
−
=
xold xnew
:= xnew g xold
( )
:= xnew 3.0346
− 1.9196i
−
=
xold xnew
:= xnew g xold
( )
:= xnew 2.9957
− 2.001i
−
=
xold xnew
:= xnew g xold
( )
:=
xnew 3
− 2i
−
=
xold xnew
:= xnew g xold
( )
:= xnew 3
− 2i
−
= <-- Converged
3.6 USE OF MATHCAD'S root AND polyroots FUNCTIONS
Use of root
The function root (f(z),z) returns the value of "z" at which the function f(z) goes to zero.
Here, both f(z) and z are to be scalar quantities. The procedure to be used will be clear
from the following example.
Let us find the root of the function in Example 3.4 which is
f x
( ) x
3
4.2 x
⋅
− 8.5
−
:=
A guess value for the root must be first defined :
x 2.5
:=
Type the following to define " a" as the root of the given function
a root f x
( ) x
,
( )
:=
Chapter 3: Roots of Equations 71

82. Type " a= " to see the root computed.
a 2.7088
=
Use of polyroots
The function polyroots is a function in Mathcad which will return all roots of a polynomial at
the same time, be they real or complex. It does not require a guess value. polyroots (v)
returns all roots of an nth degree polynomial whose coefficients are given in the vector "v"
with (n+1) components. By choosing "matrix" from the "insert" menu, type in a vector "v"
as shown , beginning with the constant term, making sure that you insert all coefficients
even if they are zero. Then, polyroots(v) returns all roots at once. The following steps will
find the root of the polynomial of Example 3.4.
f x
( ) x
3
4.2 x
⋅
− 8.5
−
:= <-- Given polynomial
This is a vector of the coefficients of the polynomial whose
roots are to be found. Include all coefficients, even zeros.
Begin with the constant term.
<--
v
8.5
−
4.2
−
0
1
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:=
polyroots v
( )
1.3544
− 1.1417i
−
1.3544
− 1.1417i
+
2.7088
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= <-- Returns all roots at the same time.
3.7 SECANT METHOD
The Secant method is very similar to the Newton-Raphson method. The one difference is
that while the derivative fprime(x) is evaluated analytically in the Newton-Raphson method, it
is determined numerically in the Secant method .
From Figure 3.4, it is clear that an approximation for the slope of the given function f(x)
at x i can be written as
fprime xi
( ) =
f xi 1
−
( ) f xi
( )
−
( )
−
xi xi 1
−
−
(3.9)
72 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

83. Figure 3.4. Secant method
By the Newton-Raphson method, a new improved guess of the root is generated using
Equation 3.7, which is
xi 1
+ xi
f xi
( )
fprime xi
( )
−
= (3.10)
Combining Equations 3.9 and 3.10 yields the equation used in the Secant method, which is
xi 1
+ xi
f xi
( ) xi 1
− xi
−
( )
⋅
f xi 1
−
( ) f xi
( )
−
−
= (3.11)
Note that the format of Equation 3.11 does utilize the derivative but computes it numerically
rather than analytically. However, two initial estimates x i-1 and xi of the solution will be
required to start the iteration process as can be seen from Equation 3.11.
Procedure for Finding Roots
1. Make initial estimates x 0 and x 1.
2. With i= 1, improve the guess x 2 using Equation 3.11, which is
Chapter 3: Roots of Equations 73

84. xi 1
+ xi
f xi
( ) xi 1
− xi
−
( )
⋅
f xi 1
−
( ) f xi
( )
−
−
=
3. Continue obtaining improved estimates x3, x4 ...... using the above equation.
4. Solution is done when a new improved value x i+1 is almost equal to the previous
value x i
Advantages and Disadvantages of the Secant Method
The Secant method has a definite advantage when the derivative of the given function is
difficult or time-consuming to evaluate analytically. Among the disadvantages are
convergence to an unintended root at times, and divergence from the root if the initial
guesses are bad. Also, if f(x) is far from linear near the root, the iterations may start to
yield points far away from the actual root.
Example 3.6
Obtain a real root of f(x)= 1.15 x3 + 1.2 x2 - 3.5 x - 3.12 between 0 and 10 by the Secant
Method.
We first draw a graph of the given function to see approximately where a real root lies in
the range given.
f x
( ) 1.15 x
3
⋅ 1.2 x
2
⋅
+ 3.5 x
⋅
− 3.12
−
:=
x 0 0.01
, 3
..
:=
0 1 2 3
10
−
0
10
20
30
Graph of functon for x= 0 to 3
f x
( )
x
From the plot, it appears like
the root lies between 1 and 3.
We will, therefore, choose x0
to be 1 and x1 to be 2
74 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

85. We will resort to Mathcad's vector notation ( subscript form ) in the use of the Secant Method
to determine the root of the given function f(x). To type a subscript, use the left bracket " [ "and
put an integer in the placeholder. Vector elements in Mathcad are ordinarily numbered
starting with the first element numbered as the zeroth element. A look at the Secant Method
suggests that this feature relates well with its recursive formula. Put in "N" as the expected
number of iterations. Then i goes from 1 to N . To find the required root, begin with the initial
estimates x0 and x1 and use the recursive formula of the Secant Method to obtain improved
estimates. Continue until convergence to a solution takes place.
N 6
:= i 1 N
..
:= x0 1
:= x1 2
:=
xi 1
+ xi
f xi
( ) xi 1
− xi
−
( )
⋅
f xi 1
−
( ) f xi
( )
−
−
:= x2 1.523926
= x3 1.662739
= x4 1.6996
=
x5 1.6953
= x6 1.6954
= x7 1.6954
=
xi 1
−
0
0
1
2
3
4
5
1
2
1.5239
1.6627
1.6996
1.6953
= xi
0
0
1
2
3
4
5
2
1.5239
1.6627
1.6996
1.6953
1.6954
= xi 1
+
0
0
1
2
3
4
5
1.5239
1.6627
1.6996
1.6953
1.6954
1.6954
=
<---- Convergence has occurred here
Let us solve this problem by Newton Raphson Method, using subscripts and compare answers
f x
( ) 1.15 x
3
⋅ 1.2 x
2
⋅
+ 3.5 x
⋅
− 3.12
−
:= fprime x
( ) 3.45 x
2
⋅ 2.4 x
⋅
+ 3.50
−
:=
N 4
:= i 1 N
..
:= x1 2
:= <--starting estimate
xi 1
+ xi
f xi
( )
fprime xi
( )
−
:=
x2 1.743046
= x3 1.696894
= x4 1.6954
= x5 1.6954
=
Chapter 3: Roots of Equations 75

86. xi
0
0
1
2
3
2
1.743
1.6969
1.6954
= xi 1
+
0
0
1
2
3
1.743
1.6969
1.6954
1.6954
=
<----Convergence has occurred here.
Let us verify the above root by resorting to the polyroots function
f x
( ) 1.15 x
3
⋅ 1.2 x
2
⋅
+ 3.5 x
⋅
− 3.12
−
:=
v
3.12
−
3.5
−
1.2
1.15
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= polyroots v
( )
1.8941
−
0.8448
−
1.6954
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
which indicates that there is one root between x = 0 and x = 10.
Example 3.7
Obtain all roots, real as well as complex, of the function f(x) of Example 3.5 by the Secant
method.
f x
( ) x
3
7 x
2
⋅
+ 19 x
⋅
+ 13
+
:=
To determine the real root, we will consider initial estimates of 1 and 2 as follows.
N 9
:= i 1 N
..
:= x0 1
:= x1 2
:=
xi 1
+ xi
f xi
( ) xi 1
− xi
−
( )
⋅
f xi 1
−
( ) f xi
( )
−
−
:= x2 0.148936
= x3 0.267833
−
= x4 0.7285
−
=
x5 0.9224
−
= x6 0.9904
−
= x7 0.9996
−
= x8 0.999998
−
=
x9 1
−
= x10 1
−
=
76 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

87. xi 1
−
0
0
1
2
3
4
5
6
7
8
1
2
0.1489
-0.2678
-0.7285
-0.9224
-0.9904
-0.9996
-1
= xi
0
0
1
2
3
4
5
6
7
8
2
0.1489
-0.2678
-0.7285
-0.9224
-0.9904
-0.9996
-1
-1
= xi 1
+
0
0
1
2
3
4
5
6
7
8
0.1489
-0.2678
-0.7285
-0.9224
-0.9904
-0.9996
-1
-1
-1
=
<--- Convergence has occurred here
To find the complex roots, let us use initial estimates of (-4+i) and (-4+2i).
x0 4
− i
+
:= x1 4
− 2i
+
:= N 7
:= j 1 N
..
:=
xj 1
+ xj
f xj
( ) xj 1
− xj
−
( )
⋅
f xj 1
−
( ) f xj
( )
−
−
:= x2 3.211618
− 1.456432i
+
=
x3 2.929182
− 1.735276i
+
= x4 2.9136
− 2.0766i
+
=
x5 3.0167
− 1.9899i
+
= x6 3.0009
− 2.0008i
+
=
x7 3
− 2i
+
= x8 3
− 2i
+
=
xj 1
−
4
− i
+
4
− 2i
+
3.2116
− 1.4564i
+
2.9292
− 1.7353i
+
2.9136
− 2.0766i
+
3.0167
− 1.9899i
+
3.0009
− 2.0008i
+
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= xj
4
− 2i
+
3.2116
− 1.4564i
+
2.9292
− 1.7353i
+
2.9136
− 2.0766i
+
3.0167
− 1.9899i
+
3.0009
− 2.0008i
+
3
− 2i
+
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= xj 1
+
3.2116
− 1.4564i
+
2.9292
− 1.7353i
+
2.9136
− 2.0766i
+
3.0167
− 1.9899i
+
3.0009
− 2.0008i
+
3
− 2i
+
3
− 2i
+
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Chapter 3: Roots of Equations 77

88. Convergence has occurred with a complex root determined as ( - 3 + 2i ). Clearly, the
other complex root will be the complex conjugate (-3 - 2i) .
Resorting to the polyroots function will confirm the roots generated above.
f x
( ) x
3
7 x
2
⋅
+ 19 x
⋅
+ 13
+
:=
v
13
19
7
1
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= polyroots v
( )
3
− 2i
+
3
− 2i
−
1
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
3.8 METHOD OF SUCCESSIVE SUBSTITUTION
This method encompasses all iteration schemes for finding roots of nonlinear functions.
Applications of this technique can be found in the use of the Newton-Raphson method and
the Secant method. Another name for this method is Fixed Point Iteration. In this
method, the equation f(x) = 0 is written in the form x = g(x). Thus, if x1 is an assumed
initial approximation to the root, then a successive approximation can be generated using
x i+ 1 = g ( x i ) (3.12)
Iteration must be pursued until convergence to a root is indicated
Advantages and Disadvantages of the Iteration Method
While the method provides a simple computational technique for finding roots of
equations, offers flexibility in the selection of the function g(x), and is easy to program, it
is still possible for the solution to diverge with improper choices of the function. To insure
convergence of the iteration, the function selected must be such that the absolute value of
its slope is always less than unity. Otherwise, divergence will occur.
Example 3.8
The function y(x)= x2 - 3 x + e x - 4 has two roots, one positive and the other negative.
Determine the negative root by the method of successive substitution.
Rewrite the given equation as follows
y x
( ) x
2
3 x
⋅
− e
x
+ 4
−
:=
78 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

89. g x
( )
x
2
e
x
+ 4
−
3
:= x g x
( )
:= gprime x
( )
1
3
2 x
⋅ e
x
+
( )
⋅
:=
Let the initial guess be 0. Using the above recursive relationship, we find revised values of x until
convergence occurs as shown below.
x 0
:= g x
( ) 1
−
=
Iteration # 1:
Iteration # 2: x g x
( )
:= x 1
−
= g x
( ) 0.8774
−
= gprime x
( ) 0.544
=
Iteration # 3: x g x
( )
:= x 0.8774
−
= g x
( ) 0.9381
−
= gprime x
( ) 0.4463
=
x g x
( )
:= x 0.9381
−
= g x
( ) 0.9095
−
= gprime x
( ) 0.495
=
x g x
( )
:= x 0.9095
−
= g x
( ) 0.9233
−
= gprime x
( ) 0.4721
=
x g x
( )
:= x 0.9233
−
= g x
( ) 0.9167
−
= gprime x
( ) 0.4832
=
x g x
( )
:= x 0.9167
−
= g x
( ) 0.9199
−
= gprime x
( ) 0.4779
=
x g x
( )
:= x 0.9199
−
= g x
( ) 0.9184
−
= gprime x
( ) 0.4804
=
x g x
( )
:= x 0.9184
−
= g x
( ) 0.9191
−
= gprime x
( ) 0.4792
=
x g x
( )
:= x 0.9191
−
= g x
( ) 0.9188
−
= gprime x
( ) 0.4798
=
Iteration # 11: x g x
( )
:= x 0.9188
−
= g x
( ) 0.9189
−
= gprime x
( ) 0.4795
=
Note that convergence has taken place at x = -0.919, and the absolute value of the slope
of the function selected is less than unity throughout the iteration process.
i 0 1
, 9
..
:= x0 0
:= xi 1
+ g xi
( )
:=
Chapter 3: Roots of Equations 79

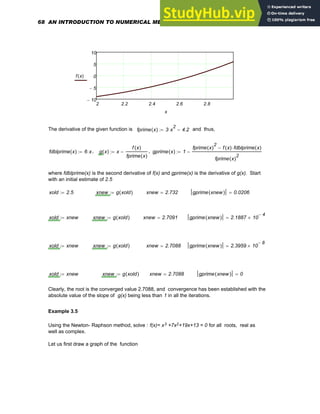
90. x
0
0
1
2
3
4
5
6
7
8
9
10
0
-1
-0.8774
-0.9381
-0.9095
-0.9233
-0.9167
-0.9199
-0.9184
-0.9191
-0.9188
=
<--- Convergence occurs here ---> y x10
( ) 5.0333
− 10
4
−
×
=
3.9 MULTIPLE ROOTS AND DIFFICULTIES IN COMPUTATION
When the given function makes contact with the x- axis and has a slope of zero, multiple roots
can occur as indicated in Figure 3.5. These roots are difficult to compute by the methods
discussed in this chapter for the following reasons.
1. In the case of the Bisection method, the function does not change sign at the root.
2. In the case of Newton-Raphson and Secant methods, the derivative at the
multiple root is zero.
Figure 3.5. Case of multiple roots
Because the Newton-Raphson and Secant methods in their orginal forms are methods that
resort to linear convergence, they cannot be employed to generate multiple roots. The following
modification to the original Newton-Raphson equation has been suggested [ 4 ].
80 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

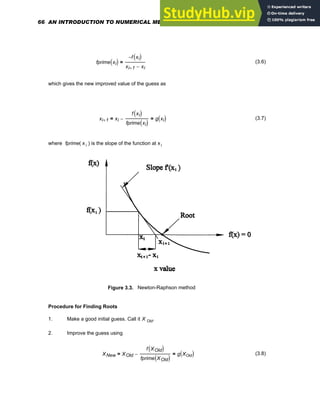
91. xi 1
+ xi m
f xi
( )
fprime xi
( )
⋅
−
= (3.13)
where m is the multiplicity of the root ( for example, m = 2 for a double root ). However, this
may not be a very practical route since it assumes prior knowledge about the multiplicity of
a root.
Another approach, also suggested [ 4 ] involves defining a new function u(x)
u x
( )
f x
( )
fprime x
( )
= (3.14)
which has the same roots as the original given function f(x), and then resorting to the
following alternative form of the Newton-Raphson formula
xi 1
+ xi
u xi
( )
uprime xi
( )
−
= (3.15)
where uprime(x) represents the derivative of the new function u(x). Substitution of Equation
(3.14) into the Newton-Raphson equation, which is now Equation (3.15), yields the desired
formula
xi 1
+ xi
f xi
( ) fprime xi
( )
⋅
fprime xi
( )2
f xi
( ) fdoubleprime xi
( )
⋅
−
−
= (3.16)
where fprime and fdoubleprime represent first and second derivatives respectively.
The modified formula for the Secant Method that will be suitable for the generation of multiple
roots can be obtained by simply substituting u(x) for f(x) in the Secant method formula giving
xi 1
+ xi
u xi
( ) xi 1
− xi
−
( )
⋅
u xi 1
−
( ) u xi
( )
−
−
= (3.17)
Example 3.9
The function
f(x)= x3 - 4 x 2 + 5 x - 2 = (x-1) (x-1) (x-2)
Chapter 3: Roots of Equations 81

92. has a double root at 1 and a single root at 2, which we will verify using Equation (3.16).
f x
( ) x
3
4 x
2
⋅
− 5 x
⋅
+ 2
−
:=
The first and second derivatives of the given function are
fprime x
( ) 3 x
2
⋅ 8 x
⋅
− 5
+
:= fdoubleprime x
( ) 6 x
⋅ 8
−
:=
In order to determine the multiple root by the modified form of the Newton-Raphson formula ,
let us employ Equation (3.16) and start with an initial estimate of 0.25.
xi 1
+ xi
f xi
( ) fprime xi
( )
⋅
fprime xi
( )2
f xi
( ) fdoubleprime xi
( )
⋅
−
−
=
xold 0.25
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1.0841
=
xold xnew
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1.0042
=
xold xnew
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1
=
xold xnew
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1
=
It is clear that the multiple root is the converged value of 1. To determine the single root, the
above approach can still be employed, but with a different starting estimate, as shown below.
xold 2.50
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1.8182
=
82 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

93. xold xnew
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1.9101
=
xold xnew
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1.9809
=
xold xnew
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 1.9992
=
xold xnew
:= xnew xold
f xold
( ) fprime xold
( )
⋅
fprime xold
( )
2
f xold
( ) fdoubleprime xold
( )
⋅
−
−
:= xnew 2
=
Thus, the single root is the converged value of 2. The following steps will now demonstrate the
application of the modified Secant Method formula, which is Equation 3.17, to the
determination of the multiple root at 1.
f x
( ) x
3
4 x
2
⋅
− 5 x
⋅
+ 2
−
:= fprime x
( ) 3 x
2
⋅ 8 x
⋅
− 5
+
:= u x
( )
f x
( )
fprime x
( )
:=
i 0 5
..
:=
xi 1
+ xi
u xi
( ) xi 1
− xi
−
( )
⋅
u xi 1
−
( ) u xi
( )
−
−
:=
i 1
−
x0 0.25
:= x1 0.26
:=
x2 x1
u x1
( ) x0 x1
−
( )
⋅
u x0
( ) u x1
( )
−
−
:= x2 1.0835
=
x3 x2
u x2
( ) x1 x2
−
( )
⋅
u x1
( ) u x2
( )
−
−
:= x3 0.9802
=
x4 x3
u x3
( ) x2 x3
−
( )
⋅
u x2
( ) u x3
( )
−
−
:= x4 0.9991
=
x5 x4
u x4
( ) x3 x4
−
( )
⋅
u x3
( ) u x4
( )
−
−
:= x5 1
= <--- Convergence at the double root x =1
Application of the polyroots and root functions confirms the correctness of the above
analysis.
Chapter 3: Roots of Equations 83

94. v
2
−
5
4
−
1
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= polyroots v
( )
0.9995
1.0005
2
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Guess x 0.5
:= a root f x
( ) x
,
( )
:= generates a 1
=
Guess x 3
:= a root f x
( ) x
,
( )
:= generates a 2
=
3.10 SOLUTION OF SYSTEMS OF NONLINEAR EQUATIONS
The methods discussed so far deal with finding the roots of functions of only a single
variable. In certain situations, it may be necessary to solve nonlinear equations in two or
more variables. In these cases, iteration can be resorted to as presented in the following
example.
Example 3.10
Solve: 1.1 x2 +1.2 xy = 10.5 ; y + 3.2 x y2 = 58.2
Let us put the given equations in the form
x
10.5 1.1 x
2
⋅
−
1.2 y
⋅
= y 58.2 3.2 x
⋅ y
2
⋅
−
=
and make the following initial guesses:
x 1
:= y 3
:=
Then, x
10.5 1.1 x
2
⋅
−
1.2 y
⋅
:= and y 58.2 3.2 x
⋅ y
2
⋅
−
:= yield
x 2.6111
= y 17
−
=
A second iteration gives
84 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

95. x
10.5 1.1 x
2
⋅
−
1.2 y
⋅
:= x 0.1471
−
= y 58.2 3.2 x
⋅ y
2
⋅
−
:= y 194.214
=
Notice that the approach resorted to is diverging and will not yield a solution. Thus, the
computations must be repeated with equations set up in a different format as shown below.
Iteration #
(1) x 1
:= y 3
:= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 2.5045
= y
58.2 y
−
3.2 x
⋅
:= y 2.6244
=
(2) x 2.5045
= y 2.6244
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.5411
= y
58.2 y
−
3.2 x
⋅
:= y 3.357
=
(3) x 1.5411
= y 3.357
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.9753
= y
58.2 y
−
3.2 x
⋅
:= y 2.9456
=
(4) x 1.9753
= y 2.9456
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.7883
= y
58.2 y
−
3.2 x
⋅
:= y 3.1073
=
(5) x 1.7883
= y 3.1073
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.8664
= y
58.2 y
−
3.2 x
⋅
:= y 3.0372
=
(6) x 1.8664
= y 3.0372
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.8335
= y
58.2 y
−
3.2 x
⋅
:= y 3.0663
=
(7) x 1.8335
= y 3.0663
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.8473
= y
58.2 y
−
3.2 x
⋅
:= y 3.054
=
(8) x 1.8473
= y 3.054
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.8415
= y
58.2 y
−
3.2 x
⋅
:= y 3.0591
=
(9) x 1.8415
= y 3.0591
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.8439
= y
58.2 y
−
3.2 x
⋅
:= y 3.057
=
(10) x 1.8439
= y 3.057
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.8429
= y
58.2 y
−
3.2 x
⋅
:= y 3.0579
=
Chapter 3: Roots of Equations 85

96. (11) x 1.8429
= y 3.0579
= x
10.5 1.2 x
⋅ y
⋅
−
1.1
:= x 1.8433
= y
58.2 y
−
3.2 x
⋅
:= y 3.0575
=
Notice that after ten iterations convergence has taken place yielding the solution as : x =1.843
and y = 3.058. This example illustrates a very serious disadvantage associated with the
successive substitution method which is the dependence of convergence on the format in which
the equations are put and utilized in the iteration process. Also , even in situations where a
converged solution can be attained, initial estimates that are fairly close to the true solution
must be resorted to, because, otherwise, divergence may occur and a solution may never be
obtained. The results of the iterative process are summarized in the following table.
----------------------------------------------------------------------------------------------------------------------------
Iteration # x y
------------------------------------------------------------------------------------------------------------------------------
0 init=1.0 3.00
1 2.505 2.624
2 1.541 3.357
3 1.975 2.946
4 1.788 3.107
5 1.866 3.037
6 1.833 3.066
7 1.847 3.054
8 1.841 3.059
9 1.844 3.057
10 1.843 3.058
11 1.843 3.058
----------------------------------------------------------------------------------------------------------------------------------
3.11 SOLVING SYSTEMS OF EQUATIONS USING MATHCAD'S Given
AND Find FUNCTIONS
Mathcad allows you to solve a system of 50 simultaneous equations in 50 unknowns. The
procedure is as follows:
1. Provide initial guesses for all unknowns. These initial guesses give Mathcad a place to
start searching for the solution.
2. Type the word Given. This tells Mathcad that what follows is a system of equations. Given
can be typed in any combination of upper and lower case letters, and in any font. However, it
should not be typed in a text region.
3. Then type the equations and inequalities in any order below the word Given . Make sure
you separate the left and right sides of an equation by an " = ". Press [Ctrl]= to type " = ".
You can of course separate the left and right sides of an inequality with the appropriate symbol.
4. a:= Find(x,y.....) returns the solution to the system of equations.
86 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

97. Example 3.11.
Using the Given and Find functions, solve
1.5 x
2
⋅ 2 y
2
⋅
+ 6.5
= . x y
+ 2.75
=
Provide initial guesses: x 1
:= y 1
:=
Given
1.5 x
2
⋅ 2 y
2
⋅
+ 6.5
=
x y
+ 2.75
=
a Find x y
,
( )
:=
a
1.5
1.25
⎛
⎜
⎝
⎞
⎟
⎠
= <--- Solution
Alternatively, do the following sequence to obtain xval and yval as the solution
Given 1.5 x
2
⋅ 2 y
2
⋅
+ 6.5
= x y
+ 2.75
=
xval
yval
⎛
⎜
⎝
⎞
⎟
⎠
Find x y
,
( )
:= xval 1.5
= yval 1.25
= <--Solution
3.12. APPLICATIONS IN ROOT-FINDING
The following are examples of situations where roots of nonlinear equations need to be
evaluated.
3.12.1 Maximum Design Load for a Column
A steel pipe with an outside diameter of 10.70 inches and a wall thickness of 0.375 inches is
to serve as a pin-ended column that is 22 feet long . It supports an eccentric load at an
eccentricity of e = 1.5 inches from the column center-line. The maximum load that the
column can carry with a factor of safety of 2.75 is to be determined. The modulus of
elasticity E for steel is 30 x 10 6 psi and its yield strength, σyld , is 40,000 psi .
The equation for the stress level σ max resulting from the application of the maximum load
P max is [ 3,18 ]
Chapter 3: Roots of Equations 87

98. (3.18)
σmax
Pmax
A
1
e c
⋅
K
2
sec
Pmax
A E
⋅
L
2 K
⋅
⋅
⎛
⎜
⎝
⎞
⎟
⎠
⋅
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
=
where A is the column cross-sectional area, e is the eccentricity at which the load is applied,
as shown in Figure 3.6 , c is the distance of the outermost fiber in the cross-section from the
neutral axis , K is the radius of gyration , L is the column length and E is the modulus of
elasticity. This relationship between σ max and P max is not linear and there is no proportionality
between the applied load and the stress that is produced. Thus, it must be solved iteratively
using trial and error. How this can be accomplished with Mathcad is demonstrated below.
Figure 3.6. Eccentrically Loaded Column
Here,
σyld 40000.
:= (psi) E 30 10
6
⋅
:= (psi) FS 2.75
:=
do 10.70
:= t 0.375
:= di do 2 t
⋅
−
:= di 9.95
= <--- all dimensions in inches
88 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

99. e 1.50
:= L 264.
:= c
do
2
:= c 5.35
=
I
π
64
do
4
di
4
−
( )
⋅
:= ( in 4 ) A
π
4
do
2
di
2
−
( )
⋅
:= (in 2 )
A 12.1639
= I 162.3057
= K
I
A
:= K 3.6528
= (in )
With a factor of safety of 2.75, the maximum stress level that the column can have is
σmax
σyld
FS
:= σmax 1.4545 10
4
×
= psi
The corresponding maximum allowable load may be determined from Equation (3.18) using
the root function as follows.
g Pmax
( )
Pmax
E A
⋅
L
2 K
⋅
⋅
:=
f Pmax
( ) σmax
Pmax
A
1
e c
⋅
K
2
sec g Pmax
( )
( )
⋅
+
⎛
⎜
⎝
⎞
⎟
⎠
⋅
−
:=
Pmax 125000.
:= (lbs) <--Guess value for the root
a root f Pmax
( ) Pmax
,
( )
:=
a 1.0221 10
5
×
= (lbs) <-- Maximum allowable load column can carry
3.12.2. Natural Frequencies of Vibration of a Uniform Beam
For a uniform beam that is clamped at one end and free at the other, a shown in Figure 3.7 ,
the natural frequencies of vibration [20] are given by the equation
1 cos βprime
( ) cosh βprime
( )
⋅
+ 0
= (3.19)
Chapter 3: Roots of Equations 89

100. where
(3.20)
βprime β L
⋅
=
and β
ρ ω
2
⋅
EI
⎛
⎜
⎝
⎞
⎟
⎠
1
4
= (3.21)
in which ρ is the mass per unit length of the beam, EI is the flexural rigidity or bending stiffness
about the neutral axis , and ω refers to the natural frequencies . For a beam with a length of 20
feet, an EI value of 16 x 10 6 lb-in 2 , and a weight per unit length of 0.03 lb/ in , the natural
frequencies may be determined as shown below.
Figure 3.7. A Fixed-Free Beam
ρwt 0.03
:= lb/in --> ρ
ρwt 12
⋅
32.2
:= --> ρ 0.0112
= (lb- ft -2 sec 2)
EI 16 10
6
⋅
:= lb-in 2 --> EI
16 10
6
⋅
144
:= --> EI 1.1111 10
5
×
= (lb- ft 2 )
L 20
:= ft
βprime 1
:= <-- Guess value for root
f βprime
( ) 1 cos βprime
( ) cosh βprime
( )
⋅
+
:=
a root f βprime
( ) βprime
,
( )
:= a 1.8751
=
90 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

101. β
a
L
:= β 0.0938
=
ω
EI β
4
⋅
ρ
:= ω 27.7106
= (rad/sec) <-- First or fundamental
natural frequency
βprime 5
:= <-- Guess value for next root
f βprime
( ) 1 cos βprime
( ) cosh βprime
( )
⋅
+
:=
a root f βprime
( ) βprime
,
( )
:=
a 4.6941
=
β
a
L
:= β 0.2347
=
ω
EI β
4
⋅
ρ
:= ω 173.6595
= (rad/sec) <-- Second natural frequency
Similarly by making appropriate guesses, higher natural frequencies can be determined
using the root function. Some of these are listed below.
Third natural frequency: 486.3 rad/sec
Fourth natural frequency: 952.8 rad/sec
Fifth natural frequency: 1575.1 rad/sec
Sixth natural frequency: 2353 rad/sec
Seventh natural frequency: 3286 rad/sec.
3.12.3. Solving the Characteristic Equation in Control Systems Engineering
A characteristic equation is an algebraic equation that is formulated from the differential
equation or equations of a control system [14] . Its solution, which often requires evaluation
of the roots of a polynomial of degree higher than two, is crucial in determining system
stability and assessing system transient response in terms of its time constant, natural
frequencies , damping qualities etc. An application involving the use of Mathcad' s polyroots
function in determining the roots of a characteristic polynomial of a control system is
presented below.
Chapter 3: Roots of Equations 91

102. For the unity - feedback system shown in Figure 3.8, the characteristic polynomial is
s
3
12 s
2
⋅
+ 20 s
⋅
+ K
+ 0
=
where K is a variable system parameter that can be selected based on the performance
requirements that may be prescribed. For varying values of this parameter, the roots of the
characteristic polynomial can be evaluated as shown below, and the system transient
response and stability studied , following which, an appropriate range for K may be
recommended.
Figure 3.8. Feedback Control System Block Diagram
K 1
:= <-- Negative real roots
indicate a stable
system
v
1
20
12
1
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= r polyroots v
( )
:= r
10.0125
−
1.9359
−
0.0516
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
K 10
:=
v
10
20
12
1
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= <-- Negative
real parts of
root
indicate a
stable
system
r polyroots v
( )
:= r
10.1216
−
0.9392
− 0.3255i
−
0.9392
− 0.3255i
+
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
92 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

103. <-- Negative
real parts
of root
indicate a
stable
system
K 100
:= v
100
20
12
1
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= r polyroots v
( )
:= r
11.0084
−
0.4958
− 2.9729i
+
0.4958
− 2.9729i
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
<-- Positive
real
parts of root
indicate an
unstable
system
K 400
:= v
400
20
12
1
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= r polyroots v
( )
:= r
12.8628
−
0.4314 5.5598i
+
0.4314 5.5598i
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
3.12.4. Horizontal Tension in a Uniform Cable
Flexible cables are often used in suspension bridges, transmission lines, telephone lines ,
mooring lines and many other applications. A cable hanging under its own weight takes the
shape of a catenary in which the deflection y along the span is given by the following
relationship [ 8 ]
y
H
w
cosh
w x
⋅
H
⎛
⎜
⎝
⎞
⎟
⎠
1
−
⎛
⎜
⎝
⎞
⎟
⎠
⋅
= (3.22)
where x is the horizontal distance along the span a shown in Figure 3.9 , H is the horizontal
component of tension in the cable and w is the weight per unit length of the cable.
Figure 3.9. Catenary cable
Chapter 3: Roots of Equations 93

104. The constant H is obtained by using the boundary condition that y = h at x = L/2, which gives
h
H
w
cosh
w L
⋅
2 H
⋅
⎛
⎜
⎝
⎞
⎟
⎠
1
−
⎛
⎜
⎝
⎞
⎟
⎠
⋅
+ (3.23)
Thus, the root of the following equation must be evaluated by using a method such as the
Secant method
h g H
( )
=
(3.24)
where
g H
( )
H
w
cosh
w L
⋅
2 H
⋅
⎛
⎜
⎝
⎞
⎟
⎠
1
−
⎛
⎜
⎝
⎞
⎟
⎠
⋅
= (3.25)
For a cable with a span of L= 22 meters, a weight per unit length of w =5.5 N/m and a
maximum sag of h= 6.5 meters,
h 6.5
:= w 5.5
:= L 22
:=
The intersection of the plot of g(H) with h= 6.5 in Figure 3.10 suggests that f(H) has a root
at about H = 50 Newtons.
g H
( )
H
w
cosh
w L
⋅
2 H
⋅
⎛
⎜
⎝
⎞
⎟
⎠
1
−
⎛
⎜
⎝
⎞
⎟
⎠
⋅
:= H 10 11
, 200
..
:= f H
( ) h
H
w
cosh
w L
⋅
2 H
⋅
⎛
⎜
⎝
⎞
⎟
⎠
1
−
⎛
⎜
⎝
⎞
⎟
⎠
⋅
−
:=
94 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

105. 0 50 100 150 200
0
100
200
300
400
h
g H
( )
H
Figure 3.10. Plot of g(H)
The use of the Secant method in obtaining the required root is shown below.
N 7
:= i 1 N
..
:= H0 25
:= H1 35
:= <--initial required guesses
Hi 1
+ Hi
f Hi
( ) Hi 1
− Hi
−
( )
⋅
f Hi 1
−
( ) f Hi
( )
−
−
:= <--recursive formula of Secant method
H2 41.1846
= H3 49.0109
= H4 53.8261
=
H5 55.9053
= H6 56.2878
= <-- improved
estimates
H7 56.31
= H8 56.3102
=
Hi 1
−
0
0
1
2
3
4
5
6
25
35
41.1846
49.0109
53.8261
55.9053
56.2878
= Hi
0
0
1
2
3
4
5
6
35
41.1846
49.0109
53.8261
55.9053
56.2878
56.31
= Hi 1
+
0
0
1
2
3
4
5
6
41.1846
49.0109
53.8261
55.9053
56.2878
56.31
56.3102
=
<----Convergence has occurred here
Mathcad's root function can also be used to determine the root of f(H) . This is done below.
Guess: H 35
:= a root f H
( ) H
,
( )
:= a 56.3102
=
Thus, by solving f(H)=0, the horizontal tension in the cable has been found as H= 56.31 N.
Chapter 3: Roots of Equations 95

106. PROBLEMS
3.1. Obtain a root of the following polynomial lying in the range 1 to 3 by the Bisection
method
f x
( ) x
3
3.45 x
2
⋅
− 3.35 x
⋅
+ 0.934
−
=
Using Mathcad, draw a graph of the polynomial for the given range of x. Label it and give it a
title . Verify your answer by using the root function. Also obtain all the roots of the polynomial
with the polyroots function.
3.2. Estimate a root of the polynomial
x
3
3.5 x
2
⋅
− 3.28 x
⋅
+ 0.924
−
between x = 2 and x = 3 using the Bisection method. Generate an answer that is good to
three decimal places.
3.3 Estimate a root of the polynomial
x
3
6.1 x
2
⋅
− 11.26 x
⋅
+ 6.336
−
between x = 1.5 and x = 2 using the Bisection method.
3.4. Obtain all roots of the following polynomial lying in the range -5.5 to 4.0 by the
Newton-Raphson method
f x
( ) 1.1 x
3
⋅ 1.15x
2
+ 17.1 x
⋅
− 15.2
+
=
Using Mathcad, draw a graph of the polynomial for the given range of x. Label it and give it a
title . Verify your answers by using the root function. Also obtain all the roots of the polynomial
with the polyroots function.
3.5. Obtain all roots of the following polynomial lying in the range -2.5 to 1.5 by the
Newton-Raphson method
f x
( ) x
3
4.25 x
2
⋅
+ 4.05
−
=
Using Mathcad, draw a graph of the polynomial for the given range of x. Label it and give it a
title . Verify your answers by using the root function. Also obtain all the roots of the polynomial
with the polyroots function.
3.6. Estimate a root of the polynomial
96 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

107. x
3
2 x
2
⋅
− 5 x
⋅
− 6
+
between x = 3 and x = 4 using the Newton-Raphson method.
3.7. Using the Newton-Raphson method, estimate a real root of the polynomial
f x
( ) e
x
−
( )
x
3
−
=
between x = 0 and x =1. Obtain an answer that is correct to at least three decimal
places.
3.8. Using the Newton-Raphson method, estimate a real root of the polynomial
f x
( ) x
3
5 cos x
( )
⋅
− 1
−
=
between x = 1 and x =2. Obtain an answer that is correct to at least three decimal places.
3.9. Using the Newton-Raphson method, estimate a real root of the polynomial
f x
( ) cos x
( ) x
−
=
between x = 0 and x =4. Obtain an answer that is correct to three decimal places.
3.10. Using the Newton-Raphson method, estimate a real root of the polynomial
f x
( ) e
x
−
x
2
−
=
between x = 0 and x =1. Obtain an answer that is correct to four decimal places.
3.11. Obtain all roots of the following polynomial lying in the range 0 to 1.0 by the
Secant method
f x
( ) x
3
1.72 x
2
⋅
− 0.85 x
⋅
+ 0.110
−
=
Using Mathcad, draw a graph of the polynomial for the given range of x. Label it and give
it a title . Verify your answers by using the root function. Also obtain all the roots of the
polynomial with the polyroots function.
3.12. Obtain all roots of the following polynomial lying in the range 0.0 to 1.0 by the
Chapter 3: Roots of Equations 97

108. Secant method
f x
( ) x
4
3.05 x
3
⋅
− 2.75 x
2
⋅
+ 0.43 x
⋅
+ 0.45
−
=
Using Mathcad, draw a graph of the polynomial for the given range of x.Label it and give it a
title . Verify your answers by using the root function. Also obtain all the roots of the polynomial
with the polyroots function.
3. 13. Using the Secant method, estimate a real root of the polynomial
x
3
x
2
+ 17 x
⋅
− 15
+
between x = 1.5 and x =4. Start with initial estimates of 1.5 and 4.0.
3.14. Using the Secant method, estimate a real root of the polynomial
x
4
2 x
3
⋅
− 15 x
2
⋅
− 4 x
⋅
− 20
+
between x = 2 and x =6. Start with initial estimates of 4.0 and 4.5.
3.15. Using the Secant method, estimate a real root of the polynomial
f x
( ) x
2
sin x
( )
− 1
−
=
between x = 1 and x =2.
3.16. Using the Secant method, estimate a real root of the polynomial
f x
( ) 5 x
4
⋅ 2 x
3
⋅
− 25 x
2
⋅
− 6 x
⋅
− 45
+
=
between x = 1 and x =2. Generate an answer that is correct to four decimal places.
3.17. Using the Secant method, estimate a real root of the polynomial
f x
( ) 2 cos x
( )
⋅ e
x
−
=
between x = 0 and x =1. Generate an answer that is correct to three decimal places.
3.18. Using the Secant method, estimate a real root of the polynomial
98 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

109. f x
( ) e
x
−
x
2
−
=
between x = 0 and x =1. Generate an answer that is correct to three decimal places.
3.19. Using the Secant method, estimate a real root of the polynomial
f x
( ) x
4
5 x
3
⋅
− 40 x
2
⋅
− 12 x
⋅
− 24
+
=
between x = 0 and x =2. Generate an answer that is correct to threer decimal places.
3.20. Obtain a root of the following polynomial lying in the range -10 to 10 by the
method of Successive Substitution
f x
( ) x
3
0.25 x
2
⋅
+ 0.75 x
⋅
− 0.350
−
:=
Using Mathcad, draw a graph of the polynomial for the given range of x. Label it and
give it a title. Notice what this plot suggests in terms of the interval where the roots may
lie. Then, draw a second graph for a narrower range (-0.60 to 1.40). Start with an initial
estimate of 0.9. Verify your answer by using the root function. Also obtain all the roots of
the polynomial with the polyroots function.
3.21. Obtain a root of the following polynomial lying in the range --5 to 25 by the
method of Successive Substitution
f x
( ) x
3
17.45 x
2
⋅
− 82.89 x
⋅
− 84.50
−
=
Using Mathcad, draw a graph of the polynomial for the given range of x. Label it and give
it a title . Start with a reasonable initial estimate. Verify your answer by using the root
function. Also obtain all the roots of the polynomial with the polyroots function.
3.22. Obtain the solution of the following system of nonlinear equations by iteration
e
x
1.1 y
⋅
− 0
= and 1.1 x
⋅ y
⋅ e
1.05 x
⋅
− 0
=
Start with an initial estimate of y= 2.2. Verify your answers with the Given and Find
functions.
3.23. Using the Given and Find functions of Mathcad, obtain the solution to the following
system of equations.
3.25x- 1.01y + 2.1z = -3.72 ; 2.12x + 3.15 y - 2.2z = -18.25 ; -x + 2.22 y + 4.15 z = -6
Chapter 3: Roots of Equations 99

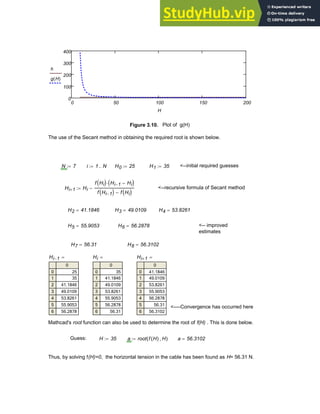
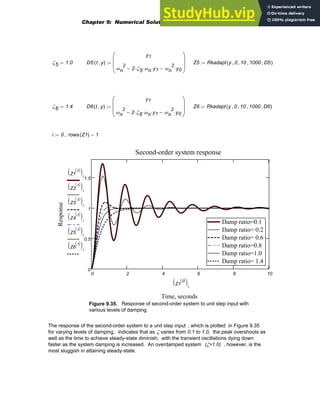
110. 3.24. The dynamic response of an underdamped second-order system, which is a
common mathematical model in control system analysis, to a unit step function is given
by [ 14 ]
c t
( ) 1
1
1 ζ
2
−
e
ζ
− ωn
⋅ t
⋅
⋅ cos ωn 1 ζ
2
−
⋅ t
⋅ ϕ
−
⎛
⎝
⎞
⎠
⎡
⎣
⎤
⎦
⋅
−
=
where ζ is the system damping ratio, ω n is the undamped natural frequency, and φ is
ϕ atan
ζ
1 ζ
2
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
=
A precise analytical relationship between the damping ratio and the rise time which is the time
required for the response to go from 10 % of the final value to 90 % ( that is, from 0.1 to 0.9 in
this case ) cannot be determined . However, using Mathcad's root function, the normalized
rise time which is ω n times the rise time, can be found for a specified damping ratio ζ by
solving for the values of ω n t that yield c(t) = 0.9 and c(t)= 0.1 . Subtracting these two values
yields the normalized rise time for the value of ζ considered . Using a range of damping ratios
from 0.1, 0.2, 0.3... .. 0.9 , construct a plot depicting normalized rise time as a function of
the damping ratio .
3.25. The frequency equation for the free undamped longitudinal vibration of a slender bar
of length L and mass m with one end fixed and with the other end carrying a mass M is
given by [ 21 ]
β tan β
( )
⋅ α
=
where
β ω
L
c0
⋅
=
c0
E
ρ
=
Figure P 3.25.
100 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

111. α
m
M
=
in which E is Young's modulus for the material of the bar, ρ is the mass per unit volume and
ω is the natural frequency .
For a steel bar with mass ratio α = 0.70, E = 30 x 10 6 psi , L = 98 in., and ρ = 7.35x 10 -4
lb-sec 2 / in 4 , determine the first three natural frequencies.
3.26. For a uniform beam of length L with one end fixed and the other simply supported, the
natural frequencies of transverse vibration are given by the relationship [ 21 ]
tan k L
⋅
( ) tanh k L
⋅
( )
=
where
k
2
ω
ρ A
⋅
E I
⋅
⋅
=
Figure P 3.26
in which ω is the natural frequency , ρ is the mass density of the beam material, A is the
area of cross section of the beam , E is Young's modulus, and I is the moment of inertia of
the beam cross section.
Determine the first three natural frequencies of a 36 in. long steel beam whose area of
cross section A is 12.50 in 2 , moment of inertia I is 12.75 in 4, and ρ = 7.35x 10 -4 lb-sec 2 /
in 4 . E for steel is 30 x 10 6 psi.
Chapter 3: Roots of Equations 101

112. NOTES:
102 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

113. C H A P T E R 4
MATRICES AND LINEAR ALGEBRA
4.1 BASIC MATRIX OPERATIONS
Basic matrix operations are addition, subtraction and multiplication. Determination of the
inverse of a matrix is linked with the concepts of transpose, minor, cofactor and adjoint.
Addition and Subtraction:
Two matrices with the same number of rows and columns can be added by adding the
corresponding terms. Similarly, subtraction is done by subtracting the corresponding
terms
Multiplication:
If the product of two matrices A and B is C , the element Cij of C is obtained by
multiplying the elements of the ith row of A by the elements of the j th column of B in
accordance with
Cij
k
aik bkj
⋅
( )
∑
= (4.1)
Transpose:
The transpose of a matrix is one in which the rows and the columns are interchanged
Minor:
The minor M ij of the element a ij is the determinant obtained by deleting the i th row and
the j th column from the given determinant.
If A
2
5
1
3
7
6
4
9
8
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= , then, M12
5
1
9
8
⎛
⎜
⎝
⎞
⎟
⎠
:= , that is, M12 31
=
Cofactor:
The cofactor C ij of the element a ij is given by:
Cij 1
−
( )
i j
+
Mij
⋅
= (4.2)
Chapter 4: Matrices and Linear Algebra 103

114. For the above case, C12 1
−
( )
3
31
( )
⋅
:= , that is, C12 31
−
=
Adjoint Matrix:
The adjoint of a square matrix is the transpose of the matrix of its cofactors.
Inverse of a Matrix:
The inverse A -1 of a matrix A must satisfy the relationship
A A -1 = I , (4.3)
where I is the Identity or the Unit matrix which is a matrix with "1" along the diagonal and
zero elsewhere. The inverse A -1 is calculated as follows
A -1 = [adjoint (A)] / Det (A) , (4.4)
where Det (A) is the determinant of the given matrix, which must be non-zero for the inverse to
exist.
Example 4.1
Determine the inverse of the following matrix A
A
1
1
1
2
3
0
3
2
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
The determinant of this matrix is A 1
−
=
The minors of A are
M11
3
0
2
4
⎛
⎜
⎝
⎞
⎟
⎠
:= M12
1
1
2
4
⎛
⎜
⎝
⎞
⎟
⎠
:= M13
1
1
3
0
⎛
⎜
⎝
⎞
⎟
⎠
:=
M21
2
0
3
4
⎛
⎜
⎝
⎞
⎟
⎠
:= M22
1
1
3
4
⎛
⎜
⎝
⎞
⎟
⎠
:= M23
1
1
2
0
⎛
⎜
⎝
⎞
⎟
⎠
:=
104 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

115. M31
2
3
3
2
⎛
⎜
⎝
⎞
⎟
⎠
:= M32
1
1
3
2
⎛
⎜
⎝
⎞
⎟
⎠
:= M33
1
1
2
3
⎛
⎜
⎝
⎞
⎟
⎠
:=
That is,
M11 12
= M12 2
= M13 3
−
= M21 8
= M22 1
= M23 2
−
=
M31 5
−
= M32 1
−
= M33 1
=
Multiplying the minors by 1
−
( )
i j
+
will yield the cofactor matrix C as :
C
12
8
−
5
−
2
−
1
1
3
−
2
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
The adjoint matrix is the transpose of the cofactor matrix, and the inverse of the matrix A
will now be the adjoint matrix divided by the determinant of A.
InverseA
adj A
( )
A
=
or,
InverseA
12
2
−
3
−
8
−
1
2
5
−
1
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
1
−
:= InverseA
12
−
2
3
8
1
−
2
−
5
1
−
1
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
The correctness of the result can now be verified as follows. Multiplying A by its inverse
obtained above gives
1
1
1
2
3
0
3
2
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
12
−
2
3
8
1
−
2
−
5
1
−
1
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
⋅
1
0
0
0
1
0
0
0
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
4.2 USE OF MATHCAD IN PERFORMING MATRIX OPERATIONS
To put in a matrix in your document, choose "Matrix" from the "Insert" menu, then enter
Chapter 4: Matrices and Linear Algebra 105

116. the number of rows and columns, click on "Insert" and start putting in the numbers in the
placeholders, as shown in Figure 4.1. How to perform matrix operations will be clear from
the following examples.
Figure 4.1. Matrix operations in Mathcad
106 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

117. Given the two matrices A and B:
A
1
1
7
0
3
8
2
2
9
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= B
3
1
1
2
2
5
1
3
9
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Addition:
A B
+
4
2
8
2
5
13
3
5
18
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Subtraction:
A B
−
2
−
0
6
2
−
1
3
1
1
−
0
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Multiplication:
<--Use the asterisk ( * ) to multiply two matrices
A B
⋅
5
8
38
12
18
75
19
28
112
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
<-- Order in which multiplication is done is important.
Note that [A] [B] is not equal to [B][A]
B A
⋅
12
24
69
14
30
87
19
33
93
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Scalar subtraction:
A 5
−
4
−
4
−
2
5
−
2
−
3
3
−
3
−
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Chapter 4: Matrices and Linear Algebra 107

118. Scalar multiplication: ( Use the asterisk "*" )
A 5
⋅
5
5
35
0
15
40
10
10
45
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Matrix inverse: Use : ^ -1
A
1
−
0.733
−
0.333
−
0.867
1.067
−
0.333
0.533
0.4
0
0.2
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Determinant of A : A 15
−
=
Transpose of A: Use [Ctrl]1
A
T
1
0
2
1
3
2
7
8
9
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
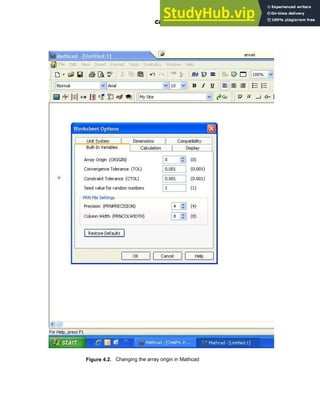
Matrix subscripts:
Use " [ " to put in subscripts. Note that, in this case, subscripts will go from 0 to 2.
because, in Mathcad, vector and matrix elements are ordinarily numbered starting with row
zero and column zero. To make " one " the " ORIGIN " , go to the Tools menu, choose
Worksheet Options , as shown in Figure 4.2 , and change the array origin from 0 to 1.
4.3 SOLUTION OF LINEAR ALGEBRAIC EQUATIONS BY USING
THE INVERSE
For a system of linear algebraic equations that can be written in matrix form as
[A]{X} = {B} (4.5)
where the matrix [A] and the column vector {B} contain known constants, the inverse of the matrix
[A] can be utilized in the determination of the solution vector {X} as follows
{X} = [A] -1 {B} (4.6)
108 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

119. Figure 4.2. Changing the array origin in Mathcad
Chapter 4: Matrices and Linear Algebra 109

120. Example 4.2
Solve: 2x + 4 y + z = -11
-x + 3 y -2 z = -16
2x - 3y + 5 z = 21
Putting the given equations in the form [A] {X}= {B}, where
A
2
1
−
2
4
3
3
−
1
2
−
5
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= B
11
−
16
−
21
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
The inverse of [A] can be easily obtained as
A
1
−
0.474
0.053
0.158
−
1.211
−
0.421
0.737
0.579
−
0.158
0.526
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
and [A] multiplied by [A]-1 will yield the identity matrix as shown
A A
1
−
⋅
1
0
0
0
1
0
0
0
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
The solution can then be generated by performing the matrix operation
X A
1
−
B
⋅
:=
yielding
X
2
4
−
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
4.4 SOLUTION OF LINEAR ALGEBRAIC EQUATIONS BY
CRAMER'S RULE
As an alternative to the above procedure, the solution {X} to the matrix equation
(Equation 4.5)
110 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

121. [A] {X} = {B}
can be computed using Cramer's rule as shown below
Letting
A
A11
A21
A31
A12
A22
A32
A13
A23
A33
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= B
B1
B2
B3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
the solution {X} can be computed using
X1
B1
B2
B3
A12
A22
A32
A13
A23
A33
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
A11
A21
A31
A12
A22
A32
A13
A23
A33
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= X2
A11
A21
A31
B1
B2
B3
A13
A23
A33
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
A11
A21
A31
A12
A22
A32
A13
A23
A33
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
(4.7)
X3
A11
A21
A31
A12
A22
A32
B1
B2
B3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
A11
A21
A31
A12
A22
A32
A13
A23
A33
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
For Example 4.2,
A
2
1
−
2
4
3
3
−
1
2
−
5
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= B
11
−
16
−
21
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= D A
:= D 19
=
Chapter 4: Matrices and Linear Algebra 111

122. ,
x
B1
B2
B3
A1 2
,
A2 2
,
A3 2
,
A1 3
,
A2 3
,
A3 3
,
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
D
:= y
A1 1
,
A2 1
,
A3 1
,
B1
B2
B3
A1 3
,
A2 3
,
A3 3
,
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
D
:= z
A1 1
,
A2 1
,
A3 1
,
A1 2
,
A2 2
,
A3 2
,
B1
B2
B3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
D
:=
where the matrix elements have been specified in the format required by Mathcad. These
calculations result in
x 2
= y 4
−
= z 1
=
4.5 SOLUTION OF LINEAR ALGEBRAIC EQUATIONS USING THE
FUNCTION lsolve
The lsolve function in Mathcad can be used to solve a system of linear algebraic equations .
Given:
[A] {X}= {B},
the function lsolve (A,B) will return the solution vector {X}, provided the matrix [A] is not
singular or nearly singular. For Example 4.2,
A
2
1
−
2
4
3
3
−
1
2
−
5
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= B
11
−
16
−
21
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
X lsolve A B
,
( )
:= gives X
2
4
−
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Example 4.3
Application of Matrices to Electrical Circuit Analysis.
Formulate a set of linear equations that represent the relationship between voltage, current and
resistances for the circuit shown in Figure 4.3. Solve the simultaneous equations generated using
(1) the inverse (2) Cramer's Rule and (3) the Mathcad function lsolve
112 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

123. Figure 4.3. Electrical circuit example
The governing equations are:
i1 + i2 = i3
7 i1 + 3 i3 = 6
7 i1 - 5 i2 = 6
These must be put in the form: [A] {X} = {B} and solved for {X}
Using the inverse
A
1
7
7
1
0
5
−
1
−
3
0
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= B
0
6
6
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
<--These are the currents i1, i2 and
i3
X A
1
−
B
⋅
:= X
0.6761
0.2535
−
0.4225
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Using Cramer's Rule
L
0
6
6
1
0
5
−
1
−
3
0
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= M
1
7
7
0
6
6
1
−
3
0
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= N
1
7
7
1
0
5
−
0
6
6
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
i1
L
A
:= i2
M
A
:= i3
N
A
:= i1 0.676
= i2 0.254
−
= i3 0.4225
=
Chapter 4: Matrices and Linear Algebra 113

124. Using Mathcad Function lsolve
X lsolve A B
,
( )
:= X
0.676
0.254
−
0.423
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= <--These are the currents i1, i2 and i3
4.6 THE EIGENVALUE PROBLEM
Eigenvalue problems occur in a variety of physical situations. Some examples of eigenvalue
problems are given below.
1. Determination of natural frequencies and mode shapes of oscillating systems.
2. Computation of principal stresses and principal directions
3. Computation of principal moments of inertia and principal axes.
4. Buckling of structures.
5. Oscillations of electrical networks.
The eigenvalue problem can be mathematically stated as
[A] {X} = λ {X} (4.8)
where [A] is a known square matrix, {X} is a column vector of unknowns, and λ is an unknown
scalar quantity. The solution of the eigenvalue problem involves the determination of vectors
{X} and associated constants λ satisfying equation (4.8). These vectors {X} are termed
eigenvectors. With each eigenvector is associated a constant λ which is called an
eigenvalue.
Equation (4.8) can be written in the form
[A- λ I ] {X} = {0} (4.9)
A trivial solution to the above is
{X} = 0
which is not of interest to us. The condition for the existence of a non-trivial solution is
det ( A- λ I ) = 0 (4.10)
114 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

125. Expansion of the above determinant produces a polynomial in λ. For instance, if [A] is a 3x 3
matrix, then Equation (4.10) would give a cubic in λ. This polynomial is called the
characteristic polynomial and its roots are called eigenvalues. Associated with each
eigenvalue is a solution vector {X} called the eigenvector.
It can be shown that the adjoint of matrix (A- λiI) contains columns, each of which is the ith
eigenvector {X} i associated with the eigenvalue λ i multiplied by an arbitrary constant.
Thus, to determine an eigenvector corresponding to an eigenvalue λi , compute the adjoint of
(A- λiI) and choose any column of it as the eigenvector.
Example 4.4
Compute the eigenvalues and eigenvectors of
17
45
6
−
16
−
⎛
⎜
⎝
⎞
⎟
⎠
A
17
45
6
−
16
−
⎛
⎜
⎝
⎞
⎟
⎠
:=
The [A- λI] matrix can be written as
A λ I
⋅
−
17 λ
−
45
6
−
16
− λ
−
⎛
⎜
⎝
⎞
⎟
⎠
=
A non-trivial solution is obtained by setting the determinant of [ A - λ I ] equal to zero
17 λ
−
45
6
−
16
− λ
−
⎛
⎜
⎝
⎞
⎟
⎠
0
=
which gives λ 2 - λ - 2 = 0, or, λ 1 = 2, λ 2 = -1. The adjoint of the matrix (A- λ I ), in
this case, is
16
− λ
−
45
−
6
17 λ
−
⎛
⎜
⎝
⎞
⎟
⎠
For λ 1 = 2, the corresponding eigenvector is the first or second column of the above
adjoint matrix with λ = λ 1 which gives
Chapter 4: Matrices and Linear Algebra 115

126. {X}
1
=
18
−
45
−
⎛
⎜
⎝
⎞
⎟
⎠
or
2
5
⎛
⎜
⎝
⎞
⎟
⎠
or
0.4
1
⎛
⎜
⎝
⎞
⎟
⎠
as the first eigenvector.
Similarly, the second eigenvector is obtained by putting λ = λ 2 in any one column of the
adjoint matrix which gives
{X}
2
=
15
−
45
−
⎛
⎜
⎝
⎞
⎟
⎠
or,
1
3
⎛
⎜
⎝
⎞
⎟
⎠
or
0.333
1
⎛
⎜
⎝
⎞
⎟
⎠
4.7 SOLVING THE EIGENVALUE PROBLEM WITH MATHCAD
The Mathcad function eigenvals(A) returns a vector containing the eigenvalues of the matrix A
Let A
1
1
1
1
2
0
1
2
3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Then,
eigenvals A
( )
3.879
0.468
1.653
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
The Mathcad function eigenvecs(A) returns a matrix containing normalized eigenvectors of
the square matrix A. The nth column of this matrix is an eigenvector corresponding to the nth
eigenvalue returned by eigenvals(A).
eigenvecs A
( )
0.433
−
0.755
−
0.493
−
0.923
−
0.127
0.364
0.535
−
0.746
−
0.397
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
The Mathcad function eigenvec(A,z) returns a matrix containing the normalized
eigenvector corresponding to the eigenvalue z of the square matrix A. For example, the
eigenvector associated with the eigenvalue 0.468 is
116 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

127. eigenvec A 0.468
,
( )
0.923
0.127
−
0.364
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
For Example 4.4, the matrix given was
A
17
45
6
−
16
−
⎛
⎜
⎝
⎞
⎟
⎠
:=
The eigenvalues and eigenvectors obtained with Mathcad are
eigenvals A
( )
2
1
−
⎛
⎜
⎝
⎞
⎟
⎠
= eigenvecs A
( )
0.371
0.928
0.316
0.949
⎛
⎜
⎝
⎞
⎟
⎠
= or
0.4
1
0.333
1
⎛
⎜
⎝
⎞
⎟
⎠
4.8 APPLICATION OF THE EIGENVALUE PROBLEM TO VIBRATION
ENGINEERING
Figure 4.4. Mathematical model of two-story building
Consider the vibration problem of a two -story building which is mathematically modeled as the two
degree of freedom system shown in Figure 4.4, in which the building is represented by lumped
masses m and 2m and springs k and 2k .
After drawing suitable free body diagrams of the two masses m and 2m, the governing
Chapter 4: Matrices and Linear Algebra 117

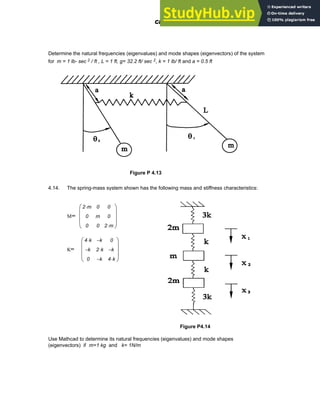
128. differential equations of motion can be seen to be
2 m d2x1 /dt2 + 3 k x1 - k x2 = 0
m d2x2 /dt2 +k ( x2 - x1 ) = 0
(4.11)
Expressing the above equations in matrix form as
..
(4.12)
[M] {x} + [K ] {x} = {0}
where [M] is the mass or inertia matrix , and [K] is the stiffness matrix, and assuming that
{x} = {A}sin ωt (4.13)
we obtain a set of linear homogeneous algebraic equations that can be written in matrix form as
(4.14)
([K]- ω2 [M ] ) {A} = 0
For a non-trivial solution, the determinant | K- ω2 M | must be zero. The problem can also be
posed slightly differently in the familiar form
|A-λI| = 0 (4.15)
where the λ 's ( λ = ω2) are the eigenvalues of the matrix [A] , which, in this case, is
[A] = [M] -1 [K] (4.16)
To find the natural frequencies and mode shapes in this case, we need to determine the
eigenvalues and eigenvectors of the matrix [A]. The square roots of the eigenvalues will then
give the natural frequencies and the corresponding eigenvectors will be the mode shapes.
Letting m = 1, and k =1 in this problem for convenience
m 1
:= k 1
:=
Then, the mass and stiffness matrices
M
2 m
⋅
0
0
m
⎛
⎜
⎝
⎞
⎟
⎠
:= K
3 k
⋅
k
−
k
−
k
⎛
⎜
⎝
⎞
⎟
⎠
:=
118 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

129. give
M
2
0
0
1
⎛
⎜
⎝
⎞
⎟
⎠
= K
3
1
−
1
−
1
⎛
⎜
⎝
⎞
⎟
⎠
=
The [A] matrix, which is called the dynamic matrix in the language of vibrations is ,
A M
1
−
K
⋅
:= which gives A
1.5
1
−
0.5
−
1
⎛
⎜
⎝
⎞
⎟
⎠
=
The eigenvalues of [A] are obtained from setting the determinant of [A-λI] equal to zero, as
follows
A λ I
⋅
− 0
=
This yields
1.5 λ
−
( ) 1 λ
−
( )
⋅ 0.5
− 0
= , or, λ1 = 0.5 , and λ2 = 2
The adjoint of the matrix [A-λI] is
1 λ
−
( )
1
0.5
1.5 λ
−
( )
⎡
⎢
⎣
⎤
⎥
⎦
In Vibration Engineering, eigenvectors are termed as natural modes or mode shapes, and
these are simply the configurations that the system takes when vibrating at a natural
frequency. Because the system considered here is a two-degree-of-freedom system, there
will be two natural frequencies and correspondingly two modes. While the natural
frequencies are simply the square roots of the eigenvalues, the associated eigenvectors or
modeshapes can be determined by putting λ = λ1(for the first mode ) and λ = λ2 (for the
second mode ) in either column of the adjoint of [A- λ I]
This procedure generates the following mode shapes
FirstMode
0.5
1
⎛
⎜
⎝
⎞
⎟
⎠
:= and SecondMode
1
1
⎛
⎜
⎝
⎞
⎟
⎠
:=
The determination of eigenvalues and eigenvectors using Mathcad is done below.
Chapter 4: Matrices and Linear Algebra 119

130. lambda eigenvals A
( )
:= lambda
2
0.5
⎛
⎜
⎝
⎞
⎟
⎠
=
By default, Mathcad arrays begin at element zero. To change this to begin at element 1,
choose "Worksheet Options" from the " Tools" menu, click on the "Built-In Variables"
tab and set "ORIGIN" to 1.
i 1 2
..
:= ωi lambdai
:= ωi
1.414
0.707
=
In Vibration Engineering, the lowest natural frequency is always considered as the first or
fundamental natural frequency. In this case, the natural frequencies are
ω2 0.707
= <--First natural frequency in rads/sec
ω1 1.414
= <--Second natural frequency in rads/sec
The eigenvectors or mode shapes can be determined, using the Mathcad function eigenvecs
as follows
X eigenvecs A
( )
:=
This gives the following matrix of eigenvectors which is referred to as the modal matrix in
Vibrations language
X
0.707
0.707
−
0.447
0.894
⎛
⎜
⎝
⎞
⎟
⎠
= <- Modal Matrix
A close inspection of the analysis will show that it is not possible to obtain unique values for the
eigenvector components. Therefore, it is traditional to select a value of unity for one of the
components of an eigenvector and compute the other one accordingly . This is called
normalization and should be clear from the calculation shown below.
The first natural mode, corresponding to the first natural frequency is
120 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

131. FirstMode
X1 2
,
0.8944
X2 2
,
0.8944
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= FirstMode
0.5
1
⎛
⎜
⎝
⎞
⎟
⎠
=
while the second natural mode, corresponding to the second natural frequency is
SecondMode
X1 1
,
0.7071
−
X2 1
,
0.7071
−
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= SecondMode
1
−
1
⎛
⎜
⎝
⎞
⎟
⎠
=
These mode shapes are sketched in Figure 4.5.
Figure 4.5. Modes shapes of the two-story building
Example 4.5.
Investigate the free vibration of a three-story building mathematically modeled as the
three-degree-of-freedom system shown in Figure 4.6.
Chapter 4: Matrices and Linear Algebra 121

132. Figure 4.6. Mathematical model of three-story building
The equations of motion of the mathematical model resorted to can be shown to be
m1
2
t
x1
d
d
2
⋅ k1 x1
⋅
+ k2 x2 x1
−
( )
⋅
− 0
=
m2
2
t
x2
d
d
2
⋅ k2 x2 x1
−
( )
⋅
+ k3 x3 x2
−
( )
⋅
− 0
= (4.17)
m3
2
t
x3
d
d
2
⋅ k3 x3 x2
−
( )
⋅
+ 0
=
These can be put in the following matrix format
[M] d2 {x} /dt2 + {K] { x } = { 0} (4.18)
where
122 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

133. [M] =
m1
0
0
0
m2
0
0
0
m3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
(4.19)
[K] =
k1 k2
+
( )
k2
−
0
k2
−
k2 k3
+
( )
k3
−
0
k3
−
k3
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
Letting m1 = 2x 10 6 kg , m2 = 14x 10 5 kg , m3 = 7x10 5 kg; and k1 = 12x10 8 N/ m,
k2= 8x 10 8 N/m , k3 = 4x 10 8 N/ m , the [A] matrix can be computed, using Mathcad ,
as follows
m1 2 10
6
⋅
:= m2 14 10
5
⋅
:= m3 7 10
5
⋅
:= k1 12 10
8
⋅
:= k2 8 10
8
⋅
:= k3 4 10
8
⋅
:=
M
m1
0
0
0
m2
0
0
0
m3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= K
k1 k2
+
( )
k2
−
0
k2
−
k2 k3
+
( )
k3
−
0
k3
−
k3
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:=
M
2 10
6
⋅
0
0
0
1.4 10
6
⋅
0
0
0
0.7 10
6
⋅
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= K
2 10
9
×
8
− 10
8
×
0
8
− 10
8
×
1.2 10
9
×
4
− 10
8
×
0
4
− 10
8
×
4 10
8
×
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
=
A M
1
−
K
⋅
:= A
1 10
3
×
571.429
−
0
400
−
857.143
571.429
−
0
285.714
−
571.429
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
The eigenvalues and the eigenvectors are
lambda eigenvals A
( )
:= lambda
1.495 10
3
×
761.106
172.146
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Chapter 4: Matrices and Linear Algebra 123

134. Note that Mathcad has found the highest eigenvalue first. The natural frequencies in Hz and the
corresponding eigenvectors are computed below.
i 1 2
, 3
..
:=
fi
lambdai
2 π
⋅
:= f1 6.154
= f2 4.391
= f3 2.088
= (Hz)
X eigenvecs A
( )
:= X
0.566
−
0.701
0.434
−
0.467
−
0.279
−
0.839
0.267
0.552
0.79
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
The normalized eigenvectors or mode shapes can be determined as shown.
Xnorm
X1 1
,
X1 1
,
X2 1
,
X1 1
,
X3 1
,
X1 1
,
X1 2
,
X1 2
,
X2 2
,
X1 2
,
X3 2
,
X1 2
,
X1 3
,
X1 3
,
X2 3
,
X1 3
,
X3 3
,
X1 3
,
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Xnorm
1
1.238
−
0.766
1
0.597
1.799
−
1
2.07
2.962
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Mode No: 3 2 1
Figure 4.7 shows the natural modes of the building as it vibrates at its natural
frequencies.
Figure 4.7. Mode shapes of three-story building
124 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

135. 4.9 APPLICATION OF THE EIGENVALUE PROBLEM TO STRESS
ANALYSIS- DETERMINATION OF PRINCIPAL STRESSES AND
PRINCIPAL DIRECTIONS
If [σ ] is the state of stress at a point in a material given by the stress components σxx ,
σyy, σzz, σxy , σyz and σzx , the principal stresses are the eigenvalues λ of the stress matrix
and the principal directions, which are the x, y and z components of the unit vectors along
the normals to the principal planes , are the eigenvectors {η} of the stress matrix. Thus ,
the eigenvalue problem in this case is stated as
[σ] - λ [ I ]) { η } = {0} (4.20)
where the eigenvalues λ and the eigenvectors η are to be determined.
Example 4.6
The two-dimensional state of stress in a mechanical element, which is shown in Figure 4.8, is
given by the components:
σ xx = 80 MPa, σyy = 0 , and σ xy = 50 MPa.
Determine the principal stresses and their associated directions.
Figure 4.8. Two-dimensional state of stress
Because the stress matrix is symmetrical, σ yx must be equal to σ xy. Thus, the matrix of
stresses is
Chapter 4: Matrices and Linear Algebra 125

136. σ
80
50
50
0
⎛
⎜
⎝
⎞
⎟
⎠
:= (MPa)
The principal stresses are the eigenvalues of the given stress matrix while the principal
directions are the associated eigenvectors. These are.
prinstress eigenvals σ
( )
:= prinstress
104.031
24.031
−
⎛
⎜
⎝
⎞
⎟
⎠
= (MPa)
prindir eigenvecs σ
( )
:= prindir
0.901
0.433
0.433
−
0.901
⎛
⎜
⎝
⎞
⎟
⎠
=
The principal direction associated with the maximum principal stress ( 104.031 MPa )
can be found in the form of a unit vector along the normal to the principal plane. Its x
and y components , prindir1, are computed below. Figure 4.9 shows the principal
stresses on the element and the associated principal directions.
prindir1 eigenvec σ 104.031
,
( )
:= prindir1
0.901
0.433
⎛
⎜
⎝
⎞
⎟
⎠
=
Figure 4.9. Principal stresses and principal directions for
two-dimensional stress example
Example 4.7
The three-dimensional state of stress in a mechanical element, which is shown in Figure
4.10, is given by:
σxx= 1000 psi, σyy = -1000 psi, σxy = 500 psi , σ yz = -200 psi, σ zx =100 psi , σ zz = 250
psi
Determine the principal stresses and their associated directions.
126 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

137. Figure 4.10. Three-dimensional state of stress
The stress matrix can be written as
(psi)
σ
1000
500
100
500
1000
−
200
−
100
200
−
250
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
The principal stresses and principal directions can be determined using Mathcad as
shown below
psi
prinstress eigenvals σ
( )
:= prinstress
1.152
− 10
3
×
1.121 10
3
×
280.707
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
prindir eigenvecs σ
( )
:= prindir
0.23
−
0.961
0.154
0.973
0.224
0.06
0.024
−
0.163
−
0.986
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
If only the principal direction associated with one of the principal stresses , say 280.707 psi, is
required, it can be found as follows.
Chapter 4: Matrices and Linear Algebra 127

138. prindir2 eigenvec σ 280.707
,
( )
:=
These are the the x and y
components of the unit
vector along the normal to the
principal plane associated with the
principal stress, 280.707 psi
prindir2
0.024
−
0.163
−
0.986
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= <-----
The principal stresses and their directions are shown in Figure 4.11. Note the orthogonality of the
principal stress directions with respect to one another.
acos 0.9730
( )
180
π
⋅ 13.344
= deg acos 0.224
( )
180
π
⋅ 77.056
= deg
acos 0.06
( )
180
π
⋅ 86.56
= deg
Figure 4.11. Principal stresses and principal directions for three-dimensional
state of stress.
4.10 REPEATED ROOTS IN THE DETERMINANTAL EQUATION
When equal roots are encountered in the determinantal equation, the associated
eigenvectors are not unique and thus a linear combination of these eigenvectors may also be
128 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

139. considered as eigenvectors. The following examples will illustrate this situation.
Example 4.8
For the given matrix [A]
A
0
1
−
1
1
−
0
1
1
1
0
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
the eigenvalues and eigenvectors are found using Mathcad as
<-- double root at λ = 1
lambda eigenvals A
( )
:= lambda
1
2
−
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
X eigenvecs A
( )
:= X
0.816
0.408
−
0.408
0.577
−
0.577
−
0.577
0.226
−
0.793
0.566
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
It is clear that the first and third eigenvectors corresponding to the repeated root λ = 1 are
arbitrary, since they are both different , while the one corresponding to λ = - 2 is
1
−
1
−
1
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
Example 4.9
The following problem is, clearly, a case of repeated roots with a double root at λ = 1
Chapter 4: Matrices and Linear Algebra 129

140. A
1
0
0
1
−
1
0
0
1
1
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
The eigenvalues and eigenvectors are
lambda eigenvals A
( )
:= lambda
1
1
1
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
X eigenvecs A
( )
:= X
1
0
0
1
0
0
0.218
−
0.436
−
0.873
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Note that the first and second eigenvectors corresponding to the repeated (double) root at λ
= 1 are, in fact , arbitrary since they have two components that are zero, while the one
corresponding to λ = -1 is the third one which is
1
−
2
−
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
Example 4.10
For the following matrix [A]
A
14
−
0
1
1
2
0
0
0
2
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
the eigenvalues and eigenvectors are
130 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

141. eigenvals A
( )
2
14
−
2
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
= eigenvecs A
( )
0
0
1
0.998
0
0.062
−
0
7.105 10
15
−
×
1
−
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
This is, again, a case of repeated roots in which the first and third eigenvectors corresponding
to the repeated roots are arbitrary. Thus, there is no unique eigenvector correponding to the
repeated root .
4.11 SOLUTION OF NONLINEAR SIMULTANEOUS EQUATIONS
There are no direct methods available for solving nonlinear simultaneous equations like you
have in the case of linear algebraic equations. In general, iterative procedures must be
resorted to, requiring initial guesses as a starting point. The following procedure utilizes an
adaptation of the Taylor series approach in obtaining a solution to a set of nonlinear
equations.
Consider the following two nonlinear equations:
f(x,y)= 0 ; g(x,y) = 0 (4.21)
which have the exact solution: x = x r and y = y r .
If x = x i and y = y i are approximate solutions, a Taylor series approximation about
( x i , y i ) gives
f( x r , y r ) = f(x i , y i ) + h ( partial deriv of f (x,y) with respect to x at (x i ,y i) ) +
j ( partial deriv of f(x,y) with respect to y at (x i , y i) ) + ... = 0
g (x r , y r ) = g( xi , y i ) + h ( partial deriv of g (x,y ) with respect to x at (xi , yi ) ) +
j ( partial deriv of g (x, y ) with respect to y at ( xi , yi ) ) + ....... = 0
(4.22)
where x r = x i + h , and y r = y i + j . (4.23)
If only linear terms are retained in the Taylor series, two linear equations are
generated in the two unknowns h and j, where h and j are approximations to ( x r - x i )
and ( yr - y i ) . Defining a, b, c and d as the partial derivatives in Equations (4.22) and
(4.23), p as f(x i , y i ) and q as g( xi , y i ) , these equations become
Chapter 4: Matrices and Linear Algebra 131

142. ah + bj = -p and ch + d j = -q (4.24)
When these two simultaneous equations are solved for h and j , we generate new
improved values for x and y, say x i+1 and y i+1 , where , x i + 1 = x i + h and y i+1 = yi +
j . These new improved values replace the old values x i and y i in the next step in an effort
to obtain still better solutions. This procedure is repeated until convergence occurs. The
following example will clarify the procedure.
Example 4.11
Determine the solution to: f(x,y) = x2 + 3 y 2 - 54 = 0 , g(x, y ) = -4 x 2 + 3x y - 2 y + 15 = 0
Iteration Number 1
f x y
,
( ) x
2
3 y
2
⋅
+ 54
−
:= g x y
,
( ) 4
− x
2
⋅ 3 x
⋅ y
⋅
+ 2 y
⋅
− 15
+
:=
partfx x y
,
( ) 2 x
⋅
:= partfy x y
,
( ) 6 y
⋅
:= partgx x y
,
( ) 8
− x
⋅ 3 y
⋅
+
:= partgy x y
,
( ) 3 x
⋅ 2
−
:=
where the above are partial derivatives of f(x,y) and g(x,y) with respect to x and y.
xold 1.5
:= yold 2.0
:= <-- Assumed starting values of solution
p f xold yold
,
( )
:= q g xold yold
,
( )
:=
a partfx xold yold
,
( )
:= b partfy xold yold
,
( )
:= c partgx xold yold
,
( )
:=
d partgy xold yold
,
( )
:=
a 3
= b 12
= c 6
−
= d 2.5
= p 39.75
−
= q 11
=
Now solve the equations obtained from the linear Taylor series approximations, namely
a h + b j = -p and c h + d j = -q
in the form: [A] {H} = {P} using lsolve as follows
A
a
c
b
d
⎛
⎜
⎝
⎞
⎟
⎠
:= P
p
−
q
−
⎛
⎜
⎝
⎞
⎟
⎠
:= H lsolve A P
,
( )
:= H
2.91
2.585
⎛
⎜
⎝
⎞
⎟
⎠
=
h H1
:= j H2
:= h 2.91
= j 2.585
=
xnew xold h
+
:= ynew yold j
+
:= xnew 4.41
= ynew 4.585
=
132 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

143. Iteration Number 2
xold xnew
:= yold ynew
:=
p f xold yold
,
( )
:= q g xold yold
,
( )
:=
a partfx xold yold
,
( )
:= b partfy xold yold
,
( )
:= c partgx xold yold
,
( )
:=
d partgy xold yold
,
( )
:=
a 8.821
= b 27.509
= c 21.528
−
= d 11.231
= p 28.516
= q 11.312
−
=
H lsolve A P
,
( )
:=
A
a
c
b
d
⎛
⎜
⎝
⎞
⎟
⎠
:= P
p
−
q
−
⎛
⎜
⎝
⎞
⎟
⎠
:= H
2.91
2.585
⎛
⎜
⎝
⎞
⎟
⎠
=
h H1
:= j H2
:= h 2.91
= j 2.585
=
xnew xold h
+
:= ynew yold j
+
:= xnew 7.321
= ynew 7.17
=
Following the same procedure as above, new improved values for x and y can be generated in
iterations 3, 4 and 5 as
Iteration Number 3: h 0.1166
−
:= j 0.0728
−
:= --> xnew 3.3804
:= ynew 3.7684
:=
Iteration Number 4: h 2.1741
− 10
3
−
⋅
:= j 6.5547
− 10
4
−
⋅
:= --> xnew 3.3782
:= ynew 3.7677
:=
Iteration Number 5: h 2.1741
− 10
3
−
⋅
:= j 6.5547
− 10
4
−
⋅
:= --> xnew 3.3782
:= ynew 3.7677
:=
f xnew ynew
,
( ) 1.075
− 10
3
−
×
= a check to see if a solution
has indeed been achieved
<---
g xnew ynew
,
( ) 2.085
− 10
4
−
×
=
Thus, it is clear that convergence has occurred in the fourth iteration because the values of
the functions f ( x, y ) and g (x, y ) are zero and the answers (xnew and ynew) obtained in the
fifth iteration are exactly the same as in the fourth. The solution is : x= 3.3782 and y =
3.7677. These answers may now be verified by using the given and find commands.
x 1
:= y 1
:= <--- Initial guesses required by Mathcad
Given x
2
3 y
2
⋅
+ 54.0
− 0
= 4
− x
2
⋅ 3 x
⋅ y
⋅
+ 2 y
⋅
− 15.0
+ 0
= <---- Press "Ctrl=" to
type "="
xval
yval
⎛
⎜
⎝
⎞
⎟
⎠
Find x y
,
( )
:= xval 3.378
= yval 3.768
= <--- Solution
Chapter 4: Matrices and Linear Algebra 133

144. PROBLEMS
4.1. Given the matrix
2
−
1
0
1
−
1
3
5
−
4
3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
find its inverse or else show that it is singular. Do calculations on a calculator.
Also check your answers with Mathcad
4.2. Given the matrix
0
1
1
0
12
2
−
1
−
0
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
Find its inverse or else show that it is singular. Do calculations on a calculator. Also
check your answers with Mathcad.
4.3. Solve the following by Cramer's rule:
(a) x + y = 4 ; 2x - y = 2
(b) 5x - 3 y = 37 ; -2x + 7 y = - 38
4.4. Solve the following system of equations
8x-y-z =4 ; x +2 y -3 z = 0 ; 2 x -y +4 z =5
Do this problem on a calculator. Check your answers with (1) Mathcad, using the inverse
and (2) Mathcad's lsolve function.
4.5. Solve the following system of equations :
x + y + z = 6 ; 2 x - y + 3z = 9 ; x + 2 y - z = 2
Do this problem on a calculator. Check your answers with (1) Mathcad, using the inverse
and (2) Mathcad's lsolve function.
134 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

145. 4.6. Solve the following system of equations :
x + y + 3 z = 96 ; 2 x - y + 7z = 6 ; x + 2 y - 5z = 2
Do this problem on a calculator. Check your answers with (1) Mathcad, using the inverse and (2)
Mathcad's lsolve function.
4.7. Solve the following by Cramer's rule:
x + y - 3z = 0 ; y - 4z = 0 ; x- y - z =5
Do this problem on a calculator. Check your answers with (1) Mathcad, using Cramer's
rule and (2) Mathcad's lsolve function.
4.8. Find the eigenvalues of the matrix
1
2
3
1
⎛
⎜
⎝
⎞
⎟
⎠
Corresponding to each eigenvalue, find an eigenvector. Do this problem on a calculator.
Check your answers with Mathcad, using the eigenvals, eigenvecs and eigenvec
functions
4.9. Find the eigenvalues of the following matrix. Find an eigenvector corresponding to
each eigenvalue.
5
−
1
0
2
⎛
⎜
⎝
⎞
⎟
⎠
Do this problem on a calculator. Check your answers with Mathcad, using the
eigenvals, eigenvecs and eigenvec functions .
4.10. Determine the eigenvalues and eigenvectors of the following matrices.
(a)
3
4
4
3
⎛
⎜
⎝
⎞
⎟
⎠
(b)
5
0
0
5
⎛
⎜
⎝
⎞
⎟
⎠
(c)
6
0
0
6
⎛
⎜
⎝
⎞
⎟
⎠
(d)
4
5
2
1
⎛
⎜
⎝
⎞
⎟
⎠
(d)
10
0
0
10
⎛
⎜
⎝
⎞
⎟
⎠
(e)
6
8
2
1
⎛
⎜
⎝
⎞
⎟
⎠
Chapter 4: Matrices and Linear Algebra 135

146. 4.11. The differential equations of motion of the spring-mass system shown are:
m
2
t
x1
d
d
2
⋅ 2 k
⋅ x1
⋅ k x2
⋅
−
( )
+ 0
= and 2 m
⋅
2
t
x2
d
d
2
⋅ 2 k
⋅ x2
⋅ k x1
⋅
−
( )
+ 0
=
Figure P 4.11
Obtain the natural frequencies ( eigenvalues ) and mode shapes ( eigenvectors) of the
system for m= 1 lb--sec 2 / ft and k = 1 lb/ ft
4.12 The two-dimensional state of stress in psi at a point on a machine element is
prescribed as:
σ
12
4
4
6
⎛
⎜
⎝
⎞
⎟
⎠
=
Obtain the eigenvalues (principal stresses) and their associated directions (eigenvectors).
4.13. For the two pendulums shown which are coupled by means of a spring "k" , the
governing differential equations are:
m L
2
⋅
2
t
θ1
d
d
2
⋅ m
− g
⋅ L
⋅ θ1
⋅ k a
2
⋅ θ1 θ2
−
( )
⋅
−
=
and
m L
2
⋅
2
t
θ2
d
d
2
⋅ m
− g
⋅ L
⋅ θ2
⋅ k a
2
⋅ θ2 θ1
−
( )
⋅
−
=
136 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

147. Determine the natural frequencies (eigenvalues) and mode shapes (eigenvectors) of the system
for m = 1 lb- sec 2 / ft , L = 1 ft, g= 32.2 ft/ sec 2, k = 1 lb/ ft and a = 0.5 ft
Figure P 4.13
4.14. The spring-mass system shown has the following mass and stiffness characteristics:
M=
2 m
⋅
0
0
0
m
0
0
0
2 m
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
K=
4 k
⋅
k
−
0
k
−
2 k
⋅
k
−
0
k
−
4 k
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
Figure P4.14
Use Mathcad to determine its natural frequencies (eigenvalues) and mode shapes
(eigenvectors) if m=1 kg and k= 1N/m
Chapter 4: Matrices and Linear Algebra 137

148. 4.15. Determine the roots of the nonlinear simultaneous equations
f(x,y) = x 2 + y 2 -4.5 = 0 and g(x,y) = x 3 - 1.5 y = 0
using the Taylor series approach. Check your answer using the Given and Find functions
of Mathcad
4. 16. Determine the roots of the nonlinear simultaneous equations
f(x,y) = x 3 + y 3 - 5.5 = 0 and g(x,y) = x 4 - 3 y2 = 0
using the Taylor series approach. Check your answer using the Given and Find functions of
Mathcad .
4.17. A two-degree-of-freedom mathematical model of an automobile suspension system
is shown . With the system modeled as a rigid bar of mass " m " and mass moment of
inertia " I " connected to springs , the governing differential equations are:
W
g 2
t
x t
( )
d
d
2
⋅ 4000 x t
( )
⋅
+ 2000 θ t
( )
⋅
+ 0
=
R eference
C .G .
x
K 1 K 2
L 1
L 2
and
I
2
t
θ t
( )
d
d
2
⋅ 2000 x t
( )
⋅
+ 65000. θ t
( )
⋅
+ 0
=
Figure P 4.17
where "x" represents the linear up and down ( bounce) motion and "θ" represents the
angular motion (pitch) of the system . Determine the natural frequencies (eigenvalues )
and mode shapes ( eigenvectors ) if W = 3000 lbs , I = 300 lb-ft-sec 2 , and g =
acceleration due to gravity = 32.2 ft / sec 2
138 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

149. 4.18. The governing differential equations of motion of the double pendulum shown in terms of
angular displacements θ1(t) and θ2(t) are
L
2
t
θ1
d
d
2
⋅ 2 g
⋅ θ1
⋅
+ g θ2
⋅
− 0
= and L
2
t
θ2
d
d
2
⋅ 2 g
⋅ θ2
⋅
+ 2 g
⋅ θ1
⋅
− 0
=
1
L
L
m
m
x 1
x 2
2
,
where "g" is the acceleration due to gravity
= 32.2 ft/ sec 2 and L is the length of each
pendulum. Using matrix methods , determine
the natural frequencies(eigenvalues) and
mode-shapes (eigenvectors) of the system
for L = 1 ft.
Figure P 4.18
4.19. An automobile is math-modeled as the two-degree-of-freedom system shown above
in Figure P 4.17. Its up and down linear motion ( bounce ) is represented by the coordinate
x(t) while its angular motion ( pitch) is represented by the coordinate θ(τ). The governing
differential equations of motion are:
m
2
t
x
d
d
2
⋅ K1 K2
+
( ) x
⋅ K1 L1
⋅ K2 L2
⋅
−
( ) θ
⋅
−
⎡
⎣ ⎤
⎦
+ 0
=
JO 2
t
θ
d
d
2
⋅ K1 L1
⋅ K2 L2
⋅
−
( ) x
⋅ K1 L1
2
⋅ K2 L2
2
⋅
+
⎛
⎝
⎞
⎠ θ
⋅
+
⎡
⎣
⎤
⎦
+ 0
=
Determine the natural frequencies (eigenvalues) and mode-shapes (eigenvectors) of an
automobile with the following data:
m = 100 lb-sec2/ ft , JO = 1600 lb-ft-sec2 , L1 = 5.5 ft , L2 = 4.5 ft,
K1= 2600 lbs / ft , K 2 = 2400 lbs/ ft.
Chapter 4: Matrices and Linear Algebra 139

150. 4.20. A rigid rod of negligible mass and length 2L is pivoted at the middle point and is
constrained to move in the vertical plane by springs and masses shown. The governing
differential equations of motion of the system are given as:
m
2
t
x
d
d
2
⋅ 2 k
⋅ x
⋅
+ k L
⋅ θ
⋅
+ 0
= , 4 m
⋅ L
2
⋅
2
t
θ
d
d
2
⋅ k L
⋅ x
⋅
+ 2 k
⋅ L
2
⋅ θ
⋅
+ 0
=
K
K
L
L
(t)
2 m
2 m
m
K
x (t)
Figure P 4.20
Determine the natural frequencies (eigenvalues) and mode-shapes (eigenvectors) of the system
for m = 1 kg, L = 1 meter, and k = 1 N/m .
4.21. The governing differential equations of motion of the double pendulum shown in
Figure P 4.18 in terms of coordinates of coordinates x1(t) and x2 (t) are
L
2
t
x1
d
d
2
⋅ 3 g
⋅ x1
⋅
+ g x2
⋅
− 0
= , L
2
t
x2
d
d
2
⋅ g x2
⋅
+ g x1
⋅
− 0
=
where "g" is the acceleration due to gravity = 32.2 ft/ sec 2 and L is the length of each
pendulum. Determine the natural frequencies (eigenvalues) and mode-shapes (eigenvectors) of
the system for L = 1 ft.
4. 22. Determine the roots of the nonlinear simultaneous equations
f(x,y) = x 2 + 2 x y - 64 = 0 and g(x,y) = 3 x 2 + 6 y2 - 264 = 0
using the Taylor series approach. Obtain answers that are correct to two decimal places.
Use starting values xold= 3 and yold = 5 . Check your answer using the Given and Find
functions of Mathcad .
140 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

151. C H A P T E R 5
NUMERICAL INTERPOLATION
In any field where measured or statistical data is involved, a need to interpolate between given
data points is bound to exist. Because measured or available data is , typically, not provided in
the form of an analytically determined function , the process known as interpolation must be
resorted to in order to obtain function values at points other thn the given data points. This
process involves the generation of a curve that must pass through the given data points and its
use in determining the function value at any intermediate point on this curve. As will be seen in
the sections following, a polynomial fitting n data points will be of order (n-1), that is one less
than the number of data points given. Thus, four data points will generate a cubic while three
data points will give a quadratic and so on.
5.1 LINEAR INTERPOLATION
Given two data points ( x k , y k ) and (x k+1 , y k+1 ), as shown in the figure below, the
connection between the coordinates of a point ( x, y) lying between the data points can be
expressed by the linear relationship
y
yk xk xk 1
+
−
( )
⋅ y
k 1
+
( ) x xk
−
( )
⋅
−
xk xk 1
+
−
= (5.1)
5.2 THE METHOD OF UNDETERMINED COEFFICIENTS
Given the data points ( x k , y k ), k= 0...n, it is required to find an interpolating polynomial
P n ( x ) such that the following constraint equations are satisfied
Pn x0
( ) y0
=
Chapter 5: Numerical Interpolation 141

152. Pn x1
( ) y1
=
(5.2)
Pn xn
( ) yn
=
Assuming the interpolating polynomial P n ( x ) is of the form
Pn x
( ) a0 a1 x
⋅
+ a2 x
2
⋅
+ ............
+ an x
n
⋅
+
= , (5.3)
Equations (5.2) yield the following matrix equation
1
1
1
x0
x1
xn
xo
( )2
x1
( )2
xn
( )2
x0
( )n
x1
( )n
xn
( )n
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
a0
a1
an
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⋅
y0
y1
yn
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= (5.4)
Once the equations represented by the matrix equation (5.4) are solved for the n unknowns
a0, a1,..... , a n , the interpolating polynomial P n ( x ) satisfying the constraint
equations is completely determined. In general, the higher the order of the interpolating
polynomial, the more accurate would be the results of the interpolation process.
EXAMPLE 5.1
Determine the polynomial f(x) that passes thru (0,2), (1,2.25) and (2,5.82), and
compute f(0.5) and f(1.5).
The given data is put in as follows. Go to the Insert menu, select Matrix, put in
the appropriate number of rows and columns and then fill in the placeholders.
142 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

153. X
0
1
2
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= Y
2
2.25
5.82
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
The order of the polynomial fitting 3 data points is 2 and the form, thus, is
f(x) = a + b x + c x 2 .
Therefore, the matrix equation that needs to be solved for the coefficients a, b and c is
1
1
1
0
1
2
0
2
1
2
2
2
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
a
b
c
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
⋅
2
2.25
5.82
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
Using Cramer's rule, the solution to the above equation can be written as :
a = m1/ D , b= m2/D and c = m3/D,
where
m1
2
2.25
5.82
0
1
2
0
1
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= m2
1
1
1
2
2.25
5.82
0
1
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= m3
1
1
1
0
1
2
2
2.25
5.82
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= D
1
1
1
0
1
2
0
1
4
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
a
m1
D
:= b
m2
D
:= c
m3
D
:= a 2
= b 1.41
−
= c 1.66
=
Thus, the interpolating polynomial generated is
f x
( ) a b x
⋅
+ c x
2
⋅
+
:= with a 2
= b 1.41
−
= c 1.66
=
It is plotted in Figure 5.1 below, which gives
Chapter 5: Numerical Interpolation 143

154. f 0.5
( ) 1.71
= f 1.5
( ) 3.62
=
x 0 0.1
, 2
..
:=
0 0.5 1 1.5 2
1
2
3
4
5
6
Given data points
Interpolation
Given data points
Interpolation
Interpolated function
Yi
f x
( )
Xi x
,
Figure 5.1. Interpolated function using undetermined coefficient method
5.3 THE GREGORY-NEWTON INTERPOLATING POLYNOMIAL
The form of the nth order Gregory-Newton interpolating polynomial is
f x
( ) a1 a2 x x1
−
( )
⋅
+ a3 x x1
−
( )
⋅ x x2
−
( )
⋅
+ a4 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅
+
....... an x x1
−
( )
⋅ x x2
−
( )
⋅ .... x xn 1
−
−
( )
+ an
+ 1 x x1
−
( )
⋅ x x2
−
( )
⋅ .... x xn
−
( )
+
+
...
=
(5.5)
where the a' s are unknown coefficients that can be determined as was done in the method of
undetermined coefficients. That is ,
f xk
( ) yk
= k 1 ..n 1
+
,
:= .. (5.6)
where the xk and yk are the given data points that the interpolating polynomial must pass
through.
144 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

155. To obtain a second order polynomial, put x= x1 , x= x 2 and x = x 3 in Equation (5.5)
yielding
a1 y1
=
a2
y2 y1
−
x2 x1
−
=
(5.7)
a3
y3 a1
− a2 x3 x1
−
( )
⋅
−
x3 x1
−
( ) x3 x2
−
( )
⋅
=
The interpolating polynomial is then determined as
f x
( ) a1 a2 x x1
−
( )
⋅
+ a3 x x1
−
( )
⋅ x x2
−
( )
⋅
+
= (5.8)
which is a second order polynomial passing through the three data points ( x1, y1 ),
(x2, y2 ) and (x3, y3 ).
For obtaining a third order polynomial, a fourth data point will be needed , and a fourth order
polynomial will require the use of a fourth as well as a fifth data point . In general, determining
an nth order polynomial , then, will require (n+1 ) data points to be prescribed. Thus, the
coefficients a4 , a5 and a6 can be determined using
a4
y4 a1
− a2 x4 x1
−
( )
⋅
− a3 x4 x1
−
( )
⋅ x4 x2
−
( )
⋅
−
x4 x1
−
( ) x4 x2
−
( )
⋅ x4 x3
−
( )
⋅
= (5.9)
a5
y5 a1
− a2 x5 x1
−
( )
⋅
− a3 x5 x1
−
( )
⋅ x5 x2
−
( )
⋅
− a4 x5 x1
−
( )
⋅ x5 x2
−
( )
⋅ x5 x3
−
( )
⋅
−
x5 x1
−
( ) x5 x2
−
( )
⋅ x5 x3
−
( )
⋅ x5 x4
−
( )
⋅
=
(5.10)
Chapter 5: Numerical Interpolation 145

156. a6
y6 a1
− a2 x6 x1
−
( )
⋅
− a3 x6 x1
−
( )
⋅ x6 x2
−
( )
⋅
− a4 x6 x1
−
( )
⋅ x6 x2
−
( )
⋅ x6 x3
−
( )
⋅
−
1
−
( ) a5
⋅ x6 x1
−
( ) x6 x2
−
( )
⋅ x6 x3
−
( )
⋅ x6 x4
−
( )
⋅
⎡
⎣ ⎤
⎦
⋅
+
...
x6 x1
−
( ) x6 x2
−
( )
⋅ x6 x3
−
( )
⋅ x6 x4
−
( )
⋅ x6 x5
−
( )
⋅
=
(5.11)
Example 5.2 -
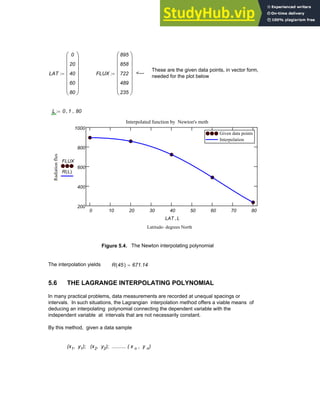
Given three data points: X: 100 200 400
Y: 975 1575 2054
Determine the Gregory -Newton Polynomial f(x) and evaluate f(251)
The form of this polynomial will be :
y = f(x) = a1 + a2(x-X1 + a3(x-X1)(x-X2)
with a1 = Y1
a2 = (Y2-Y1) / (X2-X1)
a3 = [ Y3- a1 -a2(X3-X1)] /[ (X3-X1)(X3-X2)]
The data is put in in vector form as follows.
X
100
200
400
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= Y
975
1575
2054
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
and the coefficients a1, a2 and a3 are computed using
a1 Y1
:= a2
Y2 Y1
−
X2 X1
−
:= a3
Y3 a1
− a2 X3 X1
−
( )
⋅
−
X3 X1
−
( ) X3 X2
−
( )
⋅
:=
146 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

157. a1 975
= a2 6
= a3 0.012
−
=
Thus, the interpolating polynomial generated is
f x
( ) a1 a2 x X1
−
( )
⋅
+ a3 x X1
−
( )
⋅ x X2
−
( )
⋅
+
:=
which is plotted in Figure 5.2 below, giving
f 251
( ) 1.788 10
3
×
=
x 100 105
, 400
..
:=
100 150 200 250 300 350 400
500
1000
1500
2000
2500
Given data points
Interpolation
Given data points
Interpolation
Gregory-Newton Interpolating Polynomial
x- values
Function
values
Yi
f x
( )
Xi x
,
Figure 5.2. Interpolated function obtained using Gregory-Newton
polynomial method
Example 5.3
Given: x: 0 100 200 300 400 500
y: 104.2 97.3 48.1 23.7 8.6 5.2
Determine a fifth order Gregory-Newton interpolating polynomial f(x)
and evaluate f(150 ), f(350) and f (450).
Chapter 5: Numerical Interpolation 147

158. Because six data points are given, the interpolating polynomial in this case will be of fifth
order, and will have the following form
f(x) = a1 + a2(x-x1) + a3(x-x1)(x-x2) + a4(x-x1)(x-x2)(x-x3)
+a5(x-x1)(x-x2)(x-x3)(x-x4) + a6x-x1)(x-x2)(x-x3)(x-x4)(x-x5)
where a1, a2 .... are computed as shown below.
x1 0
:= x2 100
:= x3 200
:= x4 300
:= x5 400
:= x6 500
:=
y1 104.2
:= y2 97.3
:= y3 48.1
:= y4 23.7
:= y5 8.6
:= y6 5.2
:=
a1 y1
:= a2
y2 y1
−
x2 x1
−
:= a3
y3 a1
− a2 x3 x1
−
( )
⋅
−
x3 x1
−
( ) x3 x2
−
( )
⋅
:=
a4
y4 a1
− a2 x4 x1
−
( )
⋅
− a3 x4 x1
−
( )
⋅ x4 x2
−
( )
⋅
−
x4 x1
−
( ) x4 x2
−
( )
⋅ x4 x3
−
( )
⋅
:=
a5
y5 a1
− a2 x5 x1
−
( )
⋅
− a3 x5 x1
−
( )
⋅ x5 x2
−
( )
⋅
− a4 x5 x1
−
( )
⋅ x5 x2
−
( )
⋅ x5 x3
−
( )
⋅
−
x5 x1
−
( ) x5 x2
−
( )
⋅ x5 x3
−
( )
⋅ x5 x4
−
( )
⋅
:=
a6
y6 a1
− a2 x6 x1
−
( )
⋅
− a3 x6 x1
−
( )
⋅ x6 x2
−
( )
⋅
− a4 x6 x1
−
( )
⋅ x6 x2
−
( )
⋅ x6 x3
−
( )
⋅
−
1
−
( ) a5
⋅ x6 x1
−
( )
⋅ x6 x2
−
( )
⋅ x6 x3
−
( )
⋅ x6 x4
−
( )
⋅
+
...
x6 x1
−
( ) x6 x2
−
( )
⋅ x6 x3
−
( )
⋅ x6 x4
−
( )
⋅ x6 x5
−
( )
⋅
:=
The above equations generate the following computed coefficients
a1 104.2
= a2 0.069
−
= a3 2.115
− 10
3
−
×
= a4 1.118 10
5
−
×
=
a5 3.442
− 10
8
−
×
= a6 8.375 10
11
−
×
=
which are inserted into the interpolating polynomial
f x
( ) a1 a2 x x1
−
( )
⋅
+ a3 x x1
−
( )
⋅ x x2
−
( )
⋅
+ a4 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅
+
a5 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅
+
...
a6 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅ x x5
−
( )
⋅
+
...
:=
148 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

159. yielding
f 150
( ) 70.68
= f 350
( ) 16.435
= f 450
( ) 1.84
=
The interpolated curve f(x) is shown below in Figure 5.3 along with the given data points
X
0
100
200
300
400
500
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Y
104.2
97.3
48.1
23.7
8.6
5.2
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
x 0 5
, 500
..
:=
0 100 200 300 400 500
0
50
100
150
Given data points
Interpolation
Given data points
Interpolation
Interpolated function( Gregory-Newton)
x-values
Function
values
Yi
f x
( )
Xi x
,
Figure 5.3. Fifth order Gregory-Newton interpolating polynomial
5.4 INTERPOLATION USING FINITE DIFFERENCES
A finite difference table can furnish a way of developing an interpolating polynomial so long
as the known values of the independent variable are equally spaced. For an increment Δx in
the independent variable x, the first finite difference of the dependent variable y = f(x) is
Chapter 5: Numerical Interpolation 149

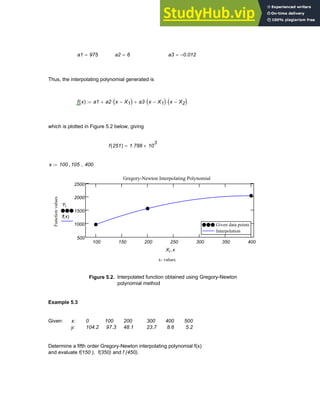
160. Δf = f(x+Δx)- f(x) (5.12)
The second finite difference is
Δ 2 f = Δ[Δf] =[f(x+2Δx)-f(x+Δx)]-[f(x+Δx)- f(x)] (5.13)
Similarly, the (n-1)th finite difference will be
Δn f = Δ[Δ n-1 f ] (5.14)
The finite differences as derived above are arranged in a table as shown in Table 5.1 which
can be used to generate an interpolating polynomial, as will be demonstrated later.
TABLE 5.1
Table of finite differences
--------------------------------------------------------------------------------------------------------------------------------
x f x
( ) Δf Δ
2
f Δ
3
f Δ
n
f
-------------------------------------------------------------------------------------------------------------------------------
x f x
( )
Δf x
( )
x Δx
+ f x Δx
+
( ) Δ
2
f x
( )
Δf x Δx
+
( ) Δ
3
f x
( )
x 2 Δx
⋅
+ f x 2 Δx
⋅
+
( ) Δ
2
f x Δx
+
( )
Δf x 2 Δx
⋅
+
( )
x 3 Δx
⋅
+ f x 3 Δx
⋅
+
( )
------------------------------------------------------------------------------------------------------------------------------------
150 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

161. An alternate representation of the above is shown in Table 5.2, in which the independent
variable goes from x0 to x3 and successive finite differences up to the fourth are generated
TABLE 5.2
Alternate form of finite-difference table
------------------------------------------------------------------------------------------------------------------------------------
xi yi Δyi Δ
2
yi Δ
3
yi Δ
4
yi
----------------------------------------------------------------------------------------------------------------------------------
x0 y0
Δy0 y1 y0
−
=
x1 y1 Δ
2
y0 Δy1 Δy0
−
=
Δy1 y2 y1
−
= Δ
3
y0 Δ
2
y1 Δ
2
y0
−
=
x2 y2 Δ
2
y1 Δy2 Δy1
−
= Δ
4
y0 Δ
3
y1 Δ
3
y0
−
=
Δy2 y3 y2
−
=
Δ
3
y1 Δ
2
y2 Δ
2
y1
−
=
x3 y3 Δ
2
y2 Δy3 Δy2
−
=
------------------------------------------------------------------------------------------------------------------------------------
5.5 NEWTON'S METHOD UTILIZING FINITE DIFFERENCES
Let ( x0, y0 ), (x1, y1 ) , ( x2, y2 )and ( x3, y3 ) be four given data points for which
a third degree Newton interpolating polynomial utilizing finite differences has to be determined .
Assume the interpolating polynomial to be
f x
( ) C0 C1 x x0
−
( )
⋅
+ C2 x x0
−
( )
⋅ x x1
−
( )
⋅
+ C3 x x0
−
( )
⋅ x x1
−
( )
⋅ x x2
−
( )
⋅
+
= (5.15)
Chapter 5: Numerical Interpolation 151

162. where the C's are undetermined coefficients that must be computed using the following constraint
equations that the polynomial must satisfy .
y0 f x0
( )
= y1 f x1
( )
= y2 f x2
( )
= y3 f x3
( )
=
(5.16)
which yield
y0 C0
=
y1 C0 C1 x1 x0
−
( )
⋅
+
=
(5.17)
y2 C0 C1 x2 x0
−
( )
⋅
+ C2 x2 x0
−
( )
⋅ x2 x1
−
( )
⋅
+
=
y3 C0 C1 x3 x0
−
( )
⋅
+ C2 x3 x0
−
( )
⋅ x3 x1
−
( )
⋅
+ C3 x3 x0
−
( )
⋅ x3 x1
−
( )
⋅ x3 x2
−
( )
⋅
+
=
Using the finite differences
x1 x0
− Δx
= x2 x0
− 2Δx
= x3 x0
− 2Δx
= (5.18)
the undetermined coefficients are obtained as
C0 y0
= C1
Δy0
Δx
=
(5.19)
C2
Δ
2
y0
2! Δx
2
⋅
= C3
Δ
3
y0
3! Δx
3
⋅
=
Defining
x x0
− n Δx
⋅
=
x x1
− n 1
−
( ) Δx
⋅
= (5.20)
x x2
− n 2
−
( ) Δx
⋅
=
152 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

163. where
n
x x0
−
Δx
= (5.21)
the interpolating polynomial of equation (5.15) can now be written as
f x
( ) f x0
( ) n Δf x0
( )
⋅
+
n n 1
−
( )
⋅
2!
Δ
2
⋅ f x0
( )
+
n n 1
−
( )
⋅ n 2
−
( )
⋅
3!
Δ
3
⋅ f x0
( )
+ ...............
+
=
(5.22)
From the above process, it can be seen that the form of an mth order interpolating polynomial will
be
f x
( ) f x0
( ) n Δf x0
( )
⋅
+
n n 1
−
( )
⋅
2!
Δ
2
⋅ f x0
( )
+
n n 1
−
( )
⋅ n 2
−
( )
⋅
3!
Δ
3
⋅ f x0
( )
+ ......
+
n n 1
−
( )
⋅ . n m
− 1
+
( )
m!
Δ
m
⋅ f x0
( )
+
...
=
(5.23)
Example 5.4
The following data is given on the radiation flux R in gram-calories per square centimeter per
day for a certain month in a given year as a function of latitude L
(deg N.)
L 0 20 40 60 80
R 895 858 722 489 235
Generate the finite difference table and obtain an interpolating polynomial using Newton's
method. Estimate the flux R at a latitude of 45 degrees.
The following finite difference table can be generated using the given data.
Chapter 5: Numerical Interpolation 153

164. ________________________________________________
Lat R delta R del 2 R del 3 R del 4 R
____________________________________________________
0 895
-37
20 858 -99
-136 2
40 722 -97 74
-233 76
60 489 -21
-254
80 235
____________________________________________________
The interpolating poly can now be written as:
R(L) = R(L0) + n del R(L0) + (1/2) n(n-1) del 2 R(L0) + (1/6) n(n-1)(n-2)del 3 R ( L0)
+ (1/24) n(n-1)(n-2)(n-3) del 4 R(L0)
where R(L0)= 895; del R (L0)=-37; del 2 R(L0)= -99; del 3 R(L0)=2;
del 4 R(L0)=74; n=( L- L0)/ del L = ( L- 0)/ 20 = L/20
Calculations are done below and the interpolating polynomial plotted in Figure 5.4
RL0 895
:= L0 0
:= delRL0 37
−
:= del2RL0 99
−
:= del3RL0 2
:= del4RL0 74
:=
delL 20
:= n L
( )
L L0
−
delL
:=
R L
( ) RL0 n L
( ) delRL0
⋅
+
n L
( ) n L
( ) 1
−
( )
⋅ del2RL0
⋅
2
+
n L
( ) n L
( ) 1
−
( )
⋅ n L
( ) 2
−
( )
⋅ del3RL0
⋅
6
+
n L
( ) n L
( ) 1
−
( )
⋅ n L
( ) 2
−
( )
⋅ n L
( ) 3
−
( )
⋅ del4RL0
⋅
24
+
...
:=
154 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

165. These are the given data points, in vector form,
needed for the plot below
LAT
0
20
40
60
80
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= FLUX
895
858
722
489
235
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= <---
L 0 1
, 80
..
:=
0 10 20 30 40 50 60 70 80
200
400
600
800
1000
Given data points
Interpolation
Given data points
Interpolation
Interpolated function by Newton's meth
Latitude- degrees North
Radiation
flux
FLUX
R L
( )
LAT L
,
Figure 5.4. The Newton interpolating polynomial
The interpolation yields R 45
( ) 671.14
=
5.6 THE LAGRANGE INTERPOLATING POLYNOMIAL
In many practical problems, data measurements are recorded at unequal spacings or
intervals. In such situations, the Lagrangian interpolation method offers a viable means of
deducing an interpolating polynomial connecting the dependent variable with the
independent variable at intervals that are not necessarily constant.
By this method, given a data sample
(x1, y1); (x2, y2); .......... ( x n , y n)
Chapter 5: Numerical Interpolation 155

166. an interpolating polynomial can be generated using
f x
( )
1
n
i
wi x
( ) . yi
⋅
( )
∑
=
=
(5.24)
where
wi x
( )
1
n
j
x xj
−
( )
∏
=
1
n
j
xi xj
−
( )
∏
=
= j i
≠ (5.25)
For example, if three data points are prescribed, n is 3 and the interpolating polynomial will
be
f x
( )
1
3
i
wi x
( ) .yi
( )
∑
=
=
with
w1 x
( )
x x2
−
( ) x x3
−
( )
⋅
x1 x2
−
( ) x1 x3
−
( )
⋅
= w2 x
( )
x x1
−
( ) x x3
−
( )
⋅
x2 x1
−
( ) x2 x3
−
( )
⋅
=
(5.26)
w3 x
( )
x x1
−
( ) x x2
−
( )
⋅
x3 x1
−
( ) x3 x2
−
( )
⋅
=
Example 5.5
Given the following data
x: 96 207 375 450
y: 932 850 767 1235
Determine the Lagrange Interpolating Polynomial f(x) that passes through the above points .
Determine f(102) , f(322) and f(415)
156 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

167. The given data is
x1 96
:= x2 207
:= x3 375
:= x4 450
:=
y1 932
:= y2 850
:= y3 767
:= y4 1235
:=
The Lagrange interpolating polynomial, in this case, will be a cubic of the following form
f x
( ) w1 x
( ) y1
⋅ w2 x
( ) y2
⋅
+ w3 x
( ) y3
⋅
+ w4 x
( ) y4
⋅
+
=
where
w1 x
( )
x x2
−
( ) x x3
−
( )
⋅ x x4
−
( )
⋅
x1 x2
−
( ) x1 x3
−
( )
⋅ x1 x4
−
( )
⋅
:= w2 x
( )
x x1
−
( ) x x3
−
( )
⋅ x x4
−
( )
⋅
x2 x1
−
( ) x2 x3
−
( )
⋅ x2 x4
−
( )
⋅
:=
w3 x
( )
x x1
−
( ) x x2
−
( )
⋅ x x4
−
( )
⋅
x3 x1
−
( ) x3 x2
−
( )
⋅ x3 x4
−
( )
⋅
:= w4 x
( )
x x1
−
( ) x x2
−
( )
⋅ x x3
−
( )
⋅
x4 x1
−
( ) x4 x2
−
( )
⋅ x4 x3
−
( )
⋅
:=
Note that the equations for w1(x), w2(x) etc have to be written in Mathcad as shown above
and not in the form of Equation 5.25. Then, the interpolating polynomial is generated using
f x
( ) w1 x
( ) y1
⋅ w2 x
( ) y2
⋅
+ w3 x
( ) y3
⋅
+ w4 x
( ) y4
⋅
+
:=
and is shown in Figure 5.5. It yields f 102
( ) 940.053
= f 322
( ) 683.419
=
f 415
( ) 955.728
=
X
96
207
375
450
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= Y
932
850
767
1235
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:=
<--- Given data points in vector form, used in the plot below
Chapter 5: Numerical Interpolation 157

168. x 96 97
, 450
..
:=
100 150 200 250 300 350 400 450
600
800
1000
1200
1400
Given data points
Interpolation
Given data points
Interpolation
Lagrange Interpolating Polynomial
X- Values
Function
values
Y
f x
( )
X x
,
Figure 5.5. The Lagrange interpolating polynomial
5.7 INTERPOLATION USING LINEAR, QUADRATIC AND CUBIC
SPLINES.
For n data points that are provided, the highest- order interpolating polynomial that can be
generated will be of order (n-1) . Although, in general, the accuracy of the interpolation
process increases with the order of the polynomial , there are situations when the accuracy
can, in fact, decrease with the polynomial order. This can happen when the measured data
reflects abrupt changes in the dependent variable values for steady changes in the
independent variable . In these cases, accuracy can be improved by resorting to lower
order polynomials, commonly referred to as splines . Splines normally used are linear,
quadratic and cubic.
Linear Splines: A linear spline results from connecting adjacent data points with straight
lines. Given n data points (x1, y1), (x2, y2), ( x3, y3 ),..... (x n, y n ) , the interpolation
function for x between x1 and x2 is
f x
( ) y1
x x1
−
x2 x1
−
y2 y1
−
( )
⋅
+
= (5.27)
Similarly, for x between x2 and x3 the interpolation function will be
158 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

169. f x
( ) y2
x x2
−
x3 x2
−
y3 y2
−
( )
⋅
+
=
(5.28)
It follows ,then, that for x between x n-1 and x n
f x
( ) yn 1
−
x xn 1
−
−
xn xn 1
−
−
yn yn 1
−
−
( )
⋅
+
=
(5.29)
The resulting linear spline, however, must satisfy the following constraint equations
f xi
( ) fi 1
+ xi
( )
= for i 1
= 2.....
, n 1
−
, (5.30)
Quadratic Splines: Quadratic splines are of the form : ax 2 + bx + c The conditions to be
satisfied are
(1) The spline function must pass through the given data points.
(2) The spline is to be continuous at the interior data points .
(3) The second derivative of the spline between the first two data points is to be zero.
Cubic Splines: Cubic splines have the form: ax 3 + b x 2 + cx + d and must satisfy the
following conditions
(1) The spline function must pass through the given data points
(2) The first derivatives of the spline must be continuous.
(3) The second derivatives of the spline must also be continuous.
(4) The second derivative must be zero at the first and second data points.
5.8 INTERPOLATION WITH MATHCAD
Interpolation in Mathcad allows you to either connect the data points with straight lines
( linear interpolation ) or with sections of a cubic polynomial ( cubic spline interpolation ).
These interpolation functions return a curve passing through the points you specify.
Linear interpolation: This is done using the linterp function as shown below.
linterp(vx,vy,x): Uses the data vectors vx and vy to return a linearly interpolated value of y
corresponding to x . The quantities vx and vy must be specified as vectors and vx must
contain real values in ascending order. The linterp function is intended for interpolation and not
for extrapolation.
Chapter 5: Numerical Interpolation 159

170. Cubic spline interpolation: Cubic spline interpolation enables you to pass a curve through a
set of points such that the first and second derivatives of the curve are continuous at each
point. Mathcad does this by taking three adjacent points and constructing a cubic polynomial
that passes through these points. These cubics are then connected together to make up the
interpolated curve.
In order to fit a cubic spline curve through a set of points, the procedure shown below
must be followed:
1. Create the vectors vx and vy containing the x and y coordinates of the points of
interest through which you want to go through. The elements of vx must be put in in
ascending order.
2. Generate the vector vs:= cspline( vx,vy). This vector vs is a vector of intermediate
results to be used with interp.
3. To evaluate the spline at a point x1, do the following: interp(vs,vx,vy,x1) .
Note: Steps 2 and 3 can be combined by doing : interp(cspline(vx,vy),vx,vy,x1)
Mathcad has two other cubic spline functions as given below:
lspline(vx,vy) : This generates a spline curve that approaches a straight line at the endpoints.
pspline(vx,vy) : This generates a spline curve that approaches a parabola at the
endpoints.
The function interp(vs,vx,vy,x) returns the interpolated y value corresponding to x. The vector
vs is a vector of intermediate results obtained by utilizing the option of using lspline, pspline
or cspline on the vectors of given data , namely, vx and vy .
For Example 5.1 , the vx and vy vectors are
vx
0
1
2
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= vy
2
2.25
5.82
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
As shown below, the linterp function is used to do a linear interpolation. The resulting spline
function is drawn in Figure 5.6 and the values of the interpolated function at
x= 0.5 and 1.5 are:
160 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

171. x 0 0.1
, 2
..
:=
0 0.5 1 1.5 2
2
4
6
vy
linterp vx vy
, x
,
( )
vx x
,
Figure 5.6. Interpolated function obtained with linterp
linterp vx vy
, 0.5
,
( ) 2.125
= linterp vx vy
, 1.5
,
( ) 4.035
=
The interp function along with lspline, pspline and cspline can be utilized as follows to
generate cubic splines
vs1 lspline vx vy
,
( )
:= vs2 pspline vx vy
,
( )
:= vs3 cspline vx vy
,
( )
:=
f1 x
( ) interp vs1 vx
, vy
, x
,
( )
:= f2 x
( ) interp vs2 vx
, vy
, x
,
( )
:= f3 x
( ) interp vs3 vx
, vy
, x
,
( )
:=
flin x
( ) linterp vx vy
, x
,
( )
:=
Values of the interpolated cubic splines at x= 0.5 and 1.5 are
f1 0.5
( ) 1.814
= f2 0.5
( ) 1.71
= f3 0.5
( ) 1.502
= f1 1.5
( ) 3.724
= f2 1.5
( ) 3.62
=
f3 1.5
( ) 3.828
= flin 0.5
( ) 2.125
= flin 1.5
( ) 4.035
=
Figure 5.7 shows a comparison of the various splines generated using Mathcad
Chapter 5: Numerical Interpolation 161

172. x 0 0.1
, 2
..
:=
0 0.5 1 1.5 2
1
2
3
4
5
6
Given data points
Using lspline
Using pspline
Using cspline
Using linterp
Given data points
Using lspline
Using pspline
Using cspline
Using linterp
Comparison of Mathcad splines
x- Values
function
values
vy
f1 x
( )
f2 x
( )
f3 x
( )
flin x
( )
vx x
,
Figure 5.7. Comparison of spline functions obtained with Mathcad
For the problem of Example 5.2, interpolations using the Mathcad linterp and interp functions yield
the following. The results are sketched in Figure 5.8.
vx
100
200
400
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= vy
975
1575
2054
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
vs cspline vx vy
,
( )
:= fcspline x
( ) interp vs vx
, vy
, x
,
( )
:= flin x
( ) linterp vx vy
, x
,
( )
:=
fcspline 251
( ) 1.737 10
3
×
= flin 251
( ) 1.697 10
3
×
=
162 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

173. x 100 105
, 400
..
:=
100 150 200 250 300 350 400
800
1000
1200
1400
1600
1800
2000
2200
Given data points
Mathcad's cubic spline
Mathcad's linear interpolation with linterp
Given data points
Mathcad's cubic spline
Mathcad's linear interpolation with linterp
Interpolation with Mathcad
x- values
function
values
vy
fcspline x
( )
flin x
( )
vx x
,
Figure 5.8. Interpolation with Mathcad
For the problem of Example 5.3 , interpolation using the Mathcad spline functions is shown
below
vx
0
100
200
300
400
500
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= <---vx and vy vectors
vy
104.2
97.3
48.1
23.7
8.6
5.2
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
flin x
( ) linterp vx vy
, x
,
( )
:=
Linear interpolation values at x= 150, x= 350 and x= 450 are
Chapter 5: Numerical Interpolation 163

174. linterp vx vy
, 150
,
( ) 72.7
= linterp vx vy
, 350
,
( ) 16.15
= linterp vx vy
, 450
,
( ) 6.9
=
The linearly interpolated function is shown in Figure 5.9.
x 0 5
, 500
..
:=
0 100 200 300 400 500
0
50
100
150
Given data points
Mathcad's linear interpolation
Given data points
Mathcad's linear interpolation
x- values
Interpolated
values
vy
linterp vx vy
, x
,
( )
vx x
,
Figure 5.9. Linear interpolation for Example 5.3
The Gregory Newton polynomial for this problem has been derived earlier and is the function
f(x) shown below .
x1 0
:= x2 100
:= x3 200
:= x4 300
:= x5 400
:= x6 500
:=
<--data points
y1 104.2
:= y2 97.3
:= y3 48.1
:= y4 23.7
:= y5 8.6
:= y6 5.2
:=
a1 104.2
:= a2 0.069
−
:= a3 2.115
− 10
3
−
⋅
:=
<--Coefficients
obtained in
Example 5.3
a4 1.118 10
5
−
⋅
:= a5 3.442
− 10
8
−
⋅
:= a6 8.375 10
11
−
⋅
:=
f x
( ) a1 a2 x x1
−
( )
⋅
+ a3 x x1
−
( )
⋅ x x2
−
( )
⋅
+ a4 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅
+
a5 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅
+
...
a6 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅ x x5
−
( )
⋅
+
...
:=
vs1 lspline vx vy
,
( )
:= vs2 pspline vx vy
,
( )
:= vs3 cspline vx vy
,
( )
:=
164 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

175. <-- Mathcad
splines
flin x
( ) linterp vx vy
, x
,
( )
:= flspline x
( ) interp vs1 vx
, vy
, x
,
( )
:=
fpspline x
( ) interp vs2 vx
, vy
, x
,
( )
:= fcspline x
( ) interp vs3 vx
, vy
, x
,
( )
:=
Figure 5.10 shows a comparison of the Mathcad spline functions with the
Gregory-Newton interpolation f(x)
vx
0
100
200
300
400
500
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vy
104.2
97.3
48.1
23.7
8.6
5.2
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
<--- Given data in vector form
x 0 5
, 500
..
:=
0 100 200 300 400 500
0
50
100
150
Given data points
Linterp
interp/lspline
interp/pspline
interp/cspline
Gregory-Newton interpolation
Given data points
Linterp
interp/lspline
interp/pspline
interp/cspline
Gregory-Newton interpolation
Interpolation with Mathcad Splines and Gregory-Newton interpolation
x values
Interpolated
values
vy
flin x
( )
flspline x
( )
fpspline x
( )
fcspline x
( )
f x
( )
vx x
,
Figure 5.10. Comparison of Mathcad splines with the
Gregory-Newton interpolating polynomial
The Mathcad interpolated values at x = 150, 350 and 450 are shown below.
flin 150
( ) 72.7
= flin 350
( ) 16.15
= flin 450
( ) 6.9
=
flspline 150
( ) 73.947
= flspline 350
( ) 15.3
= flspline 450
( ) 5.721
=
fpspline 150
( ) 73.207
= fpspline 350
( ) 15.425
= fpspline 450
( ) 5.069
=
Chapter 5: Numerical Interpolation 165

176. fcspline 150
( ) 72.343
= fcspline 350
( ) 15.48
= fcspline 450
( ) 4.645
=
In the following paragraphs, Mathcad splines for the problem of Example 5.5 are generated
and compared with the Lagrange interpolating polynomial obtained earlier. The data given is
x1 96
:= x2 207
:= x3 375
:= x4 450
:=
y1 932
:= y2 850
:= y3 767
:= y4 1235
:=
w1 x
( )
x x2
−
( ) x x3
−
( )
⋅ x x4
−
( )
⋅
x1 x2
−
( ) x1 x3
−
( )
⋅ x1 x4
−
( )
⋅
:= w2 x
( )
x x1
−
( ) x x3
−
( )
⋅ x x4
−
( )
⋅
x2 x1
−
( ) x2 x3
−
( )
⋅ x2 x4
−
( )
⋅
:=
w3 x
( )
x x1
−
( ) x x2
−
( )
⋅ x x4
−
( )
⋅
x3 x1
−
( ) x3 x2
−
( )
⋅ x3 x4
−
( )
⋅
:= w4 x
( )
x x1
−
( ) x x2
−
( )
⋅ x x3
−
( )
⋅
x4 x1
−
( ) x4 x2
−
( )
⋅ x4 x3
−
( )
⋅
:=
f x
( ) w1 x
( ) y1
⋅ w2 x
( ) y2
⋅
+ w3 x
( ) y3
⋅
+ w4 x
( ) y4
⋅
+
:= <-- Lagrange interpolating polynomial
f 102
( ) 940.053
= f 322
( ) 683.419
= f 415
( ) 955.728
=
The Mathcad vx and vy vectors are
vx
x1
x2
x3
x4
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= vy
y1
y2
y3
y4
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:=
vs1 lspline vx vy
,
( )
:= vs2 pspline vx vy
,
( )
:= vs3 cspline vx vy
,
( )
:=
flspline x
( ) interp vs1 vx
, vy
, x
,
( )
:= fpspline x
( ) interp vs2 vx
, vy
, x
,
( )
:=
<-- Mathcad
splines
fcspline x
( ) interp vs3 vx
, vy
, x
,
( )
:= flin x
( ) linterp vx vy
, x
,
( )
:=
A comparison of the Mathcad spline functions generated with linterp, lspline, pspline and cspline
functions is shown in Figure 5.11.
166 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

177. x 96 97
, 450
..
:=
100 150 200 250 300 350 400 450
600
700
800
900
1000
1100
1200
1300
Given data points
interp/lspline
interp/pspline
interp/cspline
linterp
Lagrangian interpolation
Given data points
interp/lspline
interp/pspline
interp/cspline
linterp
Lagrangian interpolation
Lagrange Poly/ Mathcad Interpolations compared
x- Values
y-
Values
vy
flspline x
( )
fpspline x
( )
fcspline x
( )
flin x
( )
f x
( )
vx x
,
Figure 5.11. Comparison of Mathcad splines with Lagrangian interpolation
The various interpolations resorted to give the following interpolated function values for x = 102,
322 and 415.
x=102: f 102
( ) 940.053
= flin 102
( ) 927.568
= flspline 102
( ) 930.335
=
fpspline 102
( ) 932.981
= fcspline 102
( ) 940.053
=
x=322: f 322
( ) 683.419
= flin 322
( ) 793.185
= flspline 322
( ) 669.542
=
fpspline 322
( ) 684.098
= fcspline 322
( ) 683.419
=
x=415: f 415
( ) 955.728
= flin 415
( ) 1.017 10
3
×
= flspline 415
( ) 985.191
=
Chapter 5: Numerical Interpolation 167

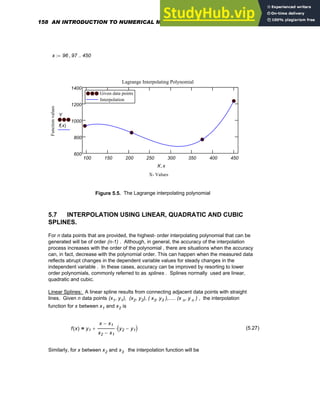
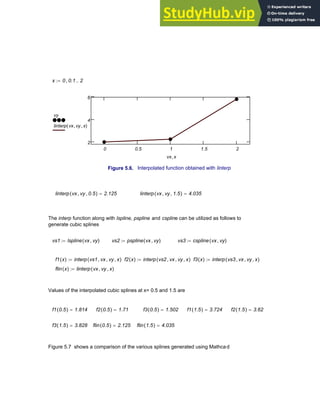
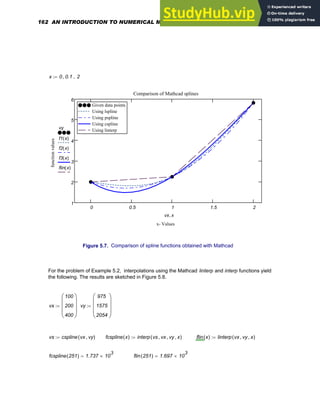
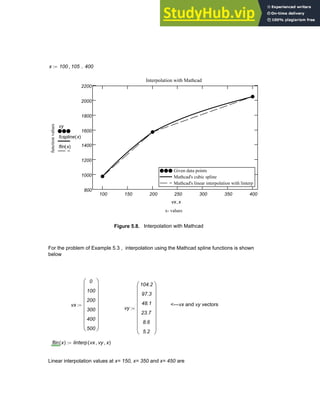
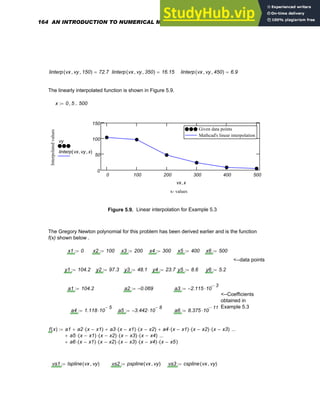
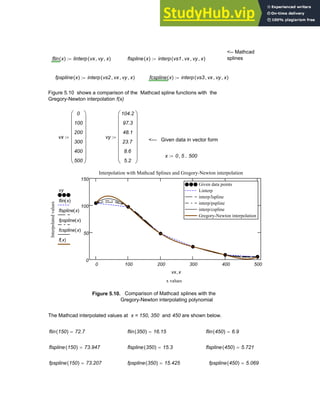
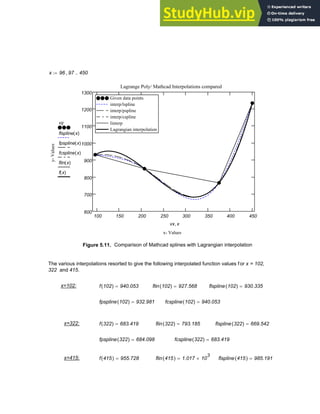
178. fpspline 415
( ) 962.582
= fcspline 415
( ) 955.728
=
5.9. APPLICATIONS IN NUMERICAL INTERPOLATION
In the examples that follow, data from various practical areas such as design of
machinery, noise control and vibration analysis, is utilized in interpolation procedure s to
generate function values at points other than the given data points.
5.9.1. Stress-Strain Data for Titanium
The stress versus strain data given in the table below is obtained from a tensile test of
annealed A-40 titanium [ 18 ]. A cubic spline can be developed using Mathcad as follows
and the stresses interpolated for any values of strain in the range provided.
The cubic spline interpolation generated together with the given data points is presented in
Figure 5.12. Notice that the spline generated passes through all the given data points as is
expected of an interpolating polynomial.
Strain (in/in) Stress (kpsi)
<--Given stress versus strain data
σ
0
5
10
15
20
25
30
34.9
39.9
44.9
49.9
60.9
73.3
78.2
86.2
94.5
98.7
118.2
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
ε
0
0.00030
0.00060
0.00090
0.00120
0.00175
0.00220
0.00285
0.00349
0.00469
0.00698
0.01610
0.04807
0.07676
0.14364
0.26677
0.34470
0.72202
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Vε ε
:= Vσ σ
:=
Vs cspline Vε Vσ
,
( )
:=
168 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

179. fspline ε
( ) interp Vs Vε
, Vσ
, ε
,
( )
:= <-- Generates a cubic spline function for given data
fspline 0.004
( ) 42.699
=
<-- interpolated values of stress at strains of 0.004 and 0.65
fspline 0.65
( ) 114.503
=
i 1 18
..
:= ε 0 0.00010
, 0.722
..
:=
1 .10
4
1 .10
3
0.01 0.1 1
1
10
100
1 .10
3
fspline ε
( )
Vσi
ε Vεi
,
Figure 5.12. Mathcad cubic spline for given stress-strain data
5.9.2. Notch Sensitivity of Aluminum
The fatigue stress concentration factor K f is used with the nominal stress σ 0 to compute
the maximum resulting stress σ max at a discontinuity in a machine part via the following
relationship [18] .
σmax Kf σ0
⋅
= (5.31)
The fatigue stress concentration factor K f , which is, in fact , just a reduced value of the
geometrical stress concentration factor K t, is a function of the sensitivity of the material of
which the part is made to notches ( known as notch sensitivity q ). These quantities are
connected by the following relationship .
Chapter 5: Numerical Interpolation 169

180. Kf 1 q Kt 1
−
( )
⋅
+
= (5.32)
Notch sensitivity charts which are graphs of notch sensitivity versus notch radius are
available for metals and alloys subjected to reversed bending or reversed axial loads. The
data given below provides notch sensitivity (q) versus notch radius (r) information for an
aluminum alloy and can be used to generate an interpolation from which notch sensitivity
values at points other than the given data points can be readily obtained.
r ( in) 0.015 0.04 0.06 0.10 0.12 0.14 0.16
q 0.25 0.55 0.65 0.75 0.775 0.80 0.825
Since seven data points are given , the interpolating polynomial that can be generated will
be of order 6 , having the form
f r
( ) a b r
⋅
+ c r
2
⋅
+ d r
3
⋅
+ e r
4
⋅
+ f r
5
⋅
+ g r
6
⋅
+
=
Resorting to the method of undetermined coefficients results in the following matrix equation
M C
⋅ A
=
where
M
1
1
1
1
1
1
1
0.015
0.04
0.06
0.10
0.12
0.14
0.16
0.015
2
0.04
2
0.06
2
0.10
2
0.12
2
0.14
2
0.16
2
0.015
3
0.04
3
0.06
3
0.10
3
0.12
3
0.14
3
0.16
3
0.015
4
0.04
4
0.06
4
0.10
4
0.12
4
0.14
4
0.16
4
0.015
5
0.04
5
0.06
5
0.10
5
0.12
5
0.14
5
0.16
5
0.015
6
0.04
6
0.06
6
0.10
6
0.12
6
0.14
6
0.16
6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= C
a
b
c
d
e
f
g
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= A
0.25
0.55
0.65
0.75
0.775
0.80
0.825
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
The coefficients in the column vector {C} can be obtained using the Mathcad function lsolve
C lsolve M A
,
( )
:=
170 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

181. C
0.187
−
40.462
922.431
−
1.27 10
4
×
1.01
− 10
5
×
4.228 10
5
×
7.169
− 10
5
×
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= a C1
:= b C2
:= c C3
:= d C4
:= e C5
:=
f C6
:= g C7
:=
Thus, the interpolating polynomial f(x) is completely determined with
a 0.187
−
= b 40.462
= c 922.431
−
= d 1.27 10
4
×
= e 1.01
− 10
5
×
=
f 4.228 10
5
×
= g 7.169
− 10
5
×
=
f r
( ) a b r
⋅
+ c r
2
⋅
+ d r
3
⋅
+ e r
4
⋅
+ f r
5
⋅
+ g r
6
⋅
+
:= <---- interpolating polynomial obtained by
the method of undetermined
coefficients
Mathcad cubic spline interpolation can also be employed as shown below and the resulting
plot compared with the results of the undetermined coefficients method and with the given
data points. This is done in in Figure 5.13.
Vr
0.015
0.04
0.06
0.10
0.12
0.14
0.16
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vq
0.25
0.55
0.65
0.75
0.775
0.80
0.825
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Vs cspline Vr Vq
,
( )
:= fspline r
( ) interp Vs Vr
, Vq
, r
,
( )
:=
Chapter 5: Numerical Interpolation 171

182. fspline 0.13
( ) 0.787
= fspline 0.15
( ) 0.813
= f 0.15
( ) 0.814
= fspline 0.15
( ) 0.813
=
r 0.015 0.016
, 0.16
..
:= i 1 7
..
:=
0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16
0.2
0.4
0.6
0.8
Given data points
Interpolation by undet coeff method
Mathcad cubic spline interpolation
Given data points
Interpolation by undet coeff method
Mathcad cubic spline interpolation
Mathcad interpolation/ notch sensitivity
Notch radius, r, inches
Notch
sensitivity,
q
Vqi
f r
( )
fspline r
( )
Vri r
,
Figure 5.13. Interpolation of notch sensitivity data
5.9.3 Speech Interference Level
In the field of Noise and Vibration Control, it often becomes necessary to determine the
effect of steady background noise on speech communication in a given setting. The
preferred speech interference level (PSIL) was established in an effort to study this effect
under the constraint that speech sounds would not be allowed to be reflected back to the
listener [ 2, 10 ]. For effective communication at a given voice level , the maximum
distance that there can be between the speaker and the listener is a function of the
preferred speech interference level existing at the location. The following data which is
provided for communication at the level of a normal male voice can be utilized in an
interpolation scheme to determine the maximum PSIL permitted for a given distance
between the speaker and the listener.
Dist (ft) 0 2 4 6 8 10 12
PSIL(dB) 83 62.5 56 52.5 50 47.5 46.5
172 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

183. Because there are 7 data points prescribed, the interpolating polynomial to be generated will
be of order 6 and if a Gregory-Newton interpolating polynomial is to be determined , it will
have the form
f x
( ) a1 a2 x x1
−
( )
⋅
+ a3 x x1
−
( )
⋅ x x2
−
( )
⋅
+ a4 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅
+
a5 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅
+
...
a6 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅ x x5
−
( )
⋅
+
...
a7 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅ x x5
−
( )
⋅ x x6
−
( )
⋅
+
...
=
where the a' s are unknown coefficients to be determined.
The given data is
x1 0
:= x2 2
:= x3 4
:= x4 6
:= x5 8
:= x6 10
:= x7 12
:=
y1 83
:= y2 62.5
:= y3 56.
:= y4 52.5
:= y5 50
:= y6 47.5
:= y7 46.5
:=
and the unknown coefficients can be determined using
a1 y1
:=
a2
y2 y1
−
x2 x1
−
:= a3
y3 a1
− a2 x3 x1
−
( )
⋅
−
x3 x1
−
( ) x3 x2
−
( )
⋅
:=
a4
y4 a1
− a2 x4 x1
−
( )
⋅
− a3 x4 x1
−
( )
⋅ x4 x2
−
( )
⋅
−
x4 x1
−
( ) x4 x2
−
( )
⋅ x4 x3
−
( )
⋅
:=
a5
y5 a1
− a2 x5 x1
−
( )
⋅
− a3 x5 x1
−
( )
⋅ x5 x2
−
( )
⋅
− a4 x5 x1
−
( )
⋅ x5 x2
−
( )
⋅ x5 x3
−
( )
⋅
−
x5 x1
−
( ) x5 x2
−
( )
⋅ x5 x3
−
( )
⋅ x5 x4
−
( )
⋅
:=
Term4 a4 x6 x1
−
( ) x6 x2
−
( )
⋅ x6 x3
−
( )
⋅
⎡
⎣ ⎤
⎦
⋅
:=
a6
y6 a1
− a2 x6 x1
−
( )
⋅
− a3 x6 x1
−
( )
⋅ x6 x2
−
( )
⋅
− Term4
−
1
−
( ) a5
⋅ x6 x1
−
( )
⋅ x6 x2
−
( )
⋅ x6 x3
−
( )
⋅ x6 x4
−
( )
⋅
+
...
x6 x1
−
( ) x6 x2
−
( )
⋅ x6 x3
−
( )
⋅ x6 x4
−
( )
⋅ x6 x5
−
( )
⋅
:=
Chapter 5: Numerical Interpolation 173

184. Termno4 a4 x7 x1
−
( )
⋅ x7 x2
−
( ) x7 x3
−
( )
⋅
⎡
⎣ ⎤
⎦
⋅
:=
a7
y6 a1
− a2 x7 x1
−
( )
⋅
− a3 x7 x1
−
( )
⋅ x7 x2
−
( )
⋅
− Termno4
−
1
−
( ) a5
⋅ x7 x1
−
( ) x7 x2
−
( )
⋅ x7 x3
−
( )
⋅ x7 x4
−
( )
⋅
⎡
⎣ ⎤
⎦
⋅
+
...
a6 x7 x1
−
( ) x7 x2
−
( )
⋅ x7 x3
−
( )
⋅ x7 x4
−
( )
⋅ x7 x5
−
( )
⋅ 1
−
( )
⋅
⎡
⎣ ⎤
⎦
⋅
+
...
x7 x1
−
( ) x7 x2
−
( )
⋅ x7 x3
−
( )
⋅ x7 x4
−
( )
⋅ x7 x5
−
( )
⋅ x7 x6
−
( )
⋅
:=
which give
a1 83
= a2 10.25
−
= a3 1.75
= a4 0.229
−
=
a5 0.023
= a6 2.083
− 10
3
−
×
= a7 2.279 10
4
−
×
=
The interpolating polynomial obtained by the Gregory-Newton method can now be obtained using
f x
( ) a1 a2 x x1
−
( )
⋅
+ a3 x x1
−
( )
⋅ x x2
−
( )
⋅
+ a4 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅
+
a5 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅
+
...
a6 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅ x x5
−
( )
⋅
+
...
a7 x x1
−
( )
⋅ x x2
−
( )
⋅ x x3
−
( )
⋅ x x4
−
( )
⋅ x x5
−
( )
⋅ x x6
−
( )
⋅
+
...
:=
Mathcad cubic spline interpolation can also be employed as shown below and the resulting plot
compared with the results of the Gregory-Newton method and with the given data points. This is
done in in Figure 5.14.
Vx
x1
x2
x3
x4
x5
x6
x7
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy
y1
y2
y3
y4
y5
y6
y7
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vx
0
2
4
6
8
10
12
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vy
83
62.5
56
52.5
50
47.5
46.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Vs cspline Vx Vy
,
( )
:= fspline x
( ) interp Vs Vx
, Vy
, x
,
( )
:=
x 0 1
, 12
..
:= i 1 2
, 7
..
:=
174 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

185. 0 2 4 6 8 10 12
40
50
60
70
80
90
Given data points
Gregory-Newton interpolation
Mathcad's interp/cspline
Given data points
Gregory-Newton interpolation
Mathcad's interp/cspline
Interpolation- speech communication
Distance from speaker to listener (ft)
Preferred
speech
interference
level
(
dB
Vyi
f x
( )
fspline x
( )
Vxi x
,
Figure 5.14. Interpolation of speech communication data
5.9.4. Load-Deflection Data for Elastomeric Mounts
Elastomeric mounts are employed when small electrical and mechanical devices have to be
isolated from high forcing frequencies [ 9, 10 ]. They are especially useful in the protection of
delicate electronic instruments . Mount performance characteristics in the form of load
versus static deflection data are provided by manufacturers of vibration control products to
enable a designer to select an appropriate isolator for a given application.
The following data is available for an elastomeric mount.
Deflection (cm): 0 0 0.02 0.04 0.06 0.08 0.10
Load (N): 5 11 17.5 23.5 28 30.5
There are six data points prescribed. Thus, if a Lagrangian interpolating polynomial is to be
generated, it will be of order 5, having the form
L D
( )
1
6
i
wi D
( ) . Li
⋅
( )
∑
=
=
where
Chapter 5: Numerical Interpolation 175

186. wi D
( )
1
6
j
D Dj
−
( )
∏
=
1
6
j
Di Dj
−
( )
∏
=
= j i
≠
Here,
D1 0
:= D2 0.02
:= D3 0.04
:= D4 0.06
:= D5 0.08
:= D6 0.10
:=
L1 5
:= L2 11.
:= L3 17.5
:= L4 23.5
:= L5 28
:= L6 30.5
:=
w1 D
( )
D D2
−
( ) D D3
−
( )
⋅ D D4
−
( )
⋅ D D5
−
( )
⋅ D D6
−
( )
⋅
D1 D2
−
( ) D1 D3
−
( )
⋅ D1 D4
−
( )
⋅ D1 D5
−
( )
⋅ D1 D6
−
( )
⋅
:=
w2 D
( )
D D1
−
( ) D D3
−
( )
⋅ D D4
−
( )
⋅ D D5
−
( )
⋅ D D6
−
( )
⋅
D2 D1
−
( ) D2 D3
−
( )
⋅ D2 D4
−
( )
⋅ D2 D5
−
( )
⋅ D2 D6
−
( )
⋅
:=
w3 D
( )
D D1
−
( ) D D2
−
( )
⋅ D D4
−
( )
⋅ D D5
−
( )
⋅ D D6
−
( )
⋅
D3 D1
−
( ) D3 D2
−
( )
⋅ D3 D4
−
( )
⋅ D3 D5
−
( )
⋅ D3 D6
−
( )
⋅
:=
w4 D
( )
D D1
−
( ) D D2
−
( )
⋅ D D3
−
( )
⋅ D D5
−
( )
⋅ D D6
−
( )
⋅
D4 D1
−
( ) D4 D2
−
( )
⋅ D4 D3
−
( )
⋅ D4 D5
−
( )
⋅ D4 D6
−
( )
⋅
:=
w5 D
( )
D D1
−
( ) D D2
−
( )
⋅ D D3
−
( )
⋅ D D4
−
( )
⋅ D D6
−
( )
⋅
D5 D1
−
( ) D5 D2
−
( )
⋅ D5 D3
−
( )
⋅ D5 D4
−
( )
⋅ D5 D6
−
( )
⋅
:=
w6 D
( )
D D1
−
( ) D D2
−
( )
⋅ D D3
−
( )
⋅ D D4
−
( )
⋅ D D5
−
( )
⋅
D6 D1
−
( ) D6 D2
−
( )
⋅ D6 D3
−
( )
⋅ D6 D4
−
( )
⋅ D6 D5
−
( )
⋅
:=
The interpolating polynomial obtained by Lagrangian interpolation may now be obtained using
L D
( ) L1 w1 D
( )
⋅ L2 w2 D
( )
⋅
+ L3 w3 D
( )
⋅
+ L4 w4 D
( )
⋅
+ L5 w5 D
( )
⋅
+ L6 w6 D
( )
⋅
+
:=
giving L 0.07
( ) 25.986
=
176 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

187. Mathcad cubic spline interpolation can also be employed as shown below and the resulting
plot compared with the results of the Lagrangian interpolation and with the given data points.
This is done in in Figure 5.15
vD
D1
D2
D3
D4
D5
D6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vL
L1
L2
L3
L4
L5
L6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
vs cspline vD vL
,
( )
:= fspline D
( ) interp vs vD
, vL
, D
,
( )
:=
D 0 0.01
, 0.1
..
:= i 1 2
, 6
..
:=
0 0.02 0.04 0.06 0.08 0.1
0
10
20
30
40
Given data points
Lagrangian interpolation
Mathcad cubic spline interpolation
Given data points
Lagrangian interpolation
Mathcad cubic spline interpolation
Interpolation-Load/deflect data
Static deflection (cm)
Load
(N)
vLi
L D
( )
fspline D
( )
vDi D
,
Figure 5.15. Interpolation of load-deflection data for elastomeric mount
PROBLEMS
In problems 5.1 through 5.15, draw graphs of the interpolating polynomial generated . Check
your results against functions obtained with Mathcad splines . Present these comparisons
as Mathcad plots with proper labels and titles.
5.1. Using the method of undetermined coefficients, derive an interpolating
polynomial f(x) of the form "a+ bx " , for the following data. Determine the interpolated
value of f (0.52).
Chapter 5: Numerical Interpolation 177

188. x 0.45 0.55 0.65 0.75
y 0.075 0.136 0.227 0.372
5.2. For the same data as in problem 1, use the method of undetermined
coefficients to derive an interpolating polynomial f(x) of form " a+bx + cx2 " . Calculate f
(0.63).
5.3. Using the method of undetermined coefficients, derive an interpolating polynomial
f(x) for the data given below.
x 0 20 40
y 892 853 725
Estimate f (37).
5.4. The following table gives the values of cos(x) for selected angles (x) in degrees
x 10 12 14 16
f(x)= cos(x) 0.0.98481 0.978150 .9703 0.96126
Using the method of undetermined coefficients, derive a cubic interpolating polynomial for
the given interval . Estimate the value of cos x for x = 12.75 deg and x = 13.5 deg. Compare
these results with the true values.
5.5. Given the following data set :
x 0.50 0.55 0.60 0.65
y 0.5823 0.6124 0.6435 0.7869
derive an interpolating polynomial f(x) using the Gregory-Newton method. Estimate f(0.535)
and f(0.625). Compare the accuracy of the estimated values if the true values are 0.6022
and 0.6978 respectively.
5.6. The deflection, δ, of a structure under loading is measured at a point for four
different values of the applied force,F. The measued data is given below.
F (kN) 0.5 1.5 2.0 2.5
δ (cm) 3.12 5.25 7.32 10.63
Using the Gregory-Newton method, compute the deflection for F = 1.75 kN.
178 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

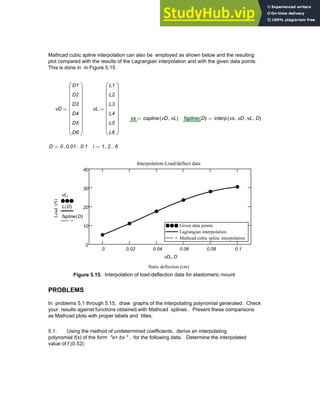
189. 5.7. The amplitude of vibration of an automobile in the vertical direction, after passing over
a road bump is found to be as follows.
Time, t (seconds) 0 0.65 1.30 1.95
Amplitude, A (mm) 5.25 2.50 0.80 0.40
Using the Gregory-Newton method, compute the amplitude for t = 1.80 seconds.
5.8. The Charpy test [ 18 ] provides material toughness data under dynamic conditions.
In this test, which is helpful in comparing several materials and in determining
low-temperature brittleness and impact strength, the specimen is struck by a pendulum
released from a fixed height and the energy absorbed by the specimen, termed the impact
value , computed from the height of the swing after fracture. The following table gives the
impact value, V, as a function of temperature, T, for a certain material. Using the
Gregory-Newton method, derive an interpolating polynomial and estimate V for T = -25 deg.
F and - 75 deg. F
T (deg F) -200 -150 -100 -50 0
V (ft-lbs) 0 1.5 3 10 35
5.9. The data in the following table are the distances traveled by a motorcycle, which was
stationary at time t = 0, for selected times.
time, t (seconds) 0 2 4 6 8 10
Distance, D (ft) 0 10 50 150 330 610
Generate a finite-difference table and obtain an interpolating polynomial using Newton's
method. Estimate the distance D traveled at t = 7 seconds.
5.10. For the given data, generate both a finite-difference table and an interpolating
polynomial.
Angle, θ, (degrees) Cosine (θ)
0 1.00000
10 0.98481
20 0.93969
30 0.86603
40 0.76604
50 0.64279
60 0.50000
Evaluate the error of the estimated value of cos (25 degrees). The true value is given to be
0.90631.
Chapter 5: Numerical Interpolation 179

190. 5.11. The following data gives the notch sensitivity , q , of a steel as a functionof the
notch radius , r [ 18 ]. Compute a finite-difference table and derive an interpolating
polynomial by Newton's method. Estimate q for r = 0.11 inches.
q 0.45 0.65 0.75 0.78 0.785
r ( in) 0.01 0.05 0.09 0.13 0.17
5.12. The deflection, δ, of a structure under loading is measured at a point for four different
values of the applied force, F. The measured data is as follows.
F (kn) 0.50 1.50 2.0 2.50
δ (cm) 3.0 5.2 7.3 10.5
Using Lagrangian interpolation , compute the deflection, δ, for F = 2.2 kN.
5.13. When a vibration problem is solved with nonlinearities included, the natural
frequencies of vibration become dependent on the amplitudes of vibration [ 9,16,20,21 ].
The following table relates the nonlinear natural frequency / linear natural frequency ratio,
r, of a rotating blade vibrating in the plane of rotation to its vibration amplitude , A.
A (in) 10 8.5 5 0
r (%) 99.9325 99.9575 99.9921 100
Derive a Lagrange interpolating polynomial and compute r for A = 4.25 in .
5.14. The behavior of a mooring line employed to control the excursions of a floating
ocean structure resembles that of a nonlinear spring with tension-displacement
characteristics which depend upon its length, weight, elastic properties, anchor holding
capacities and water depth [ 22 ]. In the table below, the horizontal component of mooring
line tension , H, is given as a function of the horizontal distance, X, between the ends of the
line.
X (ft) 440 470 485 492.5 495 498
H (Kips)0 5 10 42 150 440
Using Lagrangian interpolation, generate an interpolating polynomial and compute H for
X= 487 ft.
180 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

191. 5.15. The following table gives the pressure (P) versus temperature (T) relationship in the
liquid-vapor region for water [ 17 ]
T(deg Kelvin) 403.15 453.15 503.15 553.15 633.15
P (MPa) 0.2701 1.0021 2.795 6.412 18.651
Using Lagrangian interpolation, generate an interpolating polynomial and estimate P for T=
525 deg. K.
5.16. While the value of the endurance limit, S end , of a material is based on its
tensile strength, S ult , it is also dependent on the condition of its surface[19 ]. The following
data relates to a machined , unnotched specimen subjected to reversed bending.
S ult ( kpsi): 60 80 100 140 180 220
S end (kpsi): 22 30 38 50 60 64
Develop linear and cubic splines using linterp and interp for the above data. Also ,
graph the functions generated with proper labels and a title.
Chapter 5: Numerical Interpolation 181

192. NOTES:
182 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

193. C H A P T E R 6
CURVE-FITTING
6.1 THE NEED TO FIT A FUNCTION TO MEASURED DATA
Regression analysis plays an important role in analysis and interpretation of experimental as
well as statistical data and in their correlation with mathematical models. It involves the
determination of a function f(x) that would " best fit " a bunch of experimentally measured
values. ( x1, y1), (x2, y2) ....( xn,yn ). This function can be a linear function, a polynomial, a
nonlinear function, an exponential function , or a linear combination of known functions.
Some examples are shown in Figure 6.1. In curve- fitting a bunch of data points, typically
the number of data points would be much larger than the number of undetermined
coefficients in a given problem. Thus, there will be discrepancies between the function f(x)
determined and the data points given and it is very rare for a curve-fit to go through all the
given data points exactly. However, these differences are minimized by an adaptation of the
Method of Least Squares.
Figure 6.1. Examples of functions employed in curve-fitting
Chapter 6: Curve-Fitting 183

194. Handling of Weighted Data
When dealing with engineering, scientific and statistical data, situations may be encountered when
certain data may be considered to be more accurate than other data and consequently must be
assigned more weight in the process of generating a curve-fit. One way to include this weighting is
to make multiple inclusions of the associated data point in the regression analysis. For example,
if the following data is given and the point (2, 20) is to be assigned a "weighting factor" of 3, this
data point must simply be considered thrice in coming up with a curve-fit as shown below.
x: 1 2 3 4
y: 10 20 30 40
<--Given data
x 1 2 2 2 3 4
y: 10 20 20 20 30 40
<--- Information to be used
for curve-fitting
6.2 THE METHOD OF LEAST SQUARES
With a well-chosen approximating function, a " least squares " fit will yield a good
representation of experimental data. Suppose you want to measure the distance between
two points in a field, and let us say that you do this " n " times. You will come up with " n "
measurements which are likely to be somewhat different from one another. Let these be d1,
d2, d3,.....dn . If the true distance is "D", then the sum of the squares of the deviations from
the true distance "D" is
S d1 D
−
( )2
d2 D
−
( )2
+ ................
+ dn D
−
( )2
+
= (6.1)
This sum " S " will be a maximum or a minimum when
D
S
d
d
0
=
which yields
1
n
i
di
( )
∑
=
n D
⋅
− 0
= (6.2)
or, D
1
n
i
di
∑
=
n
= (6.3)
184 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

195. For S to be a minimum,
2
D
S
d
d
2
0
> , which it is since it comes out to be 2n.
Thus, S will be a mimimum when
D
i
di
∑
n
= ,
that is, if " n " measurements are taken, the true distance will be the arithmetic mean of the
n measurements if the sum of the squares of the deviations is to be a minimum.
6.3 STRAIGHT LINE REGRESSION
Let us assume that a plot of the given data suggests that we should fit it with a linear function.
Let this function be
f x
( ) C1 C2 x
⋅
+
= (6.4)
where C1 and C2 are coefficients to be determined. If the given data is
(x1,y1), ( x2, y2).................(xn, yn),
then the quantity "S", which is the sum of the squares of the deviations of the measured
values (y) from the function values f(x) is
S y1 C1 C2 x1
⋅
+
( )
−
⎡
⎣ ⎤
⎦
2
y2 C1 C2 x2
⋅
+
( )
−
⎡
⎣ ⎤
⎦
2
+ ..........
+ yn C1 C2 xn
⋅
+
( )
−
⎡
⎣ ⎤
⎦
2
+
= (6.5)
For S to be a minimum, the partial derivatives of S with respect to C1 and C2 must be zeros, which
leads to
n C1
⋅
1
n
i
xi
∑
=
C2
⋅
+
1
n
i
yi
∑
=
=
(6.6)
1
n
i
xi
∑
=
C1
⋅
1
n
i
xi
( )2
∑
=
C2
⋅
+
1
n
i
xi yi
⋅
( )
∑
=
=
Chapter 6: Curve-Fitting 185

196. In matrix form, this is
n
1
n
i
xi
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
C1
C2
⎛
⎜
⎝
⎞
⎟
⎠
⋅
1
n
i
yi
∑
=
1
n
i
xi yi
⋅
( )
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= (6.7)
Using Cramer's rule or the inverse of the matrix on the right hand side of the above equation or
the Mathcad function lsolve , the undetermined coefficients C1 and C2 can now be found.
Example 6.1
Given the following data:
xi yi
0.10 65.85
0.15 65.20
0.20 55.51
0.25 50.43
0.30 45.97
0.35 33.25
0.40 34.33
0.45 29.76
0.50 23.89
0.55 23.76
0.60 18.99
Fit a straight line y= f(x)= C1 + C2 x to the above data.
In this case, C1 and C2 are determined using
n
1
n
i
xi
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
C1
C2
⎛
⎜
⎝
⎞
⎟
⎠
⋅
1
n
i
yi
∑
=
1
n
i
xi yi
⋅
( )
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
186 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

197. Put in the given data as : j 1 2
, 10
..
:= x1 0.10
:= xj 1
+ xj 0.05
+
:= n 11
:=
with y
65.85
65.20
55.51
50.43
45.97
33.25
34.33
29.76
23.89
23.76
18.99
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Defining:
d
n
1
n
i
xi
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= m
1
n
i
yi
∑
=
1
n
i
xi yi
⋅
( )
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= q
n
1
n
i
xi
∑
=
1
n
i
yi
∑
=
1
n
i
xi yi
⋅
( )
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
C1
m
d
:= C1 75.497
= C2
q
d
:= C2 99.618
−
=
the fitted straight line function is then
f x
( ) C1 C2 x
⋅
+
:=
which is compared with the given data in Figure 6.2. At x= 0.20, 0.42 and 0.52, the fitted
function yields
.
f 0.20
( ) 55.574
= f 0.42
( ) 33.658
= f 0.52
( ) 23.696
=
Chapter 6: Curve-Fitting 187

198. i 1 11
..
:=
0.1 0.2 0.3 0.4 0.5 0.6
0
50
100
Given data
Fitted function
Given data
Fitted function
Comparison- Fitted Function with Data
x-values
y
and
f(x)
values
yi
f x
( )
xi x
,
Figure 6.2. Curve-fit with a linear function
6.4 CURVE- FITTING WITH A QUADRATIC FUNCTION
For some types of data, it may be appropriate to resort to a quadratic function of the
form:
f(x)= C1 + C2 x2 (6.8)
In this case, then , S will be
S y1 C1 C2 x1
( )2
⋅
+
⎡
⎣
⎤
⎦
−
⎡
⎣
⎤
⎦
2
y2 C1 C2 x2
( )2
⋅
+
⎡
⎣
⎤
⎦
−
⎡
⎣
⎤
⎦
2
+ ..................
+ yn C1 C2 xn
( )2
⋅
+
⎡
⎣
⎤
⎦
−
⎡
⎣
⎤
⎦
2
+
= (6.9)
Taking the partial derivatives of S with respect to C1 and C2 yields
(6.10)
n
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )4
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
C1
C2
⎛
⎜
⎝
⎞
⎟
⎠
⋅
1
n
i
yi
∑
=
1
n
i
xi
( )2
yi
⋅
⎡
⎣
⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
188 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

199. which can be solved for the C's using algebraic or matrix methods or by accessing the
Mathcad function lsolve. The above can be expressed as
[M]{C} = {A}, (6.11)
where
(6.12)
M
n
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )4
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= , A
1
n
i
yi
∑
=
1
n
i
xi
( )2
yi
⋅
⎡
⎣
⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
Example 6.2
A data set is given below .
x y
0.5 0.51
1.0 2.35
1.5 7.54
2.0 13.23
2.5 17.65
3.0 24.21
3.5 28.94
4.0 37.63
4.5 58.32
5.0 63.21
Determine the quadratic function that will best fit the data given
Put in the given data :
i 1 2
, 10
..
:= x1 0.5
:= xi 1
+ xi 0.5
+
:= n 10
:=
y1 0.51
:= y2 2.35
:= y3 7.54
:= y4 13.23
:= y5 17.65
:=
y6 24.21
:= y7 28.94
:= y8 37.63
:= y9 58.32
:= y10 63.21
:=
In this problem, the [M} and {A} matrices are
Chapter 6: Curve-Fitting 189

200. M
n
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )4
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= A
1
n
i
yi
∑
=
1
n
i
xi
( )2
yi
⋅
⎡
⎣
⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
Use lsolve to compute the C's:
C lsolve M A
,
( )
:=
C
0.779
2.554
⎛
⎜
⎝
⎞
⎟
⎠
= C1 0.779
= C2 2.554
=
The quadratic function fitted to the given data is f(x),
f x
( ) C1 C2 x
2
⋅
+
:=
which is now plotted and compared with the given data in Figure 6.3
x 0.5 0.51
, 5.0
..
:= i 1 2
, 10
..
:= x1 0.5
:= xi 1
+ xi 0.5
+
:=
xi
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
= yi
0.51
2.35
7.54
13.23
17.65
24.21
28.94
37.63
58.32
63.21
= f xi
( )
1.417
3.333
6.525
10.994
16.74
23.763
32.063
41.639
52.493
64.623
=
<--- Given data compared with generated function
190 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

201. 0 1 2 3 4 5
0
50
100
Curve-fitting with quadratic function
Given Data Points
Curve-fitting with quadratic function
Given Data Points
Comparison-Fitted Function with Data
x-Values
Data
(y)
and
f(x)
Values
f xi
( )
yi
xi
Figure 6.3. Curve-fit with quadratic function
6.5 CURVE-FIT WITH A POWER FUNCTION
For some data types, it may be appropriate to do a curve-fit with a function of the form
f(x)= A x B (6.13)
where A and B are undetermined coefficients to be evaluated on a least squares basis.
Taking the logarithm of the above, we obtain
ln (f) = ln (A) +B ln (x) (6.14)
or, F = C + B X (6.15)
where F= ln f , C = ln (A) and X = ln (x) (6.16)
Thus, now the problem has been reduced to one of linear regression and can be handled as done
earlier for a linear fit.
Chapter 6: Curve-Fitting 191

202. Example 6.3
For the data set given below, find a power function that will serve as a least squares fit.
x y
0.18 4.5921
0.32 5.2345
0.65 6.2321
1.12 6.5467
1.65 7.2976
2.34 7.7654
2.52 7.7237
2.85 8.2543
3.12 7.9765
3.61 8.4328
3.92 9.6322
4.51 8.8764
4.72 9.0276
5.25 9.2568
6.75 8.6432
7.85 10.2137
Using f(x)= y(x) = A x B , F=Y= C+B X, where F=Y = ln (y) , C = ln (A)
and X= ln (x), we have the following matrix equation to solve for C and B
n
1
n
i
Xi
∑
=
1
n
i
Xi
∑
=
1
n
i
Xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
C
B
⎛
⎜
⎝
⎞
⎟
⎠
⋅
1
n
i
Yi
( )
∑
=
1
n
i
Yi
( ) Xi
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= (n=16) (6.17)
Put in the given data as shown below and calculate the Y's and X's using
Yi ln yi
( )
:= Xi ln xi
( )
:=
n 16
:= i 1 2
, 16
..
:=
192 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

203. x
0.18
0.32
0.65
1.12
1.65
2.34
2.52
2.85
3.12
3.61
3.92
4.51
4.72
5.25
6.75
7.85
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= y
4.5921
5.2345
6.2321
6.5467
7.2976
7.7654
7.7237
8.2543
7.9765
8.4328
9.6322
8.8764
9.0276
9.2568
8.6432
10.2137
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Yi ln yi
( )
:= Xi ln xi
( )
:=
Equation 6.17 is: [D] { K} = {P}, where
P
1
n
i
Yi
( )
∑
=
1
n
i
Yi
( ) Xi
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
D
n
1
n
i
Xi
∑
=
1
n
i
Xi
∑
=
1
n
i
Xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
and {K} is the vector of unknown coefficients C and B
The constants C and B can be obtained using lsolve as shown below, and then the coefficients
A and B of the power function can be calculated
K lsolve D P
,
( )
:= K
1.883
0.2
⎛
⎜
⎝
⎞
⎟
⎠
= <------ This means: C= 1.883 and B = 0.2
C K1
:= B K2
:= C 1.883
= B 0.2
=
Chapter 6: Curve-Fitting 193

204. A e
C
:= A 6.571
= B 0.2
=
The fit generated is plotted and compared with the given data in Figure 6.4
f x
( ) A x
B
⋅
:=
1 2 3 4 5 6 7 8
0
5
10
Least Squares/Power Function Fit
Given Data Points
Least Squares/Power Function Fit
Given Data Points
Least Squares-Power Function Fit
x-Values
Function
Values
f xi
( )
yi
xi
Figure 6.4. Curve-fit with a power function
6.6. CURVE-FITTING WITH AN EXPONENTIAL FUNCTION
Function of Form A e Bx
Exponential functions appear frequently in the analysis of business, science as well as
engineering problems and are often employed to curve-fit experimental and statistical data. The
function, in this case, has the form .
(6.18)
f x
( ) A e
B x
⋅
⋅
=
where A and B are undetermined coefficients to be evaluated on a least squares basis. Taking the
logarithm of the above gives
ln f
( ) ln A
( ) B x
⋅
+
= (6.19)
or, F C B x
⋅
+
= (6.20)
where
194 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

205. F ln F
( )
= and C ln A
( )
= (6.21)
Thus, now the problem is again reduced to one of linear regression and can be handled as done
earlier for a linear fit.
Example 6.4
For the data set given below, find an exponential function that will serve as a least squares fit.
x y
0 16.45
1 4.47
2 1.06
3 0.45
4 0.15
5 0.03
Using f(x)= y(x) = A e Bx , F=Y= C+B x , where F=Y = ln (y) , and C = ln (A)
we have the following matrix equation to solve for C and B
n
1
n
i
xi
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
C
B
⎛
⎜
⎝
⎞
⎟
⎠
⋅
1
n
i
Yi
( )
∑
=
1
n
i
Yi
( ) xi
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= (n=6) (6.22)
which can be solved for C and B.
Put in the given data and calculate the natural logs of the y-values
i 1 2
, 6
..
:=
i 1 2
, 6
..
:= n 6
:=
y
16.45
4.47
1.06
0.45
0.15
0.03
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
x
0
1
2
3
4
5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Yi ln yi
( )
:=
Chapter 6: Curve-Fitting 195

206. The matrix in the left hand side of Equation (6.22) and the column vector in the right hand side are:
P
1
n
i
Yi
( )
∑
=
1
n
i
Yi
( ) xi
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
D
n
1
n
i
xi
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
The unknown constants C and B can be computed using lsolve and the coefficient A can then be
calculated as shown .
K lsolve D P
,
( )
:= K
2.733
1.216
−
⎛
⎜
⎝
⎞
⎟
⎠
= <------That is, C= 2.733 and B = -1.216
C K1
:= B K2
:= C 2.733
= B 1.216
−
=
A e
C
:= A 15.384
= f x
( ) A e
B x
⋅
⋅
:=
The curve-fit and its natural log are generated below and compared with the given data in Figures
6.5 (a) and 6.5(b)
i 1 6
..
:=
A 15.384
= B 1.216
−
= fi f xi
( )
:= logfunci ln fi
( )
:=
0 2 4
4
2
0
2
4
Data points
Curve-fit
Data points
Curve-fit
Natural Log of Curve- Fit
Natural
Log
of
Function
Values
Yi
logfunci
xi
f x
( ) A e
B x
⋅
⋅
:=
0 2 4
0
10
Analysis-Generated Fit
Given Data Points
Analysis-Generated Fit
Given Data Points
f z
( )
yi
z xi
,
Figure 6.5 (a) Curve-fit with an exponential function
of form A e Bx
Figure 6.5 (b) Natural log of Curve-Fit
196 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

207. Function of Form A x e Bx
There are times when exponential functions of the following form appear in the analysis of
practical problems
f(x)= y(x) = A x e Bx (6.23)
where A and B are undetermined coefficients to be evaluated on a least squares basis.
Taking the logarithm of the above, we obtain
ln (y ) = ln (f) = ln(A) + ln (x) + Bx
or, ln ( y/x) = ln ( A) + Bx
Z = C + B x (6.24)
where,
Z= ln (y/x) and C = ln (A) (6.25)
Thus, now the problem is reduced again to one of linear regression and can be handled as done
earlier for a linear fit.
Example 6.5
For the stress versus strain data given below, find an exponential function of form
S = A e exp ( B e ) that will serve as a least squares fit.
Strain (e) 300 800 1300 1800 2300 2800 (micro-in/in)
Stress (S) 1656 3521 4079 4354 4300 3675 (psi)
Using f(e)= y(e) = A e exp(Be), Z= C + B e , where Z = ln(S/e) and C= ln (A), we have
the following matrix equation to solve for C and B Here, the x-coordinate is "e" and the y -
coordinate is "S"
n
1
n
i
ei
∑
=
1
n
i
ei
∑
=
1
n
i
ei
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
C
B
⎛
⎜
⎝
⎞
⎟
⎠
⋅
1
n
i
Zi
∑
=
1
n
i
Zi ei
⋅
( )
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= (6.26)
Chapter 6: Curve-Fitting 197

208. Put in the given data and calculate the Z's : i 1 2
, 6
..
:=
e1 300
:= e2 800
:= e3 1300
:= e4 1800
:= e5 2300
:= e6 2800
:=
S1 1656
:= S2 3521
:= S3 4079
:= S4 4354
:= S5 4300
:= S6 3675
:=
Here,
n 6
:= Zi ln
Si
ei
⎛
⎜
⎝
⎞
⎟
⎠
:=
Letting
P
1
n
i
Zi
( )
∑
=
1
n
i
Zi
( ) ei
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
D
n
1
n
i
ei
∑
=
1
n
i
ei
∑
=
1
n
i
ei
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
the constants C and B of Equation (6.26) can be computed as shown below
K lsolve D P
,
( )
:= K
1.906
5.721
− 10
4
−
×
⎛
⎜
⎝
⎞
⎟
⎠
= <------That is, C= 1.906 and B = -5.7215x 10(-4)
C K1
:= B K2
:= C 1.906
= B 5.721
− 10
4
−
×
=
A exp C
( )
:= A 6.725
=
The exponential fit, then, is
f e
( ) A e
⋅ exp B e
⋅
( )
⋅
:=
which is plotted and compared with the given data in Figure 6.6
e 300 301
, 2800
..
:= i 1 2
, 6
..
:=
198 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

209. e1 300
:= e2 800
:= e3 1300
:= e4 1800
:= e5 2300
:= e6 2800
:=
<--Given
Data
Points
S1 1656
:= S2 3521
:= S3 4079
:= S4 4354
:= S5 4300
:= S6 3675
:=
500 1000 1500 2000 2500
1000
2000
3000
4000
5000
Analysis-Generated Fit
Given Data Points
Analysis-Generated Fit
Given Data Points
Curve-Fit with Exponential Function
Strain ( e) Values
Stress
(
S)
Values
f z
( )
Si
z ei
,
Figure 6.6. Curve -fit with exponential function A x e Bx
6.7 CURVE-FITTING WITH A LINEAR COMBINATION OF KNOWN
FUNCTIONS
In fitting a function to given data points, a linear combination of known functions may
have to be used at times.
Given a set of data points: (x1, y1), (x2,y2) ......... ( xn, yn), It is required to find
a function:
f(x) = C1 f1(x) + C2 f2 (x) + ......... C m fm(x) (6.27)
where the f i (x) are prescribed functions and the C's are undetermined coefficients to be
evaluated. The total number of data points given is "n" while the total number of
prescribed functions to be utilized is "m" .
In general, then, the function value at x i will be
Chapter 6: Curve-Fitting 199

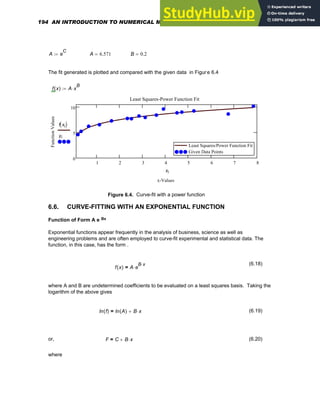
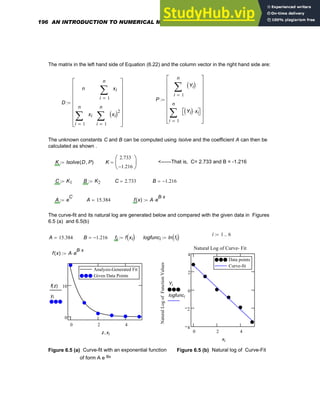
210. f xi
( )
1
m
j
Cj fj xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
= (6.28)
In this case, the sum of the squares of the deviations from the true values y i will be:
s y1 f x1
( )
−
( )2
y2 f x2
( )
−
( )2
+ ......................
+ yn f xn
( )
−
( )2
+
=
(6.29)
For S to be a minimum , the partial derivatives of S with respect to C1, C2 ....... C m
must be zero and the second partials must be positive. These requirements lead to the following
matrix equation in the unknowns, C 1, C2 ...... C m
[M] {C} = {L} (6.30)
where
C
C1
C2
Cm
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= , L
1
n
i
f1 xi
( )
⎡
⎣ ⎤
⎦ yi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
f2 xi
( )
⎡
⎣ ⎤
⎦ yi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
fm xi
( )
⎡
⎣ ⎤
⎦ yi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= , and
200 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

211. M
1
n
i
f1 xi
( )
⎡
⎣ ⎤
⎦
2
∑
=
1
n
i
f2 xi
( )
⎡
⎣ ⎤
⎦ f1 xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
fm xi
( )
⎡
⎣ ⎤
⎦ f1 xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
f1 xi
( )
⎡
⎣ ⎤
⎦ f2 xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
f2 xi
( )
⎡
⎣ ⎤
⎦
2
∑
=
1
n
i
fm xi
( )
⎡
⎣ ⎤
⎦ f2 xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
f1 xi
( )
⎡
⎣ ⎤
⎦ fm xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
f2 xi
( )
⎡
⎣ ⎤
⎦ fm xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
n
i
fm xi
( )
⎡
⎣ ⎤
⎦
2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
The above equations can now be solved for the C 's.
Example 6.6.
Fit the data points:
x: 1.0 2.0 3.0 4.0 5.0
y: 5.75 10.75 12.65 29.95 49.35
with a function of the form y x
( ) C1 f1 x
( )
⋅ C2 f2 x
( )
⋅
+
= , where f1 x
( ) 1
= , and f2 x
( ) x
3
=
In this case, n= 5 and m = 2. Equation (6.30), then, gives the following matrix equation
in C1 and C2
1
5
i
f1 xi
( )
⎡
⎣ ⎤
⎦
2
∑
=
1
5
i
f1 xi
( )
⎡
⎣ ⎤
⎦ f2 xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
5
i
f1 xi
( )
⎡
⎣ ⎤
⎦ f2 xi
( )
⎡
⎣ ⎤
⎦
⋅
⎡
⎣ ⎤
⎦
∑
=
1
5
i
f2 xi
( )
⎡
⎣ ⎤
⎦
2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
C1
C2
⎛
⎜
⎝
⎞
⎟
⎠
⋅
1
5
i
f1 xi
( )
⎡
⎣ ⎤
⎦ yi
⋅
⎡
⎣ ⎤
⎦
∑
=
1
5
i
f2 xi
( )
⎡
⎣ ⎤
⎦ yi
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
The given data is
Chapter 6: Curve-Fitting 201

212. x1 1
:= x2 2.0
:= x3 3.0
:= x4 4.0
:= x5 5.0
:=
y1 5.75
:= y2 10.75
:= y3 12.65
:= y4 29.95
:= y5 49.35
:=
The subscipts 1 and 2 are literal
subscripts , and do not denote vector
components. These are done by including a
period in the variable name . Whatever
follows the period then becomes the
subscript. For example , "vel init" is created
by typing a period after "vel " and then
typing "init"
i 1 2
, 5
..
:= f1 x
( ) 1
:= f2 x
( ) x
3
:= <----
Letting
M
1
5
i
f1 xi
( )2
∑
=
1
5
i
f2 xi
( ) f1 xi
( )
( )
⎡
⎣ ⎤
⎦
∑
=
1
5
i
f1 xi
( )
( ) f2 xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
5
i
f2 xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= L
1
5
i
f1 xi
( )
( ) yi
⋅
⎡
⎣ ⎤
⎦
∑
=
1
5
i
f2 xi
( )
( ) yi
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
the constants C 1 and C2 can be computed as shown
C lsolve M L
,
( )
:= C1 C1
:= C2 C2
:=
C
5.931
0.35
⎛
⎜
⎝
⎞
⎟
⎠
=
C1 5.931
= C2 0.35
=
The fit yielded by this analysis is: y= f(x) = 5.931 + 0.350 x 3
which is plotted in Figure 6.7 and compared with the given data.
x1 1
:= x2 2.0
:= x3 3.0
:= x4 4.0
:= x5 5.0
:=
<--- Given data points
y1 5.75
:= y2 10.75
:= y3 12.65
:= y4 29.95
:= y5 49.35
:=
202 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

213. yanal x
( ) C1 f1 x
( )
⋅ C2 f2 x
( )
⋅
+
:= <--- Curve-fit generated by analysis
yanal 1
( ) 6.281
= yanal 2
( ) 8.733
=
<---y-values generated by curve-fit
yanal 3
( ) 15.386
=
z 1 1.1
, 5
..
:= i 1 5
..
:=
1 2 3 4 5
0
20
40
60
Results of Analysis
Given data points
Results of Analysis
Given data points
Analysis - Generated Fit/ Given Data
X- Values
Y-
Values
yanal z
( )
yi
z xi
,
Figure 6.7. Curve-fit with a linear combination of known functions
6.8 CURVE-FITTING WITH POLYNOMIALS
If an mth order polynomial seems to be a good fit to the data points given, the procedure used
in fitting a linear combination of known functions can still be resorted to. In this case,
f 1 ( x) = 1, f 2 (x) = x , f 3 ( x ) = x 2, f 4 ( x ) = x 3 , ............. ,
f m+1 (x ) = x m
(6.31)
f(x) = C1 f 1 (x ) + C 2 f 2 ( x ) +....................... C m+1 f m+1 ( x ) (6.32)
in which the C 's must be solved for using
[M] {C} = {L} (6.33)
Chapter 6: Curve-Fitting 203

214. where
C
C1
C2
Cm 1
+
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
M
n
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )m
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )m
∑
=
1
n
i
xi
( )m 1
+
∑
=
1
n
i
xi
( )m 2
+
∑
=
1
n
i
xi
( )2 m
⋅
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= L
1
n
i
yi
∑
=
1
n
i
xi yi
⋅
( )
∑
=
1
n
i
xi
( )m
yi
⋅
⎡
⎣
⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
,
where the ( x i, y i ) are the "n" given data points.
Example 6.7.
Given the data points
x: 0 1 2 3 4 5
y: 0 8.47 17.48 19.57 14.69 11.23
Obtain a curve-fit of the form y x
( ) f x
( )
= C1 C2 x
⋅
+ C3 x
2
⋅
+
=
Here, n = 6 and m = 2 and the matrix equation to be solved is
[M]{C} = {L}
204 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

215. where [M] is a known 3x3 matrix and {L} is a known column vector as shown below. The
The column vector {C} , which involves the undetermined coefficients, is
C1
C2
C3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
The given data is
n 6
:= x1 0
:= x2 1
:= x3 2
:= x4 3
:= x5 4
:= x6 5
:=
y1 0
:= y2 8.47
:= y3 17.48
:= y4 19.57
:= y5 14.69
:= y6 11.23
:=
The matrices M and L are
L
1
n
i
yi
∑
=
1
n
i
xi yi
⋅
( )
∑
=
1
n
i
xi
( )2
yi
⋅
⎡
⎣
⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
M
n
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )3
∑
=
1
n
i
xi
( )2
∑
=
1
n
i
xi
( )3
∑
=
1
n
i
xi
( )4
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
The unknown constants are determined below using lsolve
C lsolve M L
,
( )
:= C
0.444
−
12.484
2.057
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
=
C1 C1
:= C2 C2
:= C3 C3
:=
C1 0.444
−
= C2 12.484
= C3 2.057
−
=
The polynomial fitting the given data , then, is
Chapter 6: Curve-Fitting 205

216. f x
( ) C1 C2 x
⋅
+ C3 x
2
⋅
+
:=
which yields
f 1
( ) 9.982
= f 2
( ) 16.294
= f 4
( ) 16.574
= f 3.5
( ) 18.047
=
f 4
( ) 16.574
= f 5
( ) 10.542
=
Figure 6.8 shows a comparison of the curve-fit generated with the given data points
i 1 6
..
:= x1 0
:= x2 1
:= x3 2
:= x4 3
:=
y1 0
:= y2 8.47
:= y3 17.48
:= y4 19.57
:=
<---- Given data
x5 4
:= x6 5
:= y5 14.69
:= y6 11.23
:=
z 0 0.01
, 5
..
:=
0 1 2 3 4 5
0
5
10
15
20
Sec order Poly
Given data points
Sec order Poly
Given data points
Curve Fitted with Sec order Poly
X- Values
Y-Values
f z
( )
yi
z xi
,
Figure 6.8. Curve-fit with polynomial
206 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

217. 6.9 USE OF MATHCAD'S REGRESSION FUNCTIONS FOR
CURVE-FITTING
6.9.1 Linear Regression with Mathcad
In Mathcad, linear regression is done on data represented by vectors vx and vy by using the
" slope" and the " intercept " functions . The function slope(vx,vy) returns a scalar, which is
the slope of the least-squares fitted straight line . The function intercept(vx,vy) returns a
scalar which is the y- axis intercept of this line. Alternatively, the function line(vx,vy) can be
used, which returns a vector containing the y-intercept as well as the slope of the regression
line. Use of these functions is demonstrated below.
Example 6.8.
Determine a linear function that would fit the data of Example 6.1 using Mathcad's linear
regression
For this example, the given data is i 1 2
, 11
..
:= x1 0.10
:= xi 1
+ xi 0.05
+
:=
y1 65.85
:= y2 65.20
:= y3 55.51
:= y4 50.43
:= y5 45.97
:= y6 33.25
:= y7 34.33
:=
y8 29.76
:= y9 23.89
:= y10 23.76
:= y11 18.99
:= n 11
:=
The function generated in the example was f(x) with C1 and C2 shown below
C1 75.497
:= C2 99.618
−
:= f x
( ) C1 C2 x
⋅
+
:=
The data points are entered in as the vx and vy vectors in Mathcad
vx
0.1
0.15
0.2
0.25
0.30
0.35
0.40
0.45
0.50
0.55
0.60
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vy
65.85
65.20
55.51
50.43
45.97
33.25
34.33
29.76
23.89
23.76
18.99
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Chapter 6: Curve-Fitting 207

218. The " slope " and the " intercept " functions are used as follows to generate the slope m and the
intercept c
m slope vx vy
,
( )
:= m 99.618
−
= c intercept vx vy
,
( )
:= c 75.497
=
Alternatively, use line(vx,vy) to generate the above quantities.
c
m
⎛
⎜
⎝
⎞
⎟
⎠
line vx vy
,
( )
:= m 99.618
−
= c 75.497
=
The straight line fit generated by Mathcad is then
ylinmathcad x
( ) m x
⋅ c
+
:= ylinmathcad 0.55
( ) 20.707
=
Figure 6.9 shows a comparison of the data with the curve-fits generated
0.1 0.2 0.3 0.4 0.5 0.6
0
20
40
60
80
Given data-
Fitted Function - f(x)
Mathcad Linear Regression
Given data-
Fitted Function - f(x)
Mathcad Linear Regression
Comparison- Fitted Function with Data
X- Values
Y
and
f(x)
values
yi
f x
( )
ylinmathcad x
( )
xi x
,
Figure 6.9. Curve-fit with Mathcad's linear regression functions
208 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

219. 6.9.2 Nonlinear Regression with Mathcad
In Mathcad, the functions "regress" and "loess" are used along with "interp" to fit a
polynomial through given data points. The " regress " function fits a single polynomial of any
desired order to fit all given data points. In practice, however, there is no need to fit a polynomial
of order higher than 4 ( n = 4 ). This function will not work very well if your data does not fit into
a single polynomial.
Unlike "regress", the " loess " function generates different second-order polynomials for
different regions of the curve . It does this by examining data in small regions. The argument
"span" controls the size of this region. With larger "span " , "loess" becomes equivalent to n =
2. A good value to use is n = 0.75 . While smaller values of "span " will make the fitted curve
track the data fluctuations in a more precise manner, a larger value of " span " , in general ,
will generate a smoother fit.
The " interp" function is the same as the one we resorted to when doing interpolation. It returns
the interpolated y- values corresponding to the x values. In the examples that follow, the vector "
vs1" relates to "regress" while " vs2" is related to the use of the " loess " function.
The formats of these functions are given below.
regress(vx,vy,n): vx and vy are are vectors containing the given
data points and n is the polynomial order required.
loess(vx, vy, span): vx and vy are are vectors containing the
given data points and span controls the size of the
regions for which second-order polynomials are to be generated.
interp(vs,vx,vy,x): This returns the interpolated y value for x. Here, vs is the vector that is
generated through the use of loess or regress and vx and vy are as defined above
Example 6.9
Do a curve-fit on the data of Example 6.2, using Mathcad's nonlinear regression.
The given data is .
i 1 2
, 10
..
:= x1 0.5
:= xi 1
+ xi 0.5
+
:=
y1 0.51
:= y2 2.35
:= y3 7.54
:= y4 13.23
:= y5 17.65
:=
y6 24.21
:= y7 28.94
:= y8 37.63
:= y9 58.32
:= y10 63.21
:=
Chapter 6: Curve-Fitting 209

220. The function generated in the example was a quadratic function of the form f(x)= C1+ C2 x 2 with
C1 0.779
:= C2 2.554
:= f x
( ) C1 C2 x
2
⋅
+
:=
The data points given are put in as the vx and vy vectors shown below
i 1 10
..
:= vxi xi
:= vyi yi
:=
Define :
vs1 regress vx vy
, 2
,
( )
:= vs2 loess vx vy
, 1.
,
( )
:=
f1 x
( ) interp vs1 vx
, vy
, x
,
( )
:= f2 x
( ) interp vs2 vx
, vy
, x
,
( )
:=
A comparison of curve-fits generated for the given data is presented in Figure 6.10 and
in Table 6.1
x1 0.5
:= xi 1
+ xi 0.5
+
:= z 0.5 0.6
, 5
..
:= z 0.5 0.51
, 5.0
..
:= i 1 10
..
:=
y1 0.51
:= y2 2.35
:= y3 7.54
:= y4 13.23
:= y5 17.65
:= <-- Given data
y6 24.21
:= y7 28.94
:= y8 37.63
:= y9 58.32
:= y10 63.21
:=
0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
50
100
Given Data Points
Curve-Fit with Quadratic
Curve-Fit with Mathcad regress function
Curve-Fit with Mathcad loess function
Given Data Points
Curve-Fit with Quadratic
Curve-Fit with Mathcad regress function
Curve-Fit with Mathcad loess function
Comparison-Fitted Function with Data
X-Values
Data
(Y)
and
f(x)
Values
yi
f z
( )
f1 z
( )
f2 z
( )
xi z
,
Figure 6.10. Curve-fitting with Mathcad's nonlinear regression functions
210 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

221. TABLE 6.1
Comparison of given data with curve-fits generated
Given data Quadratic Fit Mathcad -regress Mathcad - loess
xi
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
= yi
0.51
2.35
7.54
13.23
17.65
24.21
28.94
37.63
58.32
63.21
= f xi
( )
1.417
3.333
6.525
10.995
16.741
23.765
32.066
41.643
52.498
64.629
= f1 xi
( )
7.709
7.375
8.732
11.782
16.523
22.956
31.081
40.898
52.407
65.608
= f2 xi
( )
7.654
7.437
8.881
11.946
16.818
23.167
31.243
40.985
52.4
65.52
=
6.9.3 Use of the Function linfit
The Mathcad function "linfit" evaluates the undetermined coefficients C1, C2 ..... in a
regression function that is a linear combination of known functions f1(x), f2(x)..... .It has the
form
C1 f1 (x) + C2 f2(x) + ....... .
The function linfit(vx,vy,F) returns a vector that contains the coefficients C 1, C2 ..... in
the linear combination of known functions that would best fit the given data based on the
least squares principle. Here, "F" is a vector representing the functions that are linearly
combined to generate the best fit to the given data and vx and vy are vectors representing
the given data. Use of linfit requires that there be at least as many data points as there
are terms in F.
The use of " linfit" is illustrated in the following steps, as it is applied to the solution of
Example 6.6 .
Chapter 6: Curve-Fitting 211

222. The given data points are:
x1 1.0
:= x2 2.0
:= x3 3.0
:= x4 4.0
:= x5 5.0
:=
y1 5.75
:= y2 10.75
:= y3 12.65
:= y4 29.95
:= y5 49.35
:=
The curve-fit of Example 6.6 was obtained as a linear combination of the form:
yanal(x)=C1 f1(x) + C2 f2(x)
with C1 = 5.931, C2 = 0.35, f1(x) =1 and f2(x)= x3
C1 5.931
:= C2 0.35
:= f1 x
( ) 1
:= f2 x
( ) x
3
:=
yanal x
( ) C1 f1 x
( )
⋅ C2 f2 x
( )
⋅
+
:=
The vx and vy vectors, in this case, are
vx x
:= vy y
:=
Put in "F" as a
vector of
functions
used in the
linear
combination
resorted to
F x
( )
1
x
3
⎛
⎜
⎝
⎞
⎟
⎠
:= <---
vx
1
2
3
4
5
⎛
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎠
= vy
5.75
10.75
12.65
29.95
49.35
⎛
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎠
=
The vector "S" returned
contains the coefficients C 1,
C2 ........
S linfit vx vy
, F
,
( )
:= S
5.9309
0.3502
⎛
⎜
⎝
⎞
⎟
⎠
= <----
C1 S1
:= C1 5.9309
= C2 S2
:= C2 0.3502
=
The function " g(x) " is the linear combination of the known functions resorted to. Notice
that here both F(x) and S are vectors .
212 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

223. g x
( ) F x
( ) S
⋅
:=
which means: g(x)= C1 f1(x) + C2 f2(x) x 1.0 1.01
, 5
..
:=
The Mathcad ( linfit ) results and the linear combination analysis results are presented in
Figure 6.11 and compared with the given data points.
j 1 2
, 5
..
:=
1 1.5 2 2.5 3 3.5 4 4.5 5
0
20
40
Given Data Points
Analysis Results (Linear Combination )
Regression with linfit
Given Data Points
Analysis Results (Linear Combination )
Regression with linfit
Comparison of results
x- values
y-values
vy j
yanal x
( )
g x
( )
vxj x
,
Figure 6.11. Comparison of linfit results with given data
6.9.4 Use of the Function genfit
The function genfit(vx,vy,vg,F) returns a vector that contains the parameters that make a
nonlinear function f of x and n parameters u1, u2 ... un best fit the data represented in vectors
vx and vy. Use of this function requires that there be at least as many data points as
parameters. Here, vg is an n -element vector of guess values for the parameters u1, u2 ...
un , and F is a column vector containing the function f and its partial derivatives with respect
to the n parameters u1, u2 ... un.
While it is often faster and less sensitive to poor guess values, this process may fail to
converge in situations where the derivative vectors are done incorrectly. The method also
permits a solution that employs numerical approximations for the parameter derivatives. To
change methods, right-click on the genfit function and select the desired method from the
menu. The use of this Mathcad function is best illustrated by an example as shown below.
Chapter 6: Curve-Fitting 213

224. Example 6.11
Given the following data:x: 0.3, 0.4, 1, 1.4, 2, 4
y: 9.4 11.2, 5, 3 , 6, 0
Fit the data with a function of the form: exp ( u1 + u2 x + u3 x2 )
Assemble the column vector F as follows.
This is a column vector with:
1st row: Function fitting data
2nd row: Partial derivative of function with resp to u1
3rd row: Partial derivative of function with respect to u2
4th row: Partial derivative of function with respect to u3
<---
F x u
,
( )
e
u1 u2 x
⋅
+ u3 x
2
⋅
+
e
u1 u2 x
⋅
+ u3 x
2
⋅
+
x e
u1 u2 x
⋅
+ u3 x
2
⋅
+
⋅
x
2
e
u1 u2 x
⋅
+ u3 x
2
⋅
+
⋅
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
*
Put in the given data points as shown
vx
0.3
0.4
1
1.4
2
4
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
*
vy
9.4
11.2
5
3
6
0
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
*
Fill in the vector of guess values for u1, u2, u3 .....
vg
1
0
1
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
*
The function genfit now computes the parameters u1, u2, u3 .....
P genfit vx vy
, vg
, F
,
( )
:=
*
214 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

225. That is, u1 = 2.5654, u2 = -0.7881 , u3 = 0.0364,
as calculated by genfit.
P
2.5654
0.7881
−
0.0364
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
=
*
<-----
u1 P1
:=
*
u2 P2
:=
*
u3 P3
:=
*
The function that best fits the given data is now
This form also can be used since it
represents the zeroth column of the
vector F(x,u )
g x
( ) F x P
,
( )1
:=
*
<--
g x
( ) e
u1 u2 x
⋅
+ u3 x
2
⋅
+
:=
*
or
It is plotted in Figure 6.12 and is compared with the given data points
i 0 6
..
:=
*
x 0.3 0.31
, 4
..
:=
*
0 0.5 1 1.5 2 2.5 3 3.5 4
0
5
10
15
Given data points
Curve-fit with genfit
Given data points
Curve-fit with genfit
Comparison of curve-fit with given data
vyi
g x
( )
vxi x
,
Figure 6.12. Curve-fitting with genfit
6.9.5 Use of the Mathcad functions logfit, lnfit, pwrfit and expfit
Mathcad's logfit
The function logfit(vx,vy,vg) returns a vector containing the coefficients a, b and c for a
Chapter 6: Curve-Fitting 215

226. logarithmic curve of the form a ln(x + b ) + c that best fits the real data values represented by
vectors vx and vy. The use of this function requires that there be at least three data points The
vector vg is a three-element vector of real guess values for the parameters a, b and c. If a
logarithmic fit is desired that is different from the above form, then use genfit or linfit.
As an example, for the data represented by vectors vx and vy below and with the use of the
guess vector vg as given
vx
0
1
2
3
4
5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vy
4
5
5.5
5.8
6.2
6.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vg
2
1
5
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
the curve-fit returned by Mathcad's logfit is
a
b
c
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
logfit vx vy
, vg
,
( )
:= a 1.388
= b 1.0437
= c 3.9536
=
which is the function f(x )= 1.388 ln (x + 1.044 ) + 3.954, the plot of which is drawn below.
f x
( ) a ln x b
+
( )
⋅ c
+
:= x 0 0.01
, 5.
..
:=
0 1 2 3 4 5
4
6
8
Given data points
Mathcad's logfit
Given data points
Mathcad's logfit
vy
f x
( )
vx x
,
216 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

227. Mathcad's lnfit
The function lnfit(vx,vy) returns a vector containing the coefficients a and b for a logarithmic
curve of the form a ln(x ) + b that best fits the real data values represented by vectors vx and vy.
The use of this function requires that there be at least two data points. If a logarithmic fit is
desired that is different from the above form, then use genfit or linfit.
For the data represented by the following vx and vy vectors,
vx
1
2
3
4
5
6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vy
5
6.5
7.25
7.80
8.25
8.63
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
the curve-fit returned by Mathcad's lnfit is
a
b
⎛
⎜
⎝
⎞
⎟
⎠
lnfit vx vy
,
( )
:= a 2.0048
= b 5.04
=
which is the function f(x ) = 2.005 ln (x) + 5.04, the plot of which is shown below.
f x
( ) a ln x
( )
⋅ b
+
:= x 1 1.01
, 6.
..
:=
1 2 3 4 5 6
4
6
8
10
Given data points
Mathcad's lnfit
Given data points
Mathcad's lnfit
vy
f x
( )
vx x
,
Chapter 6: Curve-Fitting 217

228. Mathcad's pwrfit
The function pwrfit(vx,vy,vg) returns a vector containing the coefficients a, b and c for a power
curve of the form a x b + c that best fits the real data values represented by vectors vx and vy.
The use of this function requires that there be at least three data points and the vx values
must all be greater than or equal to zero. Negative x-values are not appropriate in this setting
because raising them to an arbitrary power can produce complex results that will not
correspond to the real y-values. If you need to fit a power function to data in the left-half plane,
shift it so that all x-values are positive, then adjust the fitted function accordingly to obtain
correct results. The vector vg is a three-element vector of real guess values for the parameters
a, b and c . If a logarithmic fit is desired that is different from the above form, then use genfit.
For the data points represented by the vectors vx and vy as given below, and with the use of
the vector vg of guess values shown for the coefficients a, b and c..
vx
0
1
2
3
4
5
6
7
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vy
5
9
50
192
517
1123
2121
3635
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vg
3
4
10
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
the curve-fit returned by Mathcad's pwrfit is
a
b
c
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
pwrfit vx vy
, vg
,
( )
:= giving a 3.9977
= b 3.5003
= c 4.9612
=
which is the function f(x ) = 3.998 x 3.5 + 4.961 , the plot of which is sketched below.
f x
( ) a x
b
⋅ c
+
:= x 0 0.01
, 7.
..
:=
218 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

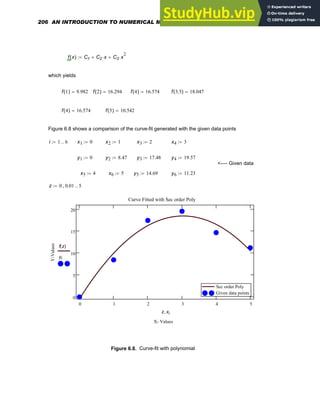
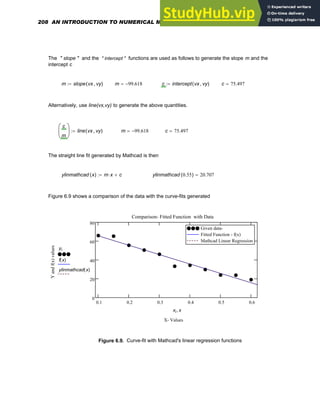
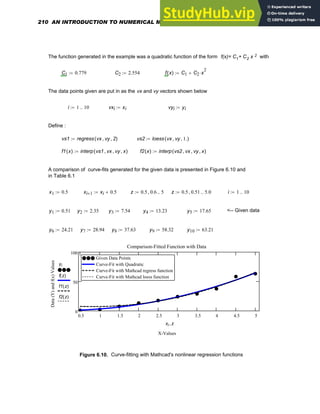
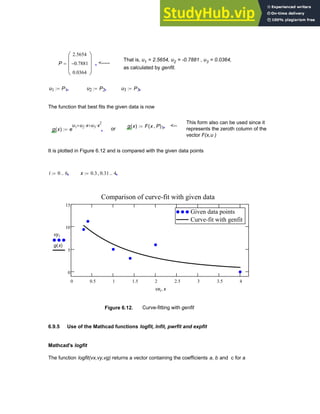
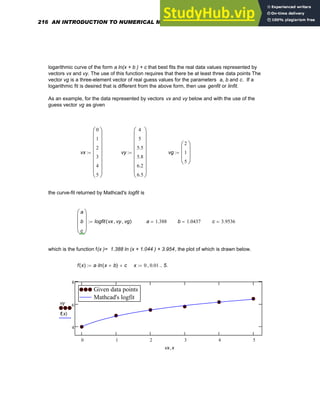
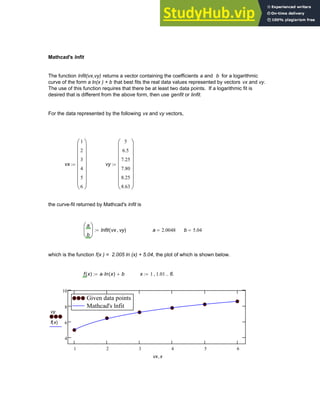
229. 0 1 2 3 4 5 6 7
0
2000
4000
Given data points
Mathcad's pwrfit
Given data points
Mathcad's pwrfit
vy
f x
( )
vx x
,
Mathcad's expfit
The function expfit(vx,vy, [vg]) returns a vector containing the coefficients a, b and c for an
exponential curve of the form A exp (b x ) + C that best fits the real data values represented by
vectors vx and vy. The use of this function requires that there be at least three data points and the
vx values must all be greater than or equal to zero. If a fit has be done on data that has negative
x-values, then the data must be shifted to the positive axis. . Otherwise, a curve-fit with erroneous
values may be generated. The vector vg is a three-element vector of real guess values for the
parameters A, b and C, but it is optional, and does not have to be used. However, if it is not
used, then expfit generates a guess that fits a line to the logs of vy. If an exponential fit is
desired that is different from the above form, then use genfit .
For the data points represented by the vectors vx and vy as given below, and with the use of the
vector vg of guess values shown for the coefficients a, b and c ,.
vg
3
2
10
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
vx
0
1
2
3
4
5
6
7
8
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vy
21
24.892
31.31
41.89
59.334
88.095
135.513
213.693
342.589
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
the curve-fit returned by Mathcad's expfit is defined by
Chapter 6: Curve-Fitting 219

230. A
b
C
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
expfit vx vy
, vg
,
( )
:=
giving A 6
= b 0.5
= C 14.9999
=
Or, if vg is not used, resort to
A
b
C
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
expfit vx vy
,
( )
:=
again, giving A 6
= b 0.5
= C 14.9999
=
which leads to the curve-fit f(x ) = 6 exp (0.5 x ) + 15 , the plot of which is sketched below.
f x
( ) A e
b x
⋅
⋅ C
+
:= x 0 0.01
, 8
..
:=
0 1 2 3 4 5 6 7 8
0
200
400
Given data points
Mathcad's expfit
Given data points
Mathcad's expfit
vy
f x
( )
vx x
,
6.9.6 More Examples with Mathcad
Example 6.12
Using Mathcad's linear regression, generate a curve-fit in the form of a power function for the
data of Example 6.3 and compare with the given data and the analytical results of Example
6.3.
220 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

231. The function generated by analysis in Example 6.3 was:
f x
( ) A x
B
⋅
=
with
A 6.571
:= B 0.2
:=
f x
( ) A x
B
⋅
:=
The data of Example 6.3 is shown below
n 16
:= i 1 2
, 16
..
:=
y
4.5921
5.2345
6.2321
6.5467
7.2976
7.7654
7.7237
8.2543
7.9765
8.4328
9.6322
8.8764
9.0276
9.2568
8.6432
10.2137
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= <-- Given data
x
0.18
0.32
0.65
1.12
1.65
2.34
2.52
2.85
3.12
3.61
3.92
4.51
4.72
5.25
6.75
7.85
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
In Mathcad, linear regression with the slope and intercept functions can be performed on
this problem or the Mathcad function pwrfit can be resorted to and curve-fits obtained as
shown in the following steps.
As was done in Section 6.5, we define:
i 1 2
, 16
..
:=
Chapter 6: Curve-Fitting 221

232. Yi ln yi
( )
:= Xi ln xi
( )
:=
vXi Xi
:= vYi Yi
:= <-- Define vectors vX and vY
The slope and the intercept of the new linear relationship Y= CSTAR+BSTAR*X can now
be computed as
BSTAR slope vX vY
,
( )
:= CSTAR intercept vX vY
,
( )
:= BSTAR 0.1996
= CSTAR 1.8827
=
ASTAR e
CSTAR
:= A 6.571
=
Using Mathcad's pwrfit function on the given data points with the guess vector
vg
6
0.1
0.1
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
yields
a
b
c
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
pwrfit x y
, vg
,
( )
:= That is, a 9.4201
= b 0.142
= c 2.7907
−
=
powerfit x
( ) a x
b
⋅ c
+
:=
The various curve-fits generated are now
fmcad x
( ) ASTAR x
BSTAR
⋅
:= <--Fit generated with Mathcad's linear regression
(slope and intercept functions)
powerfit x
( ) a x
b
⋅ c
+
:= <--Fit generated with Mathcad's pwrfit function
f x
( ) A x
B
⋅
:= <--- Fit generated with power function (Example 6.3)
222 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

233. and these are compared and presented along with the given data in Figure 6.13.
i 1 2
, 16
..
:=
1 2 3 4 5 6 7 8
4
5
6
7
8
9
10
11
Given Data Points
Power Function Fit
Mathcad's Linear Regression
Mathcad's pwrfit function
Given Data Points
Power Function Fit
Mathcad's Linear Regression
Mathcad's pwrfit function
Curve-Fitting with Power Function
x- values
y-
values
yi
f z
( )
fmcad z
( )
powerfit z
( )
xi z
,
Figure 6.13. Curve-fitting with a power function
Chapter 6: Curve-Fitting 223

234. Example 6.13
Using Mathcad's linear regression, generate a curve-fit in the form of the exponential
function A exp ( Bx ) for the data of Example 6.4 . Compare this with the given data and
with the analytical results of Example 6.4
The data given is
i 1 2
, 6
..
:=
x
0
1
2
3
4
5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= y
16.45
4.47
1.06
0.45
0.15
0.03
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
The function generated in Example 6.4 was :
n 6
:=
f x
( ) A e
B x
⋅
⋅
=
with A 15.384
:= B 1.216
−
:=
f x
( ) A e
B x
⋅
⋅
:= <-- Analysis-generated fit
As was done in Section 6.6 , define
fi f xi
( )
:= logfunci ln fi
( )
:=
Yi ln yi
( )
:= <-- log of the y-coordinates of given data
In Mathcad, linear regression with the slope and intercept functions or with the line function
can be performed on this problem and the curve-fit obtained as shown in the following steps
i 1 6
..
:=
vx x
:= vY Y
:=
BSTAR slope vx vY
,
( )
:= CSTAR intercept vx vY
,
( )
:=
224 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

235. CSTAR
BSTAR
⎛
⎜
⎝
⎞
⎟
⎠
line vx vY
,
( )
:= BSTAR 1.2164
−
= CSTAR 2.7334
=
ASTAR e
CSTAR
:= ASTAR 15.3844
=
Then,
Mathcad -generated fit using slope and
intercept or the line function
fmcad x
( ) ASTAR e
BSTAR x
⋅
⋅
:= <---
Mathcad's expfit function can also be used to generate an exponential fit of the form
a exp(bx) + c as shown below
a
b
c
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
expfit x y
,
( )
:= a 16.4172
= b 1.3222
−
= c 0.0391
=
exponfit x
( ) a e
b x
⋅
⋅ c
+
:= <-- Mathcad -generated fit using the expfit function
Figure 6.14 shows a comparison of the Mathcad fits with the results of Example 6.4 and
the given data .
z 0 0.1
, 5
..
:= i 1 6
..
:= f x
( ) A e
B x
⋅
⋅
:=
0 1 2 3 4 5
0
10
20
Given Data Points
Analysis-Generated Fit
Mathcad's Linear Regression
Mathcad's expfit function
Given Data Points
Analysis-Generated Fit
Mathcad's Linear Regression
Mathcad's expfit function
Curve-Fitting with Exponential Function
x- values
y-
values
yi
f z
( )
fmcad z
( )
exponfit z
( ) 0.05
−
xi z
,
Figure 6.14. Curve-fit with an exponential function ( AeBx) using
Mathcad's linear regression
Chapter 6: Curve-Fitting 225

236. Example 6.14
Using Mathcad's linear regression, generate a fit in the form of the exponential function
"Ax exp(Bx)" for the problem of Example 6.5 . Compare this with the results of Example
6.5 and with the given data .
The data given is
i 1 2
, 6
..
:=
e1 300
:= e2 800
:= e3 1300
:= e4 1800
:= e5 2300
:= e6 2800
:=
S1 1656
:= S2 3521
:= S3 4079
:= S4 4354
:= S5 4300
:= S6 3675
:=
The function generated in Example 6.5 was
f e
( ) A e
⋅ exp B e
⋅
( )
⋅
=
with A 6.7248
:= B 5.7205
− 10
4
−
⋅
:= f e
( ) A e
⋅ exp B e
⋅
( )
⋅
:=
n 5
:= Zi ln
Si
ei
⎛
⎜
⎝
⎞
⎟
⎠
:= Si ei exp Zi
( )
⋅
:=
e 300 301
, 3000
..
:=
In Mathcad, linear regression can be performed on this problem and the curve-fit obtained as
shown in the following steps, :
e1 300
:= e2 800
:= e3 1300
:= e4 1800
:= e5 2300
:= e6 2800
:=
S1 1656
:= S2 3521
:= S3 4079
:= S4 4354
:= S5 4300.
:= S6 3675
:=
i 1 2
, 6
..
:=
As was done in Example 6.5, define
vei ei
:= vZi Zi
:=
Zi ln
Si
ei
⎛
⎜
⎝
⎞
⎟
⎠
:=
226 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

237. BSTAR slope ve vZ
,
( )
:= CSTAR intercept ve vZ
,
( )
:= BSTAR 5.7205
− 10
4
−
×
=
CSTAR 1.9058
=
ASTAR exp CSTAR
( )
:= ASTAR 6.7248
=
fmcad e
( ) ASTAR e
⋅ exp BSTAR e
⋅
( )
⋅
:= <-- Mathcad - generated fit
f e
( ) A e
⋅ exp B e
⋅
( )
⋅
:= <-- Analysis-generated fit
Figure 6.15 shows a comparison of the Mathcad-generated fit using linear regression with the
analysis- generated fit of Example 6.5 and with the given data .
z 300 301
, 2800
..
:=
500 1000 1500 2000 2500 3000
1000
2000
3000
4000
5000
Given Data Points
Analysis -generated fit
Mathcad's Linear Regression
Given Data Points
Analysis -generated fit
Mathcad's Linear Regression
Comparison of Curve-Fit Results
Strain (e ) Values
Stress
(S)
Values
Si
f z
( )
fmcad z
( )
ei z
,
Figure 6.15. Curve-fit with an exponential function (AxeBx) using Mathcad's
linear regression
Chapter 6: Curve-Fitting 227

238. Example 6.15
Using Mathcad, generate a nonlinear fit for the data of Example 6.6. Compare these
results with the fit generated in Example 6.6 by using a linear combination of
functions and the given data.
x
1
1
:= x
2
2.0
:= x
3
3.0
:= x
4
4.0
:= x
5
5.0
:=
<--- Given data
y
1
5.75
:= y
2
10.75
:= y
3
12.65
:= y
4
29.95
:= y
5
49.35
:=
The fit generated in Example 6.6 was yanal x
( ) C1 f1 x
( )
⋅ C2 f2 x
( )
⋅
+
=
with f1 x
( ) 1
:= f2 x
( ) x
3
:= C1 5.931
:= C2 0.35
:=
Using Mathcad' s interp and loess functions , curve-fitting with a polynomial can be done
on this problem as shown in the following steps.
i 1 2
, 5
..
:= x 1 1.1
, 5.5
..
:= x
1
1
:= x
2
2.0
:= x
3
3.0
:= x
4
4.0
:= x
5
5.0
:=
y
1
5.75
:= y
2
10.75
:= y
3
12.65
:= y
4
29.95
:= y
5
49.35
:=
vx
i
x
i
:= vy
i
y
i
:= vs loess vx vy
, 1
,
( )
:= floess x
( ) interp vs vx
, vy
, x
,
( )
:=
yanal x
( ) C1 f1 x
( )
⋅ C2 f2 x
( )
⋅
+
:= floess
i
floess x
i
( )
:= yanal
i
yanal x
i
( )
:=
Figure 6.16 compares the Mathcad fit with the given data and the linear combination method
yanal x
( ) C1 f1 x
( )
⋅ C2 f2 x
( )
⋅
+
:= floess x
( ) interp vs vx
, vy
, x
,
( )
:= z 1 1.01
, 5.0
..
:= i 1 5
..
:=
1 1.5 2 2.5 3 3.5 4 4.5 5
0
20
40
60
Given Data Points
Linear Combination
Mathcad loess function
Given Data Points
Linear Combination
Mathcad loess function
Comparison- Mathcad loess / anal method
X- values
Y-
Values
yi
yanal z
( )
floess z
( )
xi z
,
Figure 6.16. Comparison of Mathcad fit with linear combination method
228 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

239. Example 6.16
Using Mathcad, generate a nonlinear fit for the data of Example 6.7. Compare these results
with the fit of form y = f(x) = C1 + C2 x + C3 x 2 generated in Example 6.7 and with the given
data .
x
1
0
:= x
2
1
:= x
3
2
:= x
4
3
:= x
5
4
:= x
6
5
:=
<--Given data
y
1
0
:= y
2
8.47
:= y
3
17.48
:= y
4
19.57
:= y
5
14.69
:= y
6
11.23
:= n 6
:=
The fit generated in Example 6.7 was f x
( ) C1 C2 x
⋅
+ C3 x
2
⋅
+
=
with C1 0.444
−
:= C2 12.484
:= C3 2.057
−
:=
Using Mathcad's interp and loess functions , curve-fitting the given data with a polynomial can
be done as shown below.
i 1 2
, 6
..
:= vx
i
x
i
:= vy
i
y
i
:= vs loess vx vy
, 1
,
( )
:= floess x
( ) interp vs vx
, vy
, x
,
( )
:=
floess
i
floess x
i
( )
:= f x
( ) C1 C2 x
⋅
+ C3 x
2
⋅
+
:= f
i
f x
i
( )
:=
The Mathcad results generated are compared with the data given and with the polynomial method
in Figure 6.17.
i 1 6
..
:= z 0 0.01
, 5
..
:= f x
( ) C1 C2 x
⋅
+ C3 x
2
⋅
+
:= floess x
( ) interp vs vx
, vy
, x
,
( )
:=
0 1 2 3 4 5
0
10
20
Given Data Points
Polynomial Method
Mathcad loess Function
Given Data Points
Polynomial Method
Mathcad loess Function
Comparison- Polynomial Method/ Mathcad
X- Values
Y-
Values
yi
f z
( )
floess z
( )
xi z
,
Figure 6.17. Comparison of Mathcad fit with polynomial method
Chapter 6: Curve-Fitting 229

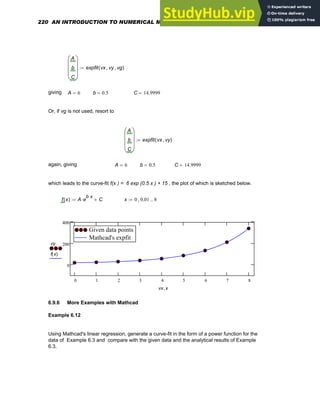
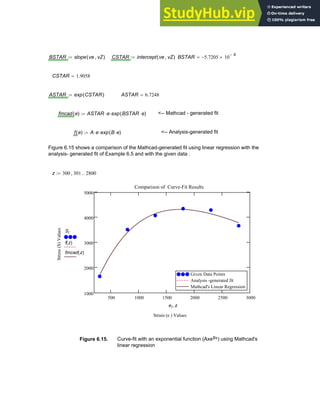
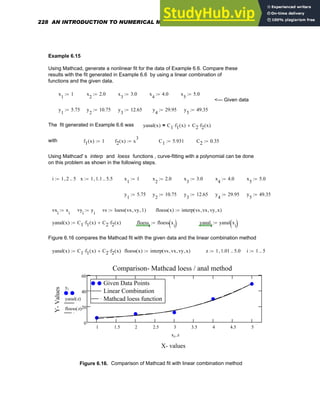
240. Example 6.17
Fit the data points :
x: 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
y: 0.59 0.83 0.90 0.95 1.02 1.43 1.75 3.15
with a function of the form : y = C1 f 1 (x ) + C2 f 2 ( x) +C 3 f 3(x) + C4 f4 (x) where
f 1 (x ) = 1 , f 2 ( x ) = x2 , f 3 ( x) = sin (2x) , f 4 ( x) = exp( 0.95x )
In this case, we have the following matrix equation
[M] {C} = {L} ,
where {C} is the column vector of unknown coefficients C1, C2, C3 and C4 , and [M] and {L} are
known matrices as generated below.
The given data is
N 8
:=
x1 0.1
:= x2 0.2
:= x3 0.3
:= x4 0.4
:= x5 0.5
:= x6 0.6
:= x7 0.7
:= x8 0.8
:=
y1 0.59
:= y2 0.83
:= y3 0.90
:= y4 0.95
:= y5 1.02
:= y6 1.43
:= y7 1.75
:= y8 3.15
:=
i 1 2
, 8
..
:= f1 x
( ) 1
:= f2 x
( ) x
2
:= <--- The subscipts 1 and 2 are literal
subscripts , and do not denote
vector components. These are
done by including a period in the variable
name . Whatever follows the period then
becomes the subscript. For
example , "vel init" is created by typing
a period after "vel" and then typing "init"
f3 x
( ) sin 2 x
⋅
( )
:=
f4 x
( ) exp 0.95 x
⋅
( )
:=
In this case, the M and L matrices are
230 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

241. N 8
:=
M
1
N
i
f1 xi
( )2
∑
=
1
N
i
f2 xi
( ) f1 xi
( )
( )
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f3 xi
( ) f1 xi
( )
( )
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f4 xi
( ) f1 xi
( )
( )
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f1 xi
( )
( ) f2 xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f2 xi
( )2
∑
=
1
N
i
f3 xi
( ) f2 xi
( )
( )
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f4 xi
( ) f2 xi
( )
( )
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f1 xi
( )
( ) f3 xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f2 xi
( )
( ) f3 xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f3 xi
( )2
∑
=
1
N
i
f4 xi
( ) f3 xi
( )
( )
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f1 xi
( )
( ) f4 xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f2 xi
( )
( ) f4 xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f3 xi
( )
( ) f4 xi
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f4 xi
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
L
1
N
i
f1 xi
( )
( ) yi
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f2 xi
( )
( ) yi
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f3 xi
( )
( ) yi
⋅
⎡
⎣ ⎤
⎦
∑
=
1
N
i
f4 xi
( )
( ) yi
⋅
⎡
⎣ ⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
The unknown coefficients in {C} can be computed using the mathcad function lsolve as
follows
C lsolve M L
,
( )
:= yielding
C
45.612
−
49.735
−
16.7
−
45.46
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
=
Chapter 6: Curve-Fitting 231

242. The constants C 1 through C4 are the components of the column vector {C} generated above. Thus,
C1 C1
:= C2 C2
:= C3 C3
:= C4 C4
:=
C1 45.612
−
= C2 49.735
−
= C3 16.7
−
= C4 45.46
=
The fit yielded by the analysis is, then,
yanal x
( ) C1 f1 x
( )
⋅ C2 f2 x
( )
⋅
+ C3 f3 x
( )
⋅
+ C4 f4 x
( )
⋅
+
:=
and has the form
-45.612 -49.735 x 2 -16.7 sin (2x)+ 45.46 exp(0.95x)I
The use of " linfit" as applied to this problem is illustrated in the following steps.
The vx and vy vectors, in this are
vx x
:= vy y
:=
Put in "F" as a
vector of
functions
used in the
linear
combination
resorted to
F x
( )
1
x
2
sin 2 x
⋅
( )
exp 0.95 x
⋅
( )
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= <---
vx
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
vy
0.59
0.83
0.9
0.95
1.02
1.43
1.75
3.15
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
S linfit vx vy
, F
,
( )
:= The vector "S" returned
contains the coefficients C 1,
C2 ........
<----
S
45.612
−
49.735
−
16.7
−
45.46
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
=
232 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

243. C1 S1
:= C2 S2
:= C3 S3
:= C4 S4
:=
C1 45.612
−
= C2 49.735
−
= C3 16.7
−
= C4 45.46
=
The function " g(x) " is then the linear combination of the known functions resorted to.
Notice that both F(x) and S are vectors here.
g x
( ) F x
( ) S
⋅
:=
which means: g(x)= C1 f1(x) + C2 f2(x) + C3 f3(x) + C4 f4 (x)
The Mathcad ( linfit ) results and the linear combination analysis results are both presented in
Figure 6.18 and compared with the given data points.
j 1 2
, 8
..
:= x 0.1 0.101
, 0.80
..
:=
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
1
2
3
4
Given Data Points
Analysis Results (Linear Combination )
Regression with linfit
Given Data Points
Analysis Results (Linear Combination )
Regression with linfit
Comparison of results
x- values
y-values
vy j
yanal x
( )
g x
( )
vxj x
,
Figure 6.18. Curve-fit with a linear combination of functions
Chapter 6: Curve-Fitting 233

244. Example 6.18
Given the following data:x: 0,1,2,3,4,5,6,7
y: 3,6.2,9.75,20.13,24.25,33.21,37.54,41.95
Using Mathcad's genfit, fit the data with a function of the form: f(x )= u1sin(2x)+u2cos(4x)+u3x,
where the u's are constants to be determined using the least squares principle.
Put in the vector of the desired function and its partial derivatives, the given data points and the
guess vector as follows
A column vector with:
1st row: Function to fit data
2nd row: Partial derivative with respect to
u1
3rd row: Partial derivative with
respect to u2
4th row: Partial derivative with respect
to u3
F x u
,
( )
u1 sin 2 x
⋅
( )
⋅ u2 cos 4 x
⋅
( )
⋅
+ u3 x
⋅
+
sin 2 x
⋅
( )
cos 4 x
⋅
( )
x
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:=
*
<---
vx
0
1
2
3
4
5
6
7
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
* vy
3
6.2
9.75
20.13
24.25
33.21
37.54
41.95
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
*
<----- Given data points
vg
1
2
3
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
*
<--- vector of guess values for u1, u2, u3.....
The function genfit now returns a vector of the u- coefficients that will best fit the given data.
P genfit vx vy
, vg
, F
,
( )
:=
*
234 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

245. That is , u1 = 1.935, u2 = 3.175, u3= 6.251, as calculated by
genfit.
P
1.935
3.175
6.251
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
=
*
u1 P1
:= u2 P2
:= u3 P3
:=
The function that best fits the given data is now
f x
( ) F x P
,
( )1
:=
*
or, use, f x
( ) u1 sin 2 x
⋅
( )
⋅ u2 cos 4 x
⋅
( )
⋅
+ u3 x
⋅
+
:=
It is plotted in Figure 6.19 and is compared with the given data points
i 1 8
..
:=
*
x 0 0.1
, 7
..
:=
*
0 1 2 3 4 5 6 7
0
10
20
30
40
50
Given data points
Curve-fit obtained
Given data points
Curve-fit obtained
Comparison of curve-fit with given data
vyi
f x
( )
vxi x
,
Figure 6.19. Curve-fitting with Mathcad's genfit
Chapter 6: Curve-Fitting 235

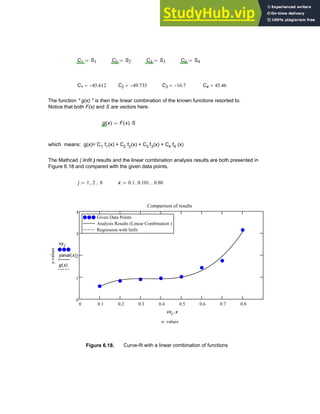
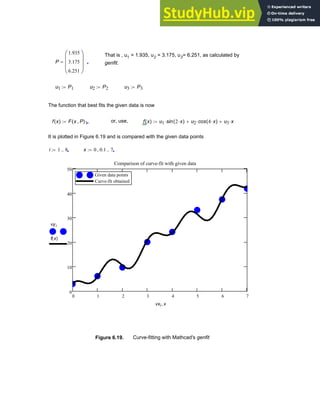
246. 6.10 APPLICATIONS IN CURVE-FITTING
In the world of engineering, science, and business, it is very common to see a function in
the form of data prescribed at many points, and in addition, there may also be
considerable scatter in the available data . The methods discussed in the earlier sections
of this chapter will now be used to generate appropriate curve-fits to actual data from
several practical applications.
6.10.1 Fatigue Failure Curve for Loading in the Finite Life Range
The fatigue failure curve of a material provides useful information pertinent to the design of
machinery for finite life [ 19 ]. It is essentially a relationship between the completely
reversed applied stress, S, and fatigue life, L , which is measured in terms of the number
of stress reversals to failure.
The following data pertains to a steel with an endurance limit of 40 kpsi and an ultimate
strength of 90 kpsi. It is required to curve-fit the data with a suitable function.
L ( million cycles) Stress (kpsi)
vL
0.02
0.03
0.04
0.05
0.075
0.1
0.2
0.4
0.6
0.8
1.0
1.1
1.2
1.3
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= vS
80
70
65
61
57
55
50
45
42
40.5
40.1
40
39.9
39.85
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
From the plot of the given data shown in Figure 6.20, it appears that a power function would
furnish a reasonable curve-fit. This has the form
S(L)= A*LB ,
236 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

247. where A and B are undetermined coefficients to be evaluated on a least squares basis.
i 1 14
..
:=
0 0.2 0.4 0.6 0.8 1 1.2
40
60
80
Given Data
Given Data
Given Data Points
Given L- values (million cycles )
Given
S-
values
(kpsi)
vSi
vLi
Figure 6.20. Fatigue life data
Using S(L) = A L B , Sstar= C+ B . Lstar , where Lstar= ln (L) , C = ln (A) and
Sstar= ln (S), the matrix equation [D]{X} = {P} is obtained , where {X} is the column vector
containing the unknowns C and B.
n 14
:= Sstar ln vS
( )
:= Lstar ln vL
( )
:= D X
⋅ P
=
D
n
1
n
i
Lstar i
∑
=
1
n
i
Lstar i
∑
=
1
n
i
Lstar i
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
P
1
n
i
Sstari
∑
=
1
n
i
Sstari Lstar i
⋅
( )
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
The unknown constants C and B can be computed using lsolve as shown below
K lsolve D P
,
( )
:= K
3.684
0.155
−
⎛
⎜
⎝
⎞
⎟
⎠
= <------Thus, C= 3.684 and B = -0.155
C K1
:= B K2
:= C 3.684
= B 0.155
−
= A e
C
:= A 39.808
=
Chapter 6: Curve-Fitting 237

248. The curve-fit generated by the linear regression analysis is now
S L
( ) A L
B
⋅
:= with A 39.808
=
Mathcad's linear regression can also be performed on this problem and the curve-fit obtained
as shown in the following steps.
vLstar ln vL
( )
:= vSstar ln vS
( )
:=
C1
B1
⎛
⎜
⎝
⎞
⎟
⎠
line vLstar vSstar
,
( )
:= B1 0.155
−
= C1 3.684
=
A1 e
C1
:= A1 39.808
= fmcad L
( ) A1 L
B1
⋅
:= <--- Mathcad -generated fit
Figure 6.21 shows a comparison of the curve-fits generated with the given data points .
L 0.02 0.03
, 1.3
..
:= i 1 14
..
:=
0 0.2 0.4 0.6 0.8 1 1.2
20
40
60
80 Given data points
Analysis-generated fit
Mathcad's linear regression
Given data points
Analysis-generated fit
Mathcad's linear regression
Curve-Fitting with Power Function
L- values (million cycles)
S-
values
(kpsi)
vSi
S L
( )
fmcad L
( )
vLi L
,
Figure 6.21. Fatigue failure curve for loading in the finite life range
238 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

249. 6.10.2. Temperature Response of an Object Placed in a Hot Stream of Air
The following data pertains to the temperatures of a solid steel sphere suspended in a hot stream
of air measured at several instants of time [ 17 ]. It is required to curve-fit the data with a suitable
function.
t= Time (secs) T=Temp (deg C) t=Time(Secs) T=Temp (deg C)
0.0 14 500 51
100 28 600 54
200 37.5 700 55
300 44 800 57.8
400 48 900 59.1
The given data is put in as follows and plotted in Figure 6.22.
n 10
:= t1 0
:= t2 100
:= t3 200
:= t4 300
:= t5 400
:= t6 500
:= t7 600
:=
T1 14
:= T2 28
:= T3 37.5
:= T4 44
:= T5 48
:= T6 51
:= T7 54
:=
t8 700
:= t9 800
:= t10 900
:= T8 55
:= T9 57.8
:= T10 59.1
:=
i 1 10
..
:=
0 200 400 600 800
0
20
40
60
Given data points
Given data points
Ti
ti
Figure 6.22. Given temperature versus time data
A glance at the plot of Figure 6.22 suggests that a function of the following form would provide a
reasonable fit to the given data
f t
( ) A B e
t
−
τ
⋅
+
=
where f(t) is a linear combination of functions in which A and B are constants to be determined
on a least squares basis. From the data plot, it appears that the temperature profile attains
steady state in approximately 1200 seconds, which , when equated to four time constants, will
yield a time constant, τ, of 300 seconds. Thus, the coefficient of t in the exponential term can
be selected as (-1/300).
Chapter 6: Curve-Fitting 239

250. In this case, the matrix equation to be solved is
[M] {C} = {A}
in which {M] and {A} contain the functions f1 t
( ) 1
:= f2 t
( ) e
1
−
300
t
⋅
:=
and
M
1
n
i
f1 ti
( )2
∑
=
1
n
i
f1 ti
( ) f2 ti
( )
⋅
( )
∑
=
1
n
i
f1 ti
( ) f2 ti
( )
⋅
( )
∑
=
1
n
i
f2 ti
( )2
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= , C
C1
C2
⎛
⎜
⎝
⎞
⎟
⎠
= , A
1
n
i
f1 ti
( ) Ti
⋅
( )
∑
=
1
n
i
f2 ti
( ) Ti
⋅
( )
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
In the above, note that n = 10 and m =2, and the unknown constants are C1 and C2 which are
determined below using lsolve.
C lsolve M A
,
( )
:= A C1
:= B C2
:=
C
60.477
45.967
−
⎛
⎜
⎝
⎞
⎟
⎠
=
The function fitting the given data , then, is
f t
( ) A B e
1
−
300
t
⋅
⋅
+
:=
which is shown in Figure 6.23 .
f 0
( ) 14.511
= f 200
( ) 36.877
= f 800
( ) 57.283
= f 900
( ) 58.189
=
Mathcad's function linfit can also be used to evaluate the undetermined coefficients A and B in
the regression function employed which is a linear combination of the functions selected for the
curve-fit. This can be done as shown in the following steps.
vt t
:= vT T
:= F t
( )
1
e
1
−
300
t
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= S linfit vt vT
, F
,
( )
:=
240 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

251. S
60.477
45.967
−
⎛
⎜
⎝
⎞
⎟
⎠
= <-- This vector returns the coefficients A and B which
are referred to here as Astar and Bstar
Astar S1
:= Bstar S2
:= Astar 60.477
= Bstar 45.967
−
=
The function g(t) which is a scalar product of the vectors F(t) and S will then yield the linear
combination employed
g t
( ) F t
( ) S
⋅
:=
That is,
g t
( ) Astar f1 t
( )
⋅ Bstar f2 t
( )
⋅
+
:=
The linfit results and those of the linear combination analysis are presented in Figure 6.23 and
compared with the given data .
f t
( ) A B e
1
−
300
t
⋅
⋅
+
:= g t
( ) F t
( ) S
⋅
:= i 1 10
..
:= t 0.5 1.0
, 900
..
:=
0 100 200 300 400 500 600 700 800 900
0
20
40
60
Given data points
Analysis fit
linfit results
Given data points
Analysis fit
linfit results
Comparison-curve-fits with data
time , seconds
temperature,
deg.
C
vTi
f t
( )
g t
( )
vti t
,
Figure 6.23. Temperature response of an object placed in a hot stream of air
Chapter 6: Curve-Fitting 241

252. 6.10.3. The Effect of Operating Temperature on the Strength of a Mechanical
Element
When a mechanical element is subjected to reversed stresses at temperatures below room
temperature, there is a strong possibility of the occurrence of brittle fracture . On the other
hand, when the operating temperatures are higher than room temperature, the yield strength
of the material drops off very rapidly with increase in temperature, and yielding can take place
. The temperature-corrected value of tensile strength, then, to be used in design calculations
is obtained by multiplying the tensile strength at room temperature by a factor K d which is
a function of the temperature of the operating environment.
The following data was collected from tests done on carbon and alloy steels and shows the
effect of operating temperature on tensile strength [ 18 ]. An appropriate curve-fit to the
given data is sought.
Temp., deg F. K d Temp.,deg F. Kd
0 0.975 600 0.963
100 1.008 700 0.927
200 1.020 800 0.872
300 1.024 900 0.797
400 1.018 1000 0.698
500 0.995 1100 0.567
The given data points, which are plotted in Figure 6.24 below, are put in as follows.
n 12
:= T1 0
:= T2 100
:= T3 200
:= T4 300
:= T5 400
:= T6 500
:=
T7 600
:= T8 700
:= T9 800
:= T10 900
:= T11 1000
:= T12 1100
:=
Kd1 0.975
:= Kd2 1.008
:= Kd3 1.020
:= Kd4 1.024
:= Kd5 1.018
:= Kd6 0.995
:=
Kd7 0.963
:= Kd8 0.927
:= Kd9 0.872
:= Kd10 0.797
:= Kd11 0.698
:= Kd12 0.567
:=
242 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

253. 0 200 400 600 800 1000
0.5
1
Given data points
Given data points
Given data points
Temperature, deg. F
Factor
Kd
Kdi
Ti
i 1 12
..
:=
Figure 6.24. Given Kd versus temperature data
We will fit the given data with a second-order polynomial of the following form.
Kd(T) = f(T) = C1 + C2 T + C3T 2
Here, n = 12 and m = 2 and the matrix equation to be solved is:
[M]{C} = {A},
where [M] is a known 3x3 matrix and {A} is a known column vector as shown below. The
column vector {C} , which involves the undetermined coefficients, is
C
C1
C2
C3
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
=
The [M] and {A} matrices are
Chapter 6: Curve-Fitting 243

254. M
n
1
n
i
Ti
∑
=
1
n
i
Ti
( )2
∑
=
1
n
i
Ti
∑
=
1
n
i
Ti
( )2
∑
=
1
n
i
Ti
( )3
∑
=
1
n
i
Ti
( )2
∑
=
1
n
i
Ti
( )3
∑
=
1
n
i
Ti
( )4
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:= A
1
n
i
Kdi
∑
=
1
n
i
Ti Kdi
⋅
( )
∑
=
1
n
i
Ti
( )2
Kdi
⋅
⎡
⎣
⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
Using the Mathcad function lsolve gives
C lsolve M A
,
( )
:= C1 C1
:= C2 C2
:= C3 C3
:=
C1 0.968
= C2 4.199 10
4
−
×
= C3 6.966
− 10
7
−
×
=
f T
( ) C1 C2 T
⋅
+ C3 T
2
⋅
+
:= f 200
( ) 1.024
= f 700
( ) 0.921
= f 900
( ) 0.782
=
The regress and loess functions in Mathcad can also be employed as shown below to
generate curve-fits to the given data .
i 1 12
..
:= vTi Ti
:= vKdi Kdi
:=
vs1 regress vT vKd
, 2
,
( )
:= vs2 loess vT vKd
, 2
,
( )
:=
freg T
( ) interp vs1 vT
, vKd
, T
,
( )
:= floess T
( ) interp vs2 vT
, vKd
, T
,
( )
:=
Figure 6.25 shows a comparison of the various curve-fits generated with the given data points.
f T
( ) C1 C2 T
⋅
+ C3 T
2
⋅
+
:= T 0 1
, 1100
..
:= i 1 12
..
:=
244 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

255. 0 200 400 600 800 1000
0.4
0.6
0.8
1
1.2
Given data points
Analysis-generated function
Mathcad regress
Mathcad loess
Given data points
Analysis-generated function
Mathcad regress
Mathcad loess
Curve-fits generated
Temperature, deg F
Multiplying
factor
Kd
vKdi
f T
( )
freg T
( )
floess T
( )
vTi T
,
Figure 6.25. Effect of operating temperature on the strength of a mechanical element
6.10.4. Drop-Testing of Packaged Articles
An interesting parameter that often warrants investigation is the height from which a package can
be dropped before it suffers any accountable damage, which can be assessed from the maximum
acceleration imparted to the package at the end of the drop [ 20 ]. This is a question that arises
when packages must be properly cushioned before shipment to another location. The maximum
acceleration to gravity ratio, a , has been found to be a function of the ratio, h , of twice the
distance dropped to the static deflection of the package.
The following a versus h data is provided , using which a reasonable curve-fit is to be
generated .
h a h a
________________________
1 1.4 9 3.25
2 1.8 10 3.3
3 2 11 3.55
4 2.25 12 3.65
5 2.65 13 3.75
6 2.8 14 3.85
7 2.9 15 4.2
8 3.01 16 4.3
_______________________________
Chapter 6: Curve-Fitting 245

256. These data points are plotted in Figure 6.26.
n 16
:= i 1 2
, 16
..
:= h1 1
:= hi 1
+ hi 1
+
:=
a1 1.4
:= a2 1.8
:= a3 2.
:= a4 2.25
:= a5 2.65
:= a6 2.8
:= a7 2.9
:= a8 3.01
:=
a9 3.25
:= a10 3.3
:= a11 3.55
:= a12 3.65
:= a13 3.75
:= a14 3.85
:= a15 4.2
:= a16 4.3
:=
We will generate a curve-fit of the form:
a = f(h) = C1 + C2 h + C3 h 2 + C 4 h 3
Here, n = 16 and m = 3 and the matrix equation to be solved is:
[M]{C} = {A},
0 2 4 6 8 10 12 14 16
1
2
3
4
5
Given data points
Given data points
Given data points
(2h/ static deflection ) ratio
(max
acceleration/
gravity)
ratio
ai
hi
Figure 6.26. Given acceleration ratio versus height ratio data
246 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

257. where [M] is a known 4x4 matrix and {A} is a known column vector as shown below. The
column vector {C} , which involves the undetermined coefficients, is
C
C1
C2
C3
C4
⎛
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎠
=
M
n
1
n
i
hi
∑
=
1
n
i
hi
( )2
∑
=
1
n
i
hi
( )3
∑
=
1
n
i
hi
∑
=
1
n
i
hi
( )2
∑
=
1
n
i
hi
( )3
∑
=
1
n
i
hi
( )4
∑
=
1
n
i
hi
( )2
∑
=
1
n
i
hi
( )3
∑
=
1
n
i
hi
( )4
∑
=
1
n
i
hi
( )5
∑
=
1
n
i
hi
( )3
∑
=
1
n
i
hi
( )4
∑
=
1
n
i
hi
( )5
∑
=
1
n
i
hi
( )6
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
A
1
n
i
ai
∑
=
1
n
i
hi ai
⋅
( )
∑
=
1
n
i
hi
( )2
ai
⋅
⎡
⎣
⎤
⎦
∑
=
1
n
i
hi
( )3
ai
⋅
⎡
⎣
⎤
⎦
∑
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
:=
C lsolve M A
,
( )
:= C
0.997
0.433
0.029
−
9.472 10
4
−
×
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
= C1 C1
:= C2 C2
:= C3 C3
:= C4 C4
:=
C1 0.997
= C2 0.433
= C3 0.029
−
= C4 9.472 10
4
−
×
=
f h
( ) C1 C2 h
⋅
+ C3 h
2
⋅
+ C4 h
3
⋅
+
:= f 15
( ) 4.114
= f 9
( ) 3.219
=
The Mathcad regress and loess functions also can be utilized as shown below to generate
curve-fits to the given data.
Chapter 6: Curve-Fitting 247

258. i 1 2
, 16
..
:=
vhi hi
:= vai ai
:= vs1 regress vh va
, 3
,
( )
:= vs2 loess vh va
, 2
,
( )
:=
freg h
( ) interp vs1 vh
, va
, h
,
( )
:= floess h
( ) interp vs2 vh
, va
, h
,
( )
:=
h 1 1.1
, 16
..
:= i 1 2
, 16
..
:=
Figure 6.27 shows a comparison of the various curve-fits obtained with the given data points.
0 2 4 6 8 10 12 14 16
1
2
3
4
5
Given data points
Analysis-generated fit
Mathcad 's regress function
Mathcad's loess function
Given data points
Analysis-generated fit
Mathcad 's regress function
Mathcad's loess function
Curve-fits generated
(2 h / static deflection ) ratio
(max
acceleration/gravity
)
ratio
vai
f h
( )
freg h
( )
floess h
( )
vhi h
,
Figure 6.27. Acceleration ratio versus height ratio curve-fit
PROBLEMS
In all problems, also obtain results with the Mathcad functions, slope, intercept, regress,
loess, interp, expfit, and pwrfit as appropriate and compare the results of your
regression analysis with the given data and results generated with Mathcad. Show this
comparison by means of Mathcad plots with proper labels, titles and traces.
6.1 Given the following data.
x: 1.3 3.2 4.6 6.1
y: 52 46 38 26
fit a straight line y= f(x)= C1 + C2 x to the above data. Determine y (5.1)
248 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

259. 6.2. Given:
x: 0 1 2 3 4
y: 11.25 12.34 18.56 28.69 44.73
determine a least squares quadratic fit. Determine y ( 3.75 )
6.3. Generate a least squares fit of the form f(x) = AxB to the following data
x: 1 2 4 5
y: 2 10 60 110
Apply a weighting factor of 3 to the last data point and determine f(3.5)
6.4. The thermal conductivity, K, of a material varies with temperature, T, as follows
T ( deg Kelvin) 200 600 1000 1400
K (W/(cm-deg Kelvin) 1.0 0.40 0.30 0.25
Determine a least squares fit of the form K = ATB. Determine K for T = 1200 deg Kelvin. Obtain
an answer that is good to two decimal places.
6.5. For the data set given below, determine a power function that will serve as a least
squares fit.
x: 1 2 3 4 5 6 7 8
y: 0.43 0.71 0.94 1.07 1.19 1.27 1.32 1.47
Compute y( 4.5)
6.6. For the data set given below, find an exponential function of form :
y= f(x) = A exp(Bx) that will serve as a least squares fit.
x: 0 1 2 2.75 3.5
y: 2.5 6.75 15.42 28.86 52.03
Determine y( 3.0)
Chapter 6: Curve-Fitting 249

260. 6.7. For the data set given below, find an exponential function of form :
y= f(x) = A exp(Bx) that will serve as a least squares fit.
x: 0 1 2 3 4
y: 2.01 1.37 0.83 0.55 0.33
Determine y(1.5)
6.8 For the experimental data given below
Strain, x, ( μ-in/in) 40 50 70 90
Displacement, y, (inches) 0.015 0.028 0.045 0.072
Determine a least squares fit of the form f(x)= Ax e (Bx). Determine f(45) and f(60)
6.9. For the strain ( e) / displacement (d) data shown below:
e: 43 57 68 84 99 115 (micro-in/in)
d: 0.009 0.017 0.029 0.043 0.067 0.097 (inches)
determine a least squares fit using an approximation of the form:
e= A x exp(-Bx)
Determine d(72)
6.10. The temperature of a a hot surface varies sinusoidally with time. The data which
is in terms of temperatures, T (deg C), measured at several time intervals , τ , where τ
is the number of hours from midnight, is given below.
τ (hours) 2 4 8
T (deg C) 80 120 105
Obtain a curve fit to the given data of the form
T = A sin ( πτ/12) + B cos ( πτ/12)
Determine T (6 hours).
250 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

261. 6.11. Fit the data points given below with a function of the form y(x) = C1 f1(x) + C2 f2(x)
where f1(x) = x and f2(x) = x3. Compute y(3.75).
x: 2.25 3.30 4.40
y: 9.75 15.60 28.27
6.12. The following data pertains to the temperatures of an object suspended in a hot
stream of air measured at several instants of time
t, Time (seconds) 0.0 400 1200
T, Temperature (deg C) 20 50 61.5
Curve-fit the data with a function of the form
f t
( ) A B e
0.0033
− t
⋅
( )
⋅
+
=
and estimate the temperature attained by the object at time t = 600 seconds
6. 13. Fit a linear combination of known functions
f(x) = A + B x + C sin (πx) + D sin (3πx )
to
x 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
( )
=
y 0.5541 2.1456 2.8021 2.5645 3.2458 2.9765 2.8521 2.4379 1.7872 0.1315
( )
=
Determine y ( 0.85)
6.14. Given the 4 data points
x: 0 2.5 4.75 6.26
y: 0 12.45 22.67 36.89
obtain a curve-fit of the form: y = f(x) = C1 + C2 x + C3 x 2 + C 4 x 3 . Apply a
weighting factor of 2 to the last two data points. Determine y ( 3.5).
6.15. Data defining the stress (S) versus strain (e) curve for an aluminum alloy is given below.
Chapter 6: Curve-Fitting 251

262. Strain,e, ( %) Stress,S, (Kpsi)
10 63
20 63.6
40 62
60 60
80 58
100 56
120 52
140 48
150 47
Using an approximating polynomial of the form
S C1 C2 e
⋅
+ C3 e
2
⋅
+
=
obtain a least squares fit to the given data. Determine S(105%)
6. 16. The following data relating the distance traveled by an object to time was obtained from a
test in an experimental test track . The distance traveled, S, is in meters and the time , t, is in
seconds.
Time, t (secs) 0.1 0.5 1.5 3.0
Distance, S (m) 0.26 1.56 7.41 30.90
Generate a curve-fit of the form S(t) = A + B t + C t 2. Compute S for t= 2 seconds.
6.17. The pressure drag , D P, on an object can be reduced in comparison with the total
drag , DT, by streamlining it , that is, making its length, L, in the direction of flow larger with
respect to its maximum thickness or diameter, D . [ 17 ] . Obtain an appropriate curve-fit to
the following data which is provided to demonstrate the effect of streamlining on the pressure
drag of a body of symmetrical airfoil cross section.
L
D
1 2 3 4 5 6 7 8 9 10 11
( )
=
DP
DT
1.25 0.65 0.42 0.25 0.20 0.10 0.08 0.06 0.04 0.02 0.01
( )
=
Determine D P / DT for L / D = 5.5
6.18. The following data , in which the time, t, is given in seconds provides the
252 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

263. response c ( t ) of a control system to a step input.
t 0 0.75 1.50 2 3 4 5 6
( )
:=
c t
( ) 0 1.30 1.40 1.10 0.85 1.02 1.01 1.009
( )
:=
Obtain a least-squares fit of the form.
c(t)= A+ B e -t sin (2.828 t ) + C e -t cos ( 2.828 t )
and determine c at t = 3.5 seconds.
6.19. The Brinell hardness number, Bhn , for steel [ 18 ] is given as a function of the
tempering temperature, T, in the following table
T, deg F. 400 600 800 1000 1200
Bhn 540 500 445 375 310
Obtain an appropriate curve-fit to the given data and determine the Brinell hardness
number for T = 850 deg F.
6.20. The average strain rate used in obtaining stress/ strain data for a material
specimen is about 0.001 in / (in-sec ). However, when the strain rate, SR, is
increased, as it happens, under conditions of impact loading, the strength of the
material also increases. [ 18 ] The following data shows the influence of the
increase in strain rate on the yield strength, SYLD, of a steel specimen
SR 10
6
−
10
5
−
10
4
−
10
2
−
1 10
2
10
3
( )
= in/(in-sec)
SYLD 30 28 30 37 45 65 78
( )
= kpsi
Obtain an appropriate least-squares fit to the given data and determine SYLD
corresponding to an SR of 50.
6.21. The endurance limit of a steel specimen is, typically, a function of the condition
of its surface [ 19 ]. For an unnotched, ground specimen in reversed bending,
the endurance limit, S end , is related to its tensile strength, S ult , as given in the
following table of data.
Sult 60 80 100 120 140 160 180 200 220
( )
= kpsi
Send 25 35 45 55 65 72 80 85 90
( )
= kpsi
Chapter 6: Curve-Fitting 253

264. Obtain a reasonable curve-fit to the given data. Determine S end corresponding to S ult = 135
kpsi .
6.22. Expected voice levels required for speech communication with various back-
ground noise levels and separations between the speaker and the listener [ 10 ]
are given in the following table of data .
Obtain appropriate curve-fits to the given data in the form of separate curves for
(a) Peak shouting (b) Shouting (c) Very loud voice (d) Raised voice and (e)
Normal voice.
Determine the voice levels required in the following situations.
(1) Speaker listener distance = 2.5 m , background noise level = 68 dBA
(2) Speaker listener distance = 4.5 m , background noise level = 86 dBA
(3) Speaker listener distance = 8.5 m , background noise level = 45 dBA
(4) Speaker listener distance = 6.5 m , background noise level = 65 dBA
BACKGROUND NOISE LEVELS (dBA)
Speaker
/listener
distance
( m )
Normal
Voice
Raised
Voice
Very
Loud
Voice
Shouting Peak
Shouting
0.25
0.5
1.0
2
3
4
5
6
7
8
9
9.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
90
80
72
63
57
54.5
52
50
49.5
49
48
47.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
62
60
57
56.5
55
54
53.5
52.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
95
88
78
72
68
66
64
62.5
61.5
60
58
57.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
100
92
84
77
74
72
68
67.5
66
65
64.5
64
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
118
112
103
96
92.5
90
88
86.5
86
85
84.5
84
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
254 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

265. C H A P T E R 7
NUMERICAL DIFFERENTIATION
7.1 INTRODUCTION TO NUMERICAL DIFFERENTIATION AND THE
USE OF THE MATHCAD DERIVATIVE OPERATORS
In the process of generating a solution to a science or an engineering problem, the need to
come up with a numerical estimate of a derivative is often encountered. We will discuss two
methods of computing derivatives as follows
1. Method of finite differences
2. Interpolating polynomial method.
These methods will be discussed in detail in the paragraphs following.
To compute the derivative of a function using the Mathcad derivative operator, first define the
point x at which the derivative is to be computed . Then click on the derivative operator in the
calculus palette of Figure 7.1 and fill in the placeholders as required. Press the equals sign
to see the derivative.
7.2 METHOD OF FINITE DIFFERENCES
In traditional calculus , a derivative of a function f(x) is defined as
x
f x
( )
d
d 0
∆x
f x ∆x
+
( ) f x
( )
−
∆x
lim
→
= (7.1)
In numerical methods, taking the above limit as Δx goes to zero is not possible , and, although, Δx
can be very small, it certainly cannot be zero. The process by which this increment Δx is made
small and utilized in calculations paves the way for the method of finite differences.
If the dependent variable x is incremented by Δx, as shown in Figure 7.2 , the difference between
the function value at (x+Δx ) and that at x is called a forward difference . In this case, the derivative
of the function f(x) at x is
x
f x
( )
d
d
f x ∆x
+
( ) f x
( )
−
∆x
= (7.2)
However, if the dependent variable is incremented by - Δx , the difference between the function
values is a backward difference, and the derivative , in this case is
x
f x
( )
d
d
f x
( ) f x ∆x
−
( )
−
∆x
= (7.3)
Chapter 7: Numerical Differentiation 255

266. Figure 7.1. Use of the Mathcad derivative operators
256 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

267. Figure 7.2. Finite differences
If a two-step difference is employed, the method of computing derivatives is called the two-step
method. An estimate of the derivative, in this case, is
x
f x
( )
d
d
f x ∆x
+
( ) f x ∆x
−
( )
−
2 ∆x
⋅
= (7.4)
For obtaining an estimate of the second derivative of f(x), we will consider the following Taylor
series expansions.
f x ∆x
+
( ) f x
( ) ∆x
( )
x
f x
( )
d
d
⋅
+
∆x
2
2! 2
x
f x
( ) .................................................................
+
(
d
d
2
⋅
+
= (7.5)
f x ∆x
−
( ) f x
( ) ∆x
( )
x
f x
( )
d
d
⋅
−
∆x
2
2! 2
x
f x
( ) .............................................................
+
(
d
d
2
⋅
+
= (7.6)
Adding Equations (7.5) and (7.6) with terms beyond the second derivative terms ignored
will give an estimate of the second derivative as
2
x
f x
( )
(
d
d
2 1
∆x
2
f x ∆x
+
( ) 2 f x
( )
⋅
− f x ∆x
−
( )
+
( )
⋅
= (7.7)
By following a similar procedure, the third and fourth derivatives can also be estimated as
Chapter 7: Numerical Differentiation 257

268. 3
x
f x
( )
d
d
3 1
∆x
3
f x 2 ∆x
⋅
+
( ) 2 f x ∆x
+
( )
⋅
− 2 f x ∆x
−
( )
⋅
+ f x 2 ∆x
⋅
−
( )
−
( )
⋅
= (7.8)
4
x
f x
( )
d
d
4 1
∆x
4
f x 2 ∆x
⋅
+
( ) 4 f x ∆x
+
( )
⋅
− 6 f x
( )
⋅
+ 4 f x ∆x
−
( )
⋅
− f x 2 ∆x
⋅
−
( )
+
( )
⋅
= (7.9)
Example 7.1.
Using the data given, compute the first derivative at x= 4 using the forward, backward as well
as the two-step finite difference approximations. Also compute the second derivative at x= 4
.
x 2 3 4 5 6
f(x) 0.703 1.212 1.456 1.723 1.853
The first derivative at x=4 using Equation (7.2) , which is the forward difference approximation is
fprimefwd
1.723 1.456
−
5 4
−
:= fprimefwd 0.267
=
The first derivative at x=4 using Equation (7.3) , which is the backward difference
approximation, is
fprimebckwd
1.456 1.212
−
4 3
−
:= fprimebckwd 0.244
=
The first derivative at x=4 using Equation (7.4) , which is the two-step difference
approximation, is
fprimetwostep
1.723 1.212
−
5 3
−
:= fprimetwostep 0.2555
=
The second, third and fourth derivatives at x =4 are given by Equations (7.7), (7.8) and (7.9),
and these are
∆x 1
:= fdblprime
1
∆x
2
1.723 2 1.456
⋅
− 1.212
+
( )
⋅
:= fdblprime 0.023
=
ftripleprime
1
∆x
3
1.853 2 1.723
⋅
− 2 1.212
⋅
+ 0.703
−
( )
⋅
:= ftripleprime 0.128
=
258 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

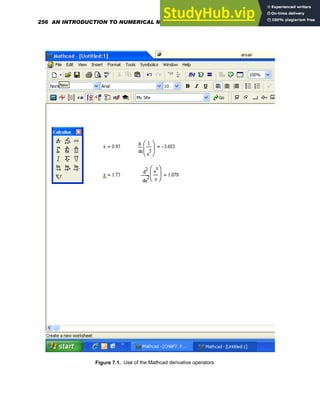
269. ffourprime
1
∆x
4
1.853 4 1.723
⋅
− 6 1.456
⋅
+ 4 1.212
⋅
− 0.703
+
( )
⋅
:= ffourprime 0.448
−
=
7.3. INTERPOLATING POLYNOMIAL METHOD
In the interpolating polynomial method, an interpolating polynomial passing through given
data points is determined by any of the methods discussed in Chapter 5. Then, the
polynomial generated can be differentiated as is done in traditional calculus. If the polynomial
derived , for instance, is
f x
( ) a0 a1 x
⋅
+ a2 x
2
⋅
+ a3 x
3
⋅
+ ............
+ an x
n
⋅
+
= (7.10)
then, its derivative can be obtained as
x
f x
( )
d
d
a1 2 a2
⋅ x
⋅
+ 3 a3
⋅ x
2
⋅
+ ..............
+ n an
⋅ x
n 1
−
⋅
+
= (7.11)
Example 7.2
Given the following data :
x 2 3 4 5 6
y 0.80354 1.23591 1.62312 1.89765 1.96789
Use the Method of Undetermined Coefficients to fit an interpolating polynomial to the given
data and estimate: yprime(4.5), yprime(2.7), ydblprime(4.5) and ydblprime(2.7).
Since 5 data points are given, we can generate a 4 th order polynomial.
Let y(x) = f(x)= a + bx + cx2 + dx3 + e x4
Substituting the given values of (x,y) in the assumed polynomial above yields the following
matrix equation:
[M]{A}= {V}
where
Chapter 7: Numerical Differentiation 259

270. M
1
1
1
1
1
2
3
4
5
6
2
2
3
2
4
2
5
2
6
2
2
3
3
3
4
3
5
3
6
3
2
4
3
4
4
4
5
4
6
4
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= V
0.80354
1.23591
1.62312
1.89765
1.96789
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Using the Mathcad function lsolve, the unknown coefficients in the column vector {A} can be
found
A lsolve M V
,
( )
:= A
0.04705
−
0.40726
7.43375 10
3
−
×
2.79917 10
3
−
×
1.00375
− 10
3
−
×
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
The coefficients a, b, c, and d of the assumed polynomial are
a A0
:= a 0.04705
−
= c A2
:= c 7.43375 10
3
−
×
= d A3
:= d 2.79917 10
3
−
×
=
b A1
:= b 0.40726
= e A4
:= e 1.00375
− 10
3
−
×
=
The polynomial derived is, then,
y x
( ) a b x
⋅
+ c x
2
⋅
+ d x
3
⋅
+ e x
4
⋅
+
:=
where a, b, c,d and e are as given above and with first and second derivatives as follows
First derivative:
yprime x
( ) b 2 c
⋅ x
⋅
+ 3 d
⋅ x
2
⋅
+ 4 e
⋅ x
3
⋅
+
:= yprime 4.5
( ) 0.27835
= yprime 2.7
( ) 0.42959
=
Second derivative:
ydblprime x
( ) 2 c
⋅ 6 d
⋅ x
⋅
+ 12 e
⋅ x
2
⋅
+
:= ydblprime 4.5
( ) 0.15347
−
= ydblprime 2.7
( ) 0.02759
−
=
260 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

271. Use of the Mathcad derivative operators yields:
x 4.5
:=
x
y x
( )
d
d
0.27835
=
2
x
y x
( )
( )
d
d
2
0.15347
−
=
x 2.7
:=
x
y x
( )
d
d
0.42959
=
2
x
y x
( )
( )
d
d
2
0.02759
−
=
Notice that the Mathcad derivative operators have yielded the same results as those
obtained through the manual process of differentiation. These are presented in Figures 7.3
and 7.4.
x 2.0 2.1
, 6.0
..
:=
2 3 4 5 6
0.2
−
0
0.2
0.4
0.6
First deriv/ inter poly
First deriv/Mathcad
A comparison of results
X-Values
First
derivative
values
yprime x
( )
x
y x
( )
d
d
x
Figure 7.3 Graph of first derivative
2 3 4 5 6
0.4
−
0.3
−
0.2
−
0.1
−
0
0.1
Second deriv/Inter poly
Second deriv/ Mathcad
A comparison of results
X-Values
Second
derivative
values
ydblprime x
( )
2
x
y x
( )
( )
d
d
2
x
Figure 7.4. Graph of second derivative
Chapter 7: Numerical Differentiation 261

272. The interpolating polynomial can also be generated by using the Mathcad function interp with
lspline, pspline or cspline, and then numerically differentiated by using the Mathcad derivative
operator, as shown below.
j 0 4
..
:= Vyj Vj
:=
<-- Generate the Vx and Vy vectors for given
data
Vy
0.80354
1.23591
1.62312
1.89765
1.96789
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Vx
2
3
4
5
6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Vs cspline Vx Vy
,
( )
:= fspline x
( ) interp Vs Vx
, Vy
, x
,
( )
:= <--- interpolating
polynomial
generated
x 4.5
:=
x
fspline x
( )
d
d
0.2786
=
2
x
fspline x
( )
( )
d
d
2
0.15547
−
=
x 2.7
:=
x
fspline x
( )
d
d
0.43082
=
2
x
fspline x
( )
( )
d
d
2
0.02671
−
=
The Mathcad results appear to be in reasonable agreement with those of the Undetermined
Coefficients method.
7.4. APPLICATIONS IN NUMERICAL DIFFERENTIATION
The following examples illustrate situations where numerical differentiation can be applied
and used to advantage in generating realistic solutions to practical problems.
7.4.1. Determination of Velocities and Accelerations from Given Displacement
Data
The following position versus time data for a train has been experimentally obtained.
Time t (secs) 0 10 20 30 35 40
Position s ( m) 0 75 175 360 480 600
262 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

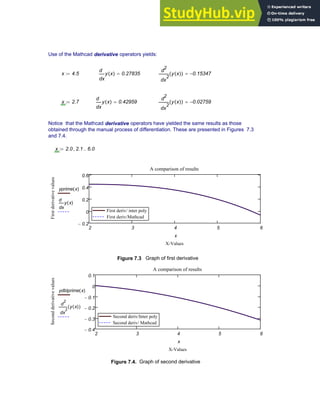
273. Determine the velocity and acceleration of the train as functions of time. Estimate the
velocity and acceleration of the train at t = 32 seconds
We first use the method of undetermined coefficients to fit an interpolating polynomial to
the given data. Since six data points are given, a fifth order polynomial of the following
form will be generated.
s(t) = f(t)= a + bt + ct2 + dt3 + e t4 + f t 5
Substituting the given values of (t,s) in the assumed polynomial above yields the following
matrix equation:
[M]{A} = {V}
where
V
0
75
175
360
480
600
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
M
1
1
1
1
1
1
0
10
20
30
35
40
0
2
10
2
20
2
30
2
35
2
40
2
0
3
10
3
20
3
30
3
35
3
40
3
0
4
10
4
20
4
30
4
35
4
40
4
0
5
10
5
20
5
30
5
35
5
40
5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Using the Mathcad function lsolve, the unknown coefficients in the column vector {A} can be found
A lsolve M V
,
( )
:=
A
0
9.41429
0.36131
−
0.01667
7.7381 10
5
−
×
4.52381
− 10
6
−
×
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Chapter 7: Numerical Differentiation 263

274. The coefficients a, b, c, d. e and f of the assumed polynomial are
a A0
:= a 0
= c A2
:= c 0.36131
−
= d A3
:= d 0.01667
=
b A1
:= b 9.41429
= e A4
:= e 7.7381 10
5
−
×
= f A5
:= f 4.52381
− 10
6
−
×
=
The polynomial derived is, then,
s t
( ) a b t
⋅
+ c t
2
⋅
+ d t
3
⋅
+ e t
4
⋅
+ f t
5
⋅
+
:=
with first and second derivatives as follows
First derivative:
velocity t
( ) b 2 c
⋅ t
⋅
+ 3 d
⋅ t
2
⋅
+ 4 e
⋅ t
3
⋅
+ 5 f
⋅ t
4
⋅
+
:= velocity 32
( ) 23.91516
= (m/sec)
Second derivative:
acceler t
( ) 2 c
⋅ 6 d
⋅ t
⋅
+ 12 e
⋅ t
2
⋅
+ 20 f
⋅ t
3
⋅
+
:= acceler 32
( ) 0.46351
= (m/sec2)
Use of the Mathcad derivative operators yields:
t 32
:=
t
s t
( )
d
d
23.91516
= m/sec
2
t
s t
( )
( )
d
d
2
0.46351
= (m/sec2)
As is expected, the results of the Mathcad derivative operators are the same as those
obtained through the process of manual differentiation of the interpolating polynomial .
They are presented in Figure 7.5.
264 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

275. t 0 1
, 40
..
:=
0 10 20 30 40
0
200
400
600
Position versus time
Time , secs
Position,
meters
s t
( )
t
0 10 20 30 40
5
10
15
20
25
Interpolating polynomial method
Mathcad's derivative operator
Velocity versus time
Time, secs
Velocity,
m/sec
velocity t
( )
t
s t
( )
d
d
t
0 10 20 30 40
1.5
−
1
−
0.5
−
0
0.5
1
Interpolating polynomial method
Mathcad's derivative operator
Acceleration versus time
Time, sec
Acceleration,
m/sec2
acceler t
( )
2
t
s t
( )
d
d
2
t
Figure 7.5. Position, velocity and acceleration versus time
Chapter 7: Numerical Differentiation 265

276. 7.4.2. Determination of Shock Absorber Parameters , and Damper and Spring
Restoring Forces from Given Vehicle Displacement Data
The following displacement (x) versus time (t) data is provided for a 200 kg motorcycle with a
shock absorber .
t,sec 0 0.5 1.0 1.5 2.0 2.5
x,mm 0 0.23 0 -0.075 0.025 0
Generate an interpolating polynomial for the displacement data given and obtain velocity and
acceleration profiles using Mathcad. Determine (a) the stiffness and the damping constant
of the shock absorber and (b) the damper and spring restoring forces of the shock absorber
as functions of time .
The given data is plotted in Figure 7.6 below.
i 1 2
, 6
..
:=
t1 0
:= ti 1
+ ti 0.5
+
:=
x1 0
:= x2 0.23
:= x3 0
:= x4 0.075
−
:= x5 0.025
:= x6 0
:=
Vxi xi
:= Vti ti
:=
0 0.5 1 1.5 2 2.5
0.1
0
0.1
0.2
Given data
Given data
Given data
Time, sec
Displacement,
mm
Vxi
Vti
Figure 7.6. Given data
266 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

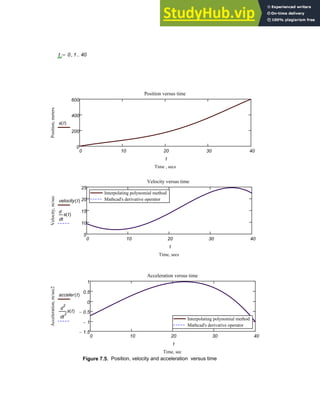
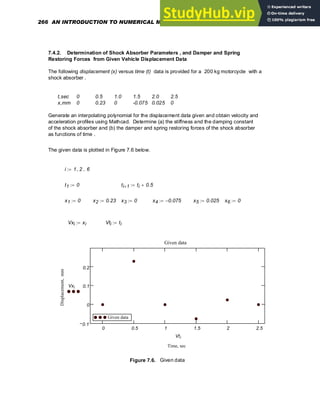
277. As done in the preceding problem, we first use the method of undetermined coefficients to fit an
interpolating polynomial to the given data. Since six data points are prescribed , a fifth order
polynomial of the following form can be generated.
x(t) = f(t)= a + bt + ct2 + dt3 + e t4 + f t 5
Substituting the given values of (t,x) in the assumed polynomial above yields the following matrix
equation:
[M]{A}= {V}
where
M
1
1
1
1
1
1
0
0.5
1
1.5
2
2.5
0
2
0.5
2
1
2
1.5
2
2
2
2.5
2
0
3
0.5
3
1
3
1.5
3
2
3
2.5
3
0
4
0.5
4
1
4
1.5
4
2
4
2.5
4
0
5
0.5
5
1
5
1.5
5
2
5
2.5
5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= V
0
0.23
0
0.075
−
0.025
0
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
A lsolve M V
,
( )
:= A
0
1.7375
3.69917
−
2.65167
0.76333
−
0.07333
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
The coefficients a, b, c, d. e and f of the assumed polynomial are
a A1
:= a 0
= c A3
:= c 3.69917
−
= d A4
:= d 2.65167
=
b A2
:= b 1.737
= e A5
:= e 0.76333
−
= f A6
:= f 0.073
=
Chapter 7: Numerical Differentiation 267

278. The interpolated polynomial which is
x t
( ) a b t
⋅
+ c t
2
⋅
+ d t
3
⋅
+ e t
4
⋅
+ f t
5
⋅
+
:=
is plotted in Figure 7.7 below. As follows, Mathcad's cspline function can also be used
with interp to generate a cubic spline interpolation which is compared with the
undetermined coefficients method and with the given data .
i 1 2
, 6
..
:=
Vs cspline Vt Vx
,
( )
:=
Vt
0
0.5
1
1.5
2
2.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vx
0
0.23
0
0.075
−
0.025
0
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
fspline t
( ) interp Vs Vt
, Vx
, t
,
( )
:=
t 0 0.01
, 2.5
..
:=
0 0.5 1 1.5 2 2.5
0
0.1
0.2
Given data points
Undetermined coefficients method
Mathcad's cubic spline interpolation
Given data points
Undetermined coefficients method
Mathcad's cubic spline interpolation
Motorcycle displacement profile
Time, seconds
Displacement,
mm
Vxi
x t
( )
fspline t
( )
Vti t
,
Figure 7.7. Interpolating polynomial generated
268 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

279. Using Mathcad's derivative operators, the velocity and the acceleration of the vehicle are also
plotted as functions of time in Figure 7.8.
0 0.5 1 1.5 2 2.5
8
6
4
2
0
2
Displacement, mm
Velocity, mm/sec
Acceleration, mm/sec2
Displacement, mm
Velocity, mm/sec
Acceleration, mm/sec2
x t
( )
t
x t
( )
d
d
2
t
x t
( )
d
d
2
t
Figure 7.8. Displacement, velocity and acceleration profiles
The system settling time is the time taken for the free vibration of the motorcycle to
completely die down. This , in this case, is 2.5 seconds. Since the settling time is
approximately equal to four time constants for a 2 % error, the system time constant τ
can be computed.
τ
2.5
4
:= τ 0.625
= seconds
The displacement profile also indicates a natural period, τ d , of one oscillation to be
approximately two seconds
τd 2
:= seconds
yielding the natural frequency of the system as
ωd 2
π
τd
⋅
:= ωd 3.142
= rad/sec
Chapter 7: Numerical Differentiation 269

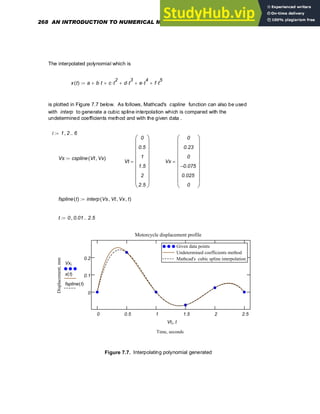
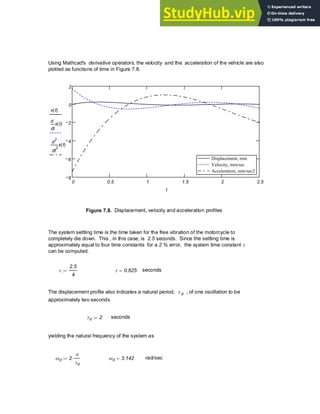
280. As shown below , the damping, c , and stiffness, k , furnished by the shock absorber
can be computed using the pertinent formulas available in textbooks in Vibrations and
Controls [ 6, 9, 14, 16, 20, 21].
Damping factor x undamped natural frequency = 1/ system time constant :
ζωn
1
τ
:= ζωn 1.6
=
Since ζωn and ωd are known , the damping factor ζ can be calculated.
ωd ωn 1 ζ
2
−
⋅
=
ωd 2
π
τd
⋅
:= ωd 3.142
= rad/sec ζ
ζωn
2
ωd
2
ζωn
2
+
:= ζ 0.454
=
The undamped natural frequency of the system along with the stiffness and damping coefficients
of the shock absorber can now be computed using
ωn
ζωn
ζ
:= ωn 3.526
= rad/sec
The stiffness and damping coefficients of the shock absorber can now be determined.
m 200
:= kg
k m ωn
2
⋅
:= k 2.486 10
3
×
= N/m
c 2 m
⋅ ωn
⋅ ζ
⋅
:= c 640
= N-sec/ m
The shock absorber spring and damper restoring forces which can now be calculated as functions
of time using
270 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

281. Fspring t
( ) k
x t
( )
1000
⋅
:=
Fdamper t
( ) c
t
x t
( )
1000
d
d
⋅
:=
are plotted in Figure 7.10.
t 0 0.1
, 2.5
..
:=
0 0.5 1 1.5 2 2.5
0.5
0
0.5
1
1.5
Shock absorber spring/damp rest forces
Time, seconds
Force,
Newtons
Fdamper t
( )
Fspring t
( )
t
Figure 7.9. Shock absorber spring and damper restoring forces
PROBLEMS
7.1. Given the following function
θ 4 5
, 6
, 7
, 8
,
( )
=
Cos θ
( ) 0.99756 0.99619
, 0.99452
, 0.99252
, 0.99027
,
( )
=
determine the first derivative of cos(θ ) at θ = 7 degrees, using forward, backward and two-step finite
difference approximations. Compare the results with the true value.
Chapter 7: Numerical Differentiation 271

282. Also obtain an answer using cspline/interp and the Mathcad derivative operator. Obtain the
Mathcad interpolated function and its derivative in the given range and graph them with proper
labels and titles.
7.2. Given the following
x 1.0 1.2 1.4 1.6 1.8 2.0
f(x) 1.1 0.9283 0.8972 0.9015 0.9422 1.1
compute first and second derivatives at x= 1.4, using finite differences . Also obtain
answers using cspline/interp and the Mathcad derivative operators. Obtain the Mathcad
interpolated function and its first and second derivatives in the given range and graph them
with proper labels and titles.
7.3. Given f(x) versus x as follows
x 1 2 3 4 5
f(x) 5.25 155.2 458.1 1682 6489
fit an interpolating polynomial using the method of undetermined coefficients and estimate
the first derivative at x=3.5 and x=4.5. Also obtain answers using cspline/interp and the
Mathcad derivative operator. Graph the polynomials obtained in the given range . Show a
comparison of the first derivative obtained by the undetermined coefficient method with that
generated using Mathcad.
7.4. Fit an interpolating polynomial to the data of Problem 7.2.
Estimate first and second derivatives at x= 1.4. Also obtain answers using cspline/interp
and the Mathcad derivative operators. Graph the polynomials obtained in the given range .
Show a comparison of the first derivative and second derivative obtained by the
undetermined coefficient method with those generated using Mathcad.
7.5. The horizontal and vertical positions of a weather balloon with respect to a station
are furnished below at various instants of time.
272 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

283. t
(seconds)
horiz distance x
(ft)
vertical distance, y
(ft)
0
8
16
24
32
40
48
54
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
0
6.4
25.6
57.6
102.4
160
230.4
291.6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
0
1
2
3
4
5
6
7
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
Using the method of undetermined coefficients, fit interpolating polynomials to the given data
and generate x versus time and y versus time curves. Estimate horizontal and vertical
velocities as well as horizontal and vertical accelerations at t = 4.5 seconds. Also obtain
answers using cspline/interp and the Mathcad derivative operators. Show a comparison of
all results generated with the help of appropriate plots.
7.6. The deflection curve of a cantilevered beam is given by the following data, in which x
is the distance in feet from the fixed end and y is the deflection in feet at x .
x 0 1 2 3 4 5 6 7 8
( )
=
y 0 0.015 0.05 0.1 0.2 0.3 0.4 0.5 0.6
( )
=
Using Mathcad's cspline/interp functions, generate an interpolating polynomial for the given
data , and obtain the beam slope at x = 5.5 ft and x= 6.5 ft. Also plot the deflection versus x
and slope versus x curves
7.7. In a slider-crank mechanism , the crank angle θ and the position x of the slider
are prescribed below at various instants of time. The position x is in feet while the angle θ is
in radians
θ 0 0.393 0.785 1.178 1.571 1.963 2.356 2.749 3.142
( )
:=
x 0.667 0.65 0.604 0.539 0.471 0.412 0.368 0.342 0.333
( )
:=
Chapter 7: Numerical Differentiation 273

284. Figure P 7.7
Using cspline/interp, generate an interpolating polynomial for the given data. If the
rotational speed of the crank is ω 2 = 1000 RPM, counterclockwise, and it is maintained
constant , estimate the velocity and acceleration of the slider at θ = π/2 and 3π/4 radians.
Plot the position x, velocity dx/dt and acceleration d2x/ dt 2 as functions of the crank
angle θ.
7,8 The data in the following table are the distances (D) traveled by a motorcycle for
selected times (t)
t(seconds): 0 2 4 6 8 10
D (ft): 0 10 50 150 330 610
(a) Determine the velocity and acceleration of the motorcycle at t = 4 , 6 and 8
seconds, using finite differences.
(b) Using only three relevant data points, determine the velocity and acceleration at t = 6
seconds by the Interpolating Polynomial method. Compare these results with those of Part
(a).
.
7.9. The deflection curve of a cantilevered beam is given by the following data, in which x is
the distance in feet from the fixed end and y is the deflection at x.
x: 1 4 8
y: 0.015 0.20 0.60
Using the Interpolating Polynomial method, compute the first and second derivatives of y(x) at
x= 3 ft and x = 6 ft.
7.10. The displacements of an instrument subjected to a random vibration test are given below
.
Time, t (seconds): 0.05 0.10 0.15 0.20 0.25 0.30
Displacement, y (in): 0.144 0.172 0.213 0.296 0.070 0.085
274 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

285. Using finite differences, determine the velocity and acceleration of the instrument at t= 0.15,
0.20 and 0.25 seconds.
Chapter 7: Numerical Differentiation 275

286. NOTES:
276 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

287. C H A P T E R 8
NUMERICAL INTEGRATION
8.1 INTRODUCTION TO NUMERICAL INTEGRATION AND THE USE
OF THE MATHCAD INTEGRAL OPERATORS
In traditional calculus, an integral of a function f(x) between limits a and b is the shaded
area shown in Figure 8.1 and is defined as
I
a
b
x
f x
( )
⌠
⎮
⌡
d
= (8.1)
Figure 8.1. Integral of a function
This analytical solution is possible only when f(x) is explicitly known. When the evaluation of
this integral becomes either impossible or extremely difficult , it is advantageous to resort to
numerical techniques.
In many science and engineering problems, data is often presented as a given bunch of
numbers for given values of the independent variable. In this case too, the evaluation of the
integral, is done by a numerical process.
There are several methods available for evaluating an integral numerically. However, only the
following will be discussed here.
1. The interpolating polynomial method.
Chapter 8: Numerical Integration 277

288. 2. Trapezoidal rule.
3. Simpson's rules.
4. Romberg integration.
To compute the definite integral of a function usiong the Mathcad integral operator, click on
the integral operator in the calculus palette shown in Figure 8.2 . Then, start filling in the
placeholders as required and press the equals sign to see the result. Mathcad resorts to
Romberg integration to approximate the integral of an expression over an interval of real
numbers.
Figure 8.2. Use of the Mathcad Integral Operator
278 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

289. 8.2 THE INTERPOLATING POLYNOMIAL METHOD
In this method, an interpolating polynomial passing through the data points is generated as
was done in the chapter on numerical differentiation and then the polynomial is integrated
anaytically over the prescribed limits of integration. If the polynomial generated is of the form
y x
( ) a bx
+ c x
2
⋅
+ d x
3
⋅
+ ..........
+
= , (8.2)
its integral is
I a x
⋅ b
x
2
2
⋅
+ c
x
3
3
⋅
+ d
x
4
4
⋅
+ ............
+
= (8.3)
which can be evaluated analytically over any prescribed integration limits.
Example 8.1.
Given the data of Example 7.2 of Chapter 7, which is
x 2 3 4 5 6
y(x) 0.80354 1.23591 1.62312 1.89765 1.96789
estimate the integral of y(x) over the range x = 2 to x = 6.
The interpolating polynomial generated in Example 7.2 for the data given was
y x
( ) a b x
⋅
+ c x
2
⋅
+ d x
3
⋅
+ e x
4
⋅
+
=
with a 0.04705
−
:= b 0.407
:= c 7.43375 10
3
−
⋅
:= d 2.79917 10
3
−
⋅
:= e 1.00375
− 10
3
−
⋅
:=
y x
( ) a b x
⋅
+ c x
2
⋅
+ d x
3
⋅
+ e x
4
⋅
+
:=
Then, the required integral is
2
6
x
y x
( )
⌠
⎮
⌡
d 6.1803
=
Chapter 8: Numerical Integration 279

290. 8.3 TRAPEZOIDAL RULE
Figure 8.3. The trapezoidal rule
The trapezoidal rule estimates the integral of a function on the basis of linear interpolation
between the given data points . If the integral of a given function f(x) is to be evaluated
between limits a and b , the interval from a to b is divided into n equal subintervals each of
width H, where
H
b a
−
n
= (8.4)
The desired integral which is, in fact, the sum of the areas in the subintervals under the
curve f(x) is then ( See Figure 8.3. )
I
1
2
H
⋅
1
n
i
f xi 1
+
( ) f xi
( )
+
( )
∑
=
⋅
= (8.5)
where the (x i , y i ) are the x and y- coordinates of the given data points at the beginning and
end of each subinterval. An alternative form of the above integral is
I
1
2
h
⋅
1
m 1
−
⋅
i
f xi 1
+
( ) f xi
( )
+
(
∑
=
⋅
= (8.6)
280 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

291. where m , now, is the number of data points given on the curve and h is, accordingly,
h
b a
−
m 1
−
= (8.7)
For example, if five data points are prescribed as shown in Figure 8.4, there will be four
segments and the trapezoidal rule will estimate the integral of the function from the first to the
last data point as
I
1
2
h
⋅ y1 2 y2
⋅
+ 2 y3
⋅
+ 2 y4
⋅
+ y5
+
( )
⋅
= (8.8)
Figure 8.4. Trapezoidal rule with five data points
If the intervals are not of equal width, the following equation should be used in place of Equation
(8.6).
I
1
2
1
m 1
−
i
xi 1
+ xi
−
( ) f xi 1
+
( ) f xi
( )
+
( )
⋅
⎡
⎣ ⎤
⎦
∑
=
⋅
= (8.9)
Chapter 8: Numerical Integration 281

292. Example 8.2.
Given:
θ (degrees): 0 15 30 45 60` 75 90
Sin(2θ): 0 0.5 0.86603 1 0.86603 0.5 0
Use the trapezoidal rule to determine the area under the curve from θ = 0 to 90 degrees.
Compare the result with the true value of the integral.
The subinterval width, in this case , is
h 15
π
180
⋅
:= h 0.2618
=
The y-coordinates of the 7 given data points are
y1 0
:= y2 0.5
:= y3 0.86603
:= y4 1.0
:= y5 0.86603
:=
y6 0.5
:= y7 0.0
:=
The value of the desired integral can be estimated by the trapezoidal rule as
Int 0.5 h
⋅ y1 2 y2
⋅
+ 2 y3
⋅
+ 2 y4
⋅
+ 2 y5
⋅
+ 2 y6
⋅
+ y7
+
( )
⋅
:= Int 0.97705
=
The true value and the error between the true and estimated values of the integral are
Trueval 1.0
:= %err
Trueval Int
−
Trueval
100
⋅
:= %err 2.2949
=
Using Mathcad, the following estimate of the integral is obtained:
x 0 0.2618
, 1.5708
..
:= y x
( ) sin 2 x
⋅
( )
:= y x
( )
0
0.5
0.866
1
0.866
0.5
-6
-7.3464·10
=
0
1.5708
θ
sin 2 θ
⋅
( )
⌠
⎮
⌡
d 1
=
282 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

293. 8.4 SIMPSON'S RULES
Simpson's rules are two in number. They are the Simpson's one-third rule and the Simpson's
three-eighth rule. The first is based on the area under a parabola passing through three equally
spaced points, while the second is based on the area under a third-order interpolating
polynomial passing through 4 points .
8.4.1 Simpson's One-Third Rule
It can be easily shown that the area under a parabola passing through the equally spaced
points ( x1, y1 ), ( x2, y2) and ( x3, y3 ), shown in Figure 8.5 is
A
h
3
y1 4 y2
⋅
+ y3
+
( )
⋅
= (8.10)
Figure 8.5. Basis of Simpson's one-third rule
In general, if the area under a curve is divided into n segments, there are (n+1 ) points on the
curve
x1 y1
,
( ) x2 y2
,
( )................ xn 1
+ yn 1
+
,
( )
If each segment is of width "h" and there are "n" segments, "n" being an even number, the area
under the parabola passing through the first three points will be
Chapter 8: Numerical Integration 283

294. A1
h
3
y1 4 y2
⋅
+ y3
+
( )
⋅
= (8.11)
Similarly, the areas under the parabolas passing through the third, fourth and fifth points, and
through the last three points on the curve will be
A2
h
3
y3 4 y4
⋅
+ y5
+
( )
⋅
=
........................................
(8.12)
Alast
h
3
yn 1
− 4 yn
⋅
+ yn 1
+
+
( )
⋅
=
The integral according to Simpson's one-third rule is the sum of the above areas and can be written
as
I
h
3
y1
⋅ 4
ieven
yi
∑
⋅
+ 2
ioddexceptlast
yi
∑
⋅
+ yn 1
+
+
= (8.13)
For example, if there are seven data points, this integral can be estimated as
I
h
3
y1 4 y2
⋅
+ 2 y3
⋅
+ 4 y4
⋅
+ 2 y5
⋅
+ 4 y6
⋅
+ y7
+
( )
⋅
=
(8.14)
Figure 8.6 shows a comparison between the function approximations obtained with the trapezoidal
rule and Simpson's rule, and the consequent integrals which are the respective areas under these
functions.
Figure 8.6. Comparison between the trapezoidal and Simpson's one-third rules
284 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

295. Example 8.3.
For the given data, compute the area under the curve by Simpson's one-third rule and
compare the estimated value with the true value
Theta: 0 15 30 45 60 75 90
Sin(2θ) 0 0.5 0.86603 1 0.86603 0.5 0.
The interval width in this case is
h 15
π
180.
⋅
:= h 0.2618
=
The y-coordinates of the given data points are
y1 0
:= y2 0.5
:= y3 0.86603
:= y4 1.0
:= y5 0.86603
:=
y6 0.5
:= y7 0.0
:=
An estimate of the desired integral by Simpson's one-third rule is then
Int1 h
y1 4 y2
⋅
+ 2 y3
⋅
+ 4 y4
⋅
+ 2 y5
⋅
+ 4 y6
⋅
+ y7
+
3
⋅
:= Int1 1.0004
=
The true value of the integral is
Trueval
0
π
2
θ
sin 2 θ
⋅
( )
⌠
⎮
⎮
⌡
d
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Trueval 1.0
:=
The percentage error between the true and estimated values is
Chapter 8: Numerical Integration 285

296. %err1
Trueval Int1
−
Trueval
100
⋅
:= %err1 0.0433
−
=
8.4.2 Simpson's three-eighth rule
Simpson's 3/8 th rule is based on the area under a third order interpolating polynomial passing
through four points . If these points are
(x1, y1 ) , (x2, y2 ), (x3, y3 ) and (x4, y4 )
as shown in Figure 8.7, then this area can be shown to be
A
3
8
h
⋅ y1 3 y2
⋅
+ 3 y3
⋅
+ y4
+
( )
⋅
= (8.15)
Figure 8.7. Basis of Simpson's three-eighth rule
If the area under a curve is divided into n segments of equal width h giving (n+1) points on
the curve, Equation (8.15)) will give the area under the third-order interpolating polynomial
passing through the first four points . Similarly, the area under the polynomial passing
through the fourth, fifth, sixth and seventh points will be
286 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

297. A2
3
8
y4 3 y5
⋅
+ 3 y6
⋅
+ y7
+
( )
⋅ h
⋅
= (8.16)
and that under the polynomial passing through the last four points will be
Alast
3
8
yn 2
− 3 yn 1
−
⋅
+ 3 yn
⋅
+ yn 1
+
+
( )
⋅ h
⋅
= (8.17)
The integral according to Simpson's 3/8 th rule is then the sum of the above areas and can be
written as
I
3
8
h
⋅ y1 3 y2
⋅
+ 3 y3
⋅
+ 2 y4
⋅
+ 3 y5
⋅
+ 3 y6
⋅
+ 2 y7
⋅
+ 3 y8
⋅
+ 3 y9
⋅
+ 2 y10
⋅
+ .....yn 1
+
+
( )
⋅
=
(8.18)
8.4.3 Limitations of Simpson's Rules
While the one-third rule requires the number of segments under the curve to be even, the
mininum number being two, the three-eighth rule requires the number of segments to be a
number divisible by three , the minimum number being three. That is, for computation by the
one-third rule, the number of segments can be 2, 4, 6 and so on while the number of
segments required by the 3/8 th rule is 3, 6, 9, 12 etc.
Example 8.4.
For the data of Example 8.3, compute the area under the curve by Simpson's three-eighth
rule and compare the estimated value with the true value
Theta: 0 15 30 45 60 75 90
Sin(2θ): 0 0.5 0.86603 1 0.86603 0.5 0.
The interval width is , as before,
h 15
π
180.
⋅
:= h 0.2618
=
and the y-coordinates of the given data points are
y1 0
:= y2 0.5
:= y3 0.86603
:= y4 1.0
:= y5 0.86603
:=
Chapter 8: Numerical Integration 287

298. y6 0.5
:= y7 0.0
:=
The integral , according to Simpson's three-eighth rule, can be estimated as
Int2
3
8
⎛
⎜
⎝
⎞
⎟
⎠
h
⋅ y1 3 y2
⋅
+ 3 y3
⋅
+ 2 y4
⋅
+ 3 y5
⋅
+ 3 y6
⋅
+ y7
+
( )
⋅
:= Int2 1.001
=
The true value, as computed in Example 8.3 , is
Trueval 1.0
:=
and the percentage error is
%err2
Trueval Int2
−
Trueval
100
⋅
:= %err2 0.1008
−
=
8.5 ROMBERG INTEGRATION
Romberg integration is a very powerful and efficient method of computing an integral. It uses a
combination of the trapezoidal rule with an extrapolation technique known as Richardson
extrapolation, and provides much better accuracy than the trapezoidal rule.
(a) (b)
Figure 8.8. Basis of Romberg integration
288 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

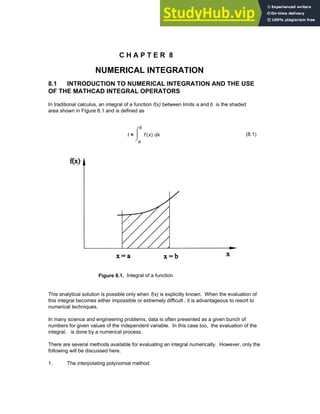
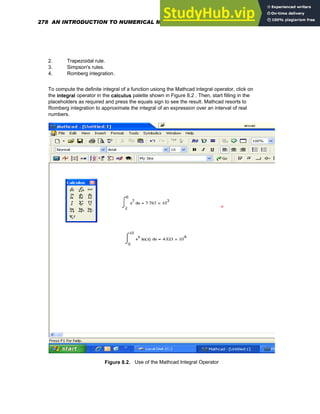
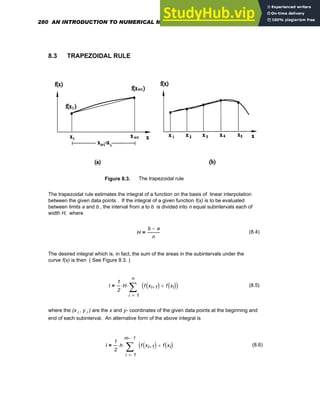
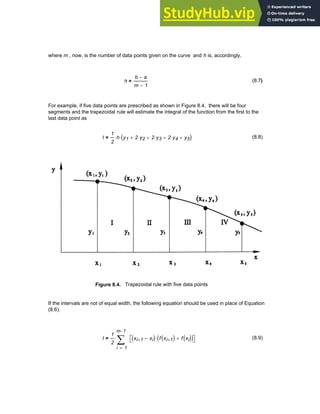
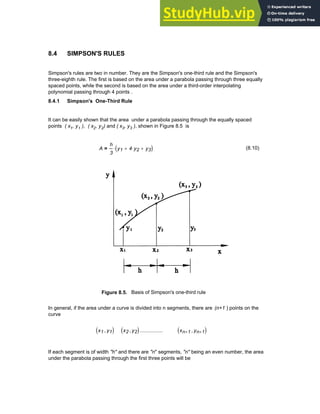
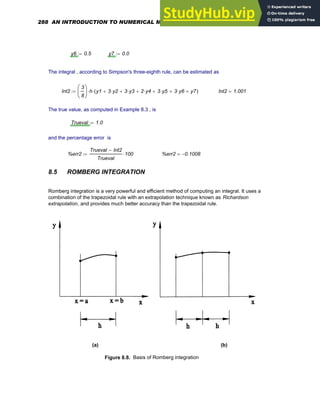
299. The procedure for computing the integral of f(x) over a prescribed range of x= a to x= b by
the Romberg method is as follows.
1. For a range of integration from x =a to x= b, a shown in Figure 8.8 (a) ,obtain
the first trapezoidal estimate I 0,1 of the integral of the given function f(x) by the trapezoidal
rule as
(8.19)
I0 1
,
1
2
h
⋅ f a
( )
( f b
( )
+
[ ]
⋅
=
where h b a
−
= (8.20)
2. Divide the given range into two segments as shown in Figure 8.8 (b) and obtain
the second trapezoidal estimate I 1,1 as
I1 1
,
h
2
y1 2 y2
⋅
+ y3
+
( )
⋅
= (8.21)
where
h
b a
−
2
=
y1 f a
( )
= <--Value of function at the beginning of the range of
integration
(8.22)
y2 f a h
+
( )
= <--Value of function at the middle of the range of
integration
y3 f a 2 h
⋅
+
( )
= <--Value of function at the end of the range of
integration
3 Now divide the given range further into four segments and obtain the third
trapezoidal estimate I 2,1 with h = one-half of the previous h = (b-a)/4 .
4. Obtain a fourth trapezoidal estimate I 3,1with eight segments and h = (b-a)/8
5. Obtain a fifth trapezoidal estimate I 4,1 with sixteen segments and h = (b-a)/16
6. Using the Richardson extrapolation formula which is
Chapter 8: Numerical Integration 289

300. Ii j
, Ii j 1
−
,
1
4
j 1
−
1
−
Ii j 1
−
, Ii 1
− j 1
−
,
−
( )
⋅
+
= (8.23)
compute the other unknown components of the matrix [I] , namely ,
I1 2
, I2 2
, I2 3
, I3 2
, I3 3
, I3 4
,
I4 2
, I4 3
, I4 4
, I4 5
, ............
and fill in the Romberg table which is shown in Table 8.1. Keep filling in the table
until the integral values converge , i.e,
I3 3
, I3 2
,
= or I4 3
, I4 2
,
= or I4 4
, I4 3
,
=
whichever occurs earlier.
TABLE 8.1
The Romberg table
R
I0 1
,
I1 1
,
I2 1
,
I3 1
,
I4 1
,
I5 1
,
I1 2
,
I2 2
,
I3 2
,
I4 2
,
I5 2
,
I2 3
,
I3 3
,
I4 3
,
I5 3
,
I3 4
,
I4 4
,
I5 4
,
I4 5
,
I5 5
, I5 6
,
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
The procedure of this method should be clear from the examples that follow.
290 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

301. Example 8.5
Use Romberg integration to find the integral of exp (- x 3 ) between the limits of a= 0.1 and b=
1.75 Use an "h" equal to (b-a) to begin with.
The given function and the integration limits are
f x
( ) e
x
3
−
:= a 0.1
:= b 1.75
:=
Computation of the first trapezoidal estimate :
f a
( ) 0.999
= f b
( ) 4.70385 10
3
−
×
=
h b a
−
:= h 1.65
= I0 1
, 0.5 h
⋅ f a
( ) f b
( )
+
( )
⋅
:= I0 1
, 0.82806
= <--- First
trapezoidal
estimate
Computation of the second trapezoidal estimate:
In this case, the interval size must be halved, giving y1, y2 and y3 as the function values at the
beginning, middle and end of the integration range.
h
b a
−
2
:= h 0.825
= y1 f a
( )
:= y1 0.999
= y2 f a h
+
( )
:= y2 0.45319
=
y3 f a 2 h
⋅
+
( )
:= y3 4.70385 10
3
−
×
=
Second trapezoidal
estimate
I1 1
, 0.5 h
⋅ y1 2 y2
⋅
+ y3
+
( )
⋅
:= I1 1
, 0.78791
= <--
Computation of the third trapezoidal estimate:
The "h" must be halved again giving h=(b-a)/4
h
h
2
:= h 0.4125
=
In this case, the computation of the number of subintervals to be used in the integration
process (n), the coordinates of the resulting data points and the third trapezoidal estimate is
done as shown below
n
b a
−
h
:= n 4
= i 1 n 1
+
( )
..
:= xi a i 1
−
( ) h
⋅
+
:= yi f xi
( )
:=
Chapter 8: Numerical Integration 291

302. xi
0.1
0.5125
0.925
1.3375
1.75
= yi
0.999
0.87406
0.45319
0.09139
-3
4.70385·10
=
I2 1
, 0.5 h
⋅ y1 2
2
4
j
yj
∑
=
⋅
+ y5
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:= I2 1
, 0.7922
= <--Third trapezoidal estimate
Computations of the fourth and fifth trapezoidal estimates:
These are very similar to that of the third estimate and are presented below
Fourth estimate: h
h
2
:= h 0.20625
= n
b a
−
h
:=
n 8
=
i 1 2
, n 1
+
( )
..
:=
xi a i 1
−
( ) h
⋅
+
:= yi f xi
( )
:=
xi
0.1
0.30625
0.5125
0.71875
0.925
1.13125
1.3375
1.54375
1.75
= yi
0.999
0.97169
0.87406
0.68983
0.45319
0.23511
0.09139
0.02525
-3
4.70385·10
=
I3 1
, 0.5 h
⋅ y1 2
2
8
j
yj
∑
=
⋅
+ y9
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:= I3 1
, 0.79249
= <--Fourth trapezoidal estimate
Fifth estimate:
h
h
2
:= h 0.10313
= n
b a
−
h
:= n 16
=
i 1 2
, n 1
+
( )
..
:= xi a i 1
−
( ) h
⋅
+
:= yi f xi
( )
:=
292 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

303. xi
0.1
0.20313
0.30625
0.40937
0.5125
0.61563
0.71875
0.82188
0.925
1.02812
1.13125
1.23438
1.3375
1.44063
1.54375
1.64688
=
yi
0.999
0.99165
0.97169
0.93369
0.87406
0.7919
0.68983
0.57398
0.45319
0.3373
0.23511
0.15247
0.09139
0.05029
0.02525
0.01149
=
y16 0.01149
=
y17 4.70385 10
3
−
×
=
I4 1
, 0.5 h
⋅ y1 2
2
16
j
yj
∑
=
⋅
+ y17
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:=
I4 1
, 0.79253
= <--Fifth trapezoidal estimate
Using the Richardson extrapolation formula for improved estimates, which is
j 2 3
, 4
..
:= i 1 2
, 4
..
:=
Ii j
, Ii j 1
−
,
1
4
j 1
−
1
−
Ii j 1
−
, Ii 1
− j 1
−
,
−
( )
⋅
+
:=
or,
Ii j
,
4
j 1
−
Ii j 1
−
,
⋅ Ii 1
− j 1
−
,
−
4
j 1
−
1
−
:= ,
improved estimates of the integral can be computed as shown below.
I2 2
, 0.79363
= I2 3
, 0.7949
= I3 2
, 0.79258
= I3 3
, 0.79251
=
I3 4
, 0.79247
= I4 2
, 0.79254
= I4 3
, 0.79254
= I4 4
, 0.79254
=
Chapter 8: Numerical Integration 293

304. However, the Romberg procedure requires the following quantities to be zeros.
I1 3
, 0
:= I1 4
, 0
:= I2 4
, 0
:=
Shown to the left is the Romberg Table
The zeros shown in the first column of
matrix, however, are to be ignored.
<--
I
0
0
0
0
0
0.82806
0.78791
0.7922
0.79249
0.79253
0
0.77452
0.79363
0.79258
0.79254
0
0
0.7949
0.79251
0.79254
0
0
0
0.79247
0.79254
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
The Romberg table of integrals is cleaned up and shown below:
TABLE 8.2
The Romberg table for the integration of exp( - x 3 )
____________________________________________________________________________
0.82806
0.78791 0.77452
0.7922 0.79363 0.79490
0.79249 0.79258 0.79251 0.79247
0.79253 0.79254 0.79254 0.79254
______________________________________________________________________________
Notice that convergence has taken place at an integral value of 0.79254 as shown in the
tabular presentation.
Use of the Mathcad integral operator gives
0.1
1.75
x
f x
( )
⌠
⎮
⌡
d 0.79254
=
where the function f(x) was already defined earlier.
294 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

305. Example 8.6
Use Romberg integration to find the integral of ln (1+ x 3) between the limits of a=1.0 and
b=4.5. Use an "h" value equal to (1/2) (b-a) to begin with .
Computation of first trapezoidal estimate:
a 1.0
:= b 4.5
:=
f x
( ) ln 1 x
3
+
( )
:=
h
b a
−
2
:= h 1.75
= y1 f a
( )
:= y1 0.69315
= y2 f a h
+
( )
:= y2 3.08177
=
y3 f a 2 h
⋅
+
( )
:= y3 4.52315
=
I1 1
, 0.5 h
⋅ y1 2 y2
⋅
+ y3
+
( )
⋅
:= I1 1
, 9.95735
= <--First trapezoidal
estimate
Computation of second trapezoidal estimate:
h
h
2
:= h 0.875
= n
b a
−
h
:= n 4
= i 1 2
, n 1
+
( )
..
:=
xi a i 1
−
( ) h
⋅
+
:= yi f xi
( )
:=
xi
1
1.875
2.75
3.625
4.5
= yi
0.69315
2.02707
3.08177
3.88434
4.52315
=
I2 1
, 0.5 h
⋅ y1 2
2
4
j
yj
∑
=
⋅
+ y5
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:= I2 1
, 10.15116
= <---- Second trapezoidal
estimate
Computation of third trapezoidal estimate:
h
h
2
:= h 0.4375
= n
b a
−
h
:= n 8
=
i 1 2
, n 1
+
( )
..
:= xi a i 1
−
( ) h
⋅
+
:= yi f xi
( )
:=
Chapter 8: Numerical Integration 295

306. xi
1
1.4375
1.875
2.3125
2.75
3.1875
3.625
4.0625
4.5
=
yi
0.69315
1.37888
2.02707
2.59275
3.08177
3.50812
3.88434
4.2202
4.52315
=
I3 1
, 0.5 h
⋅ y1 2
2
8
j
yj
∑
=
⋅
+ y9
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:= I3 1
, 10.19431
= <--- Third trapezoidal estimate
Computation of fourth trapezoidal estimate:
h
h
2
:= h 0.21875
= n
b a
−
h
:= n 16
=
i 1 2
, n 1
+
( )
..
:= xi a i 1
−
( ) h
⋅
+
:= yi f xi
( )
:=
xi
1
1.21875
1.4375
1.65625
1.875
2.09375
2.3125
2.53125
2.75
2.96875
3.1875
3.40625
3.625
3.84375
4.0625
4.28125
= yi
0.69315
1.03328
1.37888
1.7126
2.02707
2.32028
2.59275
2.84597
3.08177
3.30193
3.50812
3.70182
3.88434
4.0568
4.2202
4.3754
=
y16 4.3754
=
y17 4.52315
=
296 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

307. I4 1
, 0.5 h
⋅ y1 2
2
16
j
yj
∑
=
⋅
+ y17
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:=
I4 1
, 10.20455
= <--- Fourth trapezoidal estimate
Use of the Richardson extrapolation formula for improved estimates:
j 2 3
, 4
..
:= i 1 2
, 4
..
:=
Ii j
, Ii j 1
−
,
1
4
j 1
−
1
−
Ii j 1
−
, Ii 1
− j 1
−
,
−
( )
⋅
+
:= <---- Richardson extrapolation formula for
improved estimates
or
Ii j
,
4
j 1
−
Ii j 1
−
,
⋅ Ii 1
− j 1
−
,
−
4
j 1
−
1
−
:=
I2 2
, 10.21576
= I3 2
, 10.20869
= I3 3
, 10.20822
= I4 2
, 10.20796
=
I4 3
, 10.20791
= I4 4
, 10.20791
=
The Romberg procedure requires the following quantities to be zeros.
I0 1
, 0
:= I1 2
, 0
:= I1 3
, 0
:= I1 4
, 0
:= I2 3
, 0
:= I2 4
, 0
:= I3 4
, 0
:=
Thus, the estimates computed can be assembled in the tabular form (Romberg Table ) shown
below. The zeros shown in the matrix are to be ignored.
I
0
0
0
0
0
0
9.957348
10.151155
10.194307
10.204548
0
0
10.215758
10.20869
10.207962
0
0
0
10.208219
10.207914
0
0
0
0
10.207909
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Chapter 8: Numerical Integration 297

308. The Romberg table of integrals is cleaned up and shown below
:
TABLE 8.3
The Romberg Table for the integral of ln (1+x3)
_____________________________________________________________________________
9.957348
10.151155 10.215758
10.194307 10.20869 10.208219
10.204548 10.207962 10.207914 10.207909
______________________________________________________________________________
The tabular presentation of integral values shows that convergence has taken place at an
integral value of 10.2079
Use of the Mathcad integral operator yields
Shown on the left is the integral obtained with
Mathcad where the function f(x) was already defined
earlier.
1.0
4.5
x
f x
( )
⌠
⎮
⌡
d 10.20791
= <----
Example 8.7.
Use Romberg integration to find the integral of the given function f(x) between the limits of a=
0 and b= 8. Begin with h= (b-a) to compute the first trapezoidal estimate I 0,1 . Compute
four trapezoidal estimates, then complete the Romberg table.
x f(x)
0 3.2
0.50 2.6
1.0 1.7
1.50 1.0
2.0 0.62
2.50 0.45
3.0 0.40
3.50 0.27
4.0 0.20
298 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

309. Computation of the first trapezoidal estimate:
a 0
:= b 4
:= y1 3.2
:= y2 0.20
:= h b a
−
:= h 4
=
I0 1
, 0.5 h
⋅ y1 y2
+
( )
⋅
:= I0 1
, 6.8
= <-- FIRST TRAPEZOIDAL ESTIMATE
Computation of the second trapezoidal estimate
h
h
2
:= h 2
= n
b a
−
h
:= n 2
=
x1 0
:= y1 3.2
:= x2 2
:= y2 0.62
:= x3 4
:= y3 0.20
:=
I1 1
, 0.5 h
⋅ y1 2 y2
⋅
+ y3
+
( )
⋅
:= I1 1
, 4.64
= <-- SEC TRAPEZOIDAL ESTIMATE
Computation of the third trapezoidal estimate:
h
h
2
:= h 1
= n
b a
−
h
:= n 4
=
x1 0
:= y1 3.2
:= x2 1.
:= y2 1.7
:= x3 2.0
:= y3 0.62
:=
x4 3.0
:= y4 0.40
:= x5 4.0
:= y5 0.20
:=
I2 1
, 0.5 h
⋅ y1 2
2
4
j
yj
∑
=
⋅
+ y5
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:= I2 1
, 4.42
= <-- THIRD TRAPEZOIDAL
ESTIMATE
Computation of the fourth trapezoidal estimate:
n
b a
−
h
:= n 4
=
h
h
2
:= h 0.5
=
x1 0
:= y1 3.2
:= x2 0.50
:= y2 2.60
:= x3 1.
:= y3 1.70
:=
x4 1.50
:= y4 1.0
:= x5 2.0
:= y5 0.62
:= x6 2.50
:= y6 0.45
:=
x7 3.
:= y7 0.40
:= x8 3.50
:= y8 0.27
:= x9 4.
:= y9 0.20
:=
I3 1
, 0.5 h
⋅ y1 2
2
8
j
yj
∑
=
⋅
+ y9
+
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
⋅
:= I3 1
, 4.37
= <-- FOURTH TRAPEZOIDAL
ESTIMATE
Chapter 8: Numerical Integration 299

310. Use of the Richardson formula to obtain improved estimates:
j 2 4
..
:= i 1 2
, 3
..
:=
Ii j
,
4
j 1
−
Ii j 1
−
,
⋅ Ii 1
− j 1
−
,
−
4
j 1
−
1
−
:=
I1 2
, 3.92
= I2 2
, 4.34667
= I2 3
, 4.37511
=
I3 1
, 4.37
= I3 2
, 4.35333
= I3 3
, 4.35378
= I3 4
, 4.35344
=
I1 3
, 0
:= I1 4
, 0
:= I2 4
, 0
:=
The Romberg procedure, in
this case, requires these
quantities that are shown on
the left to be zeros.
<---
I0 2
, 0
:= I0 3
, 0
:= I0 4
, 0
:= I4 1
, 0
:=
I4 2
, 0
:= I4 3
, 0
:= I4 3
, 0
:= I4 4
, 0
:=
Shown to the left is the Romberg Table
The zeros shown in the matrix, however,
are to be ignored.
I
0
0
0
0
0
6.8
4.64
4.42
4.37
0
0
3.92
4.34667
4.35333
0
0
0
4.37511
4.35378
0
0
0
0
4.35344
0
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
<--
The Romberg table of integrals is cleaned up and shown below
:
TABLE 8.4
The Romberg Table for the integral of given function of Example 8.7
_____________________________________________________________________________
6.8
4.64 3.92
4.42 4.34667 4.37511
4.37 4.35333 4.35378 4.35344
______________________________________________________________________________
The tabular presentation of integral values shows that convergence has taken place at an
integral value of approximately 4.353.
300 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

311. 8.6 APPLICATIONS IN NUMERICAL INTEGRATION
Applications of numerical integration can be encountered in situations dealing with location of
centroids, determination of moments of inertia of cross sectional shapes and computation of
periods of oscillations in nonlinear vibration problems. Some examples are dealt with below.
8.6.1 Centroid of a Rod Bent into the Shape of a Parabola
The length of an element dL of a rod bent into the shape of the parabola shown in Figure 8.8
can be expressed in terms of the differentials dx and dy as [ 8 ]
dL dx
2
dy
2
+
= or 1
y
x
d
d
⎛
⎜
⎝
⎞
⎟
⎠
2
+ dy
⋅ (8.24)
Since x 2 y
2
⋅
= ,
y
x
d
d
4 y
×
= and dL 1 16 y
2
⋅
+ dy
⋅
=
y x
( )
x
2
:= x 0 0.001
, 0.5
..
:=
0 0.1 0.2 0.3 0.4
0
0.2
0.4
bent shape of rod
bent shape of rod
Rod of parabolic shape: x = 2 y .y
x , meters
y,
meters
y x
( )
x
Figure 8.8. Rod bent into a parabolic shape
The length of the rod , then, can be written as
L L
1
⌠
⎮
⎮
⌡
d
= or L
0
0.5
y
1 16 y
2
⋅
+
⌠
⎮
⌡
d
:= L 0.739
= meters
Chapter 8: Numerical Integration 301

312. The location of the centroid ( x CG , y CG ) can then be calculated using
xCG
L
x
⌠
⎮
⎮
⌡
d
L
= yCG
L
y
⌠
⎮
⎮
⌡
d
L
=
or,
xCG
1
L 0
0.5
y
2 y
2
⋅ 1 16 y
2
⋅
+
⋅
⌠
⎮
⌡
d
⋅
:= yCG
1
L 0
0.5
y
y 1 16 y
2
⋅
+
⋅
⌠
⎮
⌡
d
⋅
:=
giving
xCG 0.205
= m yCG 0.287
= m
8.6.2. Moment of Inertia of a Beam of Semi-Elliptic Cross Section
For the semi-elliptic beam cross section shown in Figure 8.9 , its moments of inertia about
the x and y axes can be calculated using [ 8 ]
Ixx A
y
2
⌠
⎮
⎮
⌡
d
= Iyy A
x
2
⌠
⎮
⎮
⌡
d
= (8.25)
where
dA 2 x
⋅ dy
⋅
= with x y
( ) 1
y
2
b
2
− a
⋅
= and a 4
:= in b 2
:= in
dA y dx
⋅
= with y x
( ) 1
x
2
a
2
− b
⋅
:= x 4
− 3.99
−
, 4.
..
:=
4 2 0 2 4
0
2
Semi-elliptic cross section
y x
( )
x
The moments of inertia , I xx and I yy,
can now be computed as follows,using
Equations (8.25)
Ixx 2
a
b
⋅
0
b
y
y
2
b
2
y
2
−
⋅
⌠
⎮
⌡
d
⋅
:=
Figure 8.9. Beam cross section
Iyy
b
a a
−
a
x
x
2
a
2
x
2
−
⋅
⌠
⎮
⌡
d
⋅
:= giving Ixx 12.566
= in 4 and Iyy 50.266
= in 4
302 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

313. 8.6.3. Launch of a Projectile
A projectile is launched with an initial vertical velocity vy init from a height y 0 above the ground.
Neglecting air resistance, the relationship between its vertical velocity v y at any time t and the
height y above the ground that it attains on the way up is given by [ 8 ]
vy vyinit
2
2 G
⋅ y0 y
−
( )
⋅
+
= (8.26)
where G is the acceleration due to gravity ( 32.2 ft/ sec 2 or 9.81 m/ sec 2 ) . Equating the
above quantity to dy/dt , and then integrating with respect to time from 0 to t seconds, the
following expression can be derived for the time t taken by the projectile to attain the height
y above the ground
t
y0
y
y
1
vyinit
2
2 G
⋅ y0 y
−
( )
⋅
+
⌠
⎮
⎮
⎮
⌡
d
=
(8.27)
The time taken to reach the maximum height , y max , is then the above integral with
y max as the upper limit of integration , where
ymax
vyinit
2
2 G
⋅
y0
+
=
(8.28)
For an initial velocity of 55 ft/ sec at an angle of 65 degrees from a height of 3.5 ft above ground, the
time taken to attain the maximum height is calculated below using Equations (8.27) and (8.28).
vinit 55
:= ft/sec θ 65 deg
⋅
:= sin θ
( ) 0.906
= G 32.2
:= ft/ sec 2
vyinit vinit sin θ
( )
⋅
:= vyinit 49.847
= ft/sec y0 3.5
:= ft
ymax
vyinit
2
2 G
⋅
y0
+
:= ymax 42.083
= ft
tmaxheight
y0
ymax
y
1
vyinit
2
2 G
⋅ y0 y
−
( )
⋅
+
⌠
⎮
⎮
⎮
⌡
d
:= tmaxheight 1.548
= sec
Chapter 8: Numerical Integration 303

314. 8.6.4. Large Oscillations of a Simple Pendulum
A simple pendulum, which is a mass attached to one end of a light rigid rod, is shown in Figure
8.10.
Figure 8.10. Vibration of a simple pendulum
The large-amplitude motion of this pendulum is governed by the following nonlinear differential
equation [ 6,9,16,20 ].
2
t
θ t
( )
d
d
2 G
L
sin θ t
( )
( )
⋅
+ 0
= (8.29)
where L is the length of the rod and G is the acceleration due to gravity . However, if the
amplitudes of vibration are considered small, the above differential equation assumes
its linear form
2
t
θ t
( )
d
d
2 G
L
θ t
( )
⋅
+ 0
= (8.30)
and the motion, then, has a natural period
τlinear 2 π
⋅
L
G
⋅
:= seconds (8.31)
For the nonlinear problem , it can be shown that the period of one oscillation, which is now a
function of the amplitude of vibration , is given by the integral
304 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

315. τnonlinear A
( ) 2
L
G
⋅
0
A
π
180.
⋅
θ
1
sin A
π
360
⋅
⎛
⎜
⎝
⎞
⎟
⎠
2
sin
θ
2
⎛
⎜
⎝
⎞
⎟
⎠
2
−
⌠
⎮
⎮
⎮
⎮
⎮
⌡
d
⋅
:= seconds (8.32)
where A is the maximum vibration amplitude in degrees that the pendulum attains. The
corresponding linear and nonlinear natural frequencies in Hertz can be computed using
flinear
1
τlinear
:= fnonlinear A
( )
1
τnonlinear A
( )
:= (8.33)
In a nonlinear problem, the percentage variation between the linear and nonlinear natural frequencies
is typically expressed in the following form
Percentdiff A
( )
fnonlinear A
( ) flinear
−
flinear
100
⋅
:= (8.34)
This variation, which is plotted in Figure 8.11 below as a function of the maximum amplitude of
vibration of the pendulum, confirms that there is a sharp increase in the variation from the linear
natural frequency with increase in the amplitude of vibration.
A 0.1 0.2
, 30
..
:=
5 10 15 20 25 30
0
0.5
1
1.5
2
Variation of nat freq with amplitude
Amplitude A, degrees
%
variation
from
linear
nat
frequency
Percentdiff A
( )
A
Figure 8.11. Variation of nonlinear natural frequency wiith amplitude
Chapter 8: Numerical Integration 305

316. PROBLEMS
8.1. Use the trapezoidal rule to estimate the integral of x (2/3) over the range a=0 to
b=4.0 for interval widths of h= 1.0, 0.5 and 0.25. Also obtain an answer using the Mathcad
integral operator.
8.2. Using Simpson's rules, with h= 0.25, 0.5 and 1.5, obtain estimates of the
following integral:
I
0
3
x
x
4
3
⌠
⎮
⎮
⎮
⌡
d
=
Also obtain an answer using the Mathcad integral operator
8.3. Using Simpson's rules, with h = 4, 8 and 10 subdivisions of the given range of x,
obtain estimates of the following integral:
1
4
x
1
6 5 e
2 x
⋅
⋅
+
⌠
⎮
⎮
⎮
⌡
d
Also obtain an answer using the Mathcad integral operator
8.4. Use Romberg integration to find the integral of x3 exp ( 2x ) between the
limits of a= 0 and b= 2.0. Use an "h" equal to (b-a) to begin with to compute the first
trapezoidal estimate. Also verify your answer using the Mathcad integral operator.
8.5. Use Romberg integration to find the integral of (1/x) between the limits of a= 1.0
and b= 2.0. Use an "h" equal to (b-a) to begin with. The completion of three rows of the
Romberg table should be sufficient.
8.6. Use Romberg integration to find the integral of ln(x) between the limits of a= 1.0
and b= 2.0. Use an "h" equal to (b-a) to begin with. Compute 3 trapezpoidal estimates
before completing the Romberg table.
8.7. Use Romberg integration to find the integral of
3 / (1 + x 2 )
between the limits of a= 0 and b= 4.0. Use an "h" equal to (b-a) to begin with.
Compute 3 trapezpoidal estimates before completing the Romberg table.
306 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

317. 8.8. Use Romberg integration to find the integral of ( x e 2x ) between the limits of a= 0
and b= 0.5. Use an "h" equal to (b-a) to begin with. Compute 3 trapezpoidal estimates
before completing the Romberg table.
8.9. Use Romberg integration to find the integral of x sin (x) between the limits of a= 1.0
and b= 2.0. Use an "h" equal to (b-a) to begin with. Compute an answer that is good to at
least 3 decimal places.
8.10. Use Romberg integration to find the integral of the following function f(x) between the
limits of a= 1.8 and b= 3.4. Begin with h= (b-a)/2 = 0.8 , that is , use the values marked by
asterisks to compute the first trapezoidal estimate I 1, 1 . Also verify your result by resorting
to Mathcad cubic spline interpolation and the Mathcad integral operator.
______________________________________________________________________
x f(x) x f(x) x f(x) x f(x)
----------------------------------------------------------------------------------------------------------------------------
1.6 4.751 1.8 6.152* 2.0 7.412 2.2 9.038
2.4 11.151 2.6 13.475* 2.8 16.521 3.0 20.08
3.2 24.721 3.4 30.114* 3.6 36.617 3.8 44.701
______________________________________________________________________
8.11. Use Romberg integration to find the integral of the following function f(x) between the
limits of a= 0.3 and b= 1.1. Begin with h= (b-a) to compute the first trapezoidal estimate
I 0,1 . Compute four trapezoidal estimates, then complete the Romberg table.
x f(x)
0.3 55
0.4 42
0.5 37
0.6 35
0.7 39
0.8 48
0.9 53
1.0 51
1.1 39
8.12. Use Romberg integration to find the integral of the function f(x) given in the following
table between the limits of a= 0 and b= 4. Begin with h= (b-a) to compute the first
trapezoidal estimate I 0,1 Compute four trapezoidal estimates, then complete the Romberg
table. Obtain an answer that is good to at least two decimal places.
Chapter 8: Numerical Integration 307

318. x f(x)
0 3
0.50 2.4
1.0 1.5
1.50 0.92
2.0 0.60
2.50 0.41
3.0 0.30
3.50 0.23
4.0 0.18
8.13. Use Romberg integration to find the integral of the following function f(x) between the
limits of a= 0 and b= 0.80. Begin with h= (b-a) to compute the first trapezoidal estimate I
0,1 . Compute four trapezoidal estimates, then complete the Romberg table.
x f(x)
0 0
0.1 0.12
0.2 0.30
0.3 0.55
0.4 0.89
0.5 1.36
0.6 1.99
0.7 2.84
0.8 3.96
8.14. Use Romberg integration to determine the integral of the following function f(x)
between the limits of a= 1.0 and b= 2.0. Use an "h" equal to (b-a) to begin with. Compute
three trapezoidal estimates and then complete the Romberg table. Obtain an answer that is
good to at least three decimal places.
x f(x)
1 0
1.25 0.2231
1.50 0.4055
1.75 0.5596
2.00 0.6931
8.15. The time, T, required to raise or lower the water surface in a tank with inflow
as well as outflow through an orifice at the bottom is given by the following integral
308 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

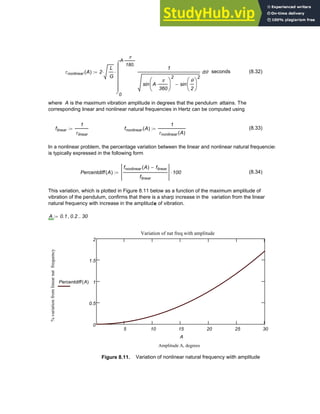
319. T
H1
H2
h
A
Q k h
0.5
⋅
−
⌠
⎮
⎮
⎮
⌡
d
=
where H1 and H2 are the initial and final heights of the water surface above the base of the
tank , A is the cross sectional area of the tank , Q is the inflow rate, and k is a constant
that depends on the coefficient of discharge and the area of the orifice. Determine how long
it will take for the water level to fall 10 ft in a tank 50 ft long by 30 ft wide with vertical sides,
when water enters the tank at the rate of 6 cu. ft / sec and the initial level of the water
surface in the tank is 16 ft above the bottom. Take k to be 3.
8.16. The motion of bodies moving with moderate speed in fluids such as
water or air is resisted by a damping force that is proportional to the square of the speed. In
order to estimate the resonant amplitude of the motion, the equivalent linear viscous
damping, C eq , is needed which is found by equating the energy dissipated by the viscous
damping in one cycle to that of the nonviscous damping [ 20 ]. The equivalent viscous
damping, in this case , can be shown to be
Ceq
2 a
⋅ ω
⋅ X
⋅
π 0
π
θ
sin θ
( )
3
⌠
⎮
⌡
d
⋅
=
where a is a proportionality constant that depends on the body geometry and the
properties of the fluid medium , ω is the frequency of excitation and X is the
amplitude of the resulting vibration. Determine C eq if a = 0.85 N-sec 2 / m , ω = 550
rads/ sec and X = 16 mm.
8.17. The moment of inertia of a sphere of radius R about a diametral axis is given by
the integral [ 8 ]
Idia
1
2
ρ
⋅ π
⋅
R
−
R
x
R
(
2
x
2
−
⎡
⎣ ⎤
⎦
2
⌠
⎮
⎮
⌡
d
⋅
=
where ρ is the mass density of the material of the sphere. Estimate I dia for a 1 m
diameter sphere made of steel with ρ = 7.8 Mg / m 3
8.18. The shear stress distribution in a beam cross section subjected to a shear force
V is given by [ 18 ]
Chapter 8: Numerical Integration 309

320. τ
V Q
⋅
I b
⋅
=
where V is the shear force acting on the cross section, I is the moment of inertia of the
entire cross section about the neutral axis , b is the cross sectional width at the level
of interest in the cross section, and Q is the first moment of the part of the area of the
cross section above the level of interest about the neutral axis. For a circular cross
section of radius R , the shear stress at a height y1 above the neutral axis is given by
the integral
τ
V
I 2
⋅ R
2
y1
2
−
⋅
2
⋅
y1
R
y
R
2
y
2
− y
⋅
⌠
⎮
⎮
⌡
d
⋅
=
Determine the shear stress distribution in the case of a beam with a circular cross section
of radius 1 inch and subjected to a shear force of magnitude 500 lbs
8.19. The time taken by an object to slide down under the action of gravity from a
point O (0,0) on a curved ramp described by the function y = y(x) to a point B is given by the
integral
T
0
xB
x
1
x
y x
( )
d
d
⎛
⎜
⎝
⎞
⎟
⎠
2
+
2 G
⋅ y x
( )
⋅
⌠
⎮
⎮
⎮
⎮
⌡
d
=
where G is the acceleration due to gravity ( 32.2 ft / sec 2 ). Estimate the time required for
a sack to slide from the top O ( 0,0) of a ramp described by
y(x) = A x 2 + B x ( with A= 0.02551, B= 0.01 )
to its bottom at x = 28 ft.
310 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

321. C H A P T E R 9
NUMERICAL SOLUTION OF ORDINARY
DIFFERENTIAL EQUATIONS
9.1 INTRODUCTION
A differential equation is an equation that expresses a relationship between a dependent
variable y , an independent variable x and derivatives of y . The order of the differential
equation is the order of the highest derivative in the equation. The following equation has
only the first derivative of y in it and is, therefore, a first order differential equation.
x
y
d
d
f x y
,
( )
= (9.1)
while one that has both first and second derivatives or just the second derivative is a
second order differential equation. Its general form is given below.
2
x
y
d
d
2
f x y
,
x
y
d
d
,
⎛
⎜
⎝
⎞
⎟
⎠
=
(9.2)
Applications of differential equations can be seen in heat transfer, electrical circuit analysis,
vibration analysis , control systems analysis and a host of other areas in science as well
as engineering.
The two broad classes of problems involving differential equations are (1) initial value
problems and (2) boundary value problems. In an initial value problem, conditions are
specified at only one value of the independent variable. An example of an initial value
problem is given below.
m
2
t
y
d
d
2
⋅ c
t
y
d
d
⋅
+ k y
⋅
+ f t
( )
= y 0
( ) dispinit
=
t
y 0
( )
d
d
velinit
= (9.3)
Although the independent variable in the above equation represents time, it can, just as well,
represent a spatial coordinate also such as x . In a boundary value problem, conditions are
prescribed at two values of the independent variable, as in the following.
A
2
x
y
d
d
2
⋅ B
x
y
d
d
⋅
+ C y
⋅
+ g x
( )
= y 0
( ) y0
= y L
( ) yL
= (9.4)
There are many methods of solving differential equations numerically. However, our discussion is
going to be limited to the Taylor series method, the Euler and Modified Euler methods, and the
Runge-Kutta methods.
Chapter 9: Numerical Solution of Ordinary Differential Equations 311

322. 9.2 TAYLOR SERIES METHOD
Given y= y(x) and the value of the independent variable at x= x0 as y(x0), a Taylor series
will give the value of y at any value of the dependent variable x as
y x
( ) y x0
( ) x x0
−
( )
x
y 0
( )
d
d
⋅
+
x x0
−
( )2
2! 2
x
y 0
( )
d
d
2
⋅
+ ...................
+
= (9.5)
If the problem to be solved is a first- order differential equation of the form
x
y
d
d
f x
( )
= (9.6)
with initial condition
y y0
= at x x0
= , (9.7)
the Taylor series expansion of Equation (9.5) can, clearly, be made use of in generating a
solution to the given differential equation. The following example should clarify this issue.
Example 9.1
Given the differential equation:
dy/dx = 7 x4 - 3 x2 +9 ,
with initial condition
y = 4 at x = 1 ,
estimate values of the function using a Taylor series expansion for x = 1 to x = 1.3 . Take
Δx to be 0.05. Compare the accuracy of the solution by comparing the computed values
with the true values computed from the true solution, which is:
312 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

323. y = (7/5)x5 - x3 +9x- (27/5)
The initial condition prescribed is
x0 1
:= y0 4.0
:=
The first, second, third, fourth and fifth derivatives of f(x) are
yprime x
( ) 7 x
4
⋅ 3 x
2
⋅
− 9
+
:= <--First derivative (given)
ydblprime x
( ) 28 x
3
⋅ 6 x
⋅
−
:= <--Second derivative
ytrprime x
( ) 84 x
2
⋅ 6
−
:= <--Third derivative
(9.8)
y4prime x
( ) 168 x
⋅
:= <--Fourth derivative
y5prime x
( ) 168.
:= <--Fifth derivative
y6prime x
( ) 0
:= <--Sixth derivative
The Taylor series of Equation (9.5) expanded to seven terms up to the sixth derivative term is
y x
( ) y0 x x0
−
( ) yprime x0
( )
⋅
+
1
2!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
2
⋅ ydblprime x0
( )
⋅
+
1
3!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
3
⋅ ytrprime x0
( )
⋅
+
1
4!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
4
⋅ y4prime x0
( )
⋅
1
5!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
5
⋅ y5prime x0
( )
⋅
+
1
6!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
6
⋅ y6prime x
(
⋅
+
+
.
:=
The true solution to the differential equation is given as (9.9)
ytrue x
( )
7
5
x
5
⋅ x
3
− 9 x
⋅
+
27
5
−
:= (9.10)
Using Equations (9.8) and (9.9), the Taylor series solution to the given differential equation
can be generated and compared with the true solution of Equation (9.10) as shown below.
Chapter 9: Numerical Solution of Ordinary Differential Equations 313

324. x 1.0 1.05
, 1.3
..
:= <--Range of interest
h 0.05
:= <--Increment for x
n
1.3 1.0
−
h
:= n 6
= <--Number of segments or subintervals in range of
interest
%error x
( )
ytrue x
( ) y x
( )
−
ytrue x
( )
100
⋅
:= <--Percent error between true and computed
values , function of x.
i 1 2
, n 1
+
..
:= xi x0 i 1
−
( ) h
⋅
+
:= <--x-values at which solution is to be
computed
%error i %error xi
( )
:= <--Percent error between true and computed
values at x= x i
yi y xi
( )
:= <--Computed Taylor solution at x= x i
ytruei ytrue xi
( )
:= <--True solution at x= x i
i
1
2
3
4
5
6
7
= xi
1
1.05
1.1
1.15
1.2
1.25
1.3
= yi
4
4.67917
5.42371
6.24503
7.15565
8.16934
9.3011
= ytruei
4
4.67917
5.42371
6.24503
7.15565
8.16934
9.3011
= %error i
0
-14
1.898·10
-14
-1.638·10
-14
-1.422·10
-14
-2.482·10
0
0
=
In what follows, several Taylor series solutions with varying number of terms are developed
and compared in Figure 9.1 with the true solution. Notice that because the sixth derivative
is zero, the six-term solution which is the same as the one with seven terms produces no
error at all.
314 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

325. y6 x
( ) y0 x x0
−
( ) yprime x0
( )
⋅
+
1
2!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
2
⋅ ydblprime x0
( )
⋅
+
1
3!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
3
⋅ ytrprime x0
( )
⋅
+
...
1
4!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
4
⋅ y4prime x0
( )
⋅
1
5!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
5
⋅ y5prime x0
( )
⋅
+
+
...
:=
<--Six-term solution
y2 x
( ) y0 x x0
−
( ) yprime x0
( )
⋅
+
:= <--Two-term solution
y1 x
( ) y0
:= <--One-term solution
ytrue x
( )
7
5
x
5
⋅ x
3
− 9 x
⋅
+
27
5
−
:= <--True solution
x 1.0 1.05
, 1.5
..
:=
1 1.05 1.1 1.15 1.2 1.25
0
5
10
15
20
Six term/ seven term solution
Two-term solution
One-term solution
True solution
Six term/ seven term solution
Two-term solution
One-term solution
True solution
Comparison of computed y with true y
X- values
Y-
values
y6 x
( )
y2 x
( )
y1 x
( )
ytrue x
( )
x
Figure 9.1. Comparison of Taylor series solutions with true solution
Chapter 9: Numerical Solution of Ordinary Differential Equations 315

326. Percentage errors for the various approximations are generated below and compared in Figure 9.2.
Notice that the error between the six-term/ seven -term approximation and the true solution is zero.
In general, the error is sizeable in the range of interest if anything short of a five-term approximation
is employed.
%error6 x
( )
ytrue x
( ) y6 x
( )
−
ytrue x
( )
100
⋅
:= %error2 x
( )
ytrue x
( ) y2 x
( )
−
ytrue x
( )
100
⋅
:=
%error1 x
( )
ytrue x
( ) y1 x
( )
−
ytrue x
( )
100
⋅
:=
x 1.0 1.01
, 3.
..
:=
1 1.05 1.1 1.15 1.2 1.25
20
0
20
40
60
80
100
Six/Seven terms
Two terms
One term
Six/Seven terms
Two terms
One term
Comparison of Errors
X- Values
Percentage
Error
%error6 x
( )
%error2 x
( )
%error1 x
( )
x
Figure 9.2. Comparison of errors generated with varying number of terms in
Taylor series
316 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

327. 9.3 EULER'S METHOD
Euler's method is a simple, programmable, one-step method which uses information from the
beginning of an interval to estimate the function value at the end of that interval . It is based
on the forward difference equation for the first derivative only , without requiring the inclusion
of higher order derivatives .
Using the forward difference representation , the derivative of a function f(x) is
x
f x
( )
d
d
f x Δx
+
( ) f x
( )
−
Δx
= (9.11)
If the slope of a curve y(x) at xn is known, say y' n , the function value y n+1 at an
adjacent point x n+1 is given by
y n+1 = y n + h y' n with h = x n+1 - xn (9.12)
so long as h, which is the difference between x n+1 and xn is small. ( See Figure 9.3)
Figure 9.3. Basis of Euler's method
If the problem to be solved is the following first-order initial value problem
Chapter 9: Numerical Solution of Ordinary Differential Equations 317

328. x
y x
( )
d
d
f x y
,
( )
= (9.13)
with initial condition y 0
( ) y0
= (9.14)
a numerical solution can be generated using Equation (9.12) which gives
yn 1
+ yn h f xn yn
,
( )
⋅
+
= (9.15)
Now, given the initial condition (9.14), Equation 9.15 can be used to do the computations one step
at a time until the solution at a desired x value is generated, which is why, this method is also
referred to as Euler's one-step method . It is to be noted that the smaller the h, the more accurate
will be the results, and , clearly, the method is not going to be very accurate for large values of h.
Example 9.2 will illustrate the procedure of Euler's method.
Because the relationship of Equation 9.12 is based on a straight line segment between
( xn , y n ) and ( x n+1 , y n+1 ), the error due to the use of Euler's method is
(y predicted - y true)
as shown in Figure 9.4. An approximate estimate of this error is given by the second order
term of the Taylor series expansion which is
ε
x x0
−
( )2
2! 2
x
y
d
d
2
⋅
= (9.16)
Figure 9.4. Error of Euler's method
318 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

329. Example 9.2
Solve: dy/dx = y' =f(x,y)=-4x3+18x2-22x +9 by Euler's method. The prescribed initial
conditions are: x=0, y=2, and the range for the solution is to be x=0 to 4.0 with a step size of
h= 0.5.
The function f(x,y) which is the derivative of y(x) is given as
f x y
,
( ) 4
− x
3
⋅ 18 x
2
⋅
+ 22 x
⋅
− 9
+
:=
The initial condition for this initial-value problem is prescribed as
x0 0
:= y0 2
:=
By integrating the given equation, its true solution can be easily seen to be
ytrue x
( ) x
4
− 6 x
3
⋅
+ 11 x
2
⋅
− 9 x
⋅
+ 2
+
:=
The procedure of Euler's method is utilized as shown below to generate solutions at x =
0.5 and 1.0.
f x0 y0
,
( ) 9
= h 0.5
:=
x1 0.5
:= y1 y0 h f x0 y0
,
( )
⋅
+
:= y1 6.5
= f x1 y1
,
( ) 2
=
x2 1.0
:= y2 y1 h f x1 y1
,
( )
⋅
+
:= y2 7.5
= f x2 y2
,
( ) 1
=
The percentage errors between the true values at x = 0.5 and 1.0 and those computed by
Euler's method are:
ytrue x1
( ) 4.438
= error
ytrue x1
( ) y1
−
ytrue x1
( )
100
⋅
:= error 46.479
−
=
ytrue x2
( ) 5
= error
ytrue x2
( ) y2
−
ytrue x2
( )
100
⋅
:= error 50
−
=
Similarly, solutions as well as errors at x = 1.5, 2.0,.....4 can also be generated easily
Chapter 9: Numerical Solution of Ordinary Differential Equations 319

330. Alternatively, Euler solutions as well as the associated percentage errors at x = 0.5, 1.0,
1.5,........4.0. can be generated by resorting to the following procedure .
x0 0
:= y0 2
:= <-- Prescribed initial condition
xlast 4
:= <--End-point of prescribed range of solution
h 0.5
:= <-- Step size
f x y
,
( ) 4
− x
3
⋅ 18 x
2
⋅
+ 22 x
⋅
− 9
+
:= <--- Prescribed derivative of y(x) at (x,y)
f x0 y0
,
( ) 9
= <-- Derivative value at starting point
Number of points beyond the starting point at
which solution is desired
N
xlast x0
−
h
:= N 8
= <--
i 0 1
, N
..
:=
xi 1
+ xi h
+
:=
<--Formulas to be used in Euler's method
yi 1
+ yi h f xi yi
,
( )
⋅
+
:=
ytruei ytrue xi
( )
:= <---True solution value at x i
error i
ytruei yi
−
ytruei
100
⋅
:= <-- Percentage Error between true value
and value computed by Euler's method
The computed and true solutions and the error due to Euler's method for the range of interest are
tabulated and shown in Table 9.1 below.
320 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

331. TABLE 9.1
Comparison between true and computed solutions and error due to Euler's method
x-value Computed solution True solution Percentage error
xi
0
0.5
1
1.5
2
2.5
3
3.5
4
= yi
2
6.5
7.5
8
9.5
12
14
12.5
3
= ytruei
2
4.438
5
5.938
8
10.438
11
5.938
-10
= error i
0
-46.479
-50
-34.737
-18.75
-14.97
-27.273
-110.526
130
=
Mathcad's cubic spline interpolation can now be resorted to as shown below to generate a plot
of the computed solution . This solution is compared with the true solution in Figure 9.5. The
errors due to Euler's method for the range of interest are presented in Figure 9.6, which shows
that the Euler error for this problem can be as large as 98 % , thus making the method
extremely inaccurate.
Vxi xi
:= Vyi yi
:= ytrue x
( ) x
4
− 6 x
3
⋅
+ 11 x
2
⋅
− 9 x
⋅
+ 2
+
:=
Vx
0
0.5
1
1.5
2
2.5
3
3.5
4
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vy
2
6.5
7.5
8
9.5
12
14
12.5
3
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= <-- Vx and Vy vectors for Euler solution generated
Vs cspline Vx Vy
,
( )
:=
fspline x
( ) interp Vs Vx
, Vy
, x
,
( )
:= <--Cubic spline solution generated with interp/
cspline
ytrue x
( ) x
4
− 6 x
3
⋅
+ 11 x
2
⋅
− 9 x
⋅
+ 2
+
:= <-- True solution
Chapter 9: Numerical Solution of Ordinary Differential Equations 321

332. %error x
( )
ytrue x
( ) fspline x
( )
−
ytrue x
( )
100
⋅
:= <--Percentage error between computed and true
solutions, function of x
x 0 0.01
, 4
..
:=
0 0.5 1 1.5 2 2.5 3 3.5 4
0
5
10
15
true solution
Euler solution
true solution
Euler solution
Comparison- Euler with True solution
X-VALUES
Y-VALUES
ytrue x
( )
fspline x
( )
x
Figure 9.5. Comparison of Euler solution with true solution
0 0.5 1 1.5 2 2.5 3 3.5
100
50
0
ERROR VERSUS x
X-VALUES
PERCENTAGE
ERROR
%error x
( )
x
Figure 9.6. Error due to Euler's method
322 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

333. 9.4 MODIFIED EULER'S METHOD
Euler's method which was discussed in the previous section does not require the use of
higher-order derivatives but apparently yields very inaccurate answers unless the step
size used is very very small. The modified Euler's method , which is an attempt at
improving the accuracy of the Euler solution, is quite similar and is still a one-step
method but uses an average slope over the segment or step rather than that at the
beginning of the segment . Thus, in this "modified" method, Equation (9.15) is replaced
by
yn 1
+ yn h
f xn 1
+
( ) f xn
( )
+
2
⋅
+
= (9.17)
Another way to look at this method is to note that it employs the trapezoidal rule as
shown in the sketch below to compute the integral
xn
xn 1
+
x
f x
( )
⌠
⎮
⌡
d
The procedural steps to be followed in this method are given below.
1. Determine slope dy/dx at the beginning of the interval , x0
2. Estimate y at x1 using Euler's formula (Equation 9.15)
yn 1
+ yn h f xn yn
,
( )
⋅
+
=
3. Evaluate slope dy/dx at the end of the interval x1, i.e., evaluate f(x1, y1 ).
4. Determine average of the slopes at the beginning and end of the interval, i.e,
f x0 y0
,
( ) f x1 y1
,
( )
+
2
Chapter 9: Numerical Solution of Ordinary Differential Equations 323

334. 5. Compute a revised estimate of y 1 using
y1 y0 h
f x0 y0
,
( ) f x1 y1
,
( )
+
2
⋅
+
=
6. Keep improving the estimate " y 1 " until convergence to a solution takes place .
Example 9.3
Using the modified Euler method, solve: dy/dx= f(x,y) = -3x -y; y(0) = -1.5; h= 0.1;
Range of x: 0 to 0.5
The function, f(x,y) which is the derivative of y(x) is given as
f x y
,
( ) 3
− x
⋅ y
−
:= h 0.1
:=
The initial condition prescribed is
x0 0.
:= y0 1.5
−
:=
The procedure of the modified Euler method is utilized as shown in the following steps to generate
numerical solutions at x= 0.1 and 0.2. Solutions for x= 0.3, 0.4 and 0.5 are obtained in a similar
manner. The quantity y1c refers to the revised estimate of the solution in each iteration .
x1 0.1
:=
f x0 y0
,
( ) 1.5
=
y1 y0 h f x0 y0
,
( )
⋅
+
:= y1 1.35
−
= f x1 y1
,
( ) 1.05
=
f x1 y1
,
( ) f x0 y0
,
( )
+
2
1.275
=
y1c y0
f x1 y1
,
( ) f x0 y0
,
( )
+
2
h
⋅
+
:= y1c 1.373
−
= y1 y1c
:=
f x1 y1
,
( ) 1.073
= f x1 y1
,
( ) f x0 y0
,
( )
+
2
1.286
=
y1c y0
f x1 y1
,
( ) f x0 y0
,
( )
+
2
h
⋅
+
:= y1c 1.371
−
= y1 y1c
:=
f x1 y1
,
( ) 1.071
= f x1 y1
,
( ) f x0 y0
,
( )
+
2
1.286
=
324 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

335. y1c y0
f x1 y1
,
( ) f x0 y0
,
( )
+
2
h
⋅
+
:= y1c 1.371
−
= y1 y1c
:=
f x1 y1
,
( ) 1.071
= f x1 y1
,
( ) f x0 y0
,
( )
+
2
1.286
=
y1c y0
f x1 y1
,
( ) f x0 y0
,
( )
+
2
h
⋅
+
:= y1c 1.371
−
= y1 y1c
:=
x2 0.2
:=
f x1 y1
,
( ) 1.071
=
y2 y1 h f x1 y1
,
( )
⋅
+
:= y2 1.264
−
= f x2 y2
,
( ) 0.664
=
f x2 y2
,
( ) f x1 y1
,
( )
+
2
0.868
= y2c y1
f x2 y2
,
( ) f x1 y1
,
( )
+
2
h
⋅
+
:=
y2c 1.285
−
= y2 y2c
:= f x2 y2
,
( ) 0.685
=
f x2 y2
,
( ) f x1 y1
,
( )
+
2
0.878
=
y2c y1
f x2 y2
,
( ) f x1 y1
,
( )
+
2
h
⋅
+
:= y2c 1.284
−
= y2 y2c
:=
f x2 y2
,
( ) 0.684
=
f x2 y2
,
( ) f x1 y1
,
( )
+
2
0.878
=
y2c y1
f x2 y2
,
( ) f x1 y1
,
( )
+
2
h
⋅
+
:= y2c 1.284
−
= y2 y2c
:=
f x2 y2
,
( ) 0.684
=
f x2 y2
,
( ) f x1 y1
,
( )
+
2
0.878
=
y2c y1
f x2 y2
,
( ) f x1 y1
,
( )
+
2
h
⋅
+
:= y2c 1.284
−
= y2 y2c
:=
At x3, x4, and x5 , the solutions can be similarly generated as :
Chapter 9: Numerical Solution of Ordinary Differential Equations 325

336. x3 0.3
:= y3 1.2328
−
:=
x4 0.4
:= y4 1.2154
−
:=
x5 0.5
:= y5 1.2283
−
:=
The results obtained by this method are presented in Table 9.2 in a tabular format for x- values
ranging from 0 to 0.5 with a step size of 0.1. Converged values of the solution are pointed out in the
" corrected yn " column .
TABLE 9.2
Calculations by Modified Euler method
corrected
avg slope
f(xn,yn)
yn
xn
yn
at beginning
and end
1.5
-1.5
0
-1.3725
1.275
1.05
-1.35
0.1
-1.3714
1.2862
1.0725
-1.3725
-1.3714
1.2857
1.0714
-1.3714
converged
-1.3714
1.2857
1.0714
-1.3714
-1.2846
0.8679
0.6643
-1.2643
0.2
-1.2836
0.878
0.6846
-1.2846
-1.2837
0.8775
0.6836
-1.2836
converged
-1.2837
0.8776
0.6837
-1.2837
-1.2337
0.4995
0.3153
-1.2153
0.3
-1.2338
0.5087
0.3337
-1.2337
converged
-1.2338
0.5082
0.3328
-1.2328
-1.2162
0.1662
-0.0004
-1.1996
0.4
-1.2154
0.1745
0.0162
-1.2162
converged
-1.2154
0.1741
0.0154
-1.2154
-1.229
-0.1353
-0.2861
-1.2139
0.5
-1.2282
-0.1278
-0.271
-1.229
-1.2283
-0.1282
-0.2718
-1.2282
converged
-1.2283
-0.1282
-0.2717
-1.2283
The x values and the computed "y" values are assembled in the form of vectors Vx and Vy in order
to generate a cubic spline interpolation as follows which is presented as a plot of the solution in
Figure 9.7.
326 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

337. <--Vx and Vy vectors for
modified Euler solution
generated
Vx
x0
x1
x2
x3
x4
x5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vx
0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vy
y0
y1
y2
y3
y4
y5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy
1.5
−
1.371
−
1.284
−
1.233
−
1.215
−
1.228
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Vs cspline Vx Vy
,
( )
:=
fspline x
( ) interp Vs Vx
, Vy
, x
,
( )
:= <-- cubic spline interpolation for the generated
solution
A solution by the Euler method is generated below in order to obtain a comparison between the
Modified Euler solution and the not-so-accurate Euler solution
x0 0
:= y0 1.5
−
:= <-- Prescribed initial condition
xlast 0.5
:= <--End-point of prescribed range of solution
h 0.1
:= <-- Step size
f x y
,
( ) 3
− x
⋅ y
−
:= <--- Prescribed derivative of y(x) at (x,y)
f x0 y0
,
( ) 1.5
= <-- Derivative value at starting point
Number of points beyond the starting point at
which solution is desired
N
xlast x0
−
h
:= N 5
= <--
i 0 1
, N
..
:= xi 1
+ xi h
+
:=
<--Formulas of Euler's method
yi 1
+ yi h f xi yi
,
( )
⋅
+
:=
Chapter 9: Numerical Solution of Ordinary Differential Equations 327

338. x-value Computed solution
xi
0
0.1
0.2
0.3
0.4
0.5
= yi
-1.5
-1.35
-1.245
-1.181
-1.152
-1.157
=
<--- Euler solution
Mathcad's cubic spline interpolation is now used below to generate a plot of the computed Euler
solution, which is compared with the Modified Euler solution in Figure 9.7.
Vxeuleri xi
:= Vyeuleri yi
:=
Vxeuler
0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vyeuler
1.5
−
1.35
−
1.245
−
1.181
−
1.152
−
1.157
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= <-- Vx and Vy vectors for Euler solution generated
Vseuler cspline Vxeuler Vyeuler
,
( )
:=
Cubic spline solution using the
Euler method generated with
interp / cspline
fsplineeuler x
( ) interp Vseuler Vxeuler
, Vyeuler
, x
,
( )
:= <---
x 0 0.01
, 0.5
..
:=
0 0.1 0.2 0.3 0.4
1.6
1.4
1.2
1
Euler solution
Modified Euler solution
Euler solution
Modified Euler solution
Euler/ Mod Euler solutions compared
X- Values
Y-
Values
fsplineeuler x
( )
fspline x
( )
x
Figure 9.7. Comparison of the modified Euler solution with
the Euler solution .
328 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

339. 9.5 RUNGE- KUTTA METHODS
Runge-Kutta methods are among the most popular techniques employed in the numerical
solution of ordinary differential equations. These methods use the y-value at the beginning of
an interval along with some representative slope over the interval to determine the y-value at
the end of the interval. Special cases of the method are Euler's method , which uses the
slope at the beginning of the interval and the modified Euler method which uses the average
slope over the segment .
There are several orders of Runge-Kutta methods from the first order to the eighth
depending on the number of iterations involved in the solution -generating process.
However, only the fourth-order Runge-Kutta method will be disussed in detail in this
chapter. All of these still resort only to the use of the first derivative and do not require the
involvement of higher order derivatives. While the second-order Runge-Kutta method is
essentially the same as the modified Euler method, and offers the same order of accuracy,
the main difference is that it resorts only to two iterations. The third-order Runge-Kutta
method resorts to Simpson's one-third rule , which is a higher-order integration scheme
than the trapezoidal rule , and uses slopes at the beginning, middle and end of the
segment in order to estimate the y-value at the end of the segment . As its name clearly
suggests , the fourth-order method does require four iterations to determine the y-value at
the segment end. Because higher-order integration schemes are employed, the
Runge-Kutta fourth-order method gives very accurate results. Orders of the method that are
higher than fourth are not common .
Advantages of Runge-Kutta methods include ease of programming, good stability
characteristics, flexibility of step size, and self-starting capability.
9.5.1 Fourth-order Runge-Kutta Method
The fourth-order Runge-Kutta method comes in two popular versions . The first version is
based on Simpson's one-third rule while the second is based on Simpson's three-eighth
rule. The sequence of calculations to be used in these versions is given below.
Procedure for version 1- based on Simpson's one-third rule:
Figure 9.8. Basis of the fourth-order Runge-Kutta method utilizing
Simpson's one- third rule
Chapter 9: Numerical Solution of Ordinary Differential Equations 329

340. Given : dy/dx = f(x,y) = Slope , y= y0 at x= x0 ( Initial condition ),
h = interval width.
Determine: y1 , which is y ( x 1 ). ( See Figure 9.8)
1. Compute h times slope K1 at ( x0, y0): K1= h. f(x0,y0)
2. Compute y at midpoint of interval x0 to x1 using the Euler formula
yMP y0
1
2
K1
⋅
+
= (9.18)
3. Compute K2 at x = x MP, y= yMP
K2 h f xMP yMP
,
( )
⋅
=
4. Obtain a revised estimate of y MP with y0, K2 and (1/2)h
yMP y0
1
2
K2
⋅
+
= (9.19)
5. Compute revised estimate of K at mid-interval, using above value of yMP
K3 h f xMP yMP
,
( )
⋅
= (9.20)
6 Compute y1 using: . y1 y0 K3
+
= (9.21)
7. Compute K at end of interval: K4 h f x1 y1
,
( )
⋅
= (9.22)
8. Compute revised estimate of y1 using:
y1 y0
1
6
K1 2 K2
⋅
+ 2 K3
⋅
+ K4
+
( )
⋅
+
= (9.23)
per Simpson's 1/3 rd rule. Notice the four estimates of slope being used
9. Repeat above steps for computing y2, y3 etc. For example, to compute y2, repeat the
procedure with (x1,y1) replacing (x0,y0) and (x2,y2) replacing (x1,y1).
Procedure for version 2- based on Simpson's three-eighth rule :
The procedure for version 2 is very similar to version 1, except that the range x0 to x1 is
330 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

341. subdivided into three regions , the starting and ending points of which are x0, x13 , x23 and
x1. The slopes at these intermediate points within the range x0 to x1 are computed and
revised until y1 is determined as shown in the following summary of calculations.
Summary of calculations for versions 1 and 2:
VERSION 1- based on Simpson's one-third rule:
K1 h f x0 y0
,
( )
⋅
=
yMP y0
1
2
K1
⋅
+
=
K2 h f xMP yMP
,
( )
⋅
=
yMP y0
1
2
K2
⋅
+
= Revised yMP (using h times
the new slope)
(9.24)
<-----
K3 h f xMP yMP
,
( )
⋅
=
y1 y0 K3
+
=
K4 h f x1 y1
,
( )
⋅
=
y1 y0
1
6
K1 2 K2
⋅
+ 2 K3
⋅
+ K4
+
( )
⋅
+
=
VERSION 2- based on Simpson's three-eighth rule:
x13 x0
1
3
h
⋅
+
= x23 x0
2
3
h
⋅
+
= K1 h f x0 y0
,
( )
⋅
=
y13 y0
1
3
K1
⋅
+
= K2 h f x13 y13
,
( )
⋅
= y23 y0
1
3
K1
⋅
+
1
3
K2
⋅
+
=
Note that y0+(1/3)K1 is, in fact, y13
(9.25)
K3 h f x23 y23
,
( )
⋅
= y1adj y0 K1
+ K2
− K3
+
= <---
" K1 - K2 + K3 "
represents h
multiplied by a
representative average
slope over segment
x0 -> x1
K4 h f x1 y1adj
,
( )
⋅
=
y1 y0
1
8
K1 3 K2
⋅
+ 3 K3
⋅
+ K4
+
( )
⋅
+
=
Chapter 9: Numerical Solution of Ordinary Differential Equations 331

342. Example 9.4
Solve: dy/dx = f(x,y) = -2x 2 - y ; Initial condition : y(0) = -1.75 ;
h = 0.1; Range of x : 0 to 0.5
Version 1 - based on Simpson's one-third rule:
The given information is.
f x y
,
( ) 2
− x
2
⋅ y
−
:= h 0.1
:= x0 0
:= y0 1.75
−
:=
Calculations for x= x1 and x= x2 are shown below
x1 0.1
:=
f x0 y0
,
( ) 1.75
=
k1 h f x0 y0
,
( )
⋅
:= k1 0.175
= ymp y0 0.5 k1
⋅
+
:= ymp 1.6625
−
=
xmp x0 0.5 h
⋅
+
:= xmp 0.05
= k2 h f xmp ymp
,
( )
⋅
:= k2 0.166
=
ymp y0 0.5 k2
⋅
+
:= ymp 1.6671
−
= k3 h f xmp ymp
,
( )
⋅
:= k3 0.166
=
y1 y0 k3
+
:= y1 1.584
−
= k4 h f x1 y1
,
( )
⋅
:= k4 0.156
=
This formula is based on <--
Simpson's one-third rule
y1 y0
1
6
⎛
⎜
⎝
⎞
⎟
⎠
k1 2 k2
⋅
+ 2 k3
⋅
+ k4
+
( )
⋅
+
:= y1 1.584
−
=
x2 0.2
:=
f x1 y1
,
( ) 1.564
=
k1 h f x1 y1
,
( )
⋅
:= k1 0.156
= ymp y1 0.5 k1
⋅
+
:= ymp 1.50591
−
=
xmp x1 0.5 h
⋅
+
:= xmp 0.15
= k2 h f xmp ymp
,
( )
⋅
:= k2 0.146
=
ymp y1 0.5 k2
⋅
+
:= ymp 1.5111
−
= k3 h f xmp ymp
,
( )
⋅
:= k3 0.147
=
y2 y1 k3
+
:= y2 1.438
−
= k4 h f x2 y2
,
( )
⋅
:= k4 0.136
=
y2 y1
1
6
⎛
⎜
⎝
⎞
⎟
⎠
k1 2 k2
⋅
+ 2 k3
⋅
+ k4
+
( )
⋅
+
:= y2 1.438
−
=
Calculations for x= 0.3, 0.4 and 0.5 are similar to the above and lead to
332 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

343. x3 0.3
:= y3 1.31316
−
:= x4 0.4
:= y4 1.21178
−
:= x5 0.5
:= y5 1.13531
−
:=
In order to generate a cubic spline interpolation for the Runge-Kutta solution, the x and y values
are put into vectors Vx and Vy. The resulting y is plotted as a function of x in Figure 9.9.
<-- Vx and Vy vectors
for the Runge-Kutta
results generated
Vx
x0
x1
x2
x3
x4
x5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy
y0
y1
y2
y3
y4
y5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vx
0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vy
1.75
−
1.584
−
1.438
−
1.313
−
1.212
−
1.135
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Vs cspline Vx Vy
,
( )
:=
cubic spline interpolation for the
solution generated
fspline1 x
( ) interp Vs Vx
, Vy
, x
,
( )
:= <-----
Version 2 - based on Simpson's three-eighth rule:
f x y
,
( ) 2
− x
2
⋅ y
−
:= h 0.1
:= x0 0
:= y0 1.75
−
:= f x0 y0
,
( ) 1.75
=
x1 0.1
:=
k1 h f x0 y0
,
( )
⋅
:= k1 0.175
= y13 y0 0.33333 k1
⋅
+
:= y13 1.69167
−
=
x13 x0
1
3
⎛
⎜
⎝
⎞
⎟
⎠
h
⋅
+
:= x13 0.033
= k2 h f x13 y13
,
( )
⋅
:= k2 0.169
=
x23 x0
2
3
⎛
⎜
⎝
⎞
⎟
⎠
h
⋅
+
:= x23 0.067
= y23 y0
k1
3
+
k2
3
+
:= y23 1.635
−
=
k3 h f x23 y23
,
( )
⋅
:= k3 0.163
=
x1 x0 h
+
:= y1adj y0 k1
+ k2
− k3
+
:= y1adj 1.581
−
=
k4 h f x1 y1adj
,
( )
⋅
:= k4 0.156
=
This formula is based on <--
Simpson's 3/8 th rule
y1 y0
1
8
⎛
⎜
⎝
⎞
⎟
⎠
k1 3 k2
⋅
+ 3 k3
⋅
+ k4
+
( )
⋅
+
:= y1 1.584
−
=
x2 0.2
:=
Chapter 9: Numerical Solution of Ordinary Differential Equations 333

344. k1 h f x1 y1
,
( )
⋅
:= k1 0.156
= y13 y1 0.33333 k1
⋅
+
:= y13 1.53212
−
=
x13 x1
1
3
⎛
⎜
⎝
⎞
⎟
⎠
h
⋅
+
:= x13 0.133
= k2 h f x13 y13
,
( )
⋅
:= k2 0.15
=
x23 x1
2
3
⎛
⎜
⎝
⎞
⎟
⎠
h
⋅
+
:= x23 0.167
= y23 y1
k1
3
+
k2
3
+
:= y23 1.482
−
=
k3 h f x23 y23
,
( )
⋅
:= k3 0.143
=
x2 x1 h
+
:= y2adj y1 k1
+ k2
− k3
+
:= y2adj 1.435
−
=
k4 h f x2 y2adj
,
( )
⋅
:= k4 0.135
=
This formula is based on <---
Simpson's 3/8 th rule
y2 y1
1
8
⎛
⎜
⎝
⎞
⎟
⎠
k1 3 k2
⋅
+ 3 k3
⋅
+ k4
+
( )
⋅
+
:= y2 1.438
−
=
Calculations for x = 0.3 , 0.4 and 0.5 are again very similar to the above and lead to:
x3 0.3
:= y3 1.31361
−
:= x4 0.4
:= y4 1.21238
−
:= x5 0.5
:= y5 1.13605
−
:=
Generation of the Vx and Vy vectors and fspline(x) as in version 1, leads to the graph in
Figure 9.9 which compares the two solutions of the fourth-order Runge-Kutta method.
These plots definitely indicate that the two solutions are very very close to each other.
Vs cspline Vx Vy
,
( )
:=
Vx
x0
x1
x2
x3
x4
x5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy
y0
y1
y2
y3
y4
y5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Vx
0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vy
1.75
−
1.584
−
1.438
−
1.314
−
1.212
−
1.136
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
fspline2 x
( ) interp Vs Vx
, Vy
, x
,
( )
:=
fspline2 0.5
( ) 1.136
−
=
x 0 0.01
, 0.5
..
:=
0 0.1 0.2 0.3 0.4
2
1.5
1
Version 1-one-third rule
Version 2-three-eighth rule
Version 1-one-third rule
Version 2-three-eighth rule
Fourth Order R/K Method
X-VALUES
Y-VALUES
fspline1 x
( )
fspline2 x
( )
x
Figure 9.9 Solution by fourth-order Runge-Kutta method
334 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

345. 9.5.2 Mathcad Solutions to a First-Order Differential Equation
The Mathcad function " rkfixed" is a general-purpose Runge-Kutta solver which can handle
both nth order differential equations with initial conditions as well as systems of differential
equations.
The arguments to the function rkfixed are
rkfixed( y,x1, x2, npoints, D)
where y is a vector of n initial values, n being the order of the differential equation or the
size of the system of equations being solved. In this case, where we have a first-order
differential equation, the vector reduces to one point. which is the initial value of y . The
quantities x1 and x2 are the endpoints of the interval over which the solution is to be
generated, and npoints is the number of points beyond the initial point at which the
solution is to be approximated. This controls the number of rows ( 1+ npoints ) in the
matrix that rkfixed returns. Here, D(x,y) is an n -element vector function containing the
first derivatives of the unknown functions. and, for a first-order differential equation, this will
be just one function , namely the given derivative.
Another Mathcad function that can be used is "Rkadapt". While "rkfixed" evaluates the
solution at equally spaced intervals , " Rkadapt " examines how fast the solution is
changing and adjusts the step size accordingly. Although "Rkadapt " may use non-uniform
step sizes in generating the solution, it will still return a solution at equally spaced points.
The arguments used by " Rkadapt " are the same as those of " rkfixed " .
To illustrate the use of these Mathcad functions, the Mathcad solution to the problem of
Example 9.1 presented in the section on the Taylor series method is outlined below.
Define the initial y value: Use the left bracket " [ " to make the subscript:
y0 4.0
:=
Put in the first derivative that is given: yprime = 7x4 -3 x 2 + 9
D x y
,
( ) 7 x
4
⋅ 3 x
2
⋅
− 9
+
:=
Evaluate the solution at 50 points between 1.0 and 1.3
Z rkfixed y 1.0
, 1.3
, 50
, D
,
( )
:=
Chapter 9: Numerical Solution of Ordinary Differential Equations 335

346. i 0 rows Z
( ) 1
−
..
:=
Plot the solution. Use Ctrl + 6 to get the superscript. ( See Figure 9.10).
To use Rkadapt , the procedure, which is presented below , is essentially the same as
with the use of rkfixed.
Define the initial y value: Use the left bracket " [ " to make the subscript:
y0 4.0
:=
Put in the first derivative that is given: yprime = 7x4 - 3 x 2 + 9
D x y
,
( ) 7 x
4
⋅ 3 x
2
⋅
− 9
+
:=
Evaluate the solution at 50 points between 1.0 and 1.3
Y Rkadapt y 1.0
, 1.3
, 50
, D
,
( )
:=
i 0 rows Y
( ) 1
−
..
:=
Plot the solution. Use Ctrl + 6 to get the superscript. (See Figure 9.10 ).
The solutions to the differential equation obtained with rkfixed and Rkadapt are presented
in Figure 9.10 and compared with the Taylor series solution, which is redone here in order to
obtain its plot.
x0 1
:= y0 4.0
:= yprime x
( ) 7 x
4
⋅ 3 x
2
⋅
− 9
+
:= ydblprime x
( ) 28 x
3
⋅ 6 x
⋅
−
:=
ytrprime x
( ) 84 x
2
⋅ 6
−
:= y4prime x
( ) 168 x
⋅
:= y5prime x
( ) 168.
:= y6prime x
( ) 0
:=
x 1.0 1.05
, 1.3
..
:=
336 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

347. y x
( ) y0 x x0
−
( ) yprime x0
( )
⋅
+
1
2!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
2
⋅ ydblprime x0
( )
⋅
+
1
3!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
3
⋅ ytrprime x0
( )
⋅
+
...
1
4!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
4
⋅ y4prime x0
( )
⋅
1
5!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
5
⋅ y5prime x0
( )
⋅
+
+
...
1
6!
⎛
⎜
⎝
⎞
⎟
⎠
x x0
−
( )
6
⋅ y6prime x0
( )
⋅
+
...
:=
<-- Taylor series
solution
xi Y
0
〈 〉
( )i
:= yi y xi
( )
:=
1 1.05 1.1 1.15 1.2 1.25
4
6
8
10
Rkadapt solution
rkfixed solution
Taylor series solution
Rkadapt solution
rkfixed solution
Taylor series solution
Comparison of solutions
X-Values
Y-Values
Y
1
〈 〉
( )i
Z
1
〈 〉
( )i
yi
Y
0
〈 〉
( )i
Figure 9.10. Comparison of Mathcad solutions with the Taylor series solution
As can be seen from the solution plots, the Mathcad solutions agree well with the Taylor series
solution.
Example 9.5
Using the Mathcad functions, solve the problem of Example 9.3 presented in the section on the
modified Euler method, namely,
dy/dx= f(x,y) = -3x -y; y(0) = -1.5 ; h= 0.1; Range of x: 0 to 0.5
The Mathcad statements necessary for the computation of the solution with rkfixed as well as
Rkadapt are
Chapter 9: Numerical Solution of Ordinary Differential Equations 337

348. y0 1.5
−
:= D x y
,
( ) 3
− x
⋅ y
−
:= Z rkfixed y 0.
, 0.5
, 50
, D
,
( )
:= i 0 rows Z
( ) 1
−
..
:=
Y Rkadapt y 0.
, 0.5
, 50
, D
,
( )
:=
The modified Euler solution is partially redone here in the following steps in order to generate a
solution plot.
Vx
0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy
1.5
−
1.3714
−
1.2837
−
1.2328
−
1.2154
−
1.2283
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vx and Vy vectors for the modified Euler
solution
<---
Vs cspline Vx Vy
,
( )
:= fspline x
( ) interp Vs Vx
, Vy
, x
,
( )
:= <---- modified Euler
solution
x 0 0.01
, 0.5
..
:= xi Y
0
〈 〉
( )i
:= fsplinei fspline xi
( )
:=
Figure 9.11 shows a comparison of the Mathcad solutions with the modified Euler solution. The
agreement between the results is, clearly, very good.
0 0.1 0.2 0.3 0.4
1.5
1.4
1.3
rkfixed solution
Rkadapt solution
modified Euler solution
rkfixed solution
Rkadapt solution
modified Euler solution
Comparison of solutions
X-VALUES
Y-VALUES
Z
1
〈 〉
( )i
Y
1
〈 〉
( )i
fsplinei
Z
0
〈 〉
( )i
Figure 9.11. Comparison of Mathcad solutions with modified Euler method
338 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

349. Example 9.6
Using the Mathcad functions , solve the problem of Example 9.4 presented in the sub-section
on the Runge-Kutta fourth order method, which is repeated below.
Solve: dy/dx = f(x,y) = - 2x 2 - y ; Initial condition : y(0) = -1.75 ;
h = 0.1; Range of x: 0 to 0.5
The Mathcad statements needed to solve the problem are
y0 1.75
−
:= D x y
,
( ) 2
− x
2
⋅ y
−
:= Z rkfixed y 0.
, 0.5
, 50
, D
,
( )
:=
Y Rkadapt y 0.
, 0.5
, 50
, D
,
( )
:= i 0 rows Z
( ) 1
−
..
:=
The Runge-Kutta solutions (Versions 1 and 2 ) are repeated here in the following steps in order to
generate solution plots in Figure 9.12 for comparison with the solutions generated with the
Mathcad functions rkfixed and Rkadapt.
Vx and Vy vectors for the Runge-Kutta
solution (Version 1 - one-third rule)
Vx1
0.0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy1
1.75
−
1.58412
−
1.43786
−
1.31316
−
1.21178
−
1.13531
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= <------
Vs1 cspline Vx1 Vy1
,
( )
:= fspline1 x
( ) interp Vs1 Vx1
, Vy1
, x
,
( )
:= <-- R/K solution (Version 1)
fspline1i fspline1 Z
0
〈 〉
( )i
⎡
⎣
⎤
⎦
:=
Vx2
0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy2
1.75
−
1.58426
−
1.43815
−
1.31361
−
1.21238
−
1.13605
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= <---- Vx and Vy vectors for the Runge-Kutta
solution (Version 2- three-eighth rule )
Chapter 9: Numerical Solution of Ordinary Differential Equations 339

350. Vs2 cspline Vx2 Vy2
,
( )
:= fspline2 x
( ) interp Vs2 Vx2
, Vy2
, x
,
( )
:= <--R/K solution- version 2
x 0 0.01
, 0.5
..
:=
fspline2i fspline2 Z
0
〈 〉
( )i
⎡
⎣
⎤
⎦
:=
0 0.1 0.2 0.3 0.4 0.5
1.8
1.6
1.4
1.2
1
rkfixed solution
Rkadapt solution
version 1- one-third rule
version 2- three-eighth rule
rkfixed solution
Rkadapt solution
version 1- one-third rule
version 2- three-eighth rule
Comparison of solutions
x- values
y-values
Z
1
〈 〉
( )i
Y
1
〈 〉
( )i
fspline1i
fspline2i
Z
0
〈 〉
( )i
Figure 9.12 Comparison of Mathcad solutions with Runge-Kutta fourth order
methods
The functions " rkfixed " and " Rkadapt " generate the solution to the given differential
equation for a number of uniformly spaced x values in the integration range bounded by x1
and x2 . If you are interested in seeing the solution only at a value of x, say x2 , it is
preferable to resort to the function " rkadapt " . Although " rkfixed " and " Rkadapt " will give
you the solution at x2 , they also go through a lot of unnecessary work returning intermediate
values of the solution at x- values in which you may not have any interest at all. The use of the
function " rkadapt " is illustrated below:
rkadapt ( y, x1, x2, acc, D, kmax, save)
where y is a vector of initial values, x1 and x2 are the endpoints of the interval of interest
over which the solution to the differential equation is to be generated. The initial values in " y "
are the values, then, at x1. The parameter "acc" controls the accuracy of the solution.
340 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

351. Small values of " acc " yield accurate solutions. A value of " acc " around 0.001 is
recommended. The parameter " kmax " is the maximum number of intermediate points at
which the solution will be computed. This value places an upper limit on the number of rows of
the matrix returned by " rkadapt" . The parameter " save " is the smallest allowable spacing
between the x- values at which the solutions are to be computed .
This command computes y values for the x-
values given in the first column.
Y rkadapt y 0
, 0.5
, 0.001
, D
, 50
, 0.001
,
( )
:= <----
x y
This is the solution returned by "rkadapt" for
the interval x= 0 to 0.5, with acc= 0.001. The
solution is generated at kmax = 50 points in
the interval where the maximum allowable
spacing between the x-values at which the
solution is to be computed is save = 0.001.
The last row is the solution generated by
"Rkadapt" at the endpoint x= 0.5
Y
0 1
0
1
2
3
4
0 -1.75
-3
5·10 -1.741272
0.03 -1.698298
0.155 -1.501116
0.5 -1.135307
=
<----
9.6 SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS
Sometimes, in engineering and the physical sciences, the need to solve a system of first-order
ordinary differential equations is encountered. Such a system is
dy1/dx = f ( x, y1, y2, ....... yn)
dy2/dx = g ( x, y1, y2, ....... yn)
..................................................
dyn/dx = z ( x, y1, y2, ....... yn)
(9.26)
with n initial conditions specified at the starting value of the independent variable x . This
system of equations can be easily solved using any of the methods discussed in sections 9.2-
9.5. However, here, the application of the the fourth order Runge-Kutta procedure to obtain a
solution to a problem involving a pair of first-order differential equations will be illustrated. Notice
that in a problem involving a pair of differential equations , where x and y are the dependent
variables and t is the independent variable , x and y calculations have to be alternately
performed as illustrated in the following example.
Chapter 9: Numerical Solution of Ordinary Differential Equations 341

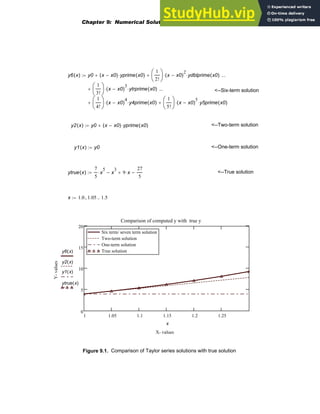
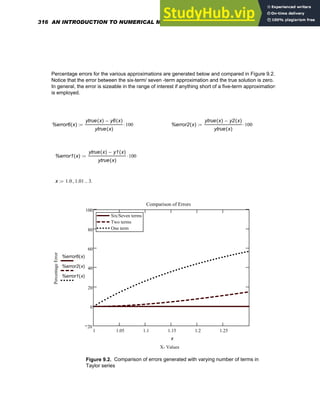
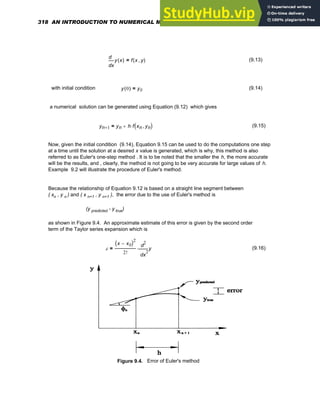
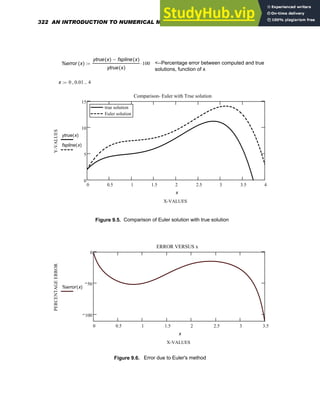
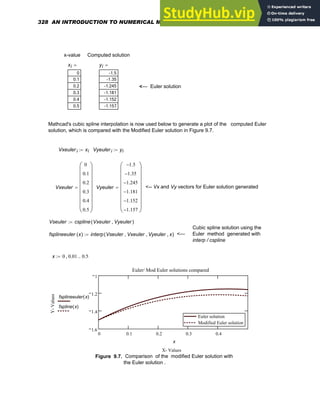
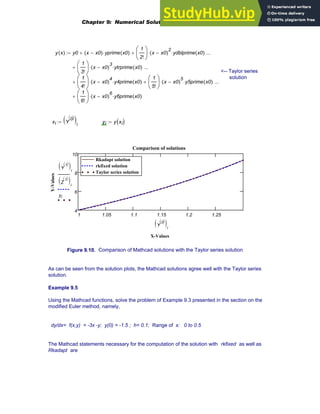
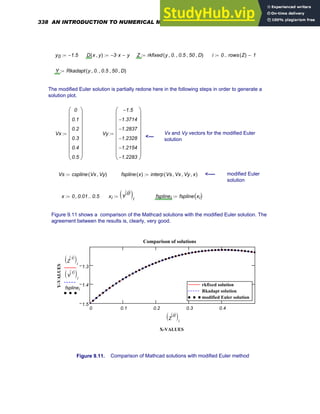
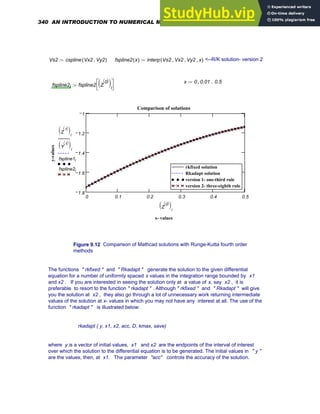
352. Example 9.7.
Using the Runge-Kutta fourth-order method, obtain a solution to
dx/dt = f(x,y,t) = xy2 + t; dy/dt= g(x,y,t) = ty + x2
for t = 0 to t= 0.5 seconds. The initial conditions are given as: x(0)= -1; y (0) = 1
Use a time increment of h = 0.1 second.
Note that both x and y are functions of the independent variable " t".
Thus, in this case,
dx/dt = f(x,y,t ) = xy2 + t ,
and dy/dt = g(x,y,t) = ty + x2
Version 1 of the Runge-Kutta Method which utilizes Simpson's one-third rule, will then resort
to the following sequential equations to compute x and y at t1, where t1 = t0 + h., and h is
the increment or step size
k1 = h f(x0, y0, t0) ; m1= h g(x0,y0, t0) ;
tmp = t0 + 0.5 h ; xmp= x0+ 0.5 k1; ymp= y0+0.5 m1
k2= h f(xmp, ymp, tmp) ; m2 = h g( xmp, ymp, tmp )
xmp* = x0 + 0.5 k2 ; ymp* = y0+ 0.5 m2
k3 = h f ( xmp*, ymp*, tmp ) ; m3 = h g ( xmp*, ymp*, tmp )
x1 = x0 + k3 ; y1 = y0 + m3 ; t1 = t0 + h
k4 = h f ( x1, y1, t1 ) ; m4 = h g ( x1, y1, t1 )
x1= x0 + (1/6) [ k1 +2 k2 + 2 k3 + k4 ] ; y1 = y0 + (1/6 ) [ m1 + 2 m2 + 2 m3 + m4 ]
In order to compute the solution (x1,y1) at t1, we start with known values x0, y0 and t0 as
shown above. Similarly, to compute the solution (x2, y2) at t2, the above procedure needs to
be repeated with ( x1, y1 , t1) replacing (x0, y0,t0) and (x2,y2,t2) replacing (x1,y1,t1).
Define the functions f(x,y,t) and g(x,y,t), the step size and the initial conditions:.
342 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

353. f x y
, t
,
( ) x y
2
⋅ t
+
:= g x y
, t
,
( ) t y
⋅ x
2
+
:= <--Define functions f(x,y,t) and g(x,y,t)
h 0.1
:= <--Time increment or step size
t0 0
:= x0 1
−
:= y0 1
:= <-- Given initial conditions
Calculations for generating solution at t1:
t1 t0 h
+
:= t1 0.1
=
k1 h f x0 y0
, t0
,
( )
⋅
:= k1 0.1
−
=
m1 h g x0 y0
, t0
,
( )
⋅
:= m1 0.1
=
tmp t0 0.5 h
⋅
+
:= tmp 0.05
=
xmp x0 0.5 k1
⋅
+
:= xmp 1.05
−
=
ymp y0 0.5 m1
⋅
+
:= ymp 1.05
=
k2 h f xmp ymp
, tmp
,
( )
⋅
:= k2 0.110763
−
=
m2 h g xmp ymp
, tmp
,
( )
⋅
:= m2 0.1155
=
xmpstar x0 0.5 k2
⋅
+
:= xmpstar 1.055381
−
=
ympstar y0 0.5 m2
⋅
+
:= ympstar 1.05775
=
k3 h f xmpstar ympstar
, tmp
,
( )
⋅
:= k3 0.11308
−
=
m3 h g xmpstar ympstar
, tmp
,
( )
⋅
:= m3 0.116672
=
x1 x0 k3
+
:= x1 1.11308
−
=
y1 y0 m3
+
:= y1 1.116672
=
t1 t0 h
+
:= t1 0.1
=
k4 h f x1 y1
, t1
,
( )
⋅
:= k4 0.128796
−
=
m4 h g x1 y1
, t1
,
( )
⋅
:= m4 0.135061
=
Chapter 9: Numerical Solution of Ordinary Differential Equations 343

354. x1 x0
1
6
⎛
⎜
⎝
⎞
⎟
⎠
k1 2 k2
⋅
+ 2 k3
⋅
+ k4
+
( )
⋅
+
:= x1 1.112747
−
=
y1 y0
1
6
m1 2 m2
⋅
+ 2 m3
⋅
+ m4
+
( )
⋅
+
:= y1 1.116567
=
Calculations for generating solution at t2:
t2 t1 h
+
:= t2 0.2
=
k1 h f x1 y1
, t1
,
( )
⋅
:= k1 0.128729
−
=
m1 h g x1 y1
, t1
,
( )
⋅
:= m1 0.134986
=
tmp t1 0.5 h
⋅
+
:= tmp 0.15
=
xmp x1 0.5 k1
⋅
+
:= xmp 1.177111
−
=
ymp y1 0.5 m1
⋅
+
:= ymp 1.184061
=
k2 h f xmp ymp
, tmp
,
( )
⋅
:= k2 0.150031
−
=
m2 h g xmp ymp
, tmp
,
( )
⋅
:= m2 0.15632
=
xmpstar x1 0.5 k2
⋅
+
:= xmpstar 1.187762
−
=
ympstar y1 0.5 m2
⋅
+
:= ympstar 1.194727
=
k3 h f xmpstar ympstar
, tmp
,
( )
⋅
:= k3 0.154538
−
=
m3 h g xmpstar ympstar
, tmp
,
( )
⋅
:= m3 0.158999
=
x2 x1 k3
+
:= x2 1.267285
−
=
y2 y1 m3
+
:= y2 1.275566
=
k4 h f x2 y2
, t2
,
( )
⋅
:= k4 0.186196
−
=
m4 h g x2 y2
, t2
,
( )
⋅
:= m4 0.186112
=
344 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

355. x2 x1
1
6
⎛
⎜
⎝
⎞
⎟
⎠
k1 2 k2
⋅
+ 2 k3
⋅
+ k4
+
( )
⋅
+
:= x2 1.266757
−
=
y2 y1
1
6
m1 2 m2
⋅
+ 2 m3
⋅
+ m4
+
( )
⋅
+
:= y2 1.27519
=
Caculations for t= 0.3, 0.4 and 0.5 seconds can be performed in a similar way , giving the
following results.
t3 0.3
:= x3 1.506
−
:= y3 1.5
:=
t4 0.4
:= x4 1.945
−
:= y4 1.848
:=
t5 0.5
:= x5 3.025
−
:= y5 2.522
:=
Plots of the results of the Runge-Kutta process can be obtained by an interpolation procedure
involving the generation of the Vt, Vx and Vy vectors and the spline functions xspline(t) and
yspline(t) as shown below.
Vt
t0
t1
t2
t3
t4
t5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Vx
x0
x1
x2
x3
x4
x5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy
y0
y1
y2
y3
y4
y5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Vt
0
0.1
0.2
0.3
0.4
0.5
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vx
1
−
1.112747
−
1.266757
−
1.506
−
1.945
−
3.025
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vy
1
1.116567
1.27519
1.5
1.848
2.522
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Vsx cspline Vt Vx
,
( )
:= Vsy cspline Vt Vy
,
( )
:=
Chapter 9: Numerical Solution of Ordinary Differential Equations 345

356. xspline t
( ) interp Vsx Vt
, Vx
, t
,
( )
:= yspline t
( ) interp Vsy Vt
, Vy
, t
,
( )
:=
The Mathcad solution process using " rkfixed " and " Rkadapt " is done below.
t 0 0.1
, 0.5
..
:= f x y
, t
,
( ) x y
2
⋅ t
+
:= g x y
, t
,
( ) t y
⋅ x
2
+
:=
Define initial conditions:
x
1
−
1
⎛
⎜
⎝
⎞
⎟
⎠
:= <-- Define initial conditions x(0) = x0 = -1 and y(0) = y1 = 1.
Define derivatives:
Note that the vector
function "D" has 2
rows in this case. If
the problem had
involved 3 first order
eqs, there would be 3
rows.
< First derivative
< Second derivative
<---
D t x
,
( )
x0 x1
( )2
⋅ t
+
t x1
⋅ x0
( )2
+
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
:=
Evaluate solution at 50 points between 0 and 0.5.
The following commands will generate the solution matrix which will contain 3 columns- the "t"
values, the corresponding "x" values and the "y " values.
Z rkfixed x 0
, 0.5
, 50
, D
,
( )
:= Y Rkadapt x 0
, 0.5
, 50
, D
,
( )
:= i 0 rows Z
( ) 1
−
..
:=
xsplinei xspline Z
0
〈 〉
( )i
⎡
⎣
⎤
⎦
:= ysplinei yspline Z
0
〈 〉
( )i
⎡
⎣
⎤
⎦
:=
The Mathcad solution generated through the above procedure is compared with the analytical
Runge-Kutta results in Figures 9.13 and 9.14.
346 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

357. 0 0.1 0.2 0.3 0.4
4
3
2
1
rkfixed solution
Rkadapt solution
R/K 4th order-
rkfixed solution
Rkadapt solution
R/K 4th order-
System of first order differential equations
Time, t, seconds
x-
values
Z
1
〈 〉
( )i
Y
1
〈 〉
( )i
xsplinei
Z
0
〈 〉
( )i
Figure 9.13. Solution to differential equation pair- x (t)
0 0.1 0.2 0.3 0.4
1
1.5
2
2.5
rkfixed solution
Rkadapt solution
R/K 4th order
rkfixed solution
Rkadapt solution
R/K 4th order
System of first-order differential equations
Time , t , seconds
y-
Values
Z
2
〈 〉
( )i
Y
2
〈 〉
( )i
ysplinei
Z
0
〈 〉
( )i
Figure 9.14. Solution to differential equation pair - y (t)
Chapter 9: Numerical Solution of Ordinary Differential Equations 347

358. t x(t) y(t) t x(t) y(t)
( obtained with rkfixed ) (obtained with Rkadapt )
Z
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 -1 1
0.01 -1.010102 1.010151
0.02 -1.020419 1.020611
0.03 -1.030966 1.031388
0.04 -1.041759 1.042491
0.05 -1.052815 1.05393
0.06 -1.064154 1.065717
0.07 -1.075794 1.077862
0.08 -1.087758 1.090377
0.09 -1.100067 1.103275
0.1 -1.112747 1.11657
0.11 -1.125822 1.130277
0.12 -1.139322 1.144412
0.13 -1.153276 1.158991
0.14 -1.167716 1.174032
0.15 -1.182678 1.189556
= Y
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 -1 1
0.01 -1.010102 1.010151
0.02 -1.020419 1.020611
0.03 -1.030966 1.031388
0.04 -1.041759 1.042491
0.05 -1.052815 1.05393
0.06 -1.064154 1.065717
0.07 -1.075794 1.077862
0.08 -1.087758 1.090377
0.09 -1.100067 1.103275
0.1 -1.112747 1.11657
0.11 -1.125822 1.130277
0.12 -1.139322 1.144412
0.13 -1.153276 1.158991
0.14 -1.167716 1.174032
0.15 -1.182678 1.189556
=
Note that the first column of the above matrices is the time " t " column, the second is the
solution "x" while the third is the solution "y".
Using " rkadapt " , the solution can be found at any point in time as follows.
This command generates the
solution to the differential
equation at the endpoint t = 0.5
secs with acc = 0.001, kmax =
50 ( maximum number of
intermediate points at which the
solution will be approximated)
and save = 0.00001 which is the
smallest spacing between
the t- values at which the
solutions are to be
computed.
Value rkadapt x 0
, 0.5
, 0.001
, D
, 50
, 0.00001
,
( )
:=
<--
348 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

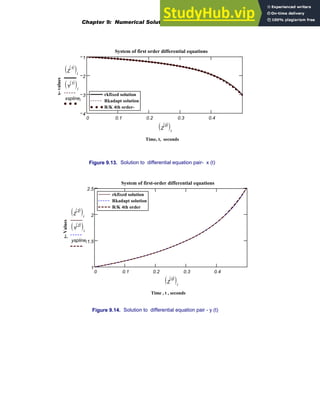
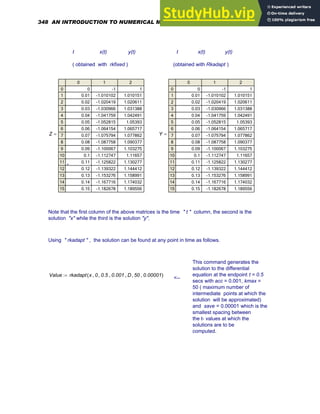
359. t x y
Note: The first column contains the
t-values, the second column contains
the x-values, and the third contains the
y- values
Value
0
5 10
3
−
×
0.03
0.155
0.374387
0.5
1
−
1.005025
−
1.030966
−
1.190367
−
1.800212
−
3.026613
−
1
1.005038
1.031388
1.197505
1.741152
2.524711
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
<---
It is noted that the Runge-Kutta- Version 1 solution agrees reasonably well with the
Mathcad solutions.
9.7 SOLUTION OF HIGHER-ORDER ORDINARY DIFFERENTIAL
EQUATIONS
In many areas of engineering and physics, the solution of higher-order differential equations is
often required. Examples can be encountered in vibration engineering, control systems
engineering , electrical circuit analysis etc.
The general form of a second-order differential equation is
d2y/dx2 = f ( x, y, dy/dx ) (9.27)
A more special form often encountered in vibrations, control systems, and electrical circuit
analysis is
a d2y/dx2 + b dy/dx + c y = q(x) (9.28)
with initial conditions y(0) and dy/dx(0) specified.
Although any of the methods discussed in sections 9.2-9.5 can certainly be used to obtain
solutions to Equation 9.28, it must first be converted to a system of first-order differential
equations as follows.
dy/dx = z = f ( x,y, z)
dz/dx = [q(x) - b z - c y] / a = g (x,y, z )
(9.29)
Chapter 9: Numerical Solution of Ordinary Differential Equations 349

360. with the initial conditions now becoming y(0) and z(0) . Thus, if a solution to the second-order
differential equation, which is now represented by the two first-order equations of Equations
9.29 , is to be generated by Version 1 of the fourth-order Runge-Kutta method, the
calculations shown in the following procedure must be resorted to.
k1 = h f (y0, z0, x0) ; m1= h g (y0,z0, x0) ;
xmp = x0 + 0.5 h ; ymp= y0+ 0.5 k1; zmp= z0+0.5 m1
k2= h f (ymp, zmp, xmp) ; m2 = h g ( ymp, zmp, xmp )
ymp* = y0 + 0.5 k2 ; zmp* = z0+ 0.5 m2
k3 = h f ( ymp*, zmp*, xmp ) ; m3 = h g ( ymp*, zmp*, xmp )
y1 = y0 + k3 ; z1 = z0 + m3 ; x1 = x0 + h
k4 = h f ( y1, z1, x1 ) ; m4 = h g ( y1, z1, x1 )
y1= y0 + (1/6) [ k1 +2 k2 + 2 k3 + k4 ] ; z1 = z0 + (1/6 ) [ m1 + 2 m2 + 2 m3 + m4 ]
(9.30)
where h is the increment or step size. Note that in order to generate the solution
(y1, z1), we started with known values ( x0, y0, z0 ). Similarly, to obtain ( y2, z2) , the above
procedure must be repeated with (x1,y1,z1) replacing ( x0, y0,z0) and (x2, y2,z2) replacing
(x1,y1,z1).
Example 9.8
Using the Runge-Kutta fourth-order
method, obtain a solution to
m d2y/dt2 +c dy/dt + k y = F(t) ;
m= 1kg, c= 3 N-sec/m, k = 9 N/m , F(t)= 9 N.
for t = 0 to t= 3 seconds. The initial conditions
are given as: y(0)=0; dy/dt (0) = 0 .
Use a time increment of 0.5 seconds.
350 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

361. The above differential equation represents the equation of motion of a linear
spring-mass-damper system subjected to a step forcing function as shown in the above figure.
As mentioned earlier , application of the fourth order Runge- Kutta Method to the solution of a
second-order differential equation is quite similar to that of a first order differential equation ,
except that the following two first-order equations must now be considered.
dy/dt = z ;
and m dz/dt + c z +k y = F(t)
Note that, now, both y and z are functions of the independent variable " t".
Thus, in this case,
dy/dt = f( y,z, t ) = z ,
and dz/dt = g(y,z,t) =[F(t) - ( k y + c z)] /m
Version 1 of the R-K procedure will then resort to the following equations to compute y and z at
t1:
k1 = h f(y0, z0, t0) ; m1= h g(y0,z0, t0) ;
tmp = t0 + 0.5 h ; ymp= y0+ 0.5 k1; zmp= z0+0.5 m1
k2= h f(ymp, zmp, tmp) ; m2 = h g( ymp, zmp, tmp )
ymp* = y0 + 0.5 k2 ; zmp* = z0+ 0.5 m2
k3 = h f ( ymp*, zmp*, tmp ) ; m3 = h g ( ymp*, zmp*, tmp )
y1 = y0 + k3 ; z1 = z0 + m3 ; t1 = t0 + h
k4 = h f ( y1, z1, t1 ) ; m4 = h g ( y1, z1, t1 )
y1= y0 + (1/6) [ k1 +2 k2 + 2 k3 + k4 ] ; z1 = z0 + (1/6 ) [ m1 + 2 m2 + 2 m3 + m4 ]
Chapter 9: Numerical Solution of Ordinary Differential Equations 351

362. F t
( ) 9
:= m 1
:= c 3
:= k 9
:= <--Given data
f y z
, t
,
( ) z
:= g y z
, t
,
( )
F t
( ) c z
⋅
− k y
⋅
−
m
:= <--Define functions f(y,z,t) and g(y,z,t)
h 0.5
:= <--Time increment or step size
t0 0
:= y0 0
:= z0 0
:= <-- Given initial conditions
Calculations for generating solution at t1:
t1 t0 h
+
:= t1 0.5
=
k1 h f y0 z0
, t0
,
( )
⋅
:= m1 h g y0 z0
, t0
,
( )
⋅
:= tmp t0 0.5 h
⋅
+
:=
k1 0
= m1 4.5
=
ymp y0 0.5 k1
⋅
+
:= zmp z0 0.5 m1
⋅
+
:= k2 h f ymp zmp
, tmp
,
( )
⋅
:=
m2 h g ymp zmp
, tmp
,
( )
⋅
:= k2 1.125
= m2 1.125
=
ympstar y0 0.5 k2
⋅
+
:= zmpstar z0 0.5 m2
⋅
+
:=
k3 h f ympstar zmpstar
, tmp
,
( )
⋅
:= m3 h g ympstar zmpstar
, tmp
,
( )
⋅
:=
k3 0.28125
= m3 1.125
=
y1 y0 k3
+
:= z1 z0 m3
+
:= t1 t0 h
+
:=
k4 h f y1 z1
, t1
,
( )
⋅
:= m4 h g y1 z1
, t1
,
( )
⋅
:=
k4 0.5625
= m4 1.546875
=
y1 y0
1
6
⎛
⎜
⎝
⎞
⎟
⎠
k1 2 k2
⋅
+ 2 k3
⋅
+ k4
+
( )
⋅
+
:= y1 0.5625
=
352 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

363. z1 z0
1
6
m1 2 m2
⋅
+ 2 m3
⋅
+ m4
+
( )
⋅
+
:= z1 1.757813
=
Calculations for generating solution at t2:
t2 t1 h
+
:= t2 1
=
k1 h f y1 z1
, t1
,
( )
⋅
:= m1 h g y1 z1
, t1
,
( )
⋅
:= tmp t1 0.5 h
⋅
+
:=
k1 0.878906
= m1 0.667969
−
=
ymp y1 0.5 k1
⋅
+
:= zmp z1 0.5 m1
⋅
+
:= k2 h f ymp zmp
, tmp
,
( )
⋅
:=
m2 h g ymp zmp
, tmp
,
( )
⋅
:= k2 0.711914
= m2 2.144531
−
=
ympstar y1 0.5 k2
⋅
+
:= zmpstar z1 0.5 m2
⋅
+
:=
k3 h f ympstar zmpstar
, tmp
,
( )
⋅
:= m3 h g ympstar zmpstar
, tmp
,
( )
⋅
:=
k3 0.342773
= m3 0.661377
−
=
y2 y1 k3
+
:= z2 z1 m3
+
:= t2 t1 h
+
:=
k4 h f y2 z2
, t2
,
( )
⋅
:= m4 h g y2 z2
, t2
,
( )
⋅
:=
k4 0.548218
= m4 1.218384
−
=
y2 y1
1
6
⎛
⎜
⎝
⎞
⎟
⎠
k1 2 k2
⋅
+ 2 k3
⋅
+ k4
+
( )
⋅
+
:= y2 1.151917
=
z2 z1
1
6
m1 2 m2
⋅
+ 2 m3
⋅
+ m4
+
( )
⋅
+
:= z2 0.508118
=
Caculations for t = 1.5,2.0,2.5 and 3.0 can be performed in a similar way , giving the
following results.
t3 1.5
:= y3 1.166
:= z3 0.342
−
:= t4 2
:= y4 1.006
:= z4 0.24
−
:=
Chapter 9: Numerical Solution of Ordinary Differential Equations 353

364. t5 2.5
:= y5 0.938
:= z5 2.889 10
3
−
⋅
:= t6 3
:= y6 0.94
:= z6 0.019
−
:=
Plots of the results of the Runge-Kutta process can be obtained by an interpolation
procedure involving the generation of the Vt, Vy and Vz vectors and the spline functions
yspline(t) and zspline(t) as shown below.
Vt
t0
t1
t2
t3
t4
t5
t6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vy
y0
y1
y2
y3
y4
y5
y6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:= Vz
z0
z1
z2
z3
z4
z5
z6
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
:=
Vt
0
0.5
1
1.5
2
2.5
3
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vy
0
0.5625
1.151917
1.166
1.006
0.938
0.94
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= Vz
0
1.757813
0.508118
0.342
−
0.24
−
2.889 10
3
−
×
0.019
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Vsy cspline Vt Vy
,
( )
:= Vsz cspline Vt Vz
,
( )
:= yspline t
( ) interp Vsy Vt
, Vy
, t
,
( )
:=
zspline t
( ) interp Vsz Vt
, Vz
, t
,
( )
:=
The Mathcad solution process using " rkfixed " and " Rkadapt " is done below.
t 0 0.1
, 3
..
:= F t
( ) 9
:= m 1
:= c 3
:= k 9
:=
f y z
, t
,
( ) z
:= g y z
, t
,
( )
F t
( ) c z
⋅
− k y
⋅
−
m
:=
Define initial conditions:
354 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

365. Define initial conditions y(0) = y0 = 0 and z(0) = y1 = 0.
y0 is initial displacement and y 1 is initial velocity
y
0
0
⎛
⎜
⎝
⎞
⎟
⎠
:= <--
Define first and second derivatives:
Note that the vector
function "D" has 2
rows in this case. If the
problem had involved 3
first order eqs, there
would be 3 rows.
< First derivative
< Second derivative
D t y
,
( )
y1
F t
( ) c y1
⋅
− k y0
⋅
−
m
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Evaluate solution at 100 points between 0 and 3:
The following commands will generate the solution matrix which will contain 3 columns- the
"t" values, the corresponding "y" values and the "dy/dt " values.
Z rkfixed y 0
, 3.0
, 100
, D
,
( )
:= Y Rkadapt y 0
, 3.0
, 100
, D
,
( )
:= i 0 rows Z
( ) 1
−
..
:=
ysplinei yspline Z
0
〈 〉
( )i
⎡
⎣
⎤
⎦
:= zsplinei zspline Z
0
〈 〉
( )i
⎡
⎣
⎤
⎦
:=
The displacement and velocity profiles generated are compared in Figures 9.15 and 9.16.
_________________________________________________________________________________
N O T E S:
Chapter 9: Numerical Solution of Ordinary Differential Equations 355

366. 0 0.5 1 1.5 2 2.5 3
0
0.5
1
1.5
rkfixed solution
Rkadapt solution
R/K 4th order-
rkfixed solution
Rkadapt solution
R/K 4th order-
Sec-order differential equation solution
TIME
DISPLACEMENT
Z
1
〈 〉
( )i
Y
1
〈 〉
( )i
ysplinei
Z
0
〈 〉
( )i
Figure 9.15. Solution to second- order differential equation - displacement as a
function of time
0 0.5 1 1.5 2 2.5 3
0
1
2
rkfixed solution
Rkadapt solution
R/K 4th order
rkfixed solution
Rkadapt solution
R/K 4th order
Second-order differential equation solution
Time values
Velocity
(
dy/dt)
Values
Z
2
〈 〉
( )i
Y
2
〈 〉
( )i
zsplinei
Z
0
〈 〉
( )i
Figure 9.16. Solution to second-order differential equation- velocity as a function
of time
356 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

367. t y(t) ydot(t)
( obtained with rkfixed )
Z
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0
0.03 -3
3.9285·10 0.257858
0.06 0.015229 0.491527
0.09 0.033181 0.701279
0.12 0.057071 0.887549
0.15 0.086205 1.050917
0.18 0.119904 1.192089
0.21 0.157516 1.311883
0.24 0.198412 1.41121
0.27 0.241994 1.491065
0.3 0.287692 1.552504
0.33 0.334971 1.596638
0.36 0.383329 1.624613
0.39 0.432298 1.637605
0.42 0.481447 1.636801
0.45 0.53038 1.623397
=
t y(t) ydot(t)
( obtained with Rkadapt )
Y
0 1 2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0
0.03 -3
3.928548·10 0.257858
0.06 0.01523 0.491526
0.09 0.033181 0.701278
0.12 0.057071 0.887549
0.15 0.086205 1.050917
0.18 0.119904 1.192088
0.21 0.157516 1.311882
0.24 0.198413 1.411209
0.27 0.241994 1.491064
0.3 0.287692 1.552503
0.33 0.334971 1.596637
0.36 0.383329 1.624612
0.39 0.432298 1.637603
0.42 0.481447 1.6368
0.45 0.53038 1.623396
=
Note that the first column of the above matrices is the time " t " column, the second is the
displacement " y " and the last is velocity " dy/dt "
Chapter 9: Numerical Solution of Ordinary Differential Equations 357

368. Using " rkadapt " , the solution can be found at any point in time as follows. This command
generates the solution to the differential equation at the endpoint t = 0.1 secs with acc =
0.001, kmax = 100 ( maximum number of intermediate points at which the solution will be
approximated) and save = 0.00001 which is the smallest spacing between the t- values at
which the solutions are to be computed.
Value rkadapt y 0
, 0.1
, 0.001
, D
, 100
, 0.00001
,
( )
:=
Time Displacement Velocity
First column is the
"time" column.
Second column is
"Displacement" .
Third is " Velocity ".
Value
0
1.638135 10
5
−
×
8.192772 10
5
−
×
4.096596 10
4
−
×
2.048319 10
3
−
×
0.010242
0.051208
0.1
0
1.207549 10
9
−
×
3.020221 10
8
−
×
7.54885 10
7
−
×
1.884157 10
5
−
×
4.671742 10
4
−
×
0.011197
0.040519
0
1.474285 10
4
−
×
7.372589 10
4
−
×
3.684671 10
3
−
×
0.018378
0.090759
0.42554
0.765952
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= <--
It is noted that the Runge-Kutta- Version 1 solution agrees reasonably well with the Mathcad
solutions.
9.8 BOUNDARY-VALUE PROBLEMS AND THE SHOOTING METHOD
As mentioned in the introduction, a boundary value problem is one in which conditions are
prescribed at two different values of the independent variable. An example of a boundary-value
problem is
2
x
y
d
d
2
C y
⋅
+ F x
( )
= , y 0
( ) 0
= , y L
( ) 2
= (9.31)
Because the two conditions given in Equations 9.31 deal with different values of the independent
variable x , this problem cannot be solved by the methods discussed so far. Other methods,
therefore, have to be resorted to in order to obtain a solution. One such method is the Shooting
Method in which a boundary-value problem is converted to a pseudo- initial-value problem
involving a trial and error approach that can make use of any of the methods discussed in this
chapter. Since only one initial condition is prescribed at x= 0 , the second initial condition,
which is not given, must be assumed at x = 0, in order to start the
358 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

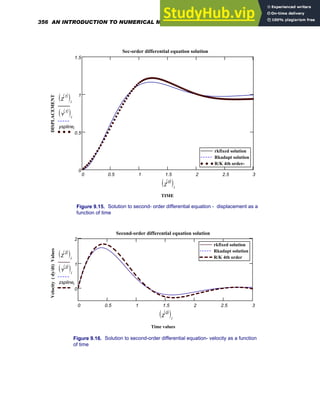
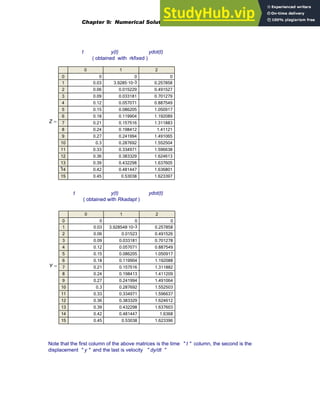
369. solution process. Upon completion of the solution process, a check must be made to
determine if the condition prescribed at the point x = L is satisfied or not. If not, a second
guess must be made and the procedure redone. If the second guess still does not satisfy the
prescribed end condition, a third guess has to be estimated. This can be accomplished by
noting the difference between the given and the computed conditions at x = L and resorting to
a linear interpolation process that utilizes the results of the first two trials. This iteration
process must be repeated until the prescribed end condition is , in fact, satisfied. In this
method, it is important for the analyst to be skillful at estimating the unprescribed initial
condition properly at the starting point in order to maintain efficiency and avoid divergence.
Because the method is analogous to aiming properly and shooting at a given object, it has
been appropriately labelled as the shooting method. When higher-order differential equations
must be solved involving several boundary conditions, this method has proven to be quite
uncouth and laborious and, thus, inefficient.
Although any of the methods discussed in this chapter can be employed in the solution of a
boundary-value problem by the shooting method. the following example will illustrate its
application with Mathcad's Rkadapt and rkadapt functions.
Example 9.9
Solve: d2y/ dx2 = M/EI = (30 x - 1.5 x^2)/ EI , where EI = 121,500 kips-ft 2
The boundary conditions prescribed are:
x = 0, y = 0 and x= 20, y =0
This differential equation represents the relationship between the bending moment M and
the deflection "y" at a distance "x" along the span from the left hand end of a 20 foot long
simply supported beam loaded with a uniformly distributed load of 3 kips/ ft. as shown in
Figure 9.17. The slope and deflection at any point " x " can be obtained by solving the above
differential equation.
Consider the two equations:
dy/dx = z ; and
(9.32)
dz/dx = M/EI = (30 x - 1.5 x^2 )/ EI
Note that, now, both y and z are functions of the dependent variable " x". Thus, in this
case,
dy/dx = f ( x, y, z ) = z ,
(9.33)
and dz/dx = g( x, y, z ) =[30 x - 1.5 x ^2 ] / EI
As said earlier, the shooting method is a trial- and- error method used in the solution of
boundary-value problems. Although two boundary conditions are prescribed here, there is
only one initial condition ( x= 0, y = 0 ) provided to begin the solution process. The initial
Chapter 9: Numerical Solution of Ordinary Differential Equations 359

370. slope ( derivative ) at x= 0 is not known. Thus, the second initial condition, namely, the value
of dy/dx at x = o has to be assumed so that the solution process can be initiated. With these
initial values of y and dy/dx , the solution " y" at x= 20 ft must then be computed by any
appropriate method such as Modified Euler or Runga- Kutta. If this solution does not agree
with the true value of y at x= 20 ft , which, in this case is zero , the initial condition dy/dx at
x= 0 used must be revised and a new solution y at x= 20 computed. This process has to be
repeated until the solution obtained at x= 20 ft agrees with the actual condition prescribed at
that point on the beam.
In the following paragraphs, an iteration process utilizing Mathcad's Rkadapt and rkadapt
functions is presented by which a solution to this boundary value problem is arrived at :
EI 121500
:= <-- Given EI value in kips-ft 2
Figure 9.17. A simply supported beam with a uniformly distributed load
Define initial conditions:
Define initial conditions y(0) = y0 = 0 and z(0) = y1
= -1.000 (assumed). y0 is y at x = 0, and y 1 is slope
(dy/dx) at x = 0.
<---
y
0
y1
⎛
⎜
⎝
⎞
⎟
⎠
:=
Define first and second derivatives:
(Note that the vector
function "D" has 2
rows in this case. If
the problem had
involved 3 first order
equations, there
would be 3 rows.)
< First derivative
< Second derivative
D x y
,
( )
y1
30 x
⋅ 1.5 x
2
⋅
−
EI
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
360 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

371. Using " rkadapt " :
Because y1 which is the slope at x = 0 is not
known, a reasonable starting value has
to be assumed.
This command generates the
solution to the differential equation
at the endpoint x= 20 Ft with acc
= 0.001, kmax = 1000
( max number of intermediate
points at which the solution will be
approximated) and save = 0.00001
which is the smallest spacing
between the x- values at which the
solutions are to be computed.
y1 1.0
−
:=
Value1 rkadapt y 0
, 20
, 0.001
, D
, 1000
, 0.00001
,
( )
:= <--
First column is the " x" column
Second column is "y "
Third is " dy/dx "
Value1
0
0.2
1.2
6.2
20
0
0.2
−
1.199931
−
6.191712
−
19.835391
−
1
−
0.999995
−
0.999829
−
0.996235
−
0.983539
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
<--
The above computation indicates that the deflection at x = 20 Ft generated with the
assumed dy/dx value at x= 0 is non-zero. Therefore, try a new value of y1:
y1 0.5
−
:= Value2 rkadapt y 0
, 20
, 0.001
, D
, 1000
, 0.00001
,
( )
:=
Value2
0
0.2
1.2
6.2
20
0
0.1
−
0.599931
−
3.091712
−
9.835391
−
0.5
−
0.499995
−
0.499829
−
0.496235
−
0.483539
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
The above analysis has yielded a deflection of 9.835 ft at the end x= 20 Ft.
With the assumed value of y1, the deflection at the end is , clearly, still non-zero. Therefore, a
third value of y1 must be tried which can be arrived at by a process of linear interpolation
utilizing the results of the first two trials. The formula arrived at that must be used for
estimating the next guess is the following.
Chapter 9: Numerical Solution of Ordinary Differential Equations 361

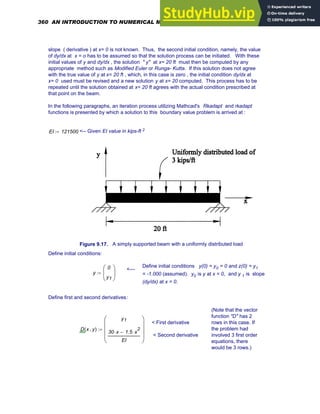
372. New value of y1 to be tried = [second value of the first derivative y1 assumed times the
first deflection value at the end computed - first value of the first derivative y1 assumed
times the second deflection value at the end computed ] / [ first deflection value at the end
computed - the second deflection value at the end computed ] . That is,
y1
Value20 2
, Value14 1
,
⋅ Value10 2
, Value24 1
,
⋅
−
Value14 1
, Value24 1
,
−
:=
y1 8.23045
− 10
3
−
×
=
Then, the solution with the new guess is
Value3 rkadapt y 0
, 20
, 0.001
, D
, 1000
, 0.00001
,
( )
:=
which yields
Note the negligible
deflection
computed at the end with
the current assumed value
of the slope (derivative) at
x= 0
<----
Value3
0
0.2
1.2
6.2
20
0
1.645763
− 10
3
−
×
9.807565
− 10
3
−
×
0.042741
−
1.922074
− 10
15
−
×
8.230453
− 10
3
−
×
8.225547
− 10
3
−
×
8.059786
− 10
3
−
×
4.465547
− 10
3
−
×
8.230453 10
3
−
×
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Now , using Rkadapt , the solution can be evaluated at 100 points between 0 and 20 with the
above initial slope value put in which led to the computation of the true displacement (y= 0) at the
end x= 20 Ft. The following commands will then generate the solution matrix [ Z ] which will
contain 3 columns- the "x" values, the corresponding "y" values and the "dy/dx " values.
Z Rkadapt y 0
, 20
, 100
, D
,
( )
:=
i 0 rows Z
( ) 1
−
..
:=
The results of the above Mathcad computation are plotted in Figures 9.18 and 9.19.
362 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

373. 0 10 20
0.01
0
0.01
Beam Slope ( dy/dx )
x- Values
dy/
dx
values
Z
2
〈 〉
( )i
Z
0
〈 〉
( )i
0 10 20
0.06
0.04
0.02
0
Beam Displacement (y)
x- Values (Feet)
Y-
values
(
Feet
)
Z
1
〈 〉
( )i
Z
0
〈 〉
( )i
Figure 9.18. Beam displacement along span Figure 9.19. Beam slope along span
9.9 APPLICATIONS IN NUMERICAL SOLUTION OF ORDINARY
DIFFERENTIAL EQUATIONS
9.9.1 Response of an Electric R-L Circuit to a Unit-Step Voltage Input
Consider the electric circuit shown in Figure 9.20 which is subjected to a unit step input
voltage .
Figure 9.20. R-L circuit with a unit-step voltage input
Summing voltages around the loop, the governing differential equation for the circuit can be
seen to be
R I t
( )
⋅ L
t
I t
( )
d
d
⋅
+ u t
( )
= (9.34)
where R is the resistance of the circuit, L its inductance and I(t) the current in it at any time
t . With no initial energy in the network, the following initial condition is applicable
I 0
( ) 0
= (9.35)
Chapter 9: Numerical Solution of Ordinary Differential Equations 363

374. The Mathcad statements that are needed to generate the solution using Rkadapt are
R 1
:= L 1
:= I0 0
:= D t I
,
( )
1 R I
⋅
−
L
:= Z Rkadapt I 0.
, 8.
, 50
, D
,
( )
:= i 0 rows Z
( ) 1
−
..
:=
0 1 2 3 4 5 6
0
0.5
1
Current in a an electric circuit
Time, seconds
Current,
amperes
Z
1
〈 〉
( )i
Z
0
〈 〉
( )i
Figure 9.21. Response of R-L circuit to unit step input voltage
The Mathcad solution generated is shown in Figure 9.21. Notice how the current attains its
steady-state value in a time t equal to 4 τ, where τ is the system time constant, which, in this
case, is L/ R or 1 second.
9.9.2. Deflection Curve of a Cantilevered Beam with a Uniformly Distributed
Load
Consider a uniform beam fixed at one end at free at the other as shown with a uniformly
distributed load of w per unit length. The bending moment at a distance x from the left hand end
of the beam is given by
M x
( ) w L
⋅ x
⋅ w
L
2
2
⋅
− w
x
2
2
⋅
−
=
(9.36)
Figure 9.22. Cantilevered beam with uniformly distributed load
364 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

375. The displacement at x is then given by
2
x
y x
( )
d
d
2 M x
( )
EI
= (9.37)
where E is Young's modulus of elasticity for the material of the beam, and I is the moment
of inertia of the beam cross section about its neutral axis. In order to determine the
deflection curve of the beam, Equation (9.37) must be integrated and the appropriate
boundary conditions applied , which are
y 0
( ) 0
= ,
x
y 0
( )
d
d
0
=
For a beam of length L= 165 inches, w = 12 lb/in, EI = 75 x 10 6 lb- in 2 , Equation (9.37)
can be solved with Mathcad's Rkadapt function as follows.
L 165
:= EI 75 10
6
⋅
:= w 12
:= y0 0
:= y1 0
:=
Define initial conditions to start the solution process: y(0)= 0 , dy/dx (0)
= 0 ( y 0 is the displacement at x=0 and y 1 is the slope at x= 0 )
y
y0
y1
⎛
⎜
⎝
⎞
⎟
⎠
:= <---
<--Bending moment expression at x
M x
( ) w L
⋅ x
⋅ w
L
2
2
⋅
− w
x
2
2
⋅
−
:=
D x y
,
( )
y1
M x
( )
EI
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= <--Define first and second derivatives
Z Rkadapt y 0
, L
, 100
, D
,
( )
:= <------ Evaluates solution at 100 points between 0 and L with
the given initial conditions
i 0 rows Z
( ) 1
−
..
:=
The results of the Mathcad computation are shown in Figures 9.23 and 9.24, with the maximum
deflection and slope occurring at the free end as anticipated.
Chapter 9: Numerical Solution of Ordinary Differential Equations 365

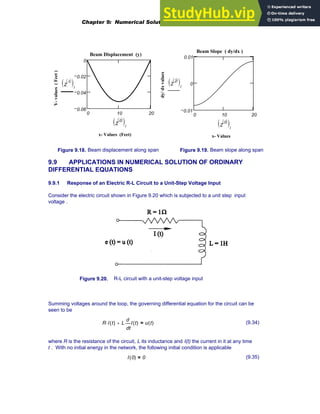
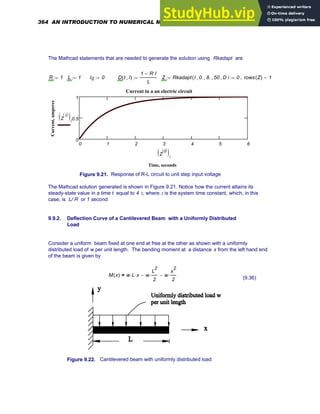
376. 0 100
0.2
0.1
0
Slope along beam span
Distance from left end
Slope
Z
2
〈 〉
( )i
Z
0
〈 〉
( )i
0 50 100 150
20
10
0
Deflection along beam span
Distance from left end, inches
Deflection
,
inches
Z
1
〈 〉
( )i
Z
0
〈 〉
( )i
Figure 9.23. Beam deflection curve Figure 9.24. Beam slope along span
9.9.3. Temperature Response of a Solid Steel Ball Placed in a Hot Stream Of Air
When a body which is initially at a uniform temperature T 0 is suddenly placed in a hot
fluid, the rate at which the temperature T(t) of the body changes with time is given by the
differential equation [ 17 ]
ρ c
⋅ Lc
⋅
t
T t
( )
d
d
⋅ h Tinf T t
( )
−
( )
⋅
= (9.38)
where ρ is the mass density of the body, c is its specific heat at constant pressure, T inf is
the temperature of the surrounding fluid, h is the average convection heat transfer coefficient,
and L c is the characteristic length. For a solid steel sphere of diameter 2 cm initially at 10 deg
C., and placed in a stream of hot air at temperature, T inf = 75 deg C. , with h =25 W/ m 2 . K,
we have
d 0.02
:= m ρ 7854
:= kg/ m 3
c 434
:= J/ kg . K h 25
:= W/ m 2 . K
Tinf 75
:= deg. K T0 10
:= deg. K V π
d
3
6
⋅
:= A π d
2
⋅
:=
Lc
V
A
:= Lc 3.333333 10
3
−
×
= m
and the Mathcad statements needed to generate the temperature response of the steel
ball to the hot stream of air are
366 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

377. T0 10
:= D t T
,
( )
h
ρ c
⋅ Lc
⋅
Tinf T
−
( )
⋅
:= Z Rkadapt T 0.
, 2000
, 100
, D
,
( )
:=
i 0 rows Z
( ) 1
−
..
:=
0 500 1000 1500 2000
0
50
100
Temp response of steel ball
Time, seconds
Temperature,
deg.
C.
Z
1
〈 〉
( )i
Z
0
〈 〉
( )i
Figure 9.25. Temperature response of steel ball
The Mathcad solution generated, which is plotted in Figure 9.25 shows how the steel ball attains
its steady-state temperature of 75 deg C. in a time t equal to 4τ, where τ is the system time
constant which, in this case, is ρ c
⋅
Lc
h
⋅ = 454.5 seconds.
9.9.4. Nonlinear Vibration of a Simple Pendulum
The natural frequency of large oscillation of a simple pendulum, which is a mass attached
to one end of a light rigid rod, has been generated in Section 6 of Chapter 8 as a function
of the maximum amplitude of the pendulum. The nonlinear behavior of the pendulum is
governed by the differential equation [ 6, 9, 16, 20 ]
2
t
θ t
( )
d
d
2 G
L
sin θ t
( )
( )
⋅
+ 0
= (9.39)
where L is the length of the pendulum and G is the acceleration due to gravity .
Chapter 9: Numerical Solution of Ordinary Differential Equations 367

378. For a pendulum of of length L= 12 inches, with a maximum initial amplitude of A= 60
degrees and zero initial velocity, the initial conditions are defined by
θ 0
( ) 0
=
t
θ 0
( )
d
d
0
= (9.40)
Equation (9.39) can then be solved with Mathcad's Rkadapt function as follows.
L 12
:= in G 386.4
:= in/ sec2
A 60
π
180
⋅
:= θ0 A
:= θ1 0
:=
Define initial conditions to start the solution process: θ(0)= A ,
dθ/dt (0) = 0 ( θ 0 is the angular displacement at t=0 and θ 1 is the
angular velocity at t= 0 )
<----
θ
θ0
θ1
⎛
⎜
⎝
⎞
⎟
⎠
:=
D t θ
,
( )
θ1
G
−
L
sin θ0
( )
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:= <---- Define first and second derivatives
Z Rkadapt θ 0
, 5
, 100
, D
,
( )
:= <---- Evaluates solution at 100 points between t=0
and t=5 seconds with the given initial conditions
Results are generated below with Mathcad for several initial amplitudes of the pendulum ranging
from 10 degrees to 120 degrees and these are plotted in Figure 9.26.
Amplitude = 10 degrees:
A 10
π
180
⋅
:= θ0 A
:= θ1 0
:= θ
θ0
θ1
⎛
⎜
⎝
⎞
⎟
⎠
:= D1 t θ
,
( )
θ1
G
−
L
sin θ0
( )
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Z1 Rkadapt θ 0
, 5
, 100
, D1
,
( )
:=
Amplitude = 50 degrees:
A 50
π
180
⋅
:= θ0 A
:= θ1 0
:= θ
θ0
θ1
⎛
⎜
⎝
⎞
⎟
⎠
:=
D2 t θ
,
( )
θ1
G
−
L
sin θ0
( )
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Z2 Rkadapt θ 0
, 5
, 100
, D2
,
( )
:=
368 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

379. Amplitude = 90 degrees:
A 90
π
180
⋅
:= θ0 A
:= θ1 0
:= θ
θ0
θ1
⎛
⎜
⎝
⎞
⎟
⎠
:= D3 t θ
,
( )
θ1
G
−
L
sin θ0
( )
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Z3 Rkadapt θ 0
, 5
, 100
, D3
,
( )
:=
Amplitude = 120 degrees:
A 120
π
180
⋅
:= θ0 A
:= θ1 0
:= θ
θ0
θ1
⎛
⎜
⎝
⎞
⎟
⎠
:= D4 t θ
,
( )
θ1
G
−
L
sin θ0
( )
⋅
⎛
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎠
:=
Z4 Rkadapt θ 0
, 5
, 100
, D4
,
( )
:= i 0 rows Z
( ) 1
−
..
:=
0 1 2 3 4 5
100
0
100
200
A= 10 degrees
A= 50 degrees
A= 90 degrees
A= 120 degrees
A= 10 degrees
A= 50 degrees
A= 90 degrees
A= 120 degrees
Nonlinear pendulum response
Time, seconds
Angular
position
,
degrees
Z1
1
〈 〉
( )i
180
π
⋅
Z2
1
〈 〉
( )i
180
π
⋅
Z3
1
〈 〉
( )i
180
π
⋅
Z4
1
〈 〉
( )i
180
π
⋅
Z
0
〈 〉
( )i
Figure 9.26. Dynamic response of nonlinear pendulum
The graphs plotted in Figure 9.26 clearly indicate that there is an increase in the magnitude of
the period of vibration of the nonlinear pendulum with increase in the oscillation amplitude .
Also, as can be seen from the response plots , because there is no damping present in the
system, the free vibration of the pendulum never decays out.
Chapter 9: Numerical Solution of Ordinary Differential Equations 369

380. 9.9.5. Transient Vibration of a Spring-Mass-Damper System Excited by a Pulse
Function
The differential equation of the spring-mass-damper system of Figure 9.27 excited by the
pulse function F(t) shown is
M
2
t
x
d
d
2
⋅ c
t
x
d
d
⋅
+ k x
⋅
+ F t
( )
= (9.41)
Figure 9.27. Spring-mass-damper system excited by pulse function
For a system with m= 3 kg, c =12 N-sec/ m, k= 120 N/m, and initially at rest, the solution to
Equation (9.41) can be obtained using Mathcad as follows
M 3
:= c 12
:= k 120
:= <--Specify the parameters of the given system
xinit 0
:= vinit 0
:= <-- Specify initial displacement and velocity
Express initial conditions as a vector y , the first
component being the initial displacement and the
second being the initial velocity.
<----
y
xinit
vinit
⎛
⎜
⎝
⎞
⎟
⎠
:=
These steps create the forcing
function F(t) using linear
interpolation and the " if "
function.
if(cond,tval,fval) returns
tval if cond is true but
returns fval if cond is false .
<-----
vt
0
0.5
1.0
2
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:= vf
0
2.
0.5
0
⎛
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎠
:=
G t
( ) linterp vt vf
, t
,
( )
:= F t
( ) if t 2.0
> 0
, G t
( )
,
( )
:=
t 0 0.001
, 2
..
:=
370 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

381. 0 0.5 1 1.5 2
0
1
2
Plot of exciting pulse
Time, seconds
Force,
Newtons
F t
( )
t
Set up the derivative vector function. In this case, it
has two rows . If the problem had involved three
first-order equations, there would be three rows
<--
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
−
( )
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:=
T 4.0
:= N 500
:= <--- Specify the time period in seconds and the
number of points beyond the initial point at
which the solution is to be approximated .
This command will generate the solution at
N points between 0 and T seconds using the
Rkadapt function. The solution matrix will
contain three columns- the "t " values, the
corresponding "y" and the "v" values .
Z Rkadapt y 0
, T
, N
, D
,
( )
:= <----
The results can be plotted as shown below. The first column ( the zeroth one according to
Mathcad ) is a vector of time values, the second ( first one according to Mathcad ) is a
column of displacements while the last is a column of velocities.
i 0 N
..
:= ti Zi 0
,
:= xi Zi 1
,
:= <---- Note that the t's are in the
zeroth column of "Z" , while the
displacements "x" and the
velocities " v" are in the first
and second columns
respectively
vi Zi 2
,
:=
The displacement and velocity time histories plotted in Figures 9.28 and 9.29 indicate that,
because of the presence of damping in the system, the response, which is in fact transient in
nature, dies out soon after the forcing function is withdrawn at t = 2 seconds.
Chapter 9: Numerical Solution of Ordinary Differential Equations 371

382. 0 0.5 1 1.5 2 2.5 3 3.5 4
0
0.01
0.02
Disp Time Hist Obt with Rkadapt
Time, seconds
Displacement
,
m
xi
ti
Figure 9.28. Displacement response of spring-mass-damper system
0 0.5 1 1.5 2 2.5 3 3.5 4
0.05
0
0.05
Velocity Time Hist Obt with Rkadapt
Time, seconds
Velocity
,
m/
sec
vi
ti
Figure 9.29. Velocity response of spring-mass-damper system
372 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

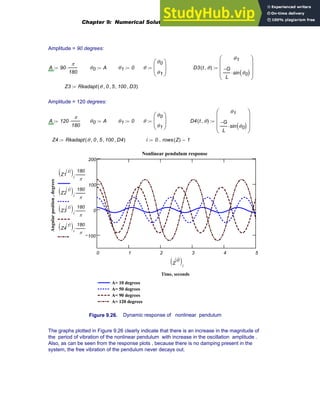
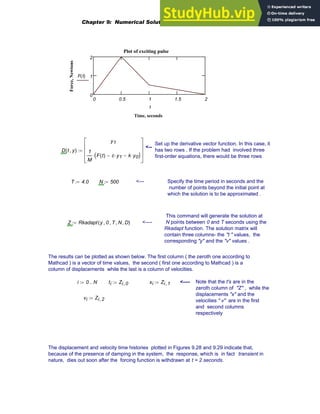
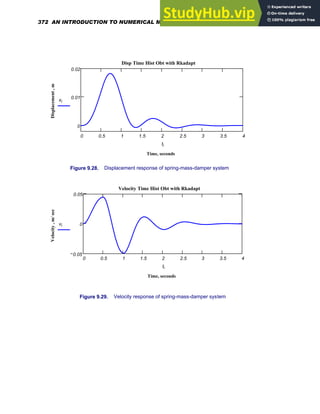
383. 9.9.6. Nonlinear Vibration of a Damped System with a Hardening Spring.
Consider the following nonlinear equation known as Duffing's equation [ 6, 16, 20, 21 ],
which is the differential equation of motion of a spring-mass-damper system with a
hardening spring
M
2
t
x
d
d
2
⋅ c
t
x
d
d
⋅
+ k x
⋅
+ μ x
3
⋅
+ F t
( )
= (9.42)
where the last term on the right hand side of the equation is due to the effect of the hardening
spring in which the spring stiffness increases as the load on it increases.
The term F(t) on the right hand side of the equation is the exciting force that the system
is subjected to. We will utilize Mathcad to obtain solutions to Equation (9.42) for m
= 1.2 kg, c= 0.6 N-sec/m , k= 1.2 N/ m and F(t) = (a) a step function and then (b) a
ramp function for values of μ ranging from 0.01 to 1.0. The results will then be compared with
those for μ =0
(a) Step input with μ =0, 0.01, 0.1, 1.0:
M 1.2
:= k 1.2
:= c 0.6
:=
xinit 0
:= vinit 0
:= <-- Specify initial displacement and velocity
Express initial conditions as a vector y , the first
component being the initial displacement and the
second being the initial velocity.
y
xinit
vinit
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:= <----
F t
( ) Φ t
( )
:= This creates a unit step function (Φ(t)= unit
step or Heaviside function )
<----
0 0.2 0.4 0.6 0.8
0.998
0.999
1
1.001
Unit step input
Time, seconds
F(t),
Newtons
F t
( )
t
t 0 0.1
, 1.0
..
:=
Chapter 9: Numerical Solution of Ordinary Differential Equations 373

384. μ = 0.01:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
− 0.01 y0
( )3
⋅
−
⎡
⎣
⎤
⎦
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= <-- Set up the derivative vector function.
T 20.0
:= N 500
:= <--- Specify the time period in seconds and the
number of points beyond the initial point at
which the solution is to be approximated .
Z1 Rkadapt y 0
, T
, N
, D
,
( )
:= <--- Generate the solution at N points between 0
and T seconds. The solution matrix will
contain three columns- the "t " values, the
corresponding "y" and the "v" values as
shown below
μ = 0.1:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
− 0.1 y0
( )3
⋅
−
⎡
⎣
⎤
⎦
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= T 20.0
:= N 500
:=
Z2 Rkadapt y 0
, T
, N
, D
,
( )
:=
μ = 1.0:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
− 1.0 y0
( )3
⋅
−
⎡
⎣
⎤
⎦
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= T 20.0
:= N 500
:=
Z3 Rkadapt y 0
, T
, N
, D
,
( )
:=
374 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

385. μ = 0.0:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
−
( )
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= T 20.0
:= N 500
:=
Z4 Rkadapt y 0
, T
, N
, D
,
( )
:=
The results can be plotted as shown below. The first column ( the zeroth one according to
Mathcad ) is a vector of time values, the second ( first one according to Mathcad ) is a
column of displacements while the last is a column of velocities.
i 0 N
..
:= ti Z1i 0
,
:=
xlowmui Z1i 1
,
:= xmidmui Z2i 1
,
:=
Note that the t's are in the
zeroth column of the "Z1 " ,
"Z2", "Z3" and "Z4 " matrices ,
while the displacements "x"
and the velocities " v" are in the first and
second columns respectively
xhighmui Z3i 1
,
:=
<-----
xzeromui Z4i 1
,
:=
0 5 10 15 20
0
0.5
1
1.5
mu=0.01
mu=0.1
mu=1.0
mu= 0
mu=0.01
mu=0.1
mu=1.0
mu= 0
Step Response
Time, seconds
Displacement,
m
xlowmui
xmidmui
xhighmui
xzeromui
ti
Figure 9.30. Response of system with hardening spring to unit step input
Chapter 9: Numerical Solution of Ordinary Differential Equations 375

386. (b) Ramp input with μ = 0, 0.01, 0.1, 1.0:
M 1.2
:= k 1.2
:= c 0.6
:= μ 1.0
:=
xinit 0
:= vinit 0
:= <-- Specify initial displacement and velocity
Express initial conditions as a vector y , the first
component being the initial displacement and the
second being the initial velocity.
y
xinit
vinit
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:= <---
F t
( ) Φ t
( ) t
⋅
:= <--This creates the unit ramp function
t 0 0.1
, 1.0
..
:=
0 0.2 0.4 0.6 0.8
0
0.5
1
The unit ramp input
Time, seconds
F(t),
Newtons
F t
( )
t
mu = 0.01:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
− 0.01 y0
( )3
⋅
−
⎡
⎣
⎤
⎦
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= T 20.0
:= N 500
:=
Z1 Rkadapt y 0
, T
, N
, D
,
( )
:=
376 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

387. mu= 0.1:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
− 0.1 y0
( )3
⋅
−
⎡
⎣
⎤
⎦
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= T 20.0
:= N 500
:=
Z2 Rkadapt y 0
, T
, N
, D
,
( )
:=
mu= 1.0:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
− 1.0 y0
( )3
⋅
−
⎡
⎣
⎤
⎦
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= T 20.0
:= N 500
:=
Z3 Rkadapt y 0
, T
, N
, D
,
( )
:=
mu= 0.0:
D t y
,
( )
y1
1
M
F t
( ) c y1
⋅
− k y0
⋅
− 0.0 y0
( )3
⋅
−
⎡
⎣
⎤
⎦
⋅
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
:= T 20.0
:= N 500
:=
Z4 Rkadapt y 0
, T
, N
, D
,
( )
:=
The results are generated below and are plotted in Figure 9.31.
i 0 N
..
:= ti Z1i 0
,
:= xlowmui Z1i 1
,
:= xmidmui Z2i 1
,
:= xhighmui Z3i 1
,
:=
xzeromui Z4i 1
,
:=
Chapter 9: Numerical Solution of Ordinary Differential Equations 377

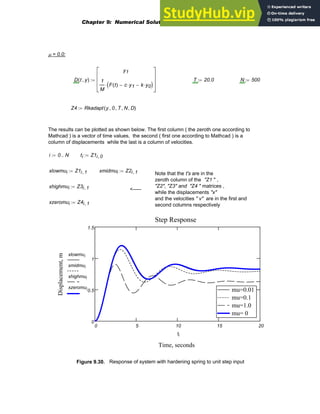
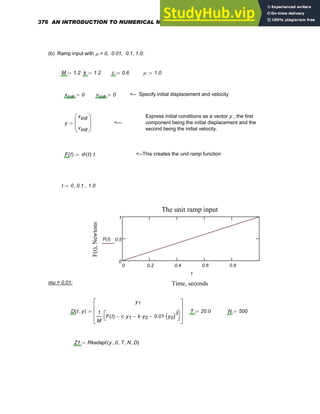
388. 0 5 10 15 20
0
5
10
15
20
mu= 0.01
mu= 0.1
mu= 1.0
mu = 0
mu= 0.01
mu= 0.1
mu= 1.0
mu = 0
Reponse to ramp input
Time, seconds
Displacement
,
m
xlowmui
xmidmui
xhighmui
xzeromui
ti
Figure 9.31. Response of system with hardening spring to a unit ramp input
9.9.7. Temperature Distribution in the Wall of a Pipe Carrying a Hot Fluid
The differential equation relating temperature in the wall of a metal pipe to radial distance is
[ 17 ]
r
2
r
T r
( )
d
d
2
⋅
t
T r
( )
d
d
+ 0
= (9.43)
where T(r) is the temperature in the pipe wall at a radial distance r from the pipe centerline. The
inner radius of the pipe is r i and the outer radius is r o . The temperature of the fluid inside the
pipe is T f while the temperature of the outer wall of the pipe is T o. Although two boundary
conditions are prescribed here, namely the temperatures at the inner and outer walls of the pipe,
there is only one initial condition available, that is , T(r i )= T f to begin the solution process.
The initial temperature gradient, namely, dT/dr , is not known. Thus, in order to resort to the
Shooting Method, this initial temperature gradient must be assumed so that the process of
generating a solution may be initiated. The solution T at ro must then be determined with these
initial values of T and dT/dr ( at r i ). If the solution obtained does not match up with the given
condition at r = r o , the assumed initial condition must be revised and a new solution T(r o )
determined. This process must be repeated until the solution obtained at r o agrees with the
prescribed condition . As discussed in Section 9.7, Equation (9.43) must first be converted to
the following two first- order differential equations before a solution can be obtained.
r
T
d
d
0
= ,
r
z
d
d
1
−
r
z
⋅
= (9.44)
378 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

389. In the following paragraphs, an iteration process utilizing Mathcad's Rkadapt and rkadapt
functions is presented by which a solution to this boundary value problem is arrived at for r i =
1 cm, r o = 2 cm, T f = 650 deg C. and T o = 10 deg C.
ri 1
:= ro 2
:= Tf 650
:= TO 10
:= <-- Given data
Define initial conditions:
initgrad 100
−
:= <--- Define initial conditions T 0 = T(ri) = Tf = 650 deg C.
and dT/dr (r i ) = z(ri) = initgrad.
T
650
initgrad
⎛
⎜
⎝
⎞
⎟
⎠
:=
Define first and second derivatives:
Note that the vector
function "D" has 2 rows in
this case. If the problem
had involved 3 first order
equations, there would be
3 rows.
< First derivative
< Second derivative
D r T
,
( )
initgrad
1
−
r
initgrad
⋅
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
The use of the Mathcad function " rkadapt " is demonstrated below. Because initgrad which
is the temperature gradient at r = r i is not known, a reasonable starting value has been
assumed. The following command generates the solution to the differential equation at the
endpoint r= r o with acc = 0.001, kmax = 1000 ( max number of intermediate points at which
the solution will be approximated) and save = 0.00001 which is the smallest spacing between
the r- values at which the solutions are to be computed.
.
Value1 rkadapt T ri
, ro
, 0.001
, D
, 1000
, 0.00001
,
( )
:=
First column is the " r" column
Second column is "T "
Third is " dT/dr "
Value1
1
1.01
1.06
1.31
2
650
649
644
619
550
100
−
99.005
−
94.173
−
72.997
−
30.685
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
= <--
Chapter 9: Numerical Solution of Ordinary Differential Equations 379

390. The above computation indicates that, with the assumed dT/dr value at r= r i , a temperature of
550 deg. C. is generated at r = ro , which is not the prescribed temperature. Therefore, try a
new value of initgrad:
initgrad 200
−
:= D r T
,
( )
initgrad
1
−
r
initgrad
⋅
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
T
650
initgrad
⎛
⎜
⎝
⎞
⎟
⎠
:=
Value2 rkadapt T ri
, ro
, 0.001
, D
, 1000
, 0.00001
,
( )
:=
Value2
1
1.01
1.06
1.31
2
650
648
638
588
450
200
−
198.01
−
188.346
−
145.995
−
61.369
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
The above analysis has yielded a temperature of 450 deg. C . at the outer wall of the pipe.
With the second assumed value of initgrad, the temperature of the outer pipe wall is ,
clearly, still not what it should be . Therefore, a third value of initgrad must be tried which
can be arrived at by a process of linear interpolation utilizing the results of the first two
trials. The formula generated that must be used for estimating the next guess is given
below.
Tdiff1 firstTouter Touterprescribed
−
=
Tdiff2 secondTouter Touterprescribed
−
=
guess
secguess Tdiff1
⋅ firstguess Tdiff2
⋅
−
firstTouter secondTouter
−
=
That is,
initgrad
Value20 2
, Value14 1
, TO
−
( )
⋅ Value10 2
, Value24 1
, TO
−
( )
⋅
−
Value14 1
, Value24 1
,
−
:=
initgrad 640
−
=
380 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

391. Then, the solution with the new initgrad is
initgrad 640
−
= T
650
initgrad
⎛
⎜
⎝
⎞
⎟
⎠
:=
D r T
,
( )
initgrad
1
−
r
initgrad
⋅
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
Value3 rkadapt T ri
, ro
, 0.001
, D
, 1000
, 0.00001
,
( )
:=
which yields
Note that the temperature
generated at the outer wall now
matches the prescribed
temperature (10 deg. C. ).
<----
Value3
1
1.01
1.06
1.31
2
650
643.6
611.6
451.6
10
640
−
633.632
−
602.708
−
467.183
−
196.382
−
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
Now , using Rkadapt , the solution can be evaluated at 100 points between r= 1 and r =
2 cm with the above initial dT/dr value put in which led to the computation of the true
temperature at the outer wall . The following commands will then generate the solution
matrix [ Z ] which will contain 3 columns- the "r" values, the corresponding "T" values
and the "dT/dr " values.
initgrad 640
−
= Z Rkadapt T ri
, ro
, 100
, D
,
( )
:=
D r T
,
( )
initgrad
1
−
r
initgrad
⋅
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
i 0 rows Z
( ) 1
−
..
:=
The results of the above Mathcad computation are plotted in Figures 9.32 and 9.33.
Chapter 9: Numerical Solution of Ordinary Differential Equations 381

392. 1 1.2 1.4 1.6 1.8
0
200
400
600
Temperature in pipe wall
r, cm
Temperature,
deg.
C.
Z
1
〈 〉
( )i
Z
0
〈 〉
( )i
Figure 9.32. Temperature in pipe outer wall
1 1.2 1.4 1.6 1.8
800
600
400
200
0
Temp gradient in pipe wall
r, cm
dT/dr,
(deg.C./
cm)
Z
2
〈 〉
( )i
Z
0
〈 〉
( )i
Figure 9.33. Temperature gradient in pipe outer wall
9.9.8 Response of an R-L Circuit with a Nonlinear Resistor
Consider a series R-L circuit having a nonlinear resistor R with the voltage drop across it is
given by
VR R I t
( ) I t
( )
3
−
( )
⋅
= (9.45)
382 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

393. Summing voltages around the loop, the governing differential equation for the circuit is
R I t
( ) I t
( )
3
−
( )
⋅ L
t
I t
( )
d
d
⋅
+ 0
= (9.46)
where R is the resistance of the circuit, L its inductance and I(t) the current in it at any
time t . If R= 2.25 Ω, L= 1.10 H and the initial current in the circuit is I(0) = 0.75
amperes, the following Mathcad statements will be needed to generate the solution
using Rkadapt and compare it with that for the corresponding linear problem.
R 2.25
:= L 1.10
:= I0 0.75
:=
D1 t I
,
( )
0 R I I
3
−
( )
⋅
−
L
:= Z Rkadapt I 0.
, 3
, 100
, D1
,
( )
:= <-- Nonlinear resistor
D2 t I
,
( )
0 R I
⋅
−
L
:= Y Rkadapt I 0.
, 3
, 100
, D2
,
( )
:= <--Linear resistor
i 0 rows Z
( ) 1
−
..
:=
0 0.5 1 1.5 2 2.5 3
0
0.5
Nonlinear resistor
Linear resistor
Nonlinear resistor
Linear resistor
Current in R-L circuit
Time, seconds
Current,
amperes
Z
1
〈 〉
( )i
Y
1
〈 〉
( )i
Z
0
〈 〉
( )i
Figure 9.34. Response of R-L circuit with a nonlinear
resistor
The Mathcad solutions generated are shown in Figure 9.34. Notice how the current decays
down to a zero value in a time t approximately equal to 4 τ, where τ is the system time
constant, which, in this case, is L / R or 0.5 seconds .
Chapter 9: Numerical Solution of Ordinary Differential Equations 383

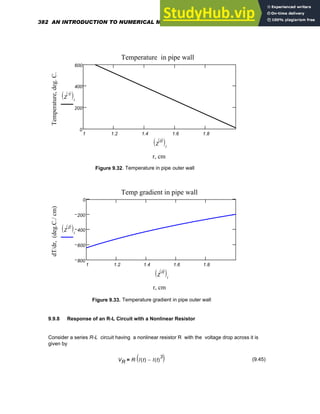
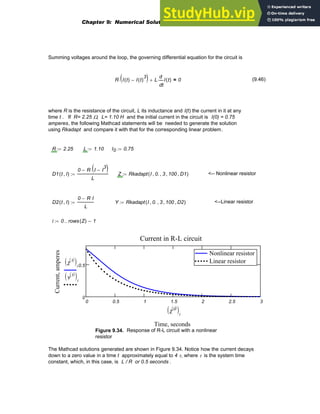
394. 9.9.9. The Effect of Damping on the Step Response of a Second-Order Control System
The general differential equation governing the behavior of a second-order control system
subjected to a unit step input is [ 14 ]
2
t
y t
( )
d
d
2
2 ζ
⋅ ωn
⋅
t
y t
( )
d
d
⎛
⎜
⎝
⎞
⎟
⎠
+ ωn
2
y t
( )
⋅
+ ωn
2
= (9.47)
where y(t) is the system response to the unit step input, ζ is the system damping ratio,
and ω n is the natural frequency of the undamped system. We want to investigate the dynamic
response of the system to different levels of damping obtained by varying ζ. If ωn = 5 rad/sec
and ζ is varied from 0.1 to1.4, the following Mathcad statements will be needed to generate the
rseponses .
ωn 5
:= y
0
0
⎛
⎜
⎝
⎞
⎟
⎠
:=
ζ1 0.1
:= D1 t y
,
( )
y1
ωn
2
2 ζ1
⋅ ωn
⋅ y1
⋅
− ωn
2
y0
⋅
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:= Z1 Rkadapt y 0
, 10
, 1000
, D1
,
( )
:=
ζ2 0.2
:= D2 t y
,
( )
y1
ωn
2
2 ζ2
⋅ ωn
⋅ y1
⋅
− ωn
2
y0
⋅
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:= Z2 Rkadapt y 0
, 10
, 1000
, D2
,
( )
:=
ζ3 0.6
:= D3 t y
,
( )
y1
ωn
2
2 ζ3
⋅ ωn
⋅ y1
⋅
− ωn
2
y0
⋅
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
Z3 Rkadapt y 0
, 10
, 1000
, D3
,
( )
:=
ζ4 0.8
:= D4 t y
,
( )
y1
ωn
2
2 ζ4
⋅ ωn
⋅ y1
⋅
− ωn
2
y0
⋅
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:= Z4 Rkadapt y 0
, 10
, 1000
, D4
,
( )
:=
384 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

395. ζ5 1.0
:= D5 t y
,
( )
y1
ωn
2
2 ζ5
⋅ ωn
⋅ y1
⋅
− ωn
2
y0
⋅
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:= Z5 Rkadapt y 0
, 10
, 1000
, D5
,
( )
:=
ζ6 1.4
:= D6 t y
,
( )
y1
ωn
2
2 ζ6
⋅ ωn
⋅ y1
⋅
− ωn
2
y0
⋅
−
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:= Z6 Rkadapt y 0
, 10
, 1000
, D6
,
( )
:=
i 0 rows Z1
( ) 1
−
..
:=
0 2 4 6 8 10
0
0.5
1
1.5
Damp ratio=0.1
Damp ratio= 0.2
Damp ratio= 0.6
Damp ratio=0.8
Damp ratio=1.0
Damp ratio= 1.4
Damp ratio=0.1
Damp ratio= 0.2
Damp ratio= 0.6
Damp ratio=0.8
Damp ratio=1.0
Damp ratio= 1.4
Second-order system response
Time, seconds
Response
Z1
1
〈 〉
( )i
Z2
1
〈 〉
( )i
Z3
1
〈 〉
( )i
Z4
1
〈 〉
( )i
Z5
1
〈 〉
( )i
Z6
1
〈 〉
( )i
Z1
0
〈 〉
( )i
Figure 9.35. Response of second-order system to unit step input with
various levels of damping
The response of the second-order system to a unit step input , which is plotted in Figure 9.35
for varying levels of damping, indicates that as ζ varies from 0.1 to 1.0, the peak overshoots as
well as the time to achieve steady-state diminish, with the transient oscillations dying down
faster as the system damping is increased. An overdamped system (ζ>1.0) , however, is the
most sluggish in attaining steady-state.
Chapter 9: Numerical Solution of Ordinary Differential Equations 385

396. PROBLEMS
In all problems, also obtain numerical solutions using the Mathcad functions rkfixed and
Rkadapt and graph them with proper labels , traces and titles
9.1 Given the differential equation
dy/dx = ( 1 - 2 x) e -2x
with initial condition: y = 3 at x =0 , estimate values of the function using a Taylor series
expansion for x = 0 to x = 0.5 . Take Δx to be 0.10. Construct a Mathcad plot to
determine the accuracy of the Taylor series solution by comparing the computed values
with the true values computed from the true solution, which is y =3 + x e-2x . Also plot
the percentage error as a function of x .
9.2 Given the differential equation
dy/dx = e x + x e x+ 2 x
with boundary condition y = 0 at x = 0 , estimate values of the function using a Taylor
series expansion for x = 0 to x = 1.0 . Take Δx to be 0.20. Construct a Mathcad plot to
determine the accuracy of the Taylor series solution by comparing the computed values
with the true values computed from the true solution, which is y = x e x + x 2 . Also plot the
percentage error as a function of x .
9.3. Given the differential equation
dy/dx = x + y +xy ,
with boundary condition y = 1 at x = 0 , estimate values of the function using a 5-term Taylor
series expansion for the range x = 0.1 to x = 0.5 . Take Δx to be 0.10.
9.4. Solve Problem 9.1 using Euler's method. The step size is to be h= 0.1 and the
range for the solution is to be x= 0 to x= 1. Compare the Euler solution with the true
solution y =3 + x e-2x by constructing a Mathcad plot. Also plot the percentage error as a
function of x .
9.5. Using Euler's method, solve
dy/dx = y' = f(x,y) = 3 x 2 / 2y
The initial condition given is y=3 at x = 2 , and the step size, h is to be 0.1. The range for
the solution is to be : x= 2 to x = 3. By constructing a Mathcad plot, compare the Euler
solution with the true solution y 1 x
3
+
= . Also plot the percentage error as a function of
x.
386 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

397. 9.6. Given the following information:
dy/dt = -y 2 + 2, y(t=0) = 10 , h = 0.1.
(a) Determine y(0.1), using the modified Euler method. The answer should be correct to 3
decimal places. (b) Continue the computation process until t= 0.5 is reached. (c) Use
Mathcad to generate a plot of y(t) in the range : t= 0 to 0.5. Compare with results of
"rkfixed" and "Rkadapt" .
9.7. Given the differential equation
dy/dt = y2 + t2 , with initial condition y = 0 at t=1,
determine (a) y(1.1) and y(1.2) by Euler's Method using an interval size h = 0.1.
(b) y(1.1) and y(1.2) by Modified Euler's Method, using an interval size h= 0.1 again
9.8. Given the differential equation
dy/dt = y2 + t3 , with initial condition y = 1 at t=2,
determine (a) y(2.1) and y(2.2) by Euler's Method using an interval size h = 0.1
(b) y(2.1) by Modified Euler's Method, using an interval size h= 0.1
9.9. Given the differential equation
dy/dt = y + t2 , with initial condition y = 2 at t=1,
determine (a) y(1.1) and y(1.2) by Euler's Method using an interval size h = 0.1
(b) y(1.1) by Modified Euler's Method, using an interval size h= 0.1
9.10. Given the differential equation
dy/dx = y + x5 , with initial condition y = 3 at x =2
determine (a) y(2.1) and y(2.2) by Euler's Method using an interval size h = 0.1 (b) y(2.1)
by Modified Euler's Method, using an interval size h= 0.1. Obtain answers that are good to at
least three decimal places
9.11. Given the differential equation
dy/dx = 4x/y - xy3 , with initial condition y = 3 at x =0,
determine (a) y(0.1) and y(0.2) by Euler's Method using an interval size h = 0.1
Chapter 9: Numerical Solution of Ordinary Differential Equations 387

398. (b) y(0.1) by Modified Euler's Method, using an interval size h= 0.1.Obtain answers that are
good to at least three decimal places.
9.12. Given the differential equation
dy/dx = y + x 2 ,
with initial condition y = 0.515 at x = 1, determine y at x = 1.2 by Modified Euler's Method,
using an interval size of h = 0.2 .
9.13. Given the differential equation
dy/dt + y = 1 , with initial condition y = 0 at t =0,
determine (a) y(0.10) and y(0.20) by Euler's Method using an interval size h =0.10
(b) y(0.10) by Modified Euler's Method, using an interval size h= 0.10 . You will
require about 4- 5 iterations to converge to a solution. Obtain answers that are good to at
least three decimal places.
9.14. Given the differential equation
dy/dx = y+2x5, with initial condition y = 3.525 at x =2,
determine (a) y(2.1) and y(2.2) by Euler's Method using an interval size h = 0.1. (b) y(2.1)
by Modified Euler's Method, using an interval size h= 0.1.Obtain answers that are good to at
least three decimal places.
9.15. Given the differential equation
dy/dx = -xy2 , with initial condition y = 2 at x =1,
determine (a) y(1.1) and y(1.2) by Euler's Method using an interval size h = 0.1.(b) y(1.1)
by Modified Euler's Method, using an interval size h= 0.1.Obtain answers that are good to at
least three decimal places.
9.16. Given the differential equation
dy/dx = -xy2 , with initial condition y = 0.3333 at x = 2,
determine (a) y(2.2) and y(2.4) by Euler's Method using an interval size h = 0.2.
(b) y(2.2) by Modified Euler's Method, using an interval size h= 0.2. Obtain answers that
are good to four decimal places.
9.17. Given the initial-value problem
388 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

399. dy/dx = f(x,y) = x 3 - 2 y 2 ; Initial condition : y(x=0) = 1;
h = step size =0.3 ,
obtain the solution at x = 0.3, using Version 1 of the Runge-Kutta method, which is based on
Simpson's one-third rule.
9.18.. Given the initial-value problem
dy/dx = 4 x 3 - 9 x 2 + 4 x - 1 , y= 5 at x = 1 , h= 0.2 ,
obtain a solution by the Runge-Kutta fourth-order method for the range x =1 to 2. Compare
the solution generated solution generated with the true solution which is
y = x 4 - 3 x 3 + 2 x 2 - x + 6. Using Mathcad, plot the results of the Runge-Kutta
solution and compare with the results of rkfixed and Rkadapt .
9.19. Using the Runge-Kutta fourth order method (Version2- that employs Simpson's
three-eighth rule),.obtain a solution at x= 0.1 and x= 0.2 to the differential equation
dy/dx = 4x/y - xy
with initial condition y(0)= 3. Use a step size of h = 0.1
9.20. Given
dy/dx = ( 3 x 3 + 6 x y 2 - x) / ( 2 y ) , y = 0.707 at x = 0 , h= 0.1 ,
obtain a solution by the fourth-order Runge-Kutta method for the range x=0 to 0.5.
Compare the solution generated with the true solution, which is
ln (x 2 + 2 y 2 ) - 3 x 2 . Using Mathcad, plot the results of the Runge-Kutta solution and
compare with the results of rkfixed and Rkadapt .
9.21. The governing differential equation of a series R-L circuit with a nonlinear resistor is
L dy/dt = - R { y - y 3 }
where R and L are the resistance and inductance in the circuit, and y(t) is the current. The
prescribed initial condition is: at t = o, y = 0.75 (ampere). Using Version 1 (that employs
Simpson's 1/3rd rule) as well as Version 2 ( that employs Simpson's 3/8th rule ) of the
Runge-Kutta fourth order method, obtain solutions at t= 0.5 seconds, that is, determine
y( 0.5) and dy/dt (0.5). Use a step size of h = 0.5 seconds. Take R = 2.25 Ohms, and L =
1.10 Henries. Obtain answers that are good to at least two decimal places.
9.22. Given the initial value problem
Chapter 9: Numerical Solution of Ordinary Differential Equations 389

400. c dy/dx + k y = F(x) with c= 0.4 , k= 1, F(x)=1 and initial condition: y(0)=0.
Using Version 1 ( that employs Simpson's 1/3 rd rule ) as well as Version 2 ( that employs
Simpson's 3/8 th rule ) of Runga-Kutta's fourth order method, obtain solutions at
t= 0.5 sec, i.e, find y(0.5) and dy/dx ( 0.5 ). Use a step size of h= 0.5
9.23. Using the Runge-Kutta fourth-order method, obtain a solution to
dx/dt = f(x,y,t) = xy3 + t2; dy/dt= g(x,y,t) = ty + x3
for t = 0 to t= 1 second. The initial conditions are given as: x(0)=0; y (0) = 1. Use a time
increment of 0.2 second.
9.24. Given the initial value problem
d2y/dt2 = (y / (e t + 1) , y(0)=1, and dy/dt (0) =0 ,
obtain a solution at t= 0.1 , i.e., find y(0.1) and dy/dt (0.1), using Version 1 of Runge-Kutta's
fourth order method . Use a step size of 0.1
9.25. Given the initial value problem:
d2y/ dt2 + 2 dy/dt + 4 y =0, y(0)=2, and dy/dt (0) =0
obtain a solution at t= 0.1 , i.e., find y(0.1) and dy/dt (0.1), using Version 1 of
Runge-Kutta's fourth order method . Use a step size of 0.1 .
9.26. Given the initial value problem
m d2y/dt2 +c dy/dt + k y3 = F(t)
with m= 1, c= 0.5 , k= 9, and F(t)=9 t and initial condns: y(0)=0; dy/dt (0) = 1 ,obtain a
solution at t= 0.5 seconds, i.e, find y(0.5) and dy/dt ( 0.5 ) using Runga-Kutta's fourth order
method. Use a step size of h= 0.5
9.27. Given the initial value problem
d2 y/ dt2 + 3 dy/dt + 4 y = 3
and initial conditions y(t=0) = 0 , dy/dt(t=0) =1, obtain a solution at t = 0.5 seconds , i.e,
determine y ( 0.5 ) and dy/dt ( 0.5 ) using Runge-Kutta's fourth order method. Use a step
size of h = 0.5. Obtain answers that are good to at least three decimal places.
390 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

401. 9.28. Given the initial value problem
d2 y/ dt2 + 4 dy/dt + 6 y = 6
and initial conditions y(t=0) = 0 , dy/dt(t=0) =2, obtain a solution at t = 0.5 seconds , i.e,
determine y ( 0.5 ) and dy/dt ( 0.5 ) using Runge-Kutta's fourth order method. Use a step
size of h = 0.5. Obtain answers that are good to at least three decimal places.
9.29. Given the initial value problem
d2 y/ dt2 + 2 dy/dt + 3 y = 3
and initial conditions y(t=0) = 0 , dy/dt(t=0) =1, obtain a solution at t = 0.5 seconds , i.e,
determine y ( 0.5 ) and dy/dt ( 0.5 ) using Runge-Kutta's fourth order method. Use a step
size of h = 0.5. Obtain answers that are good to at least three decimal places.
9.30. Given the initial value problem
d2y/ dt2 + 4 dy/dt +6 y =0, y(0)=0, and dy/dt (0) =2 ,
obtain a solution at t= 0.1 , i.e., find y(0.1) and dy/dt (0.1), using Version 1 of
Runge-Kutta's fourth order method). Use a step size of 0.1
9.31. The differential equation for a series R-C circuit with an applied voltage v(t) is
R i t
( )
⋅ t vC 0
( )
+
1
C
i t
( )
⋅
⌠
⎮
⎮
⎮
⌡
d
+ v t
( )
=
where v C (0) is the initial voltage across the capacitor and i(t) is the resulting current in
the circuit.
Figure P 9.31
Obtain a numerical solution to this differential equation for R = 1 Ω , C = 1 F, and v(t) =
u(t), a unit step function . Assume that there is no initial energy in the network .
Chapter 9: Numerical Solution of Ordinary Differential Equations 391

402. 9.32. The differential equation governing the vertical fall of an object in air from a height is
M
t
v t
( )
d
d
⋅ C v t
( )
2
⋅
+ M G
⋅
=
where M is the mass of the object, C is a proportionality constant that defines the aerodynamic
drag on the object which is proportional to the square of the velocity, v(t) is
the vertical velocity ( positive downward ) the object acquires at time t measured from the start
of the fall and G is the acceleration due to gravity . Obtain and plot the numerical solution of
this differential equation over 30 seconds for M = 100 kg, and C = 0.30 N- sec 2 / m 2 .
Assume that the initial vertical velocity of the object at t= 0 is zero .
9.33. In a tank with inflow as well as outflow, the relationship between the liquid
level or head h (t) and the rate of inflow q in (t) is given by the following
differential equation
A
t
h t
( )
d
d
⋅
h t
( )
R
+ qin t
( )
=
where A is the cross sectional area of the tank and R is the hydraulic resistance which is the
change in head required to cause a unit change in the rate of outflow .
Figure P 9.33
If the hydraulic resistance is given by R C h t
( )
⋅
= ,where C is a constant, obtain a numerical
solution to the differential equation for A = 0.04 m 2 , q in = 5 x 10 - 4 m 3 / sec and C = 3500 .
The initial level in the tank is h = 0 at t= 0. Plot h versus time and determine how long it will
take for the level in the tank to rise to 2.5 m . Also determine the steady state value of h and the
time taken to achieve it.
9.34. The large-angle deflection of a cantilevered beam of length L loaded with a vertical
392 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

403. load P at the free end is given by
2
x
y x
( )
d
d
2 P
− L x
−
( )
⋅
E I
⋅
1
x
y x
( )
d
d
⎛
⎜
⎝
⎞
⎟
⎠
2
+
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
3
2
⋅
=
where y(x) is the beam deflection at a distance x from the left hand end which is the
cantilevered end, L is its length, I is the moment of inertia of the cross- section about the
neutral axis , and E is the modulus of elasticity. Using Mathcad, obtain numerical
solutions to this differential equation and generate deflection curves for a beam with a load
P = 10 kips, length L = 15 feet , and moment of inertia I = 200 in 4 in the following cases.
Figure P 9.34
a) The beam is made of steel, with modulus of elasticity E = 30 x 10 6 psi. (b) The beam
is made of wood, with modulus of elasticity E = 1.8 x 10 6 psi. Compare your results in the
two cases with those for small-angle bending (linear beam theory ) generated by ignoring
the effect of the nonlinearity in the right hand side of the equation.
9.35. The differential equation governing the behavior of a control system is
2
t
y t
( )
d
d
2
6
t
y t
( )
d
d
⎛
⎜
⎝
⎞
⎟
⎠
⋅
+ 9 y t
( )
⋅
+ u t
( )
=
Using Mathcad, obtain and plot the numerical solution to the differential equation for zero
initial conditions. What is the steady-state value of the response and how long does it
take to achieve it ?
9.36. A spring-mass-damper system is subjected to a force pulse F(t) which is one half
of a sine wave. The governing differential equation is, thus,
Chapter 9: Numerical Solution of Ordinary Differential Equations 393

404. M
2
t
x t
( )
d
d
2
⋅ C
t
x t
( )
d
d
⋅
+ K x t
( )
⋅
+ F t
( )
=
where M is the mass , C is the damping coefficient, K is the spring constant and x(t) is
the displacement of the mass at time t. The forcing function F(t) is
F t
( ) F0 sin ωf t
⋅
( )
⋅
= 0 t
≤ 1
≤
F t
( ) 0
:= t 1
≥
0 0.2 0.4 0.6 0.8
10
0
10
Time, sec
Force
F(t)
10 sin π t
⋅
( )
⋅
t
Figure P 9.36
Using Mathcad, obtain and plot the numerical solution ( displacement and velocity )
to the above differential equation for M= 1 kg, C = 1.25 N-sec / m, K = 10 N / m , F0 =
10 N, ω f = π, and zero initial conditions. How long does it take for the transient
vibration to die out?
9.37. The system of Problem 9.36 is now excited by the trapezoidal pulse F(t)
shown below. Using Mathcad, obtain and plot the numerical solution (displacement and
velocity ). How long does it take for the transients to die out ?
394 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

405. Figure P 9.37
9.38. The Van der Pol oscillator is a spring-mass system with a damping mechanism that
depends on position as well as velocity . The motion of this system is a sustained oscillation
that is independent of initial conditions and is governed by the following differential equation
2
t
x
d
d
2
μ
t
x
d
d
⎛
⎜
⎝
⎞
⎟
⎠
⋅ 1 x
2
−
( )
⋅
− x
+ F t
( )
=
Using Mathcad, obtain numerical solutions to this equation for μ = 0.01, 0.1 , 1 , when F(t) is a
unit step function, and the initial conditions are zero.
9.39. Verify, using Mathcad, that the motion of the Van der Pol oscillator of Problem 9.38
subjected to a unit step forcing function is a sustained oscillation that is independent of
initial conditions. Consider four sets of initial conditions as follows : (1) t= 0, x= 0 , dx/dt
=0 (2) t = 0 , x=0 , dx/dt = 10 (3) t=0 , x=2, dx/dt = 0 (4) t=0 , x=2, dx/dt =10.
Obtain numerical solutions for μ = 1 only.
9.40. The differential equation for a series R-L-C circuit with an applied voltage v(t) is
R i t
( )
⋅ L
t
i t
( )
d
d
⎛
⎜
⎝
⎞
⎟
⎠
⋅
+ t vC 0
( )
+
1
C
i t
( )
⋅
⌠
⎮
⎮
⎮
⌡
d
+ v t
( )
=
where v C (0) is the initial voltage across the capacitor and i(t) is the resulting current in
the circuit.
Chapter 9: Numerical Solution of Ordinary Differential Equations 395

406. Figure P 9.40
Using Mathcad, obtain a numerical solution to this differential equation for R = 1 Ω , L = 1
H , C = 0.04 F, and v(t) = u(t), a unit step function . Assume that there is initially no
current in the circuit.
9.41. A simply supported steel beam of length L is loaded with a distributed load that
increases from zero at the left hand end to a maximum value of w 0 at the right hand end.
Its deflection curve is given by the following differential equation
2
x
y x
( )
d
d
2 M x
( )
E I
⋅
=
where EI is the bending stiffness of the beam and the bending moment M(x) at x is
M x
( )
w0 x
⋅
6 L
⋅
L
2
x
2
−
( )
⋅
=
Figure P 9.41
Using the Shooting Method, obtain a numerical solution to this boundary value problem in the
form of deflection and slope curves for w 0 = 2.5 kips/ ft, L = 15 ft , EI= 2.5x 10 9 lbs- in 2
9.42. A cylindrical metal pipe of inner radius r i and outer radius r o transports cold air at T f
396 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

407. degrees C in a building which has a room temperature of T R degrees C. The differential
equation that relates the temperature in the pipe wall to radial distance is known to be
r
2
r
T r
( )
d
d
2
⋅
r
T r
( )
d
d
+ 0
=
By employing the Shooting Method, obtain the numerical solution to the differential equation
in the form of temperature and temperature gradient profiles in the pipe wall for T f = 2 deg C ,
T R = 30 deg C , r i = 2 cm and r o = 4 cm.
Chapter 9: Numerical Solution of Ordinary Differential Equations 397

408. NOTES:
398 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

409. BIBLIOGRAPHY
1. Ayyub, Bilal M. and McCuen, Richard H., Numerical Methods for Engineers, Prentice-
Hall , Inc., 1996.
2. Bell, Lewis H. and Bell, Douglas H., Industrial Noise Control Fundamentals and
Applications, Second Edition, Marcell Dekker, Inc., 1994.
3. Cernica, John J., Strength of Materials, Holt, Rinehart and Winston, Inc., 1966.
4. Chapra, Stephen C. and Canale, Raymond P., Numerical Methods for Engineers, Fourth
Edition, McGraw Hill Book Company, 2002.
5. Deutschman, Aaron D., Michels, Walter J. and Wilson, Charles E., Machine Design,
Macmillan Publishing Company, Inc., 1975.
6. Dimargonas, Andrew D., Vibration for Engineers, Second Edition, Prentice-Hall, Inc.,
1996.
7. Gerald, Curtis F. and Wheatley, Patrick O., Applied Numerical Analysis, Fifth Edition,
Addison-Wesley Publishing Company, 1994.
8. Hibbeler, Russel C., Engineering Mechanics, Tenth Edition, Pearson Prentice-Hall,
2004.
9. Inman, Daniel J., Engineering Vibration, Second Edition, Prentice- Hall Inc., 2001.
10. Irwin, J. D., and Graf, E. R. , Industrial Noise and Vibration Control, Prentice- Hall ,
Inc., 1979 .
11. James, M. L. , Smith, G.M. and Wolford , J. C., Applied Numerical Methods for Digital
Computation, Fourth Edition, Harper Collins College Publishers, 1993.
12. Juvinall, Robert C. and Marshek, Kurt M, Fundamentals of Machine Component Design,
Third Edition, John Wiley and Sons, 2000.
13. Nakamura, Shoichiro, Numerical Analysis and Graphic Visualization with MATLAB,
Prentice-Hall, Inc., 1996 .
14. Nise, Norman S. , Control Systems Engineering, Fourth Edition , John Wiley and Sons,
Inc., 2004
15. Norton, Robert L., Machine Design- An Integrated Approach, Third Edition, Pearson
Prentice-Hall, 2006
399

410. 16. Rao, Singiresu S., Mechanical Vibrations, Fourth Edition, Pearson Prentice Hall, 2004
17. Schmidt, Frank W., Henderson, Robert E. and Wolgemuth, Carl H., Introduction to
Thermal Sciences, John Wiley and Sons, Inc., 1984.
18. Shigley, Joseph E., and Mischke, Charles R., Mechanical Engineering Design, Fifth
Edition, McGraw-Hill Book Company, 1989.
19. Spotts, M. F., Shoup, T. E. and Hornberger, L. E. , Design of Machine Elements, Eighth
Edition, Pearson Prentice- Hall, 2004
20. Thomson, William T. and Dahleh, Marie Dillon, Theory of Vibration with Applications,
Fifth Edition, Prentice-Hall, Inc., 1998.
21. Volterra, Enrico, and Zachmanoglou, E. C., Dynamics of Vibrations, Charles E. Merrill
Books, Inc., Columbus, Ohio, 1965.
22. Wilson, James F. , Ed., Dynamics of Offshore Structures, John Wiley and Sons, 1984.
400 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

411. INDEX
Accuracy, 43
Analytical methods, 43
Approximation, 44
Animation, 7
Applications,
curve-fitting, 236-248
matrices, 117-128
numerical differentiation, 262-271
numerical integration, 301-305
numerical interpolation , 168-177
numerical solution of ordinary
differential Equations , 363-
385
roots of equations, 87-95
Backward differences, 255
Bisection method, 53
advantages and disadvantages , 55
convergence criterion, 54
finding roots, 53
Boundary conditions, differential equations,
311,358,365,378
Boundary value problems,
differential equations, 311
shooting method, 358,378
Characteristic equation, 53,91
Cofactor, 103
Column vector, 108,114
Convergence,
Bisection method, 54
Iteration method, 78,84
Modified Euler’s method, 324
Newton-Raphson method , 67
Romberg integration, 290
Secant method, 74
Successive substitution method,
78,86
Cramer’s rule, 110
cspline function. 160
Cubic spline, 159-160
Mathcad’s lspline function, 160
Mathcad’s pspline function, 160
Mathcad’s cspline function, 160
in interpolation, 159
Curve-fitting (or regression analysis), 183
applications, 236-248
least squares method, 184
linear regression , 191,195,197
regression with Mathcad, 207
expfit function, 219
genfit function, 213
intercept function , 207
interp function , 209
line fuinction, 208
linear regression, 207
linfit function , 211
lnfit function , 217
loess function , 209
logfit function , 215
nonlinear regression, 209
pwrfit function. 218
regress function , 209
slope function , 207
straight line regression, 185
weighted data, 184
with exponential function, 194
with linear combination of functions,
199
with polynomials, 203
with power function, 191
with quadratic function , 188
Degrees of freedom, 117,121
Dependent variable,
differential equations, 311
Determinant, 104
Differential equations, ordinary, ( see
numerical solution of ordinary
differential equations ), 311
Differentiation, (see Numerical
differentiation ), 255
Eigenvalue problem, 114,116, 117
in stress analysis, 125
Index 401

412. in vibration engineering, 117
solving with Mathcad , 116
eigenvals function, 116
eigenvec function, 116
eigenvecs function , 116
Error,
Euler’s method, 318
relative error, 44
Taylor series, 44
Taylor series solution,
differential equation, 312
true error, 44
Euler’s method, 317
expfit function , 219
Exponential function,curve-fitting, 194
False position or
Regula falsi method, 58
find function , 86
Finite differences,
differentiation, 255
interpolation , 149
First-order differential equation, 311
Euler’s method, 317
4th-order Runge-Kutta method,
Simpson’s 1/3 rule, 329
Simpson’s 3/8 rule, 330
Mathcad solution,
335, 346, 354
Modified Euler’s method, 323
Runge-Kutta methods, 329
Taylor series method, 312
Forward differences, 255
given function , 85
Gregory-Newton method, 144
Higher order differential equations, 349
Independent variable, differential equations,
311-312
Initial conditions, differential equations, 311
Initial-value problems, 311
Integration, ( see Numerical integration), 277
intercept function, 207
interp function , 160
Interpolating polynomial, 141- 177, 259,279
Interpolation, ( see Numerical
interpolation ), 141
Inverse of matrix, 104,108
Inversion, matrix, 104,108
Iteration method , 78,84
Lagrangian interpolation, 155
Least squares method, 184
Linear algebraic equations, 108-114
Linear combination of functions, 199
Linear interpolation, 141
Linear interpolation with Mathcad, 159
Linear spline, 158
line function , 207
linfit function ,211
linterp function , 159
lnfit function, 217
loess function, 209
logfit function , 215
lsolve function , 112
lspline function, 160
Mathcad,
advantages, 7
building math expressions, 21
computation , 10
defining functions, 19
defining range variables, 23
editing expressions, 21
entering math, 16
entering text, 16
exact answers , 3
feedback, 4
formatting math, 35
formatting results and graphs, 36
formatting text, 35
functions, 19
graphing of functions, 5
graphics, 5
402 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

413. graphs, 5, 28
live math, 3
Mathcad screen, 1
matrices, 24, 103
palettes, 2,13
plotting of data, 5, 28
regions, 15
styles, 17
templates, 17
toolbars, 13
tutorial, 7
using units, 39
variables, 18
vectors, 24
window, 13
Mathcad functions,
cspline , 160
eigenvals, 116
eigenvec, 116
eigenvecs, 116
expfit, 219
find , 86
genfit, 213
given , 86
intercept, 207
interp, 209
linfit, 211
linterp, 159
lnfit, 217
loess, 209
logfit, 215
lsolve, 112
lspline , 160
polyroots, 71, 72
pspline, 160
pwrfit, 218
regress, 209
rkadapt, 340,348,360
Rkadapt, 335, 346, 354
rkfixed , 335,346, 354
root, 71
slope, 207
Matrices, 103
addition, 103
adjoint, 104
cofactor, 103
Cramer’s rule, 110
determinant, 103
eigenvalues, 114-131
identity matrix, 104,114
inverse, 104
minor, 103
multiplication, 103
nonlinear simultaneous
equations, 131
operations, 103
stress analysis application, 125
transpose, 103
unit matrix , 104
use of eigenvals, 116
use of eigenvec, 116
use of eigenvecs, 116
use of lsolve, 112
vibration engineering
application, 117-124
Modified Euler’s method, 323
Mode shapes, 118-121,124
Multiple roots, 80
Natural frequencies, 118-119,124
Natural modes, 120, 124
Newton-Raphson method, 65
Advantages, 67
Disadvantages, 67
Newton interpolating polynomial, 151
Newton interpolation, 151
Normal modes, see natural modes, 120,124
Normalization , 120
Numerical methods, 43
Numerical differentiation, 255
applications, 262- 271
calculus definition , 255
finite differences, 255
first derivative, 255, 257
interpolating polynomial
method, 259
Mathcad derivative operators,
255,256
second derivative, 257-259
Numerical integration , 277
applications, 301- 305
Index 403

414. interpolating polynomial
method, 279
Mathcad’s integral
operators, 277, 278
Romberg integration, 288
Simpson’s 1/3 rule, 283
Simpson’s 3/8 rule, 286
trapezoidal rule , 280
Numerical interpolation, 141
applications, 168-177
cubic spline interpolation, 158-160
finite differences, 149
Gregory-Newton method, 144
interpolation with Mathcad, 159
Lagrangian interpolation, 155
linear interpolation, 141
linear spline, 158
Newton’s method , 151
quadratic spline, 158
undetermined coefficients, 141
use of cspline , 160
use of lspsline, 160
use of pspline , 160
use of interp , 160
use of linterp , 159
Numerical solution of ordinary
differential equations, 311
applications , 363-385
boundary value problems, 311
Euler’s method, 317
first -order equations, 311,335
higher- order equations, 349
initial value problems, 317
Mathcad solution to first
order equation, 335
Mathcad solution to second order
equation, 346
modified Euler’s method, 323
Runge-Kutta fourth order
method, 329
Simpson’s 1/3 rule, 330
Simpson’s 3/8 rule, 331
Runge-Kutta methods, 329
second- order equations, 349- 363
systems of ordinary differential
equations, 349
shooting method, 358,378
Taylor series method, 312
use of rkfixed & Rkadapt,
335,346, 354
use of rkadapt , 340,348,360
One-step method, 317,323
Order, differential equation, 311
Ordinary differential equations ( See
numerical solution of ordinary
differential equations , 311
Orthogonality, 128
Polynomial, 53,141,144,149,155,203
polyroots function , 72
Power function, curve-fitting, 191
Principal directions, 125
Principal stresses, 125
pspline function , 160
pwrfit function, 218
Quadratic function, curve-fitting, 188
Quadratic spline, interpolation, 158
Regula falsi or false position
method, 58
regress function , 209
Regression analysis ( see
curve-fitting), 183
Relative error, 44
rkadapt function , 340,348,360
Rkadapt function , 336,346, 354
rkfixed function , 335,346, 354
Romberg integration , 288
root , 71
Root-finding, 53
applications, 87-95
bisection method, 53
False position or Regula falsi
method, 58
iteration method, 78,84
multiple roots , 80
404 AN INTRODUCTION TO NUMERICAL METHODS USING MATHCAD

415. Newton-Raphson method, 65
Regula falsi or false position
method, 58
secant method, 72
successive substitution, 78
using Mathcad, 71,86
using root, 71
using polyroots , 72
Runge-Kutta methods, 329
first order differential equation, 329
first order method, 329
fourth order method, 329,341, 350
second-order differential equation,
349-363
second order method, 329
Simpson’s 1/3 rule, 330
Simpson’s 3/8 rule, 331
Secant method, 72
Second order differential equation, 311,
349- 363
Shooting method,
boundary value problems,
31, 358, 378
Simpson’s one-third rule,
differential equation, 329
numerical integration, 283
Simpson’s three-eighth rule,
differential equation, 330
numerical integration, 286
slope function , 207
Successive substitution method, 78
Systems of ordinary differential equations,
349
Taylor series,
basis of approximation in numerical
analysis, 44
differential equation solution, 312
Trapezoidal rule, integration, 280
True error, 44
Undetermined coefficients,
curve-fitting, 185-206
interpolation, 141
Weighting factors,
curve-fitting, 184
Index 405