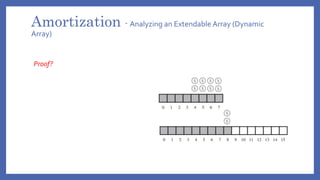
The document discusses amortized analysis, which analyzes an algorithm's time complexity by calculating the amortized cost per operation rather than worst-case cost. It describes common amortization techniques like aggregate analysis and accounting method. Aggregate analysis calculates total cost T(n) of n operations and divides by n. The accounting method assigns credits and debits to operations to show actual cost equals amortized cost minus accumulated credits. An example of dynamic array growth using amortization is given, with a theorem stating n add operations on an initially empty array have total time O(n).

1. AMORTIZED
ANALYSIS
Algorithm Design
TA Sessions
By S.Shayan Daneshvar

2. Amortized Analysis
Amortized analysis is a method for analyzing a given algorithm's complexity, or how
much of a resource, especially time or memory, it takes to execute.The motivation
for amortized analysis is that looking at the worst-case run time per operation,
rather than per algorithm.
Amortization (Amortized Analysis) is a useful tool for understanding the running
times of algorithms that have steps with widely varying performance.
CommonTechniques:
• Aggregate Analysis
• Accounting Method
• Potential Functions

3. Amortization – Aggregate Analysis
Aggregate analysis determines the upper bound T(n) on the total cost of a sequence
of n operations, then calculates the amortized cost to be T(n) / n.
Example:
A = {0, 0, …, 0} // size of k
Function increment(k):
i = 1
while i <= k and A[i] == 1 :
A[i] = 0
i = i + 1
if i < k:
A[i] = 1

4. Amortization – Aggregate Analysis
Aggregate analysis determines the upper bound T(n) on the total cost of a sequence
of n operations, then calculates the amortized cost to be T(n) / n.
Example:
A = {0, 0, …, 0} // size of k
Function increment(k):
i = 1
while i <= k and A[i] == 1 :
A[i] = 0
i = i + 1
if i < k:
A[i] = 1
FunctionT(n):
for i <- 1 until n:
increment(k)
Amortization Cost ?

5. Amortization – Accounting Method
The accounting method is a form of aggregate analysis which assigns to each
operation an amortized cost which may differ from its actual cost. Early operations
have an amortized cost higher than their actual cost, which accumulates a saved
"credit" that pays for later operations having an amortized cost lower than their
actual cost. Because the credit begins at zero, the actual cost of a sequence of
operations equals the amortized cost minus the accumulated credit.
Example?

6. Amortization – Accounting Method
Example:
A = {0, 0, …, 0} // size of k
Function increment(k):
i = 1
while i <= k and A[i] == 1 :
A[i] = 0
i = i + 1
if i < k:
A[i] = 1

7. Amortization - Analyzing an Extendable Array (DynamicArray)
Let us provide a means to grow the array A:

8. Amortization - Analyzing an Extendable Array (Dynamic
Array)
Theorem: Let S be a list implemented by means of an extendable array A, as
described above.The total time to perform a series of n add operations in S, starting
from S being empty and A having size N = 1, is O(n).
Proof?

9. Amortization - Analyzing an Extendable Array (Dynamic
Array)
Proof?