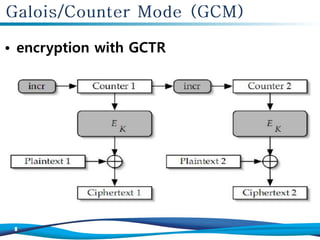
The document discusses the Galois/Counter Mode (GCM) and Message Authentication Code (MAC) used in symmetric encryption, emphasizing their roles in ensuring confidentiality, integrity, and authentication of data. It details the mechanisms and operations involved in GCM, including the use of AES for encryption and the effectiveness of GCM in protecting network traffic against attacks. Additionally, it mentions the performance benefits of GCM and the various academic references on the topic.

1. SeoulTech 알고리즘 특론
nykim@seoultech.ac.kr

2. 1. MAC and Symmetric encryption
2. Galois/Counter Mode (GCM)
3. GCM and GMAC

3. • MAC(Message Authentication Code)
– Integrity: an attacker can’t modify the data and then
compute a new MAC, because a secret key is needed
– Authentication: only the user who has got the secret
key can authenticate the message
• Symmetric encryption
– Confidentiality: data are encrypted
– Authentication: if only 2 users share the secret key

4. • Galois/Counter Mode (GCM) is authenticated
encryption with associated data.
• GCM is constructed from an approved symmetric
key block cipher with a block size of 128 bits.
• GCM provides assurance of the authenticity of
the confidential data using a universal hash
function that is defined over a NIST Special
Publication 800-38D.

5. • An authenticated encryption solution
• Encryption
– Use of the block cipher AES
– Mode of operation similar to the CTR
• Authentication
– The MAC provided is a sort of keyed digest
– Can provide authentication only → GMAC(Galois MAC)

6. • used for confidentiality and integrity
• there may be present optional not encrypted part of message
(A): e.g., network packet headers
• computation of integrity check value (ICV) is made over the
ciphertext (not plaintext): effective for network traffic protection
with denial-of-service (DoS) attack countermeasures
• the fastest mode for confidentiality and integrity
• special Intel and AMD processor assembler instruction
(PCLMULQDQ) for this mode supports
• length extensions attack protected
• small amount of weak keys may exist for integrity check

7. • Extremely fast, more than 10Gbps
• Easy to implement in software and hardware.
• Can be used for authentication only, if desired.
• Designed for AES, optimized for 128 bits.
• Arbitrary length IV, optimized for 96 bits.
• Only one key for authentication and encryption.
• No intellectual property restrictions.

8. • encryption with GCTR

9. • GCTRK
• encryption with GCTR(Galois Counter Mode)

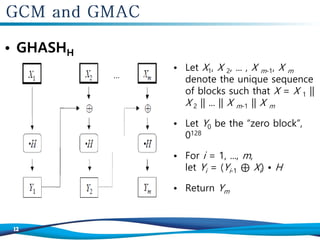
10. 1. If X is the empty string, then return the empty string as Y
2. Let n=[len(X)/128]
3. Let X1, X 2, ... , X n-1, X*n denote the unique sequence of
blocks such that X = X 1 || X 2 || ... || X n-1 || X*n
4. X1, X2,..., Xn-1 are complete blocks.
Consequently, Xn* is either a complete block or a nonempty
partial block, and if 1 ≤ len(X) ≤128, then X = X1*
5. Let CB1=ICB

11. 6. For i = 2 to n, let CBi = inc32(CBi-1)
7. For i=1 to n-1, let Yi=Xi⊕CIPHK(CBi)
8. Let Y*n=X*n⊕MSBlen(X*n)(CIPHK(CBn))
9. Let Y= Y1||Y2||…||Y*n
10. Return Y

12. • GHASHH
• Let X1, X 2, ... , X m-1, X m
denote the unique sequence
of blocks such that X = X 1 ||
X 2 || ... || X m-1 || X m
• Let Y0 be the “zero block”,
0128
• For i = 1, ..., m,
let Yi = (Yi-1 ⊕ Xi) • H
• Return Ym

13. • GCTRK – GHASHH

14. • GCTRK – GHASHH

15. • GCM-AEK

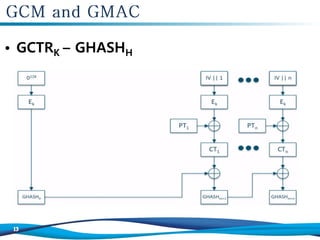
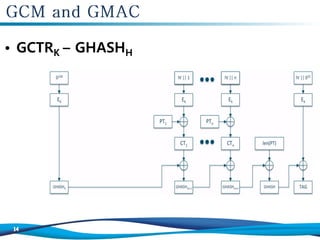
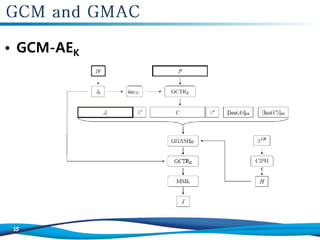
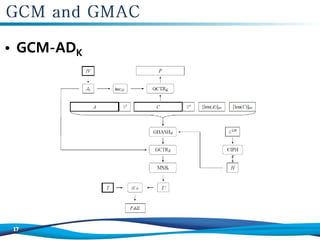
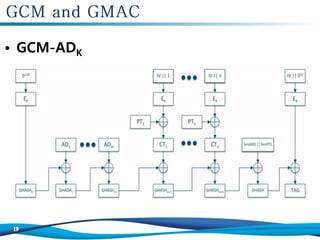
16. 1. Let H = CIPHK(0
128
).
2. Define a block, J0, as follows:
If len(IV)=96, then let J0 = IV || 0
31
||1.
If len(IV) ≠ 96, then let s = 128[len(IV)/128]–len(IV), and let
J0=GHASHH(IV||0
s+64
||[len(IV)]64).
3. Let C=GCTRK(inc32(J0), P)
4. Let u = 128 . [len(C)/128]–len(C) and let v = 128 . [len(A)/128]–len(A)
5. Define a block, S, as follows:
S = GHASHH (A || 0
v
|| C || 0
u
|| [len(A)]64 || [len(C)]64).
6. Let T = MSBt(GCTRK(J0,S))
7. Return (C, T)

17. • GCM-ADK

18. • GMAC

19. • GCM-ADK

20. • Morris Dworkin, “Recommendation for Block Cipher Modes of
Operation: Galois/Counter Mode (GCM) and GMAC”, NIST, 2007
• David A. McGrew, John Viega, “The Galois/Counter Mode of
Operation (GCM)”,
• Sharon S. Keller, Timothy A. Hall, “The Galois/Counter Mode
(GCM) and GMAC Validation System (GCMVS) with the Addition
of XPN Validation Testing”, National Institute of Standards and
Technology, 2016
• Vidder,"Galois/Counter Mode (GCM) and GMAC",youtube,2016

21. 21