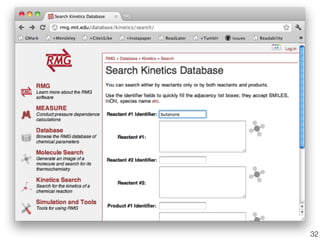
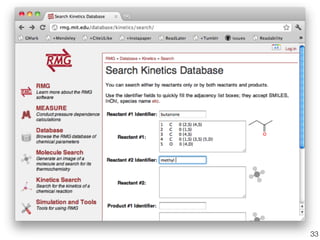
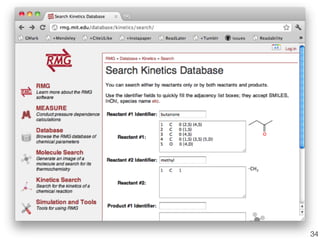
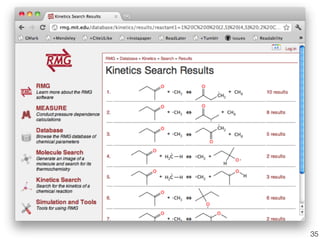
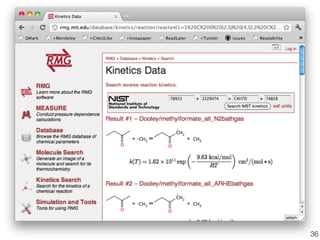
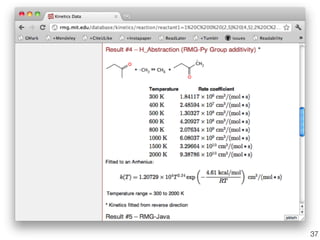
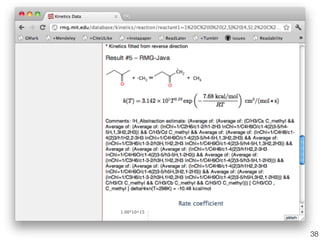
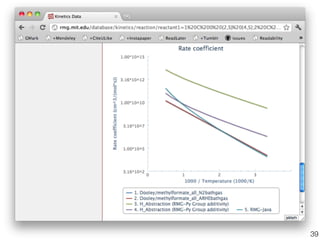
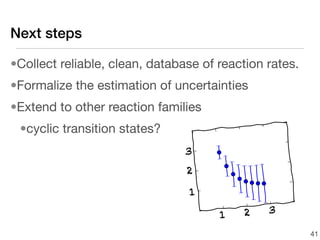
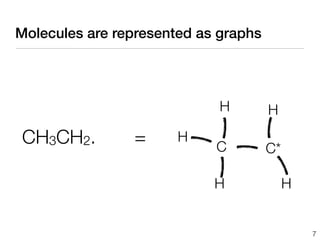
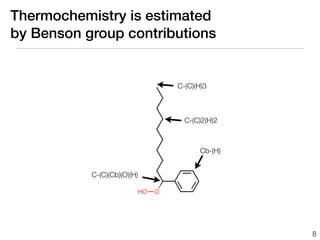
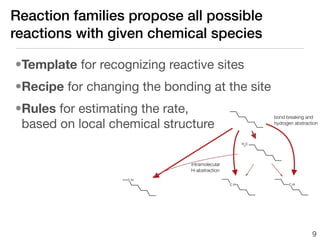
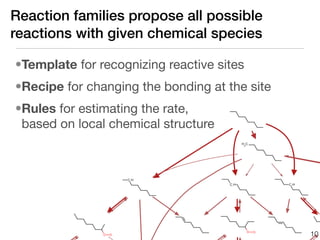
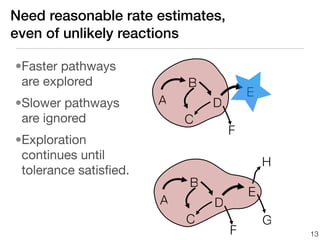
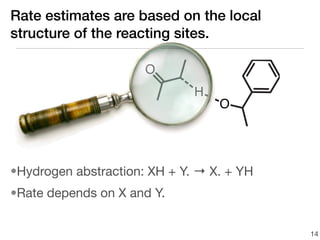
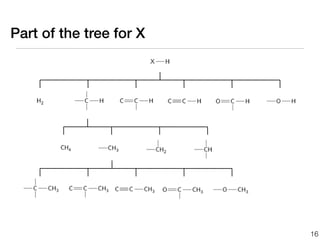
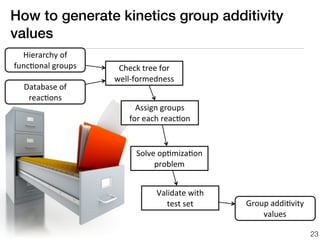
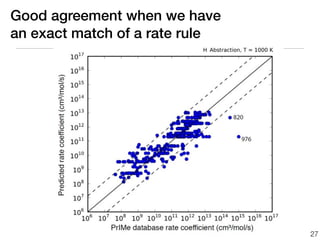
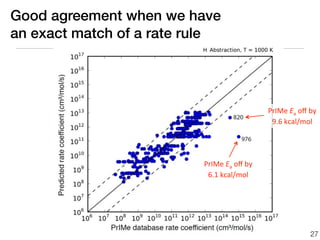
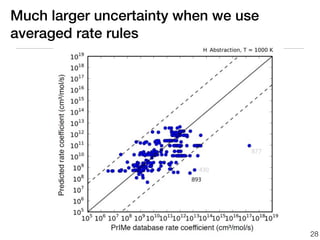
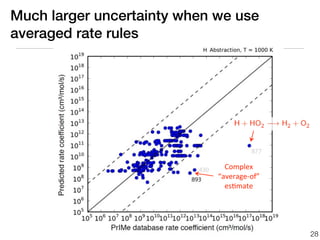
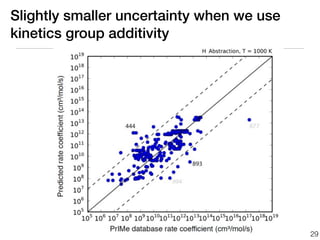
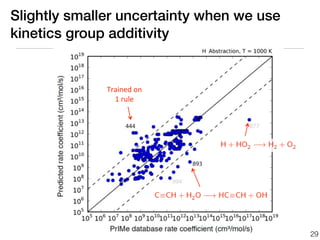
This document discusses using group additive kinetics to automatically generate chemical reaction mechanisms. It proposes representing molecules as graphs and using functional group contributions to estimate reaction rates. The approach is shown to work reasonably well for hydrogen abstraction reactions when the exact functional groups match the training data, but performs worse when using averaged rate rules. The document suggests using the group values to design a better reaction tree and collecting more reliable kinetic data to further improve the method.

1. Automatic Reaction
Mechanism Generation with
Group Additive Kinetics
Richard H. West
Joshua W. Allen
William H. Green
Massachusetts Institute of Technology

2. Combustion chemistry is complex
10
Ignition delay (ms)
1
0.1
1250 900 715
Initial temperature (K)
2

3. Modern kinetic models are large
1000
Species in kinetic model
0
1 8
C atoms in largest alkane
3

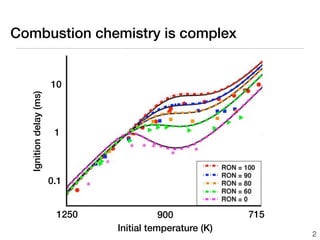
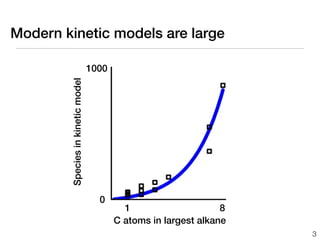
4. Detailed kinetic modeling is complex
For each chemical reaction
A + B C + D we need:
•forward rate coefficient
r = k f [A][B]
− Ea
k f = A exp
•equilibrium constant RT
kf −∆G
= Keq = exp
kr RT
∆G = ∆H − T∆S 4

5. Detailed kinetic modeling is complex
Estimating all the reactions is tedious
and error prone.
What do we do?
5

6. Detailed kinetic modeling is complex
Estimating all the reactions is tedious
and error prone.
_rp_svg2.html 12/03/2009 12:17PM
many important it is common to 1
Simulation
systems have very make simple 0.8 Raghavan
complicated chemistry
models... 0.6
chemistry
1!(N/ 0)
0.4
N
0.2
0
!0.2 1500 2000
500 1000
T (K)
p
...and fit the
parameters to
laboratory
Scale = 0.1
-
reactor data
5

7. complicated chemistry
models... 0.6
chemistry
1!(N/ 0)
0.4
N
0.2
Detailed kinetic modeling is complex !0.2
0
500 1000 1500 2000
T (K)
p
...and fit the
Estimating all the reactions is tedious parameters to
laboratory
reactor data
and error prone.
Scale = 0.1
-
and industrial
reactors are at
such different
conditions...
but these models offer
little insight into the ...that the
underlying chemistry models may be
invalid
5

8. Detailed kinetic modeling is complex
Estimating all the reactions is tedious
and error prone.
Teach the chemistry to a computer!
Reaction Mechanism Generator
•free and open source software
rmg.sourceforge.net
facebook.com/rmg.mit
5

9. Automatic reaction mechanism generation
needs methods to:
1. Represent molecules
(and identify duplicates)
2. Create reactions CH3 +
(and then new species)
3. Estimate thermo and kinetic parameters (quickly!)
6

10. Molecules are represented as graphs
H H
CH3CH2. = H
C C*
H H
7

11. Thermochemistry is estimated
by Benson group contributions
C-(C)(H)3
C-(C)2(H)2
Cb-(H)
C-(C)(Cb)(O)(H)
8

12. Reaction families propose all possible
reactions with given chemical species
•Template for recognizing reactive sites
•Recipe for changing the bonding at the site
•Rules for estimating the rate, bond breaking and
based on local chemical structure hydrogen abstraction
intramolecular
H-abstraction
9

13. Reaction families propose all possible
reactions with given chemical species
•Template for recognizing reactive sites
•Recipe for changing the bonding at the site
•Rules for estimating the rate,
based on local chemical structure
10

14. Octane autoxidation has many pathways
11

15. •Some pathways go further than others.
12

16. Need reasonable rate estimates,
even of unlikely reactions
•Faster pathways
are explored B
E
•Slower pathways A D
are ignored C
F
•Exploration
continues until
H
tolerance satisfied.
B
E
A D
C G
F 13

17. Rate estimates are based on the local
structure of the reacting sites.
O
H
O
•Hydrogen abstraction: XH + Y. → X. + YH
•Rate depends on X and Y.
14

18. Rate estimation rules are organized in a tree
•Most general structure at top
•More specific structures are children
15

19. Part of the tree for X
16

20. Part of the tree for Y

21. Ideal tree: lots of data
18

22. Typical tree: sparse data
19

23. RMG averages obscure the source of data
Ct_rad O_pri
•The pair (O_pri, Ct_rad) is not in the database.
•It is estimated by averaging pairs that are:
• H_Abstraction estimate: (Average of: (Average of: (Average of: (O_pri O2b) Average of: (O/H/NonDeC O2b) O_pri
H_rad Average of: (O/H/NonDeC H_rad O/H/OneDe H_rad) Average of: (O_pri C_methyl Average of: (O_pri
C_rad/H2/Cs)) Average of: (O/H/NonDeC C_methyl Average of: (O/H/NonDeC C_rad/H2/Cs) Average of: (O/H/
NonDeC C_rad/H/NonDeC) Average of: (Average of: (O/H/NonDeC C_rad/Cs3)) Average of: (Average of: (H2O2
C4H9O/c12345 H2O2 C4H9O/c134(2)5 H2O2 C4H9O/c134(2)5 H2O2 C4H9O/c14(2,3)5) Average of: (H2O2
C3H5/c132)) Average of: (Average of: (H2O2 C4H9O/c12345 H2O2 C4H9O/c12345 H2O2 C4H9O/c134(2)5)
Average of: (Average of: (H2O2 C4H9O/c12345))) Average of: (Average of: (Average of: (H2O2 C4H9O/c134(2)5))) O/
H/OneDe C_methyl) Average of: (O_pri Cd_pri_rad) Average of: (O/H/NonDeC Cd_pri_rad Average of: (H2O2
C4H7/c1342) Average of: (H2O2 Cd_rad/NonDeC)) Average of: (O/H/NonDeC Ct_rad) Average of: (O_pri
CO_pri_rad) Average of: (O_pri O_pri_rad Average of: (O_pri O_rad/NonDeC)) Average of: (O/H/NonDeC O_pri_rad
Average of: (H2O2 O_rad/NonDeO H2O2 O_rad/OneDe)))))
20

24. New approach: group additive log(k)
Ct_rad O_pri
•O_pri is in the database
and contributes -2.35 to log(k@1000K)
•Ct_rad is in the database
and contributes +2.53 to log(k@1000K)
•Add these to a base rate, to get rate estimate.
21

25. Group Additive Kinetics through the years
•Reference reaction + thermodynamic corrections
•Willems and Froment (1988)
•Reference reaction + generalized corrective factors
•Truong (2000)
•Estimate thermodynamics of transition state
•Sumathi et al. (2001)
•Direct estimation of Arrhenius parameters
•Saeys et al (2004-)
22

26. How to generate kinetics group additivity
values
Hierarchy
of
func.onal
groups Check
tree
for
well-­‐formedness
Database
of
reac.ons
Assign
groups
for
each
reac.on
Solve
op.miza.on
problem
Validate
with
test
set Group
addi.vity
values
23

27. The ideal training set…
... would use real reactant and product species
... would only have one k(T) for each reaction
... would only have well-known k(T) values
... would be large
24

28. The ideal training set does not exist.
•PrIMe (primekinetics.org)
•Transcription errors
•No temperature ranges
•NIST (kinetics.nist.gov)
•duplicates
•estimates
•no API
•Current RMG rules (rmg.mit.edu)
•functional groups not molecules
•current choice
25

29. Group values trained using old RMG rules,
then tested against PrIMe database.
•Take PrIMe Database warehouse.primekine.cs.org
•Filter only Hydrogen
Abstraction reactions 13654
reac.ons
•Correct obvious errors
(eg. Avogadro number) 3118
C/H/O
reac.ons
•Try to predict with RMG
1075
C/H/O
template
reac.ons
348
C/H/O
hydrogen
abstrac.on
reac.ons
26

30. Good agreement when we have
an exact match of a rate rule
27

31. Good agreement when we have
an exact match of a rate rule
PrIMe
Ea
off
by
9.6
kcal/mol
PrIMe
Ea
off
by
6.1
kcal/mol
27

32. Much larger uncertainty when we use
averaged rate rules
28

33. Much larger uncertainty when we use
averaged rate rules
Complex
“average-­‐of”
es.mate
28

34. Slightly smaller uncertainty when we use
kinetics group additivity
29

35. Slightly smaller uncertainty when we use
kinetics group additivity
Trained
on
1
rule
29

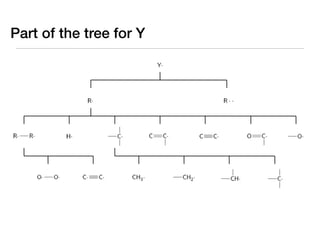
36. We can use the group values
to design a better tree
log
kXH(1000
K)
[cm3/mol*s] ±0.0
(233) Number
of
entries
trained
against
30

37. We can use the group values
to design a better tree
log
kXH(1000
K)
[cm3/mol*s] ±0.0
(233) Number
of
entries
trained
against
-­‐0.59
(19) +0.18
(120) -­‐0.55
(25) -­‐2.31
(5) +0.79
(22) -­‐0.05
(34)
-­‐0.45
(16) +0.16
(47) +0.18
(28) +0.56
(29)
-­‐0.12
(17) +0.05
(23) +1.83
(2) +2.09
(1) +1.42
(3)
30

38. We can use the group values
to design a better tree
log
kY.(1000
K)
[cm3/mol*s] ±0.0
(233) Number
of
entries
trained
against
31

39. We can use the group values
to design a better tree
log
kY.(1000
K)
[cm3/mol*s] ±0.0
(233) Number
of
entries
trained
against
-­‐0.09
(218) +1.68
(13)
-­‐7.01
(13) +2.21
(23) -­‐0.56
(97) +1.02
(26) +2.62
(7) -­‐1.13
(12) +0.77
(37)
-­‐7.82
(12) +3.52
(1) +0.54
(23) -­‐0.69
(34) -­‐0.96
(23) -­‐1.11
(17)
31

40. 32

41. 33

42. 34

43. 35

44. 36

45. 37

46. 38

47. 39

48. Benefits of group additive approach
•Easier to explain and justify than averaging method
•Possible to include uncertainty estimates
•Trained against real reactions
•Easy to modify trees and update rules
40

49. Next steps
•Collect reliable, clean, database of reaction rates.
•Formalize the estimation of uncertainties
•Extend to other reaction families
•cyclic transition states?
!
#
# !
41

50. Acknowledgements
Prof William H. Green
Joshua W. Allen
Connie Gao
Dr. Michael Harper
Amrit Jalan rmg.mit.edu
rmg.sf.net
Gregory Magoon
Shamel Merchant
42

51. Contributions
Developed framework for fitting kinetics group
additivity parameters
Group additivity kinetics estimation shows promise
for hydrogen abstraction reactions
Key challenge: Getting lots of data
43