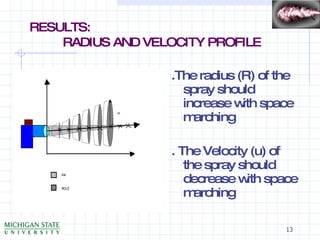
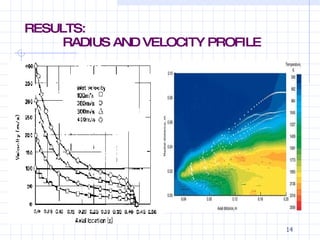
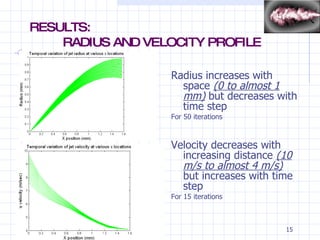
This document presents a 1-D growth model for low-speed jets in the context of spray technology, highlighting its applications in food processing, inkjet printing, and IC engines. It discusses various breakup models critical to understanding the primary breakup of sprays and outlines the governing equations used to analyze jet behavior. Numerical methods, including a semi-explicit time marching approach, are detailed for solving the governing equations, with results showing how radius and velocity profile change over space and time.

1. A 1-D Growth Model for Low Speed Jets PRESENTED TO Dr. A. BENARD BY ANUPAM DHYANI As a requirement for the partial completion of ME 872 [ F E M]

2. BRIEF INTRODUCTION TO SPRAYS . Spray technology has wide applications in many areas: - Food Processing - Inkjet Printing - IC Engines . Spraying is very complex process involving phase change,turbulence and drop interactions.Among these primary breakup model has a special importance, because it is directly related to the nozzle flow and drops generated by breakup undergo further breakup, collision and evaporation in subsequent processes. Therefore understanding the primary breakup is a key issue in the study of spray processes . Many breakup models have been generated with various assumptions as it is a very complex phenomenon

3. 1)Rayleigh model: liquid surface tension controls the breakup process. As the relative velocity b/w liquid jet and ambient gas increases, the gas internal force becomes very large relative to the surface tension force that generates drops with diameters smaller than the jet diameter, termed as “Atomization” 2)Lagrangian model: continuous liquid jets are discredited into “ blobs ”. The size of the new drops formed from a parent drop is proportional to the wavelength of the most unstable surface wave. This method has been used in engine simulations. 3)Eulerian model: resolves the detailed structure of the liquid jet. A common disadvantage of this multidimensional method is that it needs a very fine mesh to solve liquid-gas interface VARIOUS METHODS USED IN MODELS

4. METHOD USED IN PRESENT MODEL The present approach uses a 1-D model to study the growth with a finite length. A symmetric initial condition is introduced To satisfy the requirements of a 1-D model, the initial disturbance is assumed to be variable and the velocity within the jet as uniform.

5. GOVERNING EQUATIONS The surface structure of the jet is represented by the local jet radius in the axial direction. The 1-D continuity equation is set for an incompressible liquids jet as   R 2  Ru 2 ----- = - ------ …………………………….. (1)  t  x Where t = time x = axial co-ordinate ( + ve direction in jet flow direction) R=R (t,x) = radius of the jet as a function of time and axial position u=u (t,x) = velocity of the liquid

6. GOVERNING EQUATIONS contd.. The momentum equation includes the effect of a gas inertia and viscosity & is written as:  R 2 u  R 2 u 2 R 2  p 1  p G   u ------ + -------- = --- ( ---- + ----- ) = 2  --  (R 2 ------ )… (2)  t  x   x  x  x  x

7. GOVERNING EQUATIONS contd.. To help in the numerical discretization, the continuity and momentum equations were rewritten as:  R  R  R u ---- = - u ----- - ------……………………………. (3)  t  x 2  x &   u  u 1  p 1  p G  2 u 4   R  u ----- = - u -------- + --- ( ---- + ----- ) + 2  ---  + --- ---- ---- …..(4)  t  x   x  x  x 2 R  x  x

8. APPROACH TO SOLVE THE PDE A Semi-explicit time marching approach is used to solve the governing equations numerically. The Equations (3) & (4) were solved for each time step using the algorithm: u(x,t n+1 ) = u(x,t n ) + ½[ (  u/  t) x,tn + (  u/  t) x,t n+1 ]  t ……..(5) R(x,t n+1 ) = R(x,t n ) + ½[ (  R/  t) x,tn + (  R/  t) x,t n+1 ]  t …….(6) At each time step, all variables and their derivatives at time n +1 were set to be the values at time step n before iteration. The values at time n +1 were updated during the iteration.

9. APPROACH TO SOLVE THE PDE contd….. The equations are already discretized and can be solved by using the Euler First Order Unwinding [U j n+1 – U j n ]/  t + c [U j n – U j-1 n ]/  x =0 if c>0 It is a simple one step method. This scheme is explicit as only one unknown is present in each equation.

10. APPROACH TO SOLVE THE PDE contd….. since in the equations (5) & (6) the U and R do not change in space only at different time steps this technique was implemented U(x,t n+1 ) = u(x,t n ) + ½ [(u j n -u j n-1 )/  t + (u j n+1 - u j n )/  t]  t U(x,t n+1 ) = u(x,t n ) + ½ [(u j n+1 -u j n-1 )/  t]  t u j n+1 = u j n + ½[(u j n+1 - u j n-1 )] u j n+1 = 2*[u j n - ½ u j n-1 )]

11. APPROACH TO SOLVE THE PDE contd….. And similarly for Radius R R(x,t n+1 ) = R(x,t n ) + ½ [(R j n -R j n-1 )/  t + (R j n+1 - R j n )/  t]  t R(x,t n+1 ) = R(x,t n ) + ½ [( R j n+1 -R j n-1 )/  t]  t R j n+1 = R j n + ½[(R j n+1 - R j n-1 )] R j n+1 = 2*[R j n - ½ R j n-1 )]

12. APPROACH TO SOLVE THE PDE contd….. A uniform mesh with 10 elements was chosen and for every element , at different time step , the value of the previous time step was updated and added to the current. The distance was taken as Pi/2 and all the velocities and radii were calculated at these points Initial condition was chosen as per the paper Disturbance in the spray at the beginning was taken to be a sinusoidal one Initial velocity was kept at 10 m/s and the initial radius to be 0.

13. RESULTS: RADIUS AND VELOCITY PROFILE .The radius (R) of the spray should increase with space marching . The Velocity (u) of the spray should decrease with space marching

14. RESULTS: RADIUS AND VELOCITY PROFILE

15. RESULTS: RADIUS AND VELOCITY PROFILE Radius increases with space (0 to almost 1 mm) but decreases with time step For 50 iterations Velocity decreases with increasing distance (10 m/s to almost 4 m/s) but increases with time step For 15 iterations

16. ACKNOWLWDGEMENTS . Dr. A BENARD . SHRIDHARAN NARAYANAN . VENKATANARAYANAN RAMAKRISHNAN

17. REFERENCES . A One – Dimensional breakup Model for Low Speed Jets-----Yi Yong & Rolf D. Reitz . Introduction To Finite Element Methods by J.N. Reddy . Class notes.

18. QUESTIONS