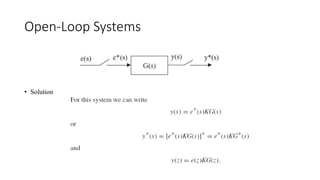
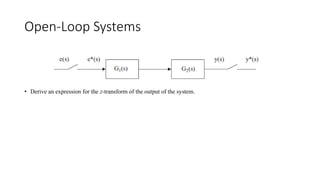
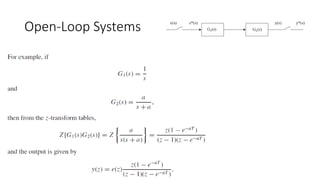
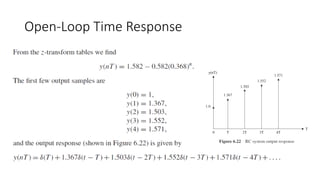
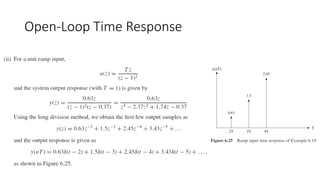
The document discusses pulse transfer functions and open-loop systems in digital control. It defines the pulse transfer function as the ratio of the z-transform of the sampled output to the input at sampling instants, emphasizing that sampling an already sampled signal has no further effect. Additionally, it covers deriving expressions for the z-transform of the output and obtaining the open-loop time response through inverse z-transforms for systems like RC circuits.

1. PULSE TRANSFER FUNCTION AND
MANIPULATION OF BLOCK DIAGRAMS
– Open loop systems
Digital control
Dr. Ahmad Al-Mahasneh

2. Pulse transfer
function
• The pulse transfer function is the ratio of the z-transform of the
sampled output and the input at the sampling instants.

3. Pulse transfer function
• If at least one of the continuous functions has been sampled, then the z-transform of the product is equal to the
product of the z-transforms of each function (note that [e*(s)]* = [e*(s)], since sampling an already sampled
signal has no further effect).
• G(z) is the transfer function between the sampled input and the output at the sampling instants and is called
the pulse transfer function.

4. Open-Loop Systems
• Example: Figure shows an open-loop sampled data system. Derive an expression
for the z-transform of the output of the system.

5. Open-Loop Systems
• Solution

6. Open-Loop Systems
• Derive an expression for the z-transform of the output of the system.

7. Open-Loop Systems

8. Open-Loop Systems

9. Open-Loop Systems
Derive an expression for the z-transform of the output of the system.

10. Open-Loop Systems

11. Open-Loop Systems

12. Open-Loop Time Response
• The open-loop time response of a sampled data system can be obtained by finding the inverse z-transform of
the output function.

13. Open-Loop Time Response
• The transfer function of the RC circuit can be found from KVL:
• 0 = −𝑅𝑅𝑅𝑅
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
− 𝑉𝑉𝑉𝑉 + 𝑉𝑉𝑉𝑉
• Taking Laplace transform of the above equation leads to:
• 0 = −𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅(𝑠𝑠) − 𝑉𝑉𝑉𝑉(𝑆𝑆) + 𝑉𝑉𝑉𝑉(𝑆𝑆)
• 𝑅𝑅𝑅𝑅 𝑆𝑆 𝑉𝑉𝑉𝑉(𝑠𝑠) + 𝑉𝑉𝑐𝑐(𝑆𝑆) = 𝑉𝑉𝑉𝑉(𝑆𝑆)
•
𝑉𝑉𝑉𝑉 𝑠𝑠
𝑉𝑉𝑉𝑉 𝑠𝑠
=
1
𝑅𝑅𝑅𝑅𝑅𝑅+1

14. Open-Loop Time Response

15. Open-Loop Time Response

16. Open-Loop Time Response

17. Open-Loop Time Response

18. Open-Loop Time Response

19. Open-Loop Time Response

20. Open-Loop Time Response

21. Open-Loop Time Response

22. Open-Loop Time Response

23. Open-Loop Time Response