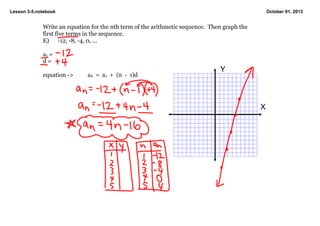
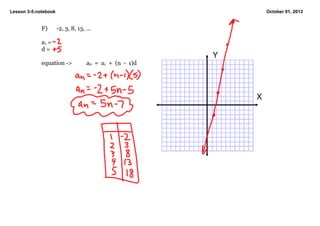
1) The document contains notes from a math lesson on arithmetic sequences. It includes examples of determining if a sequence is arithmetic, finding subsequent terms, and writing the equation for the nth term.
2) Students are assigned odd problems from the textbook section for homework due the next day.
3) There will be a chapter 3 test on Tuesday.