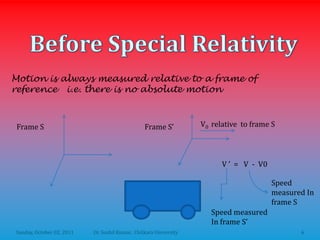
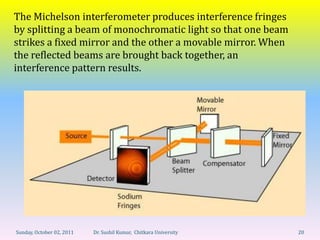
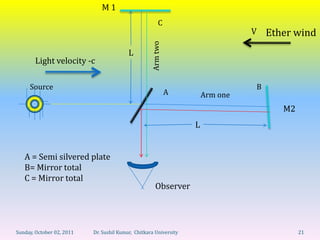
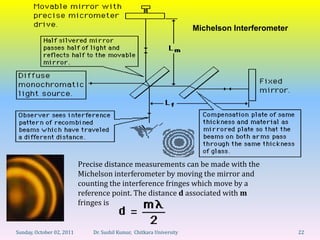
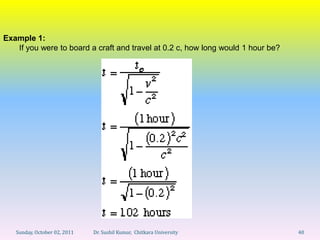
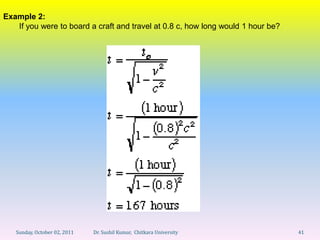
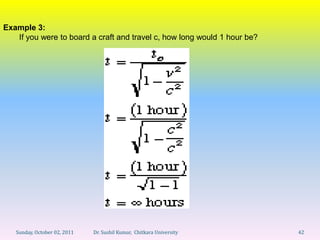
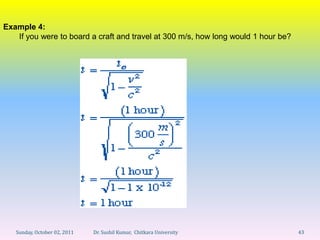
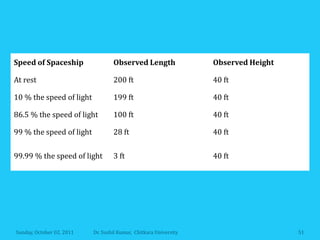
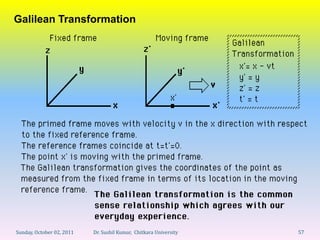
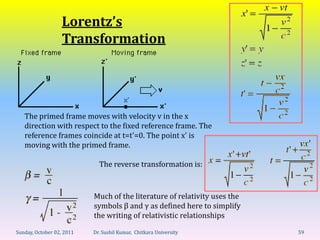
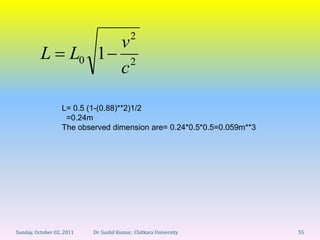Let's break this down step-by-step:
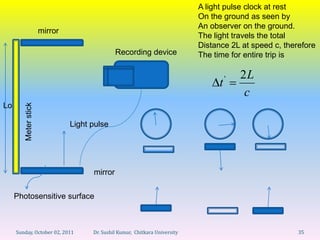
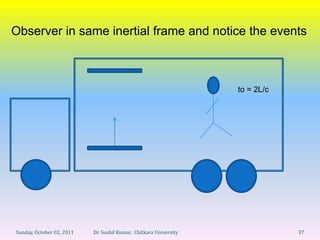
1) Event A occurs when the light pulse leaves the mirror at the back of the clock.
2) Event B occurs when the light pulse reaches the photosensitive surface at the front of the clock.
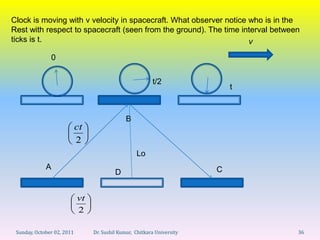
3) The time for this trip as measured by the stationary observer is t'. We know this time is 2L/c since the light travels distance 2L at speed c.
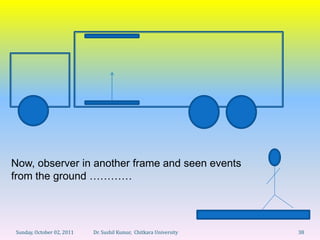
4) Meanwhile, the clock has moved a distance vt/2 during this time as seen by the stationary observer.
5) So when event B occurs, the clock has moved from its original position by vt/2.
6) Similarly, when event