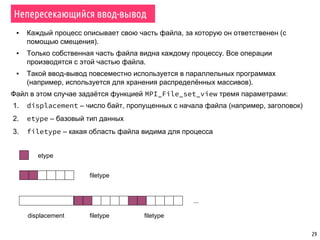
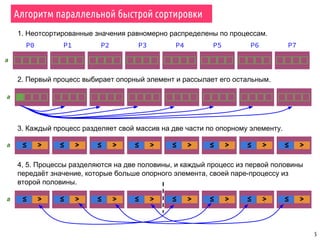
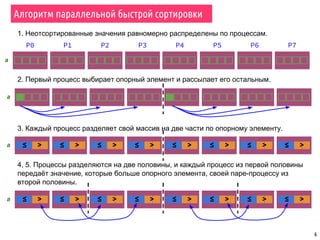
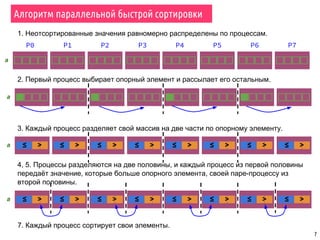
Документ охватывает темы параллельной сортировки, комбинаторного поиска и параллельного ввода-вывода в MPI. Он подробно излагает алгоритмы параллельной быстрой сортировки, гипербыстрой сортировки и поиск с возвратом, а также обсуждает методы обнаружения завершения процессов. Лекция включает примеры, иллюстрирующие принципы параллельных вычислений и различные стратегии обработки данных.

1. Лекция 6. Параллельная сортировка.
Алгоритмы комбинаторного поиска.
Параллельный ввод-вывод в MPI.
Пазников Алексей Александрович
Параллельные вычислительные технологии
СибГУТИ (Новосибирск)
Осенний семестр 2015
www: cpct.sibsutis.ru/~apaznikov/teaching
q/a: piazza.com/sibsutis.ru/fall2015/pct2015fall

2. Параллельная
сортировка в MPI

3. 3
Задача параллельной сортировки
Задача сортировки в стандарте MPI
1. Неупоредоченный список значений равномерно распределён по памяти
процессоров распределённой ВС.
2. По окончании сортировки:
▪ Списки, хранящиеся в памяти процессоров, отсортированы.
▪ Значение последнего элемента в списке процессора Pi
меньше или равно
значению первого элемента процессора Pi+1
, для 0 ≤ i ≤ p – 2.
▪ Отсортированные значения не обязательно должны быть равномерно
распределены по процессорам.
≤ ≤ ≤
P0 P1 P2 P3

4. 4
1. Неотсортированные значения равномерно распределены по процессам.
2. Выбирается опорное значение с одного из процессов и рассылается всем
процессам.
3. Каждый процесс разделяется неотсортированные значения на два списка: те,
которые меньше или равны опорному значению, и те, которые больше опорного
значения.
4. Все процессы разделяются на две части: первая половина и вторая половина.
Каждому процессору из первой половины соответствует процессор из второй
половины.
5. Каждый процесс i из первой половины передаёт свои значения, которые больше
опорного, своей паре – процессору j из второй половины. В ответ процессор
получает от j значения, которые меньше или равны опорному.
Таким образом, после выполнения этого шага максимальное значение, которое
содержится у процессора i, меньше, чем минимальное значение в массиве
процессора j.
6. Алгоритмы выполняется рекурсивно для каждой половины процессоров: в каждой
половине процессоров выбирается опорный элемент, он рассылается всем
процессам этой половины.
7. Когда деление на группы больше невозможно, каждый процесс сортирует свои
элементы.
Алгоритм параллельной быстрой сортировки

5. 5
P0 P1 P2 P3 P4 P5 P6 P7
a
1. Неотсортированные значения равномерно распределены по процессам.
a
2. Первый процесс выбирает опорный элемент и рассылает его остальным.
3. Каждый процесс разделяет свой массив на две части по опорному элементу.
a
4, 5. Процессы разделяются на две половины, и каждый процесс из первой половины
передаёт значение, которые больше опорного элемента, своей паре-процессу из
второй половины.
>≤ ≤ > ≤ > ≤ > > ≤ > ≤ > ≤ >≤
a >≤ ≤ > ≤ > ≤ > > ≤ > ≤ > ≤ >≤
Алгоритм параллельной быстрой сортировки

6. 6
P0 P1 P2 P3 P4 P5 P6 P7
a
1. Неотсортированные значения равномерно распределены по процессам.
a
2. Первый процесс выбирает опорный элемент и рассылает его остальным.
a >≤ ≤ > ≤ > ≤ > > ≤ > ≤ > ≤ >≤
a
4, 5. Процессы разделяются на две половины, и каждый процесс из первой половины
передаёт значение, которые больше опорного элемента, своей паре-процессу из
второй половины.
>≤ ≤ > ≤ > ≤ > > ≤ > ≤ > ≤ >≤
3. Каждый процесс разделяет свой массив на две части по опорному элементу.
Алгоритм параллельной быстрой сортировки

7. 7
P0 P1 P2 P3 P4 P5 P6 P7
a
1. Неотсортированные значения равномерно распределены по процессам.
a
2. Первый процесс выбирает опорный элемент и рассылает его остальным.
a >≤ ≤ > ≤ > ≤ > > ≤ > ≤ > ≤ >≤
a
4, 5. Процессы разделяются на две половины, и каждый процесс из первой половины
передаёт значение, которые больше опорного элемента, своей паре-процессу из
второй половины.
>≤ ≤ > ≤ > ≤ > > ≤ > ≤ > ≤ >≤
3. Каждый процесс разделяет свой массив на две части по опорному элементу.
Алгоритм параллельной быстрой сортировки
7. Каждый процесс сортирует свои элементы.

8. 8
Алгоритм гипербыстрой сортировки
1. Неотсортированные значения равномерно распределены по процессам.
2. Каждый процесс сортирует свою часть массива.
3. Одиз из процессов в качестве опорного элемента выбирает медиану из своих
отсортированных значений и отправляет его остальным процессам.
4. Каждый процесс разделяется неотсортированные значения на два списка: те,
которые меньше или равны опорному значению, и те, которые больше опорного
значения.
5. Процессы раздялеются на две половины, и каждый процесс i из первой половины
передаёт свои значения, которые больше опорного, своей паре – процессору j из
второй половины. В ответ процессор получает от j значения, которые меньше или
равны опорному.
6. Каждый процесс объединяет подмассив, который у него был, и значения,
полученные от другого процесса, и затем сортирует получившийся массив.
7. Алгоритмы выполняется рекурсивно для каждой половины процессоров: в каждой
половине процессоров выбирается опорный элемент, он рассылается всем
процессам этой половины.

9. 9
Алгоритм сортировки на основе равномерной выборки
15 46 48 93 39 6 72 91 14 53 97 84 58 32 27 33 72 2036 69 40 89 61 97 12 21 54
6 14 15 39 46 48 72 91 93 20 27 32 33 53 58 72 84 9712 21 36 40 54 61 69 89 97
6 39 72 12 40 69 20 33 72
6 12 20 33 39 40 69 72 72
6 14 15 39 46 48 72 91 93 20 27 32 33 53 58 72 84 9712 21 36 40 54 61 69 89 97
6 14 15 12 21 20 27 32 33 72 91 93 89 97 72 84 9739 46 48 36 40 54 61 69 53
6 12 14 15 20 21 27 32 33 72 72 84 89 91 93 97 9736 39 40 46 48 53 54 58 61 69
58
33 72 33 72 7233
1
2
3
4
5

10. Алгоритмы
комбинаторного
поиска

11. 11
Поиск с возвратом
1. Обнаружить самое длинное незаконченное слово в паззле и найти слово в словаре,
которое подходит по размеру. Если в словаре несколько слов, выбираем
случайное.
2. На каждом следующем шаге находим самое длинное незаконченное слово с как
минимум одним символом и отыскиваем в словаре слово нужной длины, которое
подходит к данным известным буквам.
Различные варианты назначения слова на каждом шаге формируют дерево
пространства состояний. Корень дерева – пустой паззл. Потомки корня –
семибуквенные слова.
Каждые последующие узлы дерева – возможные назначения слов из словаря на
незаконченные слова в паззле.
Суть поиска с возвратом заключается в следующем:
Если в какой-то момент наш очередной выбор приводит к ситуации, когда задачу решить
невозможно, мы возвращаемся к предыдущему уровню дерева и рассматриваем
альтернативное решение.
1 2 3 4 5 6
7
9
12
16
18
13
11
10
14 15
17
19

12. 12
Поиск с возвратом
1 2 3 4 5 6
7
9
12
16
18
13
11
10
14 15
17
19
1 2 3 4 5 6
7
9
12
16
18
13
11
10
14 15
17
19
T
R
O
L
L
E
Y
1 2 3 4 5 6
7
9
12
16
18
13
11
10
14 15
17
19
T
R
O
L
L
E
Y
1 2 3 4 5 6
7
9
12
16
18
13
11
10
14 15
17
19
T
R
O
L
L
E
Y
C L S E T S
C R Q U E T
1 2 3 4 5 6
7
9
12
16
18
13
11
10
14 15
17
19
T
R
O
L
L
E
Y
C R Q U E T
T
R
M
P
E
D

13. 13
Простейшая параллельная версия алгоритма
Поддерево
поиска для
процесса 0
Поддерево
поиска для
процесса 1
Поддерево
поиска для
процесса 2
Поддерево
поиска для
процесса 3
▪ Если p = bk
(b – число потомков каждого узла), то каждый процесс сначала
последовательного доходит до уровня k, а затем начинает идти по одному из k
поддеревьев на этом уровне.
▪ Такой алгоритм подходит только для числа процессоров p, равного степени b.
▪ Кроме того, дерево, как правило несбалансировано и поддеревья различаются по
сложности.

14. 14
Поиск с возвратом – параллельный алгоритм
▪ Если p = bk
(b – число потомков каждого узла), то каждый процесс доходит до уровня
k, и затем число поддеревьев равномерно распределяется между процессами по
принципу round-robin.
kk
P0
P0
P0
P1
P2
P3
P1
P2
P3
P1
P2
P3
P0
P1
P2
P3
P0
P1
P3
P2
P2
P2
P1 P1P3P0
P0

15. 15
▪ Если p = bk
(b – число потомков каждого узла), то каждый процесс доходит до уровня
k, и затем число поддеревьев равномерно распределяется между процессами.
kk
Ускорение
2
4
6
2 4 6 8 10
Глубина
Для каждого количества процессоров p и каждого
значения b можно определить оптимальную глубину,
до которой должны доходить процессы перед
распределением поддеревьев.
Поиск с возвратом – параллельный алгоритм

16. 16
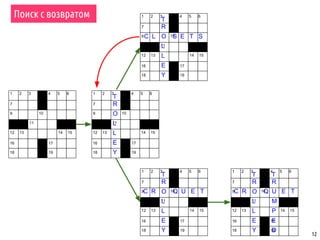
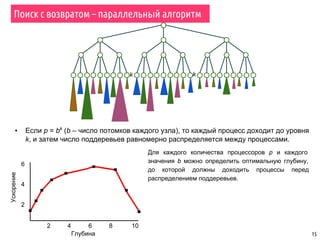
Поиск с возвратом – параллельный алгоритм
cutoff_depth; // Глубина, на которой поддеревья распределяются между процессами
cutoff_count; // Число узлов на глубине cutoff_depth
depth; // Глубина, до которой необходимо выполнять поиск
moves; // Записи позиций в дереве поиска
rank; // Ранг процесса
p; // Число процессов
ParallelBacktrack(board, level) {
if level = depth {
if board – есть решение задачи {
PrintSolution(moves)
}
} else {
if level = cutoff_depth {
cutoff_count ⟵ cutoff_count + 1
if cutoff_count mod p ≠ rank { // Если это не мой узел
return // то закончить выполнение
}
}
possible_moves ⟵ CountMoves(board) // Количество возможных решений
for i ⟵ 1 to possible_moves {
MakeMove(board, i) // Сделать ход
moves[level] ⟵ i // Записать ход
ParallelBacktrack(board, level + 1)
UnmakeMove(board, i)
}
}
}

17. 17
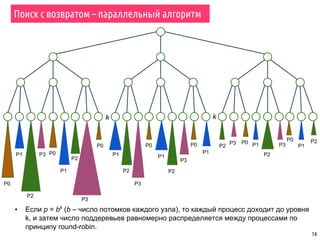
Поиск с возвратом – параллельный алгоритм
cutoff_depth; // Глубина, на которой поддеревья распределяются между процессами
cutoff_count; // Число узлов на глубине cutoff_depth
depth; // Глубина, до которой необходимо выполнять поиск
moves; // Записи позиций в дереве поиска
rank; // Ранг процесса
p; // Число процессов
ParallelBacktrack(board, level) {
if level = depth {
if board – есть решение задачи {
PrintSolution(moves)
}
} else {
if level = cutoff_depth {
cutoff_count ⟵ cutoff_count + 1
if cutoff_count mod p ≠ rank { // Если это не мой узел
return // то закончить выполнение
}
}
possible_moves ⟵ CountMoves(board) // Количество возможных решений
for i ⟵ 1 to possible_moves {
MakeMove(board, i) // Сделать ход
moves[level] ⟵ i // Записать ход
ParallelBacktrack(board, level + 1)
UnmakeMove(board, i)
}
}
}
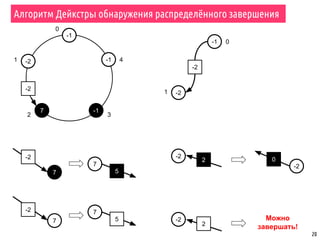
Алгоритм не позволяет обнаружить
завершение работы одного из процессов

18. 18
Неправильный способ обнаружения завершения
1. Процесс А нашёл решение и отправляет сообщения всем процессам, после чего
вызывает функцию MPI_Finalize.
2. Процесс В находит другое решение и отправляет сообщения остальным процессам
до получения сообщения от процесса А.
3. Если процесс В попытается отправить сообщение процессу А после того, как
процесс А вызвал MPI_Finalize, случится ошибка времени выполнения.
⇒ Поэтому метод обнаружения завершения, основанный на отправки сообщений всем
процессам, некорректен и может привести к аварийному завершению программы.

19. 19
Алгоритм Дейкстры обнаружения распределённого завершения
1. Процессы организованы в логическое кольцо.
2. Процесс i узнаёт состояние системы путём отправки сообщения следующему
процессу.
3. Когда сообщение возвращается процессу i, то он может определить, безопасно ли
завершать работу.
▪ Каждый процесс имеет цвет и число сообщений. Когда процесс начинает
выполнение, он белого цвета и его счетчик сообщений равен нулю.
▪ Процесс становится чёрным, когда он отправляет или получает сообщение. Когда
процесс отправляет сообщение, он увеличивает его счетчик сообщений, и когда он
принимает сообщение, он уменьшает счетчик.
▪ Как только все процессы становятся белыми и сумма сообщений равна нулю,
значит нет текущих сообщений в системе и можно завершать процессы.
▪ Когда процесс получает сообщение, он добавляет значение счетчика в нём к
счетчику в сообщении.
▪ Если процесс чёрный, он изменяет цвет сообщения на чёрный. Если процесс
белый, он не изменяет цвет сообщения.
▪ Процесс изменяет свой цвет на белый и отправляет обновлённое сообщение
следующему процессу.
▪ Если сообщение белое, процесс белый и сумма счетчика сообщения и счетчика
процесса равны нулю, в этом случае процессы безопасно завершать.

20. 20
Алгоритм Дейкстры обнаружения распределённого завершения
-1
-1
-17
-2
-2
1 4
32
0
-2
-1
-2
-2
7
7
5
7
-2 7
5
2
-2
-2
0
2
-2 Можно
завершать!
0
1

21. 21
Обнаружение завершение в алгоритме поиска с возвратом
1. Все процессы начинают выполнять поиск со счетчиками сообщений,
установленными в 0.
2. Когда процесс находит решение, он отправляет сообщение “решение найдено”
процессу 0 и устанавливает свой счетчик на 1.
3. Когда процесс 0 получает сообщение “решение найдено”, он уменьшает свой
счетчик сообщений.
4. После этого процесс 0 инициирует алгоритм обнаружения завершения.
5. Когда процесс получает сообщение “решение найдено”, он прекращает выполнение
поиска.
6. Когда процесс 0 получает сообщение и определяет, что в системе больше никакой
процесс не отправляет сообщение, он посылает сообщение “завершение”
остальным процессам и выполняет MPI_Finalize.

22. Параллельный
ввод-вывод в MPI

23. 23
Непараллельный ввод-вывод
P0 P1 P2 P3
▪ Не параллельное выполнение.
▪ Производительность хуже, чем в случае последовательного ввода-вывода.
▪ Можно использовать тот же код, что и в последовательных программах

24. 24
Независимый параллельный ввод-вывод
P0 P1 P2 P3
▪ За: параллелизм.
▪ Против: необходимо управлять многими файлами малого размера.
▪ Тот же код, что и в последовательных программах.

25. 25
Совместный параллельный ввод-вывод
P0 P1 P2 P3
▪ Паралелизм.
▪ Можно реализовать только при помощи MPI.

26. 26
Совместный параллельный ввод-вывод – пример
#include <stdio.h>
#include <mpi.h>
int main(int argc, char **argv) {
MPI_File file;
int buf[BUFSIZE], rank;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
// Коллективная операция открытия файла
MPI_File_open(MPI_COMM_WORLD, "file",
MPI_MODE_CREATE | MPI_MODE_WRONLY,
MPI_INFO_NULL, &file);
if (rank == 0)
// Ввод-вывод в файл – независимая (дифференцированная) операция
MPI_File_write(file, buf, BUFSIZE, MPI_INT, MPI_STATUS_IGNORE);
// Коллективная операция закрытия файла
MPI_File_close(&file);
MPI_Finalize();
return 0;
}

27. 27
Запись в файл
▪ Для записи используются функции MPI_File_write или MPI_File_write_at
▪ При открытии используются флаги MPI_MODE_WRONLY или MPI_MODE_RDWR
▪ Если файл до этого не существовал, необходимо добавить флаг
MPI_MODE_CREATE
MPI_File_seek
MPI_File_read
MPI_File_write
– как при обычном вводе-выводе в Linux
MPI_File_read_at
MPI_File_write_at
– комбинация перехода в определённую позицию и ввода-вывода

28. 28
Совместный параллельный ввод-вывод со смещениями
#include <stdio.h>
#include <mpi.h>
int main() {
MPI_Status status;
MPI_File file;
MPI_Offset offset;
MPI_File_open(MPI_COMM_WORLD, "/pfs/datafile",
MPI_MODE_RDONLY, MPI_INFO_NULL, &fh);
// Расчитать смещение
nints = FILESIZE / (nprocs * INTSIZE);
offset = rank * nints * INTSIZE;
MPI_File_read_at(file, offset, buf, nints, MPI_INT, &status);
MPI_Get_count(&status, MPI_INT, &count);
printf("process %d read %d intsn", rank, count);
MPI_File_close(&file);
}

29. 29
Непересекающийся ввод-вывод
▪ Каждый процесс описывает свою часть файла, за которую он ответственен (с
помощью смещения).
▪ Только собственная часть файла видна каждому процессу. Все операции
производятся с этой частью файла.
▪ Такой ввод-вывод повсеместно используется в параллельных программах
(например, используется для хранения распределённых массивов).
Файл в этом случае задаётся функцией MPI_File_set_view тремя параметрами:
1. displacement – число байт, пропущенных с начала файла (например, заголовок)
2. etype – базовый тип данных
3. filetype – какая область файла видима для процесса
etype
filetype
filetype filetypedisplacement
...

30. 30
Непересекающийся ввод-вывод
MPI_Aint lb, extent;
MPI_Datatype etype, filetype, contig;
MPI_Offset disp;
MPI_Type_contiguous(2, MPI_INT, &contig);
lb = 0;
extent = 6 * sizeof(int);
MPI_Type_create_resized(contig, lb, extent, &filetype);
MPI_Type_commit(&filetype);
disp = 5 * sizeof(int);
etype = MPI_INT;
MPI_File_open(MPI_COMM_WORLD, "/pfs/datafile",
MPI_MODE_CREATE | MPI_MODE_RDWR, MPI_INFO_NULL, &fh);
MPI_File_set_view(file, disp, etype, filetype, "native",
MPI_INFO_NULL);
MPI_File_write(file, buf, 1000, MPI_INT, MPI_STATUS_IGNORE);