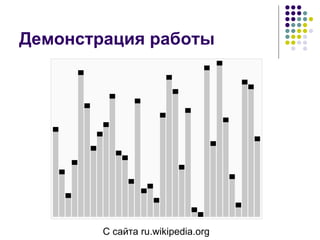
Документ посвящен алгоритмам сортировки и поиска, изучаемым в рамках специального курса по олимпиадному программированию. Рассматриваются различные методы реализации сортировки, такие как сортировка выбором, вставками, пузырьком, слиянием и быстрой сортировкой, а также алгоритмы поиска, включая линейный и двоичный. Документ включает примеры кода на языке Pascal и освещает теоретические аспекты оценки сложности алгоритмов.

1. Сортировка и поиск Федор Царев Спецкурс «Олимпиадное программирование» Лекция 2 22 .12.2008 Санкт-Петербург, Гимназия 261

2. Цель лекции Изучить алгоритмы сортировки и поиска Изучить методы их реализации на языке программирования Pascal (Delphi)

3. Зачем это надо? Сортировка и поиск в разных вариантах используются практически во всех программах : от поиска слова в файле до поиска в Интернете

4. Задача сортировки Задан набор объектов a1, a2, …, an Необходимо их переставить так, чтобы они шли в неубывающем порядке Два варианта: объекты можно только сравнивать есть доступ к их внутренней структуре

5. Обмен двух переменных Операция, с помощью которой осуществляется сортировка procedure swap( var a, b : integer); var t : integer; begin t := a; a := b; b := t; end;

6. Без дополнительной переменной (1) Можете придумать? С помощью сложения и вычитания a := a + b; // a = a + b; b = b; b := a - b; // a = a + b; b = a; a := a - b; // a = b; b = a;

7. Без дополнительной переменной (2) С помощью операции xor ( исключающее ИЛИ ) a := a xor b; // a = a xor b; b = b; b := a xor b; // a = a xor b; b = a; a := a xor b; // a = b; b = a; Методы без дополнительной переменной обладают существенным недостатком. Каким?

8. Сортировка выбором На каждом шаге выбирается минимальный из еще не просмотренных элементов Это повторяется (n-1) раз

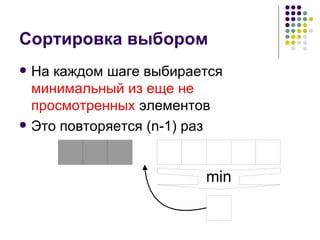
9. Программа for i := 1 to n – 1 do begin minpos := i; for j := i + 1 to n do begin if (a[j] < a[minpos]) then begin minpos := j; end; end; swap(a[i], a[minpos]); end;

10. Оценка алгоритма Время работы – O(n 2 ) Число сравнений – O(n 2 ) Число обменов – O(n) Дополнительная память – O(1)

11. Сортировка вставками Очередной элемент вставляется в уже отсортированную часть массива на соответствующее место

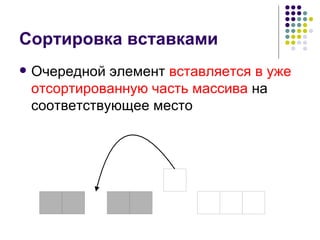
12. Программа (1) for i := 1 to n do begin pos := -1; if (a[i] < a[1]) then begin pos := 1; end; for j := i - 1 downto 1 do begin if (a[j] < a[i]) then begin pos := j + 1 ; break; end; end; // pos – позиция, на которой должен // оказаться a[i]

13. Программа (2) // Сдвиг элементов с a[pos] до a[i-1] вправо на одну позицию t := a[i]; for j := i - 1 downto pos do begin a[j + 1] := a[j]; end; a[pos] := t; end;

14. Оценка алгоритма Время работы – O(n 2 ) Число сравнений – O(n 2 ) ( можно улучшить до O(nlogn)) Число обменов – O(n 2 ) Дополнительная память – O(1)

15. Сортировка пузырьком Если два соседних элемента расположены в неправильном порядке, то их надо поменять местами Сделаем n-1 проход, на каждом из которых будем проверять все пары соседних элементов Элементы будут двигаться к своим местам как пузырьки

16. Демонстрация С сайта ru.wikipedia.org

17. Программа for i := n downto 2 do begin for j := 1 to i – 1 do begin if (a[j] > a[j + 1]) then begin swap(a[j], a[j + 1]); end; end; end;

18. Оценка алгоритма Время работы – O(n 2 ) Число сравнений – O(n 2 ) Число обменов – O(n 2 ) Дополнительная память – O(1) Сравнивает только соседние элементы Наиболее прост в реализации

19. Сортировка слиянием Сортировка слиянием предложена Джоном фон Нейманом в 1946 году Джон фон Нейман – венгро-американский математик, сделавший важный вклад в квантовую физику, квантовую логику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки

20. Метод «разделяй-и-властвуй» Один из основных методов построения алгоритмов Сложные задачи надо решать, разбивая их на более простые Отсортировать массив можно так: разбить его на две половины отсортировать каждую из них объединить отсортированные массивы

21. Дерево сортировки слиянием

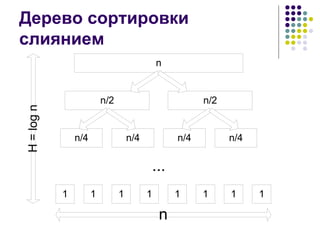
22. Слияние массивов (1) Даны два упорядоченных по возрастанию массива: a[1..n] и b[1..m] Необходимо построить упорядоченный массив c[1..n+m] , содержащий эти же элементы Число действий должно быть порядка n+m

23. Слияние массивов (2) На каждом шаге выбираем минимальный из первых непросмотренных элементов массивов Надо хранить их номера: pa, pb

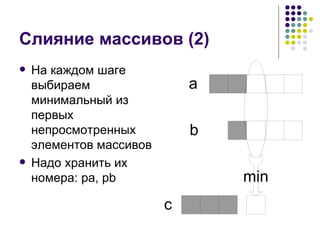
24. Слияние массивов – программа (1) pa := 1; pb := 1; pc := 1; while ((pa <= n) and (pb <= m)) do begin if (pa <= n) then begin min := a[pa]; end; if (pb <= m) and ((b[pb] < min) or (pa > n)) then begin min := b[pb]; end;

25. Слияние массивов – программа (2) if (pa <= n) and (min = a[pa]) then begin c[pc] := a[pa]; inc(pc); inc(pa); continue; end; if (pb <= m) and (min = b[pb]) then begin c[pc] := b[pb]; inc(pc); inc(pb); continue; end; end;

26. И, наконец… procedure mergeSort(l, r : integer); begin if (l >= r) then begin exit; end; m := (l + r) div 2; mergeSort(l, m); mergeSort( m + 1 , r); // m плюс один // Слияние частей массива a: a[l..m] и a[m + 1..r] – напишите сами end;

27. Оценка времени работы Время работы – O(nlogn) Число сравнений – O(nlogn) Число обменов – O(nlogn) Дополнительная память – O(n)

28. Быстрая сортировка Предложена Чарльзом Хоаром в 1964 году Основана на методе «разделяй-и-властвуй»

29. Идея алгоритма Выберем в массиве разделяющий элемент X Переставим элементы в массиве так, чтобы сначала шли меньшие X (первая часть) , затем равные (вторая часть), а в конце – большие (третья часть) Осталось отсортировать первую и третью части массива

30. Демонстрация работы С сайта ru.wikipedia.org

31. Дерево в лучшем случае

32. Дерево в худшем случае

33. Программа procedure qsort(l, r : integer); var m, i, j : integer; begin m := a[l + random(r – l + 1)]; i := l; j := r; while (i <= j) do begin while (a[i] < m) do inc(i); while (a[j] > m) do dec(j); if (i <= j) then begin swap(a[i], a[j]); inc(i); dec(j); end; end; if (l < j) then qsort(l, j); if (i < r) then qsort(i, r); end;

34. Упражнения Постройте массивы, на которых будет достигаться квадратичное время работы алгоритма с выбором разделяющего элемента без использования рандомизации: m := a[l]; m := a[r]; m := a[(l + r) div 2];

35. Оценка времени работы Время работы – в среднем O(nlogn) , в худшем случае O(n 2 ) Число сравнений – в среднем O(nlogn) , в худшем случае O(n 2 ) Число обменов – в среднем O(nlogn) , в худшем случае O(n 2 ) Дополнительная память – O( 1 ) Наиболее быстрый на практике алгоритм – при условии использования рандомизации

36. Сортировка с помощью кучи Использует особую структуру данных – кучу ( heap ) Будет рассмотрена в одной из следующих лекций Также обладает временем работы O(nlogn)

37. Устойчивость сортировки Алгоритм сортировки устойчив , если в упорядоченном массиве порядок элементов с одинаковыми ключами такой же, как в исходном Упражнение. Проанализируйте изученные алгоритмы сортировки на устойчивость Упражнение. Придумайте способ сделать любой алгоритм сортировки устойчивым

38. Упражнение Написать программу, визуализирующую работу алгоритмов сортировки

39. Задача поиска Задан набор объектов a1, a2, …, an Задан объект X Необходимо проверить, присутствует ли он в указанном наборе Два варианта: объекты можно только сравнивать есть доступ к их внутренней структуре

40. Линейный поиск found := false; for i := 1 to n do begin if (a[i] = x) then begin found := true; break; end; end; Время работы – O(n)

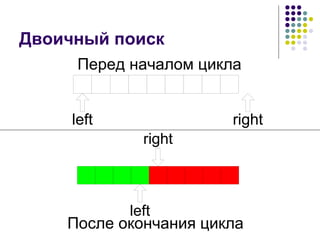
41. Двоичный поиск Пусть исходный набор уже отсортирован Сравним X со средним элементом a[n/2] набора В зависимости от результата перейдем либо к левой половине, либо к правой Размер рассматриваемой части на каждом шаге будет сокращать вдвое Время работы будет O(logn)

42. Инвариант цикла Логическое выражение, которое истинно непосредственно перед началом выполнения цикла после выполнения каждой его итерации сразу после окончания выполнения цикла

43. Инвариант для двоичного поиска Задан массив a[1] ≤ a[2] ≤ … ≤ a[n] Задано искомое число x Границы текущего отрезка поиска: left и right Инвариант цикла : a[left] ≤ x < a[right]

44. Программа function binsearch(x : integer) : integer; begin result := -1; // Не найдено if (a[1] > x) then begin exit; end; left := 1; right := n + 1; while (right – left > 1) do begin mid := left + (right - left) / 2; if (a[mid] > x) then begin // Вспомните right := mid; // инвариант end else begin // цикла! left := mid; end; end; if (a[left] = x) then begin result := left; // Вспомните инвариант цикла! end; end;

45. Двоичный поиск После окончания цикла Перед началом цикла

46. Упражнения Пусть в массиве несколько элементов равны x. Какой из них будет найден? Как найти число элементов, равных X , в заданном упорядоченном массиве за время O(logn)? Модифицируйте сортировку вставками так, чтобы в ней выполнялось O(nlogn) сравнений.

47. Другие варианты поиска Поиск подстроки в строке Поиск строки в множестве строк Двоичные деревья поиска Хэш-таблицы … Все это будет рассмотрено в следующих лекциях!

48. Выводы Алгоритм быстрой сортировки является наиболее быстрым на практике алгоритмом сортировки (при использовании случайного выбора разделяющего элемента) С помощью двоичного поиска можно быстро искать в упорядоченном массиве Существует множество методов поиска, которые будут рассмотрены в следующих лекциях

49. Спасибо за внимание! Вопросы? Комментарии? [email_address]